1 Introduction

Black hole solution is one of the interesting consequences of general relativity. Although the existence of black holes is vivid, it is an open question to realize interior nature of them in quantitative detail; the main reason comes from the fact that a perfect theory of quantum gravity does not yet exist. Studying the semiclassical phase structure of black holes provides at least preliminary steps for understanding the quantum gravity.

The phase transition plays an important role for exploring the critical behavior of the system near critical point. After the discovery of a phase transition by Hawking and Page [2], black hole phase transitions have been of great interest. It is well known that the asymptotically flat vacuum black hole solutions are thermally unstable [3]. While asymptotically AdS black holes are the famous examples of the Hawking–Page phase transition [2] between two stable phases. In order to characterize the critical behavior of a system during the phase transition, one may calculate its critical exponents which are not completely independent. Meanwhile two systems belong to the same universality class if their critical behavior is expressed by the same critical exponents.

The semiclassical phase transition which occurs in the asymptotically AdS space-times can be translated to a confinement/deconfinement phase transition in the context of AdS/CFT [4]. Regarding the applications of AdS/CFT correspondence in recent years, the similarities between the phase transition of black holes and holographic superconductivity, have achieved a great deal of attention [5, 6].

The local (thermal) stability of a system is concerned with how the system responds to small fluctuations of its thermodynamic coordinates. There are various methods that one can employ to investigate the phase structure of a black hole system near its critical point. One of the well-known standard analyses of the locally stability is based on the canonical ensemble by studying the specific heats. Phase structure may also be explained by critical quantities that are extracted in the extended phase space. In addition, one may apply the geometrical thermodynamics method for studying the phase transition.

One of the methods for constructing the phase structure of a thermodynamical system is through the use of geometry. Meaning, by considering a thermodynamical potential and its corresponding extensive parameters, it is possible to introduce a metric which describes thermodynamical properties of the system. The information regarding thermodynamical properties of the system is extracted from Ricci scalar of the metric. The divergencies of the Ricci scalar of the thermodynamical metric mark two important points of the thermodynamical system; the bound point and the phase transition. There are several methods regarding thermodynamical geometry which are; Weinhold [7, 8], Ruppeiner [9, 10], Quevedo [11, 12] and HPEM [13–15]. The geometrical thermodynamics has been employed in the context of different types of black holes [16–22]. In addition, this method was also used to study the phase transition of superconductors [23]. A comparative study regarding different geometrical thermodynamical metrics is done in Ref. [24]. A successful method of the geometrical thermodynamics include all bound and phase transition points in its Ricci scalar through the divergencies. In other words, divergencies of the Ricci scalar and mentioned points must coincide with each other. A mismatch and extra divergency indicate the existence of anomaly which contradict with principles of thermodynamics. Such anomaly was reported for Weinhold, Ruppeiner and Quevedo metrics for different types of black holes [13–15, 25]. To overcome such problem, HPEM metric was introduced [13]. In this paper, we will regard HPEM method for studying geometrical thermodynamics of black holes under consideration.

Einstein gravity introduces gravitons as massless particles, whereas there are several arguments that state gravitons should be massive particles. In order to have massive graviton, theory of general relativity should be modified to include mass terms. The first attempt for constructing a massive theory was referred to the works of Fierz and Pauli [26] which was done in the context of linear theory. This theory has specific problem which is known as van Dam, Veltman and Zakharov discontinuity. Meaning that propagator of the massive gravity in limit \(m=0\) is not consistent with one derived for massless case. The resolution to this problem was Vainshtein mechanism which requires the system to be considered in nonlinear regime. In other words, according to the Vainshtein mechanism [27], at some distance below the so-called Vainshtein radius, the linear regime breaks down and the theory enters into a nonlinear framework. Based on this mechanism, the usual general relativity can be recovered from high curvature space-times which are introduced with a wide class of non-Einsteinian theories. In the context of a static and spherically symmetric base space, it is also shown that the Vainshtein mechanism can work, correctly, both inside and outside the compact objects [28, 29] (See Refs. [30–34] for more details regarding Vainshtein mechanism). On the other hand, generalization of the Fierz and Pauli massive theory to nonlinear one leads to the existence of a Boulware–Deser ghost [35]. While solutions to these problems had existed for some time in three dimensional spacetime [36, 37], they were not solved in four and higher dimensions. In order to solve such problems de Rham, Gabadadze and Tolley (dRGT) proposed another class of massive gravity [38, 39]. Contrary to previous theories, dRGT theory is valid in higher dimensions and it was shown that such theory enjoys absence of the Boulware–Deser ghost [40, 41]. This theory builds up massive terms by employing a reference metric. A modification in reference metric could lead to another dRGT like massive theory [42]. Black hole solutions of dRGT massive gravity and their thermodynamical properties have been investigated for d dimensions (\(d\ge 3\)) in Refs. [25, 43–48].

On the other hand, one of the well-known theories of higher derivative gravity is Lovelock theory which is a natural generalization of Einstein gravity in higher dimensions. Taking into account the first additional term of Einstein gravity in the context of Lovelock theory (Gauss–Bonnet (GB) gravity), it is believed that GB gravity can solve some of the shortcomings of Einstein gravity [49–51]. In addition, GB gravity consists of curvature-squared terms which, interestingly, is free of ghosts and the corresponding field equations contain no more than second derivatives of the metric (see Refs. [52–57] for more details). Another interesting aspect of GB gravity is that it can be arisen from the low-energy limit of heterotic string theory [58–61]. Considering the GB gravity context, black hole solutions and their interesting behavior have been investigated in much literature [62–70].

On the other hand, one of the main problems of Maxwell’s electromagnetic field theory for a point-like charge is that there is a singularity at the charge position; therefore, it has infinite self energy. In order to remove this self energy, in classical electrodynamics, Born and Infeld introduced a nonlinear electromagnetic field [71], with mainly the motivation of solving the infinite self energy problem by imposing a maximum strength of the electromagnetic field. Motivated by the interesting results mentioned above, we study the thermodynamic behavior of black holes in GB-massive gravity in the presence of a Born–Infeld (BI) source.

In order to have a better description regarding physics governing a system, it is necessary to decrease different shortcomings of different theories as much as possible. This indicates that we should apply more generalizations to solve the various shortcomings of theories describing the nature of the system. Here, we have considered three generalizations; the BI generalization to remove shortcomings of the Maxwell theory, GB gravity to solve different problems of Einstein theory such as renormalization problem, and massive gravity to solve the massless gravitons in both Einstein gravity and GB theory. Such considerations solve some of the shortcomings of the theories under consideration, but they also modify the physical properties of the system. In this paper, we intend to investigate these modifications in the context of the critical behavior of black holes, which in turn provides a reasonable framework for conducting studies in other aspects of physics such as gauge/gravity duality.

The outline of the paper will be as follows. In the next section, we introduce the action and the basic equations related to GB–BI–massive gravity. We also present a brief discussion regarding the black hole solutions and conserved and thermodynamics quantities. Section 3 is devoted to a study of the phase transition through geometrical thermodynamics. In Sect. 4, we investigate the critical behavior of the system via a new method, which comes from the maximum point of denominator of the heat capacity. We also check the Maxwell equal area law in Sect. 5. After that we calculate the critical exponents of the system in the extended phase space in Sect. 6. In Sect. 7, we examine the Ehrenfest equations at the critical point and confirm the validity of the second order phase transition. In the last section we present our conclusions.

2 Basic equations

In the current paper, we set out to discuss the geometric and thermodynamic properties of charged black holes in d-dimensional GB-massive gravity with \(d-4\) compact dimensions. Regarding compactified extra dimensions, it has been shown that, depending on the horizon topology, one can obtain black string/membrane solutions in addition to black hole solutions. Furthermore, it has been pointed out that, in the context of GB gravity, one may obtain non-trivial modified solutions with an extra asymptotic charge [72]. In this paper, we focus on the black hole solutions with usual conserved charges.

The d-dimensional action of GB-massive gravity with the negative cosmological constant and in the presence of BI electrodynamics is

$$\begin{aligned} \mathcal {I}= & {} -\frac{1}{16\pi }\int \mathrm{d}^{d}x\sqrt{-g}\,\Bigg [ \mathcal {R} -2\Lambda \nonumber \\&+\alpha ( R_{\mu \nu \gamma \delta }R^{\mu \nu \gamma \delta }-4R_{\mu \nu }R^{\mu \nu }+R^{2}) \nonumber \\&+4\beta ^{2}\left( 1-\sqrt{1+\frac{\mathcal {F}}{2\beta ^{2}}} \right) +m^{2}\sum _{i}^{4}c_{i}\mathcal {U}_{i}(g,f)\Bigg ] , \end{aligned}$$
(1)

where \(\mathcal {R}\), \(\Lambda \), m, \(\alpha \), and \(\beta \) are, respectively, the scalar curvature, the cosmological constant, the massive parameter, the GB factor, and the BI parameter. Also \(R_{\mu \nu }\) and \(R_{\mu \nu \gamma \delta }\) are the Ricci and Riemann tensors, \(\mathcal {F}=F_{\mu \nu }F^{\mu \nu }\) denotes the Maxwell invariant, and f is a fixed symmetric tensor. In Eq. (1), the \(c_{i}\) are constants and the \(\mathcal {U}_{i}\) are symmetric polynomials of the eigenvalues of \(d\times d\) matrix \( \mathcal {K}_{\nu }^{\mu }=\sqrt{g^{\mu \alpha }f_{\alpha \nu }}\), which can be written in the following form:

$$\begin{aligned} \mathcal {U}_{1}= & {} \left[ \mathcal {K}\right] , \end{aligned}$$
(2)
$$\begin{aligned} \mathcal {U}_{2}= & {} \left[ \mathcal {K}\right] ^{2}-\left[ \mathcal {K}^{2} \right] , \end{aligned}$$
(3)
$$\begin{aligned} \mathcal {U}_{3}= & {} \left[ \mathcal {K}\right] ^{3}-3\left[ \mathcal {K}\right] \left[ \mathcal {K}^{2}\right] +2\left[ \mathcal {K}^{3}\right] , \end{aligned}$$
(4)
$$\begin{aligned} \mathcal {U}_{4}= & {} \left[ \mathcal {K}\right] ^{4}-6\left[ \mathcal {K}^{2} \right] \left[ \mathcal {K}\right] ^{2}+8\left[ \mathcal {K}^{3}\right] \left[ \mathcal {K}\right] \nonumber \\&+3\left[ \mathcal {K}^{2}\right] ^{2}-6\left[ \mathcal {K} ^{4}\right] . \end{aligned}$$
(5)

Using the action (1) and variation of this action with respect to the metric tensor (\(g_{\mu \nu }\)) and the Faraday tensor (\(F_{\mu \nu }\)), respectively, leads to

$$\begin{aligned} G_{\mu \nu }+\Lambda g_{\mu \nu }+H_{\mu \nu }-\frac{1}{2}g_{\mu \nu }L( \mathcal {F})-\frac{2F_{\mu \lambda }F_{\nu }^{\lambda }}{\sqrt{1+\frac{ \mathcal {F}}{2\beta ^{2}}}}+m^{2}\chi _{\mu \nu }=0, \end{aligned}$$
(6)
$$\begin{aligned} \partial _{\mu }\left( \frac{\sqrt{-g}F^{\mu \nu }}{\sqrt{1+\frac{\mathcal {F} }{2\beta ^{2}}}}\right) =0, \end{aligned}$$
(7)

in the above equations \(G_{\mu \nu }\) is the Einstein tensor, \(H_{\mu \nu }\) and \(\chi _{\mu \nu }\) are

$$\begin{aligned} H_{\mu \nu }= & {} -\frac{\alpha }{2}[ 8R^{\rho \sigma }R_{\mu \rho \nu \sigma }-4R_{\mu }^{\rho \sigma \lambda }R_{\nu \rho \sigma \lambda }-4RR_{\mu \nu }\nonumber \\&+8R_{\mu \lambda }R_{\nu }^{\lambda } +g_{\mu \nu }( R_{\mu \nu \gamma \delta }R^{\mu \nu \gamma \delta }-4R_{\mu \nu }R^{\mu \nu }+R^{2})] \nonumber \\ \end{aligned}$$
(8)

and

$$\begin{aligned} \chi _{\mu \nu }= & {} -\frac{c_{1}}{2}(\mathcal {U}_{1}g_{\mu \nu }- \mathcal {K}_{\mu \nu }) -\frac{c_{2}}{2}( \mathcal {U}_{2}g_{\mu \nu }-2\mathcal {U}_{1}\mathcal {K}_{\mu \nu }+2\mathcal {K}_{\mu \nu }^{2})\nonumber \\&-\frac{c_{3}}{2}(\mathcal {U}_{3}g_{\mu \nu }-3\mathcal {U}_{2} \mathcal {K}_{\mu \nu } +6\mathcal {U}_{1}\mathcal {K}_{\mu \nu }^{2}-6\mathcal {K}_{\mu \nu }^{3})\nonumber \\&- \frac{c_{4}}{2}(\mathcal {U}_{4}g_{\mu \nu }-4\mathcal {U}_{3}\mathcal {K}_{\mu \nu }+12\mathcal {U}_{2}\mathcal {K}_{\mu \nu }^{2}-24\mathcal {U}_{1}\mathcal {K }_{\mu \nu }^{3}\nonumber \\&+\,24\mathcal {K}_{\mu \nu }^{4}). \end{aligned}$$
(9)

2.1 Black hole solutions

Consider the following metric of d-dimensional spacetime:

$$\begin{aligned}&\mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+f^{-1}(r)\mathrm{d}r^{2}+r^{2}h_{ij}\mathrm{d}x_{i}\mathrm{d}x_{j},\nonumber \\&\quad i,j=1,2,3,\ldots ,n, \end{aligned}$$
(10)

where \(h_{ij}\mathrm{d}x_{i}\mathrm{d}x_{j}\) is the line element with constant curvature \( \left( d-2\right) (d-3)\kappa \) and volume \(V_{d-2}\) and the ansatz metric in the following form [42]:

$$\begin{aligned} f_{\mu \nu }=\mathrm{diag}(0,0,c^{2}h_{ij}), \end{aligned}$$
(11)

in which c is a positive constant. The metric function was obtained in Ref. [1]:

$$\begin{aligned} f\left( r\right)= & {} \kappa +\frac{r^{2}}{2\alpha d_{3}d_{4}}\nonumber \\&\times \left\{ 1-\sqrt{ 1+\frac{8\alpha d_{3}d_{4}}{d_{1}d_{2}}\left[ \Lambda +\frac{d_{1}d_{2}m_{0} }{2r^{d_{1}}}+\mathcal {A}+\mathcal {B}\right] }\right\} , \nonumber \\ \\ \mathcal {A}= & {} -2\beta ^{2}\left( 1-\sqrt{1+\eta }\right) -\frac{d_{2}^{2} q^{2}}{ r^{2d_{2}}}\mathcal {H}, \nonumber \\ \mathcal {B}= & {} -m^{2}d_{1} d_{2} \left[ \frac{d_{3}d_{4}c^{4}c_{4}}{ 2r^{4}}+\frac{d_{3}c^{3}c_{3}}{2r^{3}}+\frac{c^{2}c_{2}}{2r^{2}}+\frac{cc_{1} }{2d_{2}r}\right] , \nonumber \end{aligned}$$
(12)

where \(m_{0}\) and q are integration constants, which are related to the total mass and the electric charge of black hole, respectively. The notation \(d_i\) is introduced to denote the term \(d-i\) (Recall that d is the spacetime dimensionality) so as to simplify the expressions of physical quantities in this paper. For example, \(d_1\) denotes the term \(d-1\) while \(d_2\) denotes the term \(d-2\). It is notable that, in the above solution, we used the gauge potential ansatz \(A_{\mu }=h(r)\delta _{\mu }^{0}\) in the Maxwell equation (7). Also, \(\mathcal {H}\), \(\eta \), and the consistent h(r) are of the following forms:

$$\begin{aligned}&\mathcal {H}={}_{2}F_{1}\left( \left[ \frac{1}{2},\frac{d_{3}}{2d_{2}} \right] ,\left[ \frac{3d_{7/3}}{2d_{2}}\right] -\eta \right) , \end{aligned}$$
(13)
$$\begin{aligned}&\eta =\frac{d_{2}d_{3}q^{2}}{2\beta ^{2}r^{2d_{2}}}, \end{aligned}$$
(14)
$$\begin{aligned}&h(r)=-\sqrt{\frac{d_{2}}{2d_{3}}}\frac{q}{r^{d_{3}}} \mathcal {H}. \end{aligned}$$
(15)

It was shown that the asymptotical behavior of the solutions are (a)dS solutions with an effective cosmological constant (\(\Lambda _{eff}\)) [1]. This effective cosmological constant reduces to ordinary \(\Lambda \) for vanishing \(\alpha \). It was also shown that neither massive nor BI parts affect the asymptotical behavior of the solutions. [1]

2.2 Thermodynamics

The Hawking temperature of the black hole is given by [1]

$$\begin{aligned} T= & {} \frac{1}{4\pi \mathcal {N}}\left\{ \frac{m^{2}}{r_{+}}\left[ d_{3}d_{4}( c^{3}c_{3}r_{+}+d_{5}c^{4}c_{4})\right. \right. \nonumber \\&\left. \left. +r_{+}^{2}( cc_{1}r_{+}+d_{3}c^{2}c_{2}) \right] +\frac{2r_{+}^{3}}{d_{2}}( 2\beta ^{2}-\Lambda ) \right. \nonumber \\&\left. -\frac{4\beta ^{2}r_{+}^{3}}{d_{2}\Upsilon _{+}}+\frac{\kappa d_{3} }{r_{+}}( r_{+}^{2}+\alpha \kappa d_{4}d_{5}) \right\} , \end{aligned}$$
(16)

where \(\mathcal {N}=2\alpha \kappa d_{3}d_{4}+r_{+}^{2}\) and also, \(\Upsilon _{+}=\Upsilon \left| _{r=r_{+}}\right. \) (which \(\Upsilon =\sqrt{ 1-\left( \frac{h^{\prime }(r)}{\beta }\right) ^{2}}\)). It is notable that \(r_+\) in the above expression denotes the largest real root of equation \(f(r)=0\).

The total charge, the electric potential (U), and the entropy of the black hole are [1]

$$\begin{aligned} Q= & {} \frac{V_{d_{2}}\ \sqrt{d_{2}d_{3}}}{4\pi }q, \end{aligned}$$
(17)
$$\begin{aligned} U= & {} A_{\mu }\chi ^{\mu }\left| _{r\rightarrow \infty }\right. -A_{\mu }\chi ^{\mu }\left| _{r\rightarrow r_{+}}\right. =\sqrt{\frac{d_{2}}{ 2d_{3}}}\frac{q}{r_{+}^{d_{3}}}\ \mathcal {H}_{+}, \end{aligned}$$
(18)
$$\begin{aligned} S= & {} \frac{V_{d_{2}}}{4}r_{+}^{d_{2}}\left( 1+\frac{2d_{2}d_{3}}{r_{+}^{2}} \kappa \alpha \right) , \end{aligned}$$
(19)

where \(\mathcal {H}_{+}=\mathcal {H}\left| _{r=r_{+}}\right. \) The total mass of the black hole is of the following form [1]:

$$\begin{aligned} M=\frac{\ d_{2}\ V_{d_{2}}}{16\pi }m_{0}. \end{aligned}$$
(20)

The first law of thermodynamics for black hole solution in the GB-BI-massive gravity was checked in Ref. [1] and it was found that these thermodynamical quantities satisfy the first law of black hole thermodynamics,

$$\begin{aligned} \mathrm{d}M=T\mathrm{d}S+U\mathrm{d}Q. \end{aligned}$$
(21)

3 Geometrical thermodynamics

Here, we are interested in studying the critical behavior of the black holes through the use of geometrical method. This method builds the phase space of black holes by using one of the thermodynamical quantities as thermodynamical potential and its corresponding extensive parameters as components of phase space. By doing so, a metric is obtained in which the thermodynamical properties of the system are stored in its Ricci scalar. Divergencies of the Ricci scalar point out two important places in thermodynamical behavior of the system; whether the system goes through a second order phase transition or it meets a bound point. A bound point is where heat capacity/temperature meets a root. In other words, in bound points a limit for having a physical system (positive temperature) is given. On the other hand, in the phase transition point, the heat capacity has a divergency, implying that there is a discontinuity in the heat capacity. In place of this divergency, a second order phase transition takes place.

Fig. 1
figure 1

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(q=1\), \(\Lambda =-1\), \(c=c_{1}=c_{2}=2\), \(c_{3}=c_{4}=0.2\), \(k=1\), \(\beta =0.5\), \(d=6\), and \( \alpha =0.5\); left panel: \(m=1\); three right panels: \(m=5\)

Full size image
Fig. 2
figure 2

For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(q=1\), \(\Lambda =-1\), \(c=c_{1}=c_{2}=2\), \(c_{3}=c_{4}=0.2\), \(k=1\), \(m=3\), \(d=6\), and \(\alpha =0.5\); up panels: \(\beta =0.1\); down panels: \(\beta =100\)

Full size image

There are several methods for constructing the phase space of black holes through thermodynamical quantities; see Weinhold [7, 8], Ruppeiner [9, 10], Quevedo [11, 12], and HPEM [13–15]. A successful method should cover all the mentioned points without any extra divergency for its Ricci scalar. The existence of an extra divergency or mismatch between the divergency of the Ricci scalar and the phase transition (or bound points) indicate that there is a case of anomaly. Recently, it was shown that employing Weinhold, Ruppeiner, and Quevedo may lead to the existence of anomaly [13–15]. To overcome the problems of other methods, HPEM metric was proposed. The structure of the HPEM metric is

$$\begin{aligned} \mathrm{d}s^{2}= S\frac{M_{S}}{M_{QQ}^{3}}(-M_{SS}\mathrm{d}S^{2}+M_{QQ}\mathrm{d}Q^{2}), \end{aligned}$$
(22)

where \(M_{X}=\partial M/\partial X\) and \(M_{XX}=\partial ^{2}M/\partial X^{2} \). Now, by using the total mass of black holes (20) with entropy (19) and electric charge (17), one can construct the phase space and calculate its Ricci scalar. Due to economical reasons, we will not present the Ricci scalar obtained but rather present its results in the following diagrams (Figs. 1, 2, 3).

Fig. 3
figure 3

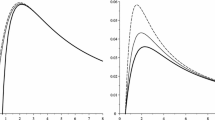
For different scales: \(\mathcal {R}\) (continuous line), \(C_{Q}\) (dotted line) and T (dashed line) versus \(r_{+}\) for \(q=1\), \(\Lambda =-1\), \(c=c_{1}=c_{2}=2\), \(c_{3}=c_{4}=0.2\), \(k=1\), \(\beta =0.5\), \(d=6\), and \( m=3\); three left panels: \(\alpha =0.5\); right panel: \(\alpha =2 \)

Full size image

Evidently, the number of phase transition points and their places are functions of massive (Fig. 1), BI (Fig. 2), and GB (Fig. 3) parameters. For considered values of different parameters, these black holes enjoy the absence of bound point. In other words, for all values of the radius of the horizon, physical black holes exist. On other hand, these black holes have a second order phase transition in their thermodynamical structure. The number of these phase transitions may vary from one (see left panel of Fig. 1 and right panel of Fig. 3) to several (see Fig. 2) phase transitions.

The system has positive temperature but depending on the choices of different parameters, temperature may acquire one to several extrema. These extrema are where the heat capacity meets a divergency. In other words, the extrema of the temperature are places in which the heat capacity is divergent. Therefore, these extrema are places in which black holes go through the second order phase transition. The number of divergencies in the heat capacity, and hence, of phase transitions, is an increasing function of the massive (see Fig. 1) and BI (see Fig. 2) parameters, while it is a decreasing function of the GB parameter (see Fig. 3).

Regarding BI theory, for large values of the nonlinearity parameter, the system behaves like Reissner–Nordström black hole. This means that for large values of this parameter, the effect of nonlinearity decreases and the system behaves like in the presence of Maxwell theory of the electromagnetic field. On the other hand, for small values of the nonlinearity parameter, the system has Schwarzschild like behavior. Taking these limits into account, one can draw the following conclusions: The highest number of phase transitions, hence, the highest complexity in the phase structure of these black holes is acquired for a linear electromagnetic field. The generalization to a nonlinear electromagnetic field reduces the number of phase transitions and it may omit some of the phase transitions. By increasing the power of the nonlinearity (decreasing the nonlinearity parameter), the system would obtain the least number of phase transitions which are acquirable for charged black holes in this theory of the nonlinear electromagnetic field.

GB gravity is a higher order gravity. In other words, the value of the Ricci scalar, which is a parameter to measure curvature of the system, is higher in this theory of gravity compared to Einstein gravity. Therefore, the gravity in this theory is stronger compared to Einstein theory of gravity. GB gravity provides an extra degree of freedom in terms of the GB parameter. Increasing the GB parameter leads to increasing the value of the Ricci scalar, and hence the power of gravity. We see, for these black holes, that by increasing the GB parameter, the number of phase transitions decreases. This means that for a system with higher power of gravity (larger curvature), the number of phase transitions and the complexity in the phase structure of these black holes decrease. Therefore, gravity here has an opposing effect on the number of phase transitions.

The massive parameter is directly related to the mass of the graviton. The plotted diagrams for the variation of the massive parameter show that as the mass of graviton increases, the black holes under consideration go through more phase transitions. In other words, by increasing the mass of the graviton the complexity in thermal behavior and the phase structure of these black holes increase.

It is evident that using the HPEM metric provides suitable divergencies in its Ricci scalar for phase transitions that are observed in the heat capacity. In other words, divergences of the Ricci scalar of the HPEM metric coincide with the phase transition points of the heat capacity. Therefore, these two approaches yield consistent results. On the other hand, depending on the type of phase transition (smaller to larger or larger to smaller black holes), the sign of the divergency of the Ricci scalar differs. If the transition is from larger to smaller, the sign of the Ricci scalar around the corresponding transition is positive, while the opposite (negative sign) is observed for the transition of smaller to larger black holes. These two differences in sign enable one to determine the type of phase transition of a system.

4 P–V criticality through new approach

In this section, we will regard critical behavior of these black holes through the use of a new method which was introduced in Ref. [73]. This method employs the denominator of the heat capacity of black holes to extract a relation for the pressure. This relation is independent from the equation of state. The maximum of the relation obtained is where the phase transition takes place. In other words, the pressure and radius of the horizon of the maximum of this relation is where the system goes through the second order phase transition and a Van der Waals like behavior is observed. In addition, the picture that this method draws for a pressure smaller/larger than the critical pressure is consistent with thermodynamical behavior for the system with the same pressure as in the usual thermodynamics in the other words, smaller than critical pressure, two horizon radii exist, which marks two different phases in the phase diagrams, while for a pressure larger than the critical pressure no phase transition is observed. This is consistent with the behavior of the T–V diagrams in which for the pressures larger than critical pressure, no phase transition region exists. The consistency of this method with other methods was investigated in Refs. [45, 46, 74, 75].

Now, we will employ this method to obtain the critical pressure and radius of the horizon of these black holes. First, we use the proportionality between the cosmological constant and pressure,

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }, \end{aligned}$$
(23)

with the heat capacity

$$\begin{aligned} C_{Q}=\frac{T}{\left( \frac{\partial ^{2}M}{\partial S^{2}}\right) _{Q}}= \frac{T}{\left( \frac{\partial T}{\partial S}\right) _{Q}}. \end{aligned}$$
(24)

Using Eq. (16), we obtain the denominator of the heat capacity \(\left( \frac{\partial T}{\partial S}\right) _{Q}\) in the following form:

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right) _{Q}= & {} \frac{\kappa d_{3}\left( \mathcal {N}-2r_{+}^{2}\right) }{\pi d_{2}\mathcal {N}^{3}r_{+}^{d_{5}}}+\frac{ \left( 3\mathcal {N}-2r_{+}^{2}\right) }{\pi d_{2}^{2}\mathcal {N} ^{3}r_{+}^{d_{7}}}\nonumber \\&\times \left( \frac{4\beta ^{2}\left( \Upsilon _{+}-1\right) }{ \Upsilon _{+}}-2\Lambda \right) -\frac{4h^{\prime }h^{\prime \prime }}{\pi d_{2}^{2}\mathcal {N}^{2}r_{+}^{d_{8}}\Upsilon _{+}^{3}}- \nonumber \\&\times \frac{\alpha \kappa ^{2}d_{3}d_{4}d_{5}\left( \mathcal {N} +2r_{+}^{2}\right) }{\pi d_{2}\mathcal {N}^{3}r_{+}^{d_{3}}}-\frac{2m^{2} \mathcal {E}}{\pi d_{2}\mathcal {N}^{3}r_{+}^{d_{3}}}, \end{aligned}$$
(25)

in which \(\mathcal {E}\) is

$$\begin{aligned} \mathcal {E}= & {} d_{3}d_{4}\left[ d_{5}c^{4}c_{4}\left( r_{+}^{2}+\frac{\mathcal {N }}{2}\right) +c^{3}c_{3}r_{+}\right] \nonumber \\&+r_{+}^{2}\left[ d_{3}c^{2}c_{2}\left( r_{+}^{2}-\frac{\mathcal {N}}{2}\right) +cc_{1}r_{+}\left( r_{+}^{2}-\mathcal { N}\right) \right] . \end{aligned}$$
(26)

Now, by solving Eq. (25) with respect to the pressure, a relation for the pressure is obtained:

$$\begin{aligned} P= & {} \frac{m^{2}d_{2}}{8\pi r_{+}^{4}\left( r_{+}^{2}+6\alpha k\right) } \left\{ d_{3}d_{4}\left[ c_{4}c^{4}d_{5}\left( \frac{3r_{+}^{2}}{2}+k\alpha \right) \right. \right. \nonumber \\&\left. \left. +c_{3}c^{3}r_{+}^{3}\right] -r_{+}^{2}\left[ c_{2}c^{2}d_{3}\left( k\alpha -\frac{r_{+}^{2}}{2}\right) +2\alpha c c_{1}k r_{+} \right] \right\} \nonumber \\&-\frac{\beta ^{2}\left( d_{3}r_{+}^{2}+2\alpha kd_{5}\right) \eta _{+}}{ 4\pi \left( r_{+}^{2}+6\alpha k\right) \sqrt{1+\eta _{+}}}\nonumber \\&+\frac{kd_{2}\left[ \alpha k\left( 2 \alpha d_{5}k+d_{9}r_{+}^{2}\right) +d_{3}r_{+}^{4}\right] }{16\pi r_{+}^{4}\left( r_{+}^{2}+6\alpha k\right) }\nonumber \\&-\frac{\beta ^{2}}{4\pi }\left( 1-\frac{1}{\sqrt{1+\eta _{+}}}\right) . \end{aligned}$$
(27)

In order to study the critical behavior of these black holes, we should see whether a maximum exists for this relation. To do so, we employ a numerical method. The results are presented in the following diagrams (Figs. 4, 5, 6, 7).

Fig. 4
figure 4

P versus \(r_{+}\) (left panel) and P versus T (right panel) for \(q=1\), \(c=c_{2}=c_{3}=c_{4}=0.2\), \(c_{1}=2\), \(\beta =0.5\), \( \alpha =0.5\), \(d=6\), and \(k=1\); Left panel: \(m=0\) (continuous line), \(m=0.3\) (dotted line), \(m=0.5\) (dashed line) and \(m=0.7\) (dash-dotted line)

Full size image
Fig. 5
figure 5

P versus \(r_{+}\) (left panel) and P versus T (right panel) for \(q=1\), \(c=c_{2}=c_{3}=c_{4}=0.2\), \(c_{1}=2\) \(m=0.5\), \(\beta =0.5\), \(d=6\), and \(k=1\); \(\alpha =0\) (continuous line), \(\alpha =0.5\) (dotted line), \( \alpha =1.5\) (dashed line) and \(\alpha =2\) (dash-dotted line)

Full size image
Fig. 6
figure 6

P versus \(r_{+}\) (left panel) and P versus T (middle and right panels) for \(q=1\), \(c=c_{2}=c_{3}=c_{4}=0.2\), \(c_{1}=2\), \(m=1\), \( \alpha =0.5\), \(d=6\), and \(k=1\); Middle panel: \(\beta =0.05\) (continuous line) and \(\beta =0.5\) (dotted line); right panel: \(\beta =0.06\) (continuous line) and \( \beta =50\) (dotted line)

Full size image

First of all, it is evident that due to the existence of maximum, these black holes enjoy a second order phase transition in their phase space. The critical pressure is a decreasing function of the massive, GB, and BI parameters while their corresponding critical radius of the horizon are increasing functions of them (left panels of Figs. 4, 5, 6). On the contrary, the critical radius of the horizon is a decreasing function of the dimension, while the critical pressure is an increasing function of this parameter (left panel of Fig. 7).

Depending on the choices of the different parameters, one may come across two interestingly different behaviors for the P–\(r_{+}\) diagrams; I) in one behavior, only one extremum exists for these diagrams (left panels of Figs. 4, 7); II) in the other one, one minimum and one maximum exist (left panels of Figs. 5, 6).

Considering the mentioned concept for this method, only in a maximum a second order phase transition exists. Therefore, we have a second order phase transition for both cases. On the other hand, for the second behavior, for critical pressure, two horizon radii exist (due to the formation of a tail). This indicates that another branch for critical behavior exists. This critical behavior is not a second order phase transition but rather another kind (considering the concept of maximum). Interestingly, the second case of behavior for P–\(r_{+}\) is observed for small values of the nonlinearity parameter and large values of the GB parameter. In other words, for small values of the BI parameter and large values of the GB parameter, the existence of an extra branch in the phase diagrams of these black holes is evident (left panels of Figs. 5, 6).

The existence of such behavior points out that another branch for the phase diagrams exists for these black holes which is absent in other black holes. Such a behavior is precisely due to the existence of massive gravity. This means that by considering a massive theory of gravity for these black holes, another type of phase transition takes place. This emphasizes the role and effects of massive gravity in the thermodynamical behavior of these black holes.

Fig. 7
figure 7

P versus \(r_{+}\) (left panel) and P versus T (right panel) for \(q=1\), \(c=c_{2}=c_{3}=c_{4}=0.2\), \(c_{1}=2\), \(m=1\), \(\alpha =0.5\), \(\beta =0.5\), and \(k=1\); \(d=6\) (continuous line), \(d=7\) (dotted line), \(d=8\) (dashed line) and \(d=9\) (dash-dotted line)

Full size image

In order to complete our study here, we will plot coexistence curves for the variation of different parameters as well (right panels of Figs. 4, 5, 6, 7). The coexistence curves are representing small/larger black holes with similar pressure and temperature. The critical point is located at the end of this line, which indicates that, after this point, the phase transition does not take place. Evidently, the critical temperature is an increasing function of the massive gravity (right panel of Fig. 4) and dimensionality (right panel of Fig. 7) while it is a decreasing function of the GB (right panel of Fig. 5) and BI parameters (right panel of Fig. 6). Here, in these phase diagrams, we see that the presence of other phase transitions is not observed. This indicates that our earlier interpretation is right. In other words, the branch for the phase transition which was observed in the P–\(r_{+}\) diagram is not a second order phase transition. Also, we should point out that plotted diagrams indicate that no reentering of the phase transition takes place for these black holes.

5 Check of Maxwell equal area law for both T–S and P–V graphs

The expressions of Hawking temperature and the entropy are listed in Eqs. (16) and (19), respectively. For the T–\(r_+\) graph, the possible critical point can be determined through

$$\begin{aligned}&\left( \frac{\partial T}{\partial r_+}\right) _{q=q_c, r=r_{+c}}=0, \end{aligned}$$
(28)
$$\begin{aligned}&\left( \frac{\partial ^2 T}{\partial r_+^2}\right) _{q=q_c, r=r_{+c}}=0. \end{aligned}$$
(29)

For the T–S graph, the possible critical point can be determined through

$$\begin{aligned}&\left( \frac{\partial T}{\partial S}\right) _{q=q_c, S=S_c}=0, \end{aligned}$$
(30)
$$\begin{aligned}&\left( \frac{\partial ^2 T}{\partial S^2}\right) _{q=q_c, S=S_c}=0. \end{aligned}$$
(31)
Table 1 Effect of m on critical quantities of T–\(r_+\) graph for \(\alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table
Table 2 Effect of \(\alpha \) on critical quantities of T–\(r_+\) graph for \(m=0.1, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table
Table 3 Effect of \(\beta \) on critical quantities of T–\(r_+\) graph for \(\alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table

Equations (30) and (31) are related to Eqs. (28) and (29) by

$$\begin{aligned} \left( \frac{\partial T}{\partial S}\right)= & {} \left( \frac{\partial T}{ \partial r_+}\right) /\left( \frac{\partial S}{\partial r_+}\right) , \end{aligned}$$
(32)
$$\begin{aligned} \left( \frac{\partial ^2 T}{\partial S^2}\right)= & {} \left( \frac{ \partial \left( \frac{\partial T}{\partial S}\right) }{\partial r_+}\right) /\left( \frac{\partial S}{\partial r_+} \right) \nonumber \\= & {} \left( \frac{\left( \frac{\partial ^2 T}{\partial r_+^2}\right) \left( \frac{\partial S}{\partial r_+}\right) -\left( \frac{\partial T}{\partial r_+} \right) \left( \frac{\partial ^2 S}{\partial r_+^2}\right) }{\left( \frac{ \partial S}{\partial r_+}\right) ^2}\right) /\left( \frac{\partial S}{\partial r_+}\right) .\nonumber \\ \end{aligned}$$
(33)

Considering the above two relations and the fact that \(\left( \frac{\partial S }{\partial r_+}\right) >0\), it is not difficult to conclude that the critical point conditions for T–\(r_+\) and T–S graphs are equivalent to each other.

To probe the effect of massive gravity on critical quantities of T–S graph, we fix other parameters and let m vary from 0 to 0.3. The results are listed in Table 1. One can see clearly that for the cases \(m=0\) and \(m=0.1\), there are two critical points, while there is only one for the cases \(m=0.2\) and \(m=0.3\). Then we let \(\alpha \) vary and keep other parameters fixed to investigate the effect of GB gravity. The results are listed in Table 2. Lastly, we let \(\beta \) vary and keep other parameters fixed to study the effect of BI theory. The results are listed in Table 3.

Fig. 8
figure 8

a T vs. \(r_+\) for \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\), b T vs. S for \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)

Full size image

To gain an intuitive understanding of the Van der Waals like behavior, we plot both T–\(r_+\) and T–S graphs for the case \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\). From Fig. 8, one can see clearly that both the graphs can be divided into three branches. The medium radius branch is unstable while both the large radius branch and the small radius branch are stable. The unstable branch in T–S curve can be removed with a bar vertical to the temperature axis \(T=T_*\) as in the approach in Ref. [76]. The possible Maxwell equal area laws for the T–S and T–\(r_+\) graphs read

$$\begin{aligned} T_*(S_3-S_1)= & {} \int ^{S_3}_{S_1}T\mathrm{d}S, \end{aligned}$$
(34)
$$\begin{aligned} T_*(r_3-r_1)= & {} \int ^{r_3}_{r_1}T\mathrm{d}r_+. \end{aligned}$$
(35)

Note that \(S_1\), \(S_2\), and \(S_3\) denote the three values of the entropy from small to large corresponding to \(T=T_*\), while \(r_1\), \(r_2\), and \(r_3\) denote the three values of \(r_+\) from small to large corresponding to \(T=T_*\).

To determine \(T_*\), one should first study the behavior of the free energy (F), which can be obtained, thus:

$$\begin{aligned} F= & {} M-TS=-\frac{V_{d_2}r_{+}^{d_5}(r_{+}^{2}+2d_3d_2\alpha \kappa )}{16\pi (r_+^2+2d_4d_3\alpha \kappa )}\nonumber \\&\times \Big \{m^2[cr_+^2(cc_2d_3+c_1r_+)+c^3d_4d_3(cc_4d_5+c_3r_+)]\nonumber \\&+d_3\kappa (r_+^2+d_5d_4\alpha \kappa ) \nonumber \\&+\frac{2r_{+}^{4}(2\beta ^2-\Lambda -2\beta ^2\sqrt{1+\eta _+})}{d_2}\Big \}\nonumber \\&+\frac{V_{d_2}}{16\pi }m^2r_+^{d_5}[cr_+^2(cc_2d_2+c_1r_+)\nonumber \\&+c^3d_3d_2(cc_4d_4+c_3r_+)] \nonumber \\&-\frac{V_{d_2}r_+^{d_1}(\Lambda -2\beta ^2+2\beta ^2 \sqrt{1+\eta _+})}{8\pi d_1}\nonumber \\&+\frac{V_{d_2}d_2}{16\pi }\left( r_+^{d_3}\kappa +d_3 d_4r_+^{d_5}\alpha \kappa ^2+\frac{2d_2q^2r_{+}^{-d_3} \mathcal {H}_+}{d_1} \right) . \end{aligned}$$
(36)

We plot the free energy for the case \(q=0.2q_c, m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\) in Fig. 9, where we can find the swallow tail characteristic of a first order phase transition.

Fig. 9
figure 9

F vs. T for \(q=0.2q_c, m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)

Full size image

Numerical checks of Maxwell equal area law for the cases \(q=0.2q_c, 0.4q_c,\) \( 0.6q_c, 0.8q_c\) are carried out in both the T–\(r_+\) and the T–S graphs. The first order phase transition temperature \(T_*\) is obtained through the intersection point of the two branches in the free energy curve. As shown in Tables 4 and 5, the relative errors are very small and the Maxwell equal area law holds for not only T–\(r_+\) curves, but also T–S curves.

Table 4 Numerical check of Maxwell equal area law for T–\(r_+\) graph for \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table
Table 5 Numerical check of Maxwell equal area law for T–S graph for \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table
Table 6 Numerical check of Maxwell equal area law for the P–\(r_+\) graph for \(m=0.5, \alpha =0.8/6, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, q=1\)
Full size table
Table 7 Numerical check of Maxwell equal area law for the P–V graph for \(m=0.2, \alpha =0.5, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, \Lambda =-0.1\)
Full size table

The possible Maxwell equal area laws for the P–\(r_+\) and P–V graphs read

$$\begin{aligned} P_*(r_3-r_1)= & {} \int ^{r_3}_{r_1}P\mathrm{d}r_+, \end{aligned}$$
(37)
$$\begin{aligned} P_*(V_3-V_1)= & {} \int ^{V_3}_{V_1}P\mathrm{d}V. \end{aligned}$$
(38)

Here, \(r_1\), \(r_2\), and \(r_3\) denote the three values of \(r_+\) from small to large corresponding to \(P=P_*\) in P–\(r_+\) graph while \(V_1\), \(V_2\), and \(V_3\) denote the three values of V from small to large corresponding to \(P=P_*\) in P–V graph. Note that the thermodynamic volume V is defined in the extended phase space as \(V=\left( \frac{\partial M}{\partial P}\right) _{S,Q}\). For the cases \(P_*=0.5P_c, 0.6P_c,\) \(0.7P_c, 0.8P_c\), we use the technique of the Gibbs free energy to determine the corresponding \(T_*\), which is shown in the first column of Tables 6 and 7. Since the mass of a black hole should be interpreted as the enthalpy in the extended phase space, the definition of the Gibbs free energy reads

$$\begin{aligned} G=H-TS=M-TS. \end{aligned}$$
(39)

We plot the Gibbs free energy for the case \(P_*=0.5P_c, m=0.5, \alpha =0.8/6, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, q=1\) in Fig. 10. The classical swallow tail behavior can also be found. We further calculate both the left hand side and the right hand side of Eqs. (37) and (38). As shown in Tables 6 and 7, the relative errors for the P–\(r_+\) graph are very large while those for the P–V graph are amazingly small, leading to the conclusion that the Maxwell equal area law holds for the P–V graph, while it fails for the P–\(r_+\) graph. Our numerical results here for the GB–BI–massive black holes further corroborate the findings in previous research [77, 78].

6 Critical exponents

To characterize the critical behavior near the critical point in the extended phase space, one usually introduces the following critical exponents:

$$\begin{aligned}&C_V\propto |t|^{-\alpha _1}, \end{aligned}$$
(40)
$$\begin{aligned}&\eta \propto |t|^{\beta _1}, \end{aligned}$$
(41)
$$\begin{aligned}&\kappa _T\propto |t|^{-\gamma }, \end{aligned}$$
(42)
$$\begin{aligned}&|P-P_c|\propto |v-v_c|^{\delta }. \end{aligned}$$
(43)

Note that we use the notations \(\alpha _1~\text {and}~\beta _1\) instead of the classical notation \(\alpha ~\text {and}~\beta \) here because \(\alpha ~\text {and}~\beta \) already have other meanings in this paper. As can be seen from the above definitions, the exponents \(\alpha _1, \beta _1, \gamma \), and \(\delta \) describe the behavior of specific heat \(C_V\), the order parameter \(\eta \), the isothermal compressibility coefficient \(\kappa _T\), and the critical isotherm, respectively.

Before calculating the above critical exponents, it would be convenient to define

$$\begin{aligned} t=\frac{T}{T_c}-1,\;\;\epsilon =\frac{v}{v_c}-1,\;\;p=\frac{P}{P_c}. \end{aligned}$$
(44)

The equation of state in the extended phase space has been derived in Ref. [1]:

$$\begin{aligned} P= & {} \frac{d_2(2\kappa \alpha ^{\prime }+r_+^2)T}{4r_+^3}\nonumber \\&-\frac{ m^2cd_2[d_3d_4c^2(d_5cc_4+c_3r_+)+r_+^2(d_3cc_2+c_1r_+)]}{16\pi r_+^4} \nonumber \\&+\frac{\beta ^2(\sqrt{1+\eta _+}-1)}{4\pi }-\frac{d_2\kappa (d_5\kappa \alpha ^{\prime }+d_3r_+^2)}{16\pi r_+^4}, \end{aligned}$$
(45)

where \(\alpha ^{\prime }=d_3d_4\alpha , \eta _+=\frac{d_2d_3q^2}{ 2\beta ^2r_+^{2d_2}}\). Identifying the specific volume v as \(v=\frac{4r_+}{ d_2}\), the equation of state can be reorganized as

$$\begin{aligned} P= & {} \frac{T}{v}+\frac{32\kappa d_3d_4\alpha T}{d_2^2v^3}\nonumber \\&-\frac{ m^2c[16d_3d_4c^2(4d_5cc_4+c_3d_2v)+d_2^2v^2(4d_3cc_2+c_1d_2v)]}{4\pi d_2^3 v^4} \nonumber \\&+\frac{\beta ^2\left( \sqrt{1+\frac{d_2d_3q^2 4^{2d_2}}{ 2\beta ^2d_2^{2d_2}v^{2d_2}}}-1\right) }{4\pi }-\frac{\kappa (16d_5\kappa d_3d_4\alpha +d_3d_2^2v^2)}{\pi d_2^3v^4}.\nonumber \\ \end{aligned}$$
(46)

Then the equation of state in the extended phase space can be expanded as

$$\begin{aligned} p=1+p_{10}t+p_{01}\epsilon +p_{11}t\epsilon +p_{02}\epsilon ^2+ p_{03}\epsilon ^3+O(t\epsilon ^2,\epsilon ^4), \end{aligned}$$
(47)

where the expansion coefficients can be calculated as

$$\begin{aligned} p_{01}= & {} p_{02}=0, \end{aligned}$$
(48)
$$\begin{aligned} p_{10}= & {} \frac{T_c}{v_cP_c}+\frac{32d_3d_4\alpha \kappa T_c}{d_2^2v_c^3P_c}, \end{aligned}$$
(49)
$$\begin{aligned} p_{11}= & {} -\frac{T_c}{v_cP_c}-\frac{96d_3d_4\alpha \kappa T_c}{d_2^2v_c^3P_c}, \end{aligned}$$
(50)
$$\begin{aligned} p_{03}= & {} -\frac{T_c}{v_cP_c}+\frac{4d_3\kappa [d_2v_c(d_2v_c-80d_4T_c\alpha )+80d_4d_5\alpha \kappa ]}{P_cd_2^3v_c^4\pi } \nonumber \\&+\frac{cm^2(1280c^3c_4d_3d_4d_5+160c^2c_3d_2d_3d_4v_c+ 16cc_2d_2^2d_3v_c^2+c_1d_2^3v_c^3)}{4P_cd_2^3v_c^4\pi } \nonumber \\&-[256^{d_2}d_2^{2-2d_2}(1+d_2)(2+d_2)d_3^2q^4+2^{1+4d_2} d_2\nonumber \\&\times (4+d_2)(1+2d_2)d_3q^2v_c^{2d_2} \beta ^2+8d_2^{2d_2}\nonumber \\&\times (1+d_2)(1+2d_2)v_c^{4d_2}\beta ^4] \nonumber \\&\times \frac{2^{\frac{1}{2}+4d_2}d_2^2d_3q^2v_c^{-2d_2}}{48P_c\pi \sqrt{ 2+\frac{16^{d_2}d_2^{1-2d_2}d_3q^2v_c^{-2d_2}}{\beta ^2}} (16^{d_2}d_2d_3q^2+2d_2^{2d_2}v_c^{2d_2}\beta ^2)^2} . \end{aligned}$$
(51)
Fig. 10
figure 10

G vs. T for \(P_*=0.5P_c, m=0.5, \alpha =0.8/6, \beta =0.5, c=c_1=c_2=2, c_3=0.2, c_4=-0.2, d=6, q=1\)

Full size image

From the equal area law, one can further derive

$$\begin{aligned} \int ^{\epsilon _s}_{\epsilon _l}\epsilon \frac{\mathrm{d} p}{\mathrm{d}\epsilon }\mathrm{d} \epsilon =0, \end{aligned}$$
(52)

where \(\frac{d p}{d\epsilon }\) can be calculated as \(p_{11}t+3p_{03} \epsilon ^2 \). Denoting by the subscripts “l” and “s” as the quantity of large black hole and small black hole, respectively, one can obtain

$$\begin{aligned} p_{11}t(\epsilon ^2_s-\epsilon ^2_l)+\frac{3}{2} p_{03}(\epsilon ^4_s- \epsilon ^4_l)=0. \end{aligned}$$
(53)

On the other hand, the pressure of the large black hole equals that of the small black hole as follows:

$$\begin{aligned} 1+p_{10}t+p_{11}t\epsilon _l+p_{03}\epsilon _l^3=1+p_{10}t+p_{11}t \epsilon _s+p_{03}\epsilon _s^3, \end{aligned}$$
(54)

because during the phase transition the pressure of the black hole keeps unchanged.

With Eqs. (53) and (54), one can get

$$\begin{aligned} \epsilon _l=-\epsilon _s=\sqrt{\frac{-p_{11}t}{p_{03}}}. \end{aligned}$$
(55)

So the order parameter can be derived as

$$\begin{aligned} \eta =v_l-v_s=v_c(\epsilon _l-\epsilon _s)=2v_c\epsilon _l\propto \sqrt{-t}, \end{aligned}$$
(56)

leading to the conclusion that \(\beta _1=1/2\).

It is not difficult to deduce that

$$\begin{aligned} \kappa _T=\left. -\frac{1}{v}\frac{\partial v}{\partial P} \right| _{v_c} \propto \left. -\frac{1}{\frac{\partial p}{\partial \epsilon }} \right| _{\epsilon =0}=-\frac{1}{p_{11}t}, \end{aligned}$$
(57)

from which one can draw the conclusion that \(\gamma =1\).

One can obtain the critical isotherm by substituting \(t=0\) into Eq. (47),

$$\begin{aligned} p-1=p_{03}\epsilon ^3, \end{aligned}$$
(58)

implying that \(\delta =3\).

The entropy S does not depend on the Hawking temperature T. So the specific heat with fixed volume \(C_V\) is equal to zero, with the critical exponent \(\alpha _1=0\).

The above exponents are totally the same as those in the previous literature. This can be attributed to the effect of mean field theory.

7 Analytical check of the Ehrenfest equations at the critical point in the extended phase space

It is important to classify the nature of the phase transition. As is well know, the Clausius–Clapeyron equation is satisfied for a first order phase transition, while for a second order phase transition one can utilize the famous Ehrenfest equations as follows:

$$\begin{aligned} \left( \frac{\partial P}{\partial T}\right) _S= & {} \frac{C_{P_2}-C_{P_1}}{VT(\tilde{\alpha } _2-\tilde{\alpha }_1)}=\frac{\Delta C_P}{VT\Delta \tilde{\alpha }}, \end{aligned}$$
(59)
$$\begin{aligned} \left( \frac{\partial P}{\partial T}\right) _V= & {} \frac{\tilde{\alpha }_2-\tilde{\alpha }_1}{ \kappa _{T_2}-\kappa _{T_1}}=\frac{\Delta \tilde{\alpha }}{\Delta \kappa _T}, \end{aligned}$$
(60)

where the volume expansion coefficient \(\tilde{\alpha }=\frac{1}{V} (\frac{ \partial V}{\partial T})_P\) and isothermal compressibility coefficient \( \kappa _T=-\frac{1}{V}(\frac{\partial V}{\partial P})_T\). Note that we use the notation \(\tilde{\alpha }\) instead of the classical notation \(\alpha \) here because \(\alpha \) already has another meaning in this paper.

Utilizing the definition of \(\tilde{\alpha }\), one can derive

$$\begin{aligned} V\tilde{\alpha }=\left( \frac{\partial V}{\partial T}\right) _P=\left( \frac{\partial V}{ \partial S}\right) _P\left( \frac{\partial S}{\partial T}\right) _P=\left( \frac{\partial V}{\partial S }\right) _P\left( \frac{C_P }{T}\right) . \end{aligned}$$
(61)

So the R.H.S. of Eq. (59) can be obtained:

$$\begin{aligned} \frac{\Delta C_P}{TV\Delta \tilde{\alpha }}=\left[ \left( \frac{\partial S}{\partial V}\right) _P\right] _c. \end{aligned}$$
(62)

The subscript “c” here denotes the corresponding quantity at the critical point. It is not difficult to obtain

$$\begin{aligned} \frac{\Delta C_P}{TV\Delta \tilde{\alpha }}=\frac{d_2(r_c^2+2d_4d_3\alpha \kappa )}{4r_c^3}. \end{aligned}$$
(63)

Utilizing Eq. (45), the L.H.S. of Eq. (59) can be derived as

$$\begin{aligned} \left[ \left( \frac{\partial P}{\partial T}\right) _S\right] _c=\frac{d_2(r_c^2+2d_4d_3\alpha \kappa )}{ 4r_c^3}. \end{aligned}$$
(64)

From Eqs. (63) and (64), we can draw the conclusion that the first equation of the Ehrenfest equations is valid at the critical point.

The L.H.S. of Eq. (60) can be obtained:

$$\begin{aligned} \left[ \left( \frac{\partial P}{\partial T}\right) _V\right] _c=\frac{d_2(r_c^2+2d_4d_3\alpha \kappa )}{ 4r_c^3}. \end{aligned}$$
(65)

With both the definitions of \(\kappa _T\) and of \(\tilde{\alpha }\), one can deduce

$$\begin{aligned} V\kappa _T=-\left( \frac{\partial V}{\partial P}\right) _T=\left( \frac{\partial T}{\partial P}\right) _V\left( \frac{\partial V}{\partial T}\right) _P=\left( \frac{\partial T}{\partial P}\right) _VV \tilde{\alpha }, \end{aligned}$$
(66)

from which we can calculate the R.H.S of Eq. (60) and get

$$\begin{aligned} \frac{\Delta \tilde{\alpha }}{\Delta \kappa _T}=\left[ \left( \frac{\partial P}{\partial T} \right) _V\right] _c=\frac{d_2(r_c^2+2d_4d_3\alpha \kappa )}{4r_c^3}. \end{aligned}$$
(67)

In the derivation of Eq. (66), we have utilized the thermodynamic identity \((\frac{\partial V}{\partial P})_T(\frac{\partial T}{\partial V})_P( \frac{\partial P}{\partial T})_V=-1\). Equation (67) reveals the validity of the second equation of the Ehrenfest equations. With Eqs. (63) and (67), the Prigogine–Defay (PD) ratio can be calculated as

$$\begin{aligned} \Pi =\frac{\Delta C_P \Delta \kappa _T}{TV(\Delta \tilde{\alpha })^2}=1. \end{aligned}$$
(68)

The above equation and the validity of the Ehrenfest equations show that GB–BI–massive black holes undergo a second order phase transition at the critical point of P–V criticality in the extended phase space. The result here is consistent with the nature of a liquid–gas phase transition at the critical point and supports the findings in the previous literature [79–81].

8 Closing remarks

In this paper, we have studied the thermodynamical behavior of Einstein–GB–massive black holes in the presence of a BI nonlinear electromagnetic field near the critical point.

First, some comments regarding the effects of mass of graviton, nonlinearity of the electromagnetic field, and power of gravity (value of the GB curvature term) on the phase structure and its complexity were given. In addition, geometrical thermodynamics was used to investigate the liquid–gas transition of these black holes based on the canonical ensemble.

Next, by using the denominator of the heat capacity and the proportionality between the cosmological constant and the thermodynamic pressure, critical behavior of these black holes was investigated. It was shown that these black holes enjoy an anomaly in their phase structure. In other words, in addition to the Van der Waals like phase transition in their phase diagrams, these black holes enjoy another type of phase transition which is different from the usual Van der Waals like phase transition. The plotted coexistence curves also confirmed that only one second order phase transition exists for these black holes.

Moreover, the Maxwell equal area law was employed to investigate the Van der Waals like behavior and structure of these black holes. It was shown that the Maxwell equal area law holds for the T–\(r_{+}\), T–S, and P–V diagrams while it fails regarding the P–\(r_{+}\) curves. Calculations regarding the critical exponent showed that these exponents are independent of massive gravity and are the same as those derived previously. Finally, the Ehrenfest equations were used to determine the type of phase transition. It was shown that these black holes undergo a second order phase transition at the critical point.