Pulsar interpretation of lepton spectra measured by AMS-02

Abstract

Alpha Magnetic Spectrometer (AMS-02) recently published its lepton spectra measurement. The results show that the positron fraction no longer increases above $\sim$200 GeV. The aim of this work is to investigate the possibility that the excess of positron fraction is due to pulsars. Nearby known pulsars from the ATNF catalog are considered to be a possible primary positron source of the high energy positrons. We find that the pulsars with age $T\simeq (0.45{-}4.5)\times 10^{5}$ year and distance $d<0.5$ kpc can explain the behavior of positron fraction of AMS-02 in the range of high energy. We show that each of the four pulsars—Geminga, J1741-2054, Monogem, and J0942-5552—is able to be a single source satisfying all considered physical requirements. We also discuss the possibility that these high energy $e{}^{\pm }$ are from multiple pulsars. The multiple pulsar contribution predicts a positron fraction with some structures at higher energies.

1 Introduction

The positron fraction spectrum ${e}^{+}$/(${e}^{+}+{e}{}^{-}$) in the cosmic ray (CR) contains two components: secondary $e{}^{\pm }$ produced by nuclei collision and primary ${e}^{-}$. It is currently believed that these two components, each of which will produce a diffused power low spectrum, predict a positron fraction which goes down with energy. However, the latest results measured by the Alpha Magnetic Spectrometer (AMS-02) with high accuracy indicate that the positron fraction increases with energy above $\sim$8 GeV and does not increase with energy above $\sim$200 GeV [1, 2]. This “increasing” behavior, which is also observed by the payload for antimatter matter exploration and light-nuclei astrophysics (PAMELA) [3–5] and the Fermi large area telescope (Fermi-LAT) [6, 7], is not compatible with only diffused power low components. The “cutoff” behavior above 200 GeV, which can be well described by a common source term with an exponential cutoff parameter in Eq. (1) of [1], indicates that potential sources produce the excess of electron and positron pairs.

AMS-02 [1, 2] is a state-of-the-art astroparticle detector installed on the International Space Station (ISS). It carries a Transition Radiation Detector (TRD) and a Electromagnetic Calorimeter (ECAL). These two sub-detectors provide independent proton/lepton identification, which will achieve a much larger proton rejection power of AMS-02 compared with PAMELA which has only one electromagnetic calorimeter for proton/lepton identification using the 3D shower shape and energy–momentum match (E/P). Compared with Fermi-LAT, AMS-02 has a large magnet which can identify charge sign of the particle. Thus, the contamination of electrons (also called “charge confusion” in [1]) in the positron sample of AMS-02 is much smaller than that of Fermi-LAT. For the reasons given above, there is much less proton or charge confusion contamination in AMS-02 measurement than that in PAMELA or Fermi-LAT. Here, we only interpret the AMS-02 result as due to the lack of knowledge of the contamination control in PAMELA and Fermi-LAT measurements.

AMS-02’s recent measurements of the positron fraction [1], ${e}{}^{+}$ flux, ${e}{}^{-}$ flux [2], and (${e}{}^{-} + {e}{}^{+}$) flux [8] were published. The ${e}{}^{-}$ flux contains three components: primary ${e}{}^{-}$, secondary $e{}^{-}$, and ${e}{}^{-}$ from unknown sources. The ${e}{}^{+}$ flux contains only two components: ${e}{}^{+}$ from secondary production and primary ${e}{}^{+}$ from sources to be identified. To avoid the unnecessary uncertainty of primary ${e}{}^{-}$, the $e{}^{+}$ flux seems to be an ideal spectrum to study extra sources. However, there is an acceptance uncertainty from the detector itself in the $e{}^{+}$ and $e{}^{-}$ fluxes. This uncertainty in $e{}^{+}$ flux is strongly correlated with that in $e{}^{-}$ flux [2], especially at high energies. The positron fraction can avoid this systematic uncertainty [1]. For example, one can clearly see a drop at the last point (350–500 GeV) in the positron fraction but cannot tell a drop at the last point (370–500 GeV) in the $e{}^{+}$ flux due to its larger error bars. Therefore, the positron fraction is used to study extra sources, while the $e{}^{-}$ flux is used to estimate the primary $e{}^{-}$, which will affect the denominator of $e{}^{+}$/($e{}^{+}+e{}^{-}$).

Recent studies have proposed some interpretations, such as dark matter annihilation or decay [9–17], supernova remnants (SNRs) [18–23], secondary production in the interstellar medium (ISM) [24], and pulsars [16, 17, 25–39]. Cosmic-ray flux data can also be taken together with other observations (like the dark matter relic density and the direct detection experimental results etc.) to give a combined constraint on dark matter models [40, 41]. Besides a dark matter scenario, the others can provide astrophysical explanations which do not require the existence of new particles. The SNRs model, for instance in [22, 42], introduces some new mechanisms for the propagation model or special distributions of the primary sources. The “model-independent” approach from [24] sets an upper limit of the positron fraction by neglecting radiative losses of electrons and positrons but does not indicate any obvious cutoff in the spectrum. Among them, the pulsar interpretation is one of the scenarios which predicts a cutoff at a few 100 GeV in the positron fraction spectrum and does not contradict other cosmic-ray spectra (e.g. boron-to-carbon). The pioneering work on a pulsar interpretation of the positron fraction has been performed [29, 31, 38] a few years ago. Combined analyses of the recent AMS-02 lepton data have been performed by [16, 23], with a global fit on the positron fraction [1], $e{}^{+}$ flux, $e{}^{-}$ flux and ($e{}^{-}+e{}^{+}$) flux. To avoid the over-estimation of the $\chi {}^{2}$, however, only two out of four spectra should be used in the fit. As for the reasons given by the previous paragraph, we only study the positron fraction and $e{}^{-}$ flux in this paper.

A pulsar is widely regarded as a rotating neutron star with a strong magnetosphere, which can accelerate electrons, which will induce an electromagnetic cascade through the emission of curvature radiation [43–46]. This leads to the production of high energy photons, which eventually induces $e{}^{+} e{}^{-}$ pair production. This process produces the same amount of high energy $e{}^{+}$ and $e{}^{-}$, which can escape from the magnetosphere and propagate to the earth. There is a cutoff energy of the photons produced in a pulsar, which leads to a cutoff in the positron fraction.

In this paper, DRAGON [47–51] is used as a numerical tool to model the propagation environment, to tune the related parameters and to estimate the $e{}^{\pm }$ background. The authors of [49–52] did a very complete work on three-dimensional cosmic-ray modeling. In the 3-D models, they pointed out that the spiral arms have an effect on the propagation parameters. A 2-D model is used in this paper because we focus on the lepton spectra implications. Due to the energy loss of the leptons, the effect of spiral arms on the high energy leptons is less important than that of the additional nearby sources contribution. ROOT is used to minimize $\chi {}^{2}$ to get the best fit results. We consider six nearby pulsars from the ATNF catalog [53, 54] as the possible extra single sources of the high energy positrons. We find only four, which are Geminga, J1741-2054, Monogem, and J0942-5552, that can survive from all considered physical requirements. We then discuss the possibility that these high energy $e{}^{\pm }$ are from multiple pulsars. The multiple pulsar contribution predicts a positron fraction with some structures at higher energies.

The paper is organized as follows. Section 2 shows the way how the $e{}^{\pm }$ background is estimated. In Sect. 3, the properties of pulsars are described and the profile of the $e{}^{\pm }$ fluxes produced by a pulsar is derived. The interpretation of the positron fraction with one single pulsar is discussed in Sect. 4 and the hypothesis as regards the multiple pulsar interpretation is tested in Sect. 5. The conclusions are drawn in Sect. 6. In Appendix A, the diffusion energy-loss equation for a burst-like source is solved in the spherically symmetric approximation.

2 Propagation parameters and $e^{\pm }$ background

The Galactic background of the lepton fluxes is considered as having three main components, which are primary electrons from CR sources, secondary electrons and positrons from the interactions between the CR, and the interstellar medium (ISM). The propagation of $e^{\pm }$ in the Galaxy obeys the Ginzburg and Syrovatskii equation [48, 55, 56]:

$$\begin{aligned}&\frac{\partial f_i}{\partial t}-\nabla \cdot [(D\nabla -\mathbf {v}_c)f_i] -\frac{\partial }{\partial p}p^2D_{pp}\frac{\partial }{\partial p}\frac{f_i}{p^2}\nonumber \\&\quad \quad +\frac{\partial }{\partial p}\left[ \left( \dot{p}-\frac{p}{3}\nabla \cdot \mathbf {v}_c\right) f_i\right] \nonumber \\&\quad =Q_i(\mathbf {x},t,p)+\sum _{j>i}c\beta n_{\mathrm {gas}}\sigma _{ji}f_j -c\beta n_{\mathrm {gas}}\sigma _{\mathrm {in}}f_i \end{aligned}$$

(1)

where $p\equiv |\mathbf {p}|$ is the particle momentum; $f_i(\mathbf {x},t,p)$ is the particle number density of a species i per unit momentum interval; $\mathbf {v}_c$ is the convection velocity, $\beta \equiv v/c$ is the ratio of the velocity to the speed of light; $\sigma _{\mathrm {in}}$ is the total inelastic cross section onto the ISM gas, whose density is $n_{\mathrm {gas}}$; $\sigma _{ji}$ is the production cross section of the species i by the fragmentation of the species j (with $j>i$); and $Q_i(\mathbf {x},t,p)$ is the source term of species i, which can be thought to be steady $Q_i=Q_i(\mathbf {x},p)$ for background CR particles.

The spatial diffusion coefficient D in the cylindrical coordinate system (r, z) may be parameterized as [48, 56, 57]

$$\begin{aligned} \left\{ \begin{array}{l} D(\rho ,r,z)= D(\rho ,r) e^{-|z|/z_t}\quad \text {or}\\ D(\rho ,r,z)=D(\rho ,r) (-L<z<L),\\ D(\rho ,r) = D_0f(r)\beta \left( \frac{\rho }{\rho _0}\right) ^\delta , \end{array} \right. \end{aligned}$$

(2)

where $\rho \equiv pc/(Ze)$ is defined as the particle magnetic rigidity, $z_t$ is the scale height of the diffusion coefficient, L is the halo size, and $\delta$ is the index of the power-law dependence of the diffusion coefficient on the rigidity. $D_0$ is the normalization of the diffusion coefficient at the reference rigidity $\rho _0=4$ GV. Previous DRAGON papers [49–51] tested a few models with the exponential profile, i.e., the left formula in (2), which is more physical than the constant one, i.e., the right one. The effect of choosing different profiles on the electron and positron background is small if the parameters are properly set. In this paper, the constant profile is used in order to compute the pulsar profile in an analytical way, i.e., Eq. (17) in Sect. 3. The function f(r) describes a possible radial dependence of D, and it can be taken to be unity for simplicity.

The diffusion coefficient in momentum space $D_{pp}$ is related to the spatial diffusion coefficient D by [14, 57–59]

$$\begin{aligned} D_{pp}D=\frac{4p^2v_A^2}{3\delta (4-\delta ^2)(4-\delta )w} \end{aligned}$$

(3)

where $v_A$ is the Alfvén velocity, and $\delta$ is the power-law index as given in (2). w is the ratio of the magnetohydrodynamic wave energy density to the magnetic field energy density, and it is usually taken to be 1.

DRAGON [47–49] is used to tune the propagation parameters according to the B/C ratio, which is sensitive to the parameters. The Markov chain Monte Carlo algorithm (MCMC, Ref. [60]) is used to determine $D_{0}$ and $\delta$. The priors are shown in Table 1. The posterior distributions are shown in a contour in the $D_{0}$ and $\delta$ plane in Fig. 1.

Table 1 The priors of $D_{0}$ and $\delta$

Fig. 1

Contour in the $D_{0}$ and $\delta$ plane. The cross shows the best fit value while the three closed curves from inside to outside show the 68.3, 95.4, and 99.7 % CL, respectively

The parameters with their 68 % CL uncertainties from the fit are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} D_{0}\big |_{\rho _{0} = 4~\mathrm {GV}} = ( 6.20 \pm 0.31 ) \times 10^{28}~ \mathrm {cm}^{2}\,\mathrm {s}^{-1},\\ \delta = 0.31 \pm 0.03,\\ L = 4 ~\mathrm {kpc},\\ v_{A} = 40~\mathrm {km}/\mathrm {s}, \end{array} \right. \end{aligned}$$

(4)

where the halo size L is taken from the MED model of [61], and the $v_{A}$ is fixed. These parameters are consistent with what the authors of Ref. [16] has got in the reacceleration propagation model.

To avoid the uncertainty of the solar modulation, the AMS-02 proton flux [62] above 45 GV is fitted to get the injection spectra using MCMC [60]. Three breaks, which are 6.7, 11, and 316 ($\pm$148) GV, are introduced in the injection spectrum of nuclei. The proton spectral indices below and above the breaks are 2.25, 2.35, 2.501 ($\pm$0.010) and 2.501–0.084 ($\pm$0.050), respectively. The high energy spectral indices of helium, carbon, and oxygen are shifted by $-$0.1 w.r.t. those of the proton according to the proton-to-helium ratio [4]. The Ferriere model [63] is used as the source distribution for the primary components, e.g. SNRs for SNe type II. To ensure that the propagation parameters are correct, we need to compare the model prediction with the boron-to-carbon ratio [5, 64–66] and the proton flux [62]. As shown in Fig. 2, the set of parameters used can reproduce the boron-to-carbon ratio and the proton flux well. According to this set of parameters, we can obtain the fluxes of the secondary positrons and electrons.

Fig. 2

a Model prediction of B/C ratio compared with measurements from PAMELA [5], ATIC02 [64], CREAM-I [65], and TRACER06 [66]. b Model prediction of proton flux compared with measurements from AMS-02 [62]. The solar modulation is taken as 500 MeV here. The red band in a shows the variation of the propagation parameters $D_{0}$ and $\delta$ within 95 % CL

A power-law spectrum with two breaks is introduced to parameterize the injection spectrum of the primary electrons as a function of rigidity,

$$\begin{aligned} Q(\rho )\propto {\left\{ \begin{array}{ll} \begin{array}{ll} (\rho /\rho _{\mathrm {br1}}^{e})^{-\gamma _{1}} &{}\quad (\rho <\rho _{\mathrm {br1}}^{e})\\ (\rho /\rho _{\mathrm {br1}}^{e})^{-\gamma _{2}} &{}\quad (\rho _{\mathrm {br1}}^{e}\le \rho \le \rho _{\mathrm {br2}}^{e})\\ (\rho _{\mathrm {br2}}^{e}/\rho _{\mathrm {br1}}^{e})^{-\gamma _{2}}\cdot (\rho /\rho _{\mathrm {br2}}^{e})^{-\gamma _{3}} &{}\quad (\rho >\rho _{\mathrm {br2}}^{e}). \end{array} \end{array}\right. } \end{aligned}$$

(5)

The parameters are adjusted according to the electron flux from AMS-02 [2]. The agreement between the model and the data is shown in Sect. 5. These spectral indices are $\gamma _{1}=1.95$, $\gamma _{2}=2.75$, and $\gamma _{3}=2.5$, respectively. The breaks are $\rho _{\mathrm {br1}}^{e}=8.6$ GV and $\rho _{\mathrm {br2}}^{e}=110$ GV. Since the high energy breaks of primary particles, such as protons and helium, are found by PAMELA [4] and recently confirmed by AMS-02 [62], it is reasonable to assume that there is also a high energy break in the primary electron flux. A more detailed discussion of the necessity of the high energy break $\rho _{\mathrm {br2}}^{e}$ can be found in [16, 67], where the high energy break hypotheses are in favor compared to the no-break ones. Reference [67] gave us an estimation by taking the primary electron flux as $\Phi _{e-}-\Phi _{e+}$ and could roughly determine the break.

3 e$^{\pm }$ from a single pulsar

The pulsars are potential sources which could produce primary e$^{\pm }$ at high energy [29–32, 38]. Electrons can be accelerated by the strong magnetosphere of the pulsars, and this acceleration produces photons. When those photons annihilate each other, they can produce e$^{\pm }$ pairs. Thus, the e$^{\pm }$ energies are related to the pulsar magnetosphere. Assuming the pulsar magnetosphere as a magnetic dipole, this magnetic dipole radiation energy is proportional to the spin-down luminosity. Due to this spin down (i.e. slowing of rotation), the rotational frequency of a pulsar $\Omega \equiv 2\pi /P$ (with P being the period) is a function of time as follows [29, 31, 38]:

$$\begin{aligned} \Omega (t)=\frac{\Omega _{0}}{\sqrt{1+t/\tau _{0}}}, \end{aligned}$$

(6)

where $\Omega _{0}$ is the initial spin frequency of the pulsar and $\tau _{0}$ is the time scale which describes the spin-down luminosity decays. $\tau _{0}$ cannot be directly obtained from pulsar timing observations, and it is assumed to be [31, 38]

$$\begin{aligned} \tau _{0}\simeq 10^{4}~\mathrm {year}. \end{aligned}$$

(7)

The rotational energy of the pulsar is $E(t)=(1/2)I\Omega ^{2}(t)$. Here I is the moment of inertia, which is related to the mass and the radius of the pulsar and can be regarded as a time independent value. The magnetic dipole radiation energy is equal to the energy-loss rate,

$$\begin{aligned} |\dot{E}(t)|=I\Omega (t)\dot{|\Omega }(t)| =\frac{I\Omega _{0}^{2}}{2}\frac{1}{\tau _{0}(1+t/\tau _{0})^{2}}. \end{aligned}$$

(8)

The total energy loss of a pulsar is [31, 32, 38]

$$\begin{aligned} E_{\mathrm {tot}}(t)\!=\!\int _0^t \mathrm{d}t'|\dot{E}(t')| \!=\!\frac{I\Omega _{0}^{2}}{2}\frac{t/\tau _{0}}{1+t/\tau _{0}} \!=\!|\dot{E}(t)|t\left( 1\!+\!\frac{t}{\tau _{0}}\right) . \end{aligned}$$

(9)

The total energy injection of $e^{\pm }$ out of a pulsar should be proportional to the total energy loss,

$$\begin{aligned} E_{\mathrm {out}}(t)=\eta E_{\mathrm {tot}}(t)=\eta |\dot{E}(t)|t\left( 1+\frac{t}{\tau _{0}}\right) \end{aligned}$$

(10)

where $\eta$ is the efficiency of the injected $e^{\pm }$ energy converted from the magnetic dipole radiation energy.

The pulsar characteristic age is defined as [54]

$$\begin{aligned} T\equiv \frac{P}{2\dot{P}}=\frac{\Omega }{2|\dot{\Omega }|}=t+\tau _0. \end{aligned}$$

(11)

For a mature pulsar with $t\gg \tau _0$, we have $T\simeq t$. Under this condition, Eqs. (8)–(10) become

$$\begin{aligned}&|\dot{E}(T)|\simeq \frac{I\Omega _{0}^{2}}{2}\frac{\tau _0}{T^2},\end{aligned}$$

(12)

$$\begin{aligned}&E_{\mathrm {tot}}(T)\simeq |\dot{E}(T)|\frac{T^2}{\tau _0},\end{aligned}$$

(13)

$$\begin{aligned}&E_{\mathrm {out}}(T)\simeq \eta |\dot{E}(T)|\frac{T^2}{\tau _0}. \end{aligned}$$

(14)

The propagation equation for the $e^{\pm }$ can be described as [29, 38]

$$\begin{aligned} \frac{\partial f}{\partial t}=D(E)\nabla ^2f+\frac{\partial }{\partial E}[b(E)f]+Q(\mathbf {x},t,E), \end{aligned}$$

(15)

where $f(\mathbf {x},t,E)$ is the number density per unit energy interval of $e^{\pm }$; $D(E)=(v/c)D_{0}(E/4~\mathrm {GeV})^{\delta }$ is the diffusion coefficient with the velocity v of the particle, the speed c of light, $D_{0}$ and $\delta$ the same as the parameters used to calculate the background in Sect. 2; and $b(E)\equiv -\mathrm{d}E/\mathrm{d}t=b_0E^{2}$ with $b_{0}=1.4\times 10^{-16}~\mathrm {GeV}^{-1}\,\mathrm {s}^{-1}$ is the rate of energy loss due to inverse Compton scattering and synchrotron radiation [6, 31, 38].

The source term $Q(\mathbf {x},t,E)$ of a pulsar can be described by a burst-like source with a power-law energy spectrum and an exponential cutoff,

$$\begin{aligned} Q(\mathbf {x},t,E)=Q_0E^{-\alpha }\exp \left( -\frac{E}{E_{\mathrm {cut}}}\right) \delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0), \end{aligned}$$

(16)

where $Q_{0}$ is the normalization factor related to the total injected energy $E_{\mathrm {out}}$, $\alpha$ is the spectral index, and $E_{\mathrm {cut}}$ is the cutoff energy.

Fig. 3

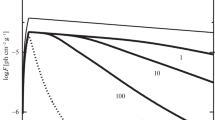
$r_{\mathrm {dif}}$ as a function of $t_{\mathrm {dif}}$ and E, which is from Eq. (18). The lepton energy E is the $e{}^{+}$ (or $e^{-}$) energy detected at a location away from the pulsar with the diffusion distance $r_{\mathrm {dif}}$. $r_{\mathrm {dif}}$ increases with E

In Appendix A, we briefly review how to solve Eq. (15) with the source (16). The method is equivalent to results of much previous work (for example, see Refs. [26, 38]). Using the results, i.e. Eqs. (56) and (60), in Appendix A, we obtain the electron or positron flux observed at the earth as follows:

$$\begin{aligned} \Phi _{e}(r,t_{\mathrm {dif}},E)= & {} \frac{c}{4\pi }f=\frac{c}{4\pi }\frac{Q_0E^{-\alpha }}{\pi ^{\frac{3}{2}}r_{\mathrm {dif}}^3}\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{\alpha -2}\nonumber \\&\times \exp \left[ -\frac{E/E_{\mathrm {cut}}}{(1-E/E_{\mathrm {max}})} -\frac{d^2}{r_{\mathrm {dif}}^2}\right] , \end{aligned}$$

(17)

where d is the distance between the earth and the source, the diffusion distance $r_{\mathrm {dif}}$ is given by

$$\begin{aligned} r_{\mathrm {dif}}(t_{\mathrm {dif}},E)= 2\sqrt{\frac{D(E)t_{\mathrm {dif}}}{(1-\delta )} \frac{E_{\mathrm {max}}}{E} \left[ 1-\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{1-\delta }\right] }, \end{aligned}$$

(18)

and the diffusion time $t_{\mathrm {dif}}$ is the time a charged particle travels in the ISM before it reaches the earth. The electrons and positrons may be trapped in the pulsar wind nebula (PWN) for some time before they escape. The age of a pulsar is $T = t_{\mathrm {escape}} + t_{\mathrm {dif}}$, where $t_{\mathrm {escape}}$ is the time before the leptons escape from the PWN. In some cases, $t_{\mathrm {escape}}$ and $t_{\mathrm {dif}}$ can be of the same order of magnitude, and then the discussion will be complicated. In some other case, $t_{\mathrm {escape}}$ could be negligible. For instance, when the SNR is evolving into the “Sedov–Taylor” phase, the leptons in it are trapped (see Ref. [68] and the references therein). In that case, the time $t_{\mathrm {escape}}$, during which the SNR reverse shock collides with the PWN forward shock, is typically a few $10^{3}$ year [68], which is small compared with the ages of the pulsars we studied here, which are around $10^{5}$ year. In this work, we consider the latter case and neglect $t_{\mathrm {escape}}$ for simplicity. We leave the case of large $t_{\mathrm {escape}}$ to a further specific study. Thus, we assume that $t_{\mathrm {dif}}\simeq T$. The maximum energy $E_{\mathrm {max}}$ is defined as

$$\begin{aligned} E_{\mathrm {max}}=1/(b_{0}T). \end{aligned}$$

(19)

Table 2 Parameters of six nearby single pulsars from the best fit results. The $\chi ^{2}/ndf$ from the fits of Geminga, J1741-2054, Monogem, J0942-5552, and J1001-5507 are smaller than 1, which show good agreement between those single pulsar models and the experiment

The positron fraction from AMS-02 implies a primary positron source with a cutoff energy $1/E_{s} = 1.84 \pm 0.58\,\mathrm{TeV}^{-1}$ in their “minimal” model [1], which corresponds to $E_{s} \in \left[ 490,790\right]$. Due to the limitation of the statistics of the high energy $e^-$ and $e^+$ measured by AMS-02, the upper bound 790 GeV is not a strict limit. Thus, we consider a primary $e^+$ and $e^-$ source contribution with a cutoff energy $E_{\mathrm {cutoff}}\simeq$ (500–5000) GeV, which corresponds to a pulsar with an age $T\simeq (0.45{-}4.5)\times 10^{5}$ year according to (19). The term $\exp \left[ -\frac{d^2}{r_{\mathrm {dif}}^2}\right]$ in (17) tells us that a pulsar with $d>r_{\mathrm {dif}}$ requires a larger normalization $Q_0$, which hints at a larger $E_{\mathrm {out}}$, a larger $\eta$ in (10), or both. $r_{\mathrm {dif}}>d$ is required in our study, whose physical interpretation is that the distance a particle travels in the ISM should be larger than the distance between the earth and the source. Equation (18) tells us that $r_{\mathrm {dif}}$ is a function of the diffusion time $t_{\mathrm {dif}}$ and the lepton energy E, as is shown by Fig. 3 where the color scale indicates $r_{\mathrm {dif}}$. For $T\simeq (0.45\sim 4.5)\times 10^{5}$ year and the lepton energy $E=1000$ GeV, $r_{\mathrm {dif}}$ is always greater than 0.5 kpc. Selecting pulsars with $d<0.5$ kpc and $T\simeq (0.45\sim 4.5)\times 10^{5}$ year, the high energy leptons they produced can reach the earth.

Thus, the pulsars with ages $T\simeq (0.45\sim 4.5)\times 10^{5}$ year and distance $d<0.5$ kpc can explain the behavior of the positron fraction of AMS-02 at a high energy range.

4 Single pulsar interpretation

A few simple examples using a single pulsar are given to explain the high energy positron fraction of AMS-02 [1]. The background electrons and positrons are described in Sect. 2. The primary electron flux is scaled by a normalization factor $A{}_{\mathrm{prim},e^{-}}$ since it is not possible to constrain the electron flux contribution from SNRs. The age T and the distance d are taken from the ATNF catalog and the positron fraction is fitted to obtain the free parameters in (17), the spectral index $\alpha$, and the normalization $Q_0$. $Q_0$ is fixed by the relation [23, 32, 37] $E_{\mathrm {out}}=\int _{E_{\mathrm {min}}}^{E_{\mathrm {max}}} dEEQ(E)\simeq \int _0^\infty dEEQ(E)$, which approximately yields $Q_{0}\simeq E_{\mathrm {out}}$ for $\alpha \simeq 2$. The cutoff energy $E_{\mathrm {cut}}$ is set to be 5000 GeV, which is large enough, as it does not change the shape of the pulsar contribution. Since we are interested in the positron excess at high energies, the fit is started from 10 GeV where the effect of solar modulation is negligible.

Six nearby single pulsars, whose ages $T\simeq (0.45$–$4.5)\times 10^{5}$ year and distance $d<0.5$ kpc, are used to fit the positron fraction. The Minuit package in ROOT is used to determine the parameters to minimize $\chi ^{2}$. The best results of the single pulsars are listed in Table 2.

The results are also shown in Fig. 4.

Fig. 4

A single pulsar model can explain the positron fraction very well. According to the fitting result, the spectral indices are almost the same

Table 3 Electron injection efficiency $\eta$ of the six nearby pulsars. For a single pulsar interpretation of the positron fraction, the results of Geminga, J1741-2054, Monogem, and J0942-5552 are thought to be reasonable while the possibilities of J1001-5507 and J1825-0935 as the high energy positron sources can be excluded

Using the parameters of the best fit results, the positron fraction can be well reproduced by these single pulsar’s contributions. Table 2 tells us that the normalizations $A{}_{\mathrm{prim},e^{-}}$ are around 0.5 and the spectral indices $\alpha$ of different pulsars are around 2.

We can estimate the injection efficiency $\eta$ from the pulsar. Taking Geminga as an example, the spin-down energy-loss rate of Geminga $|\dot{E}(T)|=3.2\times 10^{34}~\mathrm {erg}/\mathrm {s}$. The total radiation energy of the magnetic dipole can be derived from Eq. (13) as $E_{\mathrm {tot}}(T)\simeq |\dot{E}(T)|T^2/\tau _0=1.2\times 10^{49}~\mathrm {erg}$. From the fit, we get the injection energy $E_{\mathrm {out}}/2=10{}^{50.5}~\mathrm {GeV}\simeq 5.19\times 10^{47}$ erg. From (14), we get $\eta \sim 8.7\,\%$. This efficiency is consistent with the previous studies by [29, 38]. We can perform similar studies on the other five pulsars, whose results are listed in Table 3.

A smaller $\eta$ means it is easier for this pulsar to produce the same amount of positrons and electrons. The efficiency required by J1001-5507 or J1825-0935 is too large to satisfy the physics condition for a single pulsar interpretation. Geminga, J1741-2054, Monogem, and J0942-5552 are the only candidates which survive from our selection so far.¹

Fig. 5

A three pulsars fit to the positron fraction is presented here as an example of a multiple pulsar fit, as shown in a. Using the same parameters, b shows the fitted parameters from the positron fraction reproduce the electron flux when the solar modulation potential 550 MV is applied here. The error band in a shows the variation of the propagation parameters within 95 % CL, while that in b shows the combined effect of the propagation parameters and the variation of the solar modulation potential from 400 to 800 MeV

5 Multiple pulsars interpretation

The extra high energy positrons may come from several pulsars. We perform a similar study for multiple pulsars as we do for a single pulsar. Benefiting from the study in Sect. 4, we can assume that the spectral indices $\alpha$ of all the pulsars are the same. Considering the physical models of the pulsars to be similar, we make another assumption: that the electron injection efficiencies $\eta$ are the same. These two assumptions help us reduce the number of free parameters. The discussion of $\eta$ from a single pulsar in Sect. 4 tells us that Geminga, J1741-2054, and Monogem will give a much larger contribution to the high energy positron than J0942-5552. In other words, the $\eta$ of J0942-5552 in Table 3 is much larger than that of Geminga, which implies that the contribution from J0942-5552 in the multiple pulsar interpretation can be negligible compared with that from Geminga.

We choose three from the four “surviving” pulsars in the multiple pulsars discussion. The input parameters are the age T, the distance d, and the energy-loss rate $\dot{E}$ of each pulsar, while the parameters we get from the fit is the normalization factor of primary electron $A_{\mathrm{prim},e^{-}}$, the spectral index $\alpha$, and the electron injection efficiency $\eta$. As shown in Fig. 5a, we obtain a good result from the multiple pulsar fit where $\chi {}^{2}/ndf=26.9/40$. The parameters we get are $A{}_{\mathrm{prim},e^{-}}=0.50$, $\alpha =2.07$, and $\eta =2.58\,\%$.

The multiple pulsar interpretation predicts a positron fraction with a decrease up to 600 GeV and after that a bump up to 2000 GeV, which is possible to observe with more accumulating AMS-02 data.

Using the parameters from the fit, we can reproduce the electron flux measured by AMS-02 [2] in Fig. 5b. It shows that our electron background estimation in Sect. 2 $+$ pulsar contribution matches the experimental data especially at high energies. Figure 5 also shows that the effect of the uncertainty due to the propagation model is small at high energy. The solar modulation potential is taken as 550 MV in the best fit result. The solar modulation potential is varied between 400 and 800 MV, showing that its effect on low energy is quite large. To reproduce the low energy electron flux more accurately, we need monthly low energy electron fluxes, which may be published by AMS collaboration to model the solar modulation.

6 Discussion and conclusion

In this work, we investigate the possibility that the rise of the positron fraction measured by AMS-02 can be explained by pulsars. The propagation parameters and the injection spectra of nuclei and electrons are tuned according to the boron-to-carbon ratio and the proton flux. It will be better to tune those parameters with boron-to-carbon ratio and proton flux measured by AMS-02, since they are in the same data taking period as the lepton fluxes. We find that both the single pulsar model and the multiple pulsar model can explain the AMS-02 data very well. Six nearby pulsars are investigated as the single pulsar sources of the high energy positrons and finally four survive from all the conditions. The $\chi {}^{2}$s of these single pulsars in this work are much smaller that those in [17], mainly because we set the cutoff energy equal to 5000 GeV, while the authors of [17] set it to 1000 GeV. With three mostly contributing pulsars, the multiple pulsar model predicts a positron fraction with a decrease up to 600 GeV and a bump up to 2000 GeV. For the low energy, a simple solar modulation potential cannot explain the measurement well. Thus, we need the monthly electron fluxes which can describe solar activity during the whole period.

It is shown that the positron excess measured by AMS-02 can be explained by the pulsar scenario. Since the multiple pulsars can explain the experimental data well, it will be difficult to exclude the pulsar scenario by isotropy. With accumulating AMS-02 data and future experiments, we can see the positron fraction behavior up to higher energy, which will either confirm or reject the multiple pulsars scenario. If we consider other scenarios, such as dark matter, we have to look into other productions, antiproton production for instance, which have no contribution from pulsars.

Solving the diffusion energy-loss equation

To fix the notation and for pedagogical purposes, in this appendix we give a brief review on solving the diffusion energy-loss equation [26, 31, 34, 35, 38]. The diffusion energy-loss equation is given by

$$\begin{aligned} \left[ \frac{\partial }{\partial t}-D(E)\nabla ^2-\frac{\partial }{\partial E}b(E)\right] f(\mathbf {x},t,E) =Q(\mathbf {x},t,E) \nonumber \\ \end{aligned}$$

(20)

where $f(\mathbf {x},t,E)$ is the particle number density per unit energy interval, $D(E)>0$ is the diffusion coefficient, $b(E)\equiv -\mathrm{d}E/\mathrm{d}t>0$ is the energy-loss rate, and $Q(\mathbf {x},t,E)$ is the source term.

1.1 Green function for the diffusion energy-loss equation

The Green function $G(\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0)$ of (20) is defined as

$$\begin{aligned}&\left[ \frac{\partial }{\partial t}-D(E)\nabla ^2-\frac{\partial }{\partial E}b(E)\right] G(\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0)\nonumber \\&\quad =\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0)\delta (E-E_0). \end{aligned}$$

(21)

The solution of (21) has been given in Ref. [69]. To fix the notation, let us briefly review the derivation. Define

$$\begin{aligned} \phi (\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0)\equiv b(E)G(\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0). \end{aligned}$$

(22)

Substituting $G=\phi /b$ into (21) gives

$$\begin{aligned}&\left[ \frac{\partial }{\partial t}-b(E)\frac{\partial }{\partial E}-D(E)\nabla ^2\right] \phi (\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0)\nonumber \\&\quad =b(E)\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0)\delta (E-E_0). \end{aligned}$$

(23)

Let us make the variable transformation $(t,~E)\rightarrow (t',~\lambda )$ as follows:

$$\begin{aligned}&t'\equiv t-\tau (E,E_0),\quad \text {with}\quad \tau (E,E_0)\equiv \int _E^{E_0}\frac{\mathrm{d}\tilde{E}}{b(\tilde{E})}\end{aligned}$$

(24)

$$\begin{aligned}&\lambda (E,E_0) \equiv \int _E^{E_0}\mathrm{d}\tilde{E}\frac{D(\tilde{E})}{b(\tilde{E})}. \end{aligned}$$

(25)

The Jacobian matrix of this transformation is easily obtained:

$$\begin{aligned} \frac{\partial (t',~\lambda )}{\partial (t,~E)}\equiv \begin{pmatrix} \frac{\partial t'}{\partial t} &{} \frac{\partial t'}{\partial E}\\ \frac{\partial \lambda }{\partial t} &{} \frac{\partial \lambda }{\partial E} \end{pmatrix} =\begin{pmatrix} 1 &{} \frac{1}{b(E)}\\ 0 &{} -\frac{D(E)}{b(E)} \end{pmatrix} , \end{aligned}$$

(26)

whose inverse is

$$\begin{aligned} \frac{\partial (t,~E)}{\partial (t',~\lambda )}\equiv \begin{pmatrix} \frac{\partial t}{\partial t'} &{} \frac{\partial t}{\partial \lambda }\\ \frac{\partial E}{\partial t'} &{} \frac{\partial E}{\partial \lambda } \end{pmatrix} =\begin{pmatrix} 1 &{} \frac{1}{D(E)}\\ 0 &{} -\frac{b(E)}{D(E)} \end{pmatrix}. \end{aligned}$$

(27)

Thus,

$$\begin{aligned} \frac{\partial }{\partial \lambda }= \frac{\partial t}{\partial \lambda }\frac{\partial }{\partial t} +\frac{\partial E}{\partial \lambda }\frac{\partial }{\partial E} =\frac{1}{D(E)}\left[ \frac{\partial }{\partial t}-b(E)\frac{\partial }{\partial E}\right] . \end{aligned}$$

(28)

Substituting the relation $\partial _t-b(E)\partial _E=D(E)\partial _\lambda$ into (23) implies

$$\begin{aligned} \left( \frac{\partial }{\partial \lambda }-\nabla ^2\right) \phi= & {} \frac{b(E)}{D(E)}\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0)\delta (E-E_0)\nonumber \\= & {} \frac{b(E_0)}{D(E_0)}\delta ^3(\mathbf {x}\!-\!\mathbf {x}_0)\delta (t\!-\!t_0)\delta (E\!-\!E_0). \nonumber \\ \end{aligned}$$

(29)

It follows from Eq. (26) that

$$\begin{aligned} \det \left[ \frac{\partial (t',~\lambda )}{\partial (t,~E)}\right] =-\frac{D(E)}{b(E)}, \end{aligned}$$

(30)

which implies

$$\begin{aligned} \delta (t-t_0)\delta (E-E_0)= & {} \left| \frac{D(E_0)}{b(E_0)}\right| \delta (t'-t_0)\delta (\lambda )\nonumber \\= & {} \frac{D(E_0)}{b(E_0)}\delta (t'-t_0)\delta (\lambda ) \end{aligned}$$

(31)

where in the second equality we have used the properties $D(E_0)>0$ and $b(E_0)>0$. Substituting (31) into (29), we obtain

$$\begin{aligned} \left( \frac{\partial }{\partial \lambda }-\nabla ^2\right) \phi =\delta (t'-t_0)\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (\lambda ). \end{aligned}$$

(32)

As is well known, the Green function, which can be written as $G(\mathbf {x}-\mathbf {x}_0,\lambda )$ in the spherically asymmetric approximation, of the diffusion equation satisfies

$$\begin{aligned} \left( \frac{\partial }{\partial \lambda }-\nabla ^2\right) G(\mathbf {x}-\mathbf {x}_0,\lambda ) =\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (\lambda ) \end{aligned}$$

(33)

with $\lambda \ge 0$. The solution of (33) is

$$\begin{aligned} G(\mathbf {x}-\mathbf {x}_0,\lambda ) =\frac{1}{(4\pi \lambda )^{3/2}}\exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda }\right] . \end{aligned}$$

(34)

Comparing (32) with (33), we can read off the solution of $\phi$ as follows:

$$\begin{aligned} \phi= & {} \delta (t'-t_0) \frac{1}{(4\pi \lambda )^{3/2}}\exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda } \right] \nonumber \\= & {} \delta [t-t_0-\tau (E,E_0)] \frac{1}{(4\pi \lambda )^{3/2}}\exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda } \right] \nonumber \\ \end{aligned}$$

(35)

where in the second equality we have used (24). Thus, we finally get the solution of (21) as follows:

$$\begin{aligned}&G(\mathbf {x},t,E;\mathbf {x}_0,t_0,E_0)\nonumber \\&\quad =\frac{\phi }{b(E)}= \frac{\delta [t-t_0-\tau (E,E_0)]}{b(E)[4\pi \lambda (E,E_0)]^{3/2}} \exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda (E,E_0)} \right] \nonumber \\ \end{aligned}$$

(36)

where the functions $\tau (E,E_0)$ and $\lambda (E,E_0)$ are defined in Eqs. (24) and (25), respectively.

1.2 Solution for a burst-like source

Once we know the Green function, Eq. (36), we can write down the solution of Eq. (20) for a generic source as follows:

$$\begin{aligned} f(\mathbf {x},t,E)= & {} \int \mathrm{d}^3\mathbf {x'}\mathrm{d}t'\mathrm{d}E'G(\mathbf {x},t,E;\mathbf {x'},t',E')\nonumber \\&Q(\mathbf {x'},t',E'). \end{aligned}$$

(37)

In particular, for a burst-like source, the source function is proportional to $\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0)$, that is,

$$\begin{aligned} Q(\mathbf {x},t,E)=Q(E)\delta ^3(\mathbf {x}-\mathbf {x}_0)\delta (t-t_0) \end{aligned}$$

(38)

where Q(E) is an arbitrary function of E, $\mathbf {x}_0$ is the position of the source, and $t_0$ is the instantaneous time when the source bursts. Substituting Eqs. (36) and (38) into Eq. (37), we obtain

$$\begin{aligned}&f(\mathbf {x},t,E)\nonumber \\&\quad =\int \mathrm{d}^3\mathbf {x'}\mathrm{d}t'\mathrm{d}E' \frac{\delta [t-t'-\tau (E,E')]}{b(E)[4\pi \lambda (E,E')]^{3/2}}\nonumber \\&\quad \quad \times \exp \left[ -\frac{(\mathbf {x}-\mathbf {x'})^2}{4\lambda (E,E')} \right] Q(E')\delta ^3(\mathbf {x'}-\mathbf {x}_0)\delta (t'-t_0)\nonumber \\&\quad =\int \mathrm{d}E'\frac{\delta [t-t_0-\tau (E,E')]}{b(E)[4\pi \lambda (E,E')]^{3/2}} \exp \nonumber \\&\qquad \times \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda (E,E')} \right] . Q(E') \end{aligned}$$

(39)

Denote the solution of the equation

$$\begin{aligned} 0=t-t_0-\tau (E,E')=t-t_0-\int _E^{E'}\frac{\mathrm{d}\tilde{E}}{b(\tilde{E})}, \end{aligned}$$

(40)

$E'=E_0$, then we have

$$\begin{aligned} \delta [t-t_0-\tau (E,E')]=b(E_0)\delta (E'-E_0) \end{aligned}$$

(41)

where we have used

$$\begin{aligned} \left| \frac{\mathrm{d}\tau }{\mathrm{d}E'}\right| _{E'=E_0}\delta [t-t_0-\tau (E,E')]=\delta (E'-E_0). \end{aligned}$$

(42)

Substituting Eq. (41) into Eq. (39), we have

$$\begin{aligned} f(\mathbf {x},t,E)= & {} \int \mathrm{d}E'\frac{b(E_0)\delta (E'-E_0)}{b(E)[4\pi \lambda (E,E')]^{3/2}}\nonumber \\&\times \exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda (E,E')} \right] Q(E')\nonumber \\= & {} \frac{Q(E_0)}{[4\pi \lambda (E,E_0)]^{3/2}}\frac{b(E_0)}{b(E)} \exp \left[ -\frac{(\mathbf {x}-\mathbf {x}_0)^2}{4\lambda (E,E_0)} \right] \nonumber \\ \end{aligned}$$

(43)

where the initial energy $E_0$ is defined as the solution of Eq. (40). In other words, if we know $t-t_0$ and E, we can find $E_0$ by solving the equation

$$\begin{aligned} t-t_0=\tau (E,E_0)=\int _E^{E_0}\frac{\mathrm{d}\tilde{E}}{b(\tilde{E})}. \end{aligned}$$

(44)

Define the diffusion distance $r_{\mathrm {dif}}$ as

$$\begin{aligned} r_{\mathrm {dif}}(E,E_0)\equiv \sqrt{4\lambda (E,E_0)} =2\sqrt{\int _E^{E_0}\mathrm{d}\tilde{E}\frac{D(\tilde{E})}{b(\tilde{E})}} \end{aligned}$$

(45)

we can rewrite Eq. (43) as

$$\begin{aligned} f(\mathbf {x},t,E)=\frac{Q(E_0)}{\pi ^{\frac{3}{2}}r_{\mathrm {dif}}^3} \frac{b(E_0)}{b(E)}\exp \left( -\frac{r^2}{r_{\mathrm {dif}}^2}\right) \end{aligned}$$

(46)

with $r^2\equiv (\mathbf {x}-\mathbf {x}_0)^2$.

1.3 Solution for a burst-like source with power-law spectrum

Consider the case when the function Q(E) in Eq. (38) is a power-law function, that is,

$$\begin{aligned} Q(E)=Q_0E^{-\alpha }\exp \left( -\frac{E}{E_{\mathrm {cut}}}\right) \end{aligned}$$

(47)

where $Q_0$ is a normalization constant, $\alpha$ is the spectral index, and $E_{\mathrm {cut}}$ is the cutoff energy. The diffusion coefficient D(E) and the energy-loss rate b(E) are assumed to take the form

$$\begin{aligned} D(E)= & {} \beta D_0\left( \frac{E}{E_0}\right) ^\delta , \end{aligned}$$

(48)

$$\begin{aligned} b(E)= & {} b_0E^2 , \end{aligned}$$

(49)

where $\beta \equiv v/c$ is the ratio of the velocity to the speed of light, the constant $D_0$ and the index $\delta$ can be figured out by the background fitting in Sect. 2, the constant $b_0$ is given in Sect. 3, and $E_0$ should be determined by Eq. (44).

Let us calculate the initial energy $E_0$ first. Denote the diffusion time $t_{\mathrm {dif}}\equiv t-t_0$. It follows from Eqs. (44) and (49) that

$$\begin{aligned} t_{\mathrm {dif}}=\int _E^{E_0}\frac{\mathrm{d}\tilde{E}}{b_0\tilde{E}^2} =\frac{1}{b_0}\left( \frac{1}{E}-\frac{1}{E_0}\right) , \end{aligned}$$

(50)

which implies

$$\begin{aligned} \frac{1}{E}-\frac{1}{E_0}=b_0t_{\mathrm {dif}}, \end{aligned}$$

(51)

from which we see $\frac{1}{E}>b_0t_{\mathrm {dif}}$, that is, $E<\frac{1}{b_0t_{\mathrm {dif}}}$. Denote $E_{\mathrm {max}}\equiv 1/(b_0t_{\mathrm {dif}})$, then

$$\begin{aligned} \frac{1}{E}-\frac{1}{E_0}=\frac{1}{E_{\mathrm {max}}}, \end{aligned}$$

(52)

which gives

$$\begin{aligned} E_0=\frac{EE_{\mathrm {max}}}{E_{\mathrm {max}}-E}. \end{aligned}$$

(53)

Thus, we obtain the following pieces in Eq. (46):

$$\begin{aligned} Q(E_0)= & {} Q_0E_0^{-\alpha }\exp \left( -\frac{E_0}{E_{\mathrm {cut}}}\right) \nonumber \\= & {} Q_0\left( \frac{EE_{\mathrm {max}}}{E_{\mathrm {max}}-E}\right) ^{-\alpha } \exp \left( -\frac{EE_{\mathrm {max}}}{E_{\mathrm {cut}}(E_{\mathrm {max}}-E)}\right) \nonumber \\= & {} Q_0E^{-\alpha }\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^\alpha \exp \left[ -\frac{E/E_{\mathrm {cut}}}{(1-E/E_{\mathrm {max}})}\right] ,\nonumber \\ \end{aligned}$$

(54)

$$\begin{aligned} \frac{b(E_0)}{b(E)}=\frac{E_0^2}{E^2}=\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{-2}. \end{aligned}$$

(55)

Substituting Eqs. (54) and (55) into Eq. (46), we obtain

$$\begin{aligned} f(\mathbf {x},t,E)= & {} \frac{Q_0E^{-\alpha }}{\pi ^{\frac{3}{2}}r_{\mathrm {dif}}^3} \left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{\alpha -2}\nonumber \\&\times \exp \left[ -\frac{E/E_{\mathrm {cut}}}{(1-E/E_{\mathrm {max}})} -\frac{r^2}{r_{\mathrm {dif}}^2}\right] , \end{aligned}$$

(56)

which is consistent with previous work (for example, Eq. (6) of Ref. [38]).

Now let us figure out the diffusion distance $r_{\mathrm {dif}}$. To this end, we substitute Eqs. (48) and (49) into Eq. (25) and get

$$\begin{aligned} \lambda (E,E_0)= & {} \int _E^{E_0}\mathrm{d}\tilde{E}\frac{\beta D_0\left( \frac{\tilde{E}}{E_0}\right) ^\delta }{b_0\tilde{E}^2} =\frac{\beta D_0}{E_0^\delta b_0}\int _E^{E_0}\mathrm{d}\tilde{E}\tilde{E}^{\delta -2}\nonumber \\= & {} \frac{\beta D_0}{E_0^\delta b_0(\delta -1)} (E_0^{\delta -1}-E^{\delta -1}), \end{aligned}$$

(57)

which can also be written as

$$\begin{aligned} \lambda (E,E_0)\!=\!\beta D_0\left( \frac{E}{E_0}\right) ^\delta \frac{t_{\mathrm {dif}}}{b_0t_{\mathrm {dif}}(\delta \!-\!1)} \frac{1}{E}\left[ \left( \frac{E_0}{E}\right) ^{\delta \!-\!1}\!-\!1\right] .\nonumber \\ \end{aligned}$$

(58)

Comparing the above equation with Eq. (48), $E_{\mathrm {max}}\equiv 1/(b_0t_{\mathrm {dif}})$, and $E_0/E=(1-E/E_{\mathrm {max}})^{-1}$, we obtain

$$\begin{aligned} \lambda (E,E_0)=\frac{D(E)t_{\mathrm {dif}}}{(1-\delta )} \frac{E_{\mathrm {max}}}{E} \left[ 1-\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{1-\delta }\right] . \end{aligned}$$

(59)

Thus, the diffusion distance $r_{\mathrm {dif}}$ is given by

$$\begin{aligned} r_{\mathrm {dif}}\equiv & {} 2\sqrt{\lambda (E,E_0)}\nonumber \\= & {} 2\sqrt{\frac{D(E)t_{\mathrm {dif}}}{(1-\delta )} \frac{E_{\mathrm {max}}}{E} \left[ 1-\left( 1-\frac{E}{E_{\mathrm {max}}}\right) ^{1-\delta }\right] }, \end{aligned}$$

(60)

which is consistent with previous work (for example, Eq. (10) of Ref. [29] and Eq. (7) of Ref. [38]).