CGC/saturation approach for soft interactions at high energy: survival probability of central exclusive production

Abstract

We estimate the value of the survival probability for central exclusive production in a model which is based on the CGC/saturation approach. Hard and soft processes are described in the same framework. At LHC energies, we obtain a small value for the survival probability. The source of the small value is the impact parameter dependence of the hard amplitude. Our model has successfully described a large body of soft data: elastic, inelastic and diffractive cross sections, inclusive production and rapidity correlations, as well as the t-dependence of deep inelastic diffractive production of vector mesons.

1 Introduction

The large body of experimental data [1–14] on high energy soft interactions from the LHC, calls for an approach based on QCD that allows us to comprehend this data. However, due to the embryonic stage of our understanding of the confinement of quarks and gluons, we are doomed to have to introduce phenomenological model assumptions beyond that of QCD. In our recent articles [15–18] we have proposed an approach, based on the CGC/saturation effective theory of high energy interactions in QCD (see Refs. [19–38] for a review) and the Good–Walker [39] approximation for the structure of hadrons. In the next section we give a brief review of our model, however, we would like to mention here that the main ingredient of this model, is the BFKL Pomeron [40–43], which describes both hard and soft processes at high energies. In other words, in our approach, we do not separate the interactions into hard and soft, both are described in the framework of the same scheme. The second important remark concerns the description of the experimental data: we obtain a good description of the cross sections of elastic and diffractive cross sections, of inclusive productions and the rapidity correlations at high energies. Consequently, we feel that we are ready to test our model on a complicated phenomenon, the survival probability of central diffractive production.¹

Fig. 1

a Scattering amplitude of the hard process. b Description of the set of the eikonal diagrams in the BFKL Pomeron calculus, which suppress the di-jet quark production, due to the contamination of the LRG (large raridity gap) by gluons, which can be produced by different parton showers, as shown in c

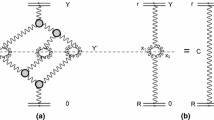
The physical meaning of “survival probability” has been clarified in the first papers on this subject (see Refs. [44–46]), and is illustrated by Fig. 1, using the example of the central production of a di-jet with large transverse momenta. At first sight we have to calculate the diagram of Fig. 1a in perturbative QCD, in which only two protons and the di-jet are produced, without any other hadrons. However, this is not sufficient, since simultaneously a number of parton showers can be produced, and gluons (quarks) from these showers will produce additional hadrons. To calculate central diffractive production, we have to exclude these processes. In other words, we multiply the cross section given by the diagram of Fig. 1a by the suppression factor, which reflects the probability of not having any additional parton showers. This factor is the “survival probability”.

Even this brief description indicates that we have a complex problem, since some of the produced parton showers can have perturbative QCD structures, while others can stem from the long distances, and can be non-perturbative by nature. Therefore, to attack this problem we need a model that describes both long and short distances.

As we have mentioned above, our model fulfills these requirements, and so we will proceed to discuss survival probability in this model, expecting reliable results.

The next section is a brief review of our approach. We include it in the paper, for the completeness of presentation, and to emphasise that both short and long distance phenomena are described in the same framework. Section 3 is devoted to a derivation of the formulae for the survival probability using the BFKL Pomeron calculus. The numerical estimates are given in Sect. 4, while in Sect. 5, we summarise our results.

Fig. 2

a Set of the diagrams in the BFKL Pomeron calculus that produce the resulting (dressed) Green function of the Pomeron in the framework of high energy QCD. b The net diagrams which include the interaction of the BFKL Pomerons with colliding hadrons are shown. After integration over positions of $G_{3 {I\!\!P}}$ in rapidity, the sum of the diagrams reduces to c

2 Our model: generalities and the elastic amplitude

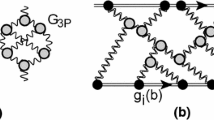
In this section we briefly review our model which successfully describes diffractive [15, 16] and inclusive cross sections [17]. The main ingredient of our model is the BFKL Pomeron Green function, which we obtained using a CGC/saturation approach [15, 51]. We determined this function from the solution of the non-linear Balitsky–Kovchegov (BK) equation [25–27], using the MPSI approximation [52–56] to sum enhanced diagrams, shown in Fig. 2a. It has the following form:

$$\begin{aligned}&G^{{\mathrm{dressed}}}(T)=a^2 (1 - \exp (-T))\nonumber \\&\qquad +\, 2 a (1 - a)\frac{T}{1 + T} + (1 - a)^2 G(T), \nonumber \\&\qquad \hbox {with} ~G(T)= 1 - \frac{1}{T} \exp (\frac{1}{T})\Gamma _0(\frac{1}{T}).\end{aligned}$$

(2.1)

$$\begin{aligned}&T(s, b)=\phi _0 S(b, m)\mathrm{e}^{0.63\lambda \ln (s/s_0)},\nonumber \\&\qquad \hbox {with}\ S(b,m )=\frac{m^2}{2 \pi } \mathrm{e}^{ - m b}. \end{aligned}$$

(2.2)

In the above formulae $a=0.65$; this value was chosen so as to attain the analytical form of the solution of the BK equation. Parameters $\lambda$ and $\phi _0$ can be estimated in the leading order of QCD, but due to the large next-to-leading order corrections, we consider them as objects to be determined from a fit to the relevant experimental data. m is a non-perturbative parameter, which characterises the large impact parameter behavior of the saturation momentum, as well, as the typical size of dipoles that take part in the interaction. The value of $m =5.25~\hbox {GeV}$ in our model, supports our main assumption that the BFKL Pomeron calculus, based on a perturbative QCD approach, is able to describe soft physics, since $m \gg \mu _{\mathrm{soft}}$, where $\mu _{\mathrm{soft}}$ is the natural scale for soft processes ($\mu _{\mathrm{soft}} \sim \Lambda _{\mathrm{QCD}}$ and/or pion mass).

Unfortunately, in the situation where the confinement problem is still far from being solved, we need to rely on a phenomenological approach for the structure of the colliding hadrons. We use a two-channel model, which allows us also to calculate the diffractive production in the region of small masses. In this model, we replace the rich structure of the diffractively produced states, by the single state with the wave function $\psi _D$. The observed physical hadronic and diffractive states are written in the form

$$\begin{aligned}&\psi _h=\alpha \,\psi _1+\beta \,\psi _2;\quad \psi _D=-\beta \,\psi _1+\alpha \,\psi _2;\nonumber \\&\qquad \hbox {where}\ \alpha ^2+\beta ^2=1. \end{aligned}$$

(2.3)

Table 1 Fitted parameters of the model. The values of the old set are taken from Ref. [16]. Values of the new set are determined by fitting to data with the additional constraint $m_{2}\le 1.5$ GeV. See Sect. 4.2

The functions $\psi _1$ and $\psi _2$ form a complete set of orthogonal functions $\{ \psi _i \}$ which diagonalise the interaction matrix $\mathbf{T}$,

$$\begin{aligned} A^{i'k'}_{i,k}=\langle \psi _i\,\psi _k|{\mathbf {T}}|\psi _{i'}\,\psi _{k'}\rangle = A_{i,k}\,\delta _{i,i'}\,\delta _{k,k'}. \end{aligned}$$

(2.4)

The unitarity constraints take the form

$$\begin{aligned} 2\,\hbox {Im}\,A_{i,k}(s,b)=|A_{i,k}(s,b)|^2+G^{in}_{i,k}(s,b), \end{aligned}$$

(2.5)

where $G^{in}_{i,k}$ denotes the contribution of all non-diffractive inelastic processes, i.e. it is the summed probability for these final states to be produced in the scattering of a state i off a state k. In Eq. (2.5) $\sqrt{s}=W$ is the energy of the colliding hadrons, and b denotes the impact parameter. A simple solution to Eq. (2.5) at high energies, has the eikonal form with an arbitrary opacity $\Omega _{ik}$, where the real part of the amplitude is much smaller than the imaginary part.

$$\begin{aligned}&A_{i,k}(s,b)=i (1 -\exp (- \Omega _{i,k}(s,b))),\end{aligned}$$

(2.6)

$$\begin{aligned}&G^{in}_{i,k}(s,b)=1-\exp (- 2\,\Omega _{i,k}(s,b)). \end{aligned}$$

(2.7)

Equation (2.7) implies that $P^S_{i,k}=\exp ( - 2\,\Omega _{i,k}(s,b))$ is the probability that the initial projectiles (i, k) will reach the final state interaction unchanged, regardless of the initial state re-scatterings.

Note that there is no factor 1 / 2. Its absence stems from our definition of the dressed Pomeron.

In the eikonal approximation we replace $\Omega _{i,k}(s,b)$ by

$$\begin{aligned} \Omega _{i,k}(s,b)= & {} \int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\, g_i({\vec {b}}') \,G^{{\mathrm{dressed}}}(T(s, {\vec {b}}''))\nonumber \\&\times \, g_k({\vec {b}} - {\vec {b}}'\ - {\vec {b}}''). \end{aligned}$$

(2.8)

where

$$\begin{aligned}&g_i(b )=g_i \,S_p(b; m_i )\nonumber \\&\quad \hbox {with}\ S_p(b,m_i)=\frac{1}{4 \pi } m^3_i \,b \,K_1(m_i b ), \end{aligned}$$

(2.9)

$S_p(b, m_i)$ is the Fourier image of the dipole form factor $1/(1 + Q_T^2/m^2_i)^2$, where $Q_T$ is the momentum transferred by the Pomeron. It is a pure phenomenological input, and this choice satisfies two theoretical limits: (1) at large $Q_T$ the dipole form factor behaves as $1/Q^4_T$, as follows from perturbative QCD estimates [47, 48]; and (2) it provides the correct ($\propto \exp (- m_ib )$ ) behaviour at large impact parameters [49, 50].

We propose a more general approach, which takes into account new small parameters that result from the fit to the experimental data (see Table 1; Fig. 2):

$$\begin{aligned} G_{3{I\!\!P}}/g_i(b=0)\ll 1;\quad m\gg m_1\ \hbox {and}\ m_2. \end{aligned}$$

(2.10)

The second equation in Eq. (2.10) means that $b''$ in Eq. (2.8) is much smaller that b and $b'$, therefore, Eq. (2.8) can be re-written in a simpler form

$$\begin{aligned} \Omega _{i,k}(s,b)= & {} \left( \int \mathrm{d}^2 b''G^{{\mathrm{dressed}}}(T(s,{\vec {b}}''))\right) \nonumber \\&\times \,\int \mathrm{d}^2 b' g_i({\vec {b}}')\,g_k({\vec {b}} - {\vec {b}}')\nonumber \\= & {} {\tilde{G}}^{{\mathrm{dressed}}}({\bar{T}})\int \mathrm{d}^2 b' g_i({\vec {b}}') \,g_k({\vec {b}} - {\vec {b}}'). \end{aligned}$$

(2.11)

Note that ${\tilde{G}}^{{\mathrm{dressed}}}(\bar{T})$ does not depend on b, and is a function of ${\bar{T}} =T(s, b=0 )=\frac{m^2}{2 \pi }\,\phi _0 \,\mathrm{e}^{0.63\,\lambda Y}$.

Selecting the diagrams using the first equation in Eq. (2.10), one can see that the main contribution stems from the net diagrams shown in Fig. 2b. The sum of these diagrams [16] leads to the following expression for $\Omega _{i,k}(s,b)$:

$$\begin{aligned}&\Omega _{i,k}(Y; b)\nonumber \\&\quad =\int \mathrm{d}^2 b' \frac{g_i(\vec {b}')\,g_k({\vec {b}} - {\vec {b}}'){\tilde{G}}^{{\mathrm{dressed}}} ({\bar{T}})}{1+G_{3{I\!\!P}}{\tilde{G}}^{{\mathrm{dressed}}}({\bar{T}})[g_i({\vec {b}}')+ g_k({\vec {b}} - {\vec {b}}')]};\nonumber \\ \end{aligned}$$

(2.12)

where

$$\begin{aligned} {\tilde{G}}^{{\mathrm{dressed}}}({\bar{T}})=\int \mathrm{d}^2 b \,G^{{\mathrm{dressed}}}(T(s, b)), \end{aligned}$$

(2.13)

and $T(s, b)$ is given by Eq. (2.2).

In the above formulae the value of the triple BFKL Pomeron vertex is known: $G_{3 {I\!\!P}} = 1.29~\hbox {GeV}^{-1}$.

For further discussion we introduce

$$\begin{aligned} N^{BK}(G^i_{{I\!\!P}}(Y,b ))= & {} a\,(1 - \exp (- G^i_{{I\!\!P}}(Y, b)))\nonumber \\&+\,(1 - a)\frac{ G^i_{{I\!\!P}}(Y, b)}{1+G^i_{{I\!\!P}}(Y, b)}, \end{aligned}$$

(2.14)

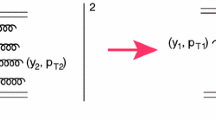
with $a = 0.65$. Equation (2.14) is the analytical approximation for the numerical solution to the BK equation [51]. $G_{{I\!\!P}}(Y; b)=g_i(b )\,\tilde{G}^{{\mathrm{dressed}}}({\bar{T}})$. We recall that the BK equation sums the ‘fan’ diagrams shown in Fig. 3.

Fig. 3

A typical example of ‘fan’ diagrams that are summed in Eq. (2.14)

3 The main formulae for the survival probability

3.1 Hard amplitude in the two-channel model

The expression for the hard amplitude is known, and it has been discussed in great detail (see Ref. [57–63]). It has the following general form (see Fig. 1a):

$$\begin{aligned} A^{{\mathrm{hard}}}= & {} \pi ^2\int \mathrm{d}^2 Q_T \frac{{\bar{\mathcal {M}}}}{Q^2_T\,({\vec {Q}}_T - {\vec {p}}_{1 T})^2\,({\vec {Q}}_T + {\vec {p}}_{2 T})^2 }\nonumber \\&\times \,\phi _G(x_1,x'_1, Q^2_T, t_1)\, \phi _G(x_2,x'_2, Q^2_T, t_2). \end{aligned}$$

(3.1)

where $Q_T$ is the transverse momentum in the gluon loop, ${\bar{\mathcal {M}}}$ is the color averaged amplitude for the process $G G \rightarrow X$, where X denotes the final state (quark–antiquark jets in Fig. 1a) with mass $M_X$.

$$\begin{aligned} {\bar{\mathcal {M}}}=\frac{2}{M^2_X}\,\frac{1}{N^2_c-1}\sum _{a,b} \delta ^{a b}({\vec {Q}}^\mu _T - {\vec {p}}^\mu _{1 T})({\vec {Q}}^\nu _T + {\vec {p}}^\nu _{2 T})\,\Gamma ^{a b}_{\mu \nu }.\nonumber \\ \end{aligned}$$

(3.2)

$\Gamma ^{a b}_{\mu \nu }$ is a vertex for $G G \rightarrow X$.

$\phi _G(x_i,x'_i, Q^2_T, t_i)$ denotes the skewed unintegrated gluon densities. These functions have been discussed and we refer the reader to Ref. [57]. The $t_i$ dependence, is of great importance for the calculation of the survival probability [46, 64, 65]. We show below that the essential $t_i$ turns out to be small in our estimates, and therefore, we have to rely on some input from non-perturbative QCD. Our assumption is that at small $t_i$ we can factorise the unintegrated gluon density as

(3.3)

We make the assumption that the hard amplitude at fixed impact parameter b has the form

$$\begin{aligned} A^{{\mathrm{hard}}}=A^{{\mathrm{hard}}}(s; p_1,p_2)\,\int \mathrm{d}^2 b' \,S^h(b')\,S^h({\vec {b}} - {\vec {b}}'), \end{aligned}$$

(3.4)

where $p_{1}$ and $p_{2}$ denote the four momenta of the outgoing protons.

The advantage of our technique is that it is based on the CGC/saturation approach, and the unintegrated structure functions, $\phi _G(x_i,x'_i, Q^2_T, t_i)$, can be calculated in this framework. In the two-channel model we have two unintegrated structure functions (see Fig. 4):

$$\begin{aligned} \phi _{1\rightarrow {\mathrm{proton}}}\propto & {} \alpha \,g_{1}(b)\equiv S^h_1(b);\nonumber \\ \phi _{2\rightarrow {\mathrm{proton}}}\propto & {} \beta \,g_{2}(b)\equiv S^h_2(b).\nonumber \end{aligned}$$

Fig. 4

Survival probability in two-channel model

We extract the b dependence of hard amplitudes i, from the experimental data for diffractive production of vector mesons in deep inelastic scattering (DIS). Presenting the t-dependence of the measure differential cross section in the form

$$\begin{aligned}&\frac{\mathrm{d}\sigma (\gamma ^* + p \rightarrow V + p )}{\mathrm{d} t} \Bigg /\frac{\mathrm{d} \sigma (\gamma ^* + p \rightarrow V + p )}{\mathrm{d} t}\Bigg |_{t=0}\nonumber \\&\quad =\mathrm{e}^{-B^h\,|t|}. \end{aligned}$$

(3.5)

In QCD

$$\begin{aligned}&\frac{\mathrm{d}\sigma (\gamma ^* + p \rightarrow V + p )}{\mathrm{d}t} \propto \phi ^2_G(x_{Bj},x'_{Bj},Q^2,t)\nonumber \\&\quad \propto \left( \int \mathrm{e}^{i {\vec {Q}}_T \cdot {\vec {b}}}(\alpha ^2 g_1 S_p(b, m_1)+\beta ^2 \,g_2\,S_p(b, m_2))\right) ^2,\nonumber \\ \end{aligned}$$

(3.6)

where $t = - Q^2_T$.

Fig. 5

Compilation of experimental data on the slope of the diffractively produced vector mesons at HERA. The figure is taken from Ref. [67, 68]

The value of the slope $B^h$ can be calculated and it is equal to

$$\begin{aligned} B^h=\frac{1}{2}\,\frac{\int b^2\, \mathrm{d}^2 b (\alpha ^2 g_1 S_p(b, m_1)+\beta ^2 \,g_2\,S_p(b, m_2))}{\int \mathrm{d}^2 b (\alpha ^2 g_1 S_p(b, m_1)+\beta ^2 \,g_2\,S_p(b, m_2))}.\nonumber \\ \end{aligned}$$

(3.7)

Using the parameters of Table 1, we find $B^h \approx 4.5~\hbox {GeV}^{-2}$. From Fig. 5 one can see that $B^h \rightarrow 4 \,\div \, 5\,\hbox {GeV}^{-2}$. Therefore, the b dependence obtained from our approach, is in accord with the HERA experimental data.

Generally speaking, both $B^h$’s depend on energy. Indeed, in Regge theory [66], the scattering amplitude $A^{{\mathrm{hard}}}\propto s^{\alpha _{{I\!\!P}}(t)}$ with $\alpha _{{I\!\!P}}(t )=\alpha _{{I\!\!P}}(0)+\alpha '_{{I\!\!P}} \,\ln (s/s_0)\,t=1+\Delta + \alpha '_{{I\!\!P}} \,\ln (s/s_0)\,t$. For hard processes we do not expect Pomeron trajectories with $\alpha '_{{I\!\!P}} \ne 0$. However, the effective $\alpha '_{{I\!\!P}}$ is due to shadowing corrections. The hard amplitude has the following generic form:

$$\begin{aligned} A^{{\mathrm{hard}}}\propto s^\Delta \,\mathrm{e}^{-\frac{b^2}{2B^h}}. \end{aligned}$$

(3.8)

At large b this amplitude is small. At some value of $b=b_0(s)$, $A^{{\mathrm{hard}}}(s, b)\sim 1$. This equation leads to

$$\begin{aligned} s^\Delta \,\mathrm{e}^{-\frac{b_0^2}{2 B^h}}=f\le 1;\quad b^2_0(s)=2\,B^h \,\Delta \ln (s/s_0). \end{aligned}$$

(3.9)

Due to unitarity (see Eq. (2.5)) the amplitude cannot exceed unity. Therefore, at $b \le b_0(s)$, $A^{{\mathrm{hard}}}(s, b)\propto \Theta (b_0(s) - b)$ where $\Theta (z)$ is a step function. Using this step function we see that $\langle b^2 \rangle =\frac{1}{2}b^2_0(s)$.

On the other hand, the t slope of the amplitude is equal to $B = \langle b^2 \rangle /4 = b^2_0(s)/8$. Note that the slope of the amplitude is equal to $\frac{1}{2}B^h$ of Eq. (3.7)). Finally, the t-slope for the scattering amplitude is proportional to $\ln (s/s_0)$, viz. $B=\frac{1}{4}\,B^h \,\Delta \ln (s/s_0)$ or

$$\begin{aligned} \alpha ^{'\,\mathrm{eff}}_{{I\!\!P}}=\frac{1}{4} \Delta \,B^h_{el,0}, \end{aligned}$$

(3.10)

where $B^h_0$ is the slope for the cross section at $s=s_0$. Choosing $s_0 = 1\,\hbox {GeV}^2$ and $\Delta = 0.2$ ² we obtain $B^h_0 \approx 3.2 \,\hbox {GeV}^{-2}$ and $\alpha _{{I\!\!P}}^{'\,\mathrm{eff}}=0.154\,\hbox {GeV}^{-2}$. While the HERA experiment gives [67–70] $B^h_{el}=4.63 \pm 0.06+4\,(0.164 \pm 0.41)\ln (W/W_0)$. We believe that our approach provides a reasonable estimate of, and an appropriate method to understand the energy behavior of the hard amplitude. Note that $B^h_0 \approx 3.2\,\hbox {GeV}^{-2}$ comes from the experimental formulae changing $W_0 = 90\,\hbox {GeV}$ to $W_0= 1\,\hbox {GeV}$. The above discussion, illustrates that our approach leads to the experimental shrinkage of the effective slope, this occurs naturally in our procedure, without any additional parameters or modification of our formulae, we discuss this in Sects. 4.1 and 4.2. In Sect. 3.4 we discuss the hard amplitude which appears in our model that describes on the same footing both soft and hard interactions. In other words, we discuss there our expressions for $\phi _G$ and $S^h(b)$ appearing in Eq. (3.3).

Fig. 6

a Set of the diagrams for the BFKL Pomeron calculus that lead to the resulting Pomeron Green function, after integrating over rapidities of the triple Pomeron vertices, can be re-written in the form of b. c Illustration that to calculate the survival probability, we need to replace one of BFKL Pomerons by the hard amplitude

Bearing in mind this estimate, we find the following hierarchy of transverse distances, in our approach for high energy scattering (see Table 1):

$$\begin{aligned} \frac{4}{m_1^2}>B^{{\mathrm{hard}}}\gg \frac{1}{m^2}, \end{aligned}$$

(3.11)

where $4/m^2_i$ is the typical slope for $g_i(b )$.

3.2 Survival probability: eikonal approach

Central exclusive production (CEP) has the typical form

$$\begin{aligned} p+p\rightarrow p(q_{1,T})+[\hbox {LRG}]+X(M_X)+[\hbox {LRG}]+p(q_{2,T}),\nonumber \\ \end{aligned}$$

(3.12)

where LRG denotes the large rapidity gap in which no hadrons are produced. We cannot restrict ourselves to the hard amplitude (see Fig. 1a) to describe this reaction. Indeed, Eq. (3.1) gives the amplitude of CEP, but only for a parton shower. However, the production of many parton showers, shown in Fig. 1c, will contaminate the LRG’s, and these have to be eliminated, in order to obtain the correct cross section for the reaction of Eq. (3.12). In simple eikonal models, such a suppression stems from the diagrams shown in Fig. 1b.

For this simple case, we can derive the formula for the survival probability, using two different approaches. The first one, relies on the s-channel unitarity constraint (see Eq. (2.5)). In the eikonal approach the contribution of all inelastic states is given by Eq. (2.7)

$$\begin{aligned} G_{in}(s, b)=1-\exp (- 2\Omega (s, b)). \end{aligned}$$

(3.13)

From Eq. (3.13) we see that multiplying the hard cross section by the factor $\exp (- 2\Omega (s, b))$, we obtain the probability that the process has no inelastic production in the entire kinematic rapidity region [44–46]. Therefore, the survival probability factor $\langle S^2\rangle$ takes the form

$$\begin{aligned} \langle S^2\rangle= & {} \frac{\int \mathrm{d}^2 b \, \mathrm{e}^{ - 2\,\Omega (s, b)}\,\, \left| A^{{\mathrm{hard}}}(s; p_1,p_2)\, \int \mathrm{d}^2 b' \,S^h(b')\,S^h({\vec {b}} - {\vec {b}}')\right| ^2 }{ \int \mathrm{d}^2 b\,\left| \,A^{{\mathrm{hard}}}(s; p_1,p_2)\, \int \mathrm{d}^2 b' \, S^h(b')\,S^h({\vec {b}} - {\vec {b}}')\right| ^2}\nonumber \\= & {} \frac{\int \mathrm{d}^2 b \, \mathrm{e}^{ - 2\,\Omega (s, b)}\,\left| \,\int \mathrm{d}^2 b' \,S^h(b')\,S^h({\vec {b}} - {\vec {b}}')\right| ^2}{ \int \mathrm{d}^2 b\,\left| \,\int \mathrm{d}^2 b' \,S^h(b')\,S^h({\vec {b}} - {\vec {b}}')\right| ^2}. \end{aligned}$$

(3.14)

Note that $A^{{\mathrm{hard}}}(s; p_1,p_2)$ does not depend on b; see Eq. (3.4).

The second derivation is based on summing the Pomeron diagrams of Fig. 1b, introducing $\Omega = g(b)^2 \tilde{G}^{{\mathrm{dressed}}}(s)$ in Eq. (3.13). The eikonal amplitude can be written as (see Eq. (2.6))

$$\begin{aligned} i(1-\exp (-\Omega (s, b)))=i\sum ^\infty _{n = 1}\,(- 1 )^{n - 1}\frac{\Omega ^n(s, b)}{n!}. \end{aligned}$$

(3.15)

In each term with the exchange of n Pomerons, we need to replace one of these Pomerons by the hard amplitude. Such a replacement leads to the following sum:

$$\begin{aligned} i\,\sum ^\infty _{n = 1}\,(- 1 )^{n - 1}\,\frac{n\,\Omega ^n(s, b)}{n!}\,A^{{\mathrm{hard}}}=i\,\mathrm{e}^{-\Omega (s, b)}A^{{\mathrm{hard}}}. \end{aligned}$$

(3.16)

Multiplying this amplitude by its complex conjugate, and integrating over b we obtain Eq. (3.14).

3.3 Survival probability: enhanced diagrams

At first sight Eq. (3.14), provides the answer for the case of eikonal rescattering. However, this is not correct, since the dressed BFKL Pomeron Green function is the sum of enhanced diagrams of Figs. 2a and 6a. To find the survival probability, we need to replace one of the Pomeron lines in Fig. 6a by the hard amplitude. As was noticed in Ref. [71] the enhanced diagrams can be reduced to a sum of diagrams which have a general form

$$\begin{aligned} G^{{\mathrm{dressed}}}(T)=\sum _{n=1}^\infty \,(-1)^{n-1}\, \Gamma ^2(P \rightarrow n P)\,T^n, \end{aligned}$$

(3.17)

after integration over positions in rapidity, of the triple Pomeron vertices. The vertices $\Gamma (P \rightarrow n P)$ can easily be found from Eq. (2.1). To obtain the survival probability, we need to replace T in Eq. (3.17) by the hard amplitude: viz

$$\begin{aligned}&G^{{\mathrm{hard}}}(Y, b)\,\equiv \, A^{{\mathrm{hard}}}_{{I\!\!P}}\sum ^\infty _{n=1}(-1 )^n \,n\, \Gamma ^2(P \rightarrow n P)\,T^{n - 1}\, \nonumber \\&\quad \rightarrow \, A^{{\mathrm{hard}}}_{{I\!\!P}}\Bigg \{ a^2\,\mathrm{e}^{-T}\,-\,(1 - a)\left( \frac{1 - a}{T^2} - \frac{2 a}{(1 + T)^2}\right) \nonumber \\&\qquad + \left. (1 - a)^2 \frac{1 + T}{T^3} \mathrm{e}^{\frac{1}{T}}\Gamma _0\left( \frac{1}{T}\right) \right\} . \end{aligned}$$

(3.18)

It should be noted that $A^{{\mathrm{hard}}}_{{I\!\!P}}$ is not the same as in Eq. (3.14), and its b distribution has a typical value of $b \propto 1/m$. In other words $A^{{\mathrm{hard}}}_{{I\!\!P}}\propto S(b)$. This expression follows from the key feature of our model that describes both the hard and the soft amplitude in the same framework. The b dependence of our hard amplitude is the same as the “soft” one and characterised by S(b).

Equation (3.18) leads to the following contribution:

$$\begin{aligned}&\Omega ^{{\mathrm{hard}}}_{i k}=\int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\,g_i(b')\,G^{{\mathrm{hard}}}(Y, b'')\, g_k({\vec {b}} - {\vec {b}}' - {\vec {b}}'')\nonumber \\&\quad \rightarrow \int \mathrm{d}^2 b'\,g_i(b')\,g_k({\vec {b}} - {\vec {b}}' )\tilde{G}^{{\mathrm{hard}}}(Y), \end{aligned}$$

(3.19)

$$\begin{aligned}&{\tilde{G}}^{{\mathrm{hard}}}(Y)=\int \mathrm{d}^2 b'' \,S(b'')\nonumber \\&\qquad \times \left\{ a^2\,\mathrm{e}^{-T}-(1 - a)\left( \frac{1 - a}{T^2} -\frac{2 a}{(1 + T)^2}\right) \,\right. \nonumber \\&\qquad +\left. (1 - a)^2 \frac{1 + T}{T^3} \mathrm{e}^{\frac{1}{T}}\Gamma _0 \left( \frac{1}{T}\right) \right\} . \end{aligned}$$

(3.20)

Inspecting Eq. (3.19) we note that at $T \rightarrow 0$, Eq. (3.19) leads to $\Omega ^{{\mathrm{hard}}}_{i k}\rightarrow \int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\,g_i (b'\,)\,g_k({\vec {b}} - {\vec {b}}')$, which coincides with our hard amplitude introduced in Eq. (3.5). Using the notation in this equation, the expression for $\Omega ^{{\mathrm{hard}}}_{i k}$ takes the final form:

$$\begin{aligned} \Omega ^{{\mathrm{hard}}}_{i k}=\int \mathrm{d}^2 b'\,S_i^h(b')\,S_k^h({\vec {b}} - {\vec {b}}')\tilde{G}^{{\mathrm{hard}}}(Y). \end{aligned}$$

(3.21)

3.4 Survival probability: general formulae

3.4.1 Survival probability: eikonal formula for two-channel model

The structure of the formula for the survival probability is shown in Fig. 4. The amplitude for the reaction of Eq. (3.12) can be written in the form

$$\begin{aligned}&A^{\mathrm{full}}(s, q_{1,T},q_{2,T}, p_1,p_1)\nonumber \\&\quad =\int \mathrm{d}^2 b' \mathrm{d}^2 b \,\mathrm{e}^{i {\vec {q}}_{1,T}\cdot {\vec {b}}'} \,\mathrm{e}^{i {\vec {q}}_{2,T}\cdot ({\vec {b}} - {\vec {b}}')} \,{\tilde{G}}^{{\mathrm{hard}}}(Y)\nonumber \\&\qquad \times \left\{ \alpha ^2 \mathrm{e}^{ - \Omega _{11}(, s,b)} S^h_1(b')\,S_1^h({\vec {b}} - {\vec {b}}')\right. \nonumber \\&\qquad +\,\beta ^2 \mathrm{e}^{- \Omega _{22}(, s,b)}S^h_2(b')\,S_2^h({\vec {b}} - {\vec {b}}')\nonumber \\&\qquad +\,\alpha \, \beta (\mathrm{e}^{ - \Omega _{12}(, s,b)}S^h_1(b')\,S_2^h({\vec {b}} - {\vec {b}}')\nonumber \\&\qquad +\left. \mathrm{e}^{ - \Omega _{21}(, s,b)}S^h_2(b')\,S_1^h({\vec {b}} - {\vec {b}}'))\right\} . \end{aligned}$$

(3.22)

The survival probability for the cross section $\mathrm{d}^2\sigma /(\mathrm{d} t_1\,\mathrm{d}t_2)$ is equal

$$\begin{aligned} \langle S^2\rangle= & {} |A^{\mathrm{full}}(s, q_{1,T},q_{2,T}, p_1,p_1)|^2/\nonumber \\&\times |A^{\mathrm{hard}}(s, q_{1,T},q_{2,T},p_1,p_1)|^2, \end{aligned}$$

(3.23)

where

$$\begin{aligned}&A^{\mathrm{hard}}(s, q_{1,T},q_{2,T}, p_1,p_1)\nonumber \\&\quad =\int \mathrm{d}^2 b' \mathrm{d}^2 b \,\mathrm{e}^{i {\vec {q}}_{1,T}\cdot {\vec {b}}'} \,\mathrm{e}^{i {\vec {q}}_{2,T}\cdot ({\vec {b}} - {\vec {b}}')}\nonumber \\&\qquad \times \left\{ \alpha ^2 S^h_1(b')\,S_1^h({\vec {b}} - {\vec {b}}')+\beta ^2 S^h_2(b')\,S_2^h({\vec {b}} - {\vec {b}}')\right. \nonumber \\&\qquad \left. +\,\alpha \, \beta (S^h_1(b')\,S_2^h({\vec {b}} - {\vec {b}}')+S^h_2(b')\,S_1^h({\vec {b}} - {\vec {b}}'))\right\} .\nonumber \\ \end{aligned}$$

(3.24)

Fig. 7

a Set of the net diagrams in the BFKL Pomeron calculus that lead to the resulting survival probability in the framework of high energy QCD. After integration over positions of $G_{3 {I\!\!P}}$ in rapidity, the sum of the diagrams reduces to b

However, if we are interested in cross sections that are integrated over $\mathrm{d}^2 q_{1,T}$ and $\mathrm{d}^2 q_{2,T}$, the expression for $\langle S^2\rangle$ can be simplified, and it has the form

$$\begin{aligned} \langle S^2\rangle = N(s, M_x,p_1,p_2)/ D(S, M_x,p_1,p_2), \end{aligned}$$

(3.25)

with

$$\begin{aligned}&N(s, M_x,p_1,p_2)=\int \mathrm{d}^2 b \ ({\tilde{G}}^{{\mathrm{hard}}}(Y))^2\nonumber \\&\qquad \times \left\{ \int \mathrm{d}^2 b'\,(\alpha ^2 \mathrm{e}^{ - \Omega _{11}(, s,b)} S^h_1(b')\,S_1^h({\vec {b}} - {\vec {b}}')\right. \nonumber \\&\qquad +\,\beta ^2 \mathrm{e}^{- \Omega _{22}(, s,b)}S^h_2(b')\,S_2^h({\vec {b}} - {\vec {b}}')\nonumber \\&\qquad +\,\alpha \, \beta (\mathrm{e}^{ - \Omega _{12}(, s,b)}S^h_1(b')\,S_2^h({\vec {b}} - {\vec {b}}')\nonumber \\&\qquad \left. +\,\mathrm{e}^{ - \Omega _{21}(, s,b)}S^h_2(b')\,S_1^h({\vec {b}} - {\vec {b}}')))\phantom {\int }\right\} ^2, \end{aligned}$$

(3.26)

and

$$\begin{aligned}&D(s, M_x,p_1,p_2)\nonumber \\&\quad =\int \mathrm{d}^2 b \left\{ \int \mathrm{d}^2 b'\, (\alpha ^2 S^h_1(b')\,S_1^h({\vec {b}} - {\vec {b}}')\right. \nonumber \\&\qquad +\,\beta ^2 S^h_2(b')\,S_2^h({\vec {b}} - {\vec {b}}')+\alpha \, \beta (S^h_1(b')\,S_2^h({\vec {b}} - {\vec {b}}')\nonumber \\&\qquad \left. +\,S^h_2(b')\,S_1^h({\vec {b}} - {\vec {b}}')))\phantom {\int }\right\} ^2. \end{aligned}$$

(3.27)

3.4.2 General case: $\Omega ^{{\mathrm{hard}}}$

The first problem that we need to solve is to find a more general expression for $\Omega ^{{\mathrm{hard}}}$, than we have obtained in Eq. (3.21). Equation (2.12) sums net diagrams, and they can be re-written in the same form as the enhanced ones [71]. Equation (3.17) is replaced by

$$\begin{aligned} \Omega _{i k}=\sum ^\infty _{n=1}\,(- 1 )^{n - 1} \Gamma (i \rightarrow n {I\!\!P})\, \Gamma (k \rightarrow n {I\!\!P})(\tilde{G}^{{\mathrm{dressed}}})^n.\nonumber \\ \end{aligned}$$

(3.28)

From Eq. (3.28) we obtain

$$\begin{aligned} \Omega ^{{\mathrm{hard}}}_{i k}= & {} A^{{\mathrm{hard}}} \sum ^\infty _{n = 0} \Gamma (i \rightarrow (n + 1) {I\!\!P})\nonumber \\&\times \Gamma (k \rightarrow (n + 1){I\!\!P})({\tilde{G}}^{{\mathrm{dressed}}})^n. \end{aligned}$$

(3.29)

Using Eqs. (2.12) and (3.29) we obtain

$$\begin{aligned}&\Omega ^{{\mathrm{hard}}}_{i k}(Y; b)\nonumber \\&\quad = \int \mathrm{d}^2 b' \frac{ S^h_i(\vec {b}')\,S^h_k({\vec {b}} - {\vec {b}}')}{(1+G_{3{I\!\!P}}\,\tilde{G}^{{\mathrm{dressed}}}({\bar{T}})[g_i({\vec {b}}')+ g_k({\vec {b}} - {\vec {b}}')])^2}.\nonumber \\ \end{aligned}$$

(3.30)

Taking into account the enhanced diagrams for $\tilde{G}^{{\mathrm{dressed}}}$ (see Eq. (3.19)) we obtain the final form for $\Omega ^{{\mathrm{hard}}} _{i k}$ (Fig. 7):

$$\begin{aligned}&\Omega ^{{\mathrm{hard}}}_{i k}(Y; b)= \int \mathrm{d}^2 b' \,\tilde{G}^{{\mathrm{hard}}}(Y)\nonumber \\&\qquad \times \frac{ S^h_i(\vec {b}')\,S^h_k({\vec {b}} - {\vec {b}}')}{(1\,+\,G_{3{I\!\!P}}\,\tilde{G}^{{\mathrm{dressed}}}({\bar{T}})[g_i({\vec {b}}')+ g_k({\vec {b}} - {\vec {b}}')])^2}\nonumber \\&\quad = {\tilde{G}}^{{\mathrm{hard}}}(Y)\, {\bar{\Omega }}^{{\mathrm{hard}}}_{i k}. \end{aligned}$$

(3.31)

3.4.3 Final formula

Finally, to obtain the general formula for the survival probability we need in Eq. (3.26), we replace $\int \mathrm{d}^2 b'\, S^i_h(\vec {b}')\,S^k_h({\vec {b}} - {\vec {b}}')$ by $\bar{ \Omega }^{{\mathrm{hard}}}_{i k}(Y, b)$. Therefore, the survival probability is equal to

$$\begin{aligned} \langle S^2\rangle = N(s, M_x,p_1,p_2)/D(s, M_x,p_1,p_2), \end{aligned}$$

(3.32)

with

$$\begin{aligned}&N(s, M_x,p_1,p_2)=\int \mathrm{d}^2 b ({\tilde{G}}^{{\mathrm{hard}}}(Y))^2 \nonumber \\&\quad \times \left\{ \alpha ^2 \mathrm{e}^{ - \Omega _{11}(s,b)} \bar{ \Omega }^{{\mathrm{hard}}}_{1 1}(Y, b)+\beta ^2 \mathrm{e}^{- \Omega _{22}(s,b)} {\bar{\Omega }}^{{\mathrm{hard}}}_{2 2}(Y, b)\right. \nonumber \\&\quad \left. +\,\alpha \, \beta (\mathrm{e}^{ - \Omega _{12}(s,b)} \bar{ \Omega }^{{\mathrm{hard}}}_{1 2 }(Y, b)+\mathrm{e}^{ - \Omega _{21}(s,b)} \bar{ \Omega }^{{\mathrm{hard}}}_{2 1 }(Y, b))\right\} ^2.\nonumber \\ \end{aligned}$$

(3.33)

while $D(s, M_x,p_1,p_2)$ remains the same as in Eq. (3.27).

From Eqs. (3.32) and (3.33) we note that $\langle S^2\rangle \propto (\tilde{G}^{{\mathrm{hard}}}(Y))^2$. This factor takes into account the contribution from the enhanced diagrams. Figure 8 shows that, on its own, it leads to a smaller survival probability.

4 Numerical estimates

4.1 Survival probability in our model

Our estimates for the survival probability are shown in Fig. 9.

Fig. 8

The suppression factor $(\tilde{G}^{{\mathrm{hard}}}(Y))^2$, which includes the contribution of the enhanced diagrams

Fig. 9

$\langle S^2\rangle$ of Eq. (3.32) versus W

Fig. 10

$\mathrm{d}\sigma /\mathrm{d}t/\mathrm{d}\sigma /\mathrm{d}t|_{t=0}$ versus |t|: a for Eq. (3.5) (blue, ‘one exponent’ curve), Eq. (3.4) for hard amplitude in our model, and black curve which is the fit to the experimental data taken from Ref. [72]; and b the blue curve corresponds to the old set of the parameters in our model, while the red line describes the prediction of our model with the new set of the parameters. The typical experimental errors are ${\pm }0.025$

We predict rather small values for the survival probability. Such small values have been discussed previously (see Ref. [64]), however, in the present model we have a different source for this small number. In Ref. [64] $\langle S^2\rangle$ turns out to be small, due to contribution of the enhanced diagram, while in the present model the enhanced diagrams give a suppression factor which is moderate (see Fig. 8). The main cause for the small value of $\langle S^2\rangle$ is the b dependence of the hard amplitude. As we have mentioned our b dependence stems from the description of the soft high energy data, based on CGC/saturation approach, in which we do not introduce a special soft amplitude. In our approach we are only dealing with hard (semi-hard) amplitudes, which provide a smooth matching of the ‘soft’ interaction with the ‘hard’ one.

4.2 Importance of b-dependence of the hard amplitude

We can illustrate the importance of the b-dependence of the hard amplitude by introducing

$$\begin{aligned} S^h_{1}= & {} \alpha \frac{1}{2 \pi B^h} \mathrm{e}^{ - \frac{b^2}{2 B^h}};\nonumber \\ S^h_{2}= & {} \beta \frac{1}{2 \pi B^h} \mathrm{e}^{ - \frac{b^2}{2 B^h}}; \end{aligned}$$

(4.1)

with $B^h = 4 \,\div \, 5\,\hbox {GeV}^{-2}$, which follows from the experimental data, as discussed previously. At first sight Eq. (4.1) follows from the experimental observation of the vector meson production in deep inelastic scattering. As we have discussed, our hard amplitude of Eq. (3.5) leads to the slope of the differential cross section which is the same as in Eq. (4.1). Indeed, as shown in Fig. 10, the t-dependence of the differential cross sections in the region of small t ($t<0.5~\hbox {GeV}^2$) are similar in both parametrisations of the hard amplitude. However, at large t there is a difference, which increases with increasing t. In Fig. 10 we compare the t-behaviour of the differential cross section for diffractive J/$\Psi$ production at the LHC, as given in Ref. [72] and shown by the black curve in Fig. 10. In place of the experimental point, we use the fit given in this paper, which has a $\chi ^2$/d.o.f. $=$ 115/96.

The difference between the amplitudes is more pronounced when plotted as a function of the impact parameter b (see Fig. 11).

The characteristic behaviour of the hard amplitude follows directly from our model’s b dependence of $g_i(b)$. If we replace the exponential type behaviour for $g_i(b)$ by a Gaussian, as assumed in Eq. (2.9), our hard amplitude will lead to larger values of the survival probability. However, as we have already mentioned above, a Gaussian behaviour contradicts both the large $Q_{T}$ behaviour of the form factors, as has been derived in perturbative QCD [47, 48], and the exponential decrease at large b, which follows from the Froissart theorem [49, 50].

The resulting difference for $\langle S^2 \rangle$ is large, values of the survival probability for the hard amplitude of Eq. (4.1) are ten or more times larger than the results of our present model (with the old set of parameters). For example, for $W=7~\hbox {TeV}$ we obtain $\langle S^2\rangle =10 \div 15~\%$.

Fig. 11

Comparison of hard amplitudes defined in Eqs. (3.5) and (4.1)

Figure 11 shows that Eq. (3.5) of our model (with the old set of parameters) leads to fast decrease of the amplitude in b.

We denote our fit which results in these very low values of $\langle S^2 \rangle$ as the “old set of parameters”. Results of this fit and figures comparing it with experimental data are given in Ref. [16]. The experimental data used were published measurements covering the energy range 0.576 $\le$ W $\le$ 7 TeV i.e. $\sigma _{\mathrm{tot}}$ (5 points), $\sigma _{el}$ (6 points), $B_{el}$ (6 points), $\sigma _{sd}$ (7 points) and $\sigma _{dd}$ (7 points). The overall $\chi ^{2}$/d.o.f. of the fit was 2.66. Excluding the $\sigma _{dd}$ data the $\chi ^{2}$/d.o.f. of the fit is 1.26.

As one can see from Table 1, the steepest decrease is due to the $A_{2 2}(b)$ amplitude, which is the smallest. This amplitude also has the smallest suppression, due to the factors $\exp (- 2 \Omega _{i k })$, since $\Omega _{2 2}$ has the smallest value. In the numerator of Eq. (3.32), only the ( 2 2) term provides the essential contribution. This term turns out to be rather large for the amplitude of Eq. (4.1), as one can see from Fig. 11. On the other hand, the same hard amplitude in Eq. (3.5) shows the steep decrease in b, resulting in a small contribution to the numerator of Eq. (3.32), as well as for the resulting $\langle S^2 \rangle$.

Based on the our diagnosis of the problem above, we attempted to find an alternate set of parameters for our model, which provides a reasonable description of the soft data and at the same time predicts larger values of the survival probability, than obtained with the “old set” of parameters.

Fig. 12

$\langle S^2\rangle$ versus W. $\langle S^2\rangle$ is calculated using Eqs. (3.32) and (3.33) with Y replaced by $Y - \Delta _{\mathrm{cor}} \, N_{G_{3{I\!\!P}}}$ with $\Delta _{\mathrm{cor}} =2$ (blue curve), while the red curve is the same as in Fig. 9. The black curve is the estimates for the survival probability with new set of parameters (see Table 1)

Consequently, we made a second fit to the same experimental data, with the additional constraint that $m_{2} \le 1.5$ GeV. We refer to this fit as “new set of parameters”. The values of the parameters for both “old” and “new” sets are given in Table 1. The comparison of the results for $\sigma _{\mathrm{tot}}, \sigma _{el}, B_{el}$, $\sigma _{sd}$ (low and high mass) and $\sigma _{dd}$ (low and high mass) for both set of parameters are shown in Table 4. We note that the values of $\sigma _{\mathrm{tot}}, \sigma _{el}$ and $B_{el}$ obtained in both fits are rather close, while the diffractive cross sections, both $\sigma _{sd}$ and $\sigma _{dd}$, are smaller in the “new” fit.

The value of $\chi ^{2}$/d.o.f. for the “new fit” is 3.79. Excluding the $\sigma _{dd}$ data the $\chi ^{2}$/d.o.f. of the “new” fit is 2.1. The increase in the value of $\chi ^{2}$/d.o.f. in the “new fit” is due to the lower values predicted for $\sigma _{sd}$ and for $\sigma _{dd}$ at LHC energies. These are smaller than the published experimental measurements, resulting in the “old fit” (with higher values for $\sigma _{sd}$ and for $\sigma _{dd}$) giving a better overall description of the data.

The results for $\langle S^2 \rangle$ with the “new set of parameters” is shown in Fig. 12, we find $\langle S^2 \rangle \approx 3~\%$ in the LHC energy range.

4.3 Kinematic corrections

In our approach we consider $G_{3{I\!\!P}}$ as a point-like vertex. This assumption is a considerable simplification. As we have discussed in [18], we expect short range correlations in rapidity, with the correlation length in rapidity $\Delta _{\mathrm{cor}} \approx 2$. Bearing in mind that the triple Pomeron vertex has a size in rapidity, we can take into consideration that in Eqs. (3.17) and (3.28), the Pomerons do not enter at rapidity Y but at $Y - \delta _{\mathrm{cor}} N_{G_{3{I\!\!P}}}$, where $N_{G_{3{I\!\!P}}}$ is the average number of triple Pomeron vertices. It is easy to see that

$$\begin{aligned} N_{G_{3{I\!\!P}}}= & {} \int \mathrm{d}^2 b T(Y, b )\frac{\mathrm{d} G^{{\mathrm{dressed}}}(T(Y, b ))}{ T(Y, b )} /\int \mathrm{d}^2b\, G^{{\mathrm{dressed}}}\nonumber \\&\times (T(Y, b )). \end{aligned}$$

(4.2)

In Fig. 12 we plot $\langle S^2 \rangle$, which is given by Eqs. (3.32) and (3.33) but $Y \rightarrow Y - \Delta _{cor} N_{G_{3{I\!\!P}}}$ with $N_{G_{3{I\!\!P}}}$ estimated using Eq. (4.2). One can see that the effect is sizeable, and leads to larger values of the survival probability.

4.4 Comparison with other estimates

Nearly 10 years ago we summarised the situation regarding the evaluation of the $\langle S^2\rangle$ by different models [73]. Unfortunately, as the results of this paper illustrate, the values obtained for $\langle S^2 \rangle$ are highly dependent on the characteristics of the models used to parametrise the soft and hard amplitudes. For details of the parametrisations used by the three groups quoted in Table 2, we refer the reader to [73–75]. Their values for the $\langle S^2 \rangle$ are given in Table 2.

Table 2 Values of $\langle S^2 \rangle$ at different energies from the three different groups [73–75]. The results are given as percentages

Table 3 Values of $\langle S^2 \rangle$ at different energies from the different groups [76, 77] and from this model: I the hard amplitude is given by Eq. (3.5) with $B = 4.5~\hbox {GeV}^{-2}$ (see Figs. 10, 11), II the hard amplitude is given by Eq. (3.4) with old set of parameters; IIn is the same as II but with the new set of parameters; and III is the same as II but the kinematic corrections are included. The $\langle S^2 \rangle$ results are in percentages

Table 4 The values of cross sections versus energy. $\sigma ^{\mathrm{LM}}_{sd}$ and $\sigma ^{\mathrm{LM}}_{dd}$ denote the cross sections for diffraction dissociation in the low mass region, for single and double diffraction, which stem from the Good–Walker mechanism. While $\sigma ^{\mathrm{HM}}_{sd}$ and $\sigma ^{\mathrm{HM}}_{dd}$ are used for diffraction in high mass, coming from the dressed Pomeron contributions

In the summary of our previous approach for constructing a model based on $N =4$ SYM for strong coupling, and matching with the perturbative QCD approach [76], we discuss the results for $\langle S^2 \rangle$ obtained from this approach. We compared our results with those obtained by the Durham group [77]. The Durham model is a two-channel eikonal model where the Pomeron coupling to the diffractive eigenstates are energy dependent. They presented four different versions, in Table 3, we quote their results for model 4, their “favoured version”.

As can be seen from Table 3, our results for $\langle S^2 \rangle$ obtained from the $N =4$ SYM approach are slightly larger than those given by the KMR approach, and larger than the results of our present model. The reasons for this have been discussed in Sect. 4.2.

Comparing the results of different calculations given in Tables 2 and 3 with our present calculation, we see that the estimates using the same b-dependence of the hard amplitude $A_{\mathrm{hard}} \propto \exp (- b^2/4 B)$ (see Table 3 ‘this model(I)’), leads to results that are similar to the estimates obtained by the other groups. The b-dependence of the hard amplitude that follows from our present approach produces small values for the survival probabilities with the old set of parameters, and reasonable values with the new set of parameters. The b-dependence of our present model, has two advantages: it leads to the correct Froissart limit at large b, $A_{\mathrm{hard}} \propto \exp (- m_{i}\,b)$; and at large momentum transfer ($Q_T$) it decreases as a power of $Q_T$, as one expects in perturbative QCD.

We wish to emphasis that we made a second (new) fit to the experimental data, and obtained a new set of parameters, which leads to an increase in the values of the survival probabilities as shown in Table 3.

5 Conclusions

In this paper we calculated the survival probability for the simplest central diffractive production e.g. gluon $+$ gluon $\rightarrow$ dijets, and we found at LHC energies that its value is small. The small value obtained does not stem from the sum of enhanced diagrams, as in our previous models [78], but is due to the impact parameter dependence of the hard amplitude. We have not included any discussion regarding the influence that final state interactions have on the value of the survival probability. In general these will lead to a decrease in the value of $\langle S^2 \rangle$.

The distinguishing feature of our model based on CGC/saturation approach is that we use a framework where soft and hard processes are treated on the same footing. Our procedure, as we have demonstrated, is able to discuss both long and short distance physics. The hard amplitude, appears as our general amplitude at short distances. To deal with final state production which includes spin/parity effects, we will have to introduce additional hard amplitudes separately to describe the production process, as discussed in Sect. 3.1. The main source for our small values of $\langle S^2 \rangle$ is the impact parameter dependence of the hard amplitude, for which we do not have any theoretical estimate. This is usually assumed to have a Gaussian form $A_{\mathrm{hard}}\propto \exp (- b^2/(2 B))$. The value of B is taken from the experimental data on the deep inelastic diffractive production of vector mesons. We demonstrated in this paper that in spite of the fact that our hard amplitude leads to experimental values of B, at small t, it yields a different behaviour than the Gaussian input, leading to small values of $\langle S^2 \rangle$ at high energies. We note that the impact parameter dependence of our hard amplitude satisfies two theoretical features that are violated in the Gaussian b-dependence: at large b, $A_{\mathrm{hard}}\propto \exp (- \mu b)$, as follows from the Froissart theorem [49, 50], and at large $Q_T$ it decreases as a power of $Q_T$, as required by perturbative QCD [47, 48].

We stress that the values obtained for the survival probability depend mostly on the b-dependence of the hard amplitude. The most interesting result is that we can describe both the soft and the hard amplitude on the same footing. At first sight, the small values of $\langle S^2 \rangle$ contradict this the most basic idea of our approach. To show that this is not an inherent problem of our approach, we made a new fit to all available soft data to show that we can obtain substantially larger values of the survival probability. It demonstrates that experimental measurements of this observable are a sensitive tool to determine the values of the phenomenological parameters of our model.

We present in this paper the result of the first consistent approach to obtain both the soft and the hard amplitude from the same model. We hope that the data from the LHC on survival probability will be instrumental in determining the impact parameter dependence of the scattering amplitude. We wish to emphasis that we have made a second (new) fit to the experimental data (see Table 4).