Abstract
We consider a condition for charge confinement and gravito-electromagnetic wave solutions in nonsymmetric Kaluza–Klein theory. We consider also the influence of the cosmological constant on a static, spherically symmetric solution. We remind the reader of some fundamentals of nonsymmetric Kaluza–Klein theory and the geometrical background behind the theory. Simultaneously we make some remarks concerning a misunderstanding connected to several notions of Kaluza–Klein Theory, Einstein Unified Field Theory, geometrization and unification of physical interactions. We reconsider the Dirac field in nonsymmetric Kaluza–Klein theory.
Similar content being viewed by others
1 Introduction
The nonsymmetric Kaluza–Klein (Jordan–Thiry) theory has been developed in the past (see Refs. [1–4]). The theory unifies gravitational theory described by NGT (Nonsymmetric Gravitational Theory) (see Ref. [5]) and Electrodynamics. The theory has been extended to Nonabelian Gauge Fields, Higgs Fields, and a scalar field with applications to cosmology. Some possibilities to get a confinement of color have been suggested. A nonsingular spherically symmetric solution has been derived. The nonsymmetric Kaluza–Klein theory can be obtained from the Nonsymmetric Jordan–Thiry Theory by putting the scalar field to zero. In this way it is the limit of the Nonsymmetric Jordan–Thiry Theory. The Nonsymmetric Jordan–Thiry Theory has several physical applications in cosmology, e.g.: (1) cosmological constant, (2) inflation, (3) quintessence, and some possible relations to the dark matter problem. Simultaneously the theory unifies gravity with gauge fields in a nontrivial way via geometrical unification of two fundamental invariance principles in physics: (1) the coordinate invariance principle, (2) the gauge invariance principle. Unification on the level of invariance principles is more important than on the level of interactions for from invariance principles we get conservation laws (via the Noether theorem). In some sense Kaluza–Klein theory unifies the energy–momentum conservation law with the conservation law of electric charge. This unification has been achieved in a higher than 4-dimensional world. It is nontrivial for we can get some additional effects unknown in conventional theories of gravity and gauge fields (electromagnetic or Yang–Mills fields). All of these effects, which we call ‘interference effects’ between gravity and gauge fields, are testable in principle in an experiment or an observation. The formalism of this unification has been described in references [1–4]. The nonsymmetric Kaluza–Klein theory is an example of the geometrization of gravitational and electromagnetic interactions according to the Einstein program. In this paper we consider conditions for charge confinement in the theory and three solutions of nonsymmetric Kaluza–Klein theory equations describing gravito-electromagnetic waves. We consider also the influence of a cosmological constant on a static, spherically symmetric solution. This solution can be considered as a model of the electron for it has remarkable properties being nonsingular in electric and gravitational fields. Simultaneously this solution has been built from elementary fields. The properties of the solution can be considered as ‘interference effects’ between electromagnetic and gravitational fields in our unification. In this way the theory realizes an old dream of Einstein, Weyl, Kaluza, Eddington, and Schrödinger of a unitary classical field theory by having particles as spherically symmetric singularity-free solutions of the field equations.
The nonsymmetric Kaluza–Klein theory should be called a Unified Field Theory according to the definition which we quote here (see Ref. [6]): “Unified Field Theory: any theory which attempts to express gravitational theory and electromagnetic theory within a single unified framework. Usually, an attempt to generalize Einstein’s general theory of relativity from a theory of gravitation alone to a theory of gravity and classical electromagnetism”. In our case this single unified framework is a multidimensional analogue of geometry from Einstein Unified Field Theory (treated as generalized gravity) defined on the electromagnetic bundle.
Summing up nonsymmetric Kaluza–Klein theory connects old ideas of unitary field theories (unified field theories) with some modern applications.
The paper has been divided into four sections. In the first section we give some elements of nonsymmetric Kaluza–Klein theory in some new setting. We give also a condition for the dielectric confinement of a charge. In the second section we give three solutions of the field equations describing gravito-electromagnetic waves. In the third section we deal with a spherically-symmetric solution in the presence of a cosmological constant. In the fourth section we give a theory of the Dirac field in nonsymmetric Kaluza–Klein theory getting CP-violation and EDM (Electric Dipole Moment) for a fermion. We reconsider some notion known from our previous papers. In Conclusions we give also some remarks concerning some misunderstanding concerning Kaluza–Klein Theory, Einstein Unified Field Theory commonly met. We put our investigations on a wider background. In Appendix A we give some notions of differential geometry used in the paper and in Appendix B some details of calculations. In Appendix C we give some elements of Clifford algebra and spinor theory. Appendix D is devoted to a redefinition of nonsymmetric Kaluza–Klein theory in terms of GR (General Relativity) and additional ‘matter fields’.
In this paper we use the following convention. Capital Latin indices \(A,B,C=1,2,3,4,5\) (Kaluza–Klein indices), lower Greek cases \(\alpha ,\beta ,\gamma =1,2,3,4\) (space–time indices), lower Latin cases \(a,b,c=1,2,3\) (space indices). In Appendix A we use Latin lower indices in the Lie algebra \(\mathfrak G\) of a Lie group \(G\), \(a,b,c=1,2,\dots ,n=\dim \mathfrak G=\dim G\). This cannot cause any misunderstanding. In Appendix B we use capital Latin indices \(A,B,C,W,N,M=1,2,\dots ,n\), where \(n\) is the dimension of the manifold equipped with nonsymmetric tensor and a nonsymmetric connection. This also does not result in any misunderstanding.
2 Elements of nonsymmetric Kaluza–Klein theory
The basic logic of the construction is as follows. We define a nonsymmetric Kaluza–Klein theory as the 5-dimensional analogue of NGT using our extension of natural metrization of the electromagnetic fiber bundle achieving in this way a unification of two fundamental principles of invariance (i.e. the coordinate invariance principle and the gauge invariance principle) reducing both to the coordinate invariance principle in 5-dimensional world (see Ref. [4] for details).
Let us notice that our construction from Ref. [4] is more general for it contains a scalar field \(\rho \) (or \(\varPsi \)) which here is put \(\rho =1\) (\({\varPsi =0}\)).
Let \(\underline{P}\) be a principal fiber bundle with the structural group \(G=U(1)\) over a space–time \(E\) with projection \(\pi \) and let us define on this bundle a connection \(\alpha \). We call this bundle an electromagnetic bundle and \(\alpha \) an electromagnetic connection (see Appendix A for details). We define a curvature \(2\)-form for the connection \(\alpha \):
where
\(A_\mu \) is the 4-potential of the electromagnetic field, \(e\) is a local section of \(\underline{P}(e:E\supset U\rightarrow P)\), \(F_{\mu \nu }\) is the electromagnetic field strength, and \(\overline{\theta }^\mu \) is a frame on \(E\). The Bianchi identity is
so the 4-potential exists. This is of course simply the first pair of Maxwell equations. On the space–time \(E\) we define a nonsymmetric metric tensor \(g_{\alpha \beta }\) such that
where the order of the indices is important. In such a way we assume that
We suppose also that
defining the inverse tensor \({\widetilde{g}}^{(\alpha \beta )}\) for \(g_{(\alpha \beta )}\) such that \({\widetilde{g}}^{(\alpha \beta )}g_{(\beta \mu )}=\delta _\mu ^\alpha \). The combination of a symmetric and antisymmetric tensor Eq. (2.4) leads to new insides in the inverse tensor. We define also on \(E\) two connections \({{\overline{w}}^\alpha }_{\!\beta }\) and \({{\overline{W}}^\alpha }_{\!\beta }\)
and
such that
where
For the connection \({{\overline{w}}^\alpha }_{\!\beta }\) we suppose the following conditions:
where \(\overline{D}\) is the exterior covariant derivative with respect to \({\overline{w}^{\alpha }}_{\!\beta }\) and \({\overline{Q}^{\alpha }}_{\!\beta \alpha }(\overline{\varGamma })\) is the torsion of \({\overline{w}^{\alpha }}_{\!\beta }\). \({\overline{W}^{\alpha }}_{\!\beta }\) is called an unconstrained connection and \({\overline{w}^{\alpha }}_{\!\beta }\) a constrained connection. Thus we have defined on space–time all quantities present in Moffat’s theory of gravitation (NGT, see Ref. [7]). In this approach we consider test particles moving along geodesics with respect to the Levi–Civita connection generated by the tensor \(g_{(\alpha \beta )}\) on \(E\), i.e. \({{\widetilde{\overline{w}}}{}^{\alpha }}_{\!\beta }={{\widetilde{\overline{\varGamma }}}{}^{\alpha }}_{\!\beta \gamma }\overline{\theta }{}^\gamma \). Let us introduce on \(P\) a frame (a lift horizontal base)
Now we turn to the natural nonsymmetric metrization of the bundle \(P\). We have
where \(\overline{g}\) is a symmetric tensor on \(E\), \(\overline{g}=g_{(\alpha \beta )}\overline{\theta }{}^\alpha \otimes \overline{\theta }{}^\beta \) and \(\underline{g}\) is a 2-form on \(E\), \(\underline{g}=g_{[\alpha \beta ]}\overline{\theta }{}^\alpha \wedge \overline{\theta }{}^\beta \). Taking both parts together we get
The nonsymmetric metric \(\gamma \) is biinvariant with respect to the action of the group \(\text {U}(1)\) on \(P\). From the classical Kaluza–Klein theory we know that \(\lambda =2\frac{\sqrt{ G_N}}{c^2}\). We work with such a system of units that \(G_N=c=1\) and \(\lambda =2\). Thus we have in matrix form
The tensor \(\gamma _{AB}\) has this shape in a lift horizontal base, which is of course nonholonomic (\({\mathrm{d}\theta ^5\ne 0}\)). We can find it in a holonomic system of coordinates. Let us take the section \(e:E\supset U\rightarrow P\) and attach to it the coordinate \(x^5\), selecting \(x^\mu =\mathrm{const}\) on the fiber in such a way that \(e\) is given by the condition \(x^5=0\) and \(\zeta _5=\partial /\partial x^5\). Then we have \(e^*\,\mathrm{d}x^5=0\) and
Taking \(\overline{\theta }{}^\mu =\mathrm{d}x^\mu \) one gets \(\theta ^5=\mathrm{d}x^5+\pi ^*(\lambda A_\mu \,\mathrm{d}x^\mu )\). Putting the last result into Eq. (2.14) one finds
In this coordinate system the tensor \(\gamma \) takes the matrix form
In order to have the correct dimension of the four-potential we should rather write \(e^*\alpha =(q/\hbar c)A=\mu A\), where \(q\) is an elementary charge and \(\hbar \) is Planck’s constant. The same is true for the curvature of connection on the electromagnetic bundle \(\varOmega =\lambda \mu \pi ^*(F)\), \(F=\frac{1}{2} F_{\mu \nu }\overline{\theta }{}^\mu \overline{\theta }{}^\nu \). Moreover, it can be absorbed by the constant \(\lambda \) (we have only one constant as in classical Kaluza theory and the appearance of Planck’s constant is illusory for the theory is classical (not quantum) and eventually demands quantization).
In this way Eq. (2.17) gives the classical Kaluza–Klein approach with a 5-dimensional metric tensor and with the Killing vector \(\zeta _5\). Even if in Eq. (2.15) we have not any four-potential \(A_\mu \), the electromagnetic field exists as an electromagnetic connection \(\alpha \).
The connection contains (potentially) all possible four-potential \(A_\mu \) (that is, in any possible gauge). To choose a gauge means here to take a section of a bundle. An electromagnetic connection \(\alpha \) is really an electromagnetic field. We can also consider \(e^*\varOmega \). Moreover, the structural group of an electromagnetic bundle \(\text {U}(1)\) is abelian. It means \(\varOmega =\mathrm{d}\alpha +\frac{1}{2}[\alpha ,\alpha ]=\mathrm{d}\alpha \). This means we can use Eq. (2.1). In this theory we have two more fiber bundles. Two fiber bundles of frames over \(E\) (a space–time) and over \(P\) (a bundle manifold). Moreover, in order to simplify the formalism we do not refer explicitly to those fiber bundles.
Tensor (2.15) in a lift horizontal base looks simpler than (2.17), moreover, we do not lose any information. Introducing nonholonomic frames we can write very complicated tensors as diagonal and sometimes it causes some misunderstanding. In this way \(F_{\mu \nu }\) tensor is connected to \(A_\mu \)—four-potential via the curvature of the electromagnetic fiber bundle and not via the metric (2.17) which has more mathematical sound. Equation (2.13) is equivalent to Eq. (2.17). The first one is written in a lift horizontal frame and the second in \(\mathrm{d}x^A= (\mathrm{d}x^\alpha ,\mathrm{d}x^5)\).
Now we define on \(P\) the connection \({w^{A}}_{\!B}\) such that
which is invariant with respect to the action of the group \(U(1)\) on \(P\). \(D\) is an exterior covariant derivative with respect to the connection \({w^{A}}_{\!B}\) and \({Q^{D}}_{\!BC}(\varGamma )\) is its torsion. Let us notice that for \({w^{A}}_{\!B}\) we do not suppose any constraints on its torsion. In Refs. [1–3] it is shown that
where \(H_{\beta \gamma }\) is a tensor on \(E\) such that
It is possible to prove that (see Appendix B)
The tensors \(H_{\mu \nu }\) and \(F_{\mu \nu }\) define a 5-dimensional connection on \(P\). In the case of the symmetric tensor \(g_{\alpha \beta }\), \(H_{\mu \nu }=F_{\mu \nu }\) and the theory reduces to ordinary Kaluza–Klein theory.
We define on \(P\) a second connection
Connection \(W^A{}_B\) is a 5-dimensional analogue of the connection \(\overline{W}{}^\alpha {}_\beta \) known in Einstein Unified Field Theory and NGT (Moffat theory of gravitation, see Ref. [7]). According to our notation ‘\(^{-\!-}\)’ over a symbol means that the quantity is defined on \(E\) (a space–time), ‘\(\,\widetilde{\,\,}\,\)’ over a symbol means that the quantity is defined with respect to Levi–Civita connections, i.e. \({{\widetilde{\overline{\varGamma }}}{}^{\alpha }}_{\!\beta \gamma }\) mean coefficients of Levi–Civita connections on \(E\).
The connections (2.19) and (2.22) unify electromagnetic and gravitational interactions in nonsymmetric Kaluza–Klein theory. In the theory we can also consider a dual frame \(\zeta _A\!=\!(\zeta _\alpha ,\zeta _5)\) such that \(\theta ^A(\zeta _B)\!=\!{\delta ^{A}}_{\!B}\). In this way \([\zeta _\alpha ,\zeta _\beta ]\!=\!\frac{\lambda }{2}F_{\alpha \beta } \zeta _5\) and the remaining commutators of the vector fields vanish. In the classical Kaluza–Klein Theory the geodetic equations describe the motion of a charged particle (test particle), i.e. we get the Lorentz force term. Moreover, in the case of classical (Riemannian) Kaluza–Klein Theory we have to do with only one (Levi–Civita) connection on \(P\). Here we have to do with several possibilities (see Ref. [4]). For we have \(H_{\mu \nu }=-H_{\nu \mu }\); it seems now that we should choose the Riemannian part of (2.19). It means we have a Levi–Civita connection generated by \(\gamma _{(AB)}\).
This means we have \(u^B\widetilde{\nabla }_B u^A=0\), where \(\widetilde{\nabla }\) means a covariant derivative with respect to \({{\widetilde{w}}^{A}}_{B}={\widetilde{\varGamma }^{A}}_{\!BC}\theta ^C\) (the Riemannian part of the connection \({w^{A}}_{\!B}\)), \(u^A(\tau )\) is a tangent vector to a geodetic line. Eventually one gets
\(2u^5\) has the interpretation of \(q/m_0\) for a test particle, where \(q\) is the charge and \(m_0\) is the rest mass of a test particle. \(\frac{\widetilde{\overline{D}}}{\mathrm{d}\tau }\) means the covariant derivative with respect to \({\widetilde{\overline{w}}^\alpha }\!_\beta \) along the curve to which \(u(\tau )\) is tangent. \({{\widetilde{\overline{w}}}{}^\alpha }\!_\beta = {{\widetilde{\overline{\varGamma }}}{}^\alpha }\!_{\beta \gamma }\widetilde{\theta }^\gamma \) is of course the Riemannian part of \({\overline{w}^{\alpha }}_{\!\beta } ={\overline{\varGamma }^{\alpha }}_{\!\beta \gamma }\overline{\theta }{}^\gamma \) (a Levi–Civita connection generated by \(g_{(\alpha \beta )}\)).
Let us calculate the Moffat–Ricci curvature scalar for \({W^{A}}_{\!B}\), \(R(W)\), \(R(W)\sqrt{\det \gamma _{AB}}\) is the 5-dimensional Lagrangian density. One gets
where
is the Moffat–Ricci scalar for the connection \({\overline{W}^{\alpha }}_{\!\beta }\) and \(\overline{R}_{\alpha \beta } (\overline{\varGamma })\) is the Moffat–Ricci tensor for the connection \({\overline{w}^{\alpha }}_{\!\beta }\). In particular
where \({\overline{R}^{\alpha }}_{\!{\mu \nu }\rho }(\overline{\varGamma })\) are components of the ordinary curvature tensor for \(\overline{\varGamma }\). In addition
The action of the theory simply reads
Using the Palatini variation principle with respect to \(g_{\alpha \beta }\), \(A_\mu \), \({\overline{W}^{\alpha }}_{\!\beta }\), i.e.
(Eqs. (2.24) and (2.28) give a 5-dimensional action in terms of 4-dimensional quantities which can be compared to the standard field theory action), where \(V=U\times U(1)\), \(U\subset E\), one gets from (2.28) fields equations
where
One can prove
and
We have also
Equations (2.29)–(2.32) can be written in the form
where \(\overline{R}_{\alpha \beta }(\overline{\varGamma })\) is the Moffat–Ricci tensor for the connection \({\overline{w}^{\alpha }}_{\!\beta }={\overline{\varGamma }^{\alpha }}_{\!\beta \gamma }{\overline{\theta }}^\gamma \) and
\(_{\gamma }\) means the partial derivative with respect to \(x^\gamma \) (as usual).
The 4-dimensional quantities in the theory \(A_\mu \), \(g_{({\mu \nu })}\), and \(g_{[{\mu \nu }]}\) are the electromagnetic field, the metric, and the skew-symmetric tensor. They correspond to the following particles: a photon (a spin one), a graviton (a spin 2) and a skewon (a spin zero).
In the theory we get a current density,
which is conserved by its definition (in this way it is a topological current). Equation (2.43) can be written in the form
where \(\overline{\nabla }_\mu \) is a covariant derivative for the connection \({\overline{w}^{\alpha }}_{\!\beta }\).
Equation (2.20) can be solved with respect to \(H_{\nu \mu }\) (see Appendix B)
However, the form of Eq. (2.20) is easier to handle from theoretical point of view. Writing \(H_{\mu \nu }\) in the form
we get
where \(Q_{\mu \nu }^5\) is the torsion in the fifth dimension for the connection \({w^{A}}_{\!B}\) on \(P\) and \(M_{\mu \nu }\) is the electromagnetic polarization tensor induced by a nonsymmetric tensor \(g_{\alpha \beta }\) (if \(g_{\alpha \beta }=g_{(\alpha \beta )}\), \(F_{\mu \nu }=H_{\mu \nu }\)). In this way \(H_{\mu \nu }\) can be considered as an induction tensor of an electromagnetic field. Moreover, the second pair of Maxwell equations (2.46) suggests that rather \(H^{\mu \nu }\) should be considered as the induction tensor. It is easy to see that if we take \(g_{[{\mu \nu }]}= F_{\mu \nu }=0\), \(g_{(\alpha \beta )}=\eta _{\alpha \beta }\) (a Minkowski tensor) we satisfy field equations, i.e. Eqs. (2.39)–(2.43). It means empty Minkowski space is a solution of the equations.
It is easy to see that the theory contains GR as the limit \(g_{[{\mu \nu }]}=0\). In this case we get Einstein equations with electromagnetic sources. If we consider a nonsymmetric Kaluza–Klein theory with external sources (see Ref. [4]), we recover GR in the limit \(g_{[{\mu \nu }]}=0\). The theory satisfies the Bohr correspondence principle to GR. Thus we recover all the achievements of GR, e.g. Newton law, post Newtonian corrections, gravitational waves. Moreover, in our theory we have gravito-electromagnetic waves which are more general (Sect. 2). Post Newtonian approximation in nonsymmetric Kaluza–Klein theory with material (external) sources can be done similarly as in NGT.
Our theory contains the antisymmetric field \(g_{[{\mu \nu }]}\). Moreover it does not results in ghosts (see Ref. [8] and references cited therein, especially Ref. [9]). One of these five theories of gravity is Moffat’s NGT (see Ref. [7]) in real version. Our approach on the level of ghost consideration corresponds to NGT. It means after linearization our theory does not differ from NGT and we can apply results from Ref. [9].
In the theory we get the electromagnetic field lagrangian
which can be written in the form
or
where
Let us consider energy–momentum tensor of the electromagnetic field in the nonsymmetric Kaluza–Klein theory, i.e. \(\overset{\mathrm{em}}{T}_{\alpha \beta }\). Using Eq. (2.48) one gets
where
is the energy–momentum tensor of the electromagnetic field in N.G.T.,
and
is a correction coming from nonsymmetric Kaluza–Klein theory.
Let us consider the second pair of Maxwell equations in nonsymmetric Kaluza–Klein theory. One writes them in the following form (using (2.48)):
where \(J^\alpha \) is the topological current and \({J^{\alpha }}_{\!p}\) is a polarization current
The energy–momentum tensor in the form (2.54) and the second pair of Maxwell equations can be obtained directly from Palatini variation principle with respect to \({\overline{W}^{\alpha }}_{\!\beta }\), \(g_{\mu \nu }\), and \(A_\mu \) for
where \(\mathcal {L}_\mathrm{em}\) is given by Eq. (2.53).
Writing as usual
and introducing Latin indices \(a,b=1,2,3\) we get
or
\(\varepsilon _{abc}\) is the usual 3-dimensional antisymmetric symbol. \(\varepsilon _{123}=1\) and it is unimportant for it if its indices are in up or down position. We keep those indices in up and down position only for convenience.
Using Eq. (2.48) one gets
In Eqs. (2.68) and (2.69) \(A^{ac}\) can be identified with \(\varepsilon _{ac}\) (a dielectric constant tensor) and \({\overline{C}}^{ab}\) with \((\mu ^{-1}) _{ab}\) (an inverse of magnetic constant tensor). Remaining coefficients have more complex interpretation. Moreover, it is possible to think about them as on material properties of some kind generalized medium. A medium with non-zero \(C^{ad}\) and \(\overline{C}{}^{ad}\) is called bianisotropic. In our case they are induced by the nonsymmetric tensor \(g_{\alpha \beta }\), where
Moreover, in Ref. [10] one can find the induction between electric and magnetic fields caused by topological effects. Another connection between our work and Ref. [10] is using a dimensional reduction which is close to the Kaluza–Klein idea.
In our theory the nonsymmetric tensor \(g_{\mu \nu }\) (a nonsymmetric gravitational field) results as a bianisotropic linear medium. Due to this we get Eqs. (2.68)–(2.69). Moreover, in classical electromagnetic theory there are some formalisms for linear bianisotropic phenomena (see Refs. [11–14]). The authors consider classical electrodynamics of continuous media in several forms including a covariant form, i.e.
(see Ref. [11]), similar to our Eqs. (2.48) and (2.20).
In the theory of spatially dispersive materials one can find the following formulas written in the dyadic formalism:
where \(\overline{\overline{\varepsilon }}\) is the permittivity and \(\overline{\overline{\mu }}\) is the permeability depending on space (and time). \(\overline{\overline{\xi }}\) is one more parameter for mirror-asymmetric structure (chiral materials). For magnetoelectric coupling media one gets
where \(\overline{\overline{\zeta }}\) is one more parameter which has to do with parity property of the material with respect to time inversion. These equations are similar to our Eqs. (2.68)–(2.69) (see Ref. [12]). In Refs. [13, 14] the authors use differential forms in classical electrodynamics also for bianisotropic media (see Ref. [14], also [15]), getting similar formulas in covariant form. In Ref. [13] the authors consider also nonlinear electrodynamics by Born–Infeld (see Ref. [16]) and also in the more general Plebański’s form (see Ref. [17]). In our approach constitutive relations are linear (in nonlinear electrodynamics they are nonlinear), but the field equations are nonlinear. In Ref. [12] one considers several currents, e.g. external, polarization. In our case we have also several currents, i.e. a polarization current and topological current, see Eq. (2.58) and (2.59), and (2.47). The covariant form of the linear constitutive equations has been considered in a general form in Ref. [11].
In GR we have also a tensor \(H^{\mu \nu }\), given by the formula
where \(g^{\mu \alpha }\) is the inverse tensor of the symmetric metric in GR. In this way we can have the induction tensor \(H^{\mu \nu }\) in curvilinear coordinates in space (e.g. spherical). Someone can define the induction ‘tensor’ in a different way, as a tensor density, i.e.
We do not follow this approach. In this way we have to do with bianisotropic medium in GR and also in flat Minkowski space in curvilinear coordinates, i.e.
It is easy to see that the ‘medium’ is bianisotropic if \(g^{4m}\ne 0\).
In nonsymmetric Kaluza–Klein theory the situation is more complex:
and \(H_{\alpha \beta }\) is given by the Eq. (2.48).
One can also consider a tensorial density
Moreover, we do not follow this approach. In Refs. [18, 19] one can find some conditions posed on \(\varepsilon _{ac}\) (or \(\varepsilon \delta _{ac}\)) and \((\mu ^{-1})_{ab}\) (or \(\frac{\delta _{ab}}{\mu }\)). In the nonsymmetric Kaluza–Klein theory such conditions are not satisfied for our ‘generalized medium’ being a gravitational field described by the nonsymmetric tensor \(g_{\mu \nu }\). Let us notice the following fact: even if \(g^{4m}=0 \ne g^{m4}\) (in the nonsymmetric case) our constitutive relations can still describe bianisotropic medium.
Let us notice that in the case of a diagonal \(g_{(\alpha \beta )}\), \(F_{\mu \nu }= H_{\mu \nu }\), also in the case of spherically symmetric \(g_{\mu \nu }\) we have \(F_{\mu \nu }=H_{\mu \nu }\), which was extensively used in order to find the exact solution for field equations (see [4]).
Equations (2.61)–(2.62) have a formal character. The physical meaning of \((\overrightarrow{D},\overrightarrow{H})\) and \((\overrightarrow{E},\overrightarrow{B})\) as induction or strength vectors of electric or magnetic fields is sound only in a stationary case.
Let us consider the nonsymmetric tensor for axially symmetric and stationary space–time in cylindrical coordinates (see Ref. [20])
where \(c=1+d^2+k^2\), \(x^1=r\), \(x^2=z\), \(x^3=\theta \), \(x^4=t\), and all the functions \(n,l,a,b,d,k\) are functions of \(r\) and \(z\) only,
The electromagnetic field is described by
and all the functions depend on \(r\) and \(z\) only.
In this case we can calculate \(H_{\mu \nu }\) and \(H^{\mu \nu }\). One gets
where \(m_1=(du-ks)e^{5n-6l}\), \(m_2=(1+d^2+k^2)e^{4(n-l)}\), \(m_3=(d(p-as)+k(q-as))e^{3n-2l}\),
where
Let us come back to Eq. (2.32) (the second part of Maxwell equations) and let us consider it for \(\alpha =4\):
or
In this equation \(\rho \) represents the density of the electric charge.
If \(\overrightarrow{D}=0\) the density of charge equals zero. The problem which we now pose is as follows. Is it possible to have \(\overrightarrow{D}=0\) and \(\overrightarrow{E}\ne 0\)? This means that we have the condition
This means we have the confinement of a charge induced by the special properties of ‘vacuum’ (i.e. a gravitational field described by the nonsymmetric tensor \(g_{\mu \nu }\)). It means non-zero electric field and zero charge distribution.
In the case of a stationary, axially symmetric field we have conditions
with \(u,s\ne 0\).
These conditions can be imposed on functions \(n,l,d,k,a\) to be satisfied for any non-zero \(u,s\) with some dependence on \(p\) and \(q\). One gets
and finally
where
or
We do not give here any quantum version of the theory. It is a classical field theory and the classical theory of charge confinement. Moreover, a confinement is a nonperturbative effect and cannot be obtained in perturbative quantum field theory. This dielectric model of a charge confinement can be considered as an ‘interference effect’ between gravity and electromagnetism in our unified classical field theory. In order to find the quantum version of the theory we should consider the Ashtekar–Lewandowski canonical quantization procedure of the theory, which is suitable here, for the theory is nonlinear and contains gravity (see Ref. [21]).
According to the Einstein program of geometrization and unification of physical interactions we should get equations where on the left-hand side we have geometrical quantities and on the right-hand side material quantities. A full program is completed if on the right-hand side we get zero. It means all quantities have been geometrized. Equations (2.29)–(2.32) give in this sense geometrization and unification of gravity and electromagnetism if we shift \(8\pi \overset{\mathrm{em}}{T}_{\alpha \beta }\) from the right-hand side to the left in Eq. (2.29) and \(2{\mathop {g}_{\sim }}^{[\alpha \beta ]}\partial _\beta (g^{[{\mu \nu }]}F_{\mu \nu })\) from the right-hand side to the left in Eq. (2.32). Having in mind Eq. (2.33) we see that \(8\pi \overset{\mathrm{em}}{T}_{\alpha \beta }\) is geometrized. According to this geometrization and unification program all quantities coming from higher dimension should get an interpretation in terms of matter defined on the space–time. In this way in the theory we geometrized all quantities completing Einstein program for the unification of gravity and electromagnetism getting ‘interference effects’ between both interactions.
3 Gravito-electromagnetic waves solutions in nonsymmetric Kaluza–Klein theory
Let us consider the following nonsymmetric metric in cartesian coordinates:
where
which describes generalized plane wave for \(g_{\mu \nu }\) and
where
which describes generalized plane electromagnetic wave. All the functions mentioned here are subject of field equations in nonsymmetric Kaluza–Klein theory. Using results form Ref. [22] one gets the following equations:
where
where \(\varDelta =\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}\) is the Laplace operator in two dimensions. Equation (3.3) is the Poisson equation for \(e\). Using Eq. (2.30) one gets
In this way we get
\(A\) and \(H\) are arbitrary harmonic functions in two dimensions with arbitrary dependence on \((z-t)\) of \(C^2\) class. \(B\) is an arbitrary solution of Poisson equation and arbitrary function for \((z-t)\) of \(C^2\) class. The function \(e\) can be obtained from the Poisson equation
where \(f\) is given in terms of \(B,A,H\) and takes the simple form
The dependence on \((z-t)\) is parametric and is given by the dependence on \((z-t)\) of \(B,A,H\). This solution describes a generalized plane gravito-electromagnetic wave.
Now we consider the following nonsymmetric tensor in cartesian coordinates:
and the electromagnetic field strength tensor
We put (3.10) and (3.11) into the field equation (2.29)–(2.35). Using the results from Ref. [23] we get the following equations:
From the remaining field equation we get
where \(\varDelta =\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}\),
where \(A\) is an arbitrary harmonic function in two variables,
The function \(b\) is given by
where \(G_1\) and \(G_2\) are arbitrary functions of \(C^2\) class (of on variable). The function \(\beta \) should be written in the form
where \(\beta _0\) is an arbitrary harmonic function and \(f_0\) is an arbitrary function of one variable (of \(C^2\) class). Let us consider Eq. (2.30). One gets
From this equation we get
where \(\varphi \) is a function (arbitrary) of two variables (of \(C^3\)) and a function of \(z-t\).
One gets
Let \(\widetilde{\varphi }\) be any arbitrary solution of Eq. (3.24) (remembering that \(A\), \(f_0\), and \(\beta _0\) are arbitrary). In this way
Let us consider Eq. (3.13) in the form
and let \(\widetilde{g}\) be any solution of this Poisson equation.
Thus
Equation (3.28) gives a consistency condition for the existence of gravito-electromagnetic wave.
Let us consider the following nonsymmetric metric:
and the electromagnetic field strength tensor
in cartesian coordinates
It is possible to consider \(x^4\) as \(z-t\). We suppose that
Using results from Refs. [24, 25] and field equation of the nonsymmetric Kaluza–Klein theory we get the following equations:
Supposing
we get further
Thus \(l\) and \(m\) are harmonically conjugate.
Writing
where \(f\) satisfies the equation
the form of \(p\) can easily be found
where \(\varphi _i\), \(s=1,2,3\), are arbitrary functions of one variable of \(C^3\) class.
This solution represents a gravito-electromagnetic wave if we interpret \(x^4\) as wave front variable \(z-t\). ‘,’ means a derivative with respect to \(x^2\) or \(x^3\), \(f\) is the solution of a Poisson equation with a parametric dependence on \(x^4\) imposed by \(\psi \), \(\varphi _i\), \(i=1,2,3\). Functions \(\psi \), \(l\), and \(m\) are arbitrary functions of \(x^4\) variable of \(C^2\) class.
For all three solutions considered here \(t_{\mu \nu }=M_{\mu \nu }=J^\mu ={J^{\mu }}_{\!p}=0\). Moreover, \(\overrightarrow{D}\ne \overrightarrow{E}\) for all solutions. Those solutions are not solutions of nonsymmetric theory of gravity coupled to the Maxwell field. They are examples of wave solutions in nonsymmetric Kaluza–Klein theory, a unified theory of gravity and the electromagnetic field.
4 The influence of the cosmological constant on a solution in nonsymmetric Kaluza–Klein theory
Let us consider Eqs. (2.29)–(2.35) and let us change \(\overset{\mathrm{em}}{T}_{\alpha \beta }\) into
It means we introduce the cosmological constant \(\Lambda \) into the theory.
In nonsymmetric Kaluza–Klein theory \(\Lambda =0\). Moreover, in the Nonsymmetric Nonabelian Kaluza–Klein Theory this constant is in general non-zero. The Yang–Mills field can be reduced to a \(U(1)\) subgroup of the group \(G\) (see Ref. [3] for more details). We also consider nonsymmetric Kaluza–Klein theory with external sources, and the cosmological constant term can be added to the external energy–momentum tensor (see Ref. [4]).
Let us consider corrected field equations in a static, spherically symmetric case. Using results from Ref. [4] we get the following exact solution:
where
\(Q\) is the electric charge and \(l\) is an integration constant of length dimension. Let us notice that a solution with a cosmological constant differs from the previous solution (see Ref. [4]) only by a term \(\frac{\Lambda r^2}{3}\) similarly as in General Relativity for a Schwarzschild solution with a cosmological constant.
Similar solution is known in Einstein Unified Field Theory and in Schrödinger Theory (see Ref. [26]) (i.e. which generalizes Schwarzschild-like solution from those theories to the case with non-zero cosmological constant). This means that cosmological constant results only via term \(\frac{\Lambda r^2}{3}\). Thus the solution is not asymptotically flat.
It is easy to see that
from Eq. (4.5). From Eq. (4.4) and the definition of the function \(g(x)\) (see Eq. (4.13) below) one gets
where
(see Ref. [4]) is the energy of the solution (a Schwarzschild-like or Kottler-like asymptotically). It is also easy to see that \(\alpha ^{-1}(0)=1\), \(F_{14}(0)=E(0)=0\).
All the details concerning the solution without a cosmological constant can be found in Ref. [4]. In Ref. [4] it has been proved that the energy of the solution is finite and the total charge is equal to \(Q\). The electric field of the solution is plotted in Fig. 3 of Ref. [4] (it is the same as in the case with non-zero cosmological constant).
Moreover, we repeat some details important for the reader. This solution is not a solution with a cosmological constant in a nonsymmetric theory of gravity coupled to the Maxwell field. This solution cannot be obtained in pure NGT with electromagnetic sources. Thus its remarkable properties concerning nonsingularity of electric and gravitational fields are ‘interference effects’ between gravity and electromagnetism in our unification of gravity and electromagnetism. The solution asymptotically behaves as Reissner–Nordström solution in NGT. Due to this it satisfies Bohr correspondence principle between our unification (nonsymmetric Kaluza–Klein theory) and NGT and General Relativity. The solution achieves an old dream by Einstein, Weyl, Kaluza, Schrödinger, Eddington on a unitary classical field theory which has spherically-symmetric singularity-free solutions of the field equations treated as particles.
The properties of the solution are traced back to Abraham–Lorentz (see Refs. [27–30]) idea and more advanced in Born–Infeld electrodynamics (see Refs. [16, 31]) of the electron being a particle-like finite-energy field configuration, the soliton, which energy is of completely field nature. It means it is the energy of field selfinteraction. The solution is in rest. In order to get a moving soliton it is enough to boost it via a Lorentz transformation.
Our theory is nonlinear (nonlinear field equations). Moreover, our constitutive equations between the field strength tensor \(F_{\mu \nu }\) and an induction tensor \(H^{\mu \nu }\) are linear.
Let us introduce the following notation:
In this notation one gets
where
(see Ref. [4]),
The function \(g(x)\) has been plotted in Fig. 2 of Ref. [4]. Similarly as in Ref. [4] one writes \(f(x)=1-P(x)\). In this way \(P(x)\) has an interpretation of a generalized Newtonian gravitational field in normalized radial coordinate, i.e. \(P(x)=-a\frac{g(x)}{x}-bx^2\) (see Schwarzschild solution in GR, see also Fig. 6 of Ref. [4] in the case of \(b=0\)). The solution described here can be considered as the classical model of an electron. We can try to quantize it using collective coordinate approach. One can also apply loop quantum gravity approach (see Ref. [21]) similarly as in Ref. [32].
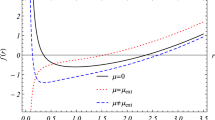
Now it is interesting to examine the influence of the cosmological constant \(\Lambda \) (via \(b\)) on properties of the solution. The most interesting case is to find horizons for such a solution. That is, to find zeros of the function
(The function \(f(x)\) gives information of gravitation field of the discussed solution. In the case of zero cosmological constant we have a plot in Fig. 6 of Ref. [4].)
All the plots of the function \(f(x)\) for some values of parameters \(a\) and \(b\) give some information on the behavior of relativistic gravitational field of the solution for some critical values of \(a\) and \(b\) and some typical behavior of the solution among critical values. For we expect horizons \(f(x)\) gives more than \(P(x)\). We have of course \(P(0)=0\) (\(f(0)=1\)).
In the previous case \(b=0\) (see Ref. [4]) we find that there is a critical value of \(a=a_\mathrm{crt}= 3.17\dots \) such that for \(a<a_\mathrm{crt}\) there is not any horizon, for \(a=a_\mathrm{crt}\) there is one horizon, and for \(a>a_\mathrm{crt}\) there are two horizons. Let us suppose that \(\Lambda >0\) (\(b>0\)) and examine \(a_\mathrm{crt}\) in this case. One gets
It means that as before we have for \(a<a_\mathrm{crt}\) not any horizon, \(a=a_\mathrm{crt}\) one horizon and for \(a>a_\mathrm{crt}\) two horizons. Thus the cosmological constant results in a higher value of \(a_\mathrm{crt}\).
It is interesting to consider a negative value of \(\Lambda \) (\(b<0\)). In this case we have always one more horizon (the so-called de Sitter horizon, the cosmological horizon). For example for \(a=0.1\), \(b=-0.001\) we have only one horizon. For \(a=5\), \(b=-0.001\) we have three horizons, two as before for \(b>0\) and one de Sitter horizon. For \(a=3\), \(b=-0.01\) we have two horizons, one de Sitter horizon and one double as before for \(b>0\). In this case \(a=3\) is a critical value for \(b=-0.001\). For lower negative values of \(b\), i.e. \(b=-0.1\), we have for \(a=0.1\), \(0.7\), \(3\) only one (de Sitter) horizon.
Summing up, for \(\Lambda >0\) we get two horizons, one horizon or no horizon, \(0<r_{H_1}<r_{H_2}\), \(0<r_H\) (as in the case of Reissner–Nordström solution). For \(\Lambda <0\) we have the de Sitter horizon
and inside it one or two horizons or the case without an inside horizon. In Figs. 1, 2, 3, 4, 5 we give plots of the function \(f(x)\) for several values of parameters \(a\) and \(b\).
Plots of the function\(f(x)\) (Eq. (4.15)) for some values of parameters \(a\) and \(b\) (see the text for explanation). a \(a=500.00000, b=-0.100\); b \(a=59.00000, b=-1.000\); c \(a=11.50000, b=1.000\); d \(a=5.00000, b=0.000\); e \(a=5.00000, b=-0.001\); f \(a=4.00000, b=0.100\); g \(a=3.17300, b=0.000\); h \(a=3.00000, b=-0.260\)
Plots of the function\(f(x)\) (Eq. (4.15)) for some values of parameters \(a\) and \(b\) (see the text for explanation). a \(a=3.00000, b=-0.200\); b \(a=3.00000, b=-0.010\); c \(a=3.00000, b=0.000\); d \(a=3.00000, b=0.001\); e \(a=3.00000, b=0.010\); f \(a=3.00000, b=0.100\); g \(a=3.00000, b=0.200\); h \(a=3.00000, b=1.000\)
Plots of the function\(f(x)\) (Eq. (4.15)) for some values of parameters \(a\) and \(b\) (see the text for explanation). a \(a=2.00000, b=0.010\); b \(a=0.79126, b=0.001\); c \(a=0.78126, b=-0.100\); d \(a=0.78126, b=-0.010\); e \(a=0.78126, b=-0.001\); f \(a=0.78126, b=0.000\); g \(a=0.78126, b=0.001\); h \(a=0.78126, b=0.010\)
Plots of the function\(f(x)\) (Eq. (4.15)) for some values of parameters \(a\) and \(b\) (see the text for explanation). a \(a=0.78126, b=0.100\); b \(a=0.10000, b=-0.100\); c \(a=0.10000, b=-0.010\); d \(a=0.10000, b=-0.001\); e \(a=0.10000, b=0.000\); f \(a=0.10000, b=0.001\); g \(a=0.10000, b=0.010\); h \(a=0.10000, b=0.100\)
Plots of the function\(f(x)\) (Eq. (4.15) for some interesting values of \(a\) and \(b\) \((b<0)\) (see the text for an explanation). a \(a\!=3.0349, b=-0.0145067\); b \(a\!=3.4281, b=-0.0163862\); c \(a=2.9677, b=-0.0207742\); d \(a=2.8446, b=-0.0302993\)
One gets the value of the critical parameter \(a_\mathrm{crt}\) and the critical value of the horizon radius from the following equations (let us remind the reader that \(x\) is \(r\) (the radius) in the convenient unit \(\sqrt{2}\,l\), see Eq. (4.14)):
After some algebra we get
Equation (4.17) has one solution for \(b\ge 0\). However, in the case of \(b_0<b<0\) it has two solutions, one solution for \(b=b_0\) and no solutions for \(b<b_0\). Thus we can write \(a_\mathrm{crt}=a_\mathrm{crt}(b)\), \(x_\mathrm{crt}(b)\) only for \(b\ge 0\) (and \(b=b_0\)). In the remaining case \(b_0<b<0\) we rewrite these equations as
The estimated value of \(b_0\) is \(-0.0302993\). It seems that in the case of de Sitter horizon for \(b<b_0=-0.0302993\) there are not any horizon except the mentioned one.
In the case of \(b<0\) we have an interesting phenomenon due to the fact that the function \(f\) has two local extrema (one minimum and one maximum). For a special value of \(b_0\) they collapse to one inflection point. This results in one horizon as a solution of a system of equations
One finds \(x_\mathrm{crt}\approx 2.30331\), \(a_\mathrm{crt}\approx 2.8446\), \(b_0 =-0.0302993\).
The points \(x_\mathrm{crt}\approx 2.30331\), \(a_\mathrm{crt}\approx 2.8446\) correspond to the minimum of the function \(b(x)\) defined by the first equation (4.19).
In Fig. 6 we give plots for \(x_\mathrm{crt}(b)\) and \(a_\mathrm{crt}(b)\) for \(b>0\) and for \(b<0\). In the case of \(b<0\) we have two branches, \(x_\mathrm{crt}\) and \(a_\mathrm{crt}\).
5 Dirac equation in nonsymmetric Kaluza–Klein theory
In this section we deal with the generalization of the Dirac equation on \(P\). Thus we consider spinor fields \(\varPsi ,\overline{\varPsi }\) on \(P\) transforming according to \(\mathrm{Spin}(1,4)\) (a double covering group of \(\mathrm{SO}(1,4)\)—de Sitter group). We want to couple these fields to gravity and electromagnetism. For \(\varPsi \) and \(\overline{\varPsi }\) we have \(\varPsi ,\overline{\varPsi }:P\rightarrow \mathbb {C}^4\) and
where \(\sigma \in \mathcal {L}(\mathbb {C}^4)\), \(p=(x,g_1)\in P\), \(g,g_1\in \text {U}(1)\).
On \(E\) we define spinor ordinary fields \(\psi ,\overline{\psi }:E\rightarrow \mathbb {C}^4\). We suppose that \(\psi \) and \(\overline{\psi }\) are defined up to a phase factor and that
where \(f:E\rightarrow P\) is a section of a bundle \(\underline{P}\). In some sense spinor fields on \(P\) are lifts of spinors on \(E\) (see Appendix C),
Let us consider a different section of the bundle \(\underline{P}\), \(e:E\rightarrow P\). In this case we have
where \(kq\) is the charge of the fermion, \(k=0,\pm 1,\pm 2, \dots \), for an electron \(k=1\), \(\chi \) is a gauge changing function.
Let us define an exterior gauge derivative \(\overset{\mathrm{gauge}}{d}\) of the field \(\varPsi \). One gets
and
Let \(\gamma _\mu \in \mathcal {L}(\mathbb {C}^4)\) be Dirac’s matrices obeying the conventional relations
(where \(\eta _{\mu \nu }\) is the Minkowski tensor of signature \((---+)\)) and let \(B=B^+\) be a matrix such that
(the indices are raised by \(\eta ^{\mu \nu }\), the inverse tensor of \(\eta _{\mu \nu }\)), where ‘\(+\)’ is the Hermitian conjugation, and we have
We define
One can easily check that
where
(the indices are raised by \(\overline{g}{}^{AB}\), the inverse tensor of \(\overline{g}_{AB}\)). We have
So
On the manifold \(P\) we have an orthonormal coordinate system \(\theta ^A\) and we can perform an infinitesimal change of the frame
If the spinor field \(\varPsi \) corresponds to \(\theta ^A\) and \(\varPsi '\) to \(\theta ^{A'}\) then we get
(\(\varPsi \) and \(\overline{\varPsi }\) are Schouten \(\sigma \)-quantities (see Refs. [33, 34]) where
Notice that the dimension of the spinor space for a \(2n\)-dimensional space is \(2^n\) and it is the same for a \((2n+1)\)-dimensional one (in our case \(n=2\)).
We take a spinor field for the 5-dimensional space \(P\) and assume that the dependence on the 5th dimension is trivial, i.e. Eq. (5.1) holds. Taking a section we obtain spinor fields on \(E\).
Let us introduce some new notions. We introduce the Levi–Civita symbol and the dual Cartan’s base
We define
We rewrite here the Riemannian part of the connection (2.19) introducing the constant \(\lambda =\frac{2\sqrt{G_N}}{c^2}\),
Let us consider exterior covariant derivative s of spinors \(\varPsi \) and \(\overline{\varPsi }\),
with respect to the Riemannian connection \({\widetilde{w}{}^{A}}_{\!B}\).
Now we introduce the derivative \(\mathcal {D}\), i.e. an exterior ‘gauge’ derivative of a new kind. This derivative may be treated as the generalization of minimal coupling scheme between spinor and electromagnetic field on \(P\),
We get
where
The derivative \(\widetilde{\overline{\mathcal {D}}}\) is the covariant derivative with respect to both \(\pi ^*({{\widetilde{\overline{w}}}{}^{\alpha }}_{\!\beta })\) and ‘gauge’ at once. It introduces interaction between the electromagnetic and gravitational fields with Dirac’s spinor in a classical well-known way (\(\widetilde{\overline{\mathcal {D}}}\varPsi =\mathrm{hor }\widetilde{\overline{D}}\varPsi \)).
In Dirac theory we have the following Lagrangian for the spinor \(\frac{1}{2}\)-spin field on \(E\):
where \(\overline{l}=\gamma _\mu \overline{\eta }{}^\mu \).
Let us lift the Lagrangian on a manifold \(P\). We pass from the spinors \(\psi \) and \(\overline{\psi }\) to \(\varPsi \) and \(\overline{\varPsi }\) and from the derivative \(d\) to \(\mathrm{\overset{\mathrm{gauge}}{d}}\) or to \(\widetilde{\overline{\mathcal {D}}}\). This is the classical way. Moreover, we have to do with a theory which unifies gravity and electromagnetism and in order to get new physical effects we should pass to our new derivative \(\mathcal {D}\). Simultaneously we pass from \(\overline{\eta }\) to \(\eta \) and from \(\overline{l}\) to \(\pi ^*(\overline{l})=l\).
In this way one gets
Using Eqs. (5.23) one obtains
where
Now we should go back to a space–time \(E\) (see Appendix C) and we get the following Lagrangian:
We get the new term
It is an interaction of the electromagnetic field with an anomalous dipole electric moment. For such an anomalous interaction it reads
Our anomalous moment reads
where \(l_\mathrm{pl}\) is the Planck length
\(q\) is the elementary charge and
is the fine structure constant.
This term can also be rewritten in a different way,
where
are Planck energy scale and Planck mass. Thus we get a term which probably gives the trace of New Physics on the Planck energy scale. This term is nonrenormalizable in Quantum Field Theory and it is of 5 order in mass units (i.e. \(c=\hbar =1\)) divided by the energy (mass) scale.
The term (5.32) can be written in a very convenient way
where
\(I\) is the identity matrix \(2\times 2\) and \(\overrightarrow{\sigma }\) are Pauli matrices. \(\overrightarrow{E}\) is the electric field and \(\overrightarrow{B}\) is the magnetic field. In this way our term introduces an anomalous dipole electric interaction and also an anomalous magnetic dipole interaction. Of course the magnetic interaction is negligible in comparison to ordinary magnetic moment interaction of the electron. One can easily calculate this anomalous magnetic moment of the electron in terms of Bohr magneton getting
where \(m_\mathrm{e}\) is the mass of the electron and \(\mu _B=\frac{q\hbar }{2m_e}\) is the Bohr magneton. From the physical point of view the most important is the electric dipole moment (EDM). So we see that using spinors \(\varPsi \) and \(\overline{\varPsi }\) and the derivative \(\widetilde{\overline{\mathcal {D}}}\) in the Kaluza–Klein Theory we have achieved an additional gravitational-electromagnetic effect. It is just the existence of a dipole moment of a fermion, which value is determined by fundamental constants (only!). This is another ‘interference effect’ between electromagnetic and gravitational fields in our unified field theory. Thirring also has achieved in his paper [37] a dipole electric moment of a fermion of the same order. In his theory the minimal rest mass of the fermion is of order of the Planck mass. Thus his theory cannot describe a fermion from the Standard Model. The anomalous moment in Thirring’s theory depends on a mass of a fermion. In order to get \(d_{kk}\) of order \(10^{-32}\,\mathrm{[cm]}q\) this must be of a Planck mass order. Otherwise the value of \(d_{kk}\) can be smaller. (In reality W. Thirring obtains two types of anomalous Pauli terms—electric and magnetic of the same order.)
In our case mass \(m\) may be arbitrary, e.g. \(m=0\). Thus we can consider also massless fermions. We can also consider chargeless fermions, i.e. for \(k=0\). It is also worth noticing that Thirring’s quantities \(\varPsi \) and \(\overline{\varPsi }\) have nothing to do with our spinor fields \(\varPsi \) and \(\overline{\varPsi }\) for the mysterious Thirring quantity \(\varphi \) which is absent in our theory (it appears also in Thirring’s definition of the parity operator). We develop the theory considered here also in ordinary Kaluza–Klein Theory and in the Kaluza–Klein theory with torsion (see Refs. [35, 38, 39]). Someone develops a theory using our spinors \(\varPsi \) and \(\overline{\varPsi }\) getting also anomalous electric dipole moments (see Refs. [40, 41]). We develop a similar approach for the Rarita–Schwinger field (see Ref. [42]). In the case of nonsymmetric Kaluza–Klein theory we consider also a different approach (see [43, 44]). However, now we consider the present as appropriate.
Let us consider operations of reflection defined on a manifold \(P\). To define them we choose first a local coordinate system on \(P\) in such a way that we pass from \(\theta ^A\) to \(\mathrm{d}x^A\) (see Sect. 1), i.e. \((\pi ^*(\mathrm{d}x^\alpha ),\mathrm{d}x^5)\). In this way
Then
and we define the following transformations: space reflection \(P\) (do not confuse with a manifold \(P\)), time reversal \(T\), charge reflection \(C\), and the combined transformations \(PC\), \(\theta =PCT\),
where \(C^{-1}\gamma _\mu C=-\gamma _\mu ^*\).
Taking a section \(f\) we get
and the charge changes sign. The reflection \(x^5\rightarrow -x^5\) as a charge reflection has been already suggested by J. Rayski (see Ref. [45]). For the space coordinate reflection we have
Taking a section \(f\) we obtain
i.e. a normal parity operator on \(E\).
This contrasts with Thirring’s definition of the parity operator (Thirring was forced to change the definition of the parity operator on 5-dimensional space and he could not obtain the normal parity operator on \(E\)). The transformation of time reversal \(T\) is defined by
Taking a section \(f\) we get
and the charge does change sign, i.e. a normal time-reversal operator on a space–time.
To define a transformation \(\theta =PCT\) we write
Taking a section \(f\) we get
and the charge changes sign. The transformation \(PC\) is as follows:
Taking a section \(f\) we have
and the charge changes sign.
It is clear now that the transformations obtained by us do not differ from those known from the literature.
The additional term in Lagrangian (5.27) breaks \(PC\) or \(T\) symmetries as in Thirring’s theory (see Ref. [37]), but Thirring defines the operator \(PC\) in a different way. This can be easily seen by acting on both sides of Eq. (5.31) with the operator defined by Eq. (5.50). Of course this breaking is very weak and it cannot be linked to \(CP\)-breaking term in Cabbibo–Kobayashi–Maskava matrix. From this breaking due to \(\delta _{PC}\)-phase, which is responsible for \(PC\)-nonconservation in \(K^0,\overline{K}{}^0\) mesons decays and also for \(D^0,\overline{D}{}^0\), \(B_s,\overline{B}_s\), \(B^0, \overline{B}{}^0\), and so on, see Ref. [46], we can get a dipole electric moment of the electron of order \(8\times 10^{-41}\,\mathrm{[cm]}q\) (if there is not New Physics beyond SM, see Ref. [47]). This is because all Feynman diagrams which induce EDM of electron vanish to three loops order.
According to Ref. [47] electron EDM
where
is EDM for the \(W\) boson, \(\Lambda \) is an energy scale for a New Physics (beyond SM),
(see Ref. [48]) is the Jarlskog invariant, \(m_b,m_s,m_c\) are masses of quarks (we suppose the existence of three families of fermions in SM) and \(s_i=\sin \theta _i\), \(c_i=\cos \theta _i\), \(i=1,2,3\).
EDMs of the electron \(d_e\) and quarks can induce EDMs of paramagnetic and diamagnetic atoms
For Thalium (Tl) and for Mercury (Hg) one gets
For the neutron
where \(d_d,d_u\) are EDM of quarks and \(\widetilde{d}_d,\widetilde{d}_u,\widetilde{d}_q\) are color EDM operators (see Ref. [49] and references cited therein). Recently we have an upper bound on EDMs (see Ref. [50] and references cited therein)
In the case of \(\theta \)-term in QCD we have also \(d_n=3\times 10^{-16} \theta \,\mathrm{[cm]}q\) (see Ref. [49]).
Recently there has been significant progress in obtaining an upper limit on the EDM of the electron by using a polar molecule thorium monoxide (ThO). The authors of Ref. [51] obtained an upper limit on \(d_e\),
This is only of three orders of magnitude bigger than our result (see Eq. (5.33)). From the other side there is also progress in calculation of SM prediction of EDM for the electron coming from a phase \(\delta _{CP}\) of CKM matrix. This calculation gives the so called equivalent EDM (see Ref. [52]),
which is bigger of three orders of magnitude than the result from Ref. [46]. Moreover, still smaller of six orders than our result. The parameter \(\theta \) from QCD is unknown and has no influence on EDM of the electron. The existence of EDM of the electron coming from Kaluza–Klein theory can help us in understanding of an asymmetry of matter-antimatter in the Universe. This EDM moment which breaks PC and T symmetry in an explicit way can have an influence on the surviving of annihilation of matter with antimatter following Big Bang.
It is interesting to notice that EDM from Kaluza–Klein Theory is the same for a muon (a \(\mu \) meson) and a tauon (a \(\tau \) meson) as for the electron. We get the same value for flavor states of neutrinos. Due to this, EDM of this value can influence oscillations of neutrinos species (see Ref. [53]).
To be honest, we write down a different, however trivial, coupling of the spinor fields \(\varPsi \) and \(\overline{\varPsi }\) in the Kaluza–Klein model. This is a coupling to a connection of the form
In this way \(\varPsi \) and \(\overline{\varPsi }\) are transforming according to \(\mathrm{SL}(2,\mathbb {C})\) and new phenomena are absent, i.e. we have to do with Lagrangian (5.28).
Let us come back to neutrino oscillations in the presence of EDM. Let us write the Lagrangian for three neutrino species neglecting gravitational field:
Despite the smallness of \(d_{kk}\) its interaction with strong electric and magnetic fields can result in sizeable effects (see Eq. (5.36)). \(m_{\lambda \lambda '}\) is the mass matrix for neutrinos which is not diagonal. In particular \(\alpha =e\), \(\beta =\mu \), \(\gamma =\tau \).
Let us consider mass eigenstates of our neutrinos \(\varPsi _a\), \(a=1,2,3\) (see [53])
The unitary matrix \(U=(U_{\lambda a})\) diagonalizes the mass matrix \(\overline{m}=(m_{\lambda \lambda '})\). The eigenvalues of the mass matrix are called \(m_a\), \(a=1,2,3\).
where \(c_{ij}=\cos \theta _{ij}\), \(s_{ij}=\sin \theta _{ij}\), the angles \(\theta _{ij} \in [0,\frac{\pi }{2}]\), \(\delta \in [0,2\pi ]\) is the Dirac CP-violation phase (see Refs. [46, 53], \(i\) means \(\lambda \)—flavor, \(j\) means \(a\)—mass eigenstate).
In the new spinor variables the Lagrangian (5.61) reads
where
(see Eq. (5.36)).
Using initial conditions for mass eigenstates
we can solve the initial value problem for linear equations corresponding to the Lagrangian (5.65), finding the evolution in time of fields \(\varPsi _a\) (they do not couple). Afterwards using (5.62) and (5.69) we find oscillations of three neutrino flavors under the influence of magnetic and electric fields due to additional term coming from Kaluza–Klein Theory. Field equations for \(\varPsi _a\) (Euler–Lagrange equations for Lagrangian (5.65)) are given in the following Hamilton form:
where
Thus eventually one gets
Equations (5.73) are typical Dirac–Pauli equations. Moreover, they have a term which explicitly breaks PC transformation. We suppose \(\overrightarrow{E}=\mathrm{const}\), \(\overrightarrow{B}=\mathrm{const}\). For Eqs. (5.73) are linear the general solutions are expressed by the Fourier integral
where \(a_a^{(\zeta )},b_a^{(\zeta )}\) are arbitrary coefficients, \(u_a^{(\zeta )},v_a^{(\zeta )}\) are base spinors such that
In the classical situation
and \(\zeta =\pm 1\) describes different polarization states of the fermions \(\varPsi _a\) (see Refs. [54, 55]). In our case \(E(+)_a^{(+1)}\), \(E(+)_a^{(-1)}\), \(E(-)_a^{(-1)}\), \(E(-)_a^{(+1)}\) are roots of the polynomial of the fourth order
where \(I\) is the identity matrix \(4\times 4\) and
Spinors \(u_a^{(\zeta )},v_a^{(\zeta )}\) are eigenvectors corresponding to those eigenvalues. They are orthogonal. Using initial conditions we can determine coefficients \(a_a^{(\zeta )}\) and \(b_a^{(\zeta )}\), i.e. we expand \(\varPsi _a^{(0)}(\overrightarrow{r})\) into Fourier integral
We can consider several possibilities of neutrino flavor oscillations supposing e.g.
In this way
which can be considered as initial conditions for oscillations.
Moreover, this problem is beyond the scope of this paper and will be considered elsewhere.
Let us notice that our generalization of the minimal coupling scheme Eq. (5.22) induces a new connectionon \(P\).
This connection is a metric but with non-vanishing torsion. The properties of this connection have been extensively examined (also in the case of nonabelian Kaluza–Klein Theories) in Ref. [56].
Let us consider the following problem. What would it mean for physics if someone measured the EDM for the electron of the value \(d_{kk}=-\frac{4l_\mathrm{pl}}{\sqrt{\alpha }}q\) as predicted in this section? It means the fifth dimension is a reality in the sense of a 5-dimensional Minkowski space.
The experiment which measures such a quantity strongly supports an idea of rotations around the fifth axis in this space (the fifth dimension is space-like). This EDM exists only due to these rotations. Otherwise spinor fields couple to the connection (5.60) and there is no new effect.
Even if \(P\) is a 5-dimensional manifold, the additional fifth dimension is not necessarily of the same nature as the remaining four dimensions, in particular three space dimensions. This dimension is a gauge dimension connected to the electromagnetic field. Moreover, we can develop this theory using Yang–Mills’ fields and also Higgs’ fields using dimensional reduction procedure, expecting some additional effects. It means we can expect something as ‘traveling’ along additional dimensions. This prediction would have tremendous importance for physics and technology.
Simultaneously the existence of the EDM of the electron has also very great impact on our understanding of PC and T symmetries breaking. This is also very important.
Thus a mentioned measurement with the answer: Yes, would have very important physical, technological and even philosophical implications.
6 Conclusions
In the paper we consider four problems:
-
1.
Charge confinement in nonsymmetric Kaluza–Klein theory.
-
2.
Gravito-electromagnetic waves solutions in this theory.
-
3.
The influence of the cosmological constant on a spherically-symmetric static solution.
-
4.
Dirac equations in nonsymmetric Kaluza–Klein theory.
There are some further prospects:
-
1.
To find similar conditions for confinement (of color) in a nonabelian version in the theory.
-
2.
To find similar gravito-Yang–Mills waves.
-
3.
To find spherical and cylindrical waves in the theory.
Finally, we give some remarks. There are some misunderstandings connecting Kaluza–Klein Theory, Einstein’s Unified Field Theory, Nonsymmetric Gravitation Theory (NGT), Nonsymmetric Kaluza–Klein Theory (NKKT), Nonsymmetric Jordan–Thiry Theory (NJTT).
-
1.
First of all we comment on the constant \(\lambda =\frac{2\sqrt{G_N}}{c^2}\). The constant \(\lambda \) appeared as a free parameter in this theory. Moreover in order to get Einstein equations with electromagnetic sources known from GR it is fixed and it is not free any more. Why is there no Planck’s length? I shall explain it briefly. The Kaluza theory is classical for the paper published by him is classical as a classical paper in the scientific literature. It is also classical for this theory is not quantum. For this we cannot get here the Planck constant. This is simply because we need Planck’s constant in order to construct the Planck length. Planck’s constant is absent in Kaluza theory for this theory is classical (non-quantum). The Planck’s length appeared in the further development done by O. Klein. O. Klein considered the Klein–Gordon equation in 5-dimensional extension. The Planck’s constant is present in Klein–Gordon equation. This equation can be considered as an equation for a classical scalar field. In Kaluza–Klein theory Planck’s length appears as the scale of length.
-
2.
The classical Kaluza theory as a realistic unified field theory has been abandoned by the 1950s. Moreover, due to some mathematical investigations a deep structure has been discovered behind the theory. Let us describe it shortly. First of all it happens that behind Maxwell theory of electromagnetism there is a principal fiber bundle over a space–time with the structural group \(\text {U}(1)\) and the connection defined on this bundle is an electromagnetic field. Gauge transformation, four-potential, the first pair of Maxwell equation obtained a clear geometrical meaning in terms of the fiber bundle approach (see Sect. 1 and Appendix A).
It happens also that the classical Kaluza theory is a theory of metrized (in a natural way) electromagnetic fiber bundle (see Ref. [57]).
This is a true unification of the two fundamental principles of invariance in physics: the gauge invariance principle and the coordinate invariance principle.
In Section 2 of Ref. [35] a classical KKT in this setting has been described (see also the last two lines of page 576 with a fixing of the constant \(\lambda \)).
Moreover this paper is devoted to the KKT with torsion in such a way that we put in the place of GR the Einstein–Cartan theory obtaining new features the so-called ‘interference effects’ between gravity and electromagnetism going to some effects which are small, moreover in principle measurable in experiment. The nonsymmetric Kaluza–Klein theory has been constructed using ideas and mathematical formalism similar to those from Ref. [35], i.e. to Kaluza–Klein Theory with torsion.
-
3.
Let us consider Einstein Unified Field Theory. A. Einstein started this theory in the 1920s. In 1950 he came back to this theory describing it in Appendix II of the fifth edition of his famous book The Meaning of Relativity (see Ref. [58]).
It is worth to mention that there are many versions of this theory. The oldest Einstein–Thomas theory and after that Einstein–Strauss theory, Einstein–Kaufmann theory. There are also two approaches, weak and strong field equations. The Einstein Unified Field Theory can be also considered as a real theory and Hermitian theory. A slight deviation is the so-called Bonnor’s Unified Field Theory. In all of these approaches there are two fundamental notions: nonsymmetric affine connection \({\varGamma ^{\lambda }}_{\!\mu \nu }\ne {\varGamma ^{\lambda }}_{\!\nu \mu }\) and the nonsymmetric metric \(g_{\mu \nu } \ne g_{\nu \mu }\). Connection and metric can be real or Hermitian. In this theory there is also a second connection \({W^{\lambda }}_{\!\mu \nu }\ne {W^{\lambda }}_{\!\nu \mu }\). Connection \({\varGamma ^{\lambda }}_{\!\mu \nu }\) is a so-called constrained connection, \({W^{\lambda }}_{\!\mu \nu }\) is called unconstrained. All of these approaches have no free parameters. Some parameters which appear in solutions of field equations are integration constants.
What was the aim to construct such theories? The aim was to find a unified theory of gravity and electromagnetism in such a way that GR and Maxwell theory appear as some limit of the theory. This approach ended with fiasco. It was impossible to obtain the Lorentz force. It was impossible to obtain the Coulomb law too.
One can find all references to all versions of Einstein Unified Field Theory in Refs. [1, 3–5] and we will not quote them here. Moreover, it is worth to mention that A. Einstein considered this theory as the theory of extended gravitation. Moreover, there is a reference of A. Einstein’s idea to treat this theory as a theory of extended gravity only. A. Einstein published a paper on it in Scientific American (the only one by Einstein in this journal, see Ref. [59]).
Geometrical–mathematical properties of Einstein Unified Field Theory have been described in a book by Vaclav Hlavatý (see Ref. [60]).
In those times A. Einstein started a program of geometrization of physics. Some notions of this program have been described in Ref. [61].
There is also an approach to this theory going in a different direction. It has been summarized in the book by A. H. Klotz (see Ref. [62]).
-
4.
Let us comment NGT (Nonsymmetric Gravitational Theory) by J. W. Moffat. J. W. Moffat reinterpreted Einstein Unified Field Theory as a theory of a pure gravitational field (see Ref. [7]). He introduced material sources to the formalism. Moreover, he introduced in his theory an additional universal constant. He and his co-workers developed this idea getting many interesting results which are in principle testable by astronomical observations in the Solar System and beyond. He was using both real and Hermitian theory. Simultaneously he developed a formalism with two connections \({\varGamma ^{\lambda }}_{\!\mu \nu }\) and \({W^{\lambda }}_{\!\mu \nu }\).
-
5.
Let us comment nonsymmetric Kaluza–Klein and the Nonsymmetric Jordan–Thiry theory. I posed and developed these theories using the nonsymmetric metrization of an electromagnetic fiber bundle using differential forms formalism as in Ref. [35].
Early results concerning nonsymmetric Kaluza–Klein theory have been published in Refs. [63, 64].
The final result of the theory with some developments has been published in Ref. [4]. The paper contains also an extension to the Nonsymmetric Jordan–Thiry Theory with the scalar field \(\varPsi \) (or \(\rho \)). In order to get a pure nonsymmetric Kaluza–Klein theory it is enough to put \({\varPsi =0}\) (or \({\rho =1}\)). All new features as some ‘interference effects’ between electromagnetic fields and gravitation have been quoted in Introduction of Ref. [4]. The theory has no free parameters except integration constants in solutions.
It is possible to get an extension of the theory to the non-Abelian case. In this case we have one free parameter. Moreover, this parameter can be fixed by a cosmological constant. The final version of this theory can be found in Ref. [3]. In Ref. [1] one can find also an extension to the case with Higgs’ field and spontaneous symmetry breaking. In the last case there are three free parameters which can be fixed by the cosmological constant and scales of masses.
I do not refer in my paper to the paper Ref. [65], for the authors are using completely different approach (it is better to say three approaches). This approach is far away from investigations in my work. Moreover, in future both approaches can meet and we will shake hands. The only one point which is now common is the starting point, the classical Kaluza Theory. We do not refer to Ref. [66]. This paper deals with some problems in NGT. However, NGT considered by them has only a little touch with NGT considered here. They introduced a mass for skew-symmetric field \(B_{\mu \nu }=-B_{\nu \mu }\) (in our notation it is \(g_{[\mu \nu ]}\)). Moreover, the \(g_{[\mu \nu ]}\) can obtain a mass in a linear approximation of Nonsymmetric Non-Abelian Kaluza–Klein Theory due to a cosmological constant and it is not necessary to introduce a mass term. It seems that this is a completely different approach (see Ref. [66]). For a cure of NGT by a cosmological constant see also Ref. [67].
Let us notice the following fact. Einstein’s Unified Field Theory has been abandoned as a realistic unified theory for it has been proved using the EIH (Einstein–Infeld–Hoffman) method that there is no Lorentz force term and no Coulomb-like law.
These are disadvantages of Einstein Unified Field Theory but not NGT. This works now for our advantage, for we do not see any term like Lorentz force and Coulomb-like law in gravitational physics (I do not mean a Newton gravitational law which can be obtained in Einstein Unified Field Theory). Someone said: ‘it is clever to use advantages, moreover, more clever is to use disadvantages’ and this is the case. Moreover, in nonsymmetric Kaluza–Klein theory we get Lorentz force term from \((N+4)\)-dimensional (5-dimensional in the electromagnetic case) geodetic equations (see Refs. [1–4]).
All additional notions in nonsymmetric Kaluza–Klein (Jordan–Thiry) theory have been described in [1]. We get from \((N+4)\)-dimensional theory (\(N=n+n_1\)) 4-dimensional al equations due to the invariance of a nonsymmetric metric and a connection with respect to the right action of the group (in the electromagnetic case this is a biinvariance of the action of the group \(\text {U}(1)\)).
Let us notice also the following fact. Equations obtained in the nonsymmetric Kaluza–Klein (Jordan–Thiry) theory are different from these in pure NGT. Due to this we can obtain nonsingular solutions of field equations in the electromagnetic case. These solutions possess a nonsingular metric \(g_{(\alpha \beta )}\) and nonsingular electric field. The asymptotic behavior is as in the case of Reissner–Nordström solution (see Refs. [1, 4] and Sect. 3). This is impossible to get in pure NGT.
-
6.
In Sect. 2 we consider gravito-electromagnetic waves. They have nothing to do with gravito-electromagnetism in General Relativity. The notion of a wave is not so easy as in Halliday’s textbook. It is more general, see Ref. [68]. A wave carries information. Roughly speaking, it can be modulated. This means that it should possess an arbitrary function of e.g. \((z-t)\). In the case of nonlinear waves we use Riemann invariants (see e.g. Ref. [69]) and the wave possesses an arbitrary function of a Riemann invariant. Moreover, a gravitational wave is more complicated, e.g. there is no plane gravitational wave. The gravitational field of such a wave is zero (the curvature tensor induced by the metric describing a plane wave is zero). Moreover, we can consider generalized plane waves (see Ref. [70]). Gravitational waves considered in [70] are not only gravitational waves in a linear approximation. There are here exact solutions of Einstein equations which can describe a very strong gravitational field. So we consider in Sect. 2 wave solutions of nonsymmetric Kaluza–Klein theory in the sense of the mentioned definition of a wave. Field equations in nonsymmetric Kaluza–Klein theory describe gravitational and electromagnetic fields. The solutions depend on arbitrary functions of \((z-t)\). In the limit of zero skewon and zero electromagnetic fields we get generalized plane waves known from the book by Zakharov. Thus those solutions are gravito-electromagnetic waves. We use some achievements in Einstein Unified Field Theory as results in a pure gravity (see Refs. [21–25]). The electromagnetic wave has remarkable properties to have both invariants of the electromagnetic field \(S=F_{\mu \nu }F^{\mu \nu }\), \(P=F_{\mu \nu }F^{*{\mu \nu }}\) equal to zero. The electromagnetic field for gravito-electromagnetic field wave has this property.
References
M.W. Kalinowski, Nonsymmetric Fields Theory and its Applications (World Scientific, Singapore, 1990)
M.W. Kalinowski, in Can We Get Confinement from Extra Dimensions, ed. by Z. Ajduk, S. Pokorski, A.K. Wróblewski. Physics of Elementary Interactions (World Scientific, Singapore, 1991)
M.W. Kalinowski, Nonsymmetric Kaluza–Klein (Jordan–Thiry) theory in a general nonabelian case. Int. J. Theor. Phys. 30, 281 (1991)
M.W. Kalinowski, Nonsymmetric Kaluza–Klein (Jordan–Thiry) theory in the electromagnetic case. Int. J. Theor. Phys. 31, 611 (1992)
M.W. Kalinowski, Scalar Fields in the Nonsymmetric Kaluza–Klein (Jordan-Thiry) Theory. arXiv:hep-th/0307242v9, 7 May 2004
McGraw-Hill Dictionary of Scientific and Technical Terms, 6th edn. (McGraw-Hill, New York, 1989)
J.W. Moffat, Generalized Theory of Gravitation and its Physical Consequences, ed. by V. de Sabbata. Proceeding of the VII International School of Gravitation and Cosmology. Erice, Sicilly (World Scientific Publishing Co., Singapore, 1982), p. 127
R.B. Mann, New ghost-free extensions of general relativity. Class. Quantum Gravity 6, 41 (1989)
R.B. Mann, Five theories of gravity. Class. Quantum Gravity 1, 561 (1984)
X.-L. Qi, T.L. Hughes, S.-C. Zhang, Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008)
E.J. Post, Formal Structure of Electromagnetics (General Covariance and Electromagnetics), (North Holland, Amsterdam, 1962, and Dover Publications Inc, Meneda, NY, 1998)
A. Serdyukov, I. Semchenko, S. Tretyakov, A. Sihvola, Electromagnetics of Bi-Anisotropic Materials (Theory and Applications) (Gordon and Breach Science Publ, Amsterdam, 2001)
F.W. Hehl, Yu.N. Obukhov, Foundations of Classical Electrodynamics (Charge, Flux and Metric) (Birkhäuser, Basel, 2003)
I.V. Lindell, Differential Forms in Electromagnetics. IEEE Press Series on Electromagnetic Wave Theory (Wiley-Blackwell and IEEE Press, New York, 2004)
H. Flanders, Differential Forms with Applications to the Physical Sciences (Academic Press, New York, 1963) and (Dover, New York, 1989)
M. Born, L. Infeld, Foundation of a new field theory. Proc. R. Soc. Lond. A 144, 425 (1934)
J. Plebański, Lectures on Nonlinear Electrodynamics, an extended version of lectures given at Niels Bohr Institute and NORDITA, Copenhagen, 1970
L.D. Landau, E.M. Lifshitz, L.P. Pitaevskii, Electrodynamics of Continuous Media. in Course of Theoretical Physics, second revised edition, vol. 8 (Elsevier-Butterworth-Heinemann, Amsterdam, 2004)
S.R. de Groot, R.G. Suttorp, Foundations of Electrodynamics (North Holland Publ. Company, Amsterdam, 1972)
S. Antoci, Stationary axially symmetric solutions of the Hermitian theory of relativity: generalization of the Papapetrou class of vacuum fields. Lettere al Nuovo Cimento 36, 16 (1983)
A. Ashtekar, J. Lewandowski, Background quantum gravity: a status report. Class. Quantum Gravity 21, R53 (2004)
K.B. Lal, A. Najaf, The wave solutions of the field equations of Einstein’s, Bonnor’s and Schrödinger’s non-symmetric unified field theories in generalized Takeno-space–time. Tensor (N.S.) 21, 241 (1970)
K.B. Lal, D.C. Khare, On solutions of Einstein’s unified field equations of gravitation and electromagnetism in \(V_2\times V_2\) space–time. Tensor (N.S.) 20, 335 (1969)
P.C. Vaidya, Unified gravitational and electromagnetic waves. Progr. Theoret. Phys. 25, 305 (1961)
R.L. Joshi, S.I. Husain, Total radiation in Einstein’s unified field theory. Tensor (N.S.) 15, 66 (1964)
H. Takeno, M. Ikeda, S. Abe, On solutions of new field equations of Einstein and those of Schrödinger. Progr. Theoret. Phys. 6, 837 (1951)
H.A. Lorentz, Weiterbildung der Maxwell’schen Theorie: Elektronentheorie, Enzyklopädie der mathematischen Wissenschaften, Band V2, Heft 1. Art. 14, 145 (1904)
M. Abraham, Theorie der Elektrizität II (Teubner, Leipzig, 1905), p. 1923
F. Rohrlich, Classical Charged Particles (Addison Wesley, Radwood City, 1990)
H. Spohn, Dynamics of Charged Particles and their Radiation Field (Cambridge University Press, Cambridge, 2004)
M. Born, L. Infeld, Electromagnetic mass. Nature 132, 970 (1933)
R. Gambini, J. Pullin, The loop quantum gravity black hole, arXiv:1302.5265 v1[gr-qc], 21 February 2013
J.A. Schouten, Der, Ricci-Kalkül (Verlag von Julius Springer, Berlin, 1924)
J.A. Schouten, Ricci-Calculus (Springer, Berlin, 1954)
M.W. Kalinowski, Gauge fields with torsion (in Polish), Ph.D. thesis submitted to the Faculty of Physics of University of Warsaw, June 1978; published in full in English. Internat. J. Theoret. Phys. 20, 563 (1981)
M.W. Kalinowski, Torsion and the Kaluza–Klein Theory. Acta Phys. Austriaca 57, 45 (1985)
W. Thirring, Fivedimensional theories and CP-violation. in Acta Phys. Austriaca Suppl., vol. IX, p. 256 (Springer, Wien-New York, 1972)
M.W. Kalinowski, CP-nonconservation and a dipole electric moment of fermion in the Klein–Kaluza Theory. Acta Phys. Austriaca 53, 229 (1981)
M.W. Kalinowski, On a dipole electric moment of fermion in the Kaluza–Klein Theory (talk). in Grand Unified Theories and Related Topics (Kyoto 1981) (World Scientific, Singapore, 1981), p. 452
T. Kawai, A five dimensional unification of the Vierbein and electromagnetic fields. Progress Theor. Phys. 67, 1946 (1982)
T. Kawai, A five dimensional unification of the Vierbein and electromagnetic fields II. Progress Theoret. Phys. 68, 1365 (1982)
M.W. Kalinowski, \(\frac{3}{2}\)-spinor field in the Kaluza-Klein Theory. Acta Phys. Austriaca 55, 167 (1983)
M.W. Kalinowski, Minimal coupling scheme for Dirac’s field in the nonsymmetric theory of gravitation. Int. J. Mod. Phys. A 1, 227 (1986)
M.W. Kalinowski, CP nonconservation and electric dipole moment of fermions in the Nonsymmetric Kaluza–Klein Theory. Int. J. Theor. Phys. 26, 21 (1987)
J. Rayski, Unified theory and modern physics. Acta Physica Polonica 31, 87 (1965)
J. Beringer et al., (Particle Data Group), 2012 review of particle physics. Phys. Rev. D 86, 010001 (2012)
M.J. Booth, The electric dipole moment of W and electron in the standard model, arXiv:hep-ph/9301293v3, 4 Feb 1993
C. Jarlskog, Commutator of the quark mass matrices in the standard electroweak model and a measure of maximal CP nonconservation. Phys. Rev. Lett. 55, 1039 (1985)
M. Raidal et al., Flavor physics of leptons and dipole moments. Eur. Phys. J. C 57, 13 (2008)
B.R. Heckel, Results form a search for an electric dipole moment of \({}^{199}{\rm Hg}\). Physics Procedia 17, 92 (2011)
J. Baron et al. (The ACME Collaboration), Order of magnitude smaller limit on the electric dipole moment of the electron, arXiv:1310.7534 v2 [physics.atom-ph], 7 Nov 2013
Pospela M., Ritz A., CKM benchmarks for electron EDM experiments, arXiv:1311.5537 v2 [hep-ph], 28 Nov 2013
C. Giunti, C.W. Kim, Fundamentals of Neutrino Physics and Astrophysics (Oxford Univ. Press, Oxford, 2007). Errata: 30 April 2013
M. Dvornikov, Field theory description of neutrino oscillations, arXiv:1011.4300 v2 [hep-ph], 6 Apr 2011
M. Dvornikov, Neutrino spin-flavor oscillations in electromagnetic fields of various configurations, arXiv:0708.3572v1 [hep-ph], 27 Aug 2007
M.W. Kalinowski, Vanishing of the cosmological constant in non-Abelian Kaluza–Klein Theories. Int. J. Theoret. Phys. 22, 385 (1983)
A. Trautman, Fibre bundles associated with space–time. Rep. Math. Phys. 1, 29 (1970/71)
A. Einstein, The Meaning of Relativity, Appendix II, Fifth Edition, revised (Methuen and Co., London, 1951), p. 127
A. Einstein, On the generalized theory of gravitation. Sci. Am. 182, 13 (1950)
V. Hlavatý, Geometry of Einstein’s Unified Field Theory (P. Noordhoff Ltd., Groningen, 1957)
M.W. Kalinowski, The program of geometrization of physics. Some philosophical remarks. Synthese 77, 129 (1988)
A.H. Klotz, Macrophysics and Geometry: From Einstein’s Unified Field Theory to Cosmology (Cambridge Univ. Press, Cambridge, 1982)
M.W. Kalinowski, The nonsymmetric Kaluza–Klein theory. J. Math. Phys. 24, 1835 (1983)
M.W. Kalinowski, Material sources in the nonsymmetric Kaluza–Klein theory. J. Math. Phys. 25, 1045 (1984)
J.M. Overduin, P.S. Wesson, Kaluza–Klein gravity. Phys. Rep. 283, 303 (1997)
T. Janssen, T. Prokopec, Instabilities in the nonsymmetric theory of gravitation. Class. Quantum Gravity 23, 4967 (2006)
T. Damour, S. Deser, J. McCarthy, Nonsymmetric gravity theories: inconsistencies and a cure. Phys. Rev. D 47, 1541 (1993)
Trautman A., On the Propagation of Information by Waves. in Recent Developments in General Relativity (Pergamon, Oxford; PWN, Warsaw, 1962)
M.W. Kalinowski, On the old-new method of solving nonlinear equations. J. Math. Phys. 25, 2620 (1984)
V.D. Zakharov, Gravitational waves in Einstein’s Theory (in Russian), Nauka, Moscow, English translation: Israel Program for Scientific Translations (Halsted Press, Jerusalem-London, 1972)
S. Kobayashi, K. Nomizu, Foundations of Differential Geometry, vols. I and II. Wiley & Sons Interscience, New York (1963 and 1969)
T.T. Wu, C.N. Yang, Concept of nonintegrable factors and global formulation of gauge fields. Phys. Rev. D 12, 3845 (1975)
S. Pokorski, Gauge Field Theories, 2nd edn. (Cambridge University Press, Cambridge, 2000)
M.W. Kalinowski, R.B. Mann, Linear approximation in the Nonsymmetric Kaluza–Klein Theory. Class. Quantum Gravity 1, 157 (1984)
R.C. Wrede, “n” Dimensional Considerations of Basic Principles A and B of the Unified Theory of Relativity, Ph.D. Thesis submitted to the Faculty of the Graduate School of Indiana University, August 1956; published partially in Tensor (N.S.) 8, p. 95 (1958)
O. Barut, R. Raczka Theory of Group Representations and Applications (PWN, Warsaw, 1977)
M.F. Atiyah, R. Bott, A. Shapiro, Clifford modules. Topol. Suppl. 3, 1 (1964)
E. Cartan, The Theory of Spinors (Hermann, Paris, 1966)
A. Trautman, The Dirac operator on hypersurfaces. Acta Physica Polonica B 26, 1283 (1995)
A. Trautman, Connections and the Dirac operator on spinor bundles. J. Geom. Phys. 58, 238 (2008)
A. Borowiec, The Dirac equation on a Kaluza–Klein bundle. Bull. Pol. Acad. Sci. Ser. Phys. XXVII.2, 65 (1979)
M. Ferrans, J. Kijowski, On the equivalence of the relativistic theories of gravitation. Gen. Rel. Gravit. 14, 165 (1982)
A. Jakubiec, J. Kijowski, On the universality of Einstein equations. Gen. Rel. Gravit. 19, 719 (1987)
A. Jakubiec, J. Kijowski, On theories of gravitation with nonlinear Lagrangian. Phys. Rev. D 37, 1406 (1988)
A. Jakubiec, J. Kijowski, On the universality of linear Lagrangians for gravitational field. J. Math. Phys. 30, 1073 (1989)
A. Jakubiec, J. Kijowski, On theories of gravitation with nonsymmetric connection. J. Math. Phys. 30, 1077 (1989)
J. Kijowski, R. Werpachowski, Universality of affine formulation in general relativity. Rep. Math. Phys. 59, 1 (2007)
A. Trautman, Einstein–Cartan Theory, in ed. by J.-P. Françoise, G.L. Naber, T.S. Tsun. Encyclopedia of Mathematical Physics, vol. 2 (Elsevier, Oxford, 2006), p. 189
M.W. Kalinowski, An Einstein–Cartan–Moffat theory. Phys. Rev. D 26, 3419 (1982)
Acknowledgments
I would like to thank Professor B. Lesyng for the opportunity to carry out computations using Mathematica™ 6 Mathematica™ is the registered mark of Wolfram Co. in the Centre of Excellence BioExploratorium, Faculty of Physics, University of Warsaw. I would like to thank an anonymous referee for critical comments to improve my paper.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
In the appendix we describe the notation and definitions of geometric quantities used in the paper. We use a smooth principal bundle which is the ordered sequence
where \(P\) is the total bundle manifold, \(F\) is a typical fiber, and \(G\), a Lie group, is the structural group, \(E\) is the base manifold and \(\pi \) is a projection. In our case \(G=\text {U}(1)\), \(E\) is a space–time, \(\pi :P\rightarrow E\). We have a map \(\varphi :P\times G\rightarrow P\) defining the action of \(G\) on \(P\). Let \(a,b\in G\) and \(\varepsilon \) be a unit element of the group \(G\), then \(\varphi (a)\circ \varphi (b)=\varphi (ba)\), \(\varphi (\varepsilon )=\mathrm{id }\), where \(\varphi (a)p =\varphi (p,a)\). Moreover, \(\pi \circ \varphi (a)=\pi \). For any open set \(U\subset E\) we have a local trivialization \(U\times G\simeq \pi ^{-1}(U)\). For any \(x\in E\), \(\pi ^{-1}(\{x\})=F_x \simeq G\), \(F_x\) is a fiber over \(x\) and is equal to \(F\). In our case we suppose \(G=F\), i.e. the Lie group \(G\) is a typical fiber. \(\omega \) is a 1-form of connection on \(P\) with values in the algebra of \(G\), \(\mathfrak G\). In the case of \(G=\text {U}(1)\) we use the notation \(\alpha \) (an electromagnetic connection). Lie algebra of \(U(1)\) is \(R\). Let \(\varphi '(a)\) be a tangent map to \(\varphi (a)\) whereas \(\varphi ^*(a)\) is the contragradient to \(\varphi '(a)\) at a point \(a\). The form \(\omega \) is a form of ad-type, i.e.
where \(\mathrm{ad }_{a^{-1}}'\) is the tangent map to the internal automorphism of the group \(G\)
In the case of \(\text {U}(1)\) (abelian) the condition (7.2) means
where \(\zeta _5\) is the Killing vector corresponding to one generator of the group \(\text {U}(1)\). Thus this is the vector tangent to the operation of the group \(\text {U}(1)\) on \(P\), i.e. to \(\varphi _{\exp (i\chi )}\), \(\chi =\chi (x)\), \(x\in E\), \(\mathop {\mathcal {L}}\limits _{\zeta _5}\) is the Lie derivative along \(\zeta _5\). We may introduce the distribution (field) of linear elements \(H_r\), \(r\in P\), where \(H_r\subset T_r(P)\) is a subspace of the space tangent to \(P\) at a point \(r\) and
So
where \(H_r\) is called a subspace of horizontal vectors and \(V_r\) of vertical vectors. For vertical vectors \(v\in V_r\) we have \(\pi '(v)=0\). This means that \(v\) is tangent to the fibers.
Let
It is proved that the distribution \(H_r\) is equal to choosing a connection \(\omega \). We use the operation \(\mathrm{hor }\) for forms, i.e.
where \(X,Y\in T(P)\).
The 2-form of the curvature is defined as follows:
where \(D\) means the exterior covariant derivative with respect to \(\omega \). This form is also of ad-type.
For \(\varOmega \) the structural Cartant equation is valid
where
Bianchi’s identity for \(\omega \) is as follows:
The map \(f:E\supset U\rightarrow P\) such that \(f\circ \pi =\mathrm{id }\) is called a section (\(U\) is an open set).
From the physical point of view it means choosing a gauge. A covariant derivative on \(P\) is defined as follows:
This derivative is called a gauge derivative . \(\varPsi \) can be a spinor field on \(P\).
In this paper we use also a linear connection on manifolds \(E\) and \(P\), using the formalism of differential forms. So the basic quantity is a 1-form of the connection \({\omega ^{A}}_{\!B}\). The 2-form of curvature is as follows:
and the 2-form of torsion is
where \(\theta ^A\) are basic forms and \(D\) means exterior covariant derivative with respect to connection \({\omega ^{A}}_{\!B}\). The following relations are established connections with common symbols:
where \({\varGamma ^{A}}_{\!BC}\) are coefficients of connection (they do not have to be symmetric in indices \(B\) and \(C\)), \({R^{A}}_{\!BCD}\) is a tensor of the curvature, and \({Q^{A}}_{\!BC}\) is the tensor of the torsion in a holonomic frame. The covariant exterior derivation with respect to \({\omega ^{A}}_{\!B}\) is given by the formula
The forms of the curvature \({\varOmega ^{A}}_{\!B}\) and the torsion \(\varTheta ^A\) obey Bianchi’s identities
All quantities introduced here can be found in Ref. [71].
In this paper we use the formalism of a fiber bundle over a space–time \(E\) with the electromagnetic connection \(\alpha \) and traditional formalism of differential geometry for linear connections on \(E\) and \(P\). In order to simplify the notation we do not use fiber bundle formalism of frames over \(E\) and \(P\). A vocabulary connected geometrical quantities and gauge fields (Yang–Mills fields) can be found in Ref. [57].
In Ref. [72] we have also a similar vocabulary (see Table I, for a translation of the terminology). Moreover, we consider a little different terminology. First of all we distinguished between a gauge potential and a connection on a fiber bundle. In our terminology a gauge potential \(A_\mu \overline{\theta }{}^\mu \) is in a particular gauge \(e\) (a section of a bundle), i.e.
where \(A_\mu \overline{\theta }{}^\mu \) is a 1-form defined on \(E\) with values in a Lie algebra \(\mathfrak G\) of \(G\). In the case of the strength of a gauge field we have similarly
where \(F_{\mu \nu }\overline{\theta }{}^\mu \wedge \overline{\theta }{}^\nu \) is a 2-form defined on \(E\) with values in a Lie algebra \(\mathfrak G\) of \(G\).
Using the generators of a Lie algebra \(\mathfrak G\) of \(G\) we get
where
are generators of \(\mathfrak G\), \({C^{c}}_{\!ab}\) are structure constants of a Lie algebra of \(G\), and \(\mathfrak G\), \([\cdot ,\cdot ]\) is the commutator of the Lie algebra elements.
In this paper we use Latin lower case letters for 3-dimensional space indices. We use Latin lower case letters as Lie algebra indices. It does not result in any misunderstanding. We have
In the case of the electromagnetic connection \(\alpha \) the field strength \(F\) does not depend on the gauge (i.e. on a section of a bundle).
Finally it is convenient to connect our approach using the gauge potentials \({A^{a}}_{\!\mu }\) with the common (see Ref. [73]) matrix valued gauge quantities \(A_\mu \) and \(F_{\mu \nu }\). It is easy to see how to do it if we consider Lie algebra generators \(X_a\) as matrices. Usually one assumes that the \(X_a\) are matrices of the adjoint representation of a Lie algebra \(\mathfrak G\), \(T^a\) with the normalization condition
where \(\{\cdot ,\cdot \}\) means the anticommutator in the adjoint representation.
In this way
One can easily see that if we take
from Ref. [73] we get
where \({F^{a}}_{\!{\mu \nu }}\) is given by (7.23). From the other side if we take a section \(f\), \(f:U\rightarrow P\), \(U\subset E\), and corresponding to it we have
and we consider both sections \(e\) and \(f\). we get the transformation from \({A^{a}}_{\!\mu }\) to \({\overline{A}{}^{a}}_{\!\mu }\) and from \({F^{a}}_{\!{\mu \nu }}\) to \({\overline{F}{}^{a}}_{\!{\mu \nu }}\) in the following way. For every \(x\in U\subset E\) there is an element \(g(x)\in G\) such that
Due to (7.2) one gets

where \(\overline{A}(x),\overline{F}(x)\) are defined by (7.29)–(7.30) and \(A(x),F(x)\) by (7.21). Equations (7.32)–(7.33) give the geometrical meaning of a gauge transformation (see Ref. [57]). In the electromagnetic case \(G=\text {U}(1)\) we have similarly, if we change the local section from \(e\) to \(f\) we get
and \(\overline{A}=A+\mathrm{d}\chi \).
Moreover, in the traditional approach (see Ref. [73]) one gets
where \(U(x)\) is the matrix of the adjoint representation of the Lie group \(G\).
For the action of the group \(G\) on \(P\) via (7.2), \(g(x)\) is exactly the matrix of the adjoint representation of \(G\). In this way (7.32)–(7.33) and (7.34)–(7.35) are equivalent.
Let us notice that usually the Lagrangian of a gauge field (Yang–Mills field) is written as
where \(F_{\mu \nu }\) is given by (7.26)–(7.27). It is easy to see that one gets
where
is the Cartan–Killing tensor for the Lie algebra \(\mathfrak G\), if we remember that the \(X_a\) in the adjoint representation are given by structure constants \({C^{c}}_{\!ab}\).
Moreover, in Refs. [1, 3] we use the notation
In this language
It is easy to see that
Thus (7.40) is equivalent to (7.37) and to (7.36). (7.36) is invariant to a change of the gauge. (7.40) is invariant with respect to the action of the group \(G\) on \(P\).
Let us notice that \(h_{ab}{F^{a}}_{\!{\mu \nu }} F^{b{\mu \nu }}=h_{ab}{H^{a}}_{\!{\mu \nu }} {H^{b}}_{\!{\mu \nu }}\), even \({H^{a}}_{\!{\mu \nu }}\) is defined on \(P\) and \({F^{a}}_{\!{\mu \nu }}\) on \(E\). In the nonabelian case it is more natural to use \({H^{a}}_{\!{\mu \nu }}\) in place of \({F^{a}}_{\!{\mu \nu }}\).
Appendix B
In this appendix we find a formula for \(H_{\nu \mu }\) from Eq. (2.48). In order to do this let us solve this equation perturbatively. According to Refs. [4, 74] one gets
where \(\overset{\mathrm{(0)}}{H}_{\alpha \beta }\) is \(H_{\alpha \beta }\) in zero order of expansion with respect to \(h_{\alpha \beta }\) where
and \(\delta \overset{(k)}{H}_{\alpha \beta }\) is the \(k\)th correction to \(\overset{\mathrm{(0)}}{H}_{\alpha \beta }\). One gets
From (8.3) one gets
where \(\delta \overset{(k)}{h}{}^{\mu \nu }\) are \(k\)th corrections to \(\eta ^{\mu \nu }\) (a zero order of the inverse tensor of \(g_{\mu \nu }\), \(\eta ^{\mu \nu }\) is the inverse Minkowski tensor). We get
Equation (2.20) can be rewritten in the more convenient form
Using Eq. (8.7) and writing
we can easily prove that \(A_{\alpha \beta }=0\). This means that \(H_{\alpha \beta }=-H_{\beta \alpha }\) if \(F_{\alpha \beta }=-F_{\beta \alpha }\). Using Eqs. (8.6) and (8.7) one gets
and eventually
where
Eq. (8.11) can be rewritten in the form
where \(\overset{\mathrm{(1)}}{g}{}^{(\tau \alpha )}\) is the inverse tensor for \(g_{(\alpha \beta )}\) up to the first order of expansion with respect to \(h_{(\alpha \beta )}\). One can easily generalize this equation to any order \(k\), getting
Taking \(k\rightarrow \infty \) we get Eq. (2.48), where \(\overset{(\infty )}{H}_{\mu \nu }=H_{\mu \nu }\), \(\overset{(\infty )}{\widetilde{g}}_{(\alpha \beta )}=\widetilde{g}_{(\alpha \beta )}\).
Let us get Eq. (2.48) from the general formula in \(n\)-dimensional generalization of Einstein Unified Field Theory obtained by Hlavatý and Wrede (see Refs. [60, 75]). One gets
where


\({\widetilde{\varGamma }{}^{N}}_{\!WM}\) is the Levi–Civita connection generated by \(h_{AB}=\gamma _{(AB)}\) (\(\gamma _{[AB]}=k_{AB}\)). \(\widetilde{\nabla }_A\) is a covariant derivative with respect to the connection \({\widetilde{\varGamma }{}^{ N}}_{\!WM}\).
The connection \({\varGamma ^{N}}_{\!WM}\) is the solution of the equation
where \(D\) is an exterior covariant derivative with respect to the connection \(\varGamma \).
and all indices are raised by \(h^{AB}\) (E. Schrödinger was surprised that it was possible to find a solution to (8.19) in a covariant form). Equation (8.15) is more general than that from Refs. [60, 75] for in Eq. (8.15) \({\widetilde{\varGamma }{}^{N}}_{\!WM}\) are coefficients of the Levi–Civita connection. This connection can be considered in a nonholonomic frame. Thus \({\widetilde{\varGamma }{}^{N}}_{\!WM}\) can be nonsymmetric in indices \(W\) and \(M\). In Refs. [60, 75] \({\widetilde{\varGamma }{}^{N}}_{\!WM}\) mean Christoffel symbols. Moreover, the proof is exactly the same as in Refs. [60, 75]. The authors of [60, 75] are using the natural nonholonomic frame connected to the nonsymmetric tensor \(\gamma _{AB}\) in order to find Eq. (8.15). Moreover, this nonholonomic frame has nothing to do with the frame we consider. They assume \(\det (\gamma _{AB})\ne 0\) and \(\det (\gamma _{(AB)})\ne 0\), which is equivalent to our assumptions (2.5) and (2.6) (in the case \(n=5\) for \(\gamma _{AB}\) given by Eq. (2.15)). Let us notice there is not any constraint imposed on the torsion of the connection.
V. Hlavatý and C. R. Wrede were first to consider an \(n\)-dimensional generalization of the geometry from Einstein Unified Field Theory with the nonsymmetric real tensor \(\gamma _{AB}\).
Here we are using capital Latin indices as indices of many-dimensional manifolds. This does not result in any misunderstanding. In general, in non-Abelian theory, even in the case with spontaneous symmetry breaking, \(n=4+N+N_1\), where \(N\) is the dimension of the Lie group and \(N_1\) is the dimension of the homogeneous space (see Refs. [1, 3, 5]).
In our case we have \(n=5\) and \(\gamma _{AB}\) is given by Eq. (2.15). It is easy to see that
(in the lift horizontal basis, an anholonomic frame). Thus it is enough to calculate \({\varGamma ^{5}}_{\!{\mu \nu }}\). One gets
where all indices are raised by \(h^{\alpha \beta }\)

We are keeping the notation from Refs. [60, 75].
Moreover in Ref. [35] (see Eq. (3.16)) Levi–Civita connection coefficients for \({\widetilde{\varGamma }{}^{N}}_{\!WN}\) generated by \(\gamma _{(AB)}=h_{AB}\) are calculated. One has \({\widetilde{\varGamma }{}^{\alpha }}_{\!\beta {5}}={F^{\alpha }}_{\!\beta }\), \({\widetilde{\varGamma }{}^{5}}_{\!\beta \gamma }=F_{\beta \gamma }\), \({\widetilde{\varGamma }{}^{\beta }}_{\! 5\gamma }={F^{\beta }}_{\!\gamma }\), \({\widetilde{\varGamma }{}^{\alpha }}_{\!\beta \gamma }={\widetilde{\overline{\varGamma }}{}^{\alpha }}_{\!\beta \gamma }\) for \(\lambda =2\) (\(n=5\) in Kaluza–Klein Theory). It is easy to see that they are not symmetric in indices (they are not Christoffel symbols for the frame is not holonomic, it is a lift horizontal basis). The remaining coefficients are zero.
Using these results one gets


where we use the fact that

Eventually we get

The remaining \(K_{ABC}\) are zero. One gets
Coming back to our notation from the paper (i.e. \(k_{\mu \nu }=g_{[{\mu \nu }]}\), \(h^{\tau \alpha } =\widetilde{g}{}^{(\tau \alpha )}\)) we get
i.e. Eq. (2.48). In this way we have consistency in our theory, leading to the same results by both methods.
Appendix C
In this paper we consider two kinds of spinor fields \(\varPsi ,\overline{\varPsi }\) and \(\psi ,\overline{\psi }\) defined, respectively, on \(P\) and \(E\). The spinor fields \(\varPsi \) and \(\overline{\varPsi }\) transform according to \(\mathrm{Spin}(1,4)\) and \(\psi ,\overline{\psi }\) according to \(\mathrm{Spin}(1,3)\simeq \mathrm{SL}(2,\mathbb {C})\). We have s
\(\mathrm{SO}(1,4)\) acts linearly in \(M^{(1,4)}\) (5-dimensional Minkowski space). The Lorentz group \(\mathrm{SO}(1,3)\subset \mathrm{SO}(1,4)\). \(D^F\) is a representation of \(\mathrm{SO}(1,4)\) (de Sitter group) such that after a restriction to its subgroup \(\mathrm{SO}(1,3)\) we get
where
is the Dirac representation of \(\mathrm{SO}(1,3)\). More precisely, we deal with representations of \(\mathrm{Spin}(1,4)\) and \(\mathrm{Spin}(1,3)\simeq \mathrm{SL}(2,\mathbb {C})\) (see Ref. [76]). In other words, we want spinor fields \(\varPsi \) and \(\overline{\varPsi }\) to transform according to such a representation of \(\mathrm{Spin}(1,4)\) which is induced by the Dirac representation of \(\mathrm{SL}(2,\mathbb {C})\). The complex dimensions of both representations are the same: 4. They are also Clifford algebras,
One gets (up to a phase)
The spinor fields \(\psi \) and \(\overline{\psi }\) transform according to Dirac representation, \(\overline{\psi }=\psi ^+B\). Our matrices \(\gamma _\mu \) and \(\gamma _A\) are representations of \(C(1,3)\) (\(C(1,4)\)). One can consider projective representations for \(\varPsi \) and \(\psi \), i.e. representations of \(\mathrm{Spin}(1,3)\otimes \text {U}(1)\) and \(\mathrm{SL}(2,\mathbb {C})\otimes \text {U}(1)\). Moreover, we do not develop this idea here.
In this paper we develop the following approach to spinor fields on \(E\) and on \(P\). We introduce orthonormal frames on \(E\) (\(\mathrm{d}x^1\), \(\mathrm{d}x^2\), \(\mathrm{d}x^3\), \(\mathrm{d}x^4\)) and on \(P\) (\(\mathrm{d}X^1=\pi ^*(\mathrm{d}x^1)\), \(\mathrm{d}X^2=\pi ^*(\mathrm{d}x^2)\), \(\mathrm{d}X^3=\pi ^*(\mathrm{d}x^3)\), \(\mathrm{d}X^4=\pi ^*(\mathrm{d}x^4)\), \(\mathrm{d}X^5\)). Our spinors \(\varPsi \) on \((P,\gamma _{(AB)})\) and \(\psi \) on \((E,g_{(\alpha \beta ))}\) are defined as complex bundles \(\mathbb {C}^4\) over \(P\) or \(E\) with homomorphisms \(\rho :C(1,4)\rightarrow \mathcal {L}(\mathbb {C}^4)\) (resp. \(\rho :C(1,3)\rightarrow \mathcal {L}(\mathbb {C}^4)\)) of bundles of algebras over \(P\) (resp. \(E\)) such that for every \(p\in P\) (resp. \(x\in E\)), the restriction of \(\rho \) to the fiber over \(p\) (resp. \(x\)) is equivalent to the spinor representation of the Clifford algebra \(C(1,4)\) (resp. \(C(1,3)\)), i.e. \(D^F\) (resp. Dirac representation, see Refs. [79, 80]). (There is also a paper on a similar subject (see Ref. [81]).) Spinor fields \(\varPsi \) and \(\psi \) are sections of these bundles. There is also an approach to consider spinor bundles for \(\varPsi \) and \(\psi \) as bundles associated to principal bundles of orthonormal frames for \((P,\gamma _{(AB)})\) or \((E,g_{(\alpha \beta )})\) (spin frames). Spinor fields \(\varPsi \) and \(\psi \) are sections of these bundles. In our case we consider spinor fields \(\varPsi \) and \(\overline{\varPsi }\) transforming according to (5.13) and (5.14). In the case of \(\psi \) and

If the spinor field \(\psi \) corresponds to \(\overline{\theta }{}^\alpha \) and \(\psi '\) to \(\overline{\theta }{}^{\alpha \prime }\) we get

Spinor fields \(\varPsi \) and \(\overline{\varPsi }\) are \(\psi \) and \(\overline{\psi }\) in any section of a bundle \(P\). Simultaneously we assume the conditions (5.2).
Similarly as for \(\varPsi ,\overline{\varPsi }\) one gets


Appendix D
In this paper we proceed toward unification and geometrization of gravitational and electromagnetic interactions. Moreover, there is an approach (see Refs. [82–87]) which is going in a different direction. In that direction, the authors of those papers are transforming all possible alternative theories of gravitation described by some geometric notions, i.e. connections, torsions, metric tensors, and also with nonstandard Lagrangians, i.e. nonlinear Lagrangians (\(f(R)\), \(f(R^{\mu \nu }R_{\mu \nu })\), \(f\left( \left( {R^{\alpha }}_{\!\beta {\mu \nu }} \varepsilon ^{{\mu \nu }\lambda \rho }{R^{\beta }}_{\!\alpha \lambda \rho }\right) ^2\right) \) etc.) to GR with additional ‘matter fields’. In our notation \(f\) means an arbitrary function, \(R\) is the scalar curvature, \(R_{\mu \nu }\) is the Ricci tensor, \({R^{\alpha }}_{\!\beta {\mu \nu }}\) means the curvature tensor (not necessarily Riemann–Christoffel tensor). One can consider also some different Lagrangians, i.e. \(f(g_{\mu \nu },R_{\mu \nu })\). In this way some unified theories, even Einstein Unified Field Theory, can be transformed into GR (General Relativity) plus some additional ‘matter fields’, i.e. scalar fields, vector fields, and so on. This is possible of course by using Legendre transformation techniques to define a new metric (symmetric) tensor and the Levi–Civita connection compatible with this tensor.
The interpretation of this new tensor and the new connection can be complex. They could not have clear physical interpretation. In the case of nonsymmetric Kaluza–Klein theory considered in this paper we proceed in a little different way.
Let us consider our nonsymmetric connection \({\overline{W}{}^{\lambda }}_{\!\mu }\) and \({\overline{w}{}^{\lambda }}_{\!\mu }\) on a space–time \(E\). Using results from Ref. [60] we can write (see Sect. 1):
and
where \({\widetilde{\overline{\varGamma }}{}^{\lambda }}_{\!{\mu \nu }}\) is the Levi–Civita connection induced by \(g_{(\alpha \beta )}\) on \(E\) and

\(\widetilde{\overline{\nabla }}{}\) is a covariant derivative with respect to the Levi–Civita connection \({\widetilde{\overline{\varGamma }}{}{}^{\alpha }}_{\!\beta \gamma } ({\widetilde{\overline{w}}{}{}^{\alpha }}_{\!\beta })\). We have of course
and
Starting from the formula for the 2-form of the curvature:
one gets
where \({\widetilde{\overline{\varOmega }}{}{}^{\alpha }}_{\!\beta }\) is the 2-form of the curvature for a Levi–Civita connection \({\widetilde{\overline{w}}{}{}^{\alpha }}_{\!\beta }\) on \(E\).
From the formula above we can easily read the tensor of the curvature \({\overline{R}{}^{\alpha }}_{\!\beta \delta \gamma }(\overline{W})\) and afterwards the Moffat–Ricci tensor as given below:

where \(\widetilde{\overline{R}}{}_{\beta \gamma }\) is the Ricci tensor for a Levi–Civita connection generated by \(g_{(\alpha \beta )}\). We get also the Moffat–Ricci tensor for \({\overline{W}{}^{\lambda }}_{\!\mu }\). One gets
The final result reads

One can also write the scalar curvature

Thus now we can write the Einstein equations
in the following way:
Taking the symmetric and anti symmetric part of equation (10.14) one gets
One can eliminate \(\overline{W}_\mu \) from the theory using (10.16) and getting
Let us consider our second Maxwell equation, i.e. Eq. (2.46) writing it in a new way. One gets
In this way we get the Einstein equations Eq. (10.15) and the second pair of Maxwell equations in GR (10.18).
Moreover, we get a supplementary condition Eq. (10.17). In this way our unified theory is equivalent to GR plus additional ‘matter fields’. Moreover, our ‘matter field’ has pure geometrical origin. We get additional terms on the right-hand side of Einstein equations (some additional terms for an effective energy–momentum tensor). We get also Eq. (2.30) (i.e. \({{\mathop {g}_{\sim }}^{[{\mu \nu }]}}_{,\nu }=0\)) which is a field equation for skewon \(g_{[{\mu \nu }]}\). We get also additional currents on the right-hand side of the second pair of Maxwell equations. This is similar to the case of Einstein–Cartan theory (see Ref. [88] and references cited therein). In this case the theory is described by the metric (symmetric) tensor and the metric connection on a space–time, which can have non-zero torsion. The external sources are the energy–momentum tensor (not necessary symmetric) and spin density. One gets the following equations:
\({Q^{\rho }}_{\!{\mu \nu }}\) is the tensor of torsion for the metric connection, \(R_{\mu \nu }\) and \(R\) are Ricci tensor and the scalar curvature for the connection, \(t_{\mu \nu }\) is an energy–momentum tensor, \({s^{\rho }}_{\!{\mu \nu }}\) is the spin density tensor. Equation (10.20) can be solved getting the torsion (and a contorsion)
Finally, we get the connection on a space–time and we can rewrite Eq. (10.19) in the following way:
where \(\widetilde{R}_{\mu \nu }\), \(\widetilde{R}\), \(\widetilde{\nabla }\) are Ricci tensor, scalar curvature, and covariant derivative with respect to the Levi–Civita connection generated by \(g_{\alpha \beta }\). Equation (10.24) gives the Belifante–Rosenfeld symmetrization of the canonical energy–momentum tensor. On the right-hand side of Eq. (10.22) we have additional ‘matter fields’, and on the left-hand side a typical term—the Einstein tensor in GR.
We can perform a very similar procedure in the case of Moffat (see Ref. [7]) and Einstein–Cartan–Moffat theory (see Ref. [89]) using both procedures described above. In the case of Kaluza–Klein Theory with torsion (see Refs. [35, 36]) a method similar to Einstein–Cartan Theory can be applied. In all of these cases GR with additional ‘matter fields’ uses the same metric tensor as in original theory, which is not true in the case of Refs. [82–87]. Thus we have no problems with the physical interpretation of the symmetric metric and we can consider our theory as GR plus additional ‘matter fields’, which have a geometrical interpretation. In this way we can complete the Einstein program of the geometrization of physical interactions getting ‘interference effects’ between gravitational and electromagnetic fields and prove that GR is a distinguished gravitational theory among alternative theories of gravitation and unified field theories.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Kalinowski, M.W. On some developments in the Nonsymmetric Kaluza–Klein Theory. Eur. Phys. J. C 74, 2742 (2014). https://doi.org/10.1140/epjc/s10052-014-2742-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-014-2742-5