Abstract
Recently, it has been argued that in the supersymmetric extension of the seesaw-extended Standard Model, heavy right-handed neutrinos and sneutrinos may give corrections as large as a few GeV to the mass of the lightest neutral CP-even Higgs boson, even if the soft supersymmetry-breaking parameters are of order the electroweak scale. The presence of such large corrections would render precise Higgs masses incalculable from measurable low-energy parameters. We show that this is not the case: decoupling is preserved in the appropriate sense and right-handed (s)neutrinos, if they exist, have negligible impact on the physical Higgs masses.


Similar content being viewed by others
Change history
08 July 2021
An Erratum to this paper has been published: https://doi.org/10.1140/epjc/s10052-021-09364-6
Notes
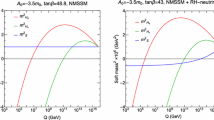
These contributions to m h are therefore quite distinct from corrections that have been found in certain parameter ranges of the NMSSM with TeV-scale right-handed neutrinos [38].
In our notation, the sum of all one-loop Feynman graphs contributing to the ϕϕ (ϕ=h,A,H) and ZZ self-energy functions are denoted by −iC ϕϕ (p 2) and iA ZZ (p 2)g μν +iB ZZ (p 2)p μν , respectively, where p is the four-momentum of the incoming boson. Only \(\varSigma_{ZZ}(p^{2})\equiv \operatorname{Re} A_{ZZ}(p^{2})\) and \(\varSigma_{\phi\phi}(p^{2})\equiv \operatorname{Re} C_{\phi\phi}(p^{2})\) are needed to define the physical on-shell boson masses. Note that the opposite sign choice in the definition of Σ(p 2) is sometimes employed in the literature.
To simplify the typography, we remove all P subscripts. However, all masses in the subsequent formulas should now be interpreted as (finite) physical masses.
The choice of evaluating the p 2-derivatives of the self-energies at p 2=0 is one of many possible choices. Employing a different value of p 2 would simply yield a tanβ definition that differs at the one-loop level. In the approximations used in this paper, the difference in the two definitions of tanβ is subdominant and can thus be neglected.
The case where \(m_{\tilde{R}}\) and/or B ν are parametrically larger than the electroweak scale will be briefly considered in Sect. 3.4.
Note that the self-energy and tadpole functions in the conventions of Ref. [27] differ by an overall sign from those defined in this paper.
References
S. Chatrchyan et al. (CMS Collaboration), Phys. Lett. B 716, 30 (2012). arXiv:1207.7235 [hep-ex]
G. Aad et al. (ATLAS Collaboration), Phys. Lett. B 716, 1 (2012). arXiv:1207.7214 [hep-ex]
S. Heinemeyer, O. Stal, G. Weiglein, Phys. Lett. B 710, 201 (2012). arXiv:1112.3026 [hep-ph]
P. Draper, P. Meade, M. Reece, D. Shih, Phys. Rev. D 85, 095007 (2012). arXiv:1112.3068 [hep-ph]
A. Arbey, M. Battaglia, A. Djouadi, F. Mahmoudi, J. Quevillon, Phys. Lett. B 708, 162 (2012). arXiv:1112.3028 [hep-ph]
L.J. Hall, D. Pinner, J.T. Ruderman, J. High Energy Phys. 1204, 131 (2012). arXiv:1112.2703 [hep-ph]
U. Ellwanger, J. High Energy Phys. 1203, 044 (2012). arXiv:1112.3548 [hep-ph]
H.E. Haber, R. Hempfling, Phys. Rev. Lett. 66, 1815 (1991)
Y. Okada, M. Yamaguchi, T. Yanagida, Prog. Theor. Phys. 85, 1 (1991)
J.R. Ellis, G. Ridolfi, F. Zwirner, Phys. Lett. B 262, 477 (1991)
M.S. Carena, J.R. Espinosa, M. Quiros, C.E.M. Wagner, Phys. Lett. B 355, 209 (1995). arXiv:hep-ph/9504316
M.S. Carena, M. Quiros, C.E.M. Wagner, Nucl. Phys. B 461, 407 (1996). arXiv:hep-ph/9508343
H.E. Haber, R. Hempfling, A.H. Hoang, Z. Phys. C 75, 539 (1997). arXiv:hep-ph/9609331
S. Heinemeyer, W. Hollik, G. Weiglein, Phys. Rev. D 58, 091701 (1998). arXiv:hep-ph/9803277
S. Heinemeyer, W. Hollik, G. Weiglein, Phys. Lett. B 440, 296 (1998). arXiv:hep-ph/9807423
S. Heinemeyer, W. Hollik, G. Weiglein, Eur. Phys. J. C 9, 343 (1999). arXiv:hep-ph/9812472
J.R. Espinosa, R.J. Zhang, J. High Energy Phys. 0003, 026 (2000). arXiv:hep-ph/9912236
J.R. Espinosa, R.J. Zhang, Nucl. Phys. B 586, 3 (2000). arXiv:hep-ph/0003246
M. Carena, H.E. Haber, S. Heinemeyer, W. Hollik, C.E.M. Wagner, G. Weiglein, Nucl. Phys. B 580, 29 (2000). arXiv:hep-ph/0001002
G. Degrassi, P. Slavich, F. Zwirner, Nucl. Phys. B 611, 403 (2001). arXiv:hep-ph/0105096
A. Brignole, G. Degrassi, P. Slavich, F. Zwirner, Nucl. Phys. B 631, 195 (2002). arXiv:hep-ph/0112177
S.P. Martin, Phys. Rev. D 67, 095012 (2003). arXiv:hep-ph/0211366
S.P. Martin, Phys. Rev. D 75, 055005 (2007). hep-ph/0701051
R.V. Harlander, P. Kant, L. Mihaila, M. Steinhauser, Phys. Rev. Lett. 100, 191602 (2008). Phys. Rev. Lett., 101, 039901, 2008. arXiv:0803.0672 [hep-ph]
P. Kant, R.V. Harlander, L. Mihaila, M. Steinhauser, J. High Energy Phys. 1008, 104 (2010). arXiv:1005.5709 [hep-ph]
G. Degrassi, S. Di Vita, J. Elias-Miro, J.R. Espinosa, G.F. Giudice, G. Isidori, A. Strumia, J. High Energy Phys. 1208, 098 (2012). arXiv:1205.6497 [hep-ph]
S. Heinemeyer, M.J. Herrero, S. Penaranda, A.M. Rodriguez-Sanchez, J. High Energy Phys. 1105, 063 (2011). arXiv:1007.5512 [hep-ph]
Y. Grossman, H.E. Haber, Phys. Rev. Lett. 78, 3438 (1997). hep-ph/9702421
J. Hisano, T. Moroi, K. Tobe, M. Yamaguchi, T. Yanagida, Phys. Lett. B 357, 579 (1995). hep-ph/9501407
J. Hisano, T. Moroi, K. Tobe, M. Yamaguchi, T. Yanagida, Phys. Rev. D 53, 2442 (1996). hep-ph/9510309
J.R. Ellis, J. Hisano, M. Raidal, Y. Shimizu, Phys. Rev. D 66, 115013 (2002). hep-ph/0206110
A. Masiero, S.K. Vempati, O. Vives, New J. Phys. 6, 202 (2004). hep-ph/0407325
E. Arganda, A.M. Curiel, M.J. Herrero, D. Temes, Phys. Rev. D 71, 035011 (2005). hep-ph/0407302
J.R. Ellis, O. Lebedev, Phys. Lett. B 653, 411 (2007). arXiv:0707.3419 [hep-ph]
A. Dedes, H.E. Haber, J. Rosiek, J. High Energy Phys. 0711, 059 (2007). arXiv:0707.3718 [hep-ph]
M. Asano, T. Kubo, S. Matsumoto, M. Senami, Phys. Rev. D 80, 095017 (2009). arXiv:0807.4922 [hep-ph]
M. Hirsch, F.R. Joaquim, A. Vicente, J. High Energy Phys. 1211, 105 (2012). arXiv:1207.6635 [hep-ph]
W. Wang, J.M. Yang, L.L. You. arXiv:1303.6465 [hep-ph]
J.F. Gunion, H.E. Haber, Nucl. Phys. B 278, 449 (1986)
A. Dobado, M.J. Herrero, S. Penaranda, Eur. Phys. J. C 7, 313 (1999). hep-ph/9710313
A. Dobado, M.J. Herrero, S. Penaranda, Eur. Phys. J. C 12, 673 (2000). hep-ph/9903211
M.S. Berger, Phys. Rev. D 41, 225 (1990)
W. Siegel, Phys. Lett. B 84, 193 (1979)
D.M. Capper, D.R.T. Jones, P. van Nieuwenhuizen, Nucl. Phys. B 167, 479 (1980). For a recent review, see T. Jones, PoS LL 2012, 011 (2012)
S. Weinberg, Phys. Lett. B 91, 51 (1980)
A. Freitas, D. Stockinger, Phys. Rev. D 66, 095014 (2002). hep-ph/0205281
Acknowledgements
We would like to acknowledge fruitful discussions with Sven Heinemeyer and Maria Herrero concerning the work of Ref. [27]. We are also grateful to the anonymous referee whose critique of earlier versions of this manuscript resulted in significant improvements to the presentation. PD and HEH are supported in part by U.S. Department of Energy grant number DE-FG02-04ER41286.
Author information
Authors and Affiliations
Corresponding author
Appendix: Approximate renormalized self-energies and tadpoles
Appendix: Approximate renormalized self-energies and tadpoles
It is convenient to have analytic approximations for the self-energy functions and tadpoles in order to see how the terms sensitive to the seesaw scale explicitly cancel in the expressions for the Higgs masses [Eqs. (2.18) and (2.19)]. Following Ref. [27], we perform a series expansion in powers of \(m_{D}^{2}\). At \(\mathcal{O}(m_{D}^{0})\), the contributions are insensitive to the seesaw scale. At \(\mathcal{O}(m_{D}^{4})\), each self-energy scales as \(m_{M}^{-2}\), exhibiting decoupling independently, in agreement with Ref. [27]. In contrast, decoupling occurs in the \(\mathcal{O}(m_{D}^{2})\) terms due to non-trivial cancellations among the various terms in Eqs. (2.18) and (2.19).
Below we give the \(\mathcal{O}(m_{D}^{2})\) contributions to the real parts of the self-energy functions and tadpolesFootnote 7 in d-spacetime dimensions using dimensional regularization, expanded to leading order with respect to the mass hierarchy
It is convenient to adopt the shorthand notation
where Q is the renormalization scale, \(\epsilon\equiv2-\frac{1}{2} d\) and γ is Euler’s constant. The \(\mathcal{O}(m_{D}^{2})\) contribution to Σ hh (p 2) at leading order in the mass hierarchy [cf. Eq. (A.1)] is given by
where p is the incoming four momentum. Likewise, Σ HH (p 2) is obtained by making the replacement \(\alpha\to\alpha-\frac{1}{2}\pi\) in Eq. (A.3),
For completeness, we provide the \(\mathcal{O}(m_{D}^{2})\) contribution to the real parts of all the other relevant self-energy functions [at leading order in the mass hierarchy, Eq. (A.1)],
Next, we compute the \(\mathcal{O}(m_{D}^{2})\) contributions [at leading order in the mass hierarchy, Eq. (A.1)] to the counterterm δtanβ in the various renormalization schemes. In the HM scheme, δtanβ is given by Eq. (2.26). Using the above expressions for the self-energy functions, along with Eq. (2.20) and the following tree-level relations (cf. Eq. (A.20) of Ref. [39]):
we obtain after considerable simplification,
Note that the \(\mathcal{O}(m_{D}^{2})\) contributions to the counterterm δtanβ in the HM and DEC schemes are equivalent, in light of the absence of non-decoupling terms in Eq. (3.8). Indeed, the \(\mathcal{O}(m_{D}^{2})\) contribution to δtanβ is independent of the tree-level Higgs mixing angle α. Although this result is obvious in the DEC scheme (which is defined via Higgs wave function counterterms that are evaluated at α=0), the cancellation of the α-dependence in the \(\mathcal{O}(m_{D}^{2})\) contribution to \(\delta\tan\beta_{\rm{HM}}\) [defined in Eq. (2.26)] is highly non-trivial.
In contrast, in the \(\overline{\rm DR}\) scheme only the ϵ −1−γ+log4π is retained, so that the corresponding \(\mathcal{O}(m_{D}^{2})\) contribution is simply
Rights and permissions
About this article
Cite this article
Draper, P., Haber, H.E. Decoupling of the right-handed neutrino contribution to the Higgs mass in supersymmetric models. Eur. Phys. J. C 73, 2522 (2013). https://doi.org/10.1140/epjc/s10052-013-2522-7
Received:
Revised:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-013-2522-7