1 Introduction

A robust description of chiral symmetry restoration and its manifestation in a medium of partially deconfined quarks and gluons is essential to making progress in understanding the properties of QCD matter under extreme conditions, such as those created in the laboratory during the ultra-relativistic heavy-ion collisions or fill the core of neutron stars.

Effective models are a flexible exploratory tool to study a dynamical system. One of the advantage is the ability to temporarily include (or suppress) a certain class of interactions or diagrams and examining the effect in isolation. One can also gain insights on the values of phenomenological parameters used and examine their connections to the properties of underlying constituents. These make this approach useful to complement the more powerful numerical methods such as lattice QCD (LQCD).

In this paper we study the in-medium dressing of the four-quark interaction by resumming a class of ring diagrams within an effective chiral quark model. Screening of the potential by ring diagram finds the most famous application in regulating the long-range Coulomb forces in an electron gas [1, 2]. (See Refs [3, 4] for discussions in condensed matter theory.) Here we shall see that it reveals rich features of the QCD phase diagram in an effective model [5,6,7,8].

In a previous work [9] we have demonstrated that polarization provides a natural mechanism to connect the large transition temperature scale (\(T_d \approx 270\) MeV) in a pure gauge theory and that of chiral symmetry restoration (\(T_{pc} \approx 156.5\) MeV) in the presence of light, dynamical quarks. It also drives the phenomenon of inverse magnetic catalysis [10, 11] at finite temperatures, i.e. the chiral condensate decreases more rapidly with temperature in the presence of a magnetic field.

In this work we explore further theoretical issues of the proposed model. We shall revisit the chiral condensate and in addition examine how the Polyakov loops are influenced by the ring diagram. We shall also elucidate some details in the calculation of the polarization tensors in the vector, scalar and pseudoscalar channels. While the calculation of ring diagram with a given quark mass is well known [12,13,14,15], its feeding back to the quark gap equation for consistent solution, and thereby including the backreaction, is usually not performed in studies of effective quark model. As we shall see, it is precisely this extra step that leads to a substantial change in the temperature and magnetic field dependences of quark condensate, and is demonstrated to improve the description of many aspects of QCD phase diagram. A merit of the current scheme is that there is no need to introduce an artificial tuning of \(T_d\) parameter in the gluon sector, nor the need to introducing an explicit B-dependent coupling, as advocated in Refs. [16, 17]. Instead, the mechanism serve as a tentative explanation for such a medium dependence.

2 Chiral quark model with dressed interaction

We begin with a brief review of the theoretical model: an effective chiral quark model motivated from the Coulomb Gauge QCD [5, 18,19,20,21,22,23,24]. The Lagrangian density reads:

(1)

where \(\rho ^a(x) = {\bar{\psi }}(x) \gamma ^0 T^a \psi (x)\) is the color quark current and \(T^a\) is a generator of the \(SU(N_c)\) symmetry group, with \(a = 1, 2, \ldots , N_c^2-1\). For the class of model where the interaction potential V is instantaneous and color-diagonal, i.e.,

$$\begin{aligned} V^{ab}(x, y) \rightarrow \delta ^{ab} \times \delta (x^0-y^0) \, V(\mathbf {x}-\mathbf {y}), \end{aligned}$$
(2)

the gap equation for the dynamical quarks has been derived [5]. The leading order result can be summarized as follows:

(3)

where

$$\begin{aligned} \varSigma (p) = C_F \, \int \frac{d^4 q}{(2 \pi )^4} \, V(\mathbf {p}-\mathbf {q}) \, i \, \gamma ^0 S(q) \gamma ^0. \end{aligned}$$
(4)

The constant \(C_F = \frac{N_c^2-1}{2 N_c}\) is introduced via the quadratic Casimir operator

$$\begin{aligned} \sum _{a=1}^{N_c^2-1} \, T^a T^a = C_F \, {\mathcal {I}}_{N_c \times N_c}. \end{aligned}$$
(5)

The solution to the gap equation (3) can be parametrized as

$$\begin{aligned} S^{-1}(p) = A_0(p) \, p^0 \gamma ^0 - A(p) \, \mathbf {p} \cdot \mathbf {\gamma } - B(p) \end{aligned}$$
(6)

with the quark dressing functions, to be determined self-consistently, given by

$$\begin{aligned}&A_0(p) = 1\nonumber \\&A(p) = 1 + C_F \, \int \frac{d^3 q}{(2 \pi )^3} \, V(\vec {p}-\vec {q}) \, \frac{A(q)\hat{p}\cdot \hat{q}}{2 \tilde{E}(q)}\varTheta \nonumber \\&B(p) = m + C_F \, \int \frac{d^3 q}{(2 \pi )^3} \, V(\vec {p}-\vec {q}) \, \frac{B(q)}{2 \tilde{E}(q)} \, \varTheta \nonumber \\&\varTheta = 1 - 2 \, N_\mathrm{th}(\tilde{E}), \end{aligned}$$
(7)

where \({\tilde{E}}(q) = \sqrt{ A(q)^2 \mathbf {q}^2 + B(q)^2} \) is a generalized energy function of the dynamical quarks, \(N_\text {th}(E) = \frac{1}{e^{\beta E}+1} \) is the Fermi-Dirac distribution.

Considering an instantaneous gluon potential (2) means that there is no \(p_0\) dependence in the gap equations. The remaining dependence on the 3-momentum \(\mathbf {p}\) disappears when considering a contact interaction: taking

$$\begin{aligned} V(\mathbf {p}-\mathbf {q}) \rightarrow V_0 \end{aligned}$$
(8)

in Eq. (7) immediately forces \(A(p) = 1\), and the quark mass function reduces to

$$\begin{aligned} M = m + C_F \, V_0 \, \int \frac{d^3 q}{(2 \pi )^3} \, \frac{M}{2 \sqrt{q^2 + M^2}} \varTheta . \end{aligned}$$
(9)

This is of the same form as the familiar result for quark mass (\(N_f\) flavors) in the model [12] of Nambu and Jona-Lasinio (NJL), with the identification

$$\begin{aligned} C_F \, V_0 \leftrightarrow 4 \, N_c \, N_f \, (2 \, G_\text {NJL}). \end{aligned}$$
(10)

In fact the present model provides a more natural starting point as an effective model of QCD: First, it closely mimics the quark-gluon interactions of QCD by implementing a vector nature of the four-quark interactions originated from a gluon exchange, both in the color and the Dirac space. Note that an effective interaction in the scalar-scalar channel is also generated from such vector-vector (from Fock-type exchange), giving rise to a spontaneous chiral symmetry breaking. This may also be understood from a Fierz transformation [25] of the original Lagrangian in Eq. (1): a vector-vector interaction can generate scalar-scalar type interactions (and vice versa). Second, it makes possible a systematic improvement on the quark potential by taking into account features of gluon propagators, e.g. momentum dependence.

The generalization of the model (9) to include an in-medium dressing of the interaction potential \(V_0\) via the polarization tensor \(\varPi _{00}\) [5] proceeds by:

$$\begin{aligned} \tilde{V_0}^{-1} = {V_0}^{-1} - \frac{1}{2} \, N_f \, \varPi _{00} \end{aligned}$$
(11)

where

(12)

Here denotes a Matsubara sum over the fermionic frequencies (\(\omega _n = (2n+1) \, \pi /\beta \)), and an integral over the momenta \(d^3 q\). In this work we work only in the static, vanishing momentum limit of the ring and thus \(p^0 =0, \mathbf {p} \rightarrow \mathbf {0}\) are eventually taken in the calculation.

Equation (11) can be understood as the dressing of the gluon propagator by the Debye mass. The factor of \(\frac{1}{2}\) in Eq. (11) originates from the color structure, i.e. \(\text {Tr} \, T^a T^b = \frac{1}{2} \, \delta ^{ab}\), and is essential to reproduce the known result [26] of the perturbative Debye mass for QCD, instead of QED.

We choose to work in an effective model with quarks and gluons as the degrees of freedom. According to quark-hadron duality one should be able to include the hadron effects by including, and iterating, multi-particle interactions among quarks and gluons. The appearance of the higher order terms in a quark-based picture, however, is different from those constructed out of mesons. There is no one-to-one mapping without further approximation [6, 7, 27, 28]. Even in the usual NJL model [12], where a Hubbard-Stratonovich transformation is used to introduce the meson fields, the kinetic terms [29] of mesons are not formally derived. In this work we shall explore the effect of quark loops and their feeding back to the quark gap equation, thus going beyond the standard mean-field treatment.

In many studies, polarization tensors are computed with the fermion propagator determined from a leading order mean-field gap equation such as Eq. (9). The use of \(\tilde{V_0}\), in lieu of \(V_0\), amounts to implementing a back-reaction of the fermion loops to the fermionic gap equation. In the language of condensed matter theory, the scheme is similar to an iteration of GW-scheme [3, 4] with polarization insertions but without vertex corrections. This effectively dresses the four-quark interaction and can substantially modify aspects of chiral phase transition, such as driving the phenomenon of inverse magnetic catalysis.

3 Polarization tensors

Many observables within an NJL-like model can be understood in terms of the following integrals [12, 15]:

(13)

Note that the (constituent) quark mass dependence enters via \(E_i = \sqrt{\mathbf {q}_i^2 + M^2}\), where \(\mathbf {q}_1 = \mathbf {q}\) and \(\mathbf {q}_2 = \mathbf {q}+\mathbf {p}\). These integrals can be decomposed into a UV-divergent vacuum piece and a finite temperature piece. For example, \(I_0\) can be written as

$$\begin{aligned} I_0 = I_0^\text {vac} + I_0^T. \end{aligned}$$
(14)

The first piece requires regularization, e.g., by a 3D regulator \({\mathcal {R}}_\text {3D}(q) = e^{-q^2/\varLambda ^2}\):

$$\begin{aligned} I_0^\text {vac} \rightarrow \int \frac{d^3 q}{(2 \pi )^3} \, \frac{1}{2 E_1} \, {\mathcal {R}}_\text {3D}(q). \end{aligned}$$
(15)

Alternatively, one can choose a 4D cutoff scheme:

$$\begin{aligned} I_0^\text {vac} \rightarrow \int \frac{d^4 q_E}{(2 \pi )^4} \, \frac{1}{q_E^2 + E_1^2} \, {\mathcal {R}}_{4D}(q), \end{aligned}$$
(16)

or a Schwinger proper-time regularization scheme:

$$\begin{aligned} I_0^\text {vac} \rightarrow \int _{1/\varLambda ^2}^{\infty } \, \frac{dt}{(16 \pi ^2)} \, \frac{1}{t^2} \, e^{-M^2 \, t}. \end{aligned}$$
(17)

The finite temperature piece, on the other hand, requires no regularization, and is given by

$$\begin{aligned} I_0^T = \int \frac{d^3 q}{(2 \pi )^3} \, \frac{-1}{2 E_1} \times 2 N_\text {th}(E_1), \end{aligned}$$
(18)

Under a general regularization scheme, the finite temperature piece of \(I_0\) can be defined in a regularization independent manner [30, 31] by

$$\begin{aligned} I_0^T = \lim _{\varLambda \rightarrow \infty } \, \left( I_0(T, \varLambda ) - I_0(T \rightarrow 0, \varLambda ) \right) . \end{aligned}$$
(19)

Similar analysis can be applied to \(I_1\) and \(I_2\). The results are:

$$\begin{aligned} \begin{aligned} I_1(p^0, \mathbf {p})&= \int \frac{d^3 q}{(2 \pi )^3} \, \frac{-1}{4 E_1 E_2} \times (Q_1 + Q_2), \\ Q_1&= ({\mathcal {R}}(q)-N_1-N_2) \, \\&\quad \times \left( \frac{1}{p^0-E_1-E_2}-\frac{1}{p^0+E_1+E_2}\right) \\ Q_2&= (N_1-N_2) \, \\&\quad \times \left( \frac{1}{p^0-E_1+E_2}-\frac{1}{p^0+E_1-E_2}\right) \end{aligned} \end{aligned}$$
(20)

and

$$\begin{aligned} \begin{aligned} I_2(p^0, \mathbf {p})&= -\int \frac{d^3 q}{(2 \pi )^3} \, \frac{\mathbf {q}^2 + \mathbf {q} \cdot \mathbf {p}}{4 E_1 E_2} \times \, (Q_1 + Q_2), \\ \end{aligned} \end{aligned}$$
(21)

where \(N_i = N_\text {th}(E_i)\).

The merit of studying these expressions (13) is that various results of the model can be written in terms of them. For example, the gap equation in Eq. (9) can be neatly expressed as

$$\begin{aligned} M = m + C_F \, V_0 \, M \times I_0. \end{aligned}$$
(22)

The chiral condensate (per flavor) is given by

$$\begin{aligned} \langle {\bar{\psi }} \, \psi \rangle = - 4 N_c M \times I_0. \end{aligned}$$
(23)

Moreover, the pion decay constant (\(N_f=2\)) can be estimated from the low energy limit of \(I_1\) by

$$\begin{aligned} f_\pi ^2 \approx 4 N_c M^2 \times I_1(p^0 \rightarrow 0, \mathbf {p}=\mathbf {0}). \end{aligned}$$
(24)

In this work the four-quark coupling \({\tilde{V}}_0\) in Eq. (11) is dressed by the \(\varPi _{00}\) polarization tensor evaluated at the static limit. Note that the full polarization tensor \(\varPi _{00}(p^0, \mathbf {p})\) can also be expressed in terms of integrals in Eq. (13) as

$$\begin{aligned} \varPi _{00}(p^0, \mathbf {p}) = 4 \left( -I_0 + (-\frac{1}{2} p^2 + 2 M^2) \, I_1 + 2 I_2 \right) . \end{aligned}$$
(25)

In the zero-temperature and static limit the expression in Eq. (25) vanishes. This is a familiar result in the Hard-Thermal-Loop (HTL) study [32], where a further \(M \rightarrow 0\) limit is implicitly taken. The relation remains true for a general M, as one can directly verify

$$\begin{aligned} \varPi _{00}(0, \mathbf {p}=\mathbf {0}) \propto \left( -I_0 + 2 M^2 \, I_1(0, \mathbf {0}) + 2 I_2(0, \mathbf {0}) \right) , \end{aligned}$$
(26)

and the second and third terms add up to \(I_0\), exactly canceling the first term. See Eqs. (20) and (21).

For the finite temperature part, besides a direct numerical evaluation of Eq. (25), an alternative convenient method to obtain the result [9] is through a formal relation to the thermal pressure of a free (single species) fermion gas at finite temperature and vanishing chemical potential:

(27)

Note that \(S^{-1}(q) = (i \, \omega _n + \mu ) \, \gamma ^0 - \mathbf {q} \cdot \mathbf {\gamma } - M\), and we set \(\mu \rightarrow 0\) after taking the derivatives. This yields an explicit expression:

$$\begin{aligned} \varPi _{00}^T(p^0=0, \mathbf {p} \rightarrow \mathbf {0}) = -\int \frac{d^3 q}{(2 \pi )^3} \, 4 \beta N_1 (1-N_1). \end{aligned}$$
(28)

Similar analysis can be performed on other channels, e.g. for scalar and pseudoscalar cases:

(29)

and

(30)

The finite temperature contribution of scalar polarization can also be extracted by taking derivatives of pressure, now with respect to M rather than to \(\mu \):

(31)

which has the following limits: (1) at small M,

$$\begin{aligned} \varPi _{S}^T(p^0=0, \mathbf {p} \rightarrow \mathbf {0}) \approx -\frac{1}{6} \, T^2 \end{aligned}$$
(32)

verifying the low mass (or high temperature) expansion by Haber and Weldon [26, 33]; and (2) the Boltzmann approximation,

$$\begin{aligned} \varPi _{S}^T(p^0=0, \vec {p} \rightarrow \vec {0})\approx & {} \frac{2}{\pi ^2} \, M^2 \times \nonumber \\&\left( K_0(M/T) - \frac{T}{M} K_1(M/T) \right) , \end{aligned}$$
(33)

where \(K_n\)’s are the modified spherical Bessel function of the second kind. Note the competition between the two terms in Eq. (33): the latter, negative contribution dominates at \(M/T \ll 1\), while the former positive contribution determines the \(M/T \gg 1\) behavior. This simply reflects the mass dependence of the thermal pressure of a free fermion gas \(P_F\): while the pressure drops, at fixed T, when M increases, the rate of change, reflected by \(\frac{\partial ^2}{\partial M \partial M} \, P_F\), starts being a negative value at small M, exhibits a peak at an intermediate M, and is suppressed (but with a positive value) at large M.

Fig. 1
figure 1

The finite temperature polarization tensors (00-channel (28) and scalar (31)) in the static limit, normalized to \(T^{-2}\) versus temperatures. We fix \(M = 0.136 \) GeV in this calculation. Dashed lines in gray are the corresponding quantities in the Boltzmann approximation. Full lines denote massless limits. See text

Full size image

Lastly, we write down the corresponding results for \(\varPi _{00}^T(p^0=0, \mathbf {p} \rightarrow \mathbf {0})\): (1) at \(M \rightarrow 0\) (or large T),

$$\begin{aligned} \varPi _{00}^T(p^0=0, \mathbf {p} \rightarrow \mathbf {0}) \approx -\frac{T^2}{3}; \end{aligned}$$
(34)

and (2) at large M (or small T), where the Boltzmann approximation is valid,

$$\begin{aligned}&\varPi _{00}^T(p^0=0, \mathbf {p} \rightarrow \mathbf {0}) \approx -\frac{2}{\pi ^2} \, M^2 \, \nonumber \\&\qquad \qquad ( K_2(M/T)-K_2(2M/T) ). \end{aligned}$$
(35)

In Fig. 1 we demonstrate a numerical calculation of these finite temperature quantities. Various limits can be readily verified. Note that the scalar channel approaches the known high temperature limit substantially slower than the 00-channel. There, the Boltzmann approximation of the former reaches \(2/\pi ^2 \times T^2\), compared to the full result of \(1/6 \times T^2\).

Fig. 2
figure 2

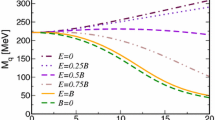
The chiral condensate (normalized to the vacuum value) (left), and the Polyakov loop (right), versus the temperature, at finite magnetic field. Dashed lines represent results obtained from a PNJL model with undressed coupling. The model with dressed coupling is capable of producing the inverse magnetic catalysis at finite temperatures

Full size image

4 Results

4.1 Condensates and Polyakov loop

Including the in-medium dressing by the \(\varPi _{00}\) polarization tensor naturally relates the deconfinement transition temperature and that of the chiral crossover transition. It also plays a pivotal role in generating the inverse magnetic catalysis at finite temperatures within the model.

The results of chiral condensate have been presented in Ref. [9] and here we show the observables obtained under the Schwinger proper-time regularization scheme. See Fig. 2 (left) The results are similar to those obtained before in a 4D cutoff scheme [9].

We highlight key theoretical features of the model:

(1) A coupling to the Polyakov loop \(\ell \) [34,35,36,37,38] is implemented in the model (9). This is done by replacing [39] the thermal weight \(N_\text {th}(E)\) with (\(N_c=3\))

$$\begin{aligned} N_\text {th}(E)\rightarrow & {} \frac{1}{3} \, \sum _{j=1}^3 \frac{{\hat{\ell }}_F^{(j)}}{e^{\beta E}+{\hat{\ell }}_F^{(j)}} \nonumber \\= & {} \frac{1}{3} \, \frac{3\ell \, e^{-\beta E} + 6 \ell \, e^{-2 \beta E} + 3 e^{-3\beta E}}{1 + 3 \ell \, e^{-\beta E} + 3 \ell \, e^{-2\beta E} + e^{-3\beta E}}, \end{aligned}$$
(36)

where [39, 40]

$$\begin{aligned} {\hat{\ell }}_F= & {} \text {diag} \, \left( e^{i \gamma _1}, 1, e^{-i \gamma _1} \right) \nonumber \\ \ell= & {} \frac{1}{3} \, \text {Tr} \, {\hat{\ell }}_F = \frac{1}{3} \, (1 + 2 \cos \gamma _1). \end{aligned}$$
(37)

The expectation value of the Polyakov loop needs to be determined from another gap equation,

$$\begin{aligned} \frac{\partial }{\partial \ell } \, (U_\text {glue}(\ell ) + U_Q(M, \ell )) = 0, \end{aligned}$$
(38)

for a given pure gauge potential \(U_\text {glue}(\ell )\) and the quark potential \(U_{Q}(M, \ell )\), the latter describes the coupling of the Polyakov loop with quarks. These potentials have been studied extensively in Refs [34, 35, 37, 38, 40, 41] and will not be repeated here. In this work we employ the pure gauge potential in Ref. [37].

(2) The final set of gap equations for quarks becomes

$$\begin{aligned} M = m + C_F \, {\tilde{V}}_0 \, M \times I_0(T; M, \ell ), \end{aligned}$$
(39)

and

$$\begin{aligned} {\tilde{V}}_0(T; M, \ell ) = \frac{1}{V_0^{-1} - \frac{1}{2} \, N_f \, \varPi _{00}^T(T; M_0, \ell )}. \end{aligned}$$
(40)

As in Ref. [9], we make a further approximation of using \(M_0 = 0.136 \) GeV in the ring. This point will be further improved in Sect. 4.2. We have made explicit the dependence on temperature and the order parameter fields \((M, \ell )\).

(3) The generalization of various quantities to a finite magnetic field B can be implemented by replacing the momentum integral with a sum over the Landau levels [10]:

$$\begin{aligned} \int \frac{d^3 q}{(2 \pi )^3} \rightarrow \frac{\vert e_f \vert B}{2 \pi } \, \sum _{n=0}^\infty \, \frac{1}{2} \, \alpha _n \int _{-\infty }^{\infty } \frac{d q_z}{2 \pi } \end{aligned}$$
(41)

where \(\alpha _n = 2 - \delta _{n0}\), \(e_f\) is the electric charge of the species, and replacing the transverse momentum by

$$\begin{aligned} q_x^2 + q_y^2 \rightarrow 2 \, n \times \vert e_f \vert B. \end{aligned}$$
(42)

The modification of the integrals in Eq. (13) is summarized in the appendix.

(4) One of the key objectives of this work is to examine the influence of ring diagram on the Polyakov loop. (See Fig. 2 (right).)

The important observation is that the Polyakov loop becomes substantial at lower temperatures as magnetic field increases, signaling lower transition temperature for deconfinement. This correct trend is brought forth by the polarization, and is quite robust against the use of different regularization schemes.

To obtain known vacuum values of the physical observables: \(f_\pi = 92.9\) MeV, \(m_\pi = 137.8\) MeV, and \(\langle {\bar{\psi }} \psi \rangle = -(250 \, \text {MeV})^3\) (per flavor) in the Schwinger proper-time regularization scheme, the set of model parameters is adjusted compared to Ref. [9]. They are given by \(\varLambda = 1.101\) GeV, \(G_\text {NJL} \, \varLambda ^2 = 3.668\) and a current quark mass \(m = 5\) MeV. We note that the constituent quark mass value in the Schwinger scheme is substantially smaller (\(\approx 200\) MeV) compared to the previous scheme (\(\approx 300\) MeV) for the same value of chiral condensate.

(5) A positive feedback mechanism: Solving Eqs. (39),  (40) and  (38) consistently, we obtain the results in Fig. 2. The reduction of the chiral transition temperature is obvious: the ring weakens the effective four-quark coupling at finite temperatures, leading to an earlier transition. Also, without the polarization dressing in Eq. (11), the PNJL model predicts an increasing chiral transition temperature with B. The dressed interaction reverses this trend, and the appearance of quarks enhances explicit Z(3) breaking, which weakens the confining effect and in turn enhances the polarization [42]. This model demonstrates such a positive feedback mechanism in a very transparent manner.

(6) Lastly we examine the effect of using a temperature (and B) dependent \((M, \ell )\), obtained as the solution to the gap equations, on the ring. This is shown in Fig. 3. The extra \((M, \ell )\) dependence turns out to give a modulation of the theoretical limits studied in Fig. 1. Note that the polarization can increase substantially at intermediate temperatures with increasing B, which can drive the phenomenon of inverse magnetic catalysis. We find no need to introduce a B-dependent coupling as advocated in Refs. [16, 17]. Instead, Eq. (11) could accommodate a theoretical explanation of such an effect.

Fig. 3
figure 3

The polarization tensor as a function of temperature, evaluated with the quark mass and Polyakov loop determined from the gap equations. Dashed lines represent results obtained from a PNJL model with undressed coupling

Full size image

4.2 Truncation schemes

Fig. 4
figure 4

The chiral condensate (with current quark mass contribution subtracted), normalized to the vacuum value, versus the temperature, at zero magnetic field. Dashed (gray) line represents result obtained from a PNJL model without screening effect. The dash-dotted (black) line is the result computed with the ring, under a further approximation of \(M=M_0 = 0.136\) GeV. Such approximation is lifted in the fully consistent scheme (”full M”)

Full size image

It was reported in Ref. [9] that the use of full M in \({\tilde{V}}_0(T; M, \ell )\) within a 4D cutoff scheme induces a first order phase transition, instead of the expected crossover behavior. This is the reason why an extra condition \(M = M_0\) is imposed. In this study, we find that the crossover nature of the transition is retained at \(B=0\) when the Schwinger proper-time regularization scheme for the vacuum term is imposed. See Fig. 4. Similar to the previous result, a transition temperature of \(\approx 160\) MeV is achieved, compared to \(>200 \) MeV without the ring. This shows that the improvement is not constructed via a judicious choice of \(M_0\), rather, it is a natural result from iterating M in the gap equation (40). Footnote 1 The ability to link different scales naturally is one of the desirable feature of implementing the ring in the chiral model. Finally, the dependence on cutoff scheme should motivate further study to explore how the chiral phase transition depends on the assumed properties of gluons.

4.3 Effect of Polyakov loop on ring

To illustrate the effect of the confinement, we perform the same calculation while setting the value of the Polyakov loop field to unity, thus removing the confining effect on quarks. This leads to a dramatic decrease in the transition temperature, as shown in Fig.  4. We have checked that such drastic change is insensitive to the choice of the cutoff scheme.

Clearly, allowing the deconfined quarks in the ring diagram to dress the 4-point interaction at the low temperature phase gives a screening effect which is too strong to produce an acceptable \(T_c\). The coupling to the Polyakov loops, as shown in Eq. (36), remedies this problem. In addition, due to the crossover nature of the transition, the chiral phase transition is now also dependent on the details of the Polyakov loop potential.

The problem of too strong screening by the quark loops has also been realized in Ref. [42] even for a more elaborated model, giving transition temperatures as low as \(\sim 30\) MeV. The study here suggests that implementing the suppression of free, though massive, quarks with a confining force in constructing the ring could provide a resolution.

5 Conclusion

In this work we have investigated the in-medium dressing of the four-quark interaction by the polarization. This provides a natural mechanism to resolve the problem of an overestimated chiral transition temperature in common PNJL models, and is capable of generating an inverse magnetic catalysis at finite temperatures. It is accomplished by a field theoretical incorporation of a quark loop dressing and its feeding back to the quark gap equation. There is no need for artificial tuning of \(T_d\) parameter in the gluon sector, nor the need to introducing an explicit B-dependent coupling. Thus, the mechanism can serve as a tentative explanation for the medium dependence discussed in the literature.

Nevertheless, the current model makes some simplifying assumptions which require improving. For example to make the problem more tractable we have employed the static approximation of the ring. However dynamical (3-momentum dependences) and timelike (energy dependence) effects can sometimes be drastic [31]. Note that similar quark loops, in their timelike limits, are computed in the model to derive pions and other mesons. In fact, it is an important question to understand how hadron loops enter in the quarks-and-gluons-based picture. In principle, it is possible to understand, in accordance to quark-hadron duality, the former by including, and iterating, multi-particle interactions in the latter. Note that the role of gluon propagator, approximated as an effective four-quark coupling, is formally recognized here. This is why quark loop dressing (40) is introduced as an extension of standard mean-field results. However, the current truncation scheme only includes these quark loops in dressing the coupling. It has yet to include additional interactions with the derived objects.

While we have explored the role of polarization in this work, vertex corrections are not examined. The contact model is not ideal for this purpose, instead it would be more satisfying to start with model which has a closer connection to QCD. In addition, further work needs to be done to include an explicit treatment of dynamical gluons (and ghosts) in the confinement model [42]. This gives a natural extension to introduce non-local interactions among quarks, and allows to study the role played by the gluons in a chiral phase transition. Finally we note an analogous dressing of the gluons is present at finite baryon density [43]. This could provide an additional handle to probe detailed features of the critical end point [8] predicted by the current model, and will be explored in the future.