1 Introduction

An understanding of exclusive charmonia decays still remains challenging and includes many open questions, see e.g. Refs.  [1, 2]. A description of the underlying QCD dynamics for charmonia is complicated because the charm quark mass is not sufficiently large. On the other hand this flaw yields a possibility to measure observables, which would be much more difficult to access in case of heavier bottomonium. This open a window to study many interesting interplays of the long and short distance QCD dynamics. For instance, many observables associated with the helicity flip amplitudes, which are strongly suppressed in the limit \( m_{Q}\rightarrow \infty \) , in case of charmonia decays can be accessed and experimentally studied with a sufficiently high accuracy. The decay \( J/\psi \rightarrow B{\bar{B}}\) into baryon-antibaryon pair is the one interesting example of such processes. The final state baryons can be easily detected and existing big statistics of samples, which has been already collected at BESIII allows one to measure not only the branching ratio but also the polarisation parameter \(\alpha _{B}\), which describes the angular behaviour of the cross section

$$\begin{aligned} \frac{dN}{d\cos \theta }=A(1+\alpha _{B}\cos ^{2}\theta ), \end{aligned}$$
(1)

where \(\theta \) is the angle between the baryon or antibaryon direction and the lepton beam, A is an overall normalisation. The value of \(\alpha _{B}\) is sensitive to the value of the helicity flip amplitude, which describes the decay of the longitudinally polarised S-wave charmonia. In the naive limit \(m_{Q}\rightarrow \infty \) this quantity is given by \( \alpha _{B}\rightarrow 1+O(m_{B}^{2}/m_{Q}^{2})\) [3]. The experimental results obtained for various baryon channels indicate that values of \(\alpha _{B}\) definitely differ from one, see Refs.  [4,5,6,7,8]. In Table 1 we summarise the existing data for the octet baryons.

The last column in this table shows the ratio \(Q_{B}\), which can be related to the similar leptonic ratio

$$\begin{aligned} Q_{l}=\frac{\text {Br}[\psi (2S)\rightarrow l{\bar{l}}]}{\text {Br}[J/\psi \rightarrow l{\bar{l}}]}\times 100=13.21. \end{aligned}$$
(2)

QCD factorisation predicts that in the limit of large mass \(m_{Q}\rightarrow \infty \)

$$\begin{aligned} Q_{l}=Q_{B}+{\mathcal {O}}(v^{2})+{\mathcal {O}}(\Lambda ^{2}/m_{Q}^{2}), \end{aligned}$$
(3)

where v is the heavy quark velocity in the quarkonium rest frame, \(v^{2}\ll 1\) and \(\Lambda \) is a typical hadronic scale. Therefore if the leading-oder contribution in the expansion with respect \(1/m_{Q}\) works sufficiently well, one finds

$$\begin{aligned} Q_{B}\simeq Q_{l}\text {.} \end{aligned}$$
(4)

It turns out that this approximate equation is not well satisfied for many decay channels. For instance, for many mesonic decays \(J/\psi \rightarrow MM\) this ratio is strongly violated, see e.g. Ref. [1]. From the Table 1 one can see that this criteria sufficiently well works for nucleon states but for other octet baryons \(Q_B\) is about factor 2 differ from \(Q_l\). However this violation effect is not too big. For example, for some mesonic decays this difference is about an order of magnitude. Therefore one can expect that the leading-order description for the baryonic decays can provide sufficiently large or perhaps even the dominant effect.

Table 1 The experimental data for decays \(J/\psi \rightarrow B{\bar{B}}\)
Full size table

The first realistic estimate of the value of \(\alpha _{N}\) was considered in Ref. [10], where it is suggested to neglect the subleading helicity flip amplitude but keep finite the ratio \(m_{N}^{2}/M_{\psi }^{2}\). Then one finds

$$\begin{aligned} \alpha _{N}\simeq \frac{1-4m_{N}^{2}/M_{\psi }^{2}}{1+4m_{N}^{2}/M_{\psi }^{2}}\simeq 0.46, \end{aligned}$$
(5)

which is a better estimate comparing with the naive limit \(m_{Q}\rightarrow \infty \). In Ref. [11] \(\alpha _{N}\) is estimated using an idea that nucleon is the non-relativistic bound state of three quarks and each quark carries approximately 1/3 of the nucleon momentum. The result of this consideration yields \(\alpha _{N} \simeq 0.66\).

A more sophisticated idea has been used in Ref. [12], where the QCD factorisation is used in order to compute the decay amplitudes. In this framework the \(c{\bar{c}}\)-pair annihilates at short distances into three hard gluons, which create light quark-antiquark pairs describing the long-distance collinear overlap with outgoing nucleon and antinucleon states. The non-perturbative physics is encoded by well defined matrix elements, which are closely associated with hadronic wave functions. Such framework allows one to build a systematic description performing the expansion with respect to small velocity v and small ratio \(\Lambda /m_{Q}\). The contribution of the helicity flip amplitude is subleading and it is suppressed by extra power \(\Lambda ^{2}/m_{Q}^{2}\) because the corresponding hard subprocess with massless quarks is sensitive to the orbital angular momentum of the light quarks, which provides an additional power suppression. In Ref.  [12] the helicity flip amplitude is obtained by introduction of the effective light quark masses, which are taken to be \( m_{q}\simeq x_{i}m_{N}\), where \(x_{i}\) are the longitudinal momentum fractions satisfying \(x_{1}+x_{2}+x_{3}=1\). All amplitudes, which are calculated in this model, are sensitive to the leading-twist light-cone distribution amplitude (DA) \(\varphi _{3}(x_{1},x_{2},x_{3})\), which describes the sharing of the nucleon longitudinal momentum between the quarks at zero transverse separation. Such calculation of the helicity flip amplitude can only be considered as a certain phenomenological model.

In Ref. [13] the helicity flip amplitude for the first time has been computed within the more systematic framework: using the three-quark higher twist DAs, which are related to the higher Fock components of the nucleon wave function. Such DAs can also be interpreted as a P-wave configurations of the three collinear constituent quarks. It turns out that the subleading helicity flip amplitude can be computed within the same collinear factorisation framework as the leading-order amplitude. The obtained result has been used for the analysis of the proton-antiproton data. The numerical estimate obtained in Ref. [13] is \(\alpha _{p}\simeq 0.71\), which allows one to conclude that the factorisation description works sufficiently well in this case. Therefore charmonium decay data may also provide an interesting information about the baryon twist-4 DAs.

Quite different idea has been developed in Refs. [14,15,16]. In these works the effective hadronic Lagrangian density has been constructed using the flavour SU(3) symmetry arguments. The unknown vertex couplings have been fitted from the data. One of the main output of this analysis is the estimate of the relative phase between the hadronic and electromagnetic amplitudes, which are defined through \(c{\bar{c}}\rightarrow ggg\) and \(c{\bar{c}}\rightarrow \gamma ^*\) subprocesses, respectively. In Ref. [16] this phase is found to be relatively closer to \(\pi /2\) than to 0 or \(\pi \). Qualitatively this does not agree with the factorisation picture, which predicts that the hadronic amplitudes are real. Basing on this observation it is concluded that this disagreement is perhaps an indication that pQCD can not provide a sufficiently good description of \(J/\psi \) decays into baryon-antibaryon pairs.

In the present work we are going to extend the analysis of the Ref. [13] to baryon–antibaryon states from the baryon octet. The results for the hard kernels obtained in Ref. [13] also allows one to calculate the amplitudes for other baryons. Therefore for such analysis one only needs the information about the twist-3 and twist-4 DAs of the baryons. Some moments of these DAs have been studied recently on the lattice in Ref. [17] and these results can be used in order to constrain the non-perturbative input.

The paper is organised as follows. In Sect. 2 we discuss the baryon DAs and describe the models, which are used in our calculations. The analytical expressions for the amplitudes and observables are discussed in the Sect. 3. The discussion of the numerical results are presented in Sect. 4. In Sect. 5 we provide the conclusions. In Appendix we provide the useful details about the baryon DAs, which are used in our calculations.

2 Baryon DAs

The long distance dynamics associated with the QCD hadronisation into outgoing hadrons is described by the matrix elements, which are parametrised in terms of the light-cone distribution amplitudes (DAs). The structure and the properties of the higher twist octet baryon DAs have already been studied in Refs. [19,20,21,22]. Here we briefly discuss the required twist-3 and twist-4 DAs and construct the phenomenological models.

In the following we assume that the baryon momentum k is directed along z-axis and can be expanded as

$$\begin{aligned} k=k_{-}\frac{{{n}}}{2}+k_{+}\frac{\bar{n}}{2},\ \ k_{+}\gg k_{-}=\frac{m_{B}^{2}}{k_{+}}, ~~ k^{2}=m_{B}^{2}. \end{aligned}$$
(6)

Here \(n,{\bar{n}}\) are the auxiliary light-cone vectors \(n^{2}={\bar{n}}^{2}=0\), \((n{\bar{n}})=2\) and

$$\begin{aligned} k_{+}=(kn),\quad k_{-}=(k{\bar{n}}). \end{aligned}$$
(7)

The baryon spinors N(k, s) satisfy Dirac equationsFootnote 1

and normalised as \({\bar{N}}(k,s)N(k,s^{\prime })=2m_{B}\delta _{ss^{\prime }}\) . It is also convenient to introduce the large and small components \(N_{\bar{ n}}\) and \(N_{{n}}\), respectively:

The similar relations also hold for the antibaryon spinors.

In this paper we only consider the contributions of the three quark operators. The contributions of the quark-gluon operators corresponds to the moments with higher conformal spin and will be neglected [19, 20]. The relevant three-quark light-cone operators are constructed from the QCD quark fields \( q={u,d,s}\) and light-cone the Wilson lines

$$\begin{aligned} W_{{\bar{n}}}[x_{-},z_{-}]=\text {P}\exp \left\{ ig\int _{(z_{-}-x_{-})/2}^{0}ds\ A_{+}(x_{-}n/2+sn)\right\} .\nonumber \\ \end{aligned}$$
(8)

The light-cone three-quark operator can be written as

$$\begin{aligned}&{\mathcal {O}}_{\alpha _{1}\alpha _{2}\alpha _{3}}(x_{-},y_{-},z_{-})\nonumber \\&\quad =\varepsilon ^{ijk}\ q_{\alpha _{1}}^{i^{\prime }}(x_{-})W_{{\bar{n}}}[x_{-},v_{-}]_{i^{\prime }i}\ q_{\alpha _{2}}^{j^{\prime }}(y_{-})\nonumber \\&\qquad W_{{\bar{n}}}[y_{-},v_{-}]_{j^{\prime }j}\ q_{\alpha _{3}}^{k^{\prime }}(z_{-})W_{{\bar{n}}}[z_{-},v_{-}]_{k^{\prime }k}, \end{aligned}$$
(9)

where we used short notation \(q(x_{-})\equiv q(x_{-}n/2)\). The set of indices \(\{ijk\}\) stands for the colour, the indices \(\alpha _{i}\) refer to the Dirac structure. Following to Ref. [21] we assume the following flavour content of the operators \(\langle 0|q_{\alpha _{1}}q_{\alpha _{2}}q_{\alpha _{3}}|B\rangle \equiv \langle 0|q_{1}q_{2}q_{3}|B\rangle \):

$$\begin{aligned}&\langle 0|u_{1}u_{2}d_{3}|p\rangle ,\, \langle 0|u_{1}d_{2}s_{3}|\Lambda \rangle , \end{aligned}$$
(10)
$$\begin{aligned}&\langle 0|u_{1}d_{2}s_{3}|\Sigma ^{0}\rangle ,\, \langle 0|u_{1}u_{2}s_{3}|\Sigma ^{+}\rangle , \end{aligned}$$
(11)
$$\begin{aligned}&\langle 0|s_{1}s_{2}u_{3}|\Xi ^{0}\rangle ,\, \langle 0|s_{1}s_{2}d_{3}|\Xi ^{-}\rangle . \end{aligned}$$
(12)

For simplicity this will not be shown explicitly. For brevity we also simplify the notation for the Dirac indices assuming \(\{\alpha _{1},\alpha _{2},\alpha _{3}\}\equiv \{1,2,3\}\).

The universal light-cone matrix elements can be defined as [19]

(13)

where we always assume that

$$\begin{aligned} k\simeq k_{+}\frac{\bar{n}}{2},\ \sigma _{kn}=\sigma _{\alpha \beta }k^{\alpha }n^{\beta }\ . \end{aligned}$$

The symbol “\(\bot \)” denotes the transverse projections with respect to the light-like vectors: \(n_{\alpha }\gamma _{\bot }^{\alpha }={\bar{n}}_{\alpha }\gamma _{\bot }^{\alpha }=0\). The symbol “FT” denotes the Fourier transformation

$$\begin{aligned} \text {FT}[f]=\int Du_{i}~e^{-i(k_{1}x)-i(k_{2}y)-i(k_{3}z)}f(u_{1},u_{2},u_{3}),~\ \end{aligned}$$
(14)

with the measure \(Du_{i}=du_{1}du_{2}du_{3}\delta (1-u_{1}-u_{2}-u_{3})\), the quark momenta in (14) are defined as

$$\begin{aligned} k_{i}=u_{i}k_{+}\frac{{\bar{n}}}{2}. \end{aligned}$$
(15)

The defined in Eq. (13) DAs are symmetric/antisymmetric with respect to interchange \(u_{1}\leftrightarrow u_{2}\)

$$\begin{aligned}&F_{i}^{B}(x_{2},x_{1},x_{3})=-(-1)_{B}F_{i}^{B}(x_{1},x_{2},x_{3}),\ \text { for }\ \ \nonumber \\&\quad F=\{S,P,A\}, \end{aligned}$$
(16)
$$\begin{aligned}&F_{i}^{B}(x_{2},x_{1},x_{3})=+(-1)_{B}F_{i}^{B}(x_{1},x_{2},x_{3}),\ \text { for }\ \ \nonumber \\&\quad F=\{V,T\}, \end{aligned}$$
(17)

with

$$\begin{aligned} (-1)_{B}=\left\{ \begin{array}{c} +1\ \ \ B\ne \Lambda \\ -1\ \ \ B=\Lambda \end{array} \right. .\text { } \end{aligned}$$
(18)

The minimal basic set of baryon light-cone DAs can be defined in terms of these DAs as [21, 22] ( below we accept the short notation \( (x_{1},x_{2},x_{3})\equiv (x_{123})\))

$$\begin{aligned} f_{B}\varphi _{3\pm }^{B}(x_{123})= & {} \frac{c_{B}^{\pm }}{2}\left\{ \left( V_{1}-A_{1}\right) ^{B}(x_{123})\right. \nonumber \\&\left. \pm \left( V_{1}-A_{1}\right) ^{B}(x_{321})\right\} , \end{aligned}$$
(19)
$$\begin{aligned} f_{B}\Pi _{3}^{B}(x_{123})= & {} c_{B}^{-}(-1)_{B}T_{1}^{B}(x_{132}), \end{aligned}$$
(20)
$$\begin{aligned} \Phi _{4\pm }^{B}(x_{123})= & {} c_{B}^{\pm }\left\{ \left( V_{2}-A_{2}\right) ^{B}(x_{123})\right. \nonumber \\&\left. \pm (-1)_{B}\left( V_{3}-A_{3}\right) ^{B}(x_{231})\right\} , \end{aligned}$$
(21)
$$\begin{aligned} \Xi _{4\pm }^{B}(x_{123})= & {} (-1)_{B}3c_{B}^{\pm }\left[ ~\left( T_{3}-T_{7}+S_{1}+P_{1}\right) ^{B}(x_{123})\right. \nonumber \\&\left. \pm \left( T_{3}-T_{7}+S_{1}+P_{1}\right) ^{B}(x_{132})\right] , \end{aligned}$$
(22)
$$\begin{aligned} \Pi _{4}^{B}(x_{123})= & {} c_{B}^{-}\left( T_{3}+T_{7}+S_{1}-P_{1}\right) ^{B}(x_{312}), \end{aligned}$$
(23)
$$\begin{aligned} \Upsilon _{4}^{B}(x_{123})= & {} 6c_{B}^{-}T_{2}^{B}(x_{321}), \end{aligned}$$
(24)

where

$$\begin{aligned} c_{B}^{+}=\left\{ \begin{array}{c} 1,~B\ne \Lambda \\ \sqrt{\frac{2}{3}},B=\Lambda \end{array} \right. ,~~\ c_{B}^{-}=\left\{ \begin{array}{c} 1,~B\ne \Lambda \\ -\sqrt{6},B=\Lambda \end{array} \right. , \end{aligned}$$
(25)

and \(f_{B}\) is the normalisation coupling. The coefficients \(c_{B}^{\pm }\) are chosen in such way that these DAs satisfy the simple relations in the SU(3) flavour symmetry limit [21].

For the nucleon state, the basic set of DAs can be further simplified by the isospin relationships, namely, it is sufficient to determine

$$\begin{aligned} f_{N~}\varphi _{3}(x_{123})= & {} \phi _{3+}^{N}(x_{123})+\phi _{3-}^{N}(x_{123})\nonumber \\= & {} \left( V_{1}-A_{1}\right) ^{N}(x_{123}), \end{aligned}$$
(26)
$$\begin{aligned} \frac{1}{2}\Phi _{4}(x_{123})= & {} \frac{1}{2}\left( \Phi _{4+}^{N}+\Phi _{4-}^{N}\right) (x_{123})\nonumber \\= & {} \left( V_{2}-A_{2}\right) ^{N}(x_{123}), \end{aligned}$$
(27)
$$\begin{aligned} \frac{1}{2}\Psi _{4}(x_{123})= & {} \frac{1}{2}\left( \Phi _{4+}^{N}-\Phi _{4-}^{N}\right) (x_{312})\nonumber \\= & {} \left( V_{3}-A_{3}\right) ^{N}(x_{231}), \end{aligned}$$
(28)
$$\begin{aligned} \frac{\lambda _{2}}{6}\Xi _{4}(x_{123})= & {} \left( \Xi _{4+}^{N}+\Xi _{4-}^{N}\right) (x_{123})\nonumber \\= & {} \left( T_{3}-T_{7}+S_{1}+P_{1}\right) ^{N}(x_{123}). \end{aligned}$$
(29)

The nucleon DAs \(\varphi _{3},\) \(\Phi _{4},\Psi _{4}\) and \(\Xi _{4}\) can be definedFootnote 2 in terms of the matrix elements of the appropriately projected light-cone operators as in Refs.  [19, 20]. Let us notice that some definitions of the DAs in Ref.  [18] differ from ones in used Ref.  [20], which are also used in this paper.

The twist-4 DAs in Eqs. (21)–(24) can be decomposed into contributions associated with the contributions of the operators with the geometrical twist-3 and twist-4. Such decomposition is often referred in the literature as Wandzura-Wilczek one. In this paper we write such decompositions in the following formFootnote 3

$$\begin{aligned}&\Phi _{4\pm }^{B}(x_{123})=f_{B}\Phi _{4\pm }^{B(3)}(x_{123})+\lambda _{1}^{B}\ {\bar{\Phi }}_{4\pm }^{B}(x_{123}), \end{aligned}$$
(30)
$$\begin{aligned}&\Pi _{4}^{B}(x_{123})=f_{\bot }^{B}\ \Pi _{4}^{B(3)}(x_{123})+\lambda _{1}^{B}{\bar{\Pi }}_{4}^{B}(x_{123}),\ \ B\ne \Lambda , \nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned}&\Pi _{4}^{\Lambda }(x_{123})=f_{\Lambda }\Pi _{4}^{\Lambda (3)}(x_{123})+\lambda _{\bot }^{\Lambda }{\bar{\Pi }}_{4}^{\Lambda }(x_{123}). \end{aligned}$$
(32)
$$\begin{aligned}&\Xi _{4\pm }^{B}(x_{123})=\lambda _{2}^{B}\ {\bar{\Xi }}_{4\pm }^{B}(x_{123}), \end{aligned}$$
(33)
$$\begin{aligned}&\Upsilon _{4}^{B}(x_{123})=\lambda _{2}^{B}{\bar{\Upsilon }}_{4}^{B}(x_{123}). \end{aligned}$$
(34)

The functions in the rhs of Eqs. (30)–(34) are dimensionless while the couplings \(f_{B},\ f_{\bot }^{B},\ \lambda _{1,2}^{B}\) and \( \lambda _{\bot }^{\Lambda }\) have dimension \(\hbox {GeV}^{2}\). The functions with the superscript “(3)” describe the contribution of geometrical twist-3, i.e. these functions are completely defined in terms of the moments of twist-3 DAs. The explicit expressions can be found in Refs. [19, 20].

The equations (19)–(24) can be easily rewritten using the symmetry properties (16)–(17) in order to get the expressions for the DAs \(\{V_{i},A_{i},T_{i},S_{i},P_{i}\}\) in terms of the basic functions \(\{\varphi _{3\pm }^{B},\Pi _{3}^{B},\Phi _{4\pm }^{B},\Xi _{4\pm }^{B},\Pi _{4}^{B},\Upsilon _{4}^{B}\}\). Therefore the non-perturbative input associated with the final baryon and antibaryon states can be unambiguously described in terms of the basic DAs. The construction of the models for these functions are based on the truncate d conformal expansions, see e.g. Refs. [19, 20].

For the nucleon DAs we take the model set “ABO1” suggested in Ref. [20]. These models have been designed in order to describe nucleon electromagnetic FFs within the light-cone sum rules. The twist-3 DA reads

$$\begin{aligned} \varphi _{3}(x_{123})= & {} 120x_{1}x_{2}x_{3}~\left( 1+\phi _{10}{\mathcal {P}} _{10}(x_{123})+\phi _{11}{\mathcal {P}}_{11}(x_{123}) \nonumber \right. \\&+ \left. \phi _{20}{\mathcal {P}} _{20}(x_{123})+\phi _{21}{\mathcal {P}}_{21}(x_{i})+\phi _{22}{\mathcal {P}} _{22}(x_{123})\right) , \nonumber \\ \end{aligned}$$
(35)

where the orthogonal polynomials \({\mathcal {P}}_{kl}(x_{i})\) are given in Appendix. The moments \(\phi _{kl}\) depends on the scale \(\mu \) and they are multiplicatively renormalisable, see the details in Appendix. The chiral-even twist-4 DAs (27) and (28) can be represented as

$$\begin{aligned}&\Phi _{4}(x_{123})=f_{N}\Phi _{4}^{(3)}(x_{123})+\lambda _{1}{\bar{\Phi }} _{4}(x_{123}), \end{aligned}$$
(36)
$$\begin{aligned}&\Psi _{4}(x_{123})=f_{N}\Psi _{4}^{(3)}(x_{123})-\lambda _{1}{\bar{\Psi }} _{4}(x_{123}), \end{aligned}$$
(37)

where the functions \(\Phi _{4}^{(3)}\) and \(\Psi _{4}^{(3)}\) are defined in terms of twist-3 moments \(\phi _{kl}\). The models for the genuine twist-4 DAs reads

$$\begin{aligned}&{\bar{\Phi }}_{4}(x_{123})=24x_{1}x_{2}\left( 1+\eta _{10}{\mathcal {R}} _{10}(x_{312})-\eta _{11}{\mathcal {R}}_{11}(x_{312})\right) , \nonumber \\ \end{aligned}$$
(38)
$$\begin{aligned}&{\bar{\Psi }}_{4}(x_{123})=24x_{1}x_{3}\left( 1+\eta _{10}{\mathcal {R}} _{10}(x_{231})+\eta _{11}{\mathcal {R}}_{11}(x_{231})\right) . \nonumber \\ \end{aligned}$$
(39)

The moments \(\eta _{ik}\) are multiplicatively renormalisable and do not mix with the moments from the quark-gluon DAs. The explicit expressions for the polynomials \({\mathcal {R}}_{1i}\) and \(\Phi _{4}^{(3)}\) and \(\Psi _{4}^{(3)}\) are also given in Appendix. The chiral-odd DA \(\Xi ^B _{4}\) and \(\Upsilon ^B_4\) (29) do not contribute at this order because the corresponding hard kernels are trivial [13].

For other baryons we consider more simple models. The twist-3 DAs are described as

$$\begin{aligned}&\varphi _{3+}^{B}(x_{i})=120x_{1}x_{2}x_{3}~\left( 1+\phi _{11}^{B}\mathcal {P }_{11}(x_{123})\right) ,\ \ \ \nonumber \\&\varphi _{3-}^{B}(x_{i})=120x_{1}x_{2}x_{3}~\phi _{10}^{B}{\mathcal {P}}_{10}(x_{123}). \end{aligned}$$
(40)
$$\begin{aligned}&\Pi _{3}^{\Lambda }(x_{123})=120x_{1}x_{2}x_{3}~\pi _{10}^{\Lambda }{\mathcal {P}}_{10}(x_{123}), \end{aligned}$$
(41)
$$\begin{aligned}&\Pi _{3}^{B}(x_{123})=120x_{1}x_{2}x_{3}(1+~\pi _{11}^{B}{\mathcal {P}} _{11}(x_{123})),\ \ B=\Sigma ,\Xi . \nonumber \\ \end{aligned}$$
(42)

The twist-3 moments \(\{ \phi _{10}^{B},\phi _{11}^{B}, \pi _{\Lambda }^{B},\pi _{11}^{B} \}\) in Eqs.(40)-(42) also enter in the expressions for the twist-4 DAs in Eqs. (30)–(32), more details can be found in Appendix. For the genuine twist-4 parts we use the following models

$$\begin{aligned}&{\bar{\Phi }}_{4+}^{B}(x_{123})=24~x_{1}x_{2}\left( -\eta _{11}^{B}\right) {\mathcal {R}}_{11}(x_{312}), \end{aligned}$$
(43)
$$\begin{aligned}&{\bar{\Phi }}_{4-}^{B}(x_{123})=~24~x_{1}x_{2}\left( 1+\eta _{10}^{B}{\mathcal {R}} _{10}(x_{312})\right) , \end{aligned}$$
(44)
$$\begin{aligned}&{{\bar{\Pi }}} _{4}^{\Lambda }(x_{123})=24x_{1}x_{2}~\left( 1+\zeta _{10}^{\Lambda } {\mathcal {R}}_{10}(x_{132})\right) , \end{aligned}$$
(45)
$$\begin{aligned}&{\bar{\Pi }}_{4}^{B}(x_{i})=24~x_{1}x_{2}\left( -\zeta _{11}^{B}\right) {\mathcal {R}}_{11}(x_{312}),\ B=\Sigma ,\Xi . \end{aligned}$$
(46)

The described DAs in the limit of exact flavour symmetry SU(3) (\(m_{u}=m_{d}=m_{s}\)) must satisfy [21]

$$\begin{aligned}&\Phi _{i+}^{N*}=\Phi _{i+}^{\Sigma *}=\Phi _{i+}^{\Xi *}=\Phi _{i+}^{\Lambda *}=\Pi _{i}^{N*}=\Pi _{i}^{B*},\ \ i=3,4\nonumber \\ \end{aligned}$$
(47)
$$\begin{aligned}&\Phi _{i-}^{N*}=\Phi _{i-}^{\Sigma *}=\Phi _{i-}^{\Xi *}=\Phi _{i-}^{\Lambda *}=\Pi _{i}^{\Lambda *},\ \ \ i=3,4. \end{aligned}$$
(48)

In terms of the moments this gives

$$\begin{aligned}&f_{N}^{*}=f_{\Sigma }^{*}=f_{\Xi }^{*}=f_{\bot }^{\Sigma *}=f_{\bot }^{\Xi *}, \end{aligned}$$
(49)
$$\begin{aligned}&\lambda _{1}^{*}=\lambda _{1}^{\Lambda *}=\lambda _{1}^{\Sigma *}=\lambda _{1}^{\Xi *}=\lambda _{\bot }^{\Lambda *}, \end{aligned}$$
(50)
$$\begin{aligned}&\phi _{10}^{*}=\phi _{10}^{\Lambda *}=\phi _{10}^{\Sigma *}=\phi _{10}^{\Xi *}=\pi _{10}^{\Lambda *}, \end{aligned}$$
(51)
$$\begin{aligned}&\eta _{10}^{*}=\eta _{10}^{\Lambda *}=\eta _{10}^{B*}=\zeta _{10}^{\Lambda *}, \end{aligned}$$
(52)
$$\begin{aligned}&\eta _{11}^{*}=\eta _{11}^{\Lambda *}=\eta _{11}^{\Sigma *}=\eta _{11}^{\Xi *}=\zeta _{11}^{\Sigma *}=\zeta _{11}^{\Xi *}. \end{aligned}$$
(53)

These relations are useful in the phenomenological analysis. The numerical values of the required moments will be discussed later.

The analytical result for the helicity flip amplitude, which involves the twist-4 DAs, can be described in terms of the so-called auxiliary DAs, which are the linear combinations of the basic DAs. Such combinations naturally appear in the calculation of hard kernels and allows one to derive a compact analytical expressions for the amplitudes. These auxiliary DAs can be defined in terms of the matrix elements of the twist-4 operators with the transverse derivative, see the details in Ref. [13]. The corresponding operators are defined using the gauge invariant collinear fields, which have definite scaling behaviour within the effective field theory framework

$$\begin{aligned} \chi (x_{-})= & {} W_{{\bar{n}}}^{\dag }(x_{-})\frac{{\bar{n}}n}{4}q(x_{-}),\nonumber \\ W_{{\bar{n}}}(x_{-})= & {} \text {P}\exp \left\{ ig\int _{-\infty }^{0}ds\ A_{+}(x_{-}n/2+sn)\right\} . \end{aligned}$$
(54)

Then the auxiliary DAs can be introduced through the following light-cone matrix elements

(55)
(56)
(57)
(58)
(59)
(60)
(61)

where the colour and the flavour structure of the operators are the same as described before. The DAs in the rhs of these equations can be expressed in terms of DAs \(\{V_{i},A_{i},T_{i},S_{i},P_{i}\}^{B}\) using the Lorentz symmetry and QCD equations of motion. This gives [13, 20]

$$\begin{aligned}&4{\mathcal {V}}_{i}^{B}(x_{123})=x_{3}\left( V_{2}+A_{2}\right) ^{B}(x_{123})\nonumber \\&\quad +(-1)^{i}\left[ (x_{1}-x_{2})V_{3}^{B}(x_{123})+{\bar{x}} _{3}A_{3}^{B}(x_{123})\right] \nonumber \\&\quad +\frac{m_{3}}{m_{B}}\left( V_{1}^{B}(x_{123})+(-1)^iA_{1}^{B}(x_{123})\right) \nonumber \\&\quad +(-1)^{i+1}2\frac{m_{1}-m_{2}}{m_{B}}T_{1}^{B}(x_{123}), \end{aligned}$$
(62)
$$\begin{aligned}&4{\mathcal {A}}_{i}^{B}(x_{123})=-x_{3}\left( V_{2}+A_{2}\right) ^{B}(x_{123})\nonumber \\&\quad +(-1)^{i}\left[ (x_{1}-x_{2})A_{3}^{B}(x_{123})+{\bar{x}} _{3}V_{3}^{B}(x_{123})\right] \nonumber \\&\quad +\frac{m_{3}}{m_{B}}\left( A_{1}^{B}(x_{123})+(-1)^iV_{1}^{B}(x_{123})\right) \nonumber \\&\quad +(-1)^{i+1}2\frac{m_{1}+m_{2}}{m_{B}}T_{1}^{B}(x_{123}), \end{aligned}$$
(63)
$$\begin{aligned}&\left( {\mathcal {T}}_{21}+{\mathcal {T}}_{41}\right) ^{B}(x_{123}) =\frac{x_{1} }{2}\left( T_{3}-T_{7}+S_{1}+P_{1}\right) ^{B}(x_{123})\nonumber \\&\quad -\frac{1}{2}\frac{m_{1}}{m_{B}}\left( V_{1}^{B}+A_{1}^{B}\right) ,\ \end{aligned}$$
(64)
$$\begin{aligned}&\quad \left( {\mathcal {T}}_{22}+{\mathcal {T}}_{42}\right) ^{B}(x_{123}) =\frac{x_{2}}{2}\left( T_{3}-T_{7}-S_{1}-P_{1}\right) ^{B}(x_{123})\nonumber \\&\quad -\frac{1}{2}\frac{m_{2}}{m_{B}}\left( V_{1}^{B}-A_{1}^{B}\right) , \end{aligned}$$
(65)
$$\begin{aligned}&\left( {\mathcal {T}}_{21}-{\mathcal {T}}_{41}\right) ^{B}(x_{123}) =\frac{x_{1} }{2}\left( T_{3}+T_{7}+S_{1}-P_{1}\right) ^{B}(x_{123})\nonumber \\&\quad +\frac{1}{2}\frac{m_{1}}{m_{B}}\left( A_{1}^{B}-V_{1}^{B}\right) , \end{aligned}$$
(66)
$$\begin{aligned}&\quad \left( {\mathcal {T}}_{22}-{\mathcal {T}}_{42}\right) ^{B}(x_{123}) = \frac{x_{2}}{2}\left( T_{3}+T_{7}-S_{1}+P_{1}\right) ^{B}(x_{123})\nonumber \\&\quad -\frac{1}{2}\frac{m_{2}}{m_{B}}\left( V_{1}^{B}+A_{1}^{B}\right) , \end{aligned}$$
(67)

where the quark masses \(m_i\) correspond to the quarks \(q_1q_2q_3\) in the matrix elements in Eqs. (10)–(12). The contributions with the quark masses appears after application QCD equations for the quark fields, see more details in Ref. [13]. In what follow we assume \(m_u=m_d\simeq 0\) and \(m_s\ne 0\). Therefore the terms with \(m_s\) represent the part of the SU(3)-breaking corrections. Because the auxiliary DAs are uniformly defined for all baryons, the description of decay amplitudes for different baryon states uses the same hard kernels, which are obtained for the nucleon case in Ref. [13].

3 Decay amplitudes

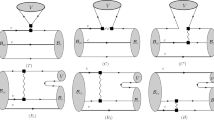
The decay amplitude \(J/\psi (P)\rightarrow B(k){\bar{B}}(k^{\prime })\) is defined as

$$\begin{aligned} M=\left( \epsilon _{\psi }\right) _{\mu }\ {\bar{N}}(k)\left\{ \gamma ^{\mu }\ A_{1}^{B}+(k^{\prime }+k)_{\nu }\frac{i\sigma ^{\mu \nu }}{2m_{B}} A_{2}^{B}\right\} V(k^{\prime }), \nonumber \\ \end{aligned}$$
(68)

where \({{\bar{N}}}\) and V denote the baryon and antibaryon spinors, respectively. The charmonium polarisation vector \(\epsilon _{\psi }^{\mu }\equiv \epsilon _{\psi }^{\mu }(P,\lambda )\) satisfies

$$\begin{aligned} \sum _{\lambda }\epsilon _{\psi }^{\mu }(P,\lambda )\epsilon _{\psi }^{\nu }(P,\lambda )=-g^{\mu \nu }+\frac{P^{\mu }P^{\nu }}{M_{\psi }^{2}}, \end{aligned}$$
(69)

where \(P^{2}=M_{\psi }^{2}\). The observables can be conveniently described in terms of linear combinations

$$\begin{aligned} {\mathcal {G}}_{M}^{B}=A_{1}^{B}+A_{2}^{B},\ \ \ {\mathcal {G}}_{E}^{B}=A_{1}^{B}+ \frac{M_{\psi }^{2}}{4m_{B}^{2}}A_{2}^{B}, \end{aligned}$$
(70)

which are similar to the Sachs redefinition for the electromagnetic FFs. These amplitudes can be computed within the standard factorisation framework. The resulting expressions can be written as

$$\begin{aligned} {\mathcal {G}}_{M/E}^{B}=\frac{f_{\psi }}{~m_{c}^{2}}\frac{~f_{B}^{~2}}{ m_{c}^{4}}~(\pi \alpha _{s})^{3}~\frac{10}{81}\ (1+\delta _{\Lambda B})\ J_{M/E}^{B}, \end{aligned}$$
(71)

where \(f_{\psi }\) is the charmonium coupling defined below in Eq. (79), \(\alpha _{s}\) is the QCD coupling and \(\delta _{\Lambda B}=1\ \ \) if \(B=\Lambda \) and \(\ \delta _{\Lambda B}=0\ \ \)if \(B\ne \Lambda .\) The leading-order dimensionless convolution integrals read

$$\begin{aligned} J_{M}^{B}= & {} \frac{1}{4f_{B}^{2}}\int \frac{Dx_{i}}{x_{1}x_{2}x_{3}}\int \frac{Dy_{i}}{y_{1}y_{2}y_{3}}\nonumber \\&\left\{ \left( V_{1}-A_{1}\right) ^{B}(x_{123})\left( V_{1}-A_{1}\right) ^{B}(y_{123})\frac{x_{1}y_{3}}{D_{1}D_{3}} \right. \nonumber \\&\left. +T_{1}^{B}(y_{123})T_{1}^{B}(x_{123})~\frac{2x_{1}y_{2}}{D_{1}D_{2}} \right\} , \end{aligned}$$
(72)

where

$$\begin{aligned} D_{i}=x_{i}(1-y_{i})+(1-x_{i})y_{i}. \end{aligned}$$
(73)

This result has been obtained already long time ago, see e.g. Refs. [23,24,25].

The second amplitude \({\mathcal {G}}_{E}^{B}\) has been computed in Ref. [13] for the nucleon case. This result can be easily generalised to other baryons taking into acount the universality of the definitions of the baryon DAs (55)–(67). Corresponding integrals read

$$\begin{aligned}&J_{E}^{B} =\frac{2}{f_{B}^{2}}\int Dy_{i}~\frac{1}{y_{1}y_{2}y_{3}}\int Dx_{i}\frac{1}{x_{1}x_{2}x_{3}}\frac{1}{ D_{1}D_{2}D_{3}} \nonumber \\&\quad \times \left\{ \ \left( {\mathcal {A}}_{1}-{\mathcal {V}}_{1}\right) ^{B}(x_{123})\left( A_{1}+V_{1}\right) ^{B}(y_{123})\ x_{1}(x_{2}(y_{2}-y_{3})-{\bar{y}}_{1}y_{2})\right. \nonumber \\&\quad +\left( {\mathcal {A}}_{1}+{\mathcal {V}}_{1}\right) ^{B}(x_{123})\left( A_{1}-V_{1}\right) ^{B}(y_{123})\ x_{2}(x_{2}-y_{2})(y_{1}-y_{3}) \nonumber \\&\quad \left. +\left( {\mathcal {T}}_{21}-{\mathcal {T}}_{41}\right) ^{B}(x_{123})T_{1}^{B}(y_{123})\ 2x_{3}(x_{2}(y_{1}-y_{2})+y_{2}{\bar{y}} _{3})\ \right\} ,\nonumber \\ \end{aligned}$$
(74)

where \({\bar{y}}_{i}=1-y_{i}\). Recall that we only consider twist-4 three-quark operators and neglect the contributions from twist-4 quark-gluon operators.

The factor \((1+\delta _{\Lambda B})\) in Eq. (71 ) takes into account the correct symmetry coefficients: the diagrams with two identical fermion lines have the symmetry coefficient 1/2. Notice also that \(\Sigma \)-baryon DAs are defined as in Ref. [21]

$$\begin{aligned} \text {DA}^{\Sigma }\equiv \text {DA}^{\Sigma ^{-}}=-\text {DA}^{\Sigma ^{+}}=\sqrt{2}\text {DA}^{\Sigma ^{0}}, \end{aligned}$$
(75)

which is also taken into account in Eq. (71).

The expression for the amplitude \({\mathcal {G}}_{E}^{N}\) given in Ref. [13] agrees with one given in Eq. (71). The properties of the DAs and the hard kernels allow one to simplify the expression for the integrand in Eq. (74) excluding the contributions with \({\mathcal {A}}_{2},\mathcal { V}_{2}\) and \({\mathcal {T}}_{22}-{\mathcal {T}}_{42}\). The integral\(J_{E}^{B}\) is well defined that can be easily seen using the following observation: all DAs in the integrand in Eq. (74) have the following structure

$$\begin{aligned} \text {DA}(x_{123})=x_{1}x_{2}x_{3}\times \sum _{k_{i}\ge 0}C_{k_{1}k_{2}k_{3}}\text { }x_{1}^{k_{1}}x_{2}^{k_{2}}x_{3}^{k_{3}}.\text { } \end{aligned}$$
(76)

Therefore the singular denominator \((x_{1}x_{2}x_{3}y_{1}y_{2}y_{3})^{-1}\) is compensated that eliminates a possibility to get the endpoint singularities. The resulting integrals for \(J_{M,E}^{B}\) can be easily computed numerically using standard integration packages accessible in Wolfram Mathematica.

Let us also mention that the baryon integrals \(J_{M,E}^{B}\) for different baryons are equal to each other in the exact SU(3) limit. The formal consideration of this point obviously involves the identities in Eqs. (47) and (48). However these equations do not lead to a simple analytical expressions at the end. In addition the equality of the integrals in the SU(3) limit imposes non-trivial relations between the different the hard kernels in Eqs. (72) and (74). It has been explicitly verified that all such relations are satisfied, which provides a powerful check of the obtained analytical expressions.

4 Phenomenology

In the previous section we described the hadronic amplitudes, which are associated with the three gluon annihilation \(J/\psi \rightarrow 3g\rightarrow B{\bar{B}}\). In order to confront theoretical predictions with the experimental data one has also to take into account the electromagnetic decay process \(J/\psi \rightarrow \gamma ^{*}\rightarrow B{\bar{B}}\). Corresponding amplitudes are described by the baryon electromagnetic time-like form factors (FFs). There are strong indications that these quantities are dominated by long distance dynamics and therefore can not be accurately computed in pQCD. In this work we assume that such contributions provide a sizeable but not very large or dominant effect and therefore can be ignored at the first step. Therefore our main task is to study the numerical effect provided by the three-gluon mechanism to the branching ratio and to the ratio \(\gamma ^{B}=|{\mathcal {G}} _{E}^{B}/{\mathcal {G}}_{M}^{B}|\), which completely defines the angular behaviour through the parameter \(\alpha ^g _{B}\)

$$\begin{aligned} \alpha _{B}^{g}=\left( 1-\frac{4m_{B}^{2}}{M_{\psi }^{2}}\left| \frac{ {\mathcal {G}}_{E}^{B}}{{\mathcal {G}}_{M}^{B}}\right| ^{2}\right) \left( 1+ \frac{4m_{B}^{2}}{M_{\psi }^{2}}\left| \frac{{\mathcal {G}}_{E}^{B}}{ {\mathcal {G}}_{M}^{B}}\right| ^{2}\right) ^{-1}, \end{aligned}$$
(77)

where the superscript \(``g''\) indicates that this is pure hadronic contribution associated with the three-gluon annihilation subprocess.

One more correction is described by the combined annihilation \( J/\psi \rightarrow \gamma ^{*}gg\rightarrow B{\bar{B}}\) . We estimate this contribution as a higher order correction and therefore it will be excluded from the current analysis.

For the branching ratio we also use simplified expression

$$\begin{aligned} Br[J/\psi \rightarrow B{\bar{B}}]=\frac{1}{\Gamma _{J/\psi }}\frac{M_{\psi }\beta }{12\pi }|{\mathcal {G}}_{M}^{B}|^{2}\left( 1+\frac{2m_{B}^{2}}{M_{\psi }^{2}}\gamma _{B}^{2}\right) ,\nonumber \\ \end{aligned}$$
(78)

where \(\gamma _{B}=\left| {\mathcal {G}}_{E}^{B}\right| /|{\mathcal {G}} _{M}^{B}|\), \(\beta =\sqrt{1-4m_{B}^{2}/M_{\psi }^{2}}\) and the total widh \(\Gamma _{J/\psi }=\) 93 MeV.

The amplitudes \({\mathcal {G}}_{M/E}^{B}\) depend on the non-perturbative parameters, which describe the overlap with initial and final hadrons. The charmonium matrix element is defined in NRQCD as

$$\begin{aligned} \left\langle 0\right| \chi _{\omega }^{\dag }(0)\gamma ^{\mu }\psi _{\omega }(0)\left| J/\psi (P)\right\rangle =\epsilon _{\psi }^{\mu }~f_{\psi }, \end{aligned}$$
(79)

where the coupling \(f_{\psi }\) is related with the quarkonium radial wave function at the origin

$$\begin{aligned} f_{\psi }=\sqrt{2M_{\psi }}\sqrt{\frac{3}{2\pi }}~R_{10}(0). \end{aligned}$$
(80)

The value \(R_{10}(0)\) has been estimated in the various potential models and in this work we use the estimate obtained for the Buchmüller-Tye potential [27]

$$\begin{aligned} \left| R_{10}(0)\right| ^{2}\simeq 0.81 \,\, \text {GeV}^{3}, \end{aligned}$$
(81)

which implies the charm quark mass to be \(m_{c}=1.48\) GeV.

The baryon and antibaryon matrix elements are defined in terms of DAs as described above. The model ABO1 is discussed in Ref. [20], the corresponding set of the parameters allows one to get reliable description of the electromagnetic nucleon form factors. The advantage of this model is that corresponding twist-3 and twist-4 DAs provide the unified theoretical description. However this model does not fix the normalisation coupling \( f_{N}\). In this work we take \(f_{N}(4\hbox {GeV}^2)=4.80\times 10^{-3}\) \(\hbox {GeV}^{2}\) , which is consistent with the sum rule calculation from Refs. [23,24,25]. This value is sufficiently larger than the lattice result \(f_{N}^{\text {lat}}(4\hbox {GeV}^2)=3.54\times 10^{-3}\) \(\hbox {GeV}^{2}\).

The DAs for other octet baryons are not well known yet. The twist-3 moments have been investigated within the various frameworks, see e.g. Refs. [23,24,25,26]. However these considerations do not include the higher twist DAs. Recently some of the twist-3 and twist-4 moments have been calculated on the lattice in Ref.  [17]. These results are quite interesting however the obtained values for the nucleon DAs are sufficiently different from the ABO1 model. In some cases this provides a substantial numerical effect and leads to a strong disagreement with the experimental data. For instance, for nucleon the largest numerical effect is related with the relatively small value of the coupling \(f_{N}\) obtained in Ref.  [17]. Nevertheless we use the results from Ref.  [17] as a first guess for baryons \(\Lambda ,\Sigma ,\Xi \) and modify the values of some parameters in order to get a more reliable description if the discrepancy with the data are large.

The twist-4 DAs depend explicitly from the strange quark mass, see Eqs. (62)–(67). For this mass we take the value \(m_s(2\,\text {GeV}^2)=100\,\)MeV.

The values of different parameters are given in Table 2 for twist-3 and twist-4 DAs, respectively.

Table 2 The parameters, which define the twist-3 and twist-4 models of the baryon DAs (upper and bottom tables, respectively)
Full size table

We will refer to these DAs as to unmodified set.

In order to provide reliable estimates for the amplitude \({\mathcal {G}}_{E}^{B}\) one also needs to estimate the twist-4 moments, which are not yet been studied. The twist-4 moments \(\{\eta _{10}^{B},\eta _{11}^{B},\zeta _{10}^{B},\zeta _{11}^{B}\}\) (except the nucleon case) are not known. Therefore to a first guess we take for these parameters the same values as for the nucleon neglecting the SU(3)-breaking effects. Further we modify them in order to improve the description of the data. The corresponding set of DAs will be referred as modified ones.

Our numerical calculations show that the value of \({\mathcal {G}}_{E}^{B}\) is quite sensitive to the parameters \(\eta _{11}^{B}\) and \(\zeta _{11}^{B}\). Therefore these unknown parameters will be modified while the computed \(\lambda _{1}^{B}\) and \(\lambda _{\bot }^{B}\) will remain unchanged.

The value of the amplitude \({\mathcal {G}}_{M}^{B}\) is quite sensitive to the normalisation coupling \(f_{B}\). One finds sufficiently strong disagreement between the lattice data and the sum rules estimates not only for nucleon but also for other baryons. The lattice results also indicate about strong SU(3)-breaking effects. These observations can be interpreted as a presence of uncertainties in the numerical values of \( f_ {B}\). Therefore the couplings \(f_{B}\) will be also modified in order to improve a qualitative description.

The DAs parameters depends on the factorisation scale \(\mu _{F}\), more details about this dependence can be found in Appendix. The branching ratios strongly depend on the QCD coupling \(\alpha _{s}(\mu _{R}^{2}),\) where the scale \( \mu _{R}\sim m_{c}\). In the given analysis we consider \(\mu _{F}=\mu _{R}=\mu \) and perform the estimates for the two values of the scale \(\mu ^{2}=2m_{c}^{2}\) and \(\mu ^{2}= 1.5~\hbox {GeV}^{2}\) in order to see the value of the corresponding uncertainty.

The obtained numerical results are presented in the Table 3.

Table 3 The results of the numerical calculations in comparison with the experimental data
Full size table

In order to estimate the branching ratios we use in Eq. (78) the experimental value for the ratio \(\gamma ^{B}\), which can be easily obtained from the data for \(\alpha _B\). Therefore in this case the only unknown quantity is the \(|{\mathcal {G}}_{M}^{B}|^{2},\) which is dominated by the leading power contribution. The values of the power suppressed term \(\sim |\gamma ^{B}_{\exp }|^{2}\) in Eq. (78) are shown in last column of Table 3. For nucleon this term is only about \(13\%\), which is not large comparing with other expected uncertainties. For heavier \(\Xi \) this term increases to \(22\%\). However for \(\Sigma \) this term is enhanced and its numerical value becomes even larger than one. This enhancement is related with the large value \(\gamma ^\Sigma _{ \exp }\sim 2\), which is the direct consequence of the negative polarisation parameter \(\alpha _{\Sigma }< 0\), see Table 1. This observation allows one to conclude that for the \(\Sigma \)-channel the value of the branching ratio is not dominated by the amplitude \({\mathcal {G}}_{M}^{B}\) as for all other baryons.

The resulting description of \({\mathcal {G}}_{M}^{B}\) shows that for the large scale \(\mu ^{2}=\) \(2m_{c}^{2}\) the obtained branching ratios are about factor 2–3 below the data. For the small scale \(\mu ^{2}=1.5\, \hbox {GeV}^{2}\) the agreement with the data is much better. The main source of the large sensitivity to the scale dependence in present case is the value of the \(\alpha _{s}(\mu ^2)\). Notice that this uncertainty cancels in the ratio \(\gamma _g ^{B}\), which becomes quite stable.

The results for the proton-antiproton decay have been discussed in Ref. [13]. In Table 3 we also added the information for the neutron-antineutron channel. The experimental value of \(\gamma _{n}\) is somewhat larger than \(\gamma _{p}\), but the experimental errors for \(\gamma _{n}\) are also larger. Potentially this relatively small difference can be attributed to the mixing with electromagnetic FFs. From the SU(2) symmetry it follows that \(\gamma _{g}^{p}=\gamma _{g}^{n}\). Numerically the obtained \(\gamma _{g}^{N} \) is less by \(20-30\%\) than \(\gamma _{\exp }^{p}\) or \(\gamma _{\exp }^{n}\), respectively. This is rather good result taking into account the underlying uncertainties. Qualitatively it shows that the leading-order contribution to \(\gamma _{g}^{N}\) is sufficiently large and indicates that the factorised contribution provides already a reliable description.

The unmodified DAs in Table 2 provide for \(\Lambda \)-baryon a relatively small value of the branching ratio, which is about factor 2 smaller than the experimental one. At the same time, the obtained value of \(\gamma _{g}^{\Lambda }\) is a bit larger than \(\gamma _{\text {exp} }^{\Lambda }\). This may indicate that the amplitude \({\mathcal {G}}_{M}^{\Lambda }\) is underestimated. Therefore in order to make the description more similar to the nucleon case, one can modify the following one parameter: \(f_{\Lambda }\rightarrow 5.5\times 10^{-3}\).Footnote 4 The larger value \(f_{\Lambda }\) increases \({\mathcal {G}}_{M}^{\Lambda }\) and at the same time this reduces the value of \({\mathcal {G}}_{E}^{\Lambda }\). After that the obtained results better agrees with the data and qualitatively better overlaps with the description for the nucleon channel. The modified value of \(f_{\Lambda }\) is larger than the value obtained from the sum rule in Ref. [23,24,25]: \(f_{\Lambda }=4.69\times 10^{-3}\) \(\hbox {GeV}^{2}\). However the SU(3) violation effect in this case is rather mild \((f_{\Lambda }-f_{N})/f_{N}\approx 0.15\).

For the \(\Sigma \)-decay channel the numerical results are different: the unmodified DAs provide sufficiently large branching ratio (only for the small scale \(\mu \) ) but the corresponding value of \(\gamma _{g}^{\Sigma }\) is about factor 2 smaller. Therefore in order to improve the description it is natural to reduce the value \(f_{\Sigma }\rightarrow 4.5\times 10^{-3}\) and to increase the values \(\eta _{11}^{\Sigma }\rightarrow 0.23\) and \(\zeta _{11}^{\Sigma }\rightarrow 0.23\). This improves the description of \(\gamma _{g}^{\Sigma }\) but also implies sufficiently large SU(3)-breaking corrections for \(\Sigma \). The modified values of \(\eta _{11}^{\Sigma }\) and \(\zeta _{11}^{\Sigma }\) are about factor two larger then ones for other baryons. At the same time the modified value \(f_{\Sigma }\) is in a good agreement with the value obtained from the sum rules \(f_{\Sigma }=4.65\times 10^{-3}\) [23,24,25] .

In case of the \(\Xi \)-decay channel the unmodified DAs provide somewhat larger values for the branching ratio and for \(\gamma _{g}^{\Xi }\). In order to reduce these numbers the following values have been modified \(f_{\Xi }\rightarrow 5.1\times 10^{-3}\), \(f_{\Xi }^{\bot }\rightarrow 5.29\times 10^{-3}\) and \(\eta _{11}^{\Xi }\rightarrow 0.11,\ \zeta _{11}^{\Xi }\rightarrow 0.11\). The new value \(f_{\Xi }\) is more close to the sum rules result [23,24,25] \(f_{\Xi }\rightarrow 4.83\times 10^{-3}\) and such modification also reduces the effect from the SU(3)-breaking corrections, which is observed for the lattice data.

5 Conclusions

The decay amplitudes for the process \(J/\psi \rightarrow B{\bar{B}}\) have been computed within the QCD collinear factorisation framework for the octet baryon states. The obtained results have been used for a qualitative phenomenological analysis. The primary goal of presented consideration is to estimate the numerical contributions provided by the factorised amplitudes and to study their dependence on the models for the baryon light-cone distribution amplitudes. In this analysis we do not consider the effect from the mixing with the baryon electromagnetic decays, which potentially can also provide a numerical impact.

The obtained results show that the branching fractions for all baryons can be reasonably described for the relatively low normalisation scale \(\mu ^{2}\simeq 1.5\,\hbox {GeV}^{2}\) only. Moreover, the qualitative description of the branching fractions can be considerably improved if the values for the leading-twist baryon coupling \( f_{B}\), which are obtained from the lattice calculations, are modified. Such modification is very important for the nucleon channel and also allows one to improve the description for other baryons. Finally the modified set of the couplings \(f_{B}\) turns out to be more close to the sum rule estimates obtained in Refs. [23,24,25]. For this modified set the expected SU(3) breaking effects are smaller than for the lattice data.

The obtained ratios \({\mathcal {G}}_{E}^{B}/{\mathcal {G}}_{M}^{B}\) describe the experimental data within the 10–30% accuracy, which is quite reasonable taking into account different theoretical uncertainties. This indicates that the obtained contributions provide sufficiently large numerical effect for this observables. The ratios \({\mathcal {G}}_{E}^{B}/{\mathcal {G}}_{M}^{B}\) weakly depend on the choice of the QCD renormalisation scale because the strong coupling \(\alpha _{s}\) and charm quark mass \(m_{c}\) cancel in the ratio.

The value of the amplitude \({\mathcal {G}}_{E}^{B}\) is sufficiently large, so that the ratio \({\mathcal {G}}_{E}^{B}/{\mathcal {G}}_{M}^{B}\sim \) 0.6 to 0.8. The convolution integrals for \({\mathcal {G}}_{E}^{B}\) are quite sensitive to the shape of the twist-4 DAs, which can be interpreted as three quark state in a P-wave. The twist-4 moments \(\eta _{11}^{B}\) and \(\zeta _{11}^{B}\) for \(\Lambda , \ \Sigma \) and \(\Xi \) have been estimated using SU(3) symmetry and the data. In the given analysis the matrix elements of twist-4 quark-gluon operators are not included because they contribute to higher order moments, which are not considered in the used models for twist-4 DAs.

The experimental data indicate that the value of \(|{\mathcal {G}}_{E}^{\Sigma }/{\mathcal {G}}_{M}^{\Sigma }|\) is about factor 2–3 larger comparing with other octet baryons. This leads to the interesting observation: the power suppressed contribution in expression for width, see Eq. (78), is strongly enhanced and provides the very large numerical effect for the branching ratio. The dynamic origin of this effect is not clear. In order to describe this effect within the considered framework it is necessary to assume sufficiently large SU(3)-breaking corrections. This implies that the twist-4 parameters \(\eta _{11}^{\Sigma }\) and \(\zeta _{11}^{\Sigma }\), are about factor 2 larger comparing with for the nucleon ones. It remains unclear whether one can explain this enhancement of \(|{\mathcal {G}}_{E}^{\Sigma }/{\mathcal {G}}_{M}^{\Sigma }|\) by some intrinsic properties of the baryon wave functions or perhaps this effect may also be related with the hadron dynamics at large distances such as final state interactions.

In conclusion let us briefly discuss different effects, which can be important for a more advanced analysis. Accounting for interference with electromagnetic amplitudes can improve phenomenological analysis. New data obtained for baryon time-like electromagnetic form factors allows one to improve the estimate of this effect, this work is in progress.

From the given analysis it also follows that the obtained description gives reliable estimates at some relatively low scale only. The scale ambiguity can be better understood performing the calculation of the next-to-leading QCD corrections. Such calculation will allow one to clarify an applicability of the collinear factorisation in exclusive charmonia decays. However the computation of the next-to-leading corrections is quite challenging because it involves a big number of the various one-loop diagrams.

In order to see a size of possible hadronic effects one can compute the power corrections to the leading-order amplitude \({\mathcal {G}}_{M}^{B}\). Such calculation also involves three-quark twist-4 and twist-5 DAs, which have been already studied in the literature [18, 20]. One can not exclude that the three-quark twist-4 DAs also provide a large power correction of order \(\Lambda ^{2}/m_{c}^{2}\) to the amplitude \({\mathcal {G}}_{M}^{B}\). If this is correct then the description of the decay observables will be considerably improved.

In addition to the studied decay mechanism there is one more contribution associated with the soft-overlap configuration of the final baryon-antibaryon state. In this case the heavy quark-antiquark pair annihilates into three hard intermediate gluons, which then create light quark and antiquark jets. The hadronisation of the jets into baryon and antibaryion involves interactions with the soft quarks and closely associated with the dynamical hard-collinear scale \(\mu _{hc}\sim \sqrt{\Lambda m_{c}}\), where \(\Lambda \) is a typical hadronic scale. Taking into account the realistic value of the charm mass \(m_{c}\) one concludes that \(\mu _{hc}\) is quite small. Therefore such soft-overlap matrix element can be considered as non-factorisable in the light-quark sector. It is not difficult to show that such contribution is of the same order in \(1/m_{c}\) as the factorisable collinear one, see e.g. Ref. [28]. The corresponding hard coefficient function is described by the two-loop diagrams and also proportional to \(\alpha _{s}^{3}\). Unlike the collinear factorisation contribution, such decay amplitude has nontrivial imaginary phase associated with the cuts perturbative diagrams. The hard-collinear matrix element(s) can be unambiguously defined within the soft-collinear effective theory. Such decay mechanism can also provide a tangible numerical effect and therefore needs to be studied. This work is postponed for a future.