1 Introduction

Semileptonic B and D meson decays have been for long considered as a good source to learn about non perturbative strong interactions, given the good knowledge of the weak vertex [1,2,3]. Refined methods have become available more recently [4,5,6] and the reactions are looked upon with interest to even learn about physics beyond the standard model [7, 8]. Explicit calculations correlating a vast amount of data with the help of some selected pieces of experimental information are also available [9]. One of the relevant cases of these reactions consist on D meson decays leading to resonances in the final state, rather than the ordinary ground state of mesons, usually studied. In particular, semileptonic decays of hadrons where the final hadron is a resonance are specially interesting. In this sense, the B and \(B_s\) semileptonic decays leading to \(D_0^*(2400)\) and \(D_{s0}^*(2317)\) resonances were studied in Ref. [10]. Similarly, the D decays into the scalar mesons \(f_0(500)\), \(K_0^*(800)\), \(f_0(980)\) and \(a_0(980)\) were addressed in Ref. [11], with relevant results concerning the nature of these scalar mesons. A review of these and related reactions can be seen in Ref. [12]. In this direction, the recent observation of the \(D^+\rightarrow \nu e^+ \bar{K}_1^0(1270)\) reaction measured by the BESIII collaboration [13] offers a new opportunity to study the properties and nature of the \(K_1(1270)\) axial-vector resonance. Prior to this measurement the CLEO collaboration presented results on the \(D^+\rightarrow \nu e^+ \bar{K}_1^0(1270)\) [14], but the quality of data is much improved in the BESIII measurements. Interestingly there are theoretical results on these reactions in Refs. [1, 2] using quark models, in Ref. [15] using QCD sum rules and factorization approach, in Ref. [16] using a covariant light front quark model and in Ref. [17] using light cone sum rules. The branching ratios obtained, within \(10^{-2}-10^{-3}\), agree qualitatively with the one measured by BESIII of about \(2.3\times 10^{-3}\).

Our interest in this reaction stems from the findings of Refs. [18, 19] that there are two \(K_1(1270)\) resonances instead of one. The idea of the present work is to see which are the particular measurements in the BESIII reaction that could show evidence of these two states, for which we do theoretical calculations looking into particular final channels. The standard quark model picture for mesons and baryons [20,21,22,23,24,25] has the great value to correlate a great amount of data on hadron spectroscopy, but the axial vector meson states are systematically not so well reproduced as the vector ones [20, 25]. With this perspective it is not surprising that other pictures have been proposed to explain these states. The chiral unitary approach (UChPT) [26, 27] was applied to the study of the pseudoscalar-vector meson interaction, using the chiral Lagrangian of Ref. [28] and it was shown that the interaction, unitarized in coupled channels, gave rise to bound states or resonances which could be identified with the low lying axial-vector resonances [18, 29, 30]. An appealing feature of these dynamically generated resonances is that the reaction mechanisms producing them proceed in a different way than ordinary mechanisms that produce resonances. Indeed, one does not produce the resonances directly, rather one produces the meson-meson components of the different coupled channels, which upon final state interaction among themselves generate the resonances. This allows one to perform calculations and relate many production channels, and often leads to particular features in the invariant mass distributions [12]. Concerning axial-vector meson production in different reactions, work has been done recently in the study of the \(J/\psi \rightarrow \eta (\eta ')h_1(1380)\) reaction [31], \(\tau ^-\rightarrow \nu _\tau P A\) with \(P=\pi ,K\) and \(A=\) \(b_1(1235)\), \(h_1(1170)\), \(h_1(1380)\), \(a_1(1260)\), \(f_1(1285)\) [32] and \(\chi _{cJ}\) decay to \(\phi h_1(1380)\) [33], among others quoted in those works.

In Refs. [18, 19] it was shown that there were two \(K_1(1270)\) states, which coupled differently to the coupled channels. One state appears at \(1195\text { MeV}\) and couples mostly to \(K^*\pi \). The other state appears at \(1284\text { MeV}\) coupling mostly to \(\rho K\). In Ref. [19] some reactions disclosing these final states were studied and it was shown that they peaked at different energies, and the state of higher mass had a smaller width. The existence of the two \(K_1(1270)\) is directly linked to the chiral dynamics of the problem and is similar to the appearance of the two \(\Lambda (1405)\) states in the baryon strange sector [34,35,36] (see the review “Pole structure of the \(\Lambda (1405)\) region” in the PDG [37]). With this picture in mind some reactions have been proposed to provide extra evidence of the existence of these two \(K_1(1270)\) states. In Ref. [32] the \(\tau ^-\rightarrow \nu _\tau K^- K_1(1270)\) reaction is proposed looking at the \(\rho K\) and \(K^* \pi \) final decay products of the \(K_1(1270)\) and two distinct peaks are seen in the results. In Ref. [38] the \(D^0 \rightarrow \pi ^+ \rho \bar{K}\) and \(D^0 \rightarrow \pi ^+ \pi \bar{K}^*\) reactions are also suggested in order to see the two peaks corresponding to the two \(K_1(1270)\) resonances.

In the present work, taking advantage of the recent BESIII measurement [13], we look at the \(D^+\rightarrow \nu e^+ \bar{K}_1^0(1270)\) reaction, evaluating explicitly the decays \(\bar{K}_1(1270)\rightarrow \rho \bar{K}\) and \(\bar{K}_1(1270)\rightarrow \pi \bar{K}^*\), showing that these final channels give different weights to the two \(K_1(1270)\) resonances and lead to invariant mass distributions that differ in the position and the shape. In view of the results obtained here we can only encourage the BESIII collaboration to perform the analysis that we suggest here, which should shed valuable light on the issue of the two \(K_1(1270)\) states and the nature of the low lying axial-vector resonances.

2 Formalism

Fig. 1
figure 1

Elementary \(D^+\rightarrow \nu e^+ V P\) process at the quark level

Full size image

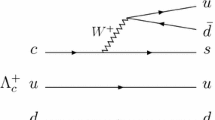
As explained in the introduction, within the UChPT of Refs. [18, 19], the axial-vector resonances are generated dynamically by the non-linear chiral dynamics involved in the unitarization procedure of the elementary VP scattering potential in s-wave, and there is no need to include them as explicit degrees of freedom (by means of Breit–Wigner like amplitudes or similar). (We refer to Ref. [18] for the seminal work on the UChPT approach for the axial-vector resonances, and to Refs. [19, 38,39,40] for brief but illustrative summaries). In particular, for the strangeness \(S=1\) and isospin \(I=1/2\) channels two poles were found in Refs. [18, 19], which were associated to two \(K_1(1270)\) resonances, looking at unphysical Riemann sheets of the unitarized VP scattering amplitudes. The poles are located at \((1195-i123)\text { MeV}\) and \((1284-i73)\text { MeV}\), where we can identify the real part with the mass and the imaginary part with half the width. In Table IV of Ref. [19] the values of the different couplings to the different VP channels can be seen. The main observation is that the lower mass pole couples dominantly to \(K^*\pi \) and the higher mass pole to \(\rho K\), but the couplings to the other VP channels are not negligible, and are actually considered. Following this philosophy, the way to produce a dynamically generated \(K_1(1270)\) resonance in a particular reaction is to create first all possible VP pairs and then implement their final state interaction. This later issue will be addressed in the second part of this section but first we need to discuss the calculation of the elementary production of the VP states, and its depiction, at the quark level, can be seen in Fig. 1. First the c quark produces an s quark through the Cabibbo favored vertex Wcs and then hadronization into a final vector and a pseudoscalar meson is implemented by producing an extra \(\bar{q} q\) with the \(^3P_0\) model [41,42,43].

We should note here, concerning the UChPT used in Refs. [18, 19], that it is based on a dispersion relation for the inverse of the scattering amplitude, which explicitly neglects the left-hand cut contribution. This might appear as a handicap but we should first warn that the contribution of the left-hand cut is usually small, only relevant in cases at small energy. The left-hand cut is explicitly considered in approaches like Roy equations [44,45,46] and other approaches [47]. In Ref. [44] it is found that for the amplitudes of the \(f_0(500)\) resonance the contribution of the left-hand cut is of the order of \(15\%\) and it is smaller in other cases where the masses of the particles involved are bigger [34, 48]. Yet, contrary to what it might look, the UChPT takes this contribution into account rather accurately, because when the left-hand cut is relatively far away from the physical energy, as in the present case, the contribution of the left-hand cut is rather energy independent and the UChPT introduces a subtraction constant in the dispersion relation which is tuned to some experimental magnitude. What is lost in the approach is only the weak energy dependence of a small quantity, which is approximated by a constant, and this is what makes the UChPT a rather accurate tool.

We are mostly interested in evaluating the relative weight and momentum dependence of the different channels modulo a global arbitrary normalization factor. The different weights among the allowed VP channels can be obtained from the following SU(3) reasoning.

The flavor state of the final hadronic part after the \(\bar{q} q\) is produced in the hadronization is

$$\begin{aligned} |H\rangle \equiv |s\,(\bar{u} u +\bar{d} d +\bar{s} s)\,\bar{d} \rangle , \end{aligned}$$
(1)

which can be written as

$$\begin{aligned} |H\rangle = \sum _{i=1}^3{|M_{3i}q_i\bar{d}} \rangle = \sum _{i=1}^3{|M_{3i}M_{i2} } \rangle = |(M^2)_{32}\rangle , \end{aligned}$$
(2)

where we have defined

$$\begin{aligned} q\equiv \left( \begin{array}{c}u\\ d\\ s\end{array}\right) \,\text {~~and~~~} M\equiv q\bar{q}^\intercal =\left( \begin{array}{ccc}u\bar{u} &{}\quad u\bar{d} &{}\quad u\bar{s}\\ d\bar{u} &{}\quad d\bar{d} &{}\quad d\bar{s}\\ s\bar{u} &{}\quad s\bar{d} &{}\quad s\bar{s} \end{array}\right) . \end{aligned}$$
(3)

The hadronic states can be identified with the physical mesons associating the M matrix with the usual SU(3) matrices containing the pseudoscalar and vector mesons:

$$\begin{aligned}&M\Rightarrow P\equiv \left( \begin{array}{ccc} \frac{\pi ^0}{\sqrt{2}} + \frac{\eta }{\sqrt{3}}+\frac{\eta '}{\sqrt{6}}&{} \quad \pi ^+ &{}\quad K^+\\ \pi ^-&{}\quad -\frac{1}{\sqrt{2}}\pi ^0 + \frac{\eta }{\sqrt{3}}+ \frac{\eta '}{\sqrt{6}}&{}\quad K^0\\ K^-&{}\quad \bar{K}^0 &{}\quad -\frac{\eta }{\sqrt{3}}+ \frac{2\eta '}{\sqrt{6}} \end{array} \right) , \nonumber \\&M\Rightarrow V \equiv \left( \begin{array}{ccc} \frac{1}{\sqrt{2}} \rho ^0 + \frac{1}{\sqrt{2}}\omega &{}\quad \rho ^+ &{}\quad K^{*+}\\ \rho ^-&{}\quad - \frac{1}{\sqrt{2}} \rho ^0 + \frac{1}{\sqrt{2}}\omega &{}\quad K^{*0}\\ K^{*-}&{}\quad \bar{K}^{*0} &{}\quad \phi \end{array} \right) , \end{aligned}$$
(4)

where the usual mixing between the singlet and octet to give \(\eta \) and \(\eta '\) [49] has been used in the P matrix. Also in the V matrix, ideal \(\omega _1\)-\(\omega _8\) mixing has been considered to produce \(\omega \) and \(\phi \), to agree with the quark content of M in Eq. (3).

Since the \(M^2\) in Eq. (2) can refer either to VP or PV, we need to evaluate the contribution

$$\begin{aligned} (VP)_{32}+(PV)_{32}&= \rho ^+ K^- - \frac{1}{\sqrt{2}} \rho ^0 \bar{K}^{0} + {K^*}^-\pi ^+ \nonumber \\&\quad - \frac{1}{\sqrt{2}} \bar{K}^{*0} \pi ^0 + \frac{1}{\sqrt{2}}\omega \bar{K}^{0} + \phi \bar{K}^{0} \end{aligned}$$
(5)

where we see that the \(\bar{K}^{*0}\eta \) channel has been cancelled mathematically and the \(\eta '\) is neglected because of its large mass as done in the original work of the VP interaction that generated the axial-vector \(K_1(1270)\) [18]. The numerical coefficients in Eq. (5) in front of each VP channel provide the relative strengths of the different VP channels.

The momentum structure of the amplitude corresponding to the mechanism in Fig. 1 can be evaluated in a similar way to what was done in Refs. [10, 11]. Indeed, the amplitude, T, for the process of Fig. 1 can be factorized into the weak part and the hadronization part, and then it will be proportional to

$$\begin{aligned} L^\mu Q_\nu \, V_\mathrm{Had} \end{aligned}$$
(6)

where global constant factors are omitted since we will perform the calculations up to a global normalization. In Eq. (6) \(L^\mu =\bar{u}_\nu \gamma ^\mu (1-\gamma _5)v_l\) is the leptonic current and \(Q_\mu =\bar{u}_s \gamma _\mu (1-\gamma _5)u_c\) the quark current. The hadronization part \(V_\mathrm{Had}\) will be discussed later on.

When evaluating the D decay width of this process, we will need to square the amplitude and sum over the quark polarizations which gives (see Ref. [11] for explicit details and calculation)

$$\begin{aligned} \frac{1}{2} \sum _\mathrm{pol} |T|^{2} = \frac{4 |V_\mathrm{had} |^{2}}{m_{l} m_{\nu } m_{D} M_\mathrm{{VP}}} ( p_{l} \cdot p_{D} ) ( p_{\nu } \cdot p_\mathrm{{VP}} ), \end{aligned}$$
(7)

where \(p_i\) are the four-momenta of the corresponding particles, \(m_i\) the masses, and the \(\mathrm {VP}\) label refers to the final VP pair, which will eventually account for the \(K_1(1270)\) resonance.

The final expression for the VP invariant mass, \(M_\mathrm{{VP}}\), distribution of the \(D^+\rightarrow \nu e^+ V P\) decay can be obtained in the same way as in Ref. [11] (see the derivation leading to Eq. (23) of Ref. [11]) and gives

$$\begin{aligned} \frac{d \Gamma }{d M_\mathrm{{VP}}}&= \frac{2 }{(2\pi )^{5}m_{D}^{3} M_\mathrm{{VP}}} \int d M_{e\nu } \, M_{e\nu }^2\,|\varvec{p}_\mathrm{{VP}}|\, |\varvec{\tilde{p}}_{\nu }| \,|\varvec{\tilde{p}}_{V}|\nonumber \\&\quad \times \left( \tilde{E}_{D} \tilde{E}_\mathrm{{VP}} - \frac{1}{3} | \tilde{\varvec{p}}_{D} |^{2} \right) |V_\mathrm{Had}|^2 \end{aligned}$$
(8)

where \(M_{e\nu }\) is the \(e\nu \) invariant mass and

$$\begin{aligned} |\varvec{p}_\mathrm{{VP}}|&=\frac{1}{2 m_D} \lambda ^{1/2}(m_D^2, M_{e\nu }^2,M_\mathrm{{VP}}^2) \theta (m_D-M_{e\nu }-M_\mathrm{{VP}}), \nonumber \\ |\varvec{\tilde{p}}_V|&=\frac{1}{2 M_\mathrm{{VP}}} \lambda ^{1/2}(M_\mathrm{{VP}}^2, m_V^2,m_P^2) \theta (M_\mathrm{{VP}}-m_V-m_P), \nonumber \\ |\varvec{\tilde{p}}_\nu |&=\frac{M_{e\nu }}{2},\nonumber \\ \tilde{E}_{D}&=\frac{m_D^2+M_{e\nu }^2-M_\mathrm{{VP}}^2}{2 M_{e\nu }}, \nonumber \\ \tilde{E}_{R}&=\frac{m_D^2-M_{e\nu }^2-M_\mathrm{{VP}}^2}{2 M_{e\nu }}, \end{aligned}$$
(9)

with \(\lambda \) and \(\theta \) standing for the Källén and step functions respectively and we have neglected the positron mass.

One of the main ingredients in the calculation of the hadronic part is the implementation of the final state interaction of the VP pairs produced in the mechanism of Fig. 1, which is depicted in Fig. 2. Note that, since the \(K_1(1270)\) resonance is generated dynamically within our approach, it is not produced directly but, instead, the different VP pairs are produced and then rescatter infinitely many times which is accounted for by the unitarized VP scattering amplitude.

Fig. 2
figure 2

VP final state interaction

Full size image

Taking into account the six different possible intermediate VP pairs, (\({K^*}^-\pi ^+\), \(\rho ^+ K^-\), \(\bar{K}^{*0} \pi ^0\), \(\rho ^0 \bar{K}^{0}\), \(\omega \bar{K}^{0}\) and \(\phi \bar{K}^{0}\)) the hadronic part of the amplitude for the decay into the \(i-\)th final VP channel can be written as

$$\begin{aligned} V_\mathrm{Had}(D^+\rightarrow \nu e^+ V_iP_i)=V_p \left( h_i + \sum _{j=1}^6 h_j G_j T^\mathrm{{I=1/2}}_{j,i}\right) \end{aligned}$$
(10)

where \(V_p\) is an arbitrary global normalization factor, and includes the weak coupling constant among other factors stemming from the quark matrix elements, \(h_i\) are the numerical coefficients in front of each VP channel in Eq. (5), \(G_j\) is the vector-pseudoscalar loop function [19] and \(T^\mathrm{{I=1/2}}_{j,i}\) is the unitarized \((VP)_j\rightarrow (VP)_i\) scattering amplitude in isospin 1/2 from Ref. [19]. These are the amplitudes that manifest the double pole structure in the complex energy plane associated to the \(K_1(1270)\). Note that in Ref. [19] the VP states are in isospin basis and here we are working with explicit charge basis, but we can easily transform from one to the other basis using that

$$\begin{aligned} | \rho \bar{K} \rangle _{I=\frac{1}{2}, I_3=\frac{1}{2}}&= \sqrt{\frac{2}{3}} |\rho ^+ K^-\rangle - \frac{1}{\sqrt{3}} |\rho ^0 \bar{K}^0\rangle ,\nonumber \\ |\bar{K}^{*} \pi \rangle _{I=\frac{1}{2}, I_3=\frac{1}{2}}&= -\sqrt{\frac{2}{3}} |K^{*-} \pi ^+\rangle + \frac{1}{\sqrt{3}} |\bar{K}^{*0}\pi ^0\rangle . \end{aligned}$$
(11)

We should note that we are taking \(V_P\) constant, while it should be a form factor that depends on \(q^2\) [4,5,6]. Yet, in the range of energies where our peaks emerge, these form factors are rather soft and, given the fact that the peaks fall down in about \(200\text { MeV}\), the effects of these form factors would only show up in the region where our amplitudes are already rather small, thus not changing the structure of the peaks discussed. Certainly, the ratio of the mass distributions obtained is independent of \(V_P\) and hence it is rid of the form factors.

On the other hand, note that these unitarized VP scattering amplitudes do not necessarily have a Breit–Wigner shape in the real axis (see explicit plots in Refs. [19, 38]). They actually contain the information of the whole VP dynamics and not only the resonant structure. However, in a actual experiment one would typically try to fit Breit–Wigner like shapes and therefore we will also compare in the results section the results using for the scattering amplitudes

$$\begin{aligned} T_{ij}=\frac{g_i g_j}{s-s_p}, \end{aligned}$$
(12)

where \(s_p\) is the pole position which can be identified with the mass and width of the generated resonances \(\sqrt{s_p}\simeq M_R -i \Gamma _R/2\) and \(g_i\) are the couplings of the resonance to the i-th VP channel which can be obtained from the residues of the amplitudes at the pole positions and can be found in Table IV of Ref. [19].

Fig. 3
figure 3

VP invariant mass distributions for \(D^+\rightarrow \nu e^+ {K}^{*-}\pi ^+\) and \(D^+\rightarrow \nu e^+ {\rho }^{+} K^-\). Left panels, a, c including the interaction with the tree level mechanism of Fig. 1. Right panels, b, d without the interference with the tree level contribution

Full size image

The usual procedure to evaluate the decay width for this process is to compute the width for some known \(D^+\rightarrow \nu e^+ V P\) reaction, which allows us to determine the coefficient \(V_P\) in Eq. (10), and then determine the widths for each of the cases that we study. This is what is done for instance in Ref. [38]. This is unnecessary here since the reaction that we study has already been measured, so its experimental feasibility is out of question. Yet, in the measured reaction \(D\rightarrow K_1(1270) e \nu \rightarrow K \pi \pi e \nu \), the final state measured is \(K \pi \pi \), and has not been separated in \(K^* \pi \) and \(\rho K\), which is what we suggest to be done here. This requires extra experimental efforts, and definitely it would be easier with much better statistics, which if not with the present facilities, will become available in future updates of these facilities or planned ones as the Super Charm-Tau factory [50, 51].

3 Results

We first show in the left panels of Fig. 3 the different contributions to the VP invariant mass distribution for the \(D^+\rightarrow \nu e^+ {K}^{*-}\pi ^+\) and \(D^+\rightarrow \nu e^+ {\rho }^{+} K^-\). The absolute normalization is arbitrary, but the relative strength between the different curves and the different channels are absolute (There is only a global normalization constant, the same for all the channels, see Eq. (10)). The label “unitarized” stands for the results using for the \(VP\rightarrow VP\) amplitudes, \(T^\mathrm{{I=1/2}}_{ij}\), the unitarized model from Ref. [19], as explained above. These curves are compared to the results using, instead, the explicit Breit–Wigner like shapes of Eq. (12), labeled as “BW poles” and also considering the contribution of only the lower mass pole (A) or the higher mass pole (B). The “tree level” curve represents the result removing the final VP state interaction, i.e. only the mechanism of Fig. 2a), which is accounted for by considering only the first \(h_i\) term in Eq. (10). We have also implemented a convolution with the final vector meson spectral function, in the same way as in Ref. [38], in order to take into account the final vector meson widths. This is specially relevant for the \(\rho \bar{K}\) case due to the large width of the \(\rho \) meson and the fact that the \(\rho K\) threshold lies around the \(K_1(1270)\) energy region.

We see that the invariant mass distributions in these \(D^+\) decays are clearly dominated by the \(K_1(1270)\) resonant contribution but the curves are clearly different in shape and position of the peaks for the two final channels considered. Actually in the \({K}^{*-}\pi ^+\) channel the peak of the distribution is located around 1160–1180 MeV, depending on whether we use the unitarized or the Breit–Wigner amplitudes for the VP scattering. However, for the \({\rho }^{+} K^-\) distribution the curve peaks at around 1250-1270 MeV and is considerable narrower. This is a clear manifestation of the different weight that the two \(K_1(1270)\) poles have in both channels. Indeed, for the \({K}^{*-}\pi ^+\) final channel, the distribution is clearly dominated by the lower mass pole, the one at \(\sqrt{s_p}=(1195-i123)\text { MeV}\). This is a consequence of the large coupling of this pole to \(\bar{K}^{*}\pi \). In the \({\rho }^{+}K^-\) channel the individual poles have a more comparable strength among themselves but the higher mass pole, the one at \((1284-i73)\text { MeV}\), shifts the final strength to higher energies and narrows the distribution.

It is also worth noting, however, that there is an important interference effect between different mechanisms, particularly with the tree level contribution. This is clearly seen by comparing to the right panels, which have been evaluated removing the tree level terms, i.e. considering only the mechanisms in Fig. 2b). This is what one would obtain if the background, non-resonant terms could be ideally removed. In this later case the distributions would more clearly manifest the effect of the individual poles.

We should make some comments concerning the possible contribution of the \(K_1(1400)\) state, which we have not considered. In the UChPT of Refs. [18, 19] two \(K_1\) states are obtained, as we have discussed previously, but none of these states was associated to the \(K_1(1400)\) state, which then remains as a state of a different nature, but which can also contribute to the mass distributions discussed above. In quark models it is customary to talk about two states, \(K_{1A}\), \(K_{1B}\), and then there are two physical states which are mixture of these two states, the \(K_1(1270)\) and \(K_1(1400)\) [16, 52]. Our picture is quite different from this one since the two \(K_1\) states that we get are not from \(q \bar{q}\) nature. Then, we have three \(K_1\) states rather than two. This means that in addition to the contribution of the two states that we have considered we should expect a contribution from the \(K_1(1400)\) which we have not evaluated, and our model cannot provide. In Ref. [19] an analysis of some reactions was done and the \(K_1(1400)\) contribution was added as an explicit resonance propagator. The good finding of Ref. [19] concerning this discussion is that the contribution of the \(K_1(1400)\) was always smaller than the one of the other two states and it could be separated from them. We expect a similar situation here.

There is also another issue that we can raise at this point. In Eq. (2) we have introduced the hadronization by creating the \(\bar{q} q\) pairs with equal weight for u, d, s quarks. This is an SU(3) singlet and we are implicitly assuming that we have SU(3) symmetry. One may worry about a possible SU(3) breaking. At this point it is worth noting that SU(3) is supposed to be a good symmetry but only in Lagrangians or elementary vertices. This is the case for instance of the chiral Lagrangians. Violations of SU(3) appear, and some times are not small, as a consequence of the different masses of particles belonging to the same SU(3) multiplets, when for instance final state interaction is done to implement unitarization of amplitudes. One can implement SU(3) breaking in our approach by putting a different weight to the \(\bar{s} s\) component in that equation than to \(\bar{u} u\) and \(\bar{d} d\), which can have the same weight to implement isospin symmetry. Something like this is hinted in the approach to the \(J/\psi \rightarrow \phi (\omega ) \pi \pi \) reaction done in Ref. [53]. However, in Ref. [31] it is shown that this is not an SU(3) breaking, but the consequence that there are several SU(3) invariant structures to accommodate the production of one vector and two pseudoscalars, and the apparent SU(3) breaking in Ref. [53] actually comes from a combination of two of these SU(3) invariant structures, \(\langle VPP \rangle \) and \(\langle V \rangle \langle PP \rangle \). Following these observations we think that the \(\bar{u} u +\bar{d} d +\bar{s} s\) combination, normally used in these type of studies, is accurate. Yet, it is still interesting to make some estimates of what a moderate SU(3) breaking in this structure produces in the present case. Let us for this purpose assume that the \(\bar{s} s\) component in Eq. (1) has a weight \(1-\alpha \) rather than 1, i.e. we consider now

$$\begin{aligned} |H\rangle \equiv |s\,(\bar{u} u +\bar{d} d +(1-\alpha )\bar{s} s)\,\bar{d} \rangle . \end{aligned}$$
(13)

This implies that Eq. (5) is changed with two extra terms: \(\alpha \, \eta \bar{K}^{*0} /\sqrt{3} - \alpha \, \phi \bar{K}^{0}\). Assuming for instance \(\alpha \) of the order of 20%, taking into account the value of the couplings of \(\eta \bar{K}^{*}\) and \(\phi \bar{K}\) to the two \(K_1\) resonances [19] and the fact that both channels are quite above the resonance masses, which makes the size of the G functions appreciable smaller, we have estimated that the contribution of these new terms to the amplitudes that we have evaluated is below \(5\%\).

4 Summary

We show theoretically that the semileptonic decays of the \(D^+\) meson into \(\nu e^+ {K}^{*-}\pi ^+\) and \(\nu e^+ {\rho }^{+} K^-\) allow to distinguish the two different poles associated to the \(K_1(1270)\) resonance as predicted by the UChPT [18, 19]. Using as only input the lowest order chiral perturbation theory Lagrangian accounting for the tree level interaction of a vector and a pseudoscalar meson, the implementation of unitarity in coupled channels allows to obtain the full VP scattering amplitude which dynamically develops two poles associated to the \(K_1(1270)\) resonance, without including them as explicit degrees of freedom. The poles show up naturally from the highly non-linear dynamics implied in the unitarization. Each pole has different features which could allow them to be distinguished in specifically devoted reactions, like those considered in the present work. Indeed, each pole couples differently to different VP channels: the lower mass pole is wider and couples mostly to \(K^*\pi \) and the higher mass pole is narrower and couples predominantly to \(\rho K\).

The semileptonic decays studied in the present work proceed first with the elementary VP production from the hadronization after the weak decay of the c quark via the creation of a \(\bar{q} q\) pair with the \(^3P_0\) model. The weights of the different channels are then related using SU(3) arguments. The \(K_1(1270)\) shows up in the decay after the implementation of the final state interaction of the VP pair, using the unitarized VP amplitudes. In spite of the fact that in the full amplitudes there is always a mixture of both poles, we obtain, by evaluating the VP invariant mass distributions, that the \(D^+\rightarrow \nu e^+ {K}^{*-}\pi ^+\) weighs more the lower mass pole while in the \(D^+\rightarrow \nu e^+ {\rho }^{+} K^-\) decay the higher mass pole has a greater influence. The shapes do not necessarily reflect directly the pure resonant shape of each pole since there are interferences between the poles and non-resonant terms, but both the position and shape of the invariant mass distributions are clearly different and reflect the dominance of either pole in both channels considered and could be observed in experiments amenable to look at these mass distributions.