Triangle singularities in $B^-\rightarrow D^{*0}\pi ^-\pi ^0\eta$ and $B^-\rightarrow D^{*0}\pi ^-\pi ^+\pi ^-$

Abstract

The possible role of the triangle mechanism in the $B^-$ decay into $D^{*0}\pi ^-\pi ^0\eta$ and $D^{*0}\pi ^-\pi ^+\pi ^-$ is investigated. In this process, the triangle singularity appears from the decay of $B^-$ into $D^{*0}K^-K^{*0}$ followed by the decay of $K^{*0}$ into $\pi ^-K^+$ and the fusion of the $K^+K^-$, which forms the $a_0(980)$ or $f_0(980)$, which finally decay into $\pi ^0\eta$ or $\pi ^+\pi ^-$, respectively. The triangle mechanism from the $\bar{K}^*K\bar{K}$ loop generates a peak around 1420 MeV in the invariant mass of $\pi ^-a_0$ or $\pi ^-f_0$, and it gives sizable branching fractions, $\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- a_0;a_0 \rightarrow \pi ^0\eta )= (1.66\pm 0.45 )\times 10^{-6}$ and $\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- f_0 ; f_0 \rightarrow \pi ^+\pi ^-)= (2.82\pm 0.75)\times 10^{-6}$.

1 Introduction

Hadron spectroscopy is a way to investigate Quantum Chromodynamics (QCD), which is the basic theory of the strong interaction. The success of the quark model in the low-lying hadron spectrum gives us an interpretation of the baryons as composed of three quarks, and the mesons as made from quark and anti-quark [1, 2]. Meanwhile, the possibility of non-conventional hadrons called exotics, which are not prohibited by QCD, have been intensively studied. One example is the $\Lambda (1405)$: the quark model predicts a mass at higher energy than the observed peak, and a $\bar{K}N$ $(I=0)$ molecular state seems to give a better description as originally studied in Ref. [3] followed by many studies which are summarized in Refs. [4, 5]. The spectrum of the low-lying scalar mesons, such as the $f_0(980)$ or $a_0(980)$ mesons, is also discussed in this picture [6,7,8], while the possible explanation as tetraquark states is also discussed in Refs. [9, 10]. These days, in the heavy sector, the XYZ [11] and the $P_c$ [12, 13] were discovered, which cannot be associated with the states predicted by the quark model. Another sort of non-conventional hadrons are the molecular states of other hadrons, which have been often invoked to describe many existing states (see the recent review in Ref. [14]). Besides ordinary hadrons, molecular states or multiquark states, triangle singularities can generate peaks, but these peaks appear from a simple kinematical effect. These singularities were pointed out by Landau [15], and the Coleman–Norton theorem says that the singularity appears when the process has a classical counterpart [16]: in the decay process of a particle 1 into the particles 2 and 3, the particle 1 decays first into particles A and B, followed by the decay of A into the particles 2 and C, and finally the particles BC merge into the particle 3. The particles A, B, and C are the intermediate particles, and the singularity appears if the momenta of these intermediate particles can take on-shell values. A novel way to understand this process is proposed in Ref. [17].

For the decay of $\eta (1405)$ into $\pi ^0\pi ^0\eta$ via $\pi ^0a_0$ and $\pi ^0\pi ^+\pi ^-$ via $\pi ^0f_0$, the triangle mechanism gives a good explanation [18,19,20]. The $K^*\bar{K}K$ loop generates the triangle singularity in this process, and the anomalously large branching fraction of the isospin-violating $\pi ^0f_0$ channel reported by BESIII [21] is well explained with the mechanism.

The peak associated with this singularity can be misidentified with a resonance state. For example, the studies in Refs. [22,23,24] suggest the possible explanation of $Z_c(3900)$ with the triangle mechanism. Similarly, a peak seen in the $\pi f_0 (980)$ mass distribution, identified as the “$a_1(1420)$” meson by the COMPASS collaboration [25], is shown to be a manifestation of the triangle mechanism as studied in Refs. [22, 26, 27]. In particular, many XYZ states are discovered as a peak of the invariant mass distribution in the heavy hadron decay. Then the thorough study on the role of the triangle singularities in the heavy hadron decay is important to clarify the properties of the reported XYZ states. In the $B^-\rightarrow K^-\pi ^-D_{s0}^+(2317)$ $(K^-\pi ^-D_{s1}^+(2460))$ process, a peak can be generated by the triangle mechanism around 2800 MeV (2950 MeV) in the $\pi ^-D_{s0}^+$ ($\pi ^-D_{s1}^+$) invariant mass spectrum, which is driven by the $K^*DK$ $(K^*D^*K)$ loop, and gives a sizable branching fraction into the channel [28]. The $D_{s0}^+$ and $D_{s1}^+$ in the final state are dynamically generated by the DK and $D^*K$, and they have large coupling with these states [29,30,31]. Because the process of the triangle mechanism contains a fusion of two hadrons, the existence of a hadronic molecular state plays an important role in having a measurable strength. Then the study of the singularity is also a useful tool to learn about the nature of the hadronic molecular states. Regarding the $P_c$ peak, discovered in the $J/\psi p$ invariant mass distribution of the $\Lambda _b$ decay [12, 13], the possibility of the interpretation as a triangle singularity was pointed out in Refs. [32, 33]. However, in Ref. [17] it was noted that if the $P_c$ quantum numbers were $\frac{1}{2}^+$ or $\frac{3}{2}^+$ the triangle mechanism could provide an interpretation of the narrow experimental peak, but not if the quantum numbers are $\frac{3}{2}^-$, $\frac{5}{2}^+$, as preferred by experiment.

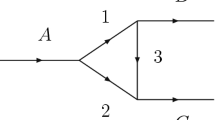
In the present study, we investigate the $B^-\rightarrow D^{*0}\pi ^-\pi ^0\eta$ and $B^-\rightarrow D^{*0}\pi ^-\pi ^+\pi ^-$ decays via $a_0$ and $f_0$ formation. The process of $B^-\rightarrow D^{*0}K^-K^{*0}$ followed by the $K^{*0}$ decay into $\pi ^-K^+$ and the merging of the $K^+K^-$ into $a_0$ or $f_0$ (see Fig. 1) generate a singularity, which would appear around 1418 MeV in the invariant mass of $\pi ^-a_0$ or $\pi ^-f_0$, as calculated using Eq. (18) of Ref. [17]. In this study, these $a_0$ and $f_0$ states appear as the dynamically generated states of $\pi \pi$, $K\bar{K}$, $\eta \eta$, and $K\bar{K}$, $\pi ^0\eta$ in the $I=0$ and $I=1$ channels, respectively, as studied in Refs. [33, 34].

Fig. 1

Diagram for the decay of $B^-$ into $D^{* 0}$, $\pi ^ -$ and R, where $R=a_0(980) \ \text {or} \ f_0(980)$

The mechanism proposed here, without the indication of how the $K^* \bar{K}$ could be formed, and without a quantitative evaluation of the process, was suggested in Ref. [22]. We provide here a realistic example of a physical process where this can occur, which also allows us to perform a quantitative calculation of the amplitudes involved.

Weak decays of heavy hadrons are turning into a good laboratory to find many triangle singularities. Apart from the work of Ref. [28], the $B_c \rightarrow B_s \pi \pi$ reaction has been suggested, where $B^+_c \rightarrow \bar{K}^{* 0} B^+$, $\bar{K}^{* 0} \rightarrow \pi ^0 \bar{K}^0$ and $\bar{K}^0 B^+ \rightarrow \pi B^0_s$ [35]. Yet, there are large uncertainties quantizing the $\bar{K}^0 B^+ \rightarrow \pi B^0_s$ amplitude and the $B^+_c \rightarrow \bar{K}^{* 0} B^+$ weak decay.

In the present case we rely upon the well-known $K\bar{K} \rightarrow \pi \pi$ ($K\bar{K} \rightarrow \pi \eta$) amplitudes, and the $B^- \rightarrow D^{* 0} \bar{K}^{* 0} K^-$ vertex can be obtained from experiment. Hence, we are able to quantize the decay rates of the mechanism proposed and we find that the mass distribution of these decay processes shows a peak associated with the triangle singularity, and finally we find the branching fractions $\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- a_0; a_0 \rightarrow \pi ^0\eta )= (1.66\pm 0.45) \times 10^{-6}$ and $\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- f_0; f_0 \rightarrow \pi ^+\pi ^-)= (2.82\pm 0.75) \times 10^{-6}$.

2 Formalism

We will analyze the effect of triangle singularities in the following decays: $B^- \rightarrow D^{* 0} \pi ^- \eta \pi ^0$ and $B^- \rightarrow D^{* 0} \pi ^- \pi ^+ \pi ^-$. The complete Feynman diagram for these decays, with the triangle mechanism through the $a_0$ or $f_0$ mesons, is shown in Fig. 2.

Fig. 2

Diagram for the decay of $B^- \rightarrow D^{* 0} \pi ^- \eta \pi ^0 (\pi ^+ \pi ^-)$

At first, we evaluate the $B^- \rightarrow D^{*} \pi R \ (R=a_0,f_0)$. This then produces the triangle diagram shown in Fig. 1. The T matrix $t_{B \rightarrow D^* \pi R}$ will have the following form:

$$\begin{aligned}&-i t_{B \rightarrow D^* \pi R} = i \sum _{\text {pol. of } K^* } \int \frac{d^4 q}{(2 \pi )^4} \frac{i \ t_{B^- \rightarrow D^{* 0} K^{* 0} K^-}}{q^2-m_K^2+i \epsilon }\nonumber \\&\quad \times \frac{i \ t_{K^*K^+ \pi ^-} }{(P-q)^2-m_{K^*}^2+i \epsilon } \frac{i \ t_{K^+K^- , R}}{(P-q-k)^2 - m_K^2+i\epsilon }.\nonumber \\ \end{aligned}$$

(2.1)

The amplitude in Eq. (2.1) is evaluated in the center-of-mass (CM) frame of $\pi R$. Now we need to calculate the three vertices, $t_{B^- \rightarrow D^{* 0} K^{* 0} K^-}$, $t_{K^*K^+ \pi ^-}$ and $t_{K^+K^- , R}$, in Eq. (2.1).

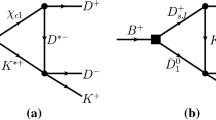
First, we discuss the $B^-\rightarrow D^{*0}K^-K^{*0}$ vertex. At the quark level, the Cabibbo-allowed vertex is formed through an internal emission of a W boson [36] (as can be seen in Fig. 3), producing a $c \bar{u}$ that forms the $D^{* 0}$, with the remaining $d \bar{u}$ quarks hadronizing and producing the $K^-$ and $K^{* 0}$ mesons with the selection of the $\bar{s}s$ pair from a created vacuum $\bar{u}u+\bar{d}d+\bar{s}s$ state.¹

Fig. 3

Diagram for the decay of $B^-$ into $D^{* 0}$, $K^{* 0}$ and $K^-$ as seen through the quark constituents of the hadrons

Since both $D^{* 0}$ and $K^{* 0}$ have $J^P=1^-$, the interaction in the $B^- \rightarrow D^{* 0} K^- K^{* 0}$ vertex can proceed via s-wave and we take the amplitude of the form

$$\begin{aligned} t_{B^- \rightarrow D^{* 0} K^{* 0} K^-} = C \ \epsilon _{\mu }(K^*) \epsilon ^{\mu }(D^*). \end{aligned}$$

(2.2)

Given that we know that the branching ratio of this decay is $\mathrm{Br}(B^- \rightarrow D^{* 0} K^{* 0} K^-)=(1.5\pm 0.4 )\times 10^{-3}$ [11, 37], we can determine the constant C by calculating the width of this decay,

$$\begin{aligned}&\frac{\mathrm{d} \Gamma _{B^- \rightarrow D^{* 0} K^{* 0} K^-}}{\mathrm{d} M_{\text {inv}}(K^* D^*)}\nonumber \\&\quad =\frac{1}{(2 \pi )^3} \frac{|{\vec {p}}_{K^-}| |{\vec {\tilde{p}}}_{K^*}|}{4 M_B^2} \overline{\sum } \sum \left| t_{B^- \rightarrow D^{* 0} K^{* 0} K^-} \right| ^2, \end{aligned}$$

(2.3)

where ${\vec {p}}_{K^-}$ is the momentum of $K^-$ in the $B^-$ rest frame, and ${\vec {\tilde{p}}}_{K^*}$ is the momentum of $K^{*0}$ in the $K^{* 0} D^{* 0}$ CM frame. The absolute values of the two momenta are given by

$$\begin{aligned} |{\vec {p}}_{K^-}|&= \frac{\lambda ^{1/2} (M_B^2, m^2_{K^-}, M^2_{\text {inv}}(K^* D^*))}{2 M_B}, \end{aligned}$$

(2.4a)

$$\begin{aligned} |{\vec {\tilde{p}}}_{K^*}|&=\frac{\lambda ^{1/2} (M^2_{\text {inv}}(K^* D^*), m^2_{K^*}, m^2_{D^*})}{2 M_{\text {inv}}(K^* D^*)}, \end{aligned}$$

(2.4b)

with $\lambda (x,y,z)$ the ordinary Källen function.

Now, if we square the T matrix in (2.2) and sum over the polarizations, we get

$$\begin{aligned} \overline{\sum } \sum&\left| t_{B^- \rightarrow D^{* 0} K^{* 0} K^-} \right| ^2\end{aligned}$$

(2.5)

$$\begin{aligned} =&C^2 \sum _{\text {pol}} \epsilon _{\mu }(K^*)\epsilon _{\nu }(K^*) \epsilon ^{\mu }(D^*) \epsilon ^{\nu }(D^*) \end{aligned}$$

(2.6)

$$\begin{aligned} =&C^2 \left( 2+ \frac{(p_{K^*} \cdot p_{D^*})^2}{m^2_{K^*} m^2_{D^*}}\right) \end{aligned}$$

(2.7)

$$\begin{aligned} =&C^2 \left( 2+ \frac{\left( M_{\text {inv}}^2(K^* D^*)-m^2_{K^*}-m^2_{D^*}\right) ^2}{4 m^2_{K^*} m^2_{D^*}}\right) , \end{aligned}$$

(2.8)

where we used the fact that $(p_{K^*}+p_{D^*})^2=M_{\text {inv}}^2(K^* D^*)$, i.e., $p_{K^*} \cdot p_{D^*}= \frac{1}{2} \left( M_{\text {inv}}^2(K^* D^*)-m^2_{K^*}-m^2_{D^*}\right)$.

Then, using this last equation in Eq. (2.3), we get

$$\begin{aligned} \frac{C^2}{\Gamma _{B^-}}=\frac{\mathrm{Br}(B^- \rightarrow D^{* 0} K^{* 0} K^-)}{\int \mathrm{d}M_{\text {inv}}(K^* D^*) \frac{1}{(2 \pi )^3} \frac{|{\vec {p}}_{K^-}| |{\vec {\tilde{p}}}_{K^*}|}{4 M_B^2}\left( 2+ \frac{\left( M_{\text {inv}}^2(K^* D^*)-m^2_{K^*}-m^2_{D^*}\right) ^2}{4 m^2_{K^*} m^2_{D^*}}\right) }, \end{aligned}$$

(2.9)

where the integral has the limits $M_{\text {inv}}(K^* D^*)|_{\text {min}}=m_{D^*}+m_{K^*}$ and $M_{\text {inv}}(K^* D^*)|_{\text {max}}=M_{B}-m_{K}$.

Now we calculate the contribution of the vertex $K^{* 0} \rightarrow \pi ^- K^+$. For that we will use the chiral invariant lagrangian with local hidden symmetry given in Refs. [38,39,40,41], which is

$$\begin{aligned} \mathcal {L}_{VPP} = -i g \langle V^{\mu } \left[ P, \partial _{\mu } P\right] \rangle , \end{aligned}$$

(2.10)

where the VPP subscript refers to the fact that we have a vertex with a vector and two pseudoscalar hadrons. The symbol $\left<...\right>$ stands for the trace over the SU(3) flavor matrices, and $g=m_V/2 f_{\pi }$ is the coupling of the local hidden gauge, with $m_V=800 \ \text {MeV}$ and $f_{\pi }=93 \ \text {MeV}$. The SU(3) matrices for the pseudoscalar and vector octet mesons P and $V^{\mu }$ are given by

$$\begin{aligned} V_{\mu }= \begin{pmatrix} \frac{1}{\sqrt{2}} \rho ^0_{\mu } + \frac{1}{\sqrt{2}} \omega _{\mu } &{} \rho ^+_{\mu } &{} K^{* +}_{\mu } \\ \rho ^-_{\mu } &{} -\frac{1}{\sqrt{2}} \rho ^0_{\mu } + \frac{1}{\sqrt{2}} \omega _{\mu } &{} K^{* 0}_{\mu } \\ K^{* -}_{\mu } &{} \bar{K}^{* 0}_{\mu } &{} \phi _{\mu } \end{pmatrix}, \end{aligned}$$

(2.11)

$$\begin{aligned} P=\begin{pmatrix} \frac{1}{\sqrt{2}} \pi ^0 + \frac{1}{\sqrt{6}} \eta &{} \pi ^+ &{} K^+\\ \pi ^- &{} -\frac{1}{\sqrt{2}} \pi ^0 + \frac{1}{\sqrt{6}} \eta &{} K^0\\ K^- &{} \bar{K}^0 &{} -\sqrt{\frac{2}{3}} \eta \end{pmatrix}. \end{aligned}$$

(2.12)

Performing the matrix operations and the trace we get

$$\begin{aligned} \mathcal {L}_{K^*K\pi } =-ig {K^{* 0}}^{\mu } \left( K^- \partial _{\mu } \pi ^+ - \pi ^+ \partial _{\mu } K^- \right) . \end{aligned}$$

(2.13)

So, for the t matrix we get

$$\begin{aligned} -i t_{K^*K^+ \pi ^-} =&-i g \epsilon ^{\mu }_{K^*} (p_{K^+}-p_{\pi })_\mu \end{aligned}$$

(2.14)

$$\begin{aligned} \simeq&-i g \vec {\epsilon }_{K^*} \cdot ({\vec {\tilde{p}}}_{\pi }-{\vec {\tilde{p}}}_{K^+}), \end{aligned}$$

(2.15)

with ${\vec {\tilde{p}}}_{K^+}$ and ${\vec {\tilde{p}}}_{\pi }$ calculated in the CM frame of $\pi R$. At the energy where the triangle singularity appears ($M_{\text {inv}}(\pi R)=1418 \ \text {MeV}$), the momentum of $K^*$ is about $150 \ \text {MeV}/c$, which is small enough, compared with the mass of $K^*$, to omit the zeroth component of the polarization vector in Eq. (2.14).

Finally we only need the $R \rightarrow K^+ K^-$ coupling before we can analyze the triangle diagram. The coupling of R with $\pi ^0 \eta$ or $\pi ^+ \pi ^-$ proceeds in s-wave. Then the vertex is written simply as a constant,

$$\begin{aligned} t_{K^+K^- , R} = g_{K^- K^+ , R}. \end{aligned}$$

(2.16)

We shall use this coupling only formally, since its product with the $g_{R,\pi ^+\pi ^-}$ ($g_{R,\pi ^0\eta }$) coupling will be traded off in favor of the $K\bar{K}\rightarrow \pi ^+\pi ^- (\pi ^0\eta )$ scattering amplitude. We can now analyze the effect of the triangle singularity on the $B^- \rightarrow D^* \pi R$ decay.

Substituting Eqs. (2.2), (2.15) and (2.16) for Eq. (2.1), the decay amplitude $t_{B^- \rightarrow D^{* 0} \pi ^- R}$ is written as

$$\begin{aligned}&t_{B^- \rightarrow D^* \pi R} = -i g_{K^- K^+, R} \ g C \sum _{\text {pol. of}\,K^{*}} \int \frac{d^4 q}{(2 \pi )^4} \nonumber \\&\quad \times \frac{\vec {\epsilon }_{D^*} \cdot \vec {\epsilon }_{K^*}}{q^2-m_K^2+i \epsilon }\nonumber \\&\quad \times \frac{\vec {\epsilon }_{K^*} \cdot ({\vec {\tilde{p}}}_{\pi }-{\vec {\tilde{p}}}_{K^+})}{(P-q)^2-m^2_{K^*}+i \epsilon } \frac{1}{(P-q-k)^2 - m_K^2+i \epsilon } \ , \end{aligned}$$

(2.17)

where for $t_{B^- \rightarrow D^{* 0} K^{* 0} K^-}$ we have also the spatial components of the polarization vectors, and ${\vec {\tilde{p}}}_{K^+}$, ${\vec {\tilde{p}}}_{K^+}$ are taken in the CM frame of $\pi R$. As we have mentioned below Eq. (2.15), the momentum of the $K^{*0}$ around the triangle peak is small compared with the mass, and we can omit the zeroth component of the polarization vector of the $K^{*0}$.

Now we only need to calculate the width $\Gamma$ associated with the diagram in Fig. 1. Right away we see that since

$$\begin{aligned} \sum _{\text {pol. of}\,K^*} \epsilon _{K^*}^i \epsilon _{K^*}^j = \delta _{ij}, \end{aligned}$$

(2.18)

Eq. (2.17) reduces to

$$\begin{aligned}&t_{B^- \rightarrow D^* \pi R} =g_{K^- K^+, R} \ g C i\int \frac{d^4 q}{(2 \pi )^4} \ \frac{\vec {\epsilon }_{D^*} \cdot ({\vec {\tilde{p}}}_{K^+}-{\vec {\tilde{p}}}_{\pi })}{q^2-m_K^2+i \epsilon }\nonumber \\&\quad \times \frac{1}{(P-q)^2-m^2_{K^*}+i \epsilon } \frac{1}{(P-q-k)^2 - m_K^2+i \epsilon },\nonumber \\ \end{aligned}$$

(2.19)

where ${\vec {\tilde{p}}}_{K^+}= \vec {P}-\vec {q}-\vec {k}= -(\vec {q}+\vec {k})$ and ${\vec {\tilde{p}}}_{\pi }= \vec {k}$.

Defining $f(\vec {q},\vec {k})$ as a product of the three propagators in Eq. (2.19), we can use the formula

$$\begin{aligned} \int d^3 q q_i f(\vec {q}, \vec {k}) = k_i \int d^3 q \frac{\vec {q} \cdot \vec {k}}{|\vec {k}|^2} f( \vec {q}, \vec {k}), \end{aligned}$$

which follows from the fact that the $\vec {k}$ is the only vector not integrated in the integrand of Eq. (2.19). Then Eq. (2.19) becomes

$$\begin{aligned} t_{B^- \rightarrow D^* \pi R} = -\vec {\epsilon }_{D^*} \cdot \vec {k} \ g_{K^- K^+, R} \ g C \ t_T, \end{aligned}$$

(2.20)

with

$$\begin{aligned}&t_T=i \int \frac{d^4 q}{(2 \pi )^4} \ \left( 2+ \frac{\vec {q} \cdot \vec {k}}{|\vec {k}|^2}\right) \nonumber \\&\, \times \frac{1}{q^2-m_K^2+i \epsilon } \frac{1}{(P-q)^2-m^2_{K^*}+i \epsilon } \frac{1}{(P-q-k)^2 - m_K^2+i \epsilon }.\nonumber \\ \end{aligned}$$

(2.21)

Squaring and summing over the polarizations of $D^*$, Eq. (2.20) becomes

$$\begin{aligned} \sum _\mathrm{pol}|t_{B^- \rightarrow D^* \pi R}|^2 =|\vec {k}|^2 \ g^2_{K^- K^+, R} \ g^2 C^2 |t_T|^2. \end{aligned}$$

(2.22)

As given in Ref. [17], the analytical integration of $t_T$ in Eq. (2.21) over $q^0$ leads to

$$\begin{aligned} t_T =&\int \frac{d^3 q}{(2 \pi )^3} \left( 2+ \frac{\vec {q} \cdot \vec {k}}{|\vec {k}|^2}\right) \frac{1}{8 \omega ^* \omega \omega '} \frac{1}{k^0-\omega '-\omega ^*}\nonumber \\&\frac{1}{P^0+\omega +\omega '-k^0} \frac{1}{P^0-\omega -\omega '-k^0 + i \epsilon } \nonumber \\&\times \frac{\{2P^0 \omega + 2 k^0 \omega ' -2[\omega +\omega '][\omega +\omega '+\omega ^*] \}}{P^0-\omega ^*-\omega +i\epsilon }, \end{aligned}$$

(2.23)

with $\omega ^*(\vec {q})=\sqrt{m^2_{K^{* 0}} +|\vec {q}|^2}$, $\omega '(\vec {q})=\sqrt{m^2_{K} +|\vec {q}+\vec {k}|^2}$ and $\omega (\vec {q})=\sqrt{m_{K}^2 +|\vec {q}|^2}$. To regularize the integral in Eq. (2.23) we use the same cutoff of the meson loop that will be used to calculate $t_{K^+ K^- \rightarrow \pi ^ 0 \eta }$ and $t_{K^+ K^- \rightarrow \pi ^+ \pi ^-}$ Eq. (2.36), $\theta (q_{\text {max}}-|q^*|)$, where $\vec {q}^{\ *}$ is the $K^-$ momentum in the R rest frame [17].

In Ref. [17] it was found that there is a singularity associated with this type of loop functions when Eq. (18) of Ref. [17] is satisfied. From that equation we can determine that the singularity will appear around $M_{\text {inv}}(\pi R) = 1418 \ \text {MeV}$.

To be completely correct in our analysis we have to use the width of $K^{* 0}$. We implement that replacing $\omega ^* \rightarrow \omega ^* - i \frac{\Gamma _{K^{*}}}{2}$ in Eq. (2.23), which will reduce the singularity to a peak [17].

For the three body decay of $B^- \rightarrow D^{* 0} \pi ^- R$ in Fig. 1, the mass distribution is given by

$$\begin{aligned} \frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi R)}= \frac{1}{(2 \pi )^3} \frac{|{\vec {p}}_{D^{*}}| |{\vec {\tilde{p}}}_{\pi }|}{4 M_B^2} \sum _\mathrm{pol.}\left| t_{B^- \rightarrow D^* \pi R} \right| ^2, \end{aligned}$$

(2.24)

with

$$\begin{aligned} |{\vec {p}}_{D^{*}}|&= \frac{\lambda ^{1/2} (M_B^2, m^2_{D^{*}}, M^2_{\text {inv}}(\pi R))}{2 M_B}, \end{aligned}$$

(2.25a)

$$\begin{aligned} |{\vec {\tilde{p}}}_{\pi }|&=|\vec {k}|=\frac{\lambda ^{1/2} (M^2_{\text {inv}}(\pi R), m^2_{\pi }, M^2_R)}{2 M_{\text {inv}}(\pi R)}. \end{aligned}$$

(2.25b)

With Eq. (2.20) and a factor $1/\Gamma _{B^-}$, the mass distribution of $B^-$ decaying into $D^* \pi R$ is written as

$$\begin{aligned}&\frac{1}{\Gamma _{B^-}}\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi R)} = \frac{C^2}{\Gamma _{B^-}}\frac{g^2}{(2 \pi )^3}\nonumber \\&\quad \times \frac{|{\vec {p}}_{D^{*}}| |\vec {k}|}{4 M_B^2} \ |\vec {k}|^2\cdot \left| t_T \times \ g_{K^- K^+, R} \right| ^2, \end{aligned}$$

(2.26)

where $\frac{C^2}{\Gamma _{B^-}}$ is given in Eq. (2.9).

However, the problem here is that the $a_0$ and $f_0$ are not stable particles, but resonances that have a width and decay to $\pi ^0 \eta$ and $\pi ^+ \pi ^-$, respectively. To solve this without having to consider R a virtual particle and having a four body decay, we can consider the resonance as a normal particle but we add a mass distribution to the decay width in Eq. (2.24),

$$\begin{aligned}&\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi R)}=\frac{1}{(2 \pi )^3} \int \mathrm{d} M^2_{\text {inv}}(R) \ \left( -\frac{1}{\pi }\text {Im}D \right) \nonumber \\&\quad \times |g_{K^- K^+, R}|^2 \frac{|{\vec {p}}_{D^{*}}| |{\vec {\tilde{p}}}_{\pi }|}{4 M_B^2} \ \overline{\sum } \sum \left| \tilde{t}_{B^- , D^* \pi R} \right| ^2, \end{aligned}$$

(2.27)

with

$$\begin{aligned} D= \frac{1}{M_{\text {inv}}^2(R) - M_R^2 + i M_R \Gamma _R}, \end{aligned}$$

(2.28)

where $M_{\text {inv}}(R)$ stands for $M_{\text {inv}}(\pi ^0 \eta )$ and $M_{\text {inv}}(\pi ^+ \pi ^-)$ for $R=a_0$ and $f_0$, respectively, and $\tilde{t}_{B^- , D^* \pi R} = t_{B^- \rightarrow D^* \pi R}/g_{K^- K^+, R}$. What Eq. (2.27) is accomplishing is a convolution of Eq. (2.24) with the mass distribution of the R resonance given by its spectral function. Note that the mass distributions of the $f_0(980)$, $a_0(980)$ states follow a Flatté distribution rather than the Breit–Wigner case of Eq. (2.28), but the use of Eq. (2.28) is only formal to arrive at an expression that uses the scattering amplitudes $t_{K^+K^-,\pi ^+\pi ^-(\pi ^0\eta )}$, which are calculated with the chiral unitary approach and automatically incorporate the Flatté form and the usual requirements of analyticity and unitarity.

Notice also that in the limit of $\Gamma _R \rightarrow 0$, $i \text {Im} D = -i \pi \delta (M_{\text {inv}}^2(R)- M_R^2)$ and we recover Eq. (2.24). Evaluating explicitly the imaginary part of D, Eq. (2.27) becomes

$$\begin{aligned}&\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi R)}= \frac{1}{(2 \pi )^3} \int \mathrm{d} M^2_{\text {inv}}(R) \ \frac{1}{\pi } \ |g_{K^- K^+, R}|^2 \frac{|{\vec {p}}_{D^{*}}| |{\vec {\tilde{p}}}_{\pi }|}{4 M_B^2}\nonumber \\&\quad \times \overline{\sum } \sum \left| \tilde{t}_{B^- , D^* \pi R} \right| ^2 \frac{M_R \Gamma _R}{(M_{\text {inv}}^2(R) - M_R^2)^2+(M_R \Gamma _R)^2}.\nonumber \\ \end{aligned}$$

(2.29)

Now, for the case of $a_0(980)$, we only have the decay $a_0 \rightarrow \pi ^0 \eta$ (we neglect the small $K \bar{K}$ decay fraction), and thus

$$\begin{aligned} \Gamma _{a_0}= \frac{1}{8 \pi } \frac{|g_{a_0 \rightarrow \pi ^0 \eta }|^2}{M^2_{\text {inv}}(\pi ^0\eta )} |\vec {\tilde{q}}_{\eta }|, \end{aligned}$$

(2.30)

with

$$\begin{aligned} |\vec {\tilde{q}}_{\eta }| = \frac{\lambda ^{1/2}(M_{\text {inv}}^2(\pi ^0\eta ), m_{\pi }^2, m_{\eta }^2)}{2 M_{\text {inv}}(\pi ^0\eta )}. \end{aligned}$$

(2.31)

Then Eq. (2.29) becomes

$$\begin{aligned}&\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi a_0)}= \frac{1}{(2 \pi )^3}\ \int \mathrm{d} M^2_{\text {inv}}(\pi ^0\eta )\nonumber \\&\quad \times \frac{|{\vec {p}}_{D^{*}}| |{\vec {\tilde{p}}}_{\pi }|}{4 M_B^2} \ \overline{\sum } \sum \left| \tilde{t}_{B^- , D^* \pi R} \right| ^2\nonumber \\&\quad \times \frac{M_{a_0} |g_{a_0 \rightarrow \pi ^0 \eta }|^2 |g_{K^- K^+ \rightarrow a_0}|^2}{(M_{\text {inv}}^2(\pi ^0\eta ) - M_{a_0}^2)^2+(M_{a_0} \Gamma _{a_0})^2}\frac{1}{8 \pi ^2} \frac{|\vec {\tilde{q}}_{\eta }|}{M^2_{\text {inv}}(\pi ^0\eta )}.\nonumber \\ \end{aligned}$$

(2.32)

But since for the resonance we have formally

$$\begin{aligned} \frac{|g_{a_0 \rightarrow \pi ^0 \eta }|^2 |g_{K^- K^+ \rightarrow a_0}|^2}{(M_{\text {inv}}^2(\pi ^0\eta ) - M_{a_0}^2)^2+(M_{a_0} \Gamma _{a_0})^2} = \left| t_{K^+ K^- \rightarrow \pi ^0 \eta } \right| ^2, \end{aligned}$$

(2.33)

Equation (2.32) reduces to

$$\begin{aligned}&\frac{\mathrm{d}^2 \Gamma }{\mathrm{d} M_{\text {inv}}(\pi a_0) \mathrm{d} M_{\text {inv}}(\pi ^0\eta )} = \frac{1}{(2 \pi )^5} \frac{|{\vec {p}}_{D^{*}}| |\vec {k}| |\vec {\tilde{q}}_{\eta }|}{4 M_B^2}\nonumber \\&\quad \times \overline{\sum } \sum \left| \tilde{t}_{B^- , D^* \pi R} \times t_{K^+ K^- \rightarrow \pi ^0 \eta }\right| ^2, \end{aligned}$$

(2.34)

where we approximated $M_\mathrm{inv}(\pi ^0\eta )$ as $M_R$. For the case of $f_0(980)$, $f_0 \rightarrow \pi ^+ \pi ^-$ is not the only possible decay and as such $\Gamma _{f_0 \rightarrow \pi ^+ \pi ^-}$ will not be the same as $\Gamma _R$ in Eq. (2.27). However, when we put $\left| t_{K^+ K^- \rightarrow \pi ^+ \pi ^-} \right| ^2$ in the end, we already select the $\pi \pi$ part of the $f_0$ decay. Thus, for the case of $f_0$ we just need to substitute, in Eq. (2.34), $t_{K^+ K^- \rightarrow \pi ^0 \eta } \rightarrow t_{K^+ K^- \rightarrow \pi ^+ \pi ^-}$, $M_{\text {inv}}(\pi a_0) \rightarrow M_{\text {inv}}(\pi f_0)$, $M_{\text {inv}}(\pi ^0\eta ) \rightarrow M_{\text {inv}}(\pi ^+\pi ^-)$, and $|\vec {\tilde{q}}_{\eta }| \rightarrow |\vec {\tilde{q}}_{\pi }|$, with

$$\begin{aligned} |\vec {\tilde{q}}_{\pi }| = \frac{\lambda ^{1/2}(M_{\text {inv}}^2(\pi ^+\pi ^-), m_{\pi ^+}^2, m_{\pi ^-}^2)}{2 M_{\text {inv}}(\pi ^+\pi ^-)}. \end{aligned}$$

(2.35)

The amplitudes $t_{K^+ K^- \rightarrow \pi ^ 0 \eta }$ and $t_{K^+ K^- \rightarrow \pi ^+ \pi ^-}$ themselves are calculated based on the chiral unitary approach, where the $a_0$ and $f_0$ appear as dynamically generated states [33, 34]. The cutoff parameter $q_{\text {max}}$, which appears for the regularization of the meson loop function in the Bethe–Salpeter equation,

$$\begin{aligned} t=[1-V G]^{-1} V, \end{aligned}$$

(2.36)

is determined as $q_{\text {max}}=600 \ \text {MeV}$ for the reproduction of the $a_0$ and $f_0$ peaks (around $980 \ \text {MeV}$ in the invariant mass of $\pi ^0 \eta$ or $\pi ^+ \pi ^-$) [42, 43]. In Eq. (2.36), t, V, and G are the meson amplitude, interaction kernel, and meson loop function, respectively.

Finally, we can substitute everything we have calculated into Eq. (2.34) and obtain

$$\begin{aligned}&\frac{1}{\Gamma _{B^-}}\frac{\mathrm{d}^2 \Gamma }{\mathrm{d} M_{\text {inv}}(\pi R) \mathrm{d} M_{\text {inv}}(R)} = \frac{g^2}{(2 \pi )^5} \frac{|{\vec {p}}_{D^{*}}| |\vec {\tilde{q}}_{\eta }| |\vec {k}|^3}{4 M_B^2} \nonumber \\&\quad \times \left| t_T \times t_{K^+ K^- \rightarrow \pi ^0 \eta (\pi ^+ \pi ^-)}\right| ^2 \frac{C^2}{\Gamma _{B^-}}. \end{aligned}$$

(2.37)

3 Results

Let us begin by showing in Fig. 4 the contribution of the triangle loop (defined in Eq. (2.23)) to the total amplitude. We plot the real and imaginary parts of $t_T$, as well as the absolute value with $M_\mathrm{inv}(R)$ fixed at 980 MeV. As can be observed, there is a peak around $1420 \ \text {MeV}$, as predicted by Eq. (18) of Ref. [17].

Fig. 4

Triangle amplitude $t_T$ for the decay $B^- \rightarrow D^{* 0}\pi R$. We take $M_\mathrm{inv}(R)=$ 980 MeV

In Figs. 5 and 6 we plot Eq. (2.37) for both $B^- \rightarrow D^{* 0} \pi ^- \eta \pi ^0$ and $B^- \rightarrow D^{* 0} \pi ^- \pi ^+ \pi ^-$, respectively, by fixing $M_{\text {inv}}(\pi R)=1418 \ \text {MeV}$, which is the position of the triangle singularity, and varying $M_{\text {inv}}(R)$. We can see a strong peak around $980 \ \text {MeV}$ and consequently we see that most of the contribution to our width $\Gamma$ will come from $M_{\text {inv}}(R)=M_R$. For Fig. 5 the dispersion is bigger, we have strong contributions for $M_{\text {inv}}(\pi ^0 \eta ) \in [880,1080]$. However, for Fig. 6 most of the contribution comes from $M_{\text {inv}}(\pi ^+ \pi ^-) \in [940,1020]$. The conclusion is that when we calculate the mass distribution $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi a_0)}$, we can restrict the integral in $M_{\text {inv}}(R)$ to the limits already mentioned.

Fig. 5

The derivative of the mass distribution of $B^- \rightarrow D^{* 0} \pi ^- \pi ^0 \eta$ with regards to $M_{\text {inv}}(a_0)$

Fig. 6

The derivative of the mass distribution of $B^- \rightarrow D^{* 0} \pi ^- \pi ^+ \pi ^-$ with regards to $M_{\text {inv}}(f_0)$

When we integrate over $M_{\text {inv}}(R)$ we obtain $\frac{\mathrm{d} \Gamma }{d M_{\text {inv}}(\pi R)}$ which we show in Fig. 7. We see a clear peak of the distribution around $1420 \ \text {MeV}$, for $f_0$ and $a_0$ production. However, we also see that the distribution stretches up to large values of $M_{\text {inv}}(\pi R)$ where the phase space of the reaction finishes. This is due to the $|\vec {k}|^3$ factor in Eq. (2.37) that contains a $|\vec {k}|$ factor from phase space and a $|\vec {k}|^2$ factor from the dynamics of the process, as we can see in Eq. (2.22). Yet, a clear peak in $M_{\text {inv}}(\pi ^- R)$ can be seen for both the $B^- \rightarrow D^{* 0} \pi ^- f_0$ and the $B^- \rightarrow D^{* 0} \pi ^- a_0$ reactions.

Fig. 7

The mass distribution of $B^- \rightarrow D^{* 0} \pi ^- \pi ^0 \eta$ (full line) and $B^- \rightarrow D^{* 0} \pi ^- \pi ^+ \pi ^-$ (dashed line)

Integrating now $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi a_0)}$ and $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi f_0)}$ over the $M_{\text {inv}}(\pi a_0)$ ($M_{\text {inv}}(\pi f_0)$) masses in Fig. 7, we obtain the branching fractions

$$\begin{aligned}&\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- a_0; a_0 \rightarrow \pi ^0\eta ) = (1.66\pm 0.45) \times 10^{-6} ,\end{aligned}$$

(3.1a)

$$\begin{aligned}&\mathrm{Br}(B^-\rightarrow D^{*0}\pi ^- f_0; f_0 \rightarrow \pi ^+\pi ^-)= (2.82\pm 0.75) \times 10^{-6}. \end{aligned}$$

(3.1b)

These numbers are within measurable range. The errors come from the experimental errors in the branching ratio of $B^-\rightarrow D^{*0}K^{*0}K^-$. Another source of uncertainty would come from the $t_{K^+K^-,\pi ^+\pi ^-(\pi ^0\eta )}$ matrices, but the errors in $|t_{K^+K^-,\pi ^+\pi ^-(\pi ^0\eta )}|^2$ are smaller than 10% from the study of many reactions, which summed in quadrature to those of the experimental branching ratio, are essentially negligible.

Note that we have assumed all the strength of $\pi ^0 \eta$ from $880 \ \text {MeV}$ to 1080 MeV to be part of the $a_0$ production, but in an experimental analysis one might associate part of this strength to a background. We note this in order to make proper comparison with these results when the experiment is performed.

The shape of $t_T$ in Fig. 4 requires some extra comment. We see that Im$(t_T)$ peaks around 1420 MeV, where the triangle singularity is expected. However, Re$(t_T)$ also has a peak around 1390 MeV. This picture is not standard. Indeed, in Ref. [44], where a triangle singularity is disclosed for the process $N (1835) \rightarrow \pi N (1535)$, $t_T$ has the real part peaking at the place of the triangle singularity and Im$(t_T)$ has no peak. In Ref. [45], a triangle singularity develops in the $\gamma p \rightarrow p \pi ^0 \eta \rightarrow \pi ^0 N (1535)$ process and there Im$(t_T)$ has a peak at the expected energy of the triangle singularity while the Re$(t_T)$ has no peak. Similarly, in the study of $N (1700) \rightarrow \pi \Delta$ in Ref. [46] a triangle singularity develops and here Im$(t_T)$ has a peak but Re$(t_T)$ has not. However, the two peaks in the real and imaginary parts of $t_T$ are also present in the study of the $B^- \rightarrow K^- \pi D_{s0}^+$ reaction in Ref. [28]. The latter work has a loop with $D^0 K^{* 0} K^+$, and by taking $\Gamma _{K^*} \rightarrow 0$, $\epsilon \rightarrow 0$ the peak of Im$(t_T)$ was identified with the triangle singularity while the peak in the Re$(t_T)$ was shown to come from the threshold of $D^0 K^{* 0}$. In the present case the situation is similar: The peak of Im$(t_T)$ at about 1420 MeV comes from the triangle singularity while the one just below 1400 MeV comes from the threshold of $K^{* 0} K^-$ in the diagram of Fig. 1, which appears at 1386 MeV. Yet, by looking at $|t_T|$ in Fig. 4 and the region of the peak of $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}}$ in Fig. 7, we can see that this latter peak comes mostly from the triangle singularity.

4 Summary

We have performed the calculations for the reactions $B^- \rightarrow D^{* 0} \pi ^- a_0(980); a_0 \rightarrow \pi ^0 \eta$ and $B^- \rightarrow D^{* 0} \pi ^- f_0(980); f_0 \rightarrow \pi ^+ \pi ^-$. The starting point is the reaction $B^- \rightarrow D^{* 0} K^{* 0} K^-$, which is a Cabibbo-favored process and for which the rates are tabulated in the PDG [11] and are relatively large. Then we allow the $K^{* 0}$ to decay into $\pi ^- K^+$ and the $K^+ K^-$ fuse to give the $f_0(980)$ or the $a_0(980)$. Both of them are allowed, since the $K^{* 0} K^-$ state does not have a particular isospin. The triangle diagram corresponding to this mechanism develops a triangle singularity at about $1420 \ \text {MeV}$ in the invariant masses of $\pi ^- f_0$ or $\pi ^- a_0$, and it makes the strength of the process studied relatively large, having a prominent peak in those invariant mass distributions around $1420 \ \text {MeV}$.

We evaluate $\frac{\mathrm{d}^2 \Gamma }{\mathrm{d} M_{\text {inv}}(\pi ^- a_0) d M_{\text {inv}}(\pi ^0 \eta )}$, and $\frac{\mathrm{d}^2 \Gamma }{\mathrm{d} M_{\text {inv}}(\pi ^- f_0) \mathrm{d} M_{\text {inv}}(\pi ^+ \pi ^-)}$ and see clear peaks in the $M_{\text {inv}}(\pi ^0 \eta )$, $M_{\text {inv}}(\pi ^+ \pi ^-)$ distributions, showing clearly the $a_0(980)$ and $f_0(980)$ shapes. Integrating over $M_{\text {inv}}(\pi ^0 \eta )$ and $M_{\text {inv}}(\pi ^+ \pi ^-)$ we obtain $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi a_0)}$ and $\frac{\mathrm{d} \Gamma }{\mathrm{d} M_{\text {inv}}(\pi f_0)}$, respectively, and these distributions show a clear peak for $M_{\text {inv}}(\pi a_0)$, $M_{\text {inv}}(\pi f_0)$ around $1420 \ \text {MeV}$. This peak is a consequence of the triangle singularity, and in this sense the work done here should be a warning not to claim a new resonance when this peak is seen in a future experiment. On the other hand, the results make predictions for an interesting effect of a triangle singularity in an experiment that is feasible in present experimental facilities. The rates obtained are also within measurable range. Finding new cases of triangle singularities is of importance also, because their study will give incentives to update present analysis tools to take into account such possibility when peaks are observed experimentally, avoiding the natural tendency to associate those peaks to resonances.