1 Introduction

The black hole (BH) solution is one of the most interesting phenomena in general relativity. Although its existence is vivid, it is an open problem to understand the interior nature of the BH in quantitative detail; the main aspects come from the fact that a perfect theory of quantum gravity does not exist [1]. Since the discovery of Hawking radiation we know that BHs have a temperature. Hence, the concept of the BH entropy, which was proposed by Bekenstein is no longer a mystery. Moreover, Hawking proposed the famous formula of entropy \(S=\frac{A}{4}\), where A represents the area of the event horizon [2]. BHs have higher entropy than any other object of the same volume [3, 4]. The maximum entropy of the BHs is expected to need corrections due to quantum fluctuations, which leads to the development of the holographic principle [5, 6]. As the BH reduces its size due to Hawking radiation, these fluctuations become very important and are expected to correct the standard relation between entropy and area [7].

There are several approaches to evaluating such corrections. Using non-pertubative quantum general relativity, one can calculate the density of microstates for asymptotically flat BHs, which leads to the construction of the logarithmic correction terms to the standard Bekenstein entropy area relation [8]. One can also use the Cardy formula to generate logarithmic correction terms for all BHs whose microscopic degrees of freedom are explained by conformal field theory [9, 10]. Ashtekar has obtained such logarithmic corrections for BTZ BHs by calculating the exact partition function [8]. These terms could also be generated by the effects of string theory on the entropy of the BH. The analysis of matter fields in the presence of the BHs has also generated them for the Bekenstein entropy area formula [11, 12]. In fact, the corrections to the entropy of dilaton BHs are obtained, which turn out to be logarithmic corrections [13]. The Rademacher expansion of the partition function can also generate such correction terms [14]. Recently, the effects of thermal fluctuations on charged ADS BHs and modified Hayward BHs have also been investigated [7, 15].

On the other hand, one of the major challenges in general relativity is the existence of essential singularities (which leads to various BHs) and it looks like the common property in most of the solutions of the Einstein field equations. Hence, regular black holes (RBHs) have been constructed to resolve this problem. Since its metric is regular everywhere, essential singularities could be avoided in the solution of Einstein equations of the BH physics [16]. The weak energy condition is satisfied by these RBHs while some of these violate the strong energy conditions somewhere in space-time [17, 18]. Since the Penrose cosmic censorship conjecture claims that singularities predicted by GR occur, they must be discussed by the concept of event horizon [19, 20]. Bardeen [21] was the pioneer who obtained a BH solution without any essential singularity at origin enclosed by an event horizon, known as ’Bardeen black hole’ which satisfies weak energy conditions. Later on, many authors found similar solutions [22,23,24]. The coupling of general relativity to non-linear electromagnetic theory has brought about new sets of charged BHs, which came into the range of RBHs solution. Ayn-Beato and Garca [22] also found such a RBH solution. Hayward [25] and Berej et al. [26] found different kinds of RBH solutions. Recently, Leonardo et al. [27] used many distribution functions in order to obtain charged RBHs.

There is an interesting non-minimal theory that couples the gravitational field to other fields using cross terms of the curvature tensor, having arisen a long time ago as alternative theories of gravity. There are five classes of the non-minimal field theories, divided accordingly to the types of fields that couple gravitation to non-minimality; for details see [28, 29]. These non-minimal theories construct exact solutions of stars [30, 31], wormholes [32, 33], BHs [34, 35] and regular magnetic BHs [36] with the Wu–Yang ansatz [37, 38]. New regular exact spherically symmetric solutions of a non-minimal Einstein–Yang–Mills theory with a gauge field of magnetic Wu–Yang and cosmological constant are presented by Balakin et al. [28, 29]. They found the most interesting solutions of BHs with metric and curvature invariant being regular everywhere. BH thermodynamics enables us to study various important thermodynamical quantities of solutions.

One of the most important thermodynamical quantities is the thermal stability of the BH. BHs should be stable in dynamical and thermodynamical frameworks due to their physical nature. The instability of the BHs means that we may ask whether it may have a phase transition or if it is completely unphysical. In this work, we analyze the effects of thermal fluctuations on RBHs of the non-minimal Einstein–Yang–Mill theory with gauge field of magnetic Wu–Yang type and a cosmological constant. We will use logarithmic correction terms to discuss various thermodynamical quantities, such as pressure, entropy, specific heats, Gibb’s free energy and Helmholtz free energy of non-minimal RBH. The outline of paper is as follows: In Sect. 2, we discuss RBHs of the non-minimal Einstein–Yang–Mill theory with gauge field of magnetic Wu–Yang type and a cosmological constant; furthermore, we will find logarithmic correction terms which produces various thermodynamical quantities. In Sect. 3, we investigate the stability of the non-minimal RBHs using a corrected value of the specific heat to analyze the phase transition. In a further subsection, we also demonstrate the grand canonical and canonical ensembles. Conclusion and observations are given in the last section.

2 Non-minimal RBH

A new exact regular spherically symmetric solution of the non-minimal Einstein–Yang–Mills theory with magnetic charge of Wu–Yang gauge field and the cosmological constant is presented by Balakin et al. [28]. Now considering their static spherically symmetric space-time with line element

$$\begin{aligned} \mathrm{d}s^{2}_e=f(r)\mathrm{d}t^{2}-(f(r))^{-1}\mathrm{d}r^{2}-r^2({\mathrm{d}\theta }^{2} +\sin \theta {\mathrm{d}\phi }^{2}), \end{aligned}$$
(1)

we see that

$$\begin{aligned} f(r)=1+\left( \frac{r^4}{r^4+2Q_m^{2}q}\right) \left( -\frac{2M}{r}+\frac{Q_m^{2}}{r^2}-\frac{\Lambda r^2}{3}\right) \end{aligned}$$
(2)

is the exact solution to the gravitational field equations. This contains four important parameters: \(\Lambda ,~q,~Q_m\) and M, which represent the cosmological constant, the non-minimal parameter of the theory, the magnetic charge of the gauge field of Wu–Yang type and the mass of the object, respectively. In this work, we consider \(q>0\), \(\Lambda >0\), \(\Lambda \le 0\), \(Q_m^{2}>0\) and \(M\ge 0\), which for the following reason. The limit case \(q=0\) gives the magnetic RN solution with cosmological constant,

$$\begin{aligned} f(r)= 1+\frac{2M}{r}-\frac{Q_m^{2}}{r^2}-\frac{\Lambda r^2}{3}. \end{aligned}$$
(3)

At \(r=0\), we find the curvature singularities. For \(q<0\) with finite positive r, we have space-time curvature singularities.

One can obtain no singularities for \(q>0\) i.e. f(r) near the center behaves like

$$\begin{aligned} f(r)= 1+\frac{r^2}{2q^2}-\frac{Mr^3}{Q_m^{2}q}+\cdots . \end{aligned}$$
(4)

One can see that \(f(0)=1\), \(f'(0)=0\) and \(f''(0)=\frac{1}{q^2}\). Hence \(r=0\) is the minimum of the regular function f(r), which is independent of the cosmological constant and the mass of the black hole. Since \(f(0)=1\) and \(R(0)=\frac{6}{q}\) shows the curvature scalar is regular at center. For \(q>0\), other curvature invariants and the quadratic scalar \(R_{\mu \nu }R^{\mu \nu }=\frac{9}{q^2}\) are also finite at the center [29]. Thus due to non-minimality of the model, space-time is truly regular in the center.

The metric function (2) is described by four parameters with different units: \(\Lambda ,~ M,~ Q_m\) and q. We can rewrite the metric function (2) in dimensionless form by introducing the following dimensionless quantities [28]:

$$\begin{aligned}&\gamma _{\Lambda } = \sqrt{\frac{3}{|\Lambda |}},\quad \gamma _{g}=2M,\quad \gamma _{q}=\big (2Q_{m}^2 q\big )^{\frac{1}{4}},\quad \gamma _{Q}=Q_m\nonumber \\&\sigma = \frac{\gamma _{g}}{ \gamma _{\Lambda }},\quad \eta = \Big (\frac{\gamma _{Q}}{\gamma _{\Lambda }}\Big )^2,\quad \zeta = \Big (\frac{\gamma _{q}}{\gamma _{\Lambda }}\Big )^4,\quad \rho = \Big (\frac{r}{\gamma _{\Lambda }}\Big )^2.\nonumber \\ \end{aligned}$$
(5)

In terms of these variables the metric function f(r) in (2) can be rewritten in \(f(\rho )\) as follows:

$$\begin{aligned} f(\rho )=1+\left( \frac{\rho ^2\big (-\rho ^4-\sigma \rho +\eta \big )}{\rho ^4+\zeta }\right) . \end{aligned}$$
(6)

The most important feature of the metric function (2) is the horizon radius which depends upon different values of the parameters. The horizon radius of a non-minimal RBH could be obtained by considering the real roots of the following equation:

$$\begin{aligned} -\frac{\Lambda r_{+}^{6}}{3} + r_{+}^4-2Mr_{+}^3+Q_m^{2}r_{+}^2 + 2Q_m^{2}q=0. \end{aligned}$$
(7)

For \(\Lambda > 0\), the non-minimal RBH solution can have three horizons depending upon different values of the parameters, the cosmological horizon, Cauchy horizon and event horizon. On the other hand, for \(\Lambda \le 0\), it can have two horizons depending upon different values of the parameters, i.e., Cauchy and event horizons. There is no cosmological horizon in this case [28]. We want to discuss the thermal quantities on the outer horizon, and we refer to it by \(r_+\).

One can obtain the mass of the non-minimal RBH in horizon radius and other parameters as follows:

$$\begin{aligned} M=\frac{-\Lambda r_{+}^6+3Q_m^{2}r_{+}^2+3r_{+}^4+6Q_m^{2}q}{6r_{+}^3}, \end{aligned}$$
(8)

which implies that \(r_{+}\ne 0\). The entropy of a non-minimal RBH which is related to the area of the BH horizon is

$$\begin{aligned} S_0=\pi r_{+}^2, \end{aligned}$$
(9)

and the volume is

$$\begin{aligned} V = \frac{4}{3} \pi r_{+}^3. \end{aligned}$$
(10)

The temperature of the non-minimal RBH can be written as

$$\begin{aligned} T= & {} \frac{f'(r)}{4 \pi } \end{aligned}$$
(11)
$$\begin{aligned}= & {} \frac{-\Lambda r_{+}^9+3Mr_{+}^6+6Q_m^{4}qr_{+}^2- 18MQ_m^{2}qr_+^{2}-(6q\Lambda +3)Q_m^{2}r^5}{6 \pi \left( r_{+}^4+2Q^2q\right) ^2}\nonumber \\ \end{aligned}$$
(12)

where the mass M is given in Eq. (8). One can examine the thermodynamics of the non-minimal RBH in terms of mass M, horizon radius \(r_+\), non-minimal parameter q, cosmological constant \(\Lambda \) and magnetic charge \(Q_m\). By utilizing Eq. (8) in the above expression, the temperature reduces to

$$\begin{aligned} T=\frac{r_{+}^4-\Lambda r_{+}^6-Q_m^{2}r_{+}^2-6Q_m^{2}q}{4\pi r_{+}\left( r_{+}^4+2Q_m^2q\right) }. \end{aligned}$$
(13)

For modeling of the metric function (2) and of the thermodynamic quantities, the dimensionless parameters (5) are used, but for visibility of the graph presentation, we use the following explicit values of the different parameters.

For real positive temperature, the following three conditions can be obtained:

  1. 1.

    For \(\Lambda = 0.01\) (positive), \(Q_m=1\), \(q=0.1\), we have \(1.2\le r_+ \le 9.95\).

  2. 2.

    For \(\Lambda = 0\), \(Q_m=2\), \(q=0.1\), we have \(r_+ \ge 2.1283\).

  3. 3.

    For \(\Lambda = -0.01\) (negative), \(Q_m=3\), \(q=0.1\), we have \(r_+ \ge 2.9713\).

If we variate the values of \(\Lambda \) then the range of horizon also change for real positive temperature. For simplicity, we discuss above three special cases throughout the paper.

The first law of thermodynamics can be defined as [39, 40],

$$\begin{aligned} \mathrm{d}M = T \mathrm{d}S + V \mathrm{d}P +\cdots . \end{aligned}$$
(14)

One can easily check the above relation is violated. For obtaining the thermodynamic quantities which have to satisfy the above relation, we will use the logarithmic corrections in the following subsections.

2.1 Logarithmic correction and thermodynamical relations

In this section, we discuss the effect of thermal fluctuations on non-minimal RBH thermodynamics. It is done by using the formalism of Euclidean quantum gravity, where temporal coordinate is rotated on complex plane. Hence, one can write the partition function for non-minimal RBH [7, 41,42,43,44,45]

$$\begin{aligned} Z=\int DgDA \exp (-I), \end{aligned}$$
(15)

where \(I\rightarrow iI\) is Euclidean action for this system. One can relate the statistical mechanical partition function [46, 47] as

$$\begin{aligned} Z=\int _{0}^{\infty } DE\eta (E) \exp (-\alpha E), \end{aligned}$$
(16)

where \(\alpha =T^{-1}\). We can calculate the density of states by using

$$\begin{aligned} \eta (E)=\frac{1}{2 \pi i}\int _{\alpha _0-\iota \infty }^{\alpha _0+i \infty } \mathrm{d}\alpha e^{S(\alpha )}, \end{aligned}$$
(17)

where \(S=\alpha E+\ln Z.\) This entropy can be obtained around the equilibrium temperature \(\alpha \) by neglecting all thermal fluctuations which becomes \(S_0=\pi r_{+}^2\). However, if thermal fluctuations are taken into account, then \(S(\alpha )\) becomes [7]

$$\begin{aligned} S=S_0+\frac{1}{2}\big (\alpha -\alpha _0\big )^2\Bigg (\frac{\partial ^2 S(\alpha )}{\partial \alpha ^2}\Bigg )_{\alpha =\alpha _0}. \end{aligned}$$
(18)

So, one can write density of states as

$$\begin{aligned} \eta (E)=\frac{1}{2 \pi i}\int _{\alpha _0-i \infty }^{\alpha _0+i \infty } \mathrm{d}\alpha e^{\frac{1}{2}\big (\alpha -\alpha _0\big )^2\Big (\frac{\partial ^2 S(\alpha )}{\partial \alpha ^2}\Big )_{\alpha =\alpha _0}}, \end{aligned}$$
(19)

which leads to

$$\begin{aligned} \eta (E)=\frac{e^{S_0}}{\sqrt{2 \pi }}\left[ \Big (\frac{\partial ^2 S(\alpha )}{\partial \alpha ^2}\Big )_{\alpha =\alpha _0}\right] ^{\frac{1}{2}}. \end{aligned}$$
(20)

We can write

$$\begin{aligned} S=S_0-\frac{1}{2}\ln \left[ \Big (\frac{\partial ^2 S(\alpha )}{\partial \alpha ^2}\Big )_{\alpha =\alpha _0}\right] ^{\frac{1}{2}}. \end{aligned}$$
(21)

One can notice that this second derivative of entropy is a fluctuation squared of energy. It is possible to simplify this expression by using the relation between the conformal field theory and the microscopic degrees of freedom of a BH [48]. Thus, we can consider the entropy of the form \(S=m_1\alpha ^{n_1}+m_2\alpha ^{-n_2}\), where \(m_1, m_2, n_1, n_2\) are all positive constants [10]. This has an extremum at \(\alpha _0=\Big (\frac{m_2 n_2}{m_1 n_1}\Big )^\frac{1}{n_1+n_2}=T^{-1}\) and expanding entropy around this extremum, we can determine [49, 50]

$$\begin{aligned} \Bigg (\frac{\partial ^2 S(\alpha )}{\partial \alpha ^2}\Bigg )_{\alpha =\alpha _0}=S_0 \alpha _0^{-2}. \end{aligned}$$
(22)

Thus, the corrected form for the entropy by neglecting higher order correction terms can be written as

$$\begin{aligned} S=S_0-\frac{1}{2}\ln S_0 T^2. \end{aligned}$$
(23)

Moreover, the quantum fluctuation in the geometry of the BH give rise to the very important problem of thermal fluctuations in the thermodynamics of the BH. When the size of the BH is small and its temperature is large then it is sufficient to contribute this correction term. Hence we can avoid the quantum fluctuations for large BH. It is evident that thermal fluctuation only become significant for BHs with large temperature and if the size of the BH reduces then its temperature increases. Hence we can conclude that this corrected terms will only come for sufficiently small BHs which temperature is large [7].

Next, we can write the general expression for entropy by neglecting higher order correction terms

$$\begin{aligned} S = S_0 - \frac{b}{2} \ln S_0T^2, \end{aligned}$$
(24)

where b is added as constant parameter to handle the logarithmic correction terms coming from thermal fluctuations. One can recover the entropy without any correction terms by setting \(b=0\). As mention before, one can take \(b\rightarrow 0\), for large BHs which temperature is very small and one can consider \(b\rightarrow 1\), for small BHs which temperature is sufficiently large. By using Eqs. (13) and (24), we can obtain the following corrected entropy:

$$\begin{aligned} S=\pi r_+^2-\frac{b}{2}\ln \left( \frac{\left( r_{+}^6\Lambda +Q_m^2r_{+}^2-r_{+}^4+6Q_m^2q\right) ^2}{16\pi (r_{+}^4+2Q_m^2q)^2}\right) .\nonumber \\ \end{aligned}$$
(25)
Fig. 1
figure 1

Plot of pressure verses horizon radius

Full size image
Table 1 Location of horizon on first law of thermodynamics satisfied
Full size table

It is suggested that the presence of logarithmic correction causes the reduction of entropy of the BH. We can calculate the pressure using Eqs. (10), (13), (24), and the following relation:

$$\begin{aligned} P = T \left( \frac{\partial S}{\partial V}\right) _V. \end{aligned}$$
(26)

which turns out to be

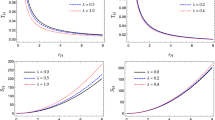
$$\begin{aligned} P= & {} \frac{1}{8 \pi ^2r_{+}^2\big (r_{+}^4+2qQ_{m}^2)^2}\nonumber \\&\times \,\big ((b\Lambda +\pi )r_{+}^8+Q_{m}^2r_{+}^4(b q \Lambda -4 \pi q-b)\nonumber \\&+2qQ_{m}^4(b-6 \pi q)-\pi r_{+}^{10} \Lambda -\pi Q_{m}^2 r_{+}^6(2q\Lambda +1)\nonumber \\&-2r_{+}^2qQ_{m}^2(\pi Q_{m}^2+8b)). \end{aligned}$$
(27)

In Fig. 1, we discuss the behavior of pressure for three cases of \(\Lambda \). If we compare \(b=0\) and \(b=1\), we see that the pressure decreases due to logarithmic correction. Further, from Fig. 1, we observe that pressure is maximum for positive cosmological constant but it becomes negative when \(r \ge 9.945\), which is evident in case 1. It means that when we increase the cosmological constant then the pressure also increases but the range of horizon for positive pressure decreases. Same behavior could be observed for temperature. We observe that the pressure is high for \(\Lambda = 0\) as compare to negative cosmological constant. Hence we conclude that the pressure will decrease due to logarithmic correction and the lower values of the cosmological constant.

Moreover, we can investigate the first law of thermodynamics by rewriting Eq. (14) as follows:

$$\begin{aligned} \mathrm{d}M-T\mathrm{d}S-V\mathrm{d}P=0, \end{aligned}$$
(28)

We construct the table for special three cases and find the horizon at which the first law of thermodynamics is satisfied. We also compare our results with respect to \(b=0\) and \(b=1\).

From Table 1, we observe that the location of horizon on which first law of thermodynamics satisfied is more for \(b=1\) as compare to \(b=0\). For positive cosmological constant, location of horizons are equal on \(b=0\) and 1 but for negative cosmological constant the location of horizons increase for \(b=1\) as compare to \(b=0\). We obtain a higher number of locations of horizons on which the first law of thermodynamics is satisfied in the absence of a cosmological constant for \(b=1\) as compared to \(b=0\). Hence, we can conclude that logarithmic correction term increases the chance of first law of thermodynamics to satisfy.

3 Stability of the non-minimal RBH

In this section, we will analyze the thermodynamical stability of non-minimal RBH due to the effect of thermal fluctuations. For this purpose we use the well-known relation

$$\begin{aligned} E = \int T \mathrm{d}S. \end{aligned}$$
(29)

We can find the internal energy and observe that it decreases dramatically due to logarithmic corrections. An important measurable physical quantity in BH thermodynamics is thermal capacity or heat capacity. It identifies the amount of heat required to change the temperature of a BH. The nature of heat capacity (positivity or negativity) represents the stability or instability of a BH. There are two different heat capacities associated with a system. \(C_\mathrm{p}\): measures the specific heat when the heat is added at constant pressure and \(C_\mathrm{v}\): measures the specific heat when the heat is added to the system by keeping the volume constant. We obtain the specific heat with constant volume by using the T and S as follows:

$$\begin{aligned} C_\mathrm{v} = T \left( \frac{\partial S}{\partial T}\right) _V. \end{aligned}$$
(30)

Using Eqs. (10), (13) and (24), we have

$$\begin{aligned} C_\mathrm{v}= & {} \Big (2 \pi r_{+}^{12} \Lambda +4\pi Q_{m}^2qr_{+}^8 \Lambda -2br_{+}^{10} \Lambda +2 \pi Q_{m}^2r_{+}^8\nonumber \\&-12Q_{m}^2 b q r_{+}^6 \Lambda -2\pi r_{+}^{10}+4 \pi Q_{m}^4 q r_{+}^4+8 \pi Q_{m}^2 q r_{+}^6\nonumber \\&+24 \pi Q_{m}^4 q^2 r_{+}^2 +2Q_{m}^2 b r_{+}^6-4 Q_{m}^4 b q r_{+}^2\nonumber \\&+32 Q_{m}^2 b q r_{+}^4\Big )\Big (r_{+}^{10}\Lambda +10Q_{m}^2 q r_{+}^6 \Lambda -3 Q_{m}^2 r_{+}^6 \nonumber \\&+r_{+}^8+2Q_{m}^4 q r_{+}^2- 36 Q_{m}^2 q r_{+}^4-12Q_{m}^4 q^2\Big )^{-1}. \end{aligned}$$
(31)

Moreover, the specific heat at constant pressure can be obtained using the relation of E, P and V as follows:

$$\begin{aligned} C_\mathrm{p} = \left( \frac{\partial (E + PV)}{\partial T}\right) _P. \end{aligned}$$
(32)

Using Eqs.(10), (13), (27) and (29), we have

$$\begin{aligned} C_\mathrm{p}= & {} \Big (64r_{+}^{12} \pi Q_{m}^2 q \Lambda +80 r_{+}^8 \pi Q_{m}^4 q^2 \Lambda +4 r_{+}^{12}\pi Q_{m}^2\nonumber \\&-\,48 r_{+}^{10} Q_{m}^2 b q \Lambda +32 r_{+}^8 \pi Q_{m}^4 q-48 \pi Q_{m}^2 q r_{+}^10\nonumber \\&-\,192 r_{+}^6 Q_{m}^4 b q^2 \Lambda +48 r_{+}^4 \pi Q_{m}^6 q^2+32 \pi Q_{m}^4 q^2 r_{+}^6\nonumber \\&+\,192 r_{+}^2 \pi Q_{m}^6 q^3 +48 r_{+}^6 Q_{m}^4 b q-64 Q_{m}^2 b q r_{+}^8\nonumber \\&-\,32 r_{+}^2 Q_{m}^6 b q^2 +384 Q_{m}^4 b q^2 r_{+}^4+12 r_{+}^{16}\pi \Lambda -8 r_{+}^{14} b \Lambda \nonumber \\&-\,8 \pi r_{+}^{14}\Big ) \Big ((r_{+}^{10}\Lambda +10Q_{m}^2 q r_{+}^6\Lambda -3Q_{m}^2 r_{+}^6+r_{+}^8\nonumber \\&+\,2Q_{m}^4 q r_{+}^2-36 Q_{m}^2 q r_{+}^4-12 Q_{m}^4 q^2)(r_{+}^4+2Q_{m}^2q)\Big )^{-1}.\nonumber \\ \end{aligned}$$
(33)

The above two specific heat relations comprise the ratio \(\gamma = C_\mathrm{p}/C_\mathrm{v}\) and its plot is given in Fig. 2 for three special cases. We observe that due to a logarithmic correction the value of \(\gamma \) increases. We obtain the maximum value of \(\gamma \) for negative cosmological constant and \(\gamma \rightarrow 1.7\) for a large horizon. Further, we observe that \(\gamma \rightarrow 1.4\) when \(\Lambda = 0\) for a large horizon. It is interesting to note that the value of \(\gamma \) decreases drastically and becomes zero at \(r_+ = 9.92\) and the value of \(\gamma \) becomes negative for a large horizon. We can say that the value of \(\gamma \) shows a stable behavior for negative and zero values of the cosmological constant but represents unstable behavior for positive cosmological constant. Hence, we can conclude that if the value of the cosmological constant decreases then the value of \(\gamma \) is higher and exhibits the more stable behavior, but it experiences an unstable behavior for higher values of the cosmological constant.

Fig. 2
figure 2

\(\gamma \) verses horizon radius

Full size image
Fig. 3
figure 3

Specific heat at constant volume verses horizon radius

Full size image

3.1 Phase transition

Another way to find the thermodynamical stability of the BH locally is to investigate the sign of the specific heat given in Eq. (31). The BH is locally stable for \(C_\mathrm{v}>0\), one can find the point of the phase transition at \(C_\mathrm{v}=0\) and the BH is locally unstable for \(C_\mathrm{v}<0\). We can find the stability range of the horizon radius of the BH for three specific cases in Fig. 3.

We discuss the range of the black hole horizon of locally thermodynamical stability for each case. We observe that when \(\Lambda =0.01\) (positive) the horizon radius for local stability \(1.3047<r_+<1.9\) and \(r_+>9.965\), when \(\Lambda = 0\) the horizon radius for local stability is \(2.1972<r_+<3.6\) and the horizon radius is \(r_+>3.0232\) for negative cosmological constant. Hence we can conclude that for negative cosmological constant the range of the horizon radius for local stability of the BH is higher than for positive and zero cosmological constant, respectively. Furthermore, we find the critical point of horizon for phase transition in each case. We obtain two critical points of the phase transition at \(r_+=1.3047\) and 9.965 for positive cosmological constant, the critical point for \(\Lambda =0\) is \(r_+=2.1972\) and the critical point is \(r_+=3.0232\) for negative cosmological constant. We notice that the phase transition for positive cosmological constant is near to BH as compare to zero and negative cosmological constant. Hence we can conclude that if we increase the value of the cosmological constant the phase transition gets shifted towards the BH and vice versa.

3.2 Grand canonical ensemble

We may treat the BH as a thermodynamical object by considering it as a grand canonical ensemble system where \(\mu = \frac{Q_m}{r_+}\) is a fixed chemical potential. The corresponding temperature and entropy with logarithmic corrected term are

$$\begin{aligned} T_\mathrm{g}= & {} \frac{1}{4 \pi r_+}\left( \frac{r_{+}^2-r_{+}^4 \Lambda - \mu ^2 r_{+}^2 - 6 \mu ^2 q}{r_+^2+2\mu ^2 q}\right) ,\end{aligned}$$
(34)
$$\begin{aligned} S= & {} \pi r_{+}^2-\frac{b}{2} \ln \left( \frac{(r_{+}^6 \Lambda + \mu ^2 r_{+}^4+6 \mu ^2 q r_{+}^2-r_{+}^4)^2}{16 \pi (r_{+}^4+2 \mu ^2 q r_{+}^2)^2}\right) .\nonumber \\ \end{aligned}$$
(35)

The effect of the chemical potential (\(\mu \)) decreases the temperature. The free energy in the grand canonical ensemble, also called Gibbs free energy, can be defined as

$$\begin{aligned} G = M - T S-\mu Q_m, \end{aligned}$$
(36)

which turns out to be

$$\begin{aligned} G= & {} \frac{-\Lambda r_{+}^6+3\mu ^{2}r_{+}^4+3r_{+}^4+6\mu ^{2} r_{+}^2 q}{6r_{+}^3}\nonumber \\&+ \left( \frac{r_{+}^2-r_{+}^4 \Lambda - \mu ^2 r_{+}^2 - 6 \mu ^2 q}{r_+^2+2\mu ^2 q}\right) \times \left( \frac{r_{+}}{4}-\frac{b}{8 \pi r_{+}} \right. \nonumber \\&\left. \times \ln \left( \frac{(r_{+}^6 \Lambda + \mu ^2 r_{+}^4+6 \mu ^2 q r_{+}^2-r_{+}^4)^2}{16 \pi (r_{+}^4+2 \mu ^2 q r_{+}^2)^2}\right) \right) -\mu ^2 r_{+}.\nonumber \\ \end{aligned}$$
(37)
Fig. 4
figure 4

Gibbs free energy in terms of horizon radius with \(\mu =0.5\)

Full size image

The effect of the chemical potential reduces the free energy as we can see from the last term in Eq. (37). Figure 4 represents the behavior of the Gibbs free energy for special three cases. We observe that the Gibbs free energy is minimum at \(r_+ \simeq 0.8\) due to the contribution of the logarithmic correction term. It means that the logarithmic correction term also reduces the Gibbs free energy. From the figure, we notice that the free energy is higher for positive cosmological constant than for zero and negative cosmological constant, respectively. It is interesting that the free energy becomes negative at \(r_+ \simeq 15\) for negative cosmological constant. It means the free energy is globally thermodynamically unstable for negative cosmological constant. Hence, we can conclude that if the value of the cosmological constant is higher, then the free energy becomes globally more stable. Moreover, thermodynamical stability does not only depend on \(\Lambda \) and q but also on the chemical potential \(\mu \).

3.3 Canonical ensemble

On the other hand, the BH could be considered as a closed system (canonical ensemble) if charge transfer is prohibited. The mass and temperature are given by Eqs. (8) and (13), respectively, and the corresponding entropy with logarithmic corrected term is given in Eq. (25). The free energy in the canonical ensemble is known as the Helmholtz free energy if the charge is fixed, which is

$$\begin{aligned} F = M- TS, \end{aligned}$$
(38)

which turns out to be

$$\begin{aligned} F= & {} \frac{-\Lambda r_{+}^6+3Q_m^{2}r_{+}^2+3r_{+}^4+6Q_m^{2}q}{6r_{+}^3}\nonumber \\&-\frac{r_{+}^4-\Lambda r_{+}^6-6Q_m^{2}q-6Q_m^{2}q}{4\pi r_{+}\left( r_{+}^4+2Q^2q\right) } \nonumber \\&\times \left( \pi r_+^2-\frac{b}{2}\ln \left( \frac{\left( r_{+}^6\Lambda +Q_m^2r_{+}^2-r_{+}^4+6Q_m^2q\right) ^2}{16\pi (r_{+}^4+2Q_m^2q)^2}\right) \right) .\nonumber \\ \end{aligned}$$
(39)
Fig. 5
figure 5

Helmholtz free energy in terms of horizon radius

Full size image

Figure 5 represents the behavior of the Helmholtz free energy for specific values of the parameters. We observe that the logarithmic corrected term reduces the free energy in every case, which is evident. Initially, the free energy for negative cosmological constant is high till \(r_+=7\), to be compare with zero and positive cosmological constant, but for a large horizon, the free energy is decreasing further, at \(r_+ = 18\) it becomes negative. The free energy is highest for positive cosmological constant as compared to \(\Lambda =0\) and \(-0.01\) for a large horizon. Hence, we can conclude that the BH is more thermodynamically stable if the value of the cosmological constant increases in large horizon and it becomes thermodynamically unstable for lower values of the cosmological constant. Moreover, thermodynamical stability does not depend only on \(\Lambda \) and q but also on magnetic charge \(Q_m\) rather than the chemical potential.

4 Concluding remarks

In this paper, we have discussed the new exact regular spherically symmetric solution of the non-minimal Einstein–Yang–Mill theory with magnetic charge of Wu–Yang gauge field and the cosmological constant. We only considered the positive non-minimal parameter q, as zero and negative values lead to space-time curvature singularities. After calculating the mass, entropy and temperature, we have discussed the effect of thermal fluctuation on non-minimal RBH. We have also utilized the logarithmic correction of the entropy and discussed the behavior of pressure and specific heat. We observed that the pressure reduces due to the logarithmic correction when decreasing the value of the cosmological constant.

We have also investigated the ratio of the specific heat at constant pressure and volume (\(\gamma \)); we observe that due to logarithmic correction the value of \(\gamma \) increases. We have also noticed that the values of \(\gamma \) are higher and more stable for negative values of the cosmological constant while it becomes unstable upon positive values of the cosmological constant for a large horizon. We observed that the first law of thermodynamics is satisfied for non-minimal RBH even in the presence of thermal fluctuations. It is mentioned here that the logarithmic correction term increases the chance of the first law of thermodynamics to be satisfied. We have also investigated the phase transition for the non-minimal RBH and found its critical points. We observed that the range of horizon radius for local stability of the BH is increased for negative cosmological constant as compared to positive and zero cosmological constant, respectively.

We have noticed that if we increase the value of the cosmological constant, the phase transition shifted towards the BH and vice versa. We have also discussed the free energy in grand canonical (Gibbs free energy) and canonical (Helmholtz free energy) ensembles. We notice that the free energy is reduced in the presence of a logarithmic correction. It is concluded that the non-minimal RBH becomes more stable globally as well as locally if we increase the value of the cosmological constant and vice versa. We have also noticed that the thermodynamics of the non-minimal RBH gets modified because of the general uncertainty principle [51, 52]. Such correction terms are non-trivial, which is evident from our results and they may lead to interesting consequences like the existence of BH remnants.