The dynamics of irreversible evaporation of a water–protein droplet and the problem of structural and dynamic experiments with single molecules

Abstract

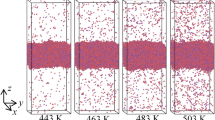
The effect of isothermal and adiabatic evaporation on the state of a water–protein droplet is discussed. The considered problem relates to the design of various approaches for structural and dynamic experiments with single molecules involving X-ray lasers. The delivery of the sample into the X-ray beam is performed by a microdroplet injector in these experiments; and the approach time is in the microsecond range. A version of molecular-dynamics simulation for all-atom modeling of an irreversible isothermal evaporation process is developed. The parameters of the isothermal evaporation of a water–protein droplet that contains sodium and chloride ions at concentrations of approximately 0.3 M have been determined in computational experiments for different temperatures. The in silico experiments showed that the energy of irreversible evaporation at the initial stages of the process was virtually the same as the specific heat of evaporation for water. An exact analytical solution of the problem for the kinetics of irreversible adiabatic evaporation has been obtained in the limit of the high heat conductivity of the droplet (or a droplet size not exceeding ~100 Å). This solution contains parameters that were derived from simulation of the isothermal evaporation of the droplets. The kinetics of the evaporation and adiabatic cooling of the droplet were shown to be scalable according to the size of the droplet. Estimation of the rate of freezing of the water–protein droplet upon adiabatic evaporation in a vacuum chamber revealed the necessity of using additional procedures for stabilizing the temperature in the droplet nucleus that contains the protein molecule. Isothermal or quasi-isothermal conditions are more favorable for the investigation of macro-molecular structural rearrangements that are related to the functioning of the object. However, the effects of dehydration and a sharp increase in the ionic strength of the aqueous microenvironment of the protein must be taken into account in this case.