Abstract
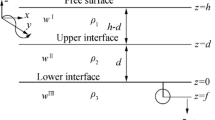
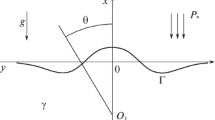
It is proved that, under a certain geometrical assumption in the linear water-wave problem, a body approaching the water surface of a symmetric three-dimensional channel gets any number of trapped modes with frequencies in the interval (0, δ) of the continuous spectrum; here δ can be any given positive number.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
J. J. Stoker, Water Waves. The Mathematical Theory with Applications. Reprint of the 1957 original. (John Wiley & Sons, Inc., New York, 1992).
R. S. Johnson, A Modern Introduction to the Mathematical Theory of Water Waves (Cambridge University Press, Cambridge, 1997).
N. Kuznetsov, V. Maz’ya, and B. Vainberg, Linear Water Waves. A Mathematical Approach (Cambridge University Press, Cambridge, 2002).
S. Campbell, The Loch Ness Monster: The Evidence (Birlinn Ltd., Edinburgh, 2002).
F. John, “On the Motion of Floating Bodies. II,” Comm. Pure Appl. Math. 3, 45–101 (1950).
F. Ursell, “Trapping Modes in the Theory of Surface Waves,” Proc. Camb. Philos. Soc. 47, 347–358 (1951).
C. M. Linton and P. McIver, “Embedded Trapped Modes in Water Waves and Acoustics,” Wave Motion 45(1–2), 16–29 (2007).
F. Ursell, “Edge Waves on a Sloping Beach,” Proc. R. Soc. Lond., Ser. A 214, 79–97 (1952).
P. McIver and D. V. Evans, “Edge Waves over a Shelf: Full Linear Theory,” J. Fluid Mech. 142, 79–95 (1984).
M. D. Groves, “On the Existence of Trapped Modes in Channels of Arbitrary Cross-Section,” Math. Methods Appl. Sci. 20, 521–545 (1997).
S. A. Nazarov, “Sufficient Conditions on the Existence of Trapped Modes in Problems of the Linear Theory of Surface Waves,” Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 369 (POMI, St. Petersburg, 2009), pp. 202–223 [J. Math. Sci. 167 (5), 713–725 (2010)].
S. A. Nazarov, “Concentration of the Trapped Modes in Problems of the Linearized Theory of Water-Waves,” Mat. Sb. 199(12), 53–78 (2008) [Sb. Math. 199 (11–12), 1783–1807 (2008)].
G. Cardone, T. Durante, and S. A. Nazarov, “Water-Waves Modes Trapped in a Canal by a Near-Surface Rough Body,” Z. Angew. Math. Mech. 90(12), 983–1004 (2010).
S. A. Nazarov, Asymptotic Theory of Thin Plates and Rods. Vol. 1. Dimension Reduction and Integral Estimates (Nauchnaya Kniga, Novosibirsk, 2001).
S. A. Nazarov and J. Taskinen, “On Essential and Continuous Spectra of the Linearized Water-Wave Problem in a Finite Pond,” Math. Scand. 106, 141–160 (2010).
D. V. Evans, M. Levitin, and D. Vasil’ev, “Existence Theorems for Trapped Modes,” J. Fluid Mech. 261, 21–31 (1994).
O. A. Ladyzhenskaya, The Boundary Value Problems of Mathematical Physics (Springer-Verlag, New York-Berlin, 1985).
M. Sh. Birman and M. Z. Solomjak [Solomyak], Spectral Theory of Self-Adjoint Operators in Hilbert Space (D. Reidel Publishing Co., Dordrecht, 1987).
S. A. Nazarov and B. A. Plamenevskii, Elliptic Problems in Domains with Piecewise Smooth Boundaries (Walter de Gruyter & Co., Berlin, 1994).
V. G. Mazja and B. A. Plamenevskii, “Estimates in L p and in Hölder Classes and the Miranda-Agmon Maximum Principle for Solutions of Elliptic Boundary Value Problems in Domains with Singular Points on the Boundary,” Amer. Math. Soc. Transl. Ser. 2 123 (American Mathematical Society, Providence, RI, 1984), pp. 1–56.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Nazarov, S.A. A body traps as many water-wave modes in a symmetric channel as it wishes. Russ. J. Math. Phys. 18, 183–194 (2011). https://doi.org/10.1134/S1061920811020075
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S1061920811020075