1 INTRODUCTION

Processes of electron–positron annihilation provide a powerful tool in studies of elementary particles. In particular, modern \({{e}^{ + }}{{e}^{ - }}\) colliders, such as VEPP-2000 (Novosibirsk), BEPC II (Beijing), KEKB (Tsukuba), etc., are well suited for production and high-precision studies of hadrons. Electron–positron colliders have significant advantages: clean signals, a low background, a high efficiency and resolution. The continuously increasing experimental accuracy challenges the theory to provide more and more precise predictions. For example, the current and upcoming experiments SuperKEKB [1], BES-III [2], Super Charm-Tau Factory [3] and Super Tau-Charm Facility [4] aim at reaching an error of a few ppm in luminosity measurements. This requires new calculations with taking into account higher order perturbative corrections and other effects including electroweak (EW) ones.

Another important advantage of \({{e}^{ + }}{{e}^{ - }}\) colliders is the possibility of using polarized beams. Several future projects of such machines foresee having at least longitudinally polarized electron beams. That will open new possibilities in high-precision studies of the charm quark and tau lepton physics. A very high accuracy of checking the universality of the neutral current vector couplings and in searches for CP violation in the lepton sector will be achieved. A new independent measurement of the effective EW mixing parameter \({{\sin }^{2}}{\kern 1pt} {{\theta }_{W}}\) through left–right asymmetries will be complementary to the corresponding studies at higher energies. Measurements with polarized beams will also help to refine the elements of the Cabibbo–Kobayashi–Maskawa matrix, study QCD at low energies and exotic hadrons, search for new physics and extensively investigate two-photon physics. The SuperKEKB team (Belle collaboration) [5] considers plans of an upgrade to have longitudinally polarized electron beam [6, 7]. That will significantly widen the collider’s capability of examining the EW sector.

BES-III has collected more than 35 fb–1 of integrated luminosity at different center-of-mass energies from 2.0 to 4.94 GeV. The upgrade of BES-III will increase the peak luminosity by a factor of 3 for beam energies from 2.0 to 2.8 GeV (center-of-mass energies from 4.0 to 5.6 GeV). Future Super Charm-Tau Factories (Super Charm-Tau Factory project [3] and High Intensity Electron Positron Advanced Facility (HIEPAF) [4]) are accelerator complexes for high-precision measurements between 2 and 5(7) GeV with luminosity up to 1035 cm−2 s–1 and longitudinal polarization. They will deliver up to 1 ab–1 of integrated luminosity per year.

In connection with these challenges, one of the most demanded processes is the lepton pair production (LPP) both for estimating luminosity and for physics program. Various experimental facilities operating at low energies are in plans or already in action demanding appropriate software for theoretical predictions. At the moment, the most advanced and widely used generators with one-loop radiative corrections (RC) for estimation of LPP at low energies are BabaYaga [8–11], KKMC [12, 13], and MCJPG [14]. Recently, a new Monte-Carlo generator [15] for the simulation of lepton pair productions and τ lepton decays up to an energy of about 11 GeV has been presented.

The SANC Monte Carlo event generator ReneSANCe [16] and integrator MCSANCee are relatively new software tools. They can be used in the mentioned energy domain of electron–positron colliders for simulation of LPP and Bhabha processes. These tools provide the possibility of evaluating the complete one-loop QED and (electro)weak RC. Some higher-order leading corrections are also implemented. In addition, the tools produce results in the full phase space and also allow taking into account longitudinal beam polarizations. To match the high precision of current and near-future experiments we plan to implement also higher-order next-to-leading QED RC.

In this article, we analyze the effects due to EW RC and polarization of the colliding beams using the SANC software. We consider the processes of electron–positron annihilation into a lepton pair

$$\begin{gathered} {{e}^{ + }}({{p}_{1}},{{\chi }_{1}}) + {{e}^{ - }}({{p}_{2}},{{\chi }_{2}}) \\ \to {{l}^{ - }}({{p}_{3}},{{\chi }_{3}}) + {{l}^{ + }}({{p}_{4}},{{\chi }_{4}})( + \gamma ({{p}_{5}},{{\chi }_{5}})), \\ \end{gathered} $$
(1)

where \(l = \mu ,\tau \) with allowance for arbitrary longitudinal polarization of the initial particles (\({{\chi }_{i}}\) correspond to the helicities of the particles). We keep in mind experiments at relatively low center-of-mass energies up to about 7 GeV which is relevant for the Super Charm-Tau Factory. Our aim is to analyze the size of different RC contributions, estimate the resulting theoretical uncertainty, and verify the necessity to include other higher-order corrections.

The article is organized as follows. In Section 2 we discuss various contributions to the cross sections. In Section 3, the corresponding numerical results are given for the total and differential cross sections. We consider in detail all possible contributions to the cross sections at center-of-mass energies of \(\sqrt s = 5\) and 7 GeV. Numerical results are obtained by an estimate of polarization effects. In Section 4 we analyze the results.

2 STATE-OF-THE-ART RADIATIVE CORRECTIONS AT LOW ENERGIES IN SANC

For a detailed analysis, we divide the contributions to the full correction into several parts: the Born level cross section, EW corrections, contribution from vacuum polarization (VP), and multiple photon emission effects.

Born level

We evaluate the Born level cross section (leading order, LO) contribution for two cases: (1) with pure photon exchange \(\sigma _{{{\text{QED}}}}^{{{\text{Born}}}}(\gamma )\) and (2) with both photon and Z boson exchange \(\sigma _{{{\text{QED}}}}^{{{\text{Born}}}}(\gamma ,Z)\).

Electroweak corrections

We have already described in detail the technique and results of the analytic calculations of the scalar form factors and helicity amplitudes of the general LPP process (1) in our recent paper [17]. For EW corrections, we calculate the following contributions and introduce the notation for them:

\( \bullet \) QED level.

Gauge invariant subsets of QED corrections are evaluated separately, i.e., the initial state radiation (ISR), the final state radiation (FSR), and the initial-final interference (IFI).

\( \bullet \) Weak and higher order corrections.

At low energies, weak-interaction contributions are typically small since they are suppressed by the ratio \(s{\text{/}}M_{Z}^{2}\). But for high-precision measurements they might be still numerically relevant. We have found it appropriate to combine the contributions of the same order of smallness, i.e., weak and higher-order corrections. The corresponding relative contributions will be further denoted as \({{\delta }^{{{\text{weak}}}}}\) and \({{\delta }^{{{\text{ho}}}}}\). We also distinguish here two possibilities: (1) the complete one-loop \({{\delta }^{{{\text{weak}}}}}\), where pure weak-interaction and VP contributions are taken into account;Footnote 1 and (2) the pure weak-interaction contribution \({{\delta }^{{{\text{weak-VP}}}}} = {{\delta }^{{{\text{weak}}}}} - {{\delta }^{{{\text{VP}}}}}\).

We evaluate the leading higher-order EW corrections \({{\delta }^{{{\text{ho}}}}}\) to four-fermion processes through the \(\Delta \alpha \) and \(\Delta \rho \) parameters. A detailed description of our implementation of this contribution was presented in [18].

Vacuum polarization

We introduce two options to account for the contribution of VP: \(\delta _{1}^{{{\text{VP}}}}\) is the choice of hadronic VP \(\Delta \alpha _{{{\text{had}}}}^{{(5)}}({{M}_{Z}})\) part using a parameterization with auxiliary quark masses; and \(\delta _{2}^{{{\text{VP}}}}\) is the choice using public versions of the AlphaQED code by F. Jegerlehner [19].

Multiple photon effects

The implementation into SANC of the multiple photon effects, i.e., ISR (FSR) corrections in the leading logarithmic approximation (LLA) through the apparatus of QED structure functions [20, 21], which was described in detail in [22]. Results are shown up to \(\mathcal{O}({{\alpha }^{3}}{{L}^{3}})\) finite terms for an exponentiated representation and up to \(\mathcal{O}({{\alpha }^{4}}{{L}^{4}})\) for order-by-order calculations. The corresponding relative corrections are denoted below as \({{\delta }^{{{\text{LLA}}{\text{,ISR(FSR}}{\text{,IFI)}}}}}\).

Particular contributions to ISR(FSR) are sensitive to experimental cuts. Our cuts are appropriate to the conditions of the Super Charm-Tau Factory project.

The master formula for a general \({{e}^{ + }}{{e}^{ - }}\) annihilation cross section with ISR QED corrections in the leading logarithmic approximation has the same structure as the one for the Drell–Yan process. For ISR corrections in the annihilation channel, the large logarithm is \(L = \ln (s{\text{/}}m_{e}^{2})\) where the total center-of-mass energy \(\sqrt s \) is chosen as the factorization scale.

In the LLA approximation we separate the pure photonic corrections (marked as γ) and the remaining ones which include the pure pair and mixed photon-pair effects (marked as \({{e}^{ + }}{{e}^{ - }}\) or \({{\mu }^{ + }}{{\mu }^{ - }}\)). Here we do not consider the correction due to light hadron pairs. Numerically, it is comparable with the muon pair con-tribution but strongly depends on the event selection procedure. So, the corrections due to hadronic effects will be treated elsewhere. The corresponding relative corrections are denoted as \({{\delta }^{{{\text{LLA}},i}}}(k)\) with \(i = \) \({\text{ISR}}{\text{,FSR}}{\text{,IFI}}\), and k suggests the correction type: γ, \({{e}^{ + }}{{e}^{ - }}\) pairs, or \({{\mu }^{ + }}{{\mu }^{ - }}\) pairs.

3 NUMERICAL RESULTS AND COMPARISONS

In this section, we show numerical results for EW RC to the annihilation process (1) obtained by means of the SANC system. Numerical results contain estimates of polarization effects. We compute total cross sections as well as angular distributions at the one-loop level.

Here we used the following set of input parameters:

$${{\alpha }^{{ - 1}}}(0) = 137.035999084,$$
(2)
$${{M}_{W}} = 80.379\;{\text{GeV}},\quad {{M}_{Z}} = 91.1876\;{\text{GeV}},$$
$${{\Gamma }_{Z}} = 2.4952\;{\text{GeV}},\quad {{m}_{e}} = 0.51099895000\;{\text{MeV}},$$
$${{m}_{\mu }} = 0.1056583745\;{\text{GeV}},\quad {{m}_{\tau }} = 1.77686\;{\text{GeV}},$$
$${{m}_{d}} = 0.083\;{\text{GeV}},\quad {{m}_{s}} = 0.215\;{\text{GeV}},$$
$${{m}_{b}} = 4.7\;{\text{GeV}},\quad {{m}_{u}} = 0.062\;{\text{GeV}},$$
$${{m}_{c}} = 1.5\;{\text{GeV}},\quad {{m}_{t}} = 172.76\;{\text{GeV}}.$$

The invariant mass and angular cuts are applied to the final state leptons:

$${\text{|}}\cos {{\theta }_{{{{\mu }^{ - }}}}}{\text{|}} < 0.9,\; {\text{|}}\cos {{\theta }_{{{{\mu }^{ + }}}}}{\text{|}} < 0.9, {{M}_{{{{l}^{ + }}{{l}^{ - }}}}} \geqslant 1\;{\text{GeV}},$$
(3)

where \({{\theta }_{{{{\mu }^{ \pm }}}}}\) are angles with respect to the beam axis.

All calculations are done in the \(\alpha (0)\) EW scheme in order to have a direct access to the effect of VP. In this scheme, the fine structure constant \(\alpha (0)\) and all particle masses are input parameters. All the results are obtained for the center-of-mass energies \(\sqrt s = 5\) and 7 GeV and for the following three sets of magnitudes of the electron \(({{P}_{{{{e}^{ - }}}}})\) and positron \(({{P}_{{{{e}^{ + }}}}})\) beam polarizations:

$$({{P}_{{{{e}^{ - }}}}},{{P}_{{{{e}^{ + }}}}}) = (0,0),( - 0.8,0),(0.8,0).$$
(4)

In order to quantify the impact of different contributions, we divide them into several parts: three gauge-invariant subsets of QED one-loop corrections, the VP contribution, the weak interaction effects, and the higher order LLA QED contributions. The three QED RC subsets are due to the initial state radiation (ISR), the final state radiation (FSR), and the interference of the initial and final state radiation (IFI).

The corresponding results for the total LPP cross section are presented in Table 1, where the relative corrections \({{\delta }^{i}}\) are computed as the ratios (in percent) of the corresponding RC contributions to the Born level cross section. Table 2 illustrates the size of the ISR higher-order QED corrections computed within the collinear leading logarithmic approximation.

Table 1. Integrated Born and one-loop cross sections and relative corrections for the \({{e}^{ + }}{{e}^{ - }} \to {{\mu }^{ - }}{{\mu }^{ + }}(\gamma )\) process at the center-of-mass energies \(\sqrt s = 5\) and \(7\) GeV
Full size table
Table 2. Higher-order ISR corrections in the LLA approximation for the \({{e}^{ + }}{{e}^{ - }} \to {{\mu }^{ - }}{{\mu }^{ + }}(n\gamma )\) process at \(\sqrt s = 5\) and 7 GeV. Here \({{\delta }_{{{\text{ISRLLA}}}}} \equiv \delta {{\sigma }_{{{\text{ISRLLA}}}}}{\text{/}}{{\sigma }_{0}} \times 100{\kern 1pt} \% \)
Full size table

In the upper panel of Fig. 1, the Born cross section and the corrected one which includes the EW NLO and higher-order corrections are shown as a function of the initial center-of-mass energy (\(\sqrt s = 2{-} 12\) GeV) of the electron and positron beams. The cross sections show the fast drop from ~20 nb at the center-of-mass energy \(\sqrt s = 2\) GeV to about 0.5 nb at \(\sqrt s = 12\) GeV.

Fig. 1.
figure 1

(Color online) (Upper panel) Born level (LO) and corrected (EW NLO + ho) cross sections of the \({{e}^{ + }}{{e}^{ - }} \to {{\mu }^{ - }}{{\mu }^{ + }}(\gamma )\) process for the center-of-mass energy range \(\sqrt s = 2{-} 12\) GeV. (Lower panel) Relative corrections of the QED, vacuum polarization (VP), and higher-order (ho) contributions.

Full size image

In the lower panel of Fig. 1 the relative corrections to the Born cross section are shown in parts, namely, the pure the QED, VP and EW higher-order contributions. The main impact is due to the QED effects, being from 5 to 10%. The VP contribution is also large, ranging from 4 to 8%. The contribution of higher order is proportional to \({{\alpha }^{n}}\) \((n \geqslant 2)\) and makes up about 0.1–0.4% because of being enhanced by large logarithms. VP is treated in two ways. In the first one, the hadronic part of VP is parameterized by auxiliary quark masses (it is marked as VP1 in the plot). In the second one, we use the parameterization by F. Jegerlehner which accounts for hadron resonances [19] (it is marked as VP2 in the plot). In both cases, leptonic contributions are taken into account. One can see that the two parameterizations agree well at higher energies in regions without resonance. But in general, the second parameterization is more appropriate for the given energy range.

4 COMPARISON WITH THE BABAYAGA CODE

In Table 3, we present a tuned comparison of the Born and QED NLO (without VP contribution) integrated cross sections produced by the SANC and BabaYaga codes. The results are obtained for two center-of-mass energies \(\sqrt s = 5\) and 7 GeV with cuts (3). Very good agreement within statistical errors of the results produced by two codes is found.

Table 3. Tuned comparison of the Born and QED NLO integrated cross sections produced by the SANC and BabaYaga codes
Full size table

Figures 2 and 3 show the comparison of the SANC and BabaYaga results produced for two center-of-mass energies \(\sqrt s = 5\) and 7 GeV. In the upper panels of the figures, the LO and QED NLO differential cross sections as functions of the cosine of the outgoing muon momentum angle are shown. In the lower panels the relative corrections are compared. For both center-of-mass energies, cross sections and the relative corrections are in good agreement. To obtain the results for Table 3 and Figs. 2, 3, additional extra efforts were made to exclude the Z boson exchange contribution in the LO and NLO cross sections in the SANC code.

Fig. 2.
figure 2

(Color online) (Upper panel) LO and NLO unpolarized pure QED cross sections and (lower panel) the relative corrections produced by the SANC and BabaYaga codes for the center-of-mass energy \(\sqrt s = 5\) GeV versus \(\cos {{\theta }_{{{{\mu }^{ + }}}}}\).

Full size image
Fig. 3.
figure 3

(Color online) Same as in Fig. 2 but for center-of-mass energy \(\sqrt s = 7\) GeV.

Full size image

5 POLARIZATION DEPENDENCE OF CROSS SECTIONS

Tables 4 and 5 present the integrated Born and one-loop cross sections in pb and relative corrections in percent for the process \({{e}^{ + }}{{e}^{ - }} \to {{l}^{ - }}{{l}^{ + }}\) at the center-of-mass energy of 5 GeV and set (4) of the initial particle degree of polarization in the \(\alpha (0)\) EW scheme. The cases with the 7 GeV center-of-mass energy for the \({{\mu }^{ + }}{{\mu }^{ - }}\) and \({{\tau }^{ + }}{{\tau }^{ - }}\) final states are presented in Tables 6 and 7, respectively. It is interesting that the Born and corrected cross sections do depend on beam polarizations while the relative correction is almost constant.

Table 4. Polarized integrated Born cross section and relative corrections for the \({{e}^{ + }}{{e}^{ - }} \to {{\mu }^{ - }}{{\mu }^{ + }}(\gamma \)) scattering for \(\sqrt s = \) 5 GeV for different degree of polarization of the initial particles
Full size table
Table 5. Polarized integrated Born cross section and relative corrections for \({{e}^{ + }}{{e}^{ - }} \to {{\tau }^{ - }}{{\tau }^{ + }}(\gamma )\) scattering for \(\sqrt s = 5\) GeV
Full size table
Table 6. Same as in Table 4, but for \(\sqrt s = 7\) GeV
Full size table
Table 7. Same as in Table 5 but for \(\sqrt s = 7\) GeV
Full size table

6 FORWARD-BACKWARD ASYMMETRY

The forward–backward asymmetry \({{A}_{{{\text{FB}}}}}\) is defined as

$${{A}_{{{\text{FB}}}}} = \frac{{{{\sigma }_{{\text{F}}}} - {{\sigma }_{{\text{B}}}}}}{{{{\sigma }_{{\text{F}}}} + {{\sigma }_{{\text{B}}}}}},$$
(5)
$${{\sigma }_{{\text{F}}}} = \int\limits_0^1 \frac{{d\sigma }}{{d\cos {{\vartheta }_{f}}}}d\cos {{\vartheta }_{f}},\quad {{\sigma }_{{\text{B}}}} = \int\limits_{ - 1}^0 \frac{{d\sigma }}{{d\cos {{\vartheta }_{f}}}}d\cos {{\vartheta }_{f}},$$

where \({{\vartheta }_{f}}\) is the angle between the momenta of the incoming electron and the outgoing negatively charged fermion. It can be measured in any \({{e}^{ + }}{{e}^{ - }} \to f{\kern 1pt} \bar {f}\) channels but for precision tests the most convenient channels are \(f = e,\mu \).

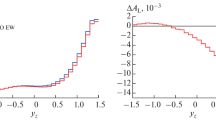
Figure 4 shows the behavior of the \({{A}_{{{\text{FB}}}}}\) asymmetry in the Born and 1-loop approximations (with weak, pure weak, QED, or complete EW RC contributions) and of the corresponding \(\Delta {{A}_{{{\text{FB}}}}}\) for the center-of-mass energy range \(2 \leqslant \sqrt s \leqslant 12\) GeV. The asymmetry in the lowest-order approximation comes from the tree-level Z boson exchange contribution. One can see that for higher energies it is comparable in size with the QED contribution which comes from one-loop RC.

Fig. 4.
figure 4

(Color online) Asymmetry \({{A}_{{{\text{FB}}}}}\) in the Born and one-loop approximations and the corresponding shifts \(\Delta {{A}_{{{\text{FB}}}}}\) for the center-of-mass energy range \(\sqrt s = 2{-} 12\) GeV.

Full size image

7 CONCLUSIONS

To summarize, we have considered different contributions of EW corrections to processes of electron–positron annihilation into a lepton pair. The corrections were evaluated within the SANC system framework in the \(\alpha (0)\) EW scheme for center-of-mass energies up to about 10 GeV which are relevant for the existing and future meson factories. In particular, our results are relevant for the Super Charm-Tau Factory project. The complete one-loop EW corrections as well as some leading higher-order corrections were analyzed. We see that the QED and VP corrections dominate in the given energy range, but in some cases the Z boson exchange amplitude also becomes nu-merically relevant. In particular, the latter is visible in the forward–backward asymmetry.

The SANC Monte Carlo event generator ReneSANCe and integrator MCSANCee were used to produce the numerical results. At the one-loop pure QED level for unpolarized beams, good agreement with the corresponding results of the BabaYaga code is found. The advantages of our codes is implementation of the complete one-loop (electro)weak corrections and taking into account particle polarizations.

From Table 2 one can see that the second order ISR corrections are numerically relevant for high-precision experiments. That brings us to the conclusion that to reduce the theoretical uncertainty we need to implement the complete two-loop, i.e., \(\mathcal{O}({{\alpha }^{2}})\) QED corrections, while starting from the third order the corrections can be computed in an approximate manner, i.e., with QED showers or even in the collinear LLA approximation.