-
PDF
- Split View
-
Views
-
Cite
Cite
N. Bucciantini, T. A. Thompson, J. Arons, E. Quataert, L. Del Zanna, Relativistic magnetohydrodynamics winds from rotating neutron stars, Monthly Notices of the Royal Astronomical Society, Volume 368, Issue 4, 1 June 2006, Pages 1717–1734, https://doi.org/10.1111/j.1365-2966.2006.10217.x
Close - Share Icon Share
Abstract
We solve for the time-dependent dynamics of axisymmetric, general relativistic magnetohydrodynamic winds from rotating neutron stars. The mass-loss rate as a function of latitude is obtained self-consistently as a solution to the magnetohydrodynamics equations, subject to a finite thermal pressure at the stellar surface. We consider both monopole and dipole magnetic field geometries and we explore the parameter regime extending from low magnetization (low σ0), almost thermally driven winds to high magnetization (high σ0), relativistic Poynting-flux-dominated outflows (σ=B2/4πργc2β2≈σ0/γ∞,β=v/c with  , where ω is the rotation rate, Φ is the open magnetic flux, and
, where ω is the rotation rate, Φ is the open magnetic flux, and 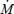 is the mass flux). We compute the angular momentum and rotational energy-loss rates as a function of σ0 and compare with analytic expectations from the classical theory of pulsars and magnetized stellar winds. In the case of the monopole, our high-σ0 calculations asymptotically approach the analytic force-free limit. If we define the spindown rate in terms of the open magnetic flux, we similarly reproduce the spindown rate from recent force-free calculations of the aligned dipole. However, even for σ0 as high as ∼20, we find that the location of the Y-type point (rY), which specifies the radius of the last closed field line in the equatorial plane, is not the radius of the Light Cylinder RL=c/ω (R= cylindrical radius), as has previously been assumed in most estimates and force-free calculations. Instead, although the Alfvén radius at intermediate latitudes quickly approaches RL as σ0 exceeds unity, rY remains significantly less than RL. In addition, rY is a weak function of σ0, suggesting that high magnetizations may be required to quantitatively approach the force-free magnetospheric structure, with rY=RL. Because rY < RL, our calculated spindown rates thus exceed the classic ‘vacuum dipole’ rate: equivalently, for a given spindown rate, the corresponding dipole field is smaller than traditionally inferred. In addition, our results suggest a braking index generically less than 3. We discuss the implications of our results for models of rotation-powered pulsars and magnetars, both in their observed states and in their hypothesized rapidly rotating initial states.
is the mass flux). We compute the angular momentum and rotational energy-loss rates as a function of σ0 and compare with analytic expectations from the classical theory of pulsars and magnetized stellar winds. In the case of the monopole, our high-σ0 calculations asymptotically approach the analytic force-free limit. If we define the spindown rate in terms of the open magnetic flux, we similarly reproduce the spindown rate from recent force-free calculations of the aligned dipole. However, even for σ0 as high as ∼20, we find that the location of the Y-type point (rY), which specifies the radius of the last closed field line in the equatorial plane, is not the radius of the Light Cylinder RL=c/ω (R= cylindrical radius), as has previously been assumed in most estimates and force-free calculations. Instead, although the Alfvén radius at intermediate latitudes quickly approaches RL as σ0 exceeds unity, rY remains significantly less than RL. In addition, rY is a weak function of σ0, suggesting that high magnetizations may be required to quantitatively approach the force-free magnetospheric structure, with rY=RL. Because rY < RL, our calculated spindown rates thus exceed the classic ‘vacuum dipole’ rate: equivalently, for a given spindown rate, the corresponding dipole field is smaller than traditionally inferred. In addition, our results suggest a braking index generically less than 3. We discuss the implications of our results for models of rotation-powered pulsars and magnetars, both in their observed states and in their hypothesized rapidly rotating initial states.
1 INTRODUCTION
Magnetically dominated winds from stars and accretion discs are central to the angular momentum evolution of these objects. Because they can efficiently extract rotational energy – transforming stored gravitational binding energy into asymptotic wind kinetic energy – magnetic outflows are ubiquitous in powering a wide variety of astrophysical systems. Schatzman (1962) first introduced the key idea that a magnetic field anchored in a rotating star with a wind can enforce plasma corotation out to radii large compared to the stellar radius, thus greatly increasing the angular momentum lost per unit mass.
Ideas of Schatzman (1962) were formalized in the steady non-relativistic flow model of Weber & Davis (1967), who assumed a pure monopole field geometry, and then by Mestel (1968a,b) who assumed a more realistic dipole magnetic field configuration. For strong dipole fields, a closed zone forms at low latitudes and the mass-loss is concentrated at high latitudes in regions where the field lines can be opened. If the extent and shape of the open field line region is known, then the physics of the magnetic wind is similar to that in the monopole geometry: the flow emerges along the open flux tubes and its character is determined by passing through the slow-magnetosonic (SM), Alfvén (AL) and fast-magnetosonic (FM) surfaces. If the thermal sound speed is small, the flow is driven primarily by magnetocentrifugal forces and the asymptotic outflow velocity is approximately vA(RA) ≈RAω, where R refers to the cylindrical radius, ω is the stellar angular velocity, and RA is the AL radius. Because RA is the point at which B2(RA)/4π=ρv2A(RA), the outflow kinetic energy is roughly equal to the magnetic energy. This remains true in the asymptotic wind.
The theory of magnetic winds has been greatly extended and applied in its non-relativistic form to a wide variety of problems in stellar astrophysics. Gosling (1996) and Aschwanden, Poland & Rabin (2001) provide reasonably modern reviews in the solar context, where many of the recent developments in non-relativistic wind modelling have occurred. Multidimensional models have been motivated in part by the fact that toroidal magnetic fields can collimate the flow along the rotation axis via hoop stress into jets, a topic of much interest in the modelling of the bipolar outflows observed from protostars (e.g. Smith 1998).
The dipole moment of the star, μ, was assumed to be related to the monopole moment m appearing in the magnetohydrodynamics (MHD) theory via m=μ/RL, a relation equivalent to assuming that the AL radius RA was equal to the radius of the Light Cylinder RL=c/ω. Since these monopole models only treated the flow in the rotational equator, the numerical coefficient k∼ 1 in equation (1) could not be determined accurately.
These simplified theoretical models revealed important differences between relativistic and non-relativistic winds. First, instead of reaching approximate energy equipartition between flow kinetic energy and magnetic energy, the asymptotic flow remains strongly magnetized. The asymptotic Lorentz factor is given by γ∞≈σ1/30, where 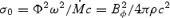 , Φ is the magnetic flux, and
, Φ is the magnetic flux, and 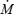 is the mass-loss rate. Thus, γ∞≪σ0. For a highly relativistic outflow (σ0≫ 1) the asymptotic magnetization σ∞=σ0/γ∞≈σ2/30≫ 1. A second important difference is that in relativistic magnetized flows the electric force cannot be neglected.1 Although it is absent by symmetry in the Michel and Goldreich & Julian models, the electric force almost exactly cancels the focusing hoop stress in multidimensional monopole models, thus undermining the usefulness of these flows for the understanding of relativistic collimated jets. This is a problem generic to all relativistic outflows (Lyubarsky & Eichler 2001) not focused by some external medium (e.g. a disc or external channel).
is the mass-loss rate. Thus, γ∞≪σ0. For a highly relativistic outflow (σ0≫ 1) the asymptotic magnetization σ∞=σ0/γ∞≈σ2/30≫ 1. A second important difference is that in relativistic magnetized flows the electric force cannot be neglected.1 Although it is absent by symmetry in the Michel and Goldreich & Julian models, the electric force almost exactly cancels the focusing hoop stress in multidimensional monopole models, thus undermining the usefulness of these flows for the understanding of relativistic collimated jets. This is a problem generic to all relativistic outflows (Lyubarsky & Eichler 2001) not focused by some external medium (e.g. a disc or external channel).
Much effort has gone into relaxing the simplifications of these early models, and in particular, on understanding what is required for an ideal MHD flow to have γ∞→σ0. Observations and models of pulsar wind nebulae suggest that at the termination shock of the outflows of young rotation-powered pulsars, the magnetic energy has been almost completely converted into flow kinetic energy (the ‘σ problem’) and the flow 4-velocity has reached γ≈σ0 (the ‘γ problem’), in contradiction with the predictions of the 1D monopole treatments. If the magnetic surfaces retain an almost monopolar shape the acceleration of the flow is only logarithmic (Begelman & Li 1994). However, various asymptotic solutions (Begelman & Li 1994; Heyvaerts & Norman 2003 and references therein) and similarity solutions (Vlahakis & Königl 2003; Vlahakis 2004) of parts of the full axisymmetric flow problem suggest that if the poloidal magnetic field is sufficiently non-monopolar beyond the FM point, the largely radial current that supports the toroidal magnetic field, might cross field lines toward the equator, causing a transfer of electromagnetic energy to flow kinetic energy. However, both a numerical solution in axisymmetric non-relativistic MHD (Sakurai 1985) and a perturbative calculation of relativistically magnetized MHD flow from the exact force-free solution (Beskin, Kuznetsova & Rafikov 1998) yield a poloidal magnetic field which hews closely to the exact monopolar form. Thus, the monopole puzzle of asymptotic winds with magnetic energy that is never converted to flow kinetic energy persists, suggesting that ideal MHD expansion of the wind contradicts the observations.
The monopole geometry for the poloidal field has long been recognized as a singular case. A dipole magnetic field aligned with the stellar rotation axis presents the simplest realistic alternative field geometry. Because the open field, where outflow occurs, has a nozzle shape that expands faster than r2 at distances comparable to the radius of the last closed field line (rY), there is a possibility of faster acceleration and larger conversion of magnetic energy into kinetic energy than occurs in the monopole geometry. However, complete solutions in axisymmetric steady flow have only been possible for the monopole; the change of topology between closed and open field lines required in the dipole case has so far escaped solution of the Grad–Shafranov equation that describes the magnetic structure in MHD flows with inertia and pressure included.
The location of the AL radius in the outflow, and its relation to the maximum equatorial radius of the last closed field line rY, where typically a Y-type neutral point occurs in the magnetic field, is a problem of equal significance. As outlined in Section 2, if rY < RL, and if rY/RL is an appropriate function of ω, one might be able to account for the observed fact that in rotation-powered pulsars T∥∝ωn, with n < 3. The strong inferred magnetization of pulsars has always suggested that the outflow structure should be treated as a problem in force-free relativistic MHD, with inertial and pressure forces completely neglected (Goldreich & Julian 1969). The force-free Grad–Shafranov equation for the case of an aligned dipole (Michel 1973; Scharlemann & Wagoner 1973) resisted solution until recently (Contopoulos, Kazanas & Fendt 1999; Gruzinov 2005 assumed strictly force-free conditions everywhere, whereas Goodwin et al. 2004 included pressure effects near the Y-point). Gruzinov found that the torque is indeed given by equation (1), with k= 1 ± 0.1, while Contopoulos et al. (1999) found k= 1.85. All of these authors assumedrY=RL, as is physically plausible.
However, subsequent work by Timokhin (2005) has found that force-free MHD allows a family of solutions with rY of the last field line within RL, contrary to naive expectations. He found that k≈ 0.47 (RL/rY)2, which, when rY=RL, is close to the force-free monopole result of Michel (1969). Importantly, these solutions indicate that beyond a few Light Cylinder radii, the poloidal magnetic field assumes a monopolar form, which suggests that acceleration in the asymptotic wind never reaches equipartition energies (the σ problem). However, since inertial forces are important beyond the FM surface (r≈σ1/30RL) the force-free approximation breaks down (Beskin et al. 1998; Arons 2004) and no strong conclusions may be drawn.
The ambiguities of the steady force-free models, and the difficulty of solving the magnetospheric structure in MHD with inertia and pressure included, suggest that an evolutionary approach to the problem would be useful. A time-dependent solution can then be sought for specified boundary conditions at the stellar surface (such as pressure or injection velocity). The system can then relax to a self-consistent steady state (if one exists) and this approach allows one to find the last closed flux surface unambiguously, for specified injection conditions. Furthermore, such a treatment allows for the possibility of intrinsic time dependence (including either limit cycle or chaotic behaviour) of the magnetosphere. The time dependence of individual radio pulses from rotation-powered pulsars, showing systematic drifting through the pulse window for many objects near the pulsar death line, and chaotic rotation phase over wider regions of the  diagram (Rankin 1986; Deshpandhe & Rankin 1999) have time-scales consistent with global magnetospheric variability causing changes in the polar current system underlying pulsar emission (Arons 1981; Wright 2001). Indeed, the torque noise exhibited by many pulsars (Cordes & Helfand 1980) may also owe its origin to instabilities of the magnetospheric current system (Arons 1981; Cheng 1987a,b).
diagram (Rankin 1986; Deshpandhe & Rankin 1999) have time-scales consistent with global magnetospheric variability causing changes in the polar current system underlying pulsar emission (Arons 1981; Wright 2001). Indeed, the torque noise exhibited by many pulsars (Cordes & Helfand 1980) may also owe its origin to instabilities of the magnetospheric current system (Arons 1981; Cheng 1987a,b).
In this paper, we carry out time-dependent relativistic MHD (RMHD) modelling of both highly magnetized Poynting-flux-dominated winds (σ0≫ 1) in which RA≈RL, as well as magnetized neutron star winds in which RA is significantly less than RL(σ0≪ 1).
Large σ0 MHD models draw their motivation from studies of rotation-powered pulsars and of magnetars (soft gamma ray repeaters and anomalous X-ray pulsars). More broadly, analogous problems appear in Poynting-flux-dominated models of jets from black holes and neutron stars. Low-σ0 (but still magnetized) neutron star winds are of interest primarily in understanding the physics of very young neutron stars. In the seconds after collapse and explosion, the neutron star is hot (surface temperatures of ∼2–5 MeV) and extended. This proto-neutron star cools and contracts on its Kelvin–Helmholtz time-scale (τKH∼ 10–100 s), radiating its gravitational binding energy (∼1053 erg) in neutrinos of all species (Burrows & Lattimer 1986; Pons et al. 1999). The cooling epoch is accompanied by a thermal wind, driven by neutrino energy deposition (primarily νen→pe− and 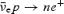 ), which emerges into the post-supernova-shock ejecta (e.g. Duncan, Shapiro & Wasserman 1986; Qian & Woosley 1996; Thompson, Burrows & Meyer 2001).
), which emerges into the post-supernova-shock ejecta (e.g. Duncan, Shapiro & Wasserman 1986; Qian & Woosley 1996; Thompson, Burrows & Meyer 2001).
A second or two after birth, the thermal pressure at the edge of the proto-neutron star surface, where the exponential atmosphere joins the wind (rν), is of order ∼1028 erg cm−3 and decreases sharply as the neutrino luminosity (Lν) decreases on a time-scale τKH, as the star cools and deleptonizes. The thermal pressure at the stellar surface is set by Lν. If the proto-neutron star has a surface magnetic field of strength B0, then at some point during the cooling epoch the magnetic energy density will exceed the thermal pressure. For fixed B0, the wind region becomes increasingly magnetically dominated as Lν decreases. For larger B0 the magnetic field dominates at earlier times. For magnetar-strength surface fields (B0∼ 1014–1015 G) the magnetic field dominates the wind dynamics from just a few seconds after the supernova (Thompson 2003).
Magnetars are thought to be born with millisecond rotation periods (Duncan & Thompson 1992; Thompson & Duncan 1993), in which case the combination of rapid rotation and strong magnetic fields makes the proto-neutron star wind magnetocentrifugally driven. Because the rotational energy of a millisecond magnetar is very large (∼2 × 1052 erg) relative to the energy of the supernova explosion (∼1051 erg) and because the spindown time-scale 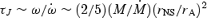 (where rNS is the neutron star radius) can be short for large rA, these proto-magnetar winds have been considered as a mechanism for producing hyperenergetic supernovae (Thompson, Chang & Quataert 2004). Because the wind becomes increasingly magnetically dominated and the flow eventually becomes Poynting-flux-dominated as the neutrino luminosity abates, the outflow must become relativistic. For this reason, proto-magnetar winds have also been considered as a possible central engine for long-duration gamma ray bursts (GRBs) (Usov 1992; Thompson 1994; Wheeler et al. 2000; Thompson et al. 2004). They may also be the source of ultrahigh energy cosmic rays (Blasi, Epstein & Olinto 2000; Arons 2003). The time dependent RMHD models of neutron star winds calculated in this paper provide a significantly improved understanding of proto-magnetar winds, and their possible role in hyperenergetic supernovae and GRBs.
(where rNS is the neutron star radius) can be short for large rA, these proto-magnetar winds have been considered as a mechanism for producing hyperenergetic supernovae (Thompson, Chang & Quataert 2004). Because the wind becomes increasingly magnetically dominated and the flow eventually becomes Poynting-flux-dominated as the neutrino luminosity abates, the outflow must become relativistic. For this reason, proto-magnetar winds have also been considered as a possible central engine for long-duration gamma ray bursts (GRBs) (Usov 1992; Thompson 1994; Wheeler et al. 2000; Thompson et al. 2004). They may also be the source of ultrahigh energy cosmic rays (Blasi, Epstein & Olinto 2000; Arons 2003). The time dependent RMHD models of neutron star winds calculated in this paper provide a significantly improved understanding of proto-magnetar winds, and their possible role in hyperenergetic supernovae and GRBs.
1.1 This paper
With these goals in mind, in Section 2 we first outline some order-of-magnitude estimates for the spindown of neutron stars in both the low- and high-σ0 limits. In Sections 3 and 4, we describe the details of our numerical model. In Section 5, we present our numerical results for the 1D monopole (Section 5.1), the 2D monopole (Section 5.2) and the aligned dipole (Section 5.3). In each case, we present a set of models for both low- and high-σ0 winds. Finally, in Section 6 we present a discussion of our results and speculate on their implications for the spindown of rotation-powered pulsars and very young, rapidly rotating magnetars.
2 PHYSICAL MODEL
As a guide to the numerical models, we describe here several simple order-of-magnitude estimates of the properties of both high- and low-σ0 winds from neutron stars.
2.1 Poynting-flux-dominated spindown
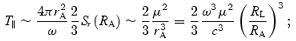
the evaluation of the constant k in equation (1) to be equal to 2/3 is the exact result for the EM torque on the force-free monopole (Michel 1973), which has no closed zone or Y-point. Since the open magnetic flux is Φo≈ (μω/c) (RL/rY), the torque can also be written as T∥≈ (2/3) (Φ2oω/c) (ry/RL)2.
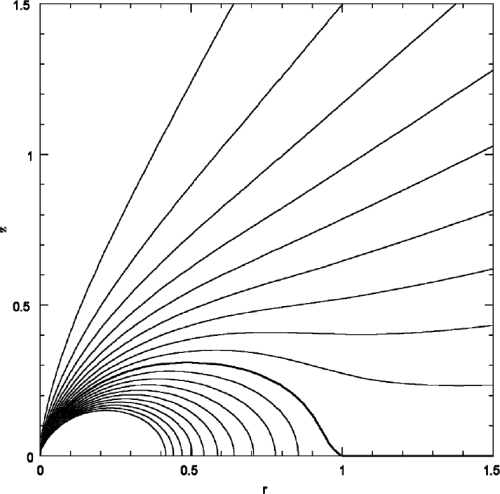
Force-free poloidal magnetic field lines from a magnetized star with dipole axis aligned with the rotation axis. The distances are scaled in units of the radius of the Light Cylinder, RLC. From Gruzinov (2005).
If mass loading (inertial forces) and pressure are negligible, the long-standing expectation has been rY=RA=RL=c/ω (Goldreich & Julian 1969), and MHD spindown torques then should have braking index 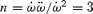 , if μ and the stellar moment of inertia are constant. Two numerical solutions for steady flow from the force-free aligned dipole rotator have found k= 1.85 (Contopoulos et al. 1999) and, at higher resolution, k= 1 ± 0.1 (Gruzinov 2005), rather than 2/3. The equality rY=RL=RA was assumed in both of these calculations.
, if μ and the stellar moment of inertia are constant. Two numerical solutions for steady flow from the force-free aligned dipole rotator have found k= 1.85 (Contopoulos et al. 1999) and, at higher resolution, k= 1 ± 0.1 (Gruzinov 2005), rather than 2/3. The equality rY=RL=RA was assumed in both of these calculations.
A long-standing empirical puzzle has been that in the four observations of braking indices not requiring major corrections for glitches in the timing, the braking index lies between 2.5 and 2.9 (Lyne, Pritchard & Graham-Smith 1993; Kaspi et al. 1994; Deeter, Nagase & Boynton 1999; Camilo et al. 2000; Livingstone et al. 2005). This reduction of the braking index for fixed μ and ω, in comparison to our simple estimate, is tantamount to rY < RL. That is, the closed zone ends within the Light Cylinder, 2and, as the star ages (ω decreases), rY/RA also decreases – the magnetosphere becomes more open with decreasing spindown power. One way to state this is to simply assert that RA=rY < RL and that rY/RL∝ωα (e.g. rY/RL= (ωrNS/c)α; Arons 1983). This implies a change in the polar cap size from rNS(rNS/RL)1/2 to the larger value (larger Φo) of rNS(rNS/RL)(1−α)/2. Using this expression, the braking index data require 1/6 ≥α≥ 1/30, with the largest value for the Crab pulsar and the smallest for the 407-ms pulsar J1119−6157.
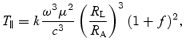
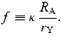
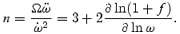
Thus, a braking index less than 3 requires RA/rY to depend on ω (more generally, to depend on time). If the time dependence of rY/RA enters solely through dependence on ω, n < 3 requires RA/rY=RL/rY to increase as the star spins down – the magnetosphere becomes more open with time, and the magnetic field at the Light Cylinder to remain larger, than is expected in the traditional model. Such behaviour requires transformation of closed field lines to open, which can occur if magnetic dissipation at and near the Y-point allows reconnection to enable this transformation.
Our RMHD numerical results presented in Section 5.3 show that although RA→RL as soon as σ0 exceeds unity, rY/RL remains substantially less than unity for σ0 as large as ∼20. We also find that, for σ0 of order a few, the ratio rY/RL decreases as ω decreases – the braking index in our models is less than 3. This suggests that seemingly small inertial and pressure forces can have a large effect on the magnetospheric structure and, in turn, the magnitude of the spindown torque and the braking index.
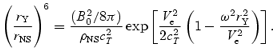
One sees that for fixed isothermal sound speed cT, if (ωrY/Ve) is greater than unity, then it becomes exponentially harder to increase RY/rNS by increasing B20/ρNS.
However, since electromagnetic stresses alone can lead to Y-point formation, as is clear from the solutions of the force-free Grad–Shafranov equation, one should treat these estimates of RY as a function of plasma stress alone with caution, when applied to the magnetically dominated regime. Simplified models along the lines pioneered by Goodwin et al. (2004) may be helpful, but at present, the best results are the simulations themselves (Section 5.3). We defer a relativistic generalization of Mestel & Spruit (1987) with a polytropic (p∝ρΓ) equation of state (more appropriate to our simulations) to a future paper.
2.2 Spindown by magnetized mass-loaded winds
Stresses due to mass loading become significant in the thermally driven winds of newly born neutron stars. These stars may have strongly mass-loaded winds which have rA large in comparison to rNS, but significantly smaller than RL (Thompson et al. 2004). Conditions for such winds in the presence of thermally driven mass-loss generally obtain when the isothermal sound speed cT is smaller than, or of order, the AL speed, vA.3
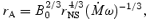
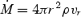 and B0 is the magnetic field strength at the stellar surface. The time evolution of the spin period of the star is then governed by the equation
and B0 is the magnetic field strength at the stellar surface. The time evolution of the spin period of the star is then governed by the equation 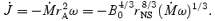
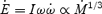 . In this limit (vA≫cT) the sonic point is approximately
. In this limit (vA≫cT) the sonic point is approximately 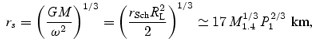
where we have scaled the spin period P to 1 ms and rSch is the Schwarzschild radius. In the cT≪vA limit, the radial velocity reaches its asymptotic value of v∞≈ (3/2)vA at the FM point (e.g. Belcher & MacGregor 1976).
In the regime we are interested in this paper we always have a supersonic outflows at the AL surface. In this case, according to the standard parameterization of MHD winds (Sakurai 1985; Daigne & Drenkhahn 2002), all solution should be considered centrifugally or marginally centrifugally driven.
A similar set of estimates for a dipole magnetic field is considerably more complicated, particularly since, as in Section 2.1, the position of the Y-point is not known a priori. In addition, since the areal function along open flux tubes adjacent to the closed zone deviates significantly from radial, a full numerical solution is required to address spindown in this context (Section 5.3). However, as a rough guide in understanding the expected differences between monopole and dipole spindown it is sufficient to imagine the scalings for the dipole as essentially those for the monopole, but with the surface magnetic field strength normalized to just the open magnetic flux.
2.3 Parametrization
These estimates and those of Section 2.1 reveal the parameters which specify the physical regimes of relevance to our models of rotating magnetospheres. Mass-loss is thermally and centrifugally driven in these models, depending upon the ratio of pressure and centrifugal forces to the gravitational force, parametrized at the injection surface (rin) by (c2T/V2e) and by (Ωrin/Ve)2. All of the models considered in this paper have the first of these parameters between 0.01 and 0.1, while the second is between 0.05 and 0.3. The values adopted can be derived from the parameter shown in Tables 1 (Section 4.1). For all of the 2D monopole and dipole models, magnetic pressure dominates gas pressure, as expressed by B2/4πc2s > 1. This is true for most of the 1D monopole models also. Again, these parameters are listed in Table 1. In all cases, the thermal energy density is smaller than the rest-mass density (p < ρc2). Thus, pressure forces do not lead to relativistic motion. The values of the ratios between the characteristic speeds at the base of the wind, for all our simulations, are provided in Appendix A.
Parameters of the numerical models (unit with c= 1).
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
| c2T(rin) | 0.033 | 0.033 | 0.028 | 0.025 | 0.021 | 0.018 | 0.033 | 0.030 | 0.030 | 0.030 |
| Br(rin)2/ρ(rin) | 0.004 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 4 | 8 | 32 | 80 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | ||||
| Br(rin)2/ρ(rin) | 0.04 | 0.4 | 0.4 | 4 | 40 | 200 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | |||||
| Br(rin, θ= 0)2/ρ(rin) | 0.64 | 6.4 | 6.4 | 6.4 | 64 | |||||
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
| c2T(rin) | 0.033 | 0.033 | 0.028 | 0.025 | 0.021 | 0.018 | 0.033 | 0.030 | 0.030 | 0.030 |
| Br(rin)2/ρ(rin) | 0.004 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 4 | 8 | 32 | 80 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | ||||
| Br(rin)2/ρ(rin) | 0.04 | 0.4 | 0.4 | 4 | 40 | 200 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | |||||
| Br(rin, θ= 0)2/ρ(rin) | 0.64 | 6.4 | 6.4 | 6.4 | 64 | |||||
In all models Ω= 0.143 except model B1 which have Ω= 0.214 and model B2 which has Ω= 0.0715. See equation (24) for the corresponding value of the rotation period. c2T=Γp/(ρh). Case A0 is a reference case for an almost thermally driven wind. In term of the standard wind parametrization (Sakurai 1985; Daigne & Drenkhahn 2002) all our cases are centrifugally driven: the value of Γp/ρ(Ωr)2 at the AL surfaces, is always less than 0.1 except in case A0 where it is 0.5. The value of the lapse at the injection radius is α(rin) = 0.79 corresponding to an escape speed 0.6 c. The unit of length corresponds to the radius of the neutron star rNS, the unit of time is rNS/c.
Parameters of the numerical models (unit with c= 1).
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
| c2T(rin) | 0.033 | 0.033 | 0.028 | 0.025 | 0.021 | 0.018 | 0.033 | 0.030 | 0.030 | 0.030 |
| Br(rin)2/ρ(rin) | 0.004 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 4 | 8 | 32 | 80 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | ||||
| Br(rin)2/ρ(rin) | 0.04 | 0.4 | 0.4 | 4 | 40 | 200 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | |||||
| Br(rin, θ= 0)2/ρ(rin) | 0.64 | 6.4 | 6.4 | 6.4 | 64 | |||||
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
| c2T(rin) | 0.033 | 0.033 | 0.028 | 0.025 | 0.021 | 0.018 | 0.033 | 0.030 | 0.030 | 0.030 |
| Br(rin)2/ρ(rin) | 0.004 | 0.04 | 0.04 | 0.04 | 0.04 | 0.04 | 4 | 8 | 32 | 80 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | ||||
| Br(rin)2/ρ(rin) | 0.04 | 0.4 | 0.4 | 4 | 40 | 200 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
| c2T(rin) | 0.033 | 0.033 | 0.033 | 0.033 | 0.033 | |||||
| Br(rin, θ= 0)2/ρ(rin) | 0.64 | 6.4 | 6.4 | 6.4 | 64 | |||||
In all models Ω= 0.143 except model B1 which have Ω= 0.214 and model B2 which has Ω= 0.0715. See equation (24) for the corresponding value of the rotation period. c2T=Γp/(ρh). Case A0 is a reference case for an almost thermally driven wind. In term of the standard wind parametrization (Sakurai 1985; Daigne & Drenkhahn 2002) all our cases are centrifugally driven: the value of Γp/ρ(Ωr)2 at the AL surfaces, is always less than 0.1 except in case A0 where it is 0.5. The value of the lapse at the injection radius is α(rin) = 0.79 corresponding to an escape speed 0.6 c. The unit of length corresponds to the radius of the neutron star rNS, the unit of time is rNS/c.
The distinction between pressure-driven and centrifugally driven wind, can be also done based on the conditions at the AL surface. In Daigne & Drenkhahn (2002) (following Sakurai (1985)) the distinction is based on the value of the ratio Γp/ρ(Ωr)2 at the AL surfaces (Γ is the adiabatic coefficient). In all our cases this ratio is less than 0.1.
The most significant parameter is Michel's magnetization parameter, σ0, defined just after expression (1). When the magnetic energy density exceeds the rest-mass density (σ0 > 1), magnetic pressure can accelerate the flow to relativistic velocities. This parameter is listed for all the models, as our major goal is to span the regimes from highly mass loaded, pressure-driven, non-relativistic outflow (σ0≪ 1) to lightly mass loaded, magnetically driven relativistic outflow (σ0≫ 1) in both monopole and dipole geometry. The values of σ0 for the various models are given in the tables in Sections 5.1–5.3.
We do not consider outflows driven by relativistically high temperature (p > ρc2), a regime more relevant to fireball models of GRBs.
3 MATHEMATICAL FORMULATION
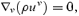
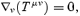
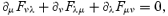
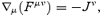
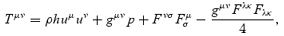
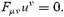
With this approximation, equations (10)–(13) can be rewritten in term of proper density, pressure, 4-velocity and magnetic field, reducing to a system of eight equations for eight variables, plus the solenoidal condition on the magnetic field, ∇·B= 0.
Although we consider winds from neutron stars with centrifugal forces large enough to affect the mass-loss, we only consider rotation rates slow enough to allow us to neglect rotational modifications of the metric. Therefore, we employ the Schwarzschild instead of the Kerr metric. The use of a diagonal metric allows one to simplify the equations and to implement them easily in any code for special relativistic MHD, as shown by Koide, Shibata & Kudoh (1999).
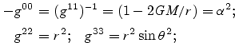
where M is the mass of the central object (1.44 M⊙).
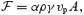
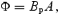
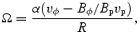
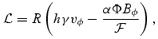
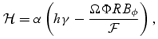
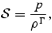
where subscript p and φ indicate poloidal and azimuthal components, respectively, γ is the Lorentz factor, A is the area of the flux tube (A=r2 in the case of radial outflow), and R=r sin θ the cylindrical radius. Again note that we have chosen units in which c= 1.
If the value of the six integrals is known on a stream line, then equations (17)–(22) can be solved for the value of primitive quantities like density, velocity and pressure. In general, quantities like 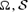 and Φ are assumed to be known and given by the physical conditions at the surface of the central object, while the values of the remaining integrals are derived by requiring the solution to pass smoothly the SM, AL and FM points. In 2D, one also requires an additional equation for the area of the flux tube, and this is provided by requiring equilibrium across streamlines.
and Φ are assumed to be known and given by the physical conditions at the surface of the central object, while the values of the remaining integrals are derived by requiring the solution to pass smoothly the SM, AL and FM points. In 2D, one also requires an additional equation for the area of the flux tube, and this is provided by requiring equilibrium across streamlines.
4 NUMERICAL METHOD
Equations (10)–(13) are solved using the shock-capturing code for relativistic MHD developed by Del Zanna, Bucciantini & Londrillo (2003). The code has been modified to solve the equations in the Schwarzschild metric following the recipes by Koide et al. (1999). The scheme is particularly simple and efficient, since solvers based on characteristic waves are avoided in favour of central-type component-wise techniques (Harten–Lax–van Leer solver based only on the FM speed). In the axisymmetric 2D approximation the equation for the evolution of Bφ can be written in conservative form and only one component of the vector potential, Aφ, is used in the evolution of the poloidal magnetic field. Moreover, we replace the energy conservation equation with the constant entropy condition, 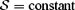 . Of course, this condition cannot be satisfied during the evolution when shocks form in the flow. However, if the wind evolves toward steady state, shocks propagate outside the computational domain, and the condition
. Of course, this condition cannot be satisfied during the evolution when shocks form in the flow. However, if the wind evolves toward steady state, shocks propagate outside the computational domain, and the condition 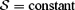 can be satisfied. There are various numerical reasons for our choice of S= constant. Most importantly, enforcing constant entropy significantly enhances code stability. For example, it is known that in strongly magnetized flows or in the supersonic regime, in deriving the thermal pressure from the conserved quantities, small errors can lead to unphysical states. In non-relativistic MHD, these unphysical states correspond to solutions with negative pressure. A common fix is to set a minimum pressure ‘floor’ that allows the computation to proceed. However, in RMHD it is possible that no state can be found (not even one with negative pressure) and the computation stops. This usually happens for high Lorentz factor γ∼ 10–100, depending on the grid-flow geometry, or in the case of high magnetization, B2/(ρh) ≳ 100. When the magnetization at the Light Cylinder is high, close to the central object it will be above this stability threshold, which prevents us from using the full equation of energy. The use of a constant entropy condition also greatly simplifies the derivation of primitive variables from the conserved quantities, thus increasing the efficiency of the code.
can be satisfied. There are various numerical reasons for our choice of S= constant. Most importantly, enforcing constant entropy significantly enhances code stability. For example, it is known that in strongly magnetized flows or in the supersonic regime, in deriving the thermal pressure from the conserved quantities, small errors can lead to unphysical states. In non-relativistic MHD, these unphysical states correspond to solutions with negative pressure. A common fix is to set a minimum pressure ‘floor’ that allows the computation to proceed. However, in RMHD it is possible that no state can be found (not even one with negative pressure) and the computation stops. This usually happens for high Lorentz factor γ∼ 10–100, depending on the grid-flow geometry, or in the case of high magnetization, B2/(ρh) ≳ 100. When the magnetization at the Light Cylinder is high, close to the central object it will be above this stability threshold, which prevents us from using the full equation of energy. The use of a constant entropy condition also greatly simplifies the derivation of primitive variables from the conserved quantities, thus increasing the efficiency of the code.
Lastly, by specifying the value of the entropy we remove entropy waves from the system. Entropy waves travel at the advection speed (and are dissipated in an advection time). If the sound speed is much smaller than c, the advection speed vr, close to the surface of the central object, is much smaller than the speed of light and the advection time can be extremely long. By removing entropy waves, perturbations are dissipated at the SM speed, which in our regime is of the order of 0.1 c.
Simulations were performed on a logarithmic spherical grid with 200 points per decade in the radial direction, and a uniform resolution on the θ direction with 100 grid points between the pole and the equator (Courant–Friedrichs–Lewy factor equal to 0.4). Higher resolutions were used in a few cases, to test convergence and accuracy. In order to model the heating and cooling processes using an ideal gas equation of state we adopt an adiabatic coefficient Γ= 1.1 (almost isothermal wind), which is reasonably representative of the wind solution by, e.g. Qian & Woosley (1996). It can be shown that in order to have a transonic outflow the thermal pressure cannot be too high (above a critical value depending on Γ the sonic point moves inside the surface of the star) nor too low (the Bernoulli integral 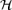 must be positive), as shown by Koide et al. (1999) in the hydrodynamical case. The available parameter space increases for smaller Γ. The value we choose allows us to investigate easily cases with p/ρ∼ 0.05, especially in the dipole case where the strong flux divergence at the base is more important.
must be positive), as shown by Koide et al. (1999) in the hydrodynamical case. The available parameter space increases for smaller Γ. The value we choose allows us to investigate easily cases with p/ρ∼ 0.05, especially in the dipole case where the strong flux divergence at the base is more important.
4.1 Initial and boundary conditions, and model parameters
Simulations in both 1D and 2D were initialized by using a hydrodynamical 1D radial solution obtained on a much finer grid (the relativistic extension of the Parker solution (Parker 1958), and projecting it on the initial magnetic field lines. In the monopole cases, initial poloidal magnetic field lines are assumed to be strictly radial while for the dipole cases we adopt the solution for the vacuum dipole in the Schwarzschild metric (i.e. Muslimov & Tsygan 1992; Wasserman & Shapiro 1983). Density and pressure were interpolated from the hydrodynamical solution, vr was derived by projecting the radial velocity on the magnetic field lines, and we set vθ= 0. We also impose corotation in the inner region vφ= min (ΩR/α, 0.6c), in order to avoid sharp temporal transients in the vicinity of the inner boundary.
Standard reflection conditions are imposed on the axis, and symmetric conditions are imposed on the equator. At the outer radial boundary, we apply standard zeroth order extrapolation for all the variables. Initial conditions are chosen in order to guarantee that during the evolution the FM surface is inside the computational domain so that no information is propagated back from the outer boundary.
Unfortunately, as we will discuss in the following section, in the 2D case such a constraint can not be satisfied close to the axis, unless one uses an excessively large computational domain. In a few cases, using larger grids that allow the FM surface to be inside the computational domain, we find that the results do not change appreciably except along the axis itself. That is, the global solution at all but the highest latitudes is not significantly affected by the fact that the FM surface is outside the computational domain very near the polar axis.
Particular care has to be taken for the inner boundary conditions. As pointed out in Section 1, we are here interested in the transition from mass loaded (σ0≪ 1) to high-σ0 winds, and our injection conditions are tuned to be as close as possible to the neutrino-driven proto-neutron star case. We chose the inner radius rin to be located at 11 km (1.1 radii of the neutron star rNS), which corresponds to the outer edge of the exponential atmosphere for a thermally driven wind (e.g. Thompson et al. 2001). The modelling of such a steep atmosphere requires very high resolution in order to avoid numerical diffusion, and the problem becomes prohibitive in terms of computational time in 2D. At the inner boundary the flow speed is smaller than the SM speed, implying that all wave modes can have incoming and outgoing characteristics. This constrains the number of physical quantities that can be specified. Density and pressure at the inner radius are set to be p/ρ∼ 0.04, thus fixing the entropy for the overall wind. The radial velocity is derived using linear extrapolation. We also fixed the value of Ω/α(rin), typically at Ωrin/α(rin) = 0.2, corresponding to a millisecond period (in the neutron star proper frame, see also equation 24), which implies RL= 6.8 rNS.
The frozen-in condition (15) requires that the electric field in the comoving frame at the inner radius vanishes: vp∥Bp→Eφ= 0 and Ep=ΩRinBp/α(rin). The condition on Eφ implies that the radial component of the magnetic field remains constant. We chose for Br(rin) different values to investigate both cases with low magnetizations and high magnetization. Bθ and Bφ where extrapolated using zeroth order reconstruction (we found that linear interpolation can lead to spurious oscillations). The value of the tangential velocities were derived using the remaining constraint of the frozen-in condition: vθ=vrBθ/Br and vφ=ΩRin/α(rin) −vrBφ/Br. Given that the three components of the velocity are derived independently, there is no guarantee that v2 < 1; so care has to be taken to avoid sharp transients and spurious oscillations in the tangential magnetic field near the inner boundary.
In Table 1 the parameters of our various models are given. Equations (17)–(22) show that the problem can be parametrized in terms of the ratio 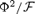 (assuming Bφ scales as Br) and not on the specific value of density and magnetic field; more generally the parameter governing the properties of the system is
(assuming Bφ scales as Br) and not on the specific value of density and magnetic field; more generally the parameter governing the properties of the system is 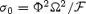 (Michel 1969). The bulk of our simulations have been done using a fixed value for Ω, in order to allow a more straightforward comparison among the various results; however in a few cases (B1 of the 2D monopole, and B1, B2 of the 2D dipole) we use a different rotation rate to check whether the energy and angular momentum loss rates indeed only scale with σ0. We note that it is computationally more efficient to increase the magnetic flux than to drop the mass flux in order to achieve higher σ0. Only in the 1D case, where resolution is not a constraint, are we able to investigate the behaviour of the system for different values of
(Michel 1969). The bulk of our simulations have been done using a fixed value for Ω, in order to allow a more straightforward comparison among the various results; however in a few cases (B1 of the 2D monopole, and B1, B2 of the 2D dipole) we use a different rotation rate to check whether the energy and angular momentum loss rates indeed only scale with σ0. We note that it is computationally more efficient to increase the magnetic flux than to drop the mass flux in order to achieve higher σ0. Only in the 1D case, where resolution is not a constraint, are we able to investigate the behaviour of the system for different values of  .
.
5 RESULTS
5.1 The 1D monopole
As a starting point for our investigation, we consider the simple case of a relativistic monopolar wind in 1D. This is the relativistic extension of the classic Weber–Davis solution for a magnetized wind (Weber & Davis 1967), and represents a simplified model for the flow in the equatorial plane. The 1D model can also be used both to verify the accuracy of the code and as a guide in understanding the 2D simulations (Section 5.2 and 5.3). Here we assume vθ=Bθ= 0. The solenoidal condition on the poloidal magnetic field reduces to Br∝r−2.
We calculate a number of wind solutions for different values of the flux Φ and the entropy  . The results are summarized in Table 2. Case A0 is a reference case for an almost unmagnetized wind, and it will be used for comparison with the weakly magnetized regime (A–D). As stated above, the solution can be parametrized in terms of
. The results are summarized in Table 2. Case A0 is a reference case for an almost unmagnetized wind, and it will be used for comparison with the weakly magnetized regime (A–D). As stated above, the solution can be parametrized in terms of 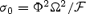 . We have verified that the mass-loss rate
. We have verified that the mass-loss rate 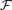 depends strongly on the value of the sound speed at rin, and drops rapidly as the pressure approaches the critical value for
depends strongly on the value of the sound speed at rin, and drops rapidly as the pressure approaches the critical value for  , which also depends on the magnetic field strength. In contrast, over the range of parameters studied,
, which also depends on the magnetic field strength. In contrast, over the range of parameters studied,  has a relatively minor dependence on the value of the magnetic field at fixed
has a relatively minor dependence on the value of the magnetic field at fixed 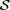 : increasing Br(rin)2 by three orders of magnitude corresponds to an increase in
: increasing Br(rin)2 by three orders of magnitude corresponds to an increase in 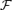 by just a factor of ∼1.7 (compare models A0 and F in Table 2). The reason for this is that in all cases listed in Table 2 the AL point is larger than the SM point. Thus, the magnetocentrifugal effect of increasing the density scale height in the region interior to the SM point, where the mass-loss rate is set, is already maximized. For all the cases investigated, the value of Γp/ρ(Ωr)2 at the AL point is always less than 0.1 (in Case A it is ≃0.1 while in case E it is ≃0.02). All the solution can thus be considered centrifugally driven. We expect and find a sharp drop in
by just a factor of ∼1.7 (compare models A0 and F in Table 2). The reason for this is that in all cases listed in Table 2 the AL point is larger than the SM point. Thus, the magnetocentrifugal effect of increasing the density scale height in the region interior to the SM point, where the mass-loss rate is set, is already maximized. For all the cases investigated, the value of Γp/ρ(Ωr)2 at the AL point is always less than 0.1 (in Case A it is ≃0.1 while in case E it is ≃0.02). All the solution can thus be considered centrifugally driven. We expect and find a sharp drop in 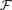 as we go to yet smaller magnetization. For example, in the purely hydrodynamical case without magnetic fields,
as we go to yet smaller magnetization. For example, in the purely hydrodynamical case without magnetic fields, 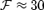 , six times lower than
, six times lower than 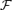 for Case F.
for Case F.
Results of the 1D models.
| Model . | σ0 . | 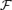 .
. | 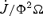 .
. | 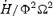 .
. | γ(100rNS) . | rA/RL . |
|---|---|---|---|---|---|---|
| A0 | 0.013 | 101 | 10.6 | 99.0 | 1.12 | 0.30 |
| A | 0.084 | 142 | 4.17 | 18.0 | 1.20 | 0.46 |
| B | 0.164 | 74 | 3.34 | 9.98 | 1.22 | 0.56 |
| C | 0.307 | 39 | 2.71 | 6.06 | 1.32 | 0.65 |
| D | 0.634 | 19 | 2.18 | 3.75 | 1.42 | 0.75 |
| E | 2.81 | 4.25 | 1.52 | 1.86 | 1.87 | 0.89 |
| F | 6.85 | 175 | 1.31 | 1.49 | 2.30 | 0.93 |
| G | 18.4 | 130 | 1.17 | 1.24 | 2.94 | 0.96 |
| H | 61.4 | 155 | 1.08 | 1.10 | 4.00 | 0.98 |
| I | 127 | 188 | 1.06 | 1.06 | 4.84 | 0.99 |
| Model . | σ0 . | 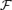 .
. | 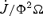 .
. | 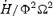 .
. | γ(100rNS) . | rA/RL . |
|---|---|---|---|---|---|---|
| A0 | 0.013 | 101 | 10.6 | 99.0 | 1.12 | 0.30 |
| A | 0.084 | 142 | 4.17 | 18.0 | 1.20 | 0.46 |
| B | 0.164 | 74 | 3.34 | 9.98 | 1.22 | 0.56 |
| C | 0.307 | 39 | 2.71 | 6.06 | 1.32 | 0.65 |
| D | 0.634 | 19 | 2.18 | 3.75 | 1.42 | 0.75 |
| E | 2.81 | 4.25 | 1.52 | 1.86 | 1.87 | 0.89 |
| F | 6.85 | 175 | 1.31 | 1.49 | 2.30 | 0.93 |
| G | 18.4 | 130 | 1.17 | 1.24 | 2.94 | 0.96 |
| H | 61.4 | 155 | 1.08 | 1.10 | 4.00 | 0.98 |
| I | 127 | 188 | 1.06 | 1.06 | 4.84 | 0.99 |
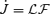 and
and 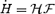 . Values of
. Values of  are given in code units, see equations (23)–(27) for conversion to physical units. In all cases Ω= 0.143.
are given in code units, see equations (23)–(27) for conversion to physical units. In all cases Ω= 0.143.
Results of the 1D models.
| Model . | σ0 . |  .
. | 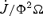 .
. | 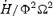 .
. | γ(100rNS) . | rA/RL . |
|---|---|---|---|---|---|---|
| A0 | 0.013 | 101 | 10.6 | 99.0 | 1.12 | 0.30 |
| A | 0.084 | 142 | 4.17 | 18.0 | 1.20 | 0.46 |
| B | 0.164 | 74 | 3.34 | 9.98 | 1.22 | 0.56 |
| C | 0.307 | 39 | 2.71 | 6.06 | 1.32 | 0.65 |
| D | 0.634 | 19 | 2.18 | 3.75 | 1.42 | 0.75 |
| E | 2.81 | 4.25 | 1.52 | 1.86 | 1.87 | 0.89 |
| F | 6.85 | 175 | 1.31 | 1.49 | 2.30 | 0.93 |
| G | 18.4 | 130 | 1.17 | 1.24 | 2.94 | 0.96 |
| H | 61.4 | 155 | 1.08 | 1.10 | 4.00 | 0.98 |
| I | 127 | 188 | 1.06 | 1.06 | 4.84 | 0.99 |
| Model . | σ0 . | 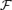 .
. | 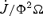 .
. | 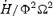 .
. | γ(100rNS) . | rA/RL . |
|---|---|---|---|---|---|---|
| A0 | 0.013 | 101 | 10.6 | 99.0 | 1.12 | 0.30 |
| A | 0.084 | 142 | 4.17 | 18.0 | 1.20 | 0.46 |
| B | 0.164 | 74 | 3.34 | 9.98 | 1.22 | 0.56 |
| C | 0.307 | 39 | 2.71 | 6.06 | 1.32 | 0.65 |
| D | 0.634 | 19 | 2.18 | 3.75 | 1.42 | 0.75 |
| E | 2.81 | 4.25 | 1.52 | 1.86 | 1.87 | 0.89 |
| F | 6.85 | 175 | 1.31 | 1.49 | 2.30 | 0.93 |
| G | 18.4 | 130 | 1.17 | 1.24 | 2.94 | 0.96 |
| H | 61.4 | 155 | 1.08 | 1.10 | 4.00 | 0.98 |
| I | 127 | 188 | 1.06 | 1.06 | 4.84 | 0.99 |
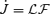 and
and 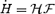 . Values of
. Values of 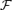 are given in code units, see equations (23)–(27) for conversion to physical units. In all cases Ω= 0.143.
are given in code units, see equations (23)–(27) for conversion to physical units. In all cases Ω= 0.143.
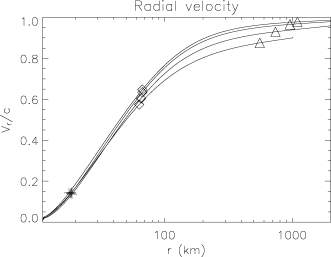
Note that the value of γ reported in Table 2 is at a fixed position, r= 100rNS, which is generally outside the FM point (see Fig. 2). Case I is an exception. For reference, the Lorentz factor at ∼300 rNS is 7.8 for this model.
Radial velocity, and position of the SM (plus), AL (diamond) and FM (triangle) points, in the 1D monopole case. From bottom to top lines refer to Cases F, G, H and I.
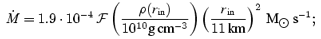
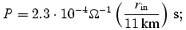
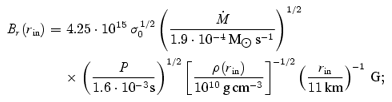
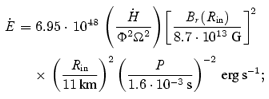
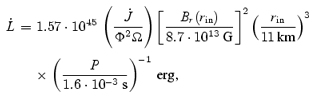
where  and
and  .
.
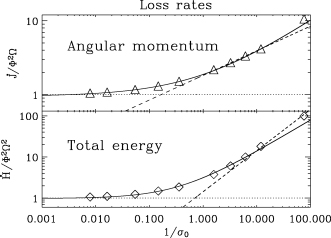
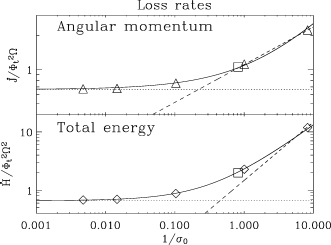
In Fig. 2, we plot the velocity profiles for Cases F, G, H and I, together with the location of the SM, AL and FM points. Note that the position of the SM point does not change significantly and is given roughly by equation (9). In Fig. 3, the angular momentum loss rate and energy loss rate are plotted as a function of σ0. The convergence to the force free solution is evident (see also Table 2). An alternative way to parametrize how close the solution is to the force free limit is by considering rA/RL (Daigne & Drenkhahn 2002), as shown in Table 2. In the mass loaded cases (σ0 < 1; models A–D) we find that 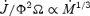 in accord with the expectations from Section 2.2. We find that all the points (we excluded case A0 because we are interested in case where rA > rSM, typical of the transition from mass loaded to force free) can be approximated by a relation of the form
in accord with the expectations from Section 2.2. We find that all the points (we excluded case A0 because we are interested in case where rA > rSM, typical of the transition from mass loaded to force free) can be approximated by a relation of the form 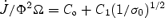 , where Co should correspond to the force free limit
, where Co should correspond to the force free limit 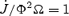 . A fit to our results gives Co= 0.98 and C1= 0.93. A similar expression can be written for the energy losses. At low σ0 the total energy loss rate scales as the mass loss rate, as expected,
. A fit to our results gives Co= 0.98 and C1= 0.93. A similar expression can be written for the energy losses. At low σ0 the total energy loss rate scales as the mass loss rate, as expected, 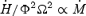 . For large σ0, the solution converges to the force free limit,
. For large σ0, the solution converges to the force free limit, 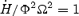 (see Fig. 3). We find that the transition between the two limits can be fit with
(see Fig. 3). We find that the transition between the two limits can be fit with 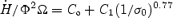 , where Co= 0.98 and C1= 2.16. We also consider the reduced energy loss rate (the difference between the total energy and the rest mass energy), and find that this too can be approximated with a power law:
, where Co= 0.98 and C1= 2.16. We also consider the reduced energy loss rate (the difference between the total energy and the rest mass energy), and find that this too can be approximated with a power law: 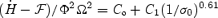 , with Co= 0.98 and C1= 0.965. We stress that these power law relations have been determined by fitting the results of our simulations. As such, there is no guarantee that these trends can be extended outside the range we investigated, but they do correspond well to the estimates given in Section 2.
, with Co= 0.98 and C1= 0.965. We stress that these power law relations have been determined by fitting the results of our simulations. As such, there is no guarantee that these trends can be extended outside the range we investigated, but they do correspond well to the estimates given in Section 2.
Loss rates for the 1D monopole calculations in non-dimensional units (Table 2). Upper panel: angular momentum loss rate. Lower panel: total energy-loss rate. Dashed curves represent the theoretical expectation for the losses in the mass loaded cases 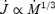 and
and 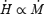 . Continuous curves represent the best power-low fit given in the text. Dotted lines are the force-free solution.
. Continuous curves represent the best power-low fit given in the text. Dotted lines are the force-free solution.
Our simulations focus on the region close to the neutron star and so the problem of the acceleration of the outflow at large distances cannot be properly addressed. However, as shown, for example, by Daigne & Drenkhahn (2002) the efficiency of conversion from magnetic to kinetic energy in the strict monopole limit is very low. Faster than radial divergence in the flux tubes is required after the FM point to increase the acceleration significantly (Section 2.1). Within our computational domain in Case I we find that the ratio of particle kinetic energy flux to electromagnetic energy flux scales approximately as r1/3 and shows a tendency towards saturation. At a radius of 300rNS in Case I, the ratio is still less than 5 per cent.
5.2 The 2D monopole
The 1D monopole discussed above does not take into account deformations of the poloidal field lines by the moving plasma. As a consequence, the conversion of magnetic energy into kinetic energy of the accelerated wind is inefficient. To understand if and how deviations from a strict monopole may affect the dynamics of the outflow it is necessary to perform 2D simulations. We focus only on the region close to the star, within 100–200rNS, and we consider both mass-loaded (σ0 < 1) and Poynting-flux-dominated (σ0 > 1) regimes (see Tables 1 and 3). In contrast to the cases considered by Bogovalov (2001), where the mass flux was fixed at rin and a cold wind (p= 0) was assumed, here the mass flux is derived self-consistently, with pressure at the base of the wind being the control parameter for the flow. Even if cT(rin) ∼ 0.1c, the difference with the pressureless case is not trivial. For example, the location of the FM point in the 1D monopole is at infinity if p= 0, so, in principle, one might expect a higher efficiency also in the 2D case. More important, in our case, the velocity at the base is much smaller that c, so that collimation in the region close to the star could be more efficient.
Results of the 2D monopole models.
| Model . | σ0 . |  .
. | 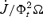 .
. | 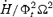 .
. | rA,equat/RL . |
|---|---|---|---|---|---|
| A | 0.121 | 98 | 1.23 | 11.9 | 0.40 |
| B | 1.00 | 119 | 1.11 | 2.28 | 0.68 |
| B1 | 1.22 | 217 | 1.05 | 1.99 | 0.70 |
| C | 9.67 | 122 | 0.755 | 0.875 | 0.92 |
| D | 68.5 | 173 | 0.678 | 0.699 | 0.98 |
| E | 211.5 | 280 | 0.671 | 0.679 | 0.99 |
| Model . | σ0 . | 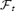 .
. | 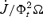 .
. | 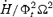 .
. | rA,equat/RL . |
|---|---|---|---|---|---|
| A | 0.121 | 98 | 1.23 | 11.9 | 0.40 |
| B | 1.00 | 119 | 1.11 | 2.28 | 0.68 |
| B1 | 1.22 | 217 | 1.05 | 1.99 | 0.70 |
| C | 9.67 | 122 | 0.755 | 0.875 | 0.92 |
| D | 68.5 | 173 | 0.678 | 0.699 | 0.98 |
| E | 211.5 | 280 | 0.671 | 0.679 | 0.99 |
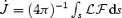 ;
; 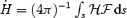 ;
; 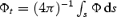 ;
; 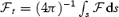 and
and 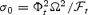 . Values are given in code units, see equations (23)–(27) for conversion to physical units. The value of
. Values are given in code units, see equations (23)–(27) for conversion to physical units. The value of 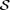 in all cases is 0.018. In all cases Ω= 0.143, except case B1 which has Ω= 0.214. rA,equat is the radial distance of the AL surface on the equatorial plane.
in all cases is 0.018. In all cases Ω= 0.143, except case B1 which has Ω= 0.214. rA,equat is the radial distance of the AL surface on the equatorial plane.
Results of the 2D monopole models.
| Model . | σ0 . | 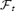 .
. | 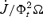 .
. | 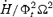 .
. | rA,equat/RL . |
|---|---|---|---|---|---|
| A | 0.121 | 98 | 1.23 | 11.9 | 0.40 |
| B | 1.00 | 119 | 1.11 | 2.28 | 0.68 |
| B1 | 1.22 | 217 | 1.05 | 1.99 | 0.70 |
| C | 9.67 | 122 | 0.755 | 0.875 | 0.92 |
| D | 68.5 | 173 | 0.678 | 0.699 | 0.98 |
| E | 211.5 | 280 | 0.671 | 0.679 | 0.99 |
| Model . | σ0 . | 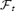 .
. | 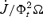 .
. | 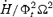 .
. | rA,equat/RL . |
|---|---|---|---|---|---|
| A | 0.121 | 98 | 1.23 | 11.9 | 0.40 |
| B | 1.00 | 119 | 1.11 | 2.28 | 0.68 |
| B1 | 1.22 | 217 | 1.05 | 1.99 | 0.70 |
| C | 9.67 | 122 | 0.755 | 0.875 | 0.92 |
| D | 68.5 | 173 | 0.678 | 0.699 | 0.98 |
| E | 211.5 | 280 | 0.671 | 0.679 | 0.99 |
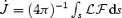 ;
; 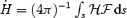 ;
; 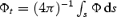 ;
; 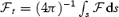 and
and 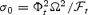 . Values are given in code units, see equations (23)–(27) for conversion to physical units. The value of
. Values are given in code units, see equations (23)–(27) for conversion to physical units. The value of 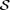 in all cases is 0.018. In all cases Ω= 0.143, except case B1 which has Ω= 0.214. rA,equat is the radial distance of the AL surface on the equatorial plane.
in all cases is 0.018. In all cases Ω= 0.143, except case B1 which has Ω= 0.214. rA,equat is the radial distance of the AL surface on the equatorial plane.
5.2.1 Magnetic, mass-loaded winds
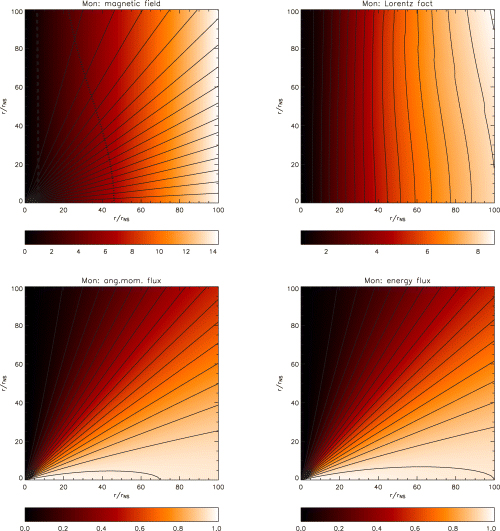
In Fig. 4 we show the results for a heavily mass-loaded case (Case A) corresponding to a 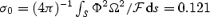 , where the integration is performed over 4π solid angle.
, where the integration is performed over 4π solid angle.
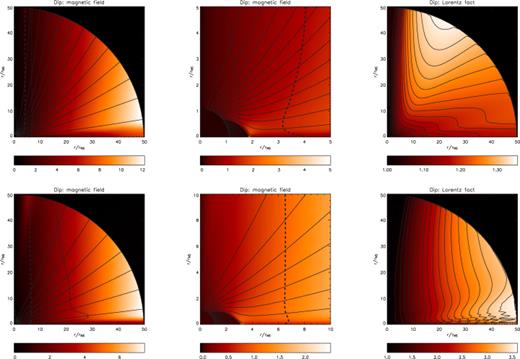
Results for the 2D monopole in the weakly magnetized Case A (Table 3). Upper left-hand panel: contours represent poloidal magnetic field lines, while colours represent the ratio |Bφ/Br|. Upper right-hand panel: colours and contour represent the Lorentz factor. Notice the presence of a slow channel on the axis and the peak in velocity at about 70°. Lower left-hand panel: angular momentum flux in adimensional units 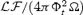 . Lower right-hand panel: total energy flux
. Lower right-hand panel: total energy flux 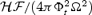 in non-dimensional units (see equations 23–27 for conversion in physical units). Note that these fluxes peak at high latitudes (compare with Fig. 5).
in non-dimensional units (see equations 23–27 for conversion in physical units). Note that these fluxes peak at high latitudes (compare with Fig. 5).
At rin the mass flux profile scales approximately as sin2θ, and is minimal at the pole. As a result of magnetic acceleration and centrifugal support at the equator, the mass flux is higher than in the corresponding 1D hydrodynamical non-rotating case and it is about the same as in the 1D monopole. However, at the pole the mass flux is lower because of magnetic collimation on the axis (Kopp & Holzer 1976). The large difference in mass flux between pole and equator is manifest in the elongated shape of the FM surface. The upper left-hand panel of Fig. 4 shows that the field lines are very close to radial and that Bφ scales approximately as sin θ. At the pole, the FM surface falls outside of the computational domain, whereas the FM surface intersects the equatorial plane at 5.2rNS(rin= 1.1rNS).
The SM surface also has a large axis ratio: it intersects the pole at a distance of 11rNS and it intersects the equator at 1.8rNS. It is interesting to look also at the position of the AL surface. Its distance from the Light Cylinder RL is an indicator of how close the solution is to the force-free limit and it strongly reflects the degree of magnetization. While on the axis where Bφ= 0 the AL and FM surfaces are coincident, away from the pole the toroidal field component does not vanish and the two critical curves separate. The AL surface intersects the equator at a distance of about 2.7rNS (to be compared with RL= 6.8rNS).
One might expect the Lorentz factor to be largest in the equatorial region, as a result of stronger magnetocentrifugal effects there. However, contrary to this expectation, we observe that γ peaks at about 70°. Such a result was also obtained by Bogovalov (2001) for cold flows. This effect is stronger in our calculations because of the lower overall Lorentz factor. We also notice the existence of a very slow channel along the axis. We want to stress that the FM surface is outside the computational domain within 3° of the axis, and so the solution has not converged fully in this region. However, by increasing the radial computational domain, we find that the main effect of failing to capture the FM surface at the pole is that the wind in this region is less collimated and somewhat faster than it should be. So we expect the wind to be more collimated and slower, with yet larger computational grids. Whether the FM surface is inside the computational domain at the pole or not has relatively little effect on those streamlines at lower latitudes that do pass through the FM point. Typical deviations are found to be less than 1 per cent.
As the lower panels of Fig. 4 show, we find that both the energy flux (which is mainly kinetic) and the angular momentum flux peak at high latitudes. In addition, the mass flux at large distance from the neutron star is higher close to the axis because of magnetic collimation. In contrast, the conversion of electromagnetic energy to kinetic energy is maximal along the equator, even though in this mass-loaded low-σ0 case the electromagnetic energy flux is lower than kinetic energy flux, and the wind terminal Lorentz factor is mainly given by the conversion of internal energy to kinetic energy.
5.2.2 Poynting-flux-dominated winds
In Fig. 5, we show the results for a Poynting-flux-dominated flow (Case E), corresponding to a ratio 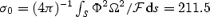 , where the integration is again performed over 4π solid angle. In this case the solution is mostly magnetically driven, and plasma effects lead to small deviations with respect to the force-free limit.
, where the integration is again performed over 4π solid angle. In this case the solution is mostly magnetically driven, and plasma effects lead to small deviations with respect to the force-free limit.
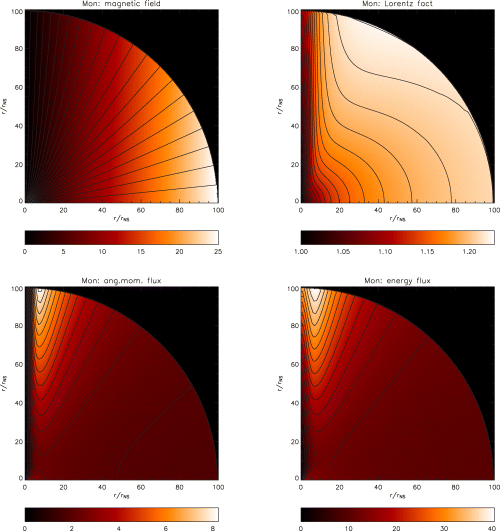
Results for the 2D monopole in the highly magnetized Case E (Table 3). Upper left-hand panel: contours represent poloidal magnetic field lines, while colours represent the ratio |Bφ/Br|. The FM surface (dotted line) is more distant from the axis while the AL surface (dashed line) is very close to the Light Cylinder. Upper right-hand panel: colours and contours represent the Lorentz factor. There is no evidence here of the relatively slow channel on the axis as in Case A (see Fig. 4) and the Lorentz factor scales as sin (θ). Lower left-hand panel: angular momentum flux in non-dimensional units 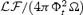 . Lower right-hand panel: total energy flux
. Lower right-hand panel: total energy flux 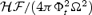 in non-dimensional units (see equations 23–27 for conversion in physical units). Here, these fluxes are higher at the equator than at the pole (compare with Fig. 4), as expected when the flow is relativistic and Poynting-flux-dominated.
in non-dimensional units (see equations 23–27 for conversion in physical units). Here, these fluxes are higher at the equator than at the pole (compare with Fig. 4), as expected when the flow is relativistic and Poynting-flux-dominated.
Similar to the mass-loaded Case A, at the neutron star surface we find that the mass flux is higher at the equator than at the pole, and that the AL and FM surfaces are extended in the direction of the pole. Here, the FM and AL surfaces intersect the equatorial plane at a distance of 46rNS (to be compared with 40.5 =σ1/30RL) and 6.7rNS, respectively, while the SM surface is more spherical than Case A and intersects the pole and the equator at a distance of 2.5rNS and 1.7rNS, respectively. Magnetic field lines are again monopolar, but while in the mass-loaded Case A this was a consequence of a originally centrifugally driven wind, now this is due to electromagnetic force balance. The dynamics of a magnetized outflow are governed by the combination of Lorentz and Coulomb forces. In the relativistic regime the Coulomb force cannot be neglected and, as the flow speed approaches c, the Coulomb force balances the Lorentz force, suppressing collimation. As a consequence, the flux tubes in a Poynting-flux-dominated wind have an areal cross-section that scales as r2. It is known that the efficiency of conversion of magnetic energy to kinetic energy increases when the flow divergence becomes more than radial (Daigne & Drenkhahn 2002). In the high-σ0 simulation presented here, at least within the limited computational domain employed, we do not see evidence for efficient conversion and acceleration. As found by (Bogovalov 2001) there is evidence for a narrow collimated channel very close to the axis, but in our case, where the mass flux at the injection is not imposed, the mass flux in the channel is not strongly enhanced. However, the FM surface on the axis does not close in our computational box so no strong conclusion can be drawn.
The upper right-hand panel of Fig. 5 shows that the Lorentz factor in the wind scales approximately as sin θ. The maximum value achieved in the computational domain is 8. The latitude dependence is not appreciable, probably because our solution does not extend far enough away from the star. As in the 1D models, for the range of parameters investigated, the total mass flux from the star is not much affected by the value of the surface magnetic field. For the Poynting-flux-dominated Case E it is about three times higher than in the mass-loaded Case A, despite the fact that the magnetic energy density is 5000 times higher. This again follows from the fact that the AL surface is larger than the SM surface. However, there are important qualitative differences between Cases A and E. In Case E, we find that on large scales magnetic acceleration is dominant and the mass flux is maximal on the equator, instead of on the axis. In addition, the lower panels of Fig. 5 show that the energy and angular momentum fluxes increase toward the equatorial plane and are almost completely magnetically dominated. In fact, the energy and angular momentum loss rates scale as sin2θ, as expected in the force-free limit. This strong transition in the angular dependence of the energy and momentum fluxes, from strongly collimated to equatorial, occurs at σ0∼ 1.
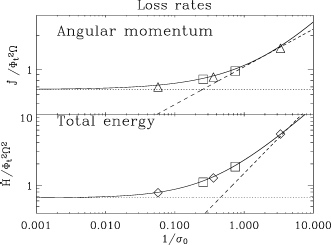
Fig. 6 shows the behaviour of the angular momentum and energy losses as σ0 increases. We again observe the convergence to the force-free limit (see also Table 3) and recover the expected behaviour 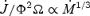 in the mass-loaded cases. The convergence to the force-free solution can be approximated, as in the 1D case, with a power law of the form Co+C1(1/σ0)β. The fits are different than the 1D models because the flux tubes deviate from being strictly monopolar. We find for the angular momentum loss rate
in the mass-loaded cases. The convergence to the force-free solution can be approximated, as in the 1D case, with a power law of the form Co+C1(1/σ0)β. The fits are different than the 1D models because the flux tubes deviate from being strictly monopolar. We find for the angular momentum loss rate 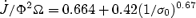 , for the total energy losses
, for the total energy losses 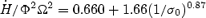 , and for the reduced energy
, and for the reduced energy 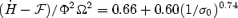 . As mentioned before, we have derived these fits within the parameter range of our simulations, and there is no guarantee that they can be extrapolated for much higher or lower magnetizations. We stress that in the highly magnetized Case E our results are very close to the force-free solution:
. As mentioned before, we have derived these fits within the parameter range of our simulations, and there is no guarantee that they can be extrapolated for much higher or lower magnetizations. We stress that in the highly magnetized Case E our results are very close to the force-free solution: 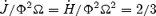 (Michel 1991). Note also that such a value is lower than what would be expected from a trivial 2D extension of the 1D monopole (0.78 =
(Michel 1991). Note also that such a value is lower than what would be expected from a trivial 2D extension of the 1D monopole (0.78 =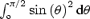 ).
).
Loss rates for a 2D monopole in non-dimensional units. Upper panel: angular momentum loss rate. Lower panel: total energy-loss rate. Dashed curves represent the theoretical expectation for the losses in the mass loaded cases 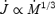 (Section 2.2) and
(Section 2.2) and 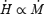 . Continuous curves represent the best power-low fit given in the text. The dotted lines are the force-free limits. The square mark indicates Case B1, which has a different rotation rate (Table 1).
. Continuous curves represent the best power-low fit given in the text. The dotted lines are the force-free limits. The square mark indicates Case B1, which has a different rotation rate (Table 1).
The efficiency of conversion of the magnetic energy to kinetic energy is maximal on the equator, but it does not exceed 10 per cent at the outer boundary. We note that conversion is faster than logarithmic in radius and at the edge of the computational box it scales as R1/3, similar to our 1D results. However, we cannot draw strong conclusions on the terminal efficiency far outside of the FM surface because of the limited size of our computational domain. As shown by Bogovalov (2001), γ seems to increase after the FM point and then saturates at larger distances.
5.3 The aligned dipole
To lowest order, currents in the neutron star should generate a dipole magnetic field. This field configuration is much more realistic than the monopolar models considered in Sections 5.1 and 5.2. A dipole field may also have interesting consequences for the asymptotic character of the outflow. For example, it is possible that the presence of a closed zone, outside of which the open field lines at first expand much more rapidly than radially, might provide for a more efficient conversion of magnetic energy into kinetic energy, leading to a higher terminal Lorentz factor (Section 1). Below, we review several numerical issues associated with our dipole wind solutions and then we present our results, which again bridge the transition from low- to high-σ0 outflows.
5.3.1 Numerical challenges
The modelling of a magnetic wind with a closed zone and an equatorial current sheet presents a number of numerical difficulties. We have encountered two problems in particular that bear mention. The first is that the outer edge of the closed zone rotates faster than what is required by equation (19). We believe this ‘supercorotation’ is connected with numerical dissipation in the equation for the evolution of Bφ and that it stems from the fact that the boundary between the closed and open field regions is not grid-aligned.4 By suppressing the upwinding term in the HLL flux we were able to reduce the deviation from the corotation condition from 10–20 per cent to ∼5 per cent, but at the price of making the code less stable when the flow is highly magnetized. Unfortunately, of the previous papers dealing with winds in the presence of a closed zone in the MHD regime, only Keppens & Goedbloed (2000) discuss deviations from corotation in the closed zone. In their paper these amount to ∼10–20 per cent, and they consider only parameters appropriate to the Sun, a slow rotator.
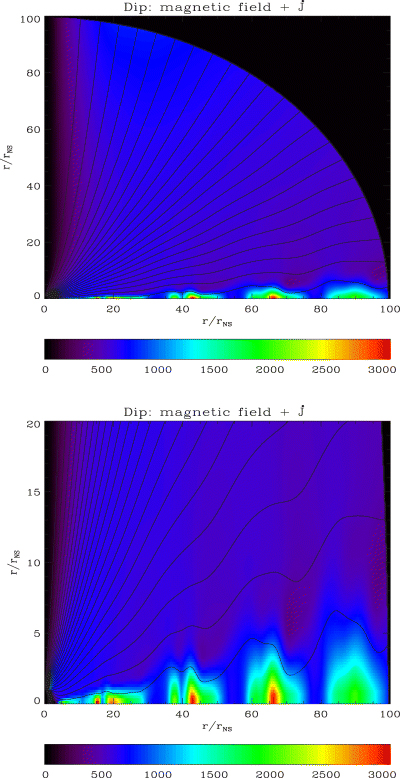
The second problem is that the magnetic field undergoes reconnection at the neutral current sheet on the equator close to the position of the Y-point, where the last closed field line intersects the equatorial plane. As a consequence, plasmoids are formed and advected away, thus preventing the system from reaching a steady-state configuration.5 At the current sheet Br and Bφ change sign, the MHD approximation fails, and a sharp discontinuity develops that cannot be well resolved. Fig. 7 shows an example of plasmoid formation. Although it is well known that current sheets in the presence of a Y-type point are subject to reconnection and the continuous formation of plasmoids (Yin et al. 2000; Endeve & Leer 2003; Tanuma & Shibata 2005), in our case the high value of σ0 does not allow us to properly resolve the current sheet. For this reason, the reconnection processes are dominated by the intrinsic numerical resistivity of our numerical scheme.
Magnetic structure of a magnetically dominated flow (Case C). The upper panel shows the poloidal magnetic field structure, with a snapshot of outflowing plasmoids forming along the equatorial current sheet outside the closed zone. The lower panel shows a blow up of these plasmoids, which travel out at close to the speed of light. The colour indicates the angular momentum density, with roughly 20 per cent of the angular momentum loss being carried by these intermittent structures. Values are in code units (equations 23–27). As stated in the text, the numerical values in the plasmoids depend on numerical resistivity.
We have found that the formation and growth of plasmoids depends on two terms in the definition of the HLL electric field (see equation 44 of Del Zanna et al. 2003): ∂Br/∂θ and Brvθ. The first behaves like an explicit resistivity and seems responsible for the evolution of the plasmoids as they are advected off the grid along the equator. The second term behaves like forced reconnection and controls the initiation of plasmoid formation (given that the current sheet is not resolved, vθ is not reconstructed to zero on the equator). Setting both terms to zero causes the closed zone to disappear entirely and the system evolves toward a modified split monopole. To deal with this issue and explicitly enforce a steady state, we opt for the following procedure: in a calculation with plasmoids we note the position of the Y-point and we then impose the conditions ∂Br/∂θ= 0 and Brvθ= 0 on the equator outside the position of the Y-point as inferred from the calculation without these boundary conditions. The condition ∂Br/∂θ= 0 can be justified because of the structure of the characteristic waves and because the solution should be symmetric about the equatorial plane. The equator is a contact discontinuity, so only the total pressure is important as a boundary conditions and not the sign of the parallel magnetic field, in fact for infinite conductivity a pure monopole and a split monopole have the same solution. The condition Brvθ= 0 corresponds to enforcing vθ= 0.
We note that the steady state solution need not be the physically correct solution found in nature. The equatorial current sheet in the vicinity of a neutron star is undoubtedly dissipative, and is thus subject to reconnection and plasmoid formation. However, a full understanding of this behaviour requires – at the very least – the use of resistive RMHD, so that the dissipation can be controlled, rather than being fully numerical, as in our current calculations. Such a treatment is beyond the scope of this paper. Thus, we focus our attention here on the forced steady state solutions described above. As a test, we have compared the global energy and angular momentum loss rates between time-dependent calculations with plasmoids and those with our forced steady state boundary conditions outside the Y-point. In general, losses are higher in the latter calculations because the open magnetic flux is larger. In Case A the difference is less than 5 per cent, while in Case C it is about 15–20 per cent (see Table 4 and Fig. 8). In the time-dependent calculations the individual plasmoids represent fractional deviations in 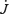 and
and 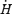 from the average of up to 15 per cent in Case C, and less for lower σ0 flows. Thus, the plasmoids do not appear to be that dynamically significant for the overall energy and angular momentum losses from the neutron star.
from the average of up to 15 per cent in Case C, and less for lower σ0 flows. Thus, the plasmoids do not appear to be that dynamically significant for the overall energy and angular momentum losses from the neutron star.
Results of the dipole models.
| Model . | σ0 . |  .
. | 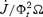 .
. | 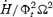 .
. | rY/RL . |
|---|---|---|---|---|---|
| A | 0.298 | 66 | 1.53 | 5.28 | 0.26 |
| B2 | 1.34 | 7.8 | 0.965 | 1.81 | 0.32 |
| B | 2.77 | 43 | 0.853 | 1.27 | 0.37 |
| B1 | 3.91 | 114 | 0.816 | 1.10 | 0.48 |
| C | 17.5 | 42 | 0.701 | 0.73 | 0.47 |
| Model . | σ0 . |  .
. | 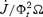 .
. | 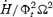 .
. | rY/RL . |
|---|---|---|---|---|---|
| A | 0.298 | 66 | 1.53 | 5.28 | 0.26 |
| B2 | 1.34 | 7.8 | 0.965 | 1.81 | 0.32 |
| B | 2.77 | 43 | 0.853 | 1.27 | 0.37 |
| B1 | 3.91 | 114 | 0.816 | 1.10 | 0.48 |
| C | 17.5 | 42 | 0.701 | 0.73 | 0.47 |
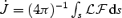 ;
; 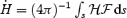 ;
; 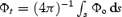 ;
; 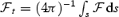 and
and 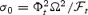 . Values are given in code units, see equations (23)–(27) for conversion to physical units. Cases B1 and B2 have different rotation rates (Table 1). All cases have
. Values are given in code units, see equations (23)–(27) for conversion to physical units. Cases B1 and B2 have different rotation rates (Table 1). All cases have 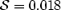 .
.
Results of the dipole models.
| Model . | σ0 . | 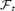 .
. | 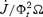 .
. | 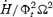 .
. | rY/RL . |
|---|---|---|---|---|---|
| A | 0.298 | 66 | 1.53 | 5.28 | 0.26 |
| B2 | 1.34 | 7.8 | 0.965 | 1.81 | 0.32 |
| B | 2.77 | 43 | 0.853 | 1.27 | 0.37 |
| B1 | 3.91 | 114 | 0.816 | 1.10 | 0.48 |
| C | 17.5 | 42 | 0.701 | 0.73 | 0.47 |
| Model . | σ0 . |  .
. | 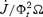 .
. | 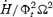 .
. | rY/RL . |
|---|---|---|---|---|---|
| A | 0.298 | 66 | 1.53 | 5.28 | 0.26 |
| B2 | 1.34 | 7.8 | 0.965 | 1.81 | 0.32 |
| B | 2.77 | 43 | 0.853 | 1.27 | 0.37 |
| B1 | 3.91 | 114 | 0.816 | 1.10 | 0.48 |
| C | 17.5 | 42 | 0.701 | 0.73 | 0.47 |
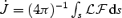 ;
; 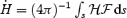 ;
; 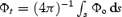 ;
; 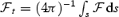 and
and 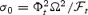 . Values are given in code units, see equations (23)–(27) for conversion to physical units. Cases B1 and B2 have different rotation rates (Table 1). All cases have
. Values are given in code units, see equations (23)–(27) for conversion to physical units. Cases B1 and B2 have different rotation rates (Table 1). All cases have 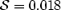 .
.
Loss rates for a 2D dipole in non-dimensional units. Upper panel: angular momentum loss rate. Lower panel: total energy-loss rate. Dashed curves represent the theoretical expectation for the losses in the mass loaded cases 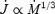 and
and 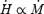 . Continuous curves represent the best power-law fit of the 2D monopole of Fig. 6. The dotted lines are the force-free solution. The squares mark cases B1 and B2, which have different rotation rates (see Table 1).
. Continuous curves represent the best power-law fit of the 2D monopole of Fig. 6. The dotted lines are the force-free solution. The squares mark cases B1 and B2, which have different rotation rates (see Table 1).
5.3.2 Results
 and Ω are known. We find that in all our cases the relation is
and Ω are known. We find that in all our cases the relation is 
Thus, the problem of relating the surface magnetic field to the loss rates is reduced to the problem of determining the size of the closed zone.
In Fig. 8, the angular momentum and energy-loss rates are plotted. The continuous lines in this figure are not a fit to our dipole results, but are simply the same curves as in Fig. 6 for the 2D monopole. In addition, as in Fig. 6, the dashed lines are the analytic expectation for the loss rates in the mass-loaded limit for the monopole (Section 2.2). This shows that if the solutions are parametrized in terms of the open magnetic flux, then the dipole and monopole winds have very similar behaviour within the parameter space we have investigated. This can be easily understood if one considers the structure of the outflow in the far region. Given that 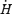 and
and 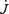 are integrals, they can be evaluated at any distance from the star. Even if the field is dipolar close to the star it is nearly monopolar outside RL. Even when we do not impose our steady-state boundary conditions at the equator, and plasmoids are present during the evolution,
are integrals, they can be evaluated at any distance from the star. Even if the field is dipolar close to the star it is nearly monopolar outside RL. Even when we do not impose our steady-state boundary conditions at the equator, and plasmoids are present during the evolution, 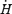 and
and 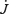 closely follow our results for the monopole (again, as long as these losses are written in terms of the open magnetic flux). Note also that in Fig. 8, we find that
closely follow our results for the monopole (again, as long as these losses are written in terms of the open magnetic flux). Note also that in Fig. 8, we find that 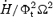 and
and 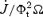 converge to the expected value of 2/3 in the force-free limit (Contopoulos et al. 1999; Gruzinov 2005). However, as we discuss below, rY < RL in all of our calculations, contrary to the assumption that rY=RL in the above force-free treatments.
converge to the expected value of 2/3 in the force-free limit (Contopoulos et al. 1999; Gruzinov 2005). However, as we discuss below, rY < RL in all of our calculations, contrary to the assumption that rY=RL in the above force-free treatments.
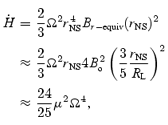
in agreement with Gruzinov (2005).
The flow structure for both low σ0 (Case A) and high σ0 (Case C) are shown in Fig. 9. These figures show that the poloidal magnetic field for R > RL has a structure very similar to that obtained from the monopole calculations. Also, Bφ scales as sin θ, except in a region close to the equatorial plane where it changes sign. This agrees with the results of Fig. 8 showing that the energy and angular momentum losses scale as for a monopole.
Result of the 2D dipole. Upper panels represent Case A, lower panels Case C. Left-hand panel: contours represents poloidal magnetic field lines, while colours represent the ratio Bφ/Br. The dotted line is the FM surface, the dashed line the AL surface. In Case C the AL surface is close to RL. Middle panel: contours represents poloidal magnetic field lines, while colours represent the ratio Bφ/Br, in a region closer to the star. Now the dotted line represents the SM surface. Right-hand panel: colours and contour represent the Lorentz factor.
As expected, we find that the size of the closed region increases with magnetization. The position of the Y-point moves from 1.8rNS in Case A, to 2.5rNS in Case B, to 3.1rNS in Case C. Thus, an increase in σ0 of a factor of ∼60 corresponds to a ∼70 per cent increase in the size of the closed zone. Importantly, even at relatively high σ0 (∼18 for Case C), these values are significantly smaller than the Light Cylinder radius RL= 6.8rNS. In order to understand the systematics of the Y-point, we have calculated several models with different rotation rates Ω (see Tables 1 and 4). The radius of the Y-point changes from 2.2rNS in Case B1, to 2.5rNS in Case B, to 4.3 rNS in Case B2. Although rY is largest in the model with slowest rotation (Case B2), this model has the smallest ratio rY/RL. Indeed, we find that rY/RL decreases as Ω decreases. This trend yields a braking index less than 3. If one takes Cases B1, B and B2 as a time-series in the life of a neutron star, one would infer a braking index ∼2.2.
In general, the size of the closed zone will depend on the physical conditions at the stellar surface, including the thermal sound speed and the mass density, which govern the mass-loss rate on each open streamline (see Section 2.1; Mestel & Spruit 1987). This shows that even a small thermal pressure can have an important effect on the torque. Fig. 9 shows that in Case A both the AL and the FM surfaces are inside the radius of the Light Cylinder. However, in the high-σ0 Case C the AL surface is very close to RL. This suggests that although the AL surface rapidly approaches RL as σ0 increases, the position of the Y-point remains inside RL and is a weak function of σ0. It is thus possible to produce a relativistic outflow, even if the Y-point is well inside RL. Because the range of parameters we have explored is fairly limited, we can only conclude that quite large magnetization is required to achieve rY=RL. A rough extrapolation of our results implies that Br(rin, θ= 0)2/ρ(rin) must be of order 105–106 to achieve rY≈RL, but at the moment we deem premature to draw strong conclusions.
We stress here that the magnetization parameter σ0 is defined as an integral average. It is known that in a dipolar field geometry with sub-SM injection, the mass flux at the edge of the closed zone is higher than the average integrated value over the entire star (Kopp & Holzer 1976). Thus, the magnetization varies from high to low latitudes. For example, in our Case C the magnetization on the open flux tubes immediately adjacent to the closed zone is less than 7, while the σ0 parameter for this model is 17.5. Because the position of the Y-point and the shape of the magnetosphere depend on local equilibrium between the closed and open zones, this strong variation in magnetization in latitude may help explain why even if the global flow has σ0≫ 1, rY is less than RL.
The upper and lower far right-hand panels of Fig. 9 show that for the Lorentz factor we recover similar behaviour as for the monopole (compare with Figs 4 and 5). In Case A, the Lorentz factor reaches its maximum at about 70° from the equator. We also notice that there is now a slower equatorial flow corresponding to what is known as the ‘slow solar wind’ in models of the Sun's outflow. In Case C the Lorentz factor appears to scale mostly as the cylindrical radius. This again was found for the monopole. The slow-wind region is still present, but now the boundary conditions we have imposed on the equator to suppress the plasmoids cause a noisy structure in vr.
The shape of the field lines outside the FM surface does show significant differences between the monopole and the dipole. In the dipolar Case C at r= 50rNS the maximum value of Bθ/Br=−0.06. Such a value for this ratio is in between Cases C (−0.08) and D (−0.03) for the 2D monopole. Our limited computational domain prohibits a more quantitative study of the poloidal field line shape at still larger distances from the neutron star.
Lastly, the angular distribution of the energy and momentum loss rates in our dipole models are qualitatively similar to those we obtained for the 2D monopole (see the bottom panels of Figs 4 and 5). For low-σ0 outflows, because of hoop stress, 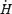 and
and  far from the neutron star are peaked at high latitudes, along the axis of rotation. In contrast, for high-σ0 outflows,
far from the neutron star are peaked at high latitudes, along the axis of rotation. In contrast, for high-σ0 outflows, 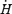 and
and 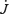 are maximum near the equator, similar to Fig. 5 (Case E).
are maximum near the equator, similar to Fig. 5 (Case E).
6 DISCUSSION AND CONCLUSIONS
We have solved for the dynamics of time-dependent relativistic MHD winds from rotating neutron stars, including the effects of general relativity on the gravitational force. The mass-loss rate along open field lines is derived self-consistently as a solution to the RMHD equations, subject to the boundary conditions at the stellar surface (finite thermal pressure) and a polytropic equation of state. We consider 1D and 2D monopole field geometries and the aligned dipole, and we explore solutions that cover the parameter regime from non-relativistic mass-loaded low-σ0 outflows to relativistic Poynting-flux-dominated high-σ0 outflows. Our primary results are
- (i)
In the 1D and 2D monopole calculations, we reproduce the expected analytic trends in both the high- and low-σ0 limits. In particular, the solutions asymptotically approach the force-free limit when σ0≫ 1.
- (ii)
In both the dipole and 2D monopole solutions, when σ0 < 1, the energy and momentum losses far from the neutron star are highly directed along the axis of rotation. The zenith angle at which these fluxes are maximized is an increasing function of σ0 so that for σ0 > 1, the losses are primarily equatorial.
- (iii)
In both the dipole and 2D monopole solutions, for winds with σ0 < 1, the Lorentz factor peaks at high latitudes.
- (iv)
For the aligned dipole, the equatorial current sheet may be unstable to the formation of plasmoids, leading to time-dependent spindown of the neutron star. A proper treatment of dissipative RMHD in the equatorial region is needed to explore this issue more completely.
- (v)
If the energy and angular momentum losses from the aligned dipole are parametrized in terms of the open magnetic flux, then the results are nearly identical to those from the 2D monopole solutions in both the mass-loaded and Poynting flux-dominated regimes. In particular, the dipole calculations quantitatively approach the force-free limit when σ0≫ 1. The normalization for the angular momentum loss rate is k≈ 24/25 (equation 29), in good agreement with the force-free results found by Gruzinov (2005) and Spitkovsky (2006).
- (vi)
For average integrated magnetization parameters as high as σ0≈ 20, the radial position of the Y-point (rY), which bounds the closed zone in the dipole models, is significantly less than the Light Cylinder distance. This result obtains despite the fact that the AL point rapidly approaches RL for σ > 1. The ratio rY/RL is a very slowly increasing function of the surface magnetic field strength. An extrapolation of our results indicates that σ0 must be very large, σ0≫ 100, for the Y-point to reach the Light Cylinder. That rY is generically much less than RL in our calculations is due in part to the fact that although σ0≈ 20 globally (Case C, Section 5.3) the magnetization along the open field lines nearest the closed zone is less than 7.
- (vii)
Over limited dynamic range, the ratio rY/RL decreases as ω decreases in the dipole models. This behaviour is consistent with a braking index less than 3 (see Sections 2.1 and 6.1).
Concerning the acceleration of the wind, we do not find any evidence for efficient magnetic to kinetic energy conversion. However, we want to stress again that our computational box does not extend far enough from the star to appreciably probe the asymptotic behaviour of the wind.
6.1 Rotation-powered pulsars
Our results have several possible implications for rotation-powered pulsars, where σ0 is high. The fact that the Y-point is interior to the Light Cylinder (and the Alfven radius) suggests that observed braking indices less than 3 might be a consequence of equilibrium magnetospheric structure. We emphasize that the position of the Y-point depends on a local equilibrium between the surface of the closed zone and the wind region. As a consequence, the value of the mass flux along the open field lines closest to the closed zone directly affects the position of the Y-point. The mass flux, in turn, depends on the boundary conditions at the stellar surface. In our simulations, the mass-loss rate is derived self-consistently, subject to a finite thermal pressure at rNS. In the case of a pulsar, the injection of matter at rNS is thought to be due to non-MHD pair creation processes (Hibschman & Arons 2001) in a ‘gap’ just above the stellar surface which, in an otherwise MHD flow, act to inject plasma with velocity already exceeding the sound speed. Then the mass-loss rate is determined by the gap physics, not by the requirement of making a smooth transition from subsonic to supersonic flow. Thus, in principle rY depends upon the injection law determined by the pair creation physics at the surface. For this reason, we caution against overinterpreting our results (vi) and (vii) in the pulsar context. Indeed, thermal pressure of the magnitude employed here is not likely to be relevant for classical pulsars.6 On the other hand, magnetic dissipation and reconnection at and near the Y-point might cause pressure and inertial forces to be significant in this localized region. In any case, our primary conclusions, that rY/RL is generally less than unity and that rY/RL decreases as Ω decreases, are intriguing possibilities now open to investigation with the advent of dynamical, large σ models of neutron star magnetopsheres. A more general study of the effect of the injection conditions on the structure of the magnetosphere and the accompanying wind is under way.7
The appearance of outwardly propagating plasmoids at and beyond the Y-point as a consequence of (numerical) magnetic dissipation raises the intriguing possibility that noise in pulsar spindown (Cordes & Helfand 1980) might arise from instability of the magnetospheric currents due to real magnetic dissipation (e.g. via the collisionless tearing instability). Our results show the possibility of 20 per cent or more torque fluctuations that could in principle give rise to a random walk in the rotation frequencies of pulsars, as is observed. Likewise, such torque fluctuations might give rise to noise and limit cycles in the observed phase of the subpulses of pulsars, as is seen in many systems (Rankin 1986; Deshpandhe & Rankin 1999). Determining whether these observed phenomena could be due to magnetospheric dissipation requires treating the dissipation with a consistent physical model, which is an investigation beyond that reported in this paper.
6.2 Proto-neutron stars and proto-magnetars
High thermal pressure at the neutron star surface is thought to be a generic feature of neutron star birth and so the calculations presented in this paper are directly relevant to young neutron stars, particularly in the hypothesized rapidly rotating and highly magnetic initial state of magnetars.
We identify five separate phases in the life of any very young neutron star: (1) a pressure-dominated essentially non-magnetic phase in which the wind is driven by neutrino-heating (as in e.g. Qian & Woosley 1996); (2) a phase in which magnetic field effects are present, but not dominant so that rAω < 0.1c≈cT, where cT is the isothermal sound speed at the proto-neutron star surface; (3) a non-relativistic magnetically dominated phase when RA is greater than rNS, but less than RL; (4) a relativistic phase in which RA∼RL, but rY < RL, and lastly (5) an epoch when the force-free limit is applicable and rY≃RA≃RL. Phases (1)–(5) represent a time evolution starting immediately after the supernova explosion commences. The time-scale for the evolution from phase (1) to phase (4) is set by the Kelvin–Helmholtz time-scale for cooling of the proto-neutron star, τKH∼ 10–100 s. The transition from phase (4) to phase (5) may occur on a longer time-scale, or not at all, depending upon the applicability of our results to classical pulsars as the MHD approximation breaks down.
For parameters appropriate to a proto-magnetar, phase (3) lasts of the order of τKH. Our simulations show that in this phase, the wind is energetic and that the energetic flux is highly directed along the axis of rotation. The characteristic rotational energy-loss rate in this phase is 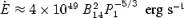 , where B14=B(rNS)/1014 G is the ‘equivalent’ monopole field (equation 28), and P1=P/1 ms. On the time-scale τKH, the total amount of energy extracted is comparable to the asymptotic supernova energy, ∼1051 erg. The magnitude of the rotational energy extracted in this phase and its collimation along the rotational axis should have profound implications both for the spindown of millisecond magnetars and for the supernova remnants that accompany their birth. We save a detailed discussion for a future paper.
, where B14=B(rNS)/1014 G is the ‘equivalent’ monopole field (equation 28), and P1=P/1 ms. On the time-scale τKH, the total amount of energy extracted is comparable to the asymptotic supernova energy, ∼1051 erg. The magnitude of the rotational energy extracted in this phase and its collimation along the rotational axis should have profound implications both for the spindown of millisecond magnetars and for the supernova remnants that accompany their birth. We save a detailed discussion for a future paper.
We thank Prof S. S. Komissarov, for providing us with a wave based Riemann solver, to verify effects of numerical diffusion in our 2D dipole calculations. Part of this work was done while N. B. and J. A. were in residence at the Kavli Institute for Theoretical Physics, with partial support from NSF Grant No. PHY99-07949. NB and JA were also supported in part by NASA grants TM4-5000X and NAG5-12031, and by NSF grant AST-0507813 to the University of California, Berkeley. EQ was supported in part by the David and Lucile Packard Foundation. TAT was supported during most of this work by NASA through Hubble Fellowship grant #HST-HF-01157.01-A awarded by the Space Telescope Science Institute, operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS 5-26555.
REFERENCES
Appendix
APPENDIX A: PARAMETRIZATION OF THE MODELS
All the simulations can be parametrized in terms of the ratios of characteristic velocities at the injection radius (rin), see Table A1. Following the work by Mestel (1968a) and Goldreich & Julian (1970), these are essentially the sound speed cT, the rotational velocity vφ, the non relativistic AL velocity 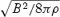 , and the escape speed
, and the escape speed 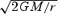 . For the 2D cases we consider the value of the rotational velocity and the magnetic field at the equator. Note that the characteristic velocities defined above do not coincide with the cited works in Newtonian gravity. For example, the escape speed differs by a factor of
. For the 2D cases we consider the value of the rotational velocity and the magnetic field at the equator. Note that the characteristic velocities defined above do not coincide with the cited works in Newtonian gravity. For example, the escape speed differs by a factor of 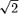 , and in the definition of vφ one must include the effect of time delay. These are corrections due to the general relativistic metric which are not present in the above cited papers (α(rin) = 0.79).
, and in the definition of vφ one must include the effect of time delay. These are corrections due to the general relativistic metric which are not present in the above cited papers (α(rin) = 0.79).
Parametrization of the numerical models.
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
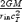 | 11.44 | 11.44 | 6.74 | 7.54 | 8.98 | 10.45 | 11.44 | 6.29 | 6.29 | 6.29 |
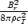 | 0.061 | 0.61 | 0.71 | 0.80 | 0.95 | 1.11 | 60.6 | 133 | 533 | 1330 |
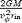 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
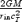 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | ||||
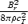 | 0.61 | 6.1 | 6.1 | 60.6 | 606 | 3030 | ||||
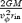 | 9.43 | 9.43 | 4.20 | 9.43 | 9.43 | 9.43 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
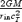 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | |||||
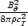 | 1.22 | 12.2 | 12.2 | 12.2 | 122 | |||||
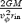 | 9.43 | 9.43 | 4.20 | 38.5 | 9.43 | |||||
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
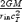 | 11.44 | 11.44 | 6.74 | 7.54 | 8.98 | 10.45 | 11.44 | 6.29 | 6.29 | 6.29 |
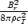 | 0.061 | 0.61 | 0.71 | 0.80 | 0.95 | 1.11 | 60.6 | 133 | 533 | 1330 |
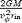 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
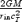 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | ||||
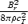 | 0.61 | 6.1 | 6.1 | 60.6 | 606 | 3030 | ||||
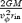 | 9.43 | 9.43 | 4.20 | 9.43 | 9.43 | 9.43 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
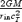 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | |||||
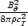 | 1.22 | 12.2 | 12.2 | 12.2 | 122 | |||||
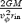 | 9.43 | 9.43 | 4.20 | 38.5 | 9.43 | |||||
Parametrization of the numerical models.
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
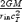 | 11.44 | 11.44 | 6.74 | 7.54 | 8.98 | 10.45 | 11.44 | 6.29 | 6.29 | 6.29 |
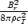 | 0.061 | 0.61 | 0.71 | 0.80 | 0.95 | 1.11 | 60.6 | 133 | 533 | 1330 |
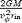 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
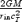 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | ||||
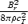 | 0.61 | 6.1 | 6.1 | 60.6 | 606 | 3030 | ||||
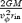 | 9.43 | 9.43 | 4.20 | 9.43 | 9.43 | 9.43 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
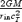 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | |||||
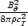 | 1.22 | 12.2 | 12.2 | 12.2 | 122 | |||||
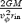 | 9.43 | 9.43 | 4.20 | 38.5 | 9.43 | |||||
| Model . | Parameters . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1D model | A0 | A | B | C | D | E | F | G | H | I |
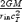 | 11.44 | 11.44 | 6.74 | 7.54 | 8.98 | 10.45 | 11.44 | 6.29 | 6.29 | 6.29 |
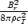 | 0.061 | 0.61 | 0.71 | 0.80 | 0.95 | 1.11 | 60.6 | 133 | 533 | 1330 |
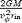 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 | 9.43 |
| 2D monopolar model | A | B | B1 | C | D | E | ||||
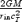 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | ||||
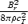 | 0.61 | 6.1 | 6.1 | 60.6 | 606 | 3030 | ||||
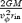 | 9.43 | 9.43 | 4.20 | 9.43 | 9.43 | 9.43 | ||||
| 2D dipolar model | A | B | B1 | B2 | C | |||||
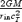 | 11.44 | 11.44 | 11.44 | 11.44 | 11.44 | |||||
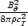 | 1.22 | 12.2 | 12.2 | 12.2 | 122 | |||||
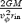 | 9.43 | 9.43 | 4.20 | 38.5 | 9.43 | |||||
Notice that for the dipole, where the open field lines originate close to the pole, the base value of the magnetic field is about twice stronger than at the equator, and the rotational velocity is much smaller than the equatorial speed.
Footnotes
In relativistic MHD, the electric field arises because of motion of the conducting fluid across the magnetic field. Equivalently, the fluid moves with the single particle E×B drift velocity. Therefore, one can eliminate the electric field by putting oneself in the local fluid rest frame and describing the electromagnetic stress as being solely due to the comoving magnetic field. Occasionally, debate occurs about which is the ‘correct’ frame in which to describe the forces, since workers used to non-relativistic MHD are sometimes uncomfortable with the explicit appearance of the electric field. When the fluid dynamics is expressed in covariant form (the electrodynamics is already covariant), as we have done in this paper, the forces are well defined and unambiguously described in every reference frame. The choice is dictated only by convenience in describing the physics, or in actually carrying out the calculations.
An alternate possibility is an increasing magnetic moment (Blandford & Romani 1988). Still another option is evolution of the angle between ω and μ, in the still unassessed dependence of the electromagnetic torque on the oblique rotator, in either force-free or RMHD models.
For very high mass-loss rates and/or high thermal pressures, ρc2T≫B2/8π. In this limit, the magnetic field is not important in accelerating matter off of the stellar surface, the wind is driven thermally, and spindown is negligible unless the star rotates at a significant fraction of breakup.
Increasing the resolution of the simulation or using a characteristics-based solver (Komissarov 1999, private communication) does not improve the accuracy of the solution.
Wind calculations performed over a full 180° show that the formation of plasmoids is not an artefact of our 90° computational domain.
If the surface magnetic field is not highly stressed, the plasma in the closed zone is likely to be non-neutral and it will fill the magnetosphere via cross-field transport driven by shear flow turbulence (Spitkovsky & Arons 2002), not via pressure, which alters the force balance at the Y-point.
We are aware of the recent work of Komissarov (2006) who obtains rY≈RL for σ≈ 100. Because the injection conditions used by Komissarov (2006) are qualitatively different from the self-consistent calculation of the mass-loss rate as a function of latitude obtained here, we do not believe our two results are mutually contradictory. Instead, our finding that rY≈RL only when σ≫ 100 serves to emphasize the point that the injection conditions are critical in determining rY.
Author notes
Hubble Fellow. Present address: Department of Astrophysical Sciences, Peyton Hall, Ivy Lane, Princeton, NJ 08544, USA.