-
PDF
- Split View
-
Views
-
Cite
Cite
R. E. Mennickent, G. Djurašević, On the accretion disc and evolutionary stage of β Lyrae, Monthly Notices of the Royal Astronomical Society, Volume 432, Issue 1, 11 June 2013, Pages 799–809, https://doi.org/10.1093/mnras/stt515
Close - Share Icon Share
Abstract
We modelled the V-band light curve of β Lyrae (Lyr) with two stellar components plus an optically thick accretion disc around the gainer assuming a semidetached configuration. We present the results of this calculation, giving physical parameters for the stars and the disc, along with general system dimensions. We discuss the evolutionary stage of the system finding the best match with one of the evolutionary models of Van Rensbergen et al. According to this model, the system is found at age 2.30 × 107 yr, in the phase of rapid mass transfer, the second one in the life of this binary, in a Case-B mass-exchange stage with |$\dot{M} = 1.58\times 10^{-5}$| M⊙ yr−1. This result, along with the reported rate of orbital period change and observational evidence of mass-loss, suggests that the mass transfer in β Lyr is quasi-conservative. The best model indicates that β Lyr finished a relatively large mass-loss episode 31 400 yr ago. The light-curve model that best fit the observations has inclination angle i = 81°, M1 = 13.2 M⊙, M2 = 3.0 M⊙, R1 = 6.0 R⊙ and R2 = 15.2 R⊙. The disc contributes 22 per cent to the total V-band light curve at quadrature, has a radius of 28.3 R⊙ and the outer edge thickness is 11.2 R⊙. The light-curve model is significantly better with two bright regions in the disc rim with temperatures 10 and 20 per cent higher than the disc outer edge temperature. We compare our results with earlier studies of this interacting binary.
1 INTRODUCTION
β Lyrae (Lyr; Sheliak) is one of the best-studied interacting binaries and also one of the more enigmatic bright objects in the sky. The literature for this object is extensive and only brief highlights will be given in this short introduction. The interested reader is directed to the reviews by Sahade (1980) and Harmanec (2002). The current picture of the system includes a B6-B8II donor star transferring mass on to an early B-type gainer. The hotter star is hidden by an optically and geometrically thick disc (Huang 1963; Wilson 1974; Hubeny & Plavec 1991; Skulskij 1992; Linnell 2000) and some peculiar features can be explained by the presence of a bipolar jet emanating from the disc (Harmanec et al. 1996; Hoffman, Nordsieck & Fox 1998; Ak et al. 2007). Interferometry of β Lyr showed for the first time the direct image of a gravitationally distorted star (Zhao et al. 2008; Schmitt et al. 2009). Non-conservative evolution was inferred from the presence of a radio nebula surrounding the binary system (Umana et al. 2000). The system has an orbital period of 12.9 d increasing at a rate of 19 s yr−1 (Harmanec & Scholz 1993). The notable properties of this system are: (1) the unexplained non-orbital 282.4 d photometric periodicity, (2) the reversal of the depth of primary and secondary eclipses and their gradual evanescence towards the ultraviolet and (3) the presence of six systems of infrared, optical and ultraviolet lines characterized by their morphology and radial velocity behaviour (e.g. Harmanec 2002).
Many solutions for the system parameters have been proposed in the literature, some of them including an accretion disc around the gainer. In this paper, we offer a complementary view of the system, and apply our light-curve (LC) synthesis code to fit the published V-band LC, obtaining a new set of representative system parameters. After obtaining these parameters, we search for a self-consistent evolutionary model by exploring a grid of theoretical evolutionary tracks for binary stars. The synthetic models are those by Van Rensbergen et al. (2008, 2011); they consider brief episodes of liberal or non-conservative evolution. The paper is organized as follows. In Section 2, we describe the LC synthesis code including an accretion disc around the gainer and present the results of the LC analysis. In Section 3, we explore the evolutionary stage of β Lyr obtaining age and mass transfer rate and a theoretical set of system parameters. In Section 4, we provide a discussion of our results and a comparison with previous investigations. In Section 5, we give our conclusions.
2 LIGHT-CURVE ANALYSIS
2.1 Model for an optically thick disc around the gainer
Here, we give a brief description of the disc model that we apply to β Lyr. The basic elements of the binary system model with a plane-parallel disc and the corresponding LC synthesis procedure are described in detail by Djurašević (1992a, 1996). The model and code have been widely used, slightly improved and tested during our recent research of intermediate-mass interacting binaries (e.g. Djurašević et al. 2010, 2011, 2012; Garrido et al. 2013; Mennickent et al. 2012).
We assume that the disc in β Lyr is optically and geometrically thick. The disc edge is approximated by a cylindrical surface. In the current version of the model (Djurašević et al. 2010), the vertical thickness of the disc can change linearly with radial distance, allowing the disc to take a conical shape (convex, concave or plane-parallel), i.e. the disc presents a triangular cross-section at both sides of the star. The geometrical properties of the disc are determined by its radius (Rd), its vertical thickness at the edge (de) and the vertical thickness at the centre or inner boundary (dc).
The model of the system is refined by introducing active regions on the edge of the disc. The existence of these active regions is supported by hydrodynamical simulations of β Lyr as we will discuss in Section 4.1. The active regions have higher local temperatures so their inclusion results in a non-uniform distribution of radiation. The model includes two such active regions: a hotspot (hs) and a bright spot (bs). These regions are characterized by their temperatures Ths,bs angular dimensions (radius) θhs,bs and longitudes λhs,bs. The longitude λ is measured clockwise (as viewed from the direction of the +Z-axis, which is orthogonal to the orbital plane) with respect to the line connecting the star centres (+X-axis), in the range 0°–360°. These parameters are also determined by solving the inverse problem.
Due to the infall of an intensive gas stream, the disc surface in the region of the hotspot becomes deformed as the material accumulates at the point of impact, producing a local deviation of radiation from the uniform azimuthal distribution. In the model, this deviation is described by the angle θrad between the line perpendicular to the local disc edge surface and the direction of the hotspot maximum radiation in the orbital plane.
The second spot in the model, i.e. the bright spot, approximates the spiral structure of an accretion disc, predicted by hydrodynamical calculations (Heemskerk 1994). The tidal force exerted by the donor star causes a spiral shock, producing one or two extended spiral arms in the outer part of the disc. The bright spot can also be interpreted as a region where the disc significantly deviates from the circular shape. For further information about these active regions in the model, see Djurašević et al. (2012).
One limitation of the code at its present implementation is the lack of a detailed treatment for the donor irradiation by the disc part facing the donor, including hotspot. This effect could be potentially important in close binaries with a large difference in stellar and disc temperatures. However, it should be a second-order effect compared with the stellar and disc flux contributions (including donor irradiation by the gainer) already implemented in our code. This is demonstrated in the very good fit obtained with the orbital LC.
Another limitation is the lack of consideration of a ‘third light’, a source of continuum emission that is not eclipsed; in the case of β Lyr it could be the jet reported by Harmanec et al. (1996). However, studies show that this third light has a minor influence in the total flux of β Lyr, being larger in the ultraviolet, but much less evident in the optical (e.g. Linnell 2000). Hence, it is reasonable to assume that the optical flux is dominated by the stars and the disc.
2.2 The V-band time series
We have used the V-band LC and non-linear ephemeris of β Lyr published by Harmanec et al. (1996). This data set consists of 2582 V-band magnitudes obtained by differential photometry in a 36 yr interval at 12 different stations. In most stations, the reported mean rms error per one observation of the corresponding check star is mostly between 0.01 and 0.03 mag. The interested reader can find more details including the procedure of homogenization of the multistation LC in Harmanec et al. (1996).
Since the long photometric cycle of 282.4 d has a low amplitude of 0.024 mag, comparable to the error of an individual data point, viz. 0.027, and this long cycle is probably not strictly periodic (Harmanec et al. 1996), we decided to work with the original V-band LC without intending to remove the long cycle, which could introduce additional uncertainties.
2.3 The fitting procedure
The LC fitting was performed using the inverse-problem solving method based on the simplex algorithm, and the model of a binary system with a disc described in the previous section. We used the Nelder–Mead simplex algorithm (see e.g. Press et al. 1992) with optimizations described by Dennis & Torczon (1991). While the direct problem comprises the calculation of the LC from model parameters given a priori, the inverse problem is the process of finding the set of parameters that will optimally fit the synthetic LC to the observations. For more detail see e.g. Djurašević (1992b).
To obtain reliable estimates of the system parameters, a good practice is to restrict the number of free parameters by fixing some of them to values obtained from independent sources. Thus, we fixed the spectroscopic mass ratio to q = 0.226 and the donor temperature to T2 = 13 300 K, based on published values (e.g. Harmanec 2002; Linnell 2000). Our own LC simulations made with the parameters of the best solution but changing the mass ratio confirmed this q value. In addition, we set the gravity darkening coefficient and the albedo of the gainer and the donor to βh, c = 0.25 and Ah, c = 1.0 in accordance with von Zeipel's law for radiative shells and complete re-radiation (Von Zeipel 1924). The limb darkening for the components was calculated in the way described by Djurašević et al. (2010).
The possible values of free parameters are constrained by imposing the lowest and highest values which seems reasonable based on previous studies of this binary. Here, are the ranges for the fitted parameters.
Inclination: 70° to 90°.
Disc dimension factor (the ratio of the disc radius and the radius of the critical Roche lobe along the y-axis): 0.5 to 1.0.
Disc edge temperature: 6000 to 12 000 K.
Disc thickness: 0.01 to 0.3 distance between the components aorb.
The exponent of the disc temperature distribution: 1 to 5.
Non-synchronous rotation coefficient for the gainer (in critical rotation regime): 5 to 25.
After the first fit, these ranges are decreased according to the results of the first iteration.
We treated the rotation of the donor as synchronous, i.e. we used the non-synchronous rotation coefficient, defined as the ratio between the actual and the Keplerian angular velocity, fc = 1.0. Since it is assumed that the donor has filled its Roche lobe (i.e. the filling factor of the donor was set to Fc = 1.0), the synchronization is expected to be the consequence of the tidal effects. In the case of the gainer, however, the accreted material from the disc is expected to transfer enough angular momentum to increase the rate of the gainer up to the critical velocity as soon as even a small fraction of the mass has been transferred (Packet 1981; de Mink, Pols & Glebbeek 2007). This means that the gainer fills its corresponding non-synchronous Roche lobe for the star rotating in the critical regime, and its dimensions and the amount of rotational distortion are uniquely determined by the factor of non-synchronous rotation. For β Lyr, we assumed critical rotation for the gainer, and estimated a non-synchronous rotation factor fh = 20.2 in the critical rotation regime. Our additional modelling, obtained considering the synchronous rotation regime for the gainer, does not differ much from the critical rotation case.
We were able to model the asymmetry of the LC very precisely by incorporating two regions of enhanced radiation on the disc: the hotspot (hs) and the bright spot (bs). The hotspot and the bright spot in our model are located on the edge side of the disc and are described by the longitude of the centre of the spot, the angular radius of the spot, and the temperature ratio of the spot and the unperturbed local temperature of the disc. The difference between the temperature of the spot and the local unperturbed temperature of the disc is what results in the difference in brightness. The hotspot can be located at longitudes between 270° and 360°, and the bright spot can be located at any longitude. The angular radius of the spots was constrained to the range from 0° to 30° for the hotspot, and from 0° to 70° for the bright spot; the temperature ratio for the spots can be from 1.0 to 1.5.
2.4 Results of the light-curve fitting
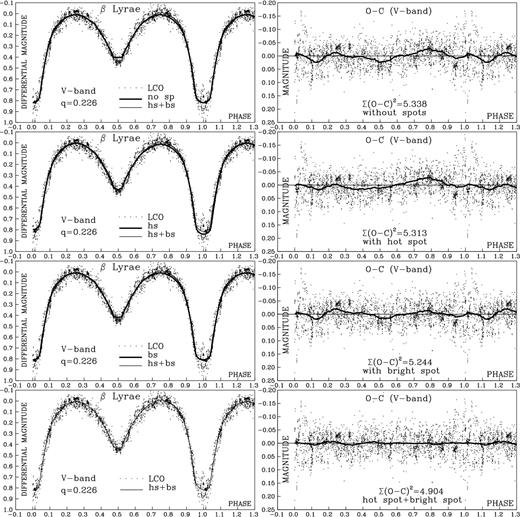
Compared to the model without the active regions on the disc, the model which includes the hot and bright spots (hs+bs) fits the observations much better (see Fig. 1). The dominant feature of our optimal model is the bright spot, and the parameters describing its size, temperature and location are the most important for improving the fit. The existence of a bright spot indicates significant deviation of the disc from cylindrical shape, or other phenomena that are not directly modelled, such as a spiral arm in the outer part of the disc. The parameters of the hotspot do not have as much influence on the quality of the fit because the bright spot is significantly larger in size.
An attempt to model the system without including the active regions on the edge of the accretion disc showed that the observed LC cannot be described well with such a model. This is especially notable in the secondary minimum and around the secondary maximum where there is a significant asymmetry in the LC (see Fig. 1). The O − C residuals between the observed (‘LCO’) and synthetic LC (‘no sp’) clearly show the deficiencies of this model for optimal fitting of the observations.
If a hotspot region is added to the model of the disc, the model fits the observations better in the secondary minimum, but still does not describe the asymmetry in the region of the secondary maximum, and introduces problems with the fitting of the primary minimum. The third model we tested has only a bright spot on the edge of the disc and gives a somewhat better fit, but with significant differences between the model and the observations in certain phase intervals (see Fig. 1). Finally, Fig. 1 shows the optimal model of the system, which contains both the hotspot and the bright spot regions (hs+bs) on the disc. The picture clearly shows that this model can successfully fit the observations and the LC asymmetries that were problematic in other models we considered.
Observed (LCO) and model's synthetic LCs (without spots – no sp, with hotspot – hs, with bright spot – bs and with hotspot and bright spot – hs+bs on the accretion disc edge) of β Lyr obtained by analysing photometric observations and the corresponding final O − C residuals between the observed and model's synthetic LCs. The O − C plots show also the final Σ(O − C)2 for the corresponding model and polynomial fit of the residuals presented by the solid line. In the right-hand column a thin horizontal line shows 0 magnitude.
Apart from this graphical presentation, the advantages of our optimal model can be demonstrated by applying the Fisher statistical F-test, which shows that the models without spots (S1 = Σ(O − C)2 = 5.338) and the models with a single (hot –S2 = Σ(O − C)2 = 5.313 or bright – S3 = Σ(O − C)2 = 5.244) spot can be discarded with the probability of 95 per cent when compared to the optimal model (hotspot and bright spot – Sopt = Σ(O − C)2 = 4.904). Namely, the mentioned values give the following quantities: F1 = S1/Sopt = 1.0885, F2 = S2/Sopt = 1.0834 and F3 = S3/Sopt = 1.0693, while the Fisher statistical F-test for the probability of 95 per cent gives the critical value of the F-distribution F = 1.064. This clearly shows that the model with active hot and bright regions on the disc fits the observations much better than models without spots (F1) and with single hotspot (F2) or bright spot (F3) because these F1, 2, 3 calculated from the data are greater than the critical value of the F-distribution for probability 95 per cent, as can also be seen in Fig. 1. On the other hand, adding more bright spot regions does not improve the quality of the fit.
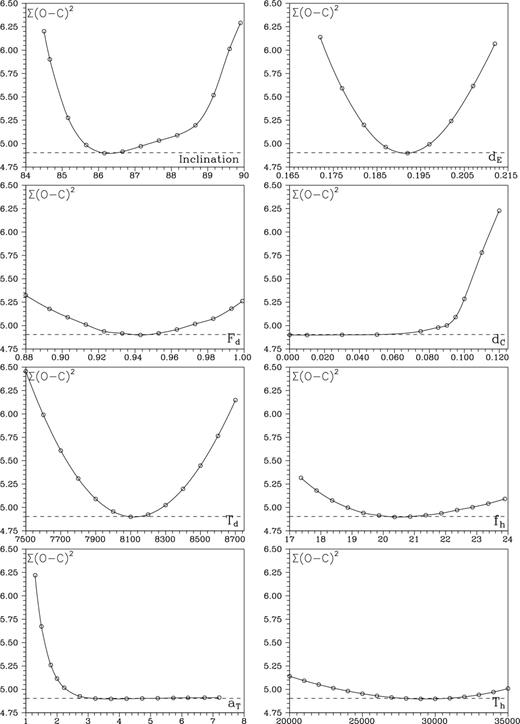
Fig. 2 shows how varying of basic model parameters around the optimal values (obtained for the best model, which includes the active regions on the disc) affects the Σ(O − C)2 value. Each panel shows the variation of one model parameter while all others are kept fixed on their optimal values. The scale in all plots is the same, to make easier to note which parameters influence the quality of the fit at most.
The dependence of Σ(O − C)2 on basic model parameters. Each panel shows the variation of one parameter while all others are kept fixed on the optimal values obtained for the best-fitting model, which includes the hot and bright spots (hs+bs) on the accretion disc. The dashed line shows the minimum value of Σ(O − C)2 = 4.904 in each panel.
The model is relatively insensitive to the temperature of the gainer and to the exponent of the disc temperature distribution. This is to be expected since the disc is seen edge-on, and it covers a large part of the gainer, so the inner regions of the disc do not contribute much to its total radiation. The value found by us, viz. Th = 30 000 K, is consistent with that used by other authors (e.g. Hubeny & Plavec 1991). The model also shows relatively low sensitivity to changes in disc radius (parameter Fd), inner disc thickness (dc), and the non-synchronous rotation coefficient of the gainer (fh). It is more sensitive to change in the orbital inclination, the outer disc thickness (de) and temperature (Td).
2.5 The best light-curve model
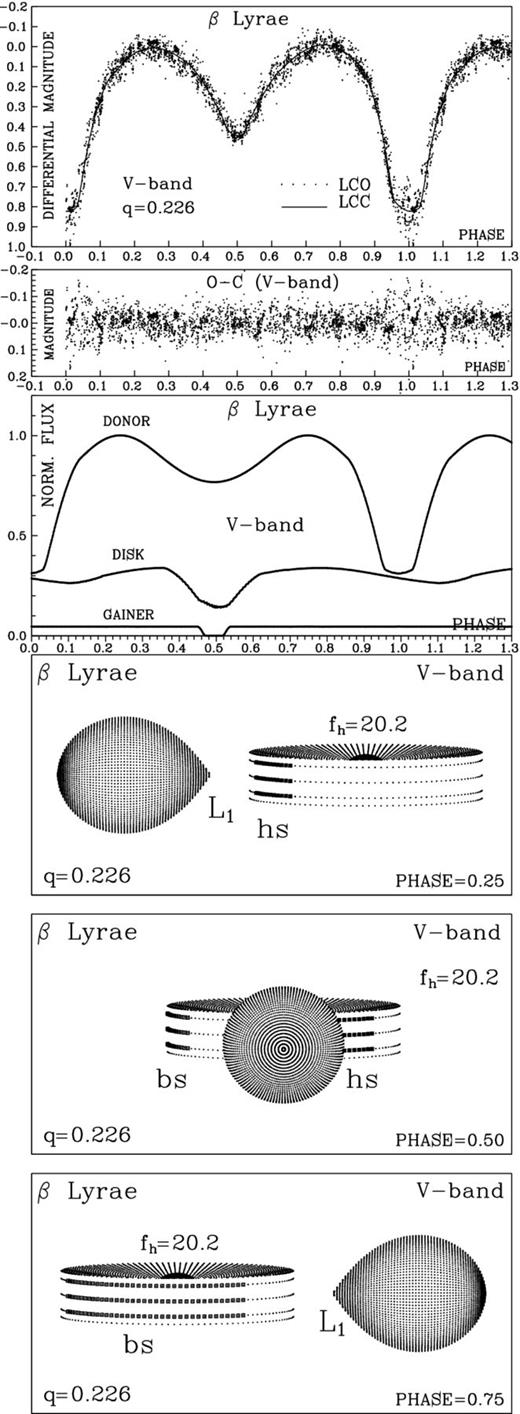
The fit, O − C residuals, individual donor, disc and gainer flux contributions and the view of the optimal model at orbital phases 0.25, 0.50 and 0.75, obtained with the parameters estimated by the LC analysis, are illustrated in Fig. 3. We note that residuals show no dependence on orbital or long-cycle phases, except a larger random scatter around main eclipse, a feature already evident in the LC. We find that the best-fitting model of β Lyr contains an optically and geometrically thick disc around the hotter, more massive gainer star (Table 1). With a radius of Rd ≈ 28.3 R⊙, the disc is 4.7 times larger than the central star (Rh ≈ 6.0 R⊙). The disc has a convex shape, with central thickness dc ≈ 0.6 R⊙ and edge thickness de ≈ 11.2 R⊙. The temperature of the disc increases from Td = 8200 K at its edge, to Th = 30 000 K at the inner radius, where it is in thermal and physical contact with the gainer. The relatively large disc temperature gradient explains the big difference between disc thickness at the inner and outer edges.
Observed (LCO) and synthetic (LCC) LCs of β Lyr, obtained by analysing photometric observations; final O − C residuals between the observed and optimum synthetic LCs; fluxes of the donor, the gainer and of the disc, normalized to the donor flux at phase 0.25; the views of the optimal model at orbital phases 0.25, 0.50 and 0.75, obtained with parameters estimated from LC analysis. We indicate the mass ratio (q), the approximate positions of the inner Lagrangian point (L1), the hotspot (hs), the bright spot (bs) and the gainer non-synchronous rotation factor defined in the text (fh).
Parameters of the best-fitting model for the β Lyr V-band LC obtained by solving the inverse problem considering an accretion disc around a gainer in critical rotation regime.
| Quantity . | . | Quantity . | . |
|---|---|---|---|
| n | 2852 | |$\cal M_{\rm _h} {(\cal M_{\odot })}$| | 13.16 ± 0.3 |
| Σ(O − C)2 | 4.9040 | |$\cal M_{\rm _c} {(\cal M_{\odot })}$| | 2.97 ± 0.2 |
| σrms | 0.0415 | |$\cal R_{\rm _h} {\rm (R_{\odot })}$| | 6.0 ± 0.2 |
| i(°) | 86.1 ± 0.5 | |$\cal R_{\rm _c} {\rm (R_{\odot })}$| | 15.2 ± 0.2 |
| Fd | 0.94 ± 0.03 | |${\rm log_{10}}g_{\rm _h}$| | 4.0 ± 0.1 |
| Td(K) | 8200 ± 400 | |${\rm log_{10}}g_{\rm _c}$| | 2.5 ± 0.1 |
| de(aorb) | 0.192 ± 0.009 | |$M^{\rm h}_{\rm bol}$| | −6.3 ± 0.2 |
| dc(aorb) | 0.01 ± 0.01 | |$M^{\rm c}_{\rm bol}$| | −4.7 ± 0.1 |
| aT | 3.8 ± 0.3 | aorb(R⊙) | 58.5 ± 0.3 |
| fh | 20.2 ± 0.5 | |$\cal {R}_{\rm d} {\rm (R_{\odot })}$| | 28.3 ± 0.3 |
| Fh | 1.00 | |$\rm {{\rm \textit {d}}_e} {\rm (R_{\odot })}$| | 11.2 ± 0.2 |
| Th(K) | 30 000 ± 2000 | |$\rm {{\rm \textit {d}}_c} {\rm (R_{\odot })}$| | 0.6 ± 0.1 |
| Ahs = Ths/Td | 1.21 ± 0.1 | log10Th | 4.48 |
| θhs(°) | 16.2 ± 2.0 | |$\rm {log_{10} {\rm \textit {T}}_c}$| | 4.12 |
| λhs(°) | 324.6 ± 7.0 | |$\rm {log_{10} {\rm \textit {L}}_h}$| | 4.42 |
| θrad(°) | −13.5 ± 5.0 | log10Lc | 3.81 |
| Abs = Tbs/Td | 1.12 ± 0.1 | ||
| θbs(°) | 53.8 ± 5.0 | ||
| λbsm(°) | 107.3 ± 9.0 | ||
| Ah, c, d | 0.10, 0.35, 0.59 | ||
| Ωh | 12.12 ± 0.02 | ||
| Ωc | 2.296 ± 0.02 |
| Quantity . | . | Quantity . | . |
|---|---|---|---|
| n | 2852 | |$\cal M_{\rm _h} {(\cal M_{\odot })}$| | 13.16 ± 0.3 |
| Σ(O − C)2 | 4.9040 | |$\cal M_{\rm _c} {(\cal M_{\odot })}$| | 2.97 ± 0.2 |
| σrms | 0.0415 | |$\cal R_{\rm _h} {\rm (R_{\odot })}$| | 6.0 ± 0.2 |
| i(°) | 86.1 ± 0.5 | |$\cal R_{\rm _c} {\rm (R_{\odot })}$| | 15.2 ± 0.2 |
| Fd | 0.94 ± 0.03 | |${\rm log_{10}}g_{\rm _h}$| | 4.0 ± 0.1 |
| Td(K) | 8200 ± 400 | |${\rm log_{10}}g_{\rm _c}$| | 2.5 ± 0.1 |
| de(aorb) | 0.192 ± 0.009 | |$M^{\rm h}_{\rm bol}$| | −6.3 ± 0.2 |
| dc(aorb) | 0.01 ± 0.01 | |$M^{\rm c}_{\rm bol}$| | −4.7 ± 0.1 |
| aT | 3.8 ± 0.3 | aorb(R⊙) | 58.5 ± 0.3 |
| fh | 20.2 ± 0.5 | |$\cal {R}_{\rm d} {\rm (R_{\odot })}$| | 28.3 ± 0.3 |
| Fh | 1.00 | |$\rm {{\rm \textit {d}}_e} {\rm (R_{\odot })}$| | 11.2 ± 0.2 |
| Th(K) | 30 000 ± 2000 | |$\rm {{\rm \textit {d}}_c} {\rm (R_{\odot })}$| | 0.6 ± 0.1 |
| Ahs = Ths/Td | 1.21 ± 0.1 | log10Th | 4.48 |
| θhs(°) | 16.2 ± 2.0 | |$\rm {log_{10} {\rm \textit {T}}_c}$| | 4.12 |
| λhs(°) | 324.6 ± 7.0 | |$\rm {log_{10} {\rm \textit {L}}_h}$| | 4.42 |
| θrad(°) | −13.5 ± 5.0 | log10Lc | 3.81 |
| Abs = Tbs/Td | 1.12 ± 0.1 | ||
| θbs(°) | 53.8 ± 5.0 | ||
| λbsm(°) | 107.3 ± 9.0 | ||
| Ah, c, d | 0.10, 0.35, 0.59 | ||
| Ωh | 12.12 ± 0.02 | ||
| Ωc | 2.296 ± 0.02 |
Fixed parameters: |$q={\cal M}_{\rm c}/{\cal M}_{\rm h}=0.226$| – mass ratio of the components, Tc = 13300 K – temperature of the less-massive (cooler) donor, Fc = 1.0 – filling factor for the critical Roche lobe of the donor, Fh = Rh/Rzc = 1.0 – filling factor for the critical non-synchronous lobe of the hotter, more massive gainer (ratio of the stellar polar radius to the critical non-synchronous lobe radius along z-axis for a star in critical rotation regime), fc = 1.00 – non-synchronous rotation coefficients of the donor, βh,c = 0.25 – gravity-darkening coefficients of the components.
Note: n – number of observations, Σ(O − C)2 – final sum of squares of residuals between observed (LCO) and synthetic (LCC) LCs, σrms – root-mean-square of the residuals, i – orbit inclination (in arc degrees), Fd = Rd/Ryc – disc dimension factor (the ratio of the disc radius to the critical Roche lobe radius along y-axis), Td – disc-edge temperature, de, dc, – disc thicknesses (at the edge and at the centre of the disc, respectively) in the units of the distance between the components, aT – disc temperature distribution coefficient, fh – non-synchronous rotation coefficient of the more massive gainer (in the critical rotation regime), Th – temperature of the gainer, Ahs,bs = Ths,bs/Td – hot and bright spots’ temperature coefficients, θhs,bs and λhs,bs – spots’ angular dimensions (radius) and longitudes (in arc degrees), θrad – angle between the line perpendicular to the local disc edge surface and the direction of the hotspot maximum radiation, Ah, c, d – albedo coefficients of the system components and the accretion disc, Ωh,c – dimensionless surface potentials of the hotter gainer and cooler donor, |$\cal M_{\rm _{h,c}} {(\cal M_{\odot })}$|, |$\cal R_{\rm _{h,c}} {\rm (R_{\odot })}$| – stellar masses and mean radii of stars in solar units, |${\rm log_{10}}g_{\rm _{h,c}}$| – logarithm (base 10) of the system components effective gravity, |$M^{\rm {h,c}}_{\rm bol}$| – absolute stellar bolometric magnitudes, aorb (R⊙), |$\cal {R}_{\rm d} {\rm (R_{\odot })}$|, de(R⊙), dc(R⊙) – orbital semimajor axis, disc radius and disc thicknesses at its edge and centre, respectively, given in solar units, log10Th,c, log10Lh,c – logarithm (base 10) of the system components effective temperature and luminosity.
Parameters of the best-fitting model for the β Lyr V-band LC obtained by solving the inverse problem considering an accretion disc around a gainer in critical rotation regime.
| Quantity . | . | Quantity . | . |
|---|---|---|---|
| n | 2852 | |$\cal M_{\rm _h} {(\cal M_{\odot })}$| | 13.16 ± 0.3 |
| Σ(O − C)2 | 4.9040 | |$\cal M_{\rm _c} {(\cal M_{\odot })}$| | 2.97 ± 0.2 |
| σrms | 0.0415 | |$\cal R_{\rm _h} {\rm (R_{\odot })}$| | 6.0 ± 0.2 |
| i(°) | 86.1 ± 0.5 | |$\cal R_{\rm _c} {\rm (R_{\odot })}$| | 15.2 ± 0.2 |
| Fd | 0.94 ± 0.03 | |${\rm log_{10}}g_{\rm _h}$| | 4.0 ± 0.1 |
| Td(K) | 8200 ± 400 | |${\rm log_{10}}g_{\rm _c}$| | 2.5 ± 0.1 |
| de(aorb) | 0.192 ± 0.009 | |$M^{\rm h}_{\rm bol}$| | −6.3 ± 0.2 |
| dc(aorb) | 0.01 ± 0.01 | |$M^{\rm c}_{\rm bol}$| | −4.7 ± 0.1 |
| aT | 3.8 ± 0.3 | aorb(R⊙) | 58.5 ± 0.3 |
| fh | 20.2 ± 0.5 | |$\cal {R}_{\rm d} {\rm (R_{\odot })}$| | 28.3 ± 0.3 |
| Fh | 1.00 | |$\rm {{\rm \textit {d}}_e} {\rm (R_{\odot })}$| | 11.2 ± 0.2 |
| Th(K) | 30 000 ± 2000 | |$\rm {{\rm \textit {d}}_c} {\rm (R_{\odot })}$| | 0.6 ± 0.1 |
| Ahs = Ths/Td | 1.21 ± 0.1 | log10Th | 4.48 |
| θhs(°) | 16.2 ± 2.0 | |$\rm {log_{10} {\rm \textit {T}}_c}$| | 4.12 |
| λhs(°) | 324.6 ± 7.0 | |$\rm {log_{10} {\rm \textit {L}}_h}$| | 4.42 |
| θrad(°) | −13.5 ± 5.0 | log10Lc | 3.81 |
| Abs = Tbs/Td | 1.12 ± 0.1 | ||
| θbs(°) | 53.8 ± 5.0 | ||
| λbsm(°) | 107.3 ± 9.0 | ||
| Ah, c, d | 0.10, 0.35, 0.59 | ||
| Ωh | 12.12 ± 0.02 | ||
| Ωc | 2.296 ± 0.02 |
| Quantity . | . | Quantity . | . |
|---|---|---|---|
| n | 2852 | |$\cal M_{\rm _h} {(\cal M_{\odot })}$| | 13.16 ± 0.3 |
| Σ(O − C)2 | 4.9040 | |$\cal M_{\rm _c} {(\cal M_{\odot })}$| | 2.97 ± 0.2 |
| σrms | 0.0415 | |$\cal R_{\rm _h} {\rm (R_{\odot })}$| | 6.0 ± 0.2 |
| i(°) | 86.1 ± 0.5 | |$\cal R_{\rm _c} {\rm (R_{\odot })}$| | 15.2 ± 0.2 |
| Fd | 0.94 ± 0.03 | |${\rm log_{10}}g_{\rm _h}$| | 4.0 ± 0.1 |
| Td(K) | 8200 ± 400 | |${\rm log_{10}}g_{\rm _c}$| | 2.5 ± 0.1 |
| de(aorb) | 0.192 ± 0.009 | |$M^{\rm h}_{\rm bol}$| | −6.3 ± 0.2 |
| dc(aorb) | 0.01 ± 0.01 | |$M^{\rm c}_{\rm bol}$| | −4.7 ± 0.1 |
| aT | 3.8 ± 0.3 | aorb(R⊙) | 58.5 ± 0.3 |
| fh | 20.2 ± 0.5 | |$\cal {R}_{\rm d} {\rm (R_{\odot })}$| | 28.3 ± 0.3 |
| Fh | 1.00 | |$\rm {{\rm \textit {d}}_e} {\rm (R_{\odot })}$| | 11.2 ± 0.2 |
| Th(K) | 30 000 ± 2000 | |$\rm {{\rm \textit {d}}_c} {\rm (R_{\odot })}$| | 0.6 ± 0.1 |
| Ahs = Ths/Td | 1.21 ± 0.1 | log10Th | 4.48 |
| θhs(°) | 16.2 ± 2.0 | |$\rm {log_{10} {\rm \textit {T}}_c}$| | 4.12 |
| λhs(°) | 324.6 ± 7.0 | |$\rm {log_{10} {\rm \textit {L}}_h}$| | 4.42 |
| θrad(°) | −13.5 ± 5.0 | log10Lc | 3.81 |
| Abs = Tbs/Td | 1.12 ± 0.1 | ||
| θbs(°) | 53.8 ± 5.0 | ||
| λbsm(°) | 107.3 ± 9.0 | ||
| Ah, c, d | 0.10, 0.35, 0.59 | ||
| Ωh | 12.12 ± 0.02 | ||
| Ωc | 2.296 ± 0.02 |
Fixed parameters: |$q={\cal M}_{\rm c}/{\cal M}_{\rm h}=0.226$| – mass ratio of the components, Tc = 13300 K – temperature of the less-massive (cooler) donor, Fc = 1.0 – filling factor for the critical Roche lobe of the donor, Fh = Rh/Rzc = 1.0 – filling factor for the critical non-synchronous lobe of the hotter, more massive gainer (ratio of the stellar polar radius to the critical non-synchronous lobe radius along z-axis for a star in critical rotation regime), fc = 1.00 – non-synchronous rotation coefficients of the donor, βh,c = 0.25 – gravity-darkening coefficients of the components.
Note: n – number of observations, Σ(O − C)2 – final sum of squares of residuals between observed (LCO) and synthetic (LCC) LCs, σrms – root-mean-square of the residuals, i – orbit inclination (in arc degrees), Fd = Rd/Ryc – disc dimension factor (the ratio of the disc radius to the critical Roche lobe radius along y-axis), Td – disc-edge temperature, de, dc, – disc thicknesses (at the edge and at the centre of the disc, respectively) in the units of the distance between the components, aT – disc temperature distribution coefficient, fh – non-synchronous rotation coefficient of the more massive gainer (in the critical rotation regime), Th – temperature of the gainer, Ahs,bs = Ths,bs/Td – hot and bright spots’ temperature coefficients, θhs,bs and λhs,bs – spots’ angular dimensions (radius) and longitudes (in arc degrees), θrad – angle between the line perpendicular to the local disc edge surface and the direction of the hotspot maximum radiation, Ah, c, d – albedo coefficients of the system components and the accretion disc, Ωh,c – dimensionless surface potentials of the hotter gainer and cooler donor, |$\cal M_{\rm _{h,c}} {(\cal M_{\odot })}$|, |$\cal R_{\rm _{h,c}} {\rm (R_{\odot })}$| – stellar masses and mean radii of stars in solar units, |${\rm log_{10}}g_{\rm _{h,c}}$| – logarithm (base 10) of the system components effective gravity, |$M^{\rm {h,c}}_{\rm bol}$| – absolute stellar bolometric magnitudes, aorb (R⊙), |$\cal {R}_{\rm d} {\rm (R_{\odot })}$|, de(R⊙), dc(R⊙) – orbital semimajor axis, disc radius and disc thicknesses at its edge and centre, respectively, given in solar units, log10Th,c, log10Lh,c – logarithm (base 10) of the system components effective temperature and luminosity.
In the best model the hotspot with 16° angular radius covers 9 per cent of the disc outer rim and it is situated at longitude λhs ≈ 325°, roughly between the components of the system, at the place where the gas stream falls on to the disc (Lubow & Shu 1975). The temperature of the hotspot is approximately 21 per cent higher than the disc edge temperature, i.e. Ths ≈ 9900 K. Although including the hotspot region into the model improves the fit, it cannot explain the LC asymmetry completely. By introducing one additional bright spot, larger than the hotspot and located on the disc edge at λbs ≈ 107°, the fit becomes much better. This bright spot has Tbs ≈ 9200 K and with 54° angular radius covers 30 per cent of the disc outer rim.
A Fourier analysis (Lenz & Breger 2005) and a Phase Dispersion Minimization analysis (Stellingwerf 1978) of residuals of the best-fitting model confirm the long periodicity of 282 d found by Harmanec et al. (1996) with the same data set but with other LC model.
3 ON THE EVOLUTIONARY STAGE OF β Lyr
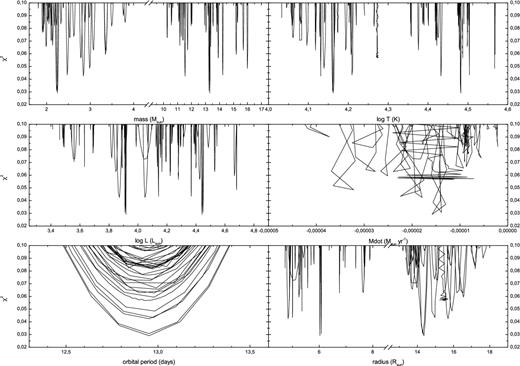
We find the absolute χ2 minimum (viz. 0.0291) in the weak interaction model with initial masses of 12 and 7.2 M⊙ and initial orbital period of 2.5 d; their parameters are shown in Table 2. All other models give larger χ2 and were rejected as reliable solutions. A comparison of χ2 for these models with the optimal solution indicates that the best fit stands out among other solutions in the multiparametric space (Fig. 4). The solution very near to the absolute minima in Fig. 4 (easily visible in the bottom panels) corresponds to the strong interaction model for the same initial conditions; it has χ2 = 0.0308 and their parameters, also given in Table 2 for reference, differ by a small and almost always neglectable amount from the adopted parameters.
The parameters of the Van Rensbergen et al. (2008, labelled vR08) models that best fit the β Lyr data of Table 1 along with those of the model by De Greve & Linnell (1994, labelled DGL94. Subindexes ‘s’ and ‘w’ refer to the strong and weak interaction models for the same set of initial parameters, where the weak case is the best solution followed by the strong case, as discussed in the text. The hydrogen and helium core mass fractions (Xc and Yc) are given for the cool and hot star. Errors are given when available, corresponding approximately to half of the grid step at a given parameter.
| Quantity . | vR08w . | vR08s . | DGL94 . | Quantity . | vR08w . | vR08s . | DGL94 . |
|---|---|---|---|---|---|---|---|
| Age (yr) | 2.30070(4) × 107 | 2.30457(1) × 107 | 3.1924 × 107 | period (d) | 12.95(9) | 12.95(8) | 13.23 |
| Mc (M⊙) | 2.248(6) | 2.231(6) | 2.95 | Mh (M⊙) | 13.308(6) | 13.251(6) | 13.27 |
| |$\dot{M_{{\rm c}}}$| (M⊙ yr−1) | −1.58(11) × 10−5 | −1.38(2) × 10−5 | −2.77E-05 | |$\dot{M_{{\rm h}}}$| (M⊙ yr−1) | 1.44(2) × 10−5 | 1.47(4) × 10−5 | 2.57 × 10−5 |
| log Tc (K) | 4.162(1) | 4.161(1) | 4.135 | log Th(K) | 4.482(1) | 4.482(1) | 4.444 |
| log Lc (L⊙) | 3.917(1) | 3.911(1) | 3.917 | log Lh (L⊙) | 4.442(1) | 4.449(1) | 4.329 |
| Rc (R⊙) | 14.36(5) | 14.29(3) | 16.26 | Rh (R⊙) | 6.023(2) | 6.076(2) | 6.33 |
| Xcc | 0.00(0) | 0.00(0) | 0.000 | Xch | 0.43(0) | 0.42(0) | 0.479 |
| Ycc | 0.98(0) | 0.98(0) | 0.980 | Ych | 0.55(0) | 0.56(0) | 0.501 |
| Quantity . | vR08w . | vR08s . | DGL94 . | Quantity . | vR08w . | vR08s . | DGL94 . |
|---|---|---|---|---|---|---|---|
| Age (yr) | 2.30070(4) × 107 | 2.30457(1) × 107 | 3.1924 × 107 | period (d) | 12.95(9) | 12.95(8) | 13.23 |
| Mc (M⊙) | 2.248(6) | 2.231(6) | 2.95 | Mh (M⊙) | 13.308(6) | 13.251(6) | 13.27 |
| |$\dot{M_{{\rm c}}}$| (M⊙ yr−1) | −1.58(11) × 10−5 | −1.38(2) × 10−5 | −2.77E-05 | |$\dot{M_{{\rm h}}}$| (M⊙ yr−1) | 1.44(2) × 10−5 | 1.47(4) × 10−5 | 2.57 × 10−5 |
| log Tc (K) | 4.162(1) | 4.161(1) | 4.135 | log Th(K) | 4.482(1) | 4.482(1) | 4.444 |
| log Lc (L⊙) | 3.917(1) | 3.911(1) | 3.917 | log Lh (L⊙) | 4.442(1) | 4.449(1) | 4.329 |
| Rc (R⊙) | 14.36(5) | 14.29(3) | 16.26 | Rh (R⊙) | 6.023(2) | 6.076(2) | 6.33 |
| Xcc | 0.00(0) | 0.00(0) | 0.000 | Xch | 0.43(0) | 0.42(0) | 0.479 |
| Ycc | 0.98(0) | 0.98(0) | 0.980 | Ych | 0.55(0) | 0.56(0) | 0.501 |
The parameters of the Van Rensbergen et al. (2008, labelled vR08) models that best fit the β Lyr data of Table 1 along with those of the model by De Greve & Linnell (1994, labelled DGL94. Subindexes ‘s’ and ‘w’ refer to the strong and weak interaction models for the same set of initial parameters, where the weak case is the best solution followed by the strong case, as discussed in the text. The hydrogen and helium core mass fractions (Xc and Yc) are given for the cool and hot star. Errors are given when available, corresponding approximately to half of the grid step at a given parameter.
| Quantity . | vR08w . | vR08s . | DGL94 . | Quantity . | vR08w . | vR08s . | DGL94 . |
|---|---|---|---|---|---|---|---|
| Age (yr) | 2.30070(4) × 107 | 2.30457(1) × 107 | 3.1924 × 107 | period (d) | 12.95(9) | 12.95(8) | 13.23 |
| Mc (M⊙) | 2.248(6) | 2.231(6) | 2.95 | Mh (M⊙) | 13.308(6) | 13.251(6) | 13.27 |
| |$\dot{M_{{\rm c}}}$| (M⊙ yr−1) | −1.58(11) × 10−5 | −1.38(2) × 10−5 | −2.77E-05 | |$\dot{M_{{\rm h}}}$| (M⊙ yr−1) | 1.44(2) × 10−5 | 1.47(4) × 10−5 | 2.57 × 10−5 |
| log Tc (K) | 4.162(1) | 4.161(1) | 4.135 | log Th(K) | 4.482(1) | 4.482(1) | 4.444 |
| log Lc (L⊙) | 3.917(1) | 3.911(1) | 3.917 | log Lh (L⊙) | 4.442(1) | 4.449(1) | 4.329 |
| Rc (R⊙) | 14.36(5) | 14.29(3) | 16.26 | Rh (R⊙) | 6.023(2) | 6.076(2) | 6.33 |
| Xcc | 0.00(0) | 0.00(0) | 0.000 | Xch | 0.43(0) | 0.42(0) | 0.479 |
| Ycc | 0.98(0) | 0.98(0) | 0.980 | Ych | 0.55(0) | 0.56(0) | 0.501 |
| Quantity . | vR08w . | vR08s . | DGL94 . | Quantity . | vR08w . | vR08s . | DGL94 . |
|---|---|---|---|---|---|---|---|
| Age (yr) | 2.30070(4) × 107 | 2.30457(1) × 107 | 3.1924 × 107 | period (d) | 12.95(9) | 12.95(8) | 13.23 |
| Mc (M⊙) | 2.248(6) | 2.231(6) | 2.95 | Mh (M⊙) | 13.308(6) | 13.251(6) | 13.27 |
| |$\dot{M_{{\rm c}}}$| (M⊙ yr−1) | −1.58(11) × 10−5 | −1.38(2) × 10−5 | −2.77E-05 | |$\dot{M_{{\rm h}}}$| (M⊙ yr−1) | 1.44(2) × 10−5 | 1.47(4) × 10−5 | 2.57 × 10−5 |
| log Tc (K) | 4.162(1) | 4.161(1) | 4.135 | log Th(K) | 4.482(1) | 4.482(1) | 4.444 |
| log Lc (L⊙) | 3.917(1) | 3.911(1) | 3.917 | log Lh (L⊙) | 4.442(1) | 4.449(1) | 4.329 |
| Rc (R⊙) | 14.36(5) | 14.29(3) | 16.26 | Rh (R⊙) | 6.023(2) | 6.076(2) | 6.33 |
| Xcc | 0.00(0) | 0.00(0) | 0.000 | Xch | 0.43(0) | 0.42(0) | 0.479 |
| Ycc | 0.98(0) | 0.98(0) | 0.980 | Ych | 0.55(0) | 0.56(0) | 0.501 |
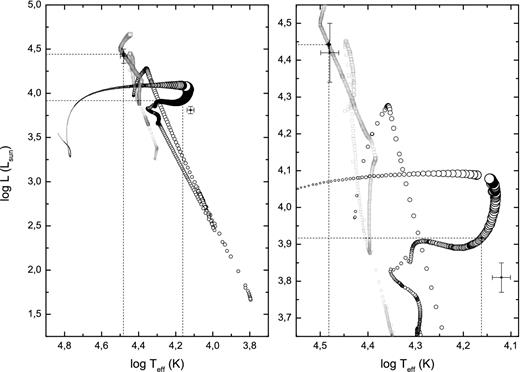
The corresponding evolutionary tracks for the gainer and donor stars are shown in Fig. 5, along with the position for the best model for β Lyr. We observe a relatively good match for the gainer star parameters but a small mismatch with the donor temperature and luminosity. The observed donor is slightly fainter and cooler than the model prediction. The difference amounts to 0.9 per cent in log T and 2.7 per cent in log L. This small discrepancy remains when considering the next more reliable solution, those with strong tidal interaction and whose parameters are given in Table 2. We propose that this mismatch could be due to a limitation of the existing grid of synthetic models available, that are not dense enough in initial orbital period and initial masses to give account of all possible evolutionary combinations, and eventually could not reproduce the β Lyr evolution perfectly. For instance, only initial masses for the donor of 7, 8, 9, 12 and 15 M⊙ are considered in the range compatible with β Lyr. Whereas this discretization of initial parameters probably does not produce a large discrepancy with the actual system parameters (as suggested by the absence of competent solutions near the absolute minima in Fig. 4), it is likely that small differences between observed and synthetic parameters, as observed with the donor, occur. At present, we cannot quantify this effect.
χ2 for all studied models versus selected parameters. Only the regions around the χ2 minima are shown. Temperatures, luminosities, masses and radii are given for both components in the corresponding panel. The significance of the best fit represented by the absolute minima, can be evaluated from the depth and proximity of secondary minima.
Evolutionary tracks for the binary star model from Van Rensbergen et al. (2008) that best fit the data. Donor (right black track) and gainer (left grey track) evolutionary paths are shown, along with the parameters derived from the LC fit. The best fit is reached at the time corresponding to the model attached to the axis by dashed lines, that is characterized in Table 2. The mismatch for the donor is discussed in the text. Stellar sizes are proportional to the circle diameters. An expanded view is shown in the right-hand panel where half of the points are shown for the donor track for best visualization.
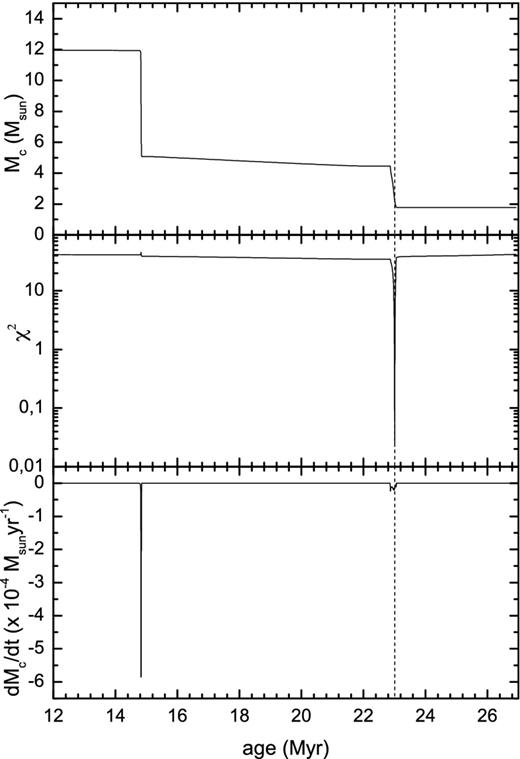
The best fit indicates that β Lyr is found inside a burst of mass transfer, the second one in the life of this binary (Fig. 6). The donor is an inflated (Rc = 14.4 R⊙) and evolved 2.2 M⊙ star with its core completely exhausted of hydrogen. According to the best model the system has now an age of 2.3 × 107 yr and |$\dot{M}$| = 1.58 × 10−5 M⊙ yr−1. The system reverted its mass ratio not at the present semidetached stage, but about 8 Myr ago, during a much stronger episode of mass transfer. The small difference between |$\dot{M_{\rm h}}$| and |$\dot{M_{\rm c}}$| in Table 2 is a purely numeric effect due to the iterative process of calculation; the transferred mass equals the accreted mass in the long term, i.e. according to the best model β Lyr is in a conservative mass transfer stage. An inspection of the best-model evolutionary track indicates that: (i) the system is found 147 000 yr after second Roche lobe contact and (ii) in this interaction episode the system has lost (previously) 0.03 M⊙ into the interstellar medium and the gainer has eventually accreted 1.55 M⊙. The last figures were derived from the mass balance between two epochs in the evolutionary track: the epoch corresponding to the start of mass-loss and the present epoch. However, if critical rotation impedes the accretion of more mass (something not considered by the binary evolution codes), part of this mass could have been ejected into the interstellar medium or remains still stored in the accretion disc.
Mc, χ2 (defined in equation 2) and |$\dot{M_{\rm c}}$| for the best evolutionary track. The vertical dashed line indicates the position for the best model.
4 DISCUSSION
In this section, we compare our β Lyr parameters with those previously reported in the literature. We also give a semblance of the future appearance of the system, just after finishing the mass transfer process, based on the prediction of the best synthetic model.
4.1 Comparison with published system and disc parameters
A range of stellar masses, inclinations and mass ratios have been published for β Lyr during the past 50 yr, but the latest calculations seems to indicate gainer and donor masses around 13 and 3 M⊙, respectively (Harmanec 2002). Our stellar masses, listed in Table 1, are consistent with these numbers.
Similar to other authors (e.g. Hubeny & Plavec 1991, hereafter HP; Linnell 2000), we have found that a geometrically thick disc significantly improves the fit to the LC in β Lyr. In our model, the disc contributes 22 per cent to the total V-band LC at quadrature, has a radius of 28.3 R⊙ (HP find 25.5 R⊙ and Linnell 30 R⊙) and the thickness goes from 0.58 R⊙ at the inner edge to 11.2 R⊙ at the rim (HP find 0.34 to 14 R⊙, respectively, and Linnell finds 16 R⊙ at the rim).
We notice two important issues here: (1) The best-fitting model is conservative, but observations (discussed in the next paragraph) suggest mass-loss at the present epoch and (2) our |$\dot{M}$| value is near the conservative figure derived from equation (4). Whereas the first point could indicate that the models still do not reproduce the actual physics of mass-loss processes, the second point suggests that the mass-loss rate probably is much smaller than the mass transfer rate, producing a mass transfer practically conservative or, in other words, quasi-conservative.
Jets and nebular radio emission have been considered signatures of mass-loss in β Lyr. From the evolutionary track discussed in Section 3, we have estimated that 0.03 M⊙ have been lost in the present episode of Roche lobe overflow. Umana et al. (2000) estimate 0.015 M⊙ from the analysis of the radio nebula but using |$\dot{M}$| ∼ 10−7 M⊙ yr−1 for the donor wind ionized by the radiation field of the hotter companion. An earlier estimate based on the mass exchange models by De Greve & Linnell (1994, hereafter DGL94) is 0.43 M⊙. Our mass-loss estimate is linked to the nature of the mass-loss process considered in the Van Rensbergen et al. (2008, 2011) models. These models consider mass-loss driven by radiation pressure from a hotspot located in the stream impact region on the stellar surface or accretion disc edge. The mass-loss extracts angular momentum from the system, specifically from the gainer. The best model indicates that β Lyr already passed by a non-conservative epoch 31 400 yr ago, and now it is in a conservative regime. The fact that observations actually show some mass-loss suggests a quasi-conservative stage instead, as stated previously.
We find two bright regions along the disc rim at longitudes λhs = 325° and λbs = 107°; the first one 1.21 times hotter than the disc rim, with 16° angular radius covering 9 per cent of the outer disc rim, and the second one 1.12 times hotter than the disc rim, with 54° angular radius, covering 30 per cent of the outer disc rim. These regions might be tentatively identified with shock regions revealed in hydrodynamical simulations of mass transfer in β Lyr by Nazarenko & Glazunova (2006) and in close binaries in general by Bisikalo et al. (1998, 1999, 2003).
Interestingly, the hotspot has also been inferred from spectropolarimetric observations by Lomax et al. (2012). They report a hotspot at the disc outer edge with a projected linear extension between 22 and 33 R⊙, equivalent to angular sizes 27.4°and 60.8°(7.6 and 16.9 per cent of the outer disc rim), depending on the photometric bandpass. The centre of the hotspot is roughly at orbital phase 0.47, near the position of the hotspot found by us at orbital phase 0.40 (λhs = 325°).
4.2 Comparison with previous evolutionary studies
We find β Lyr in a Case-B mass transfer stage with an age of 2.30 × 107 yr. The donor has exhausted hydrogen in its core and the gainer has a hydrogen concentration Xch = 0.43. The parameters for the best non-conservative evolutionary model are given in Table 2. The late evolutionary stage of the donor is consistent with the spectroscopic finding of He enrichment and extreme CNO cycling by Balachandran et al. (1986).
The evolutionary stage of β Lyr was previously investigated by DGL94. These authors determined that a conservative solution led to several discrepancies with observed data. They find that β Lyr is reaching the end of the mass transfer, having evolved in a non-conservative way from an initial system of 9 + 7.65 M⊙ and orbital period of 4 d (our best model starts with 12 + 7.2 M⊙ and orbital period 2.5 d). Their model parameters are given in Table 2 along with those of our best model.
In general, the stellar parameters derived from our evolutionary solution compares relatively well with those of DGL94. However, significant differences can be observed in the initial masses and the initial orbital period. In addition, DGL94 model gives a 9 Myr older binary, a slightly more inflated donor and a mass transfer rate 75 per cent larger than ours.
The above differences are not negligible and point to some physical difference between both models. One of the possible reasons for the differences might be the more massive binary considered in our solution, along with the shorter initial orbital period. This means not only a faster evolution (a younger system as observed) but also that non-conservative effects should be stronger than those in the case studied by DGL94. Another possible reason is the way both models deal with mass-loss, usually parametrized with the parameter β, defined as the mass fraction accreted by the gainer, so 1-β is the mass fraction lost by the system. DGL94 assume β constant through the whole mass transfer process whereas Rensbergen et al. consider β variable according to the physics of their model. In any case, we caution that we cannot go further interpreting the differences between both models since the mass-loss processes are still not well understood, nor included with all physical details in the models. At this stage, these differences can be interpreted as upper estimates for the accuracy of the initial binary parameters, their age and |$\dot{M}$|.
4.3 The future of β Lyr
According to the best synthetic model presented in Section 3, the donor will lose contact with its Roche lobe after 72 100 yr, becoming a detached binary, with stellar components of 1.78 and 13.77 M⊙. The orbital period will be 23.47 d and the stars will be in basically the same present evolutionary stage. The model does not cover the posterior evolution of the gainer, but if the disc and rapid gainer rotation still persist at that time, the system might be easily classified like a binary Be star. This conclusion depends on how the angular momentum and circumstellar mass are distributed during the interaction epochs, something that future models need to consider carefully.
5 CONCLUSIONS
In this paper, we fit the published optical LC of β Lyr with a LC synthesis code based on the simplex algorithm, considering stellar plus disc components. In addition, the evolutionary stage of the binary was studied by comparing our best system parameters with those of grids of synthetic evolutionary tracks. Hence, we have made use of the published data in an entirely new and complementary way. A comparison with earlier studies was also given. The main results of our research are as follows.
The V-band LC can be modelled with an intermediate mass semidetached binary including an accretion disc around the gainer. The best system parameters including stellar and disc temperatures, masses, luminosities and sizes are given in Table 1.
Our study of the evolutionary stage of β Lyr indicates that it is in a Case-B mass transfer stage, with age 2.30 × 107 yr and |$\dot{M} = 1.58\times 10^{-5}$| M⊙ yr−1. The donor has exhausted hydrogen in its core and the gainer is slightly evolved with central hydrogen fraction Xch = 0.43.
The best evolutionary model indicates that the system is found 147 000 yr after second Roche lobe contact. In this interaction episode, the system has lost 0.03 M⊙ into the interstellar medium and the gainer might have accreted 1.55 M⊙. A fraction of this mass could still remain in the disc.
We provide arguments supporting the view that β Lyr is in a quasi-conservative evolutionary stage, having finished a relatively large mass-loss episode 31 400 yr ago. By quasi-conservative, we mean a stage with a systemic mass-loss much less that the mass transfer rate.
Discretization of the grid of synthetic models could explain the small discrepancy observed in donor temperature. At present we cannot quantify this effect, but argue it should be small.
We find significant evidence for two bright regions in the disc rim with temperatures 10 and 20 per cent higher than the disc outer edge temperature. They are located at longitudes λ = 107° and 325°, respectively. The cooler bright spot region covers 30 per cent of the disc outer rim and the hotter one 9 per cent. These hot regions might be tentatively identified with those shock regions revealed by hydrodynamical simulations of the mass transfer process.
REM acknowledges support by Fondecyt grant 1110347 and the BASAL Centro de Astrofisica y Tecnologias Afines (CATA) PFB–06/2007. GD acknowledges the financial support of the Ministry of Education and Science of the Republic of Serbia through the project 176004 ‘Stellar physics’. We acknowledge an anonymous referee for useful indications aimed to improve the first version of this manuscript.