Photonic-crystal lasers with high-quality narrow-divergence symmetric beams and their application to LiDAR

To realize 10 W class high-power, narrow-beam-divergence operation, lasing oscillation in the fundamental mode should be maintained, and oscillation in high-order modes should be suppressed, as the lasing area is expanded. However, the threshold gain margin, defined as the threshold gain difference (Δα) between the fundamental lasing mode and 1st high-order mode, shrinks as the lasing area increases, leading to the commencement of oscillation in the high-order mode. To overcome this challenge, we have proposed a unique double-lattice structure [16, 26], where two lattices, A and B, are combined as shown in figure 4(a). In this double-lattice structure, the optical path difference between the light diffracted backward by individual lattices is set to be around λ/2 (where λ is the wavelength in the material), which leads to the destructive interaction of waves diffracted in-plane by 180°. As a result of this interaction, optical modes formed in the double-lattice photonic crystal spread out and leak more easily from the edges of the lasing area than from those edges of the previous single-lattice photonic crystal [14], as shown in figure 4(b). In particular, since the antinodes of the high-order modes are concentrated near the edges, their edge loss (i.e. in-plane loss) increases more quickly than that of the fundamental mode, and the threshold gain margin widens as a consequence. Figure 4(c) shows the calculated results of Δα for a double-lattice photonic crystal designed for 500 µmΦ resonators and referred to as structure II in [16]. Using Δα of a single-lattice photonic crystal as a benchmark (Δα ∼ 4 cm⁻¹ at 200 µmΦ) [14], the resonator area can be increased to 500 µmΦ while maintaining high-beam-quality operation. In this design, we have separately introduced a difference in the heights of the double-hole pair in order to create vertical asymmetry (see the right panel of figure 4(c)), which enhances the surface emission. In other words, the vertical asymmetry is introduced to obtain a reasonable value of radiation constant α_v.

Zoom In Zoom Out Reset image size

We fabricated PCSELs using the double-lattice design, and achieved 10 W high-power, high-beam-quality (beam-divergence angle of ∼0.2° measured at FWHM) operation under pulsed conditions [16]. However, the slope efficiency of this device was ∼0.4 W A⁻¹, and thus a high injection current was necessary to obtain the high output power of 10 W. Also, concerning device fabrication, a relatively complicated process (two-step electron-beam (EB) lithography and dry etching, including careful alignment) was required for forming air-hole pairs with the same shape but different heights, as necessary to obtain the reasonable value of α_v [16]. In the following sections, for the purpose of solving all of the above issues inherent to the previous design of double-lattice photonic crystal, we present and discuss optimization of the photonic-crystal design, as well as the use of backside refection by a DBR mirror.

We begin by designing a photonic-crystal structure that can be fabricated by a simplified process using one-step EB lithography and etching for 500 µmΦ PCSELs while maintaining a sufficiently wide threshold gain margin for oscillation in the fundamental mode. We investigate an asymmetric structure consisting of two holes with different in-plane shapes in lieu of a height difference in order to enhance the surface-emitted power while maintaining Δα. Specifically, as shown in figure 5(a), asymmetry is introduced by making one hole elliptical by changing the ratio of its minor (x) and major (y) axes while keeping the other hole circular. Here, the ratio is tuned by fixing x and changing y.

Zoom In Zoom Out Reset image size

First, we calculate the radiation constant α_v of the band-edge mode A in which the lasing oscillation occurs, as a function of the x/y ratio; the dark blue line in figure 5(b) indicates these values of α_v when the lattice separation is d= 0.250a. α_v is 0 when the two holes are circular (x/y = 1.0), but increases when the hole becomes elliptical, and is maximum at x/y = 0.7. This trend is explained by changes in the cancellation of the electric fields emitted in the surface-normal direction, depending on the degree of electric-field overlap at each hole. Note that the cancellation discussed here does not involve Bloch waves diffracted in-plane and the determination of Δα, but rather involves the light emitted in the surface-normal direction and the determination of α_v. Figure 5(c) shows the calculated electric-field distribution of the mode of band-edge A in the unit cell for x/y = 1.0, 0.7, and 0.5. When unit cell has C_2v symmetry (x/y = 1.0), the position of the node of the electric field is equidistant from the center of each hole. Consequently, the vectors of the electric fields diffracted out-of-plane at the two holes are equal in magnitude and opposite in phase, resulting in their complete cancellation and thus zero-valued α_v. On the other hand, when C_2v symmetry is broken by making one hole elliptical, such cancellation becomes incomplete. In the case of x/y = 0.7, the position of the node of the electric field shifts toward the elliptical hole and that of the antinode shifts toward the circular hole, resulting in an imbalance of the magnitude of the vertically diffracted electric-field vectors and thus alleviating their cancellation. However, when the hole becomes even more elliptical (x/y = 0.5), the overlap between the elliptical hole and the electric field increases, so the magnitude of its corresponding vertically diffracted electric-field vector approaches that of the circular hole. Therefore, the cancellation once again becomes more complete and α_v decreases. Here, although we have increased α_v by appropriately breaking C_2v symmetry as described above, α_v nevertheless does not exceed 7 cm⁻¹ even at its maximum at x/y = 0.7; considering the presence of other losses in the current device system (e.g. fundamental absorptive loss α₀ and in-plane loss α_//, which will be discussed later), this value is slightly insufficient. Note that when α₀ is decreased in the future by optimizing the device structure even further, then even a small α_v will be sufficient. To further increase α_v, we consider the lattice separation d between the two holes as an additional degree of freedom for finely tuning the degree of overlap between the holes and the electric field. As shown in figure 5(b), α_v increases as d increases from 0.250a to 0.255a. When d increases, the position of the electric-field node slightly shifts as if it is pulled by the larger elliptical hole, and the imbalance of the diffracted electric-field vectors is enhanced (see figure 5(d)). As a result, a larger radiation coefficient of ∼16 cm⁻¹ is obtained when d = 0.255a and x/y = 0.7; this value is sufficient for obtaining a high slope efficiency exceeding ∼0.8 W A⁻¹ once the effect of reflection from a DBR is considered as well, as discussed later.

Next, we evaluate whether the above design for realizing appropriate α_v is also appropriate for achieving a reasonably large value of threshold gain difference Δα to realize high-beam-quality operation in a 500 µmΦ device. Figure 5(e) shows κ_1D, a coupling coefficient which expresses the strength of in-plane 180° diffraction, as a function of the x/y ratio for structures with different d. It is seen that κ_1D increases as the x/y ratio decreases from 1.0 to 0.5. Nevertheless, a sufficiently small value of κ_1D of less than 300 cm⁻¹, which is comparable to that of our previous design, is obtained at around x/y = 0.7. Figure 5(f) shows the calculated Δα as a function of the x/y ratio for a structure with d = 0.255a in a 500 µmΦ device. As shown in this figure, although Δα decreases as the x/y ratio decreases (or, alternatively, as κ_1D increases), a sufficiently large Δα of ∼5 cm⁻¹ is nevertheless obtained when x/y = 0.7. Therefore, a coincidence of high-peak-power and high-beam-quality operation is expected from a 500 µmΦ device using this new photonic crystal structure which can be fabricated using a simplified process.

Next, we discuss improving the slope efficiency of the PCSEL by introducing and optimizing a DBR mirror on the backside of the device to act as a reflector. The slope efficiency η_SE of a PCSEL without the DBR mirror is expressed by the following equation:

$$\begin{equation}{\eta _{{\text{SE}}}} = \frac{{1.24}}{\lambda }\left( {1 - A} \right){\eta _i}\frac{{{\alpha _{{\text{v}}\_{\text{up}}}}}}{{{\alpha _{{{{\text{v}}\_{\text{up}}}}}} + {\alpha _{{{\text{v}\_{\text{down}}}}}} + {\alpha _{\left\| {} \right.}} + {\alpha _0}}}\end{equation} \tag{ 1 }$$

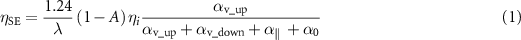
where α_{v_up} and α_{v_down} are the upward and downward radiation constants and their sum is equal to the α_v discussed above, α₀ is the fundamental absorptive loss, α_// is the in-plane loss, and λ is the lasing wavelength. A is an absorption constant, which is defined as the ratio of the power absorbed in the substrate to the total output power from the resonator, and η_i is the internal quantum efficiency of the active layer. Because nearly equal amounts of light are diffracted from the photonic crystal layer in the upward and downward directions (i.e. α_{v_up} ≈ α_{v_down} ≈ α_v/2), the introduction of the DBR mirror, which reflects the downward-diffracted light toward the output facet in the upward direction as shown in figure 6(a), is critical for increasing the slope efficiency. The light reflected by the DBR mirror interferes with the light radiated directly upward, so the resultant α_{v_up} and η_SE are expected to change depending on the interference phase of the reflected and upward-radiated light. Although a DBR mirror has been employed in our previous device, the effect of this interference on the lasing characteristics was not investigated in detail, and η_SE of our previous device was no higher than 0.4–0.5 W A⁻¹ [16].

Zoom In Zoom Out Reset image size

To indicate the effect of reflection by the DBR mirror on ${\eta _{{\text{SE}}}}$, we rewrite equation (1) as follows:

$$\begin{equation}{\eta _{{\text{SE}}}} = \frac{{1.24}}{\lambda }\left( {1 - A} \right){\eta _{\text{i}}}\frac{{\frac{1}{2}\left( {1 + 2\sqrt R \cos \theta + R} \right){\alpha _{\text{v}}}}}{{\left( {1 + \sqrt R \cos \theta } \right){\alpha _{\text{v}}} + {\alpha _{\left\| {} \right.}} + {\alpha _0}}}.\end{equation} \tag{ 2 }$$

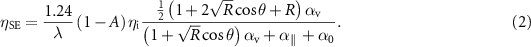
Here, R is the reflectivity of the DBR mirror and θ is interference phase between the reflected and upward-radiated light. For the above-designed photonic crystal structure, whose radiation constant α_v = 16 cm⁻¹, we calculated upward radiation constant α_{v_up}, which is expressed by the term [$\frac{1}{2}\left( {1 + 2\sqrt R \cos \theta + R} \right){\alpha _{\text{v}}}]{ }$ in equation (2), and using equation (2) as functions of θ when R = 0.9; the results of these calculations are shown in figures 6(b) and (c). For comparison, values corresponding to an equivalent device without the DBR (i.e. when R = 0.0) are also shown with broken lines. When there is no DBR mirror, the downward radiation becomes loss, and, therefore, the slope efficiency is limited to ∼0.4 W A⁻¹. On the other hand, with the DBR mirror, a periodic dependence of α_{v_up} and η_SE on θ is observed. When interference is constructive (i.e. when θ is around 0°), η_SE ⩾0.8 W A⁻¹, which is twice as high as that of our previous device, is obtained. We note that the term $\left[ {\left( {1 + \sqrt R \cos \theta } \right){\alpha _{\text{v}}} + {\alpha _\parallel } + {\alpha _0}} \right]$ in equation (2) expresses the threshold gain for the lasing oscillation. Thus, the threshold current is also dependent on the interference phase θ.

We fabricated a PCSEL based on the above-designed photonic crystal and DBR structures. Figure 7(a) shows a top-view SEM image of the fabricated photonic crystal after dry etching. The double-lattice structure, composed of circular and elliptical air holes, was successfully fabricated by an EB lithography and dry-etching process. We then performed MOVPE regrowth while retaining the air-hole structure inside the device, and formed the DBR mirror composed of 14 pairs of Al_0.1Ga_0.9As/Al_0.9Ga_0.1As layers (see figure 7(b)). For this DBR, R was measured to be ∼0.86 at the lasing wavelength of ∼940 nm as shown in figure 7(c). Figure 7(d) shows typical current–voltage (I–V) characteristics of the fabricated 500 µmΦ PCSELs with the DBR. Here, the interference phase varies with the thickness of the p-cladding layer, which determines the optical path length between the photonic crystal and the DBR mirror. In order to experimentally investigate the appropriate thickness of the p-cladding layer for realizing a high slope efficiency, we fabricated and evaluated the current–light output power (I–L) characteristics of four types of devices with p-cladding layer thicknesses of 1030 nm, 1080 nm, 1130 nm, and 1180 nm. Figures 8(a)–(d) show the I–L characteristics of each device, evaluated under pulsed conditions (with a repetition frequency of 1 kHz and a pulse width of 100 ns for a pulse duty cycle of 0.01%) at room temperature. The backside temperature of each device was kept at room temperature (∼24 °C), because the device was driven under pulsed conditions with a low duty cycle, where the temperature rise was negligible. As shown in these figures, the slope efficiency and threshold current vary with the p-cladding layer thickness. The variations in slope efficiency and threshold current were checked by measuring three devices with the same p-cladding layer thickness, and were found to be very small. Figures 8(e) and (f) show the dependence of the slope efficiency and threshold current density on the p-cladding layer thickness, evaluated from these I–L characteristics. The slope efficiency and threshold current density are periodic over a change of ∼140 nm to the p-cladding layer thickness, corresponding to a change of one wavelength in the p-cladding layer. Constructive interference of the reflected and upward-radiated light is considered to occur at a p-cladding layer thickness of ∼1130 nm, resulting in a high slope efficiency exceeding 0.8 W A⁻¹. Comparison of these experimental results with the theoretical analysis in the section 3.3 allowed us to estimate the surface radiation constant and in-plane loss to be α_v = 22 cm⁻¹ and α_// = 7 cm⁻¹, assuming that α₀ and A are 6 cm⁻¹ and 0.1, respectively. Fitting of the threshold current density was done assuming that the gain of the quantum wells, g, has a linear-fractional dependence [27] on the carrier density, N, i.e. g(N) = g_max(N− N_tr)/{N + [g_max/(−g₀)]N_tr}, where we set the transparency carrier density N_tr = 1.5 × 10¹⁸cm⁻³, the saturated gain g_max = 2000 cm⁻¹, and the absorption coefficient in the absence of carriers g₀ = − 5000 cm⁻¹.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Next, we evaluated the I–L characteristics and emitted beam patterns of a PCSEL, whose p-cladding layer thickness was set to 1130 nm, over a wider range of injected currents. Figure 9(a) shows the measured I–L characteristics. Owing to the high slope efficiency, a peak power exceeding 10 W was obtained at a lower current of ∼15 A than the previous device (∼25 A) [16]. As shown in the measured far-field patterns of figure 9(b) and a single-spot beam with a narrow divergence angle of ∼0.1° (evaluated using the FWHM beam width) and ∼0.17° (evaluated using the 1/e² beam width) was achieved at an output power of 10 W. Such high-beam-quality operation clearly suggests that the laser operates in a single fundamental mode and that the oscillations of higher-order modes have been suppressed by virtue of the newly designed photonic crystal. We also attribute the narrow divergence angle (∼0.1° at FWHM beam width) of the present device to the highly reflective DBR, which suppressed the direct nonuniform reflection effect from the p-side electrode. The nonuniform reflection from this electrode, which is only weakly reflective once it has been alloyed with the p⁺-contact laser, is nevertheless considered to have been partly responsible for the wider divergence angle (∼0.2° at FWHM beam width) in our previous device, which did not have a DBR.

Zoom In Zoom Out Reset image size

Considering LiDAR applications, it is desirable for the PCSEL to operate over a wide temperature range. Accordingly, in addition to the characterization at room temperature as described above, we also evaluated the dependence of the lasing characteristics of the PCSEL on temperature. As mentioned in the introduction, the lasing spectrum of PCSELs has a small dependence on temperature. This is because the lasing spectrum is fixed by the lattice constant of the photonic crystal. The oscillation wavelength of the photonic crystal (and thus the emission wavelength of the PCSEL) changes by ∼0.08 nm °C⁻¹ due to the change of the refractive index with temperature. However, it should be noted that the gain peak wavelength of the active layer (InGaAs/AlGaAs multiple quantum wells) also changes by ∼0.3 nm °C⁻¹, due to the change of its electronic bandgap with temperature. Due to these different rates of change, when the temperature is changed over a wide range, the deviation between the oscillation wavelength and the gain peak becomes large, which may cause an increase in the threshold current, a decrease in the output power, and mode hopping. Considering the above, for operation over a wide temperature range, we properly adjusted the lattice constant of the photonic crystal to minimize the deviation of the oscillation wavelength from the gain peak. To clarify the dependence of device performance on temperature, we evaluated the lasing characteristics under pulsed operation (with a repetition frequency of 1 kHz and a pulse width of 100 ns as above) at ambient temperatures ranging from −40 °C to 100 °C. Figure 10 shows the output power characteristics and lasing spectrum at various temperatures. Lasing oscillation was obtained over the entire temperature range, and the average rate of change of output power with respect to temperature over this range was small, at ∼0.36% °C⁻¹, which is similar to that of commercially available FP-lasers (∼0.4% °C⁻¹). It should be noted that the change in output power can be made smaller by further adjusting the lattice constant and the gain peak wavelength according to the required temperature range (for example, a range of high temperatures or low temperatures) for each application. In addition, figure 10(b) shows a narrow lasing spectrum at several temperatures, indicating that the laser operates in a stable lasing mode across the entire temperature range. The temperature dependence of the lasing wavelength is maintained at ∼0.08 nm °C⁻¹ in the range of −40 °C to 100 °C, which shows that the lasing wavelength is more stable than that of the conventional FP-lasers (∼0.30 nm °C⁻¹). These results clearly indicate that our PCSELs perform well under harsh practical conditions as required for LiDAR applications.

Zoom In Zoom Out Reset image size