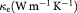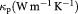Abstract
We present an implementation of the full-potential linearized augmented plane-wave method for carrying out ab initio calculations of the electronic and thermoelectric properties of d2/d0 type HfSiSb based on the density-functional theory. A most common generalized gradient approximation is taken into consideration for exchange-correlation energy. The electronic calculations show that HfSiSb is metallic in nature because of the overlap between the valence band and the conduction band. The thermoelectric properties, such as Seebeck coefficient, electronic thermal conductivity and electrical conductivity were calculated along the perpendicular and parallel directions with respect to chemical potential (µ) and temperature. In addition, we also included lattice thermal conductivity ( ) to obtain the total thermal conductivity. The presence of total thermal conductivity gave us an exact understanding of the material's thermodynamics and its efficiency (ZT). A sharp variation in ZT in the range (200–400 K) was seen, which makes this compound suitable at around room temperature.
) to obtain the total thermal conductivity. The presence of total thermal conductivity gave us an exact understanding of the material's thermodynamics and its efficiency (ZT). A sharp variation in ZT in the range (200–400 K) was seen, which makes this compound suitable at around room temperature.
Export citation and abstract BibTeX RIS
1. Introduction
The depletion of fossil fuels has led to a limitation of energy resources due to overgrowing global energy consumption. Thus, a novel renewable primary energy source is required that can supply clean energy without the emission of additional greenhouse gases [1], and this would also be a possible solution to threats due to climate change. It is believed that thermoelectric materials can solve this problem. Thermoelectric materials can directly convert waste heat into electrical energy and do not require any moving parts or other environmentally unfriendly technology. They can be used for cooling as well as power generation devices [2]. The efficiency of a thermoelectric material is defined by its dimensionless figure of merit ZT expressed as
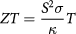
where S is the Seebeck coefficient,  the electrical conductivity, and
the electrical conductivity, and  the thermal conductivity.
the thermal conductivity.  is the electronic contribution to thermal conductivity and
is the electronic contribution to thermal conductivity and  the phononic contribution to thermal conductivity. So, the efficiency ZT can be expressed as,
the phononic contribution to thermal conductivity. So, the efficiency ZT can be expressed as,  . Materials with efficiency greater than or equal to unity are considered as efficient thermoelectric materials [3].
. Materials with efficiency greater than or equal to unity are considered as efficient thermoelectric materials [3].
In recent years, several materials have been studied to search for efficient thermoelectric materials. Other than narrow band gap semiconductors or semimetals, materials with low thermal conductivity and high carrier mobility are also suitable for thermoelectric applications [4]. Ternary antimonides are important materials for optoelectronic and microelectronic technologies [5] and are also being considered as potential thermoelectric candidates [6–8]. HfSiSb is a member of the family of ternary antimonides and has attracted much attraction for its excellent chemical, physical and structural stability. Dashjav and Kleinke have investigated the crystal structure and electronic properties of Ge based ternary antimonide HfGeSb and found it to be a thermoelectric material with a tetragonal structure [9]. HfSiSb is a hypothetical compound and it is assumed that this compound has the same tetragonal structure as that of Ge based compound. The vibrational and anisotropic elastic properties of HfSiSb were reported by Deligoz et al [10] and Ozyar et al [11], respectively. They reported that this compound crystallizes into a tetragonal ZrSiS-type structure. The studies also concluded that HfSiSb is both mechanically and dynamically stable. Furthermore, Deligoz et al [10] reported that this compound has very low heat transport, making it suitable for thermoelectric applications. In addition, HfSiSb has a metallic nature because of its high carrier mobility and low lattice thermal conductivity. The thermoelectric figure of merit ZT is a limiting factor to the efficiency of the material. Finding high ZT materials requires a complicated balancing of inter-related parameters such as charge carrier mobility with high thermopower, needed for high electrical conductivity along with low thermal conductivity [12]. Various methods exist for maximizing the efficiency, the most effective ones being the use of supperlattice or quantum well structures [13] and nanostructured engineering [14]. Studies by Slack [15] on skutterudites and Huang et al [16] on thermoelectric materials suggested that the nanocomposite approach is also very effective for increasing the thermoelectric efficiency, as it leads to strong phonon scattering, thus enhancing ZT. One simple method to enhance ZT is by optimizing the thermoelectric parameters suh as electrical and thermal conductivity, and this is what we have used. Materials with high atomic weights can decouple electrical and thermal conductivity, which leads to high ZT [17]. Metals have a high density of carriers and high  values, which are dominated by phonons, implying that the electrical and thermal conductivities are decoupled. In this context, systematic research on the inter-relationship between the electronic and thermoelectric properties for HfSiSb from the first principles approach is meager. Thus, we carried out a detailed investigation of these properties for the compound. The transport properties were calculated along the perpendicular and parallel directions. At around room temperature (from 200 K to 500 K), the perpendicular component of total thermal conductivity was calculated to be of the order of 102 and its parallel component to be of the order of 101. The thermal conductivity values are low as we expected. The paper outline is as follows: in section 2 we have present the computational details of our calculations and in section 3 we present our results, which are followed by conclusions in section 4.
values, which are dominated by phonons, implying that the electrical and thermal conductivities are decoupled. In this context, systematic research on the inter-relationship between the electronic and thermoelectric properties for HfSiSb from the first principles approach is meager. Thus, we carried out a detailed investigation of these properties for the compound. The transport properties were calculated along the perpendicular and parallel directions. At around room temperature (from 200 K to 500 K), the perpendicular component of total thermal conductivity was calculated to be of the order of 102 and its parallel component to be of the order of 101. The thermal conductivity values are low as we expected. The paper outline is as follows: in section 2 we have present the computational details of our calculations and in section 3 we present our results, which are followed by conclusions in section 4.
2. Computational details
We performed first principle calculations using the WIEN2k code [18] based upon the framework of density functional theory (DFT) [19, 20]. The electronic structure calculation was performed with the most conventional DFT exchange-potential, the generalized gradient approximation (GGA) [21] based on the full potential linearized augmented plane wave (FPLAPW) method [22, 23]. HfSiSb, when treated with the GGA, gave metallic characteristics and had a similar density of states (DOS) contribution along the spin up and spin down channels. For the well known self-consistent field calculation, we used cut off energy = −6.0 Ry, RMT × Kmax = 7 and k-points = 10 000 to create 28 × 28 × 12 k mesh in the first Brillouin zone. Out of the 10 000 k-points 1893 irreducible part of the k-points were used for first Brillouin zone integration. The charge and energy convergence criteria were set to 0.001 e− and 0.000 01 Ry, respectively. The semi-core states were treated ignoring spin orbit coupling, i.e. they were treated semi-relativistically. The calculation of transport properties involved a post DFT treatment, which involved the semiclassical Boltzmann transport theory within the constant relaxation time approximation (RTA), assuming directional independence of relaxation time τ, and the rigid band approach, as implemented in BoltzTraP code [24]. This approach has been proven to be very efficient and has been used in various similar studies [25–27]. The natural output of the energy band from the first principles calculation is taken as the key input for the calculation of thermoelectric properties. The Fermi energy at zero temperature (T = 0 K) was taken as the chemical potential (µ) in the transport calculation. In addition to electron thermal conductivity, we also considered the lattice thermal conductivity calculated from anharmonic lattice dynamics based on the RTA–BTE (relaxation time approximation-Boltzmann transport equation) [28].
3. Results and discussions
3.1. Crystal structure
HfSiSb is a hypothetical compound and we have assumed that it has the same structure as Ge based HfGeSb. HfGeSb crystallizes in a ZrSiS-type structure possessing tetragonal-phase with P4/nmm space group. A unit cell of HfSiSb consists of six atoms occupying three two-fold positions: Hf on 2c (1/4, 1/4, 0.2420), Si on 2a (3/4, 1/4, 0) and Sb on 2c (1/4, 1/4, 0.6112) [11], see figure 1. Structural optimization based on Murnaghan's equation of state [29] was performed to obtain the relax structure with minimum energy.
Figure 1. Crystal structure and corresponding volume optimization curve for HfSiSb.
Download figure:
Standard image High-resolution imageThe output of the volume optimization gives the equilibrium lattice constant, bulk modulus, its pressure derivative, etc. The smooth energy versus volumes curve is obtained by fitting the data in Murnaghan's equation of state (see figure 1). Unfortunately, to the best of our knowledge, there are no experimental results for the comparison of the calculated lattice constant, bulk modulus, etc. Thus we have compared it with that of the available theoretical ones, as shown in table 1. The change in the parameters are given by Δ. Our calculated value of the bulk modulus is 111.223 GPa, its pressure derivative is 4.644 and the optimized lattice constants are, a = 3.746 Å and c = 8.618 Å. It is seen that the present structural parameters of HfSiSb compound are in excellent agreement with the theoretical values of [11].
Table 1. Calculated equilibrium lattice parameters, bulk modulus (B) and its pressure derivative (B') of bulk modulus along with the available theoretical data.
| a (Å) | c (Å) | B (GPa) | B' | |
|---|---|---|---|---|
| Our result | 3.746 | 8.618 | 111.23 | 4.645 |
| [11] | 3.740 | 8.603 | 114.07 | 4.389 |
| Difference (Δ) | 0.006 | 0.015 | 2.84 | 0.256 |
3.2. Electronic properties
The optimal lattice constants obtained were used to study the electronic properties. To determine the thermoelectric properties it is necessary to obtain a good description of the electronic structure. The band structure, along with the DOS, is plotted in figure 2. The contribution of different electronic states in the valance and the conduction band determines the electronic property of the material. This is shown with the help of the total and partial DOS in figure 3.
Figure 2. Band structure along with the total DOS of HfSiSb.
Download figure:
Standard image High-resolution imageFigure 3. (a) Partial DOS of Hf, (b) partial DOS of Si, (c) partial DOS of Sb.
Download figure:
Standard image High-resolution imageIt can be clearly seen that no band gap is observed, implying that HfSiSb is a metal. In the Fermi level EF, there is no hybridization between the Hf-d2 and Si/Sb-d0 states and, hence, a band gap is missing. This is because of dispersed bands that are a result of the overlap between p-states of Hf with that of Si and Sb. The band structure is related to the Seebeck coefficient according to the formula  (
( is the band gap energy, e is the electronic charge, T is the absolute temperature and Smax is the maximum Seebeck coefficient) [30]. HfSiSb should have zero Seebeck coefficient as the observed band gap is zero. However, our calculated value of the Seebeck coefficient is of the order of 10−5. The band curves near the Fermi level are quite sharp in almost all directions except in the XM direction, where the band curves are flat in the valance band region. Sharp curves are beneficial for the Seebeck coefficient and this may be the reason for non-zero value of the Seebeck coefficient. From the partial DOS plots (figure 3) the maximum contribution to the total DOS is due to the Hf-d2 states (~4.2 eV) and there is an appreciable contribution from the p states of Si and Sb. Since Hf has the highest contribution near the Fermi energy, therefore the sharp peaks in the DOS are mainly due to d-state electrons. The DOS near the Fermi energy of HfSiSb is about 8 electrons eV−1, which is the main reason for high electrical conductivity. Thus, the electrons at the top of the valance band and those at the bottom of the conduction band mostly come from the d-orbital and some from the p-orbital. The sharp peak at 0–2 eV below the Fermi energy is due to the occupied dt2g (dxy, dxz, dyz) states while the peaks above the Fermi energy at around 2–6 eV are due to the unoccupied deg (dz2, dx2+y2) states. In comparison to the DOS results, it can be seen from the band structure results that the bands from 1.4 eV to 8 eV are due to the d-state electron of the Hf atom. The dense band at the vicinity of the Fermi energy (EF) is mostly due to the d-states of Hf atoms, whereas the thin bands away from EF are mainly due to the Sb-p and Si-p states. In the valance band region, from about −7.2 eV to 1.6 eV, the bands are dominated by the d-states of Hf atoms; the p-states of Si and Sb have a very low contribution. In the conduction band region, the contribution to DOS by all Hf, Si and Sb atoms is very small and is almost equal.
is the band gap energy, e is the electronic charge, T is the absolute temperature and Smax is the maximum Seebeck coefficient) [30]. HfSiSb should have zero Seebeck coefficient as the observed band gap is zero. However, our calculated value of the Seebeck coefficient is of the order of 10−5. The band curves near the Fermi level are quite sharp in almost all directions except in the XM direction, where the band curves are flat in the valance band region. Sharp curves are beneficial for the Seebeck coefficient and this may be the reason for non-zero value of the Seebeck coefficient. From the partial DOS plots (figure 3) the maximum contribution to the total DOS is due to the Hf-d2 states (~4.2 eV) and there is an appreciable contribution from the p states of Si and Sb. Since Hf has the highest contribution near the Fermi energy, therefore the sharp peaks in the DOS are mainly due to d-state electrons. The DOS near the Fermi energy of HfSiSb is about 8 electrons eV−1, which is the main reason for high electrical conductivity. Thus, the electrons at the top of the valance band and those at the bottom of the conduction band mostly come from the d-orbital and some from the p-orbital. The sharp peak at 0–2 eV below the Fermi energy is due to the occupied dt2g (dxy, dxz, dyz) states while the peaks above the Fermi energy at around 2–6 eV are due to the unoccupied deg (dz2, dx2+y2) states. In comparison to the DOS results, it can be seen from the band structure results that the bands from 1.4 eV to 8 eV are due to the d-state electron of the Hf atom. The dense band at the vicinity of the Fermi energy (EF) is mostly due to the d-states of Hf atoms, whereas the thin bands away from EF are mainly due to the Sb-p and Si-p states. In the valance band region, from about −7.2 eV to 1.6 eV, the bands are dominated by the d-states of Hf atoms; the p-states of Si and Sb have a very low contribution. In the conduction band region, the contribution to DOS by all Hf, Si and Sb atoms is very small and is almost equal.
A closer look at figures 3(b) and (c) shows that the maximum contribution of Si-p states (mainly from the pz orbital) to the total DOS is at −1.6 eV, whereas Sb-(px + py) contributed at −1.8 eV, below EF. Still, the sharp peaks at (1–2 eV) below EF are very small compared to the peaks due to Hf-d states. Thus, the hybridization between Hf-d2 and Si/Sb-d0 states are missing, and this may be the reason for deformed and dispersed DOS at EF. The band structure is directly related to the Seebeck coefficient, and from the Seebeck coefficient we can calculate the other transport coefficients. Unfortunately, there are no works reported on electronic properties of HfSiSb, either theoretical or experimental, for comparison.
3.3. Thermoelectric properties
The thermoelectric properties such as S, σ/τ, and κ/τ were calculated from the BTE in combination with the first-principles band-structure calculations using a simple rigid-band and the RTA. One of the demerit of BoltzTraP is that the relaxation time is not known. TiGeSb and TiSiSb compounds have negligible heat transport, hence it can be assumed that their relaxation time is constant [17]. Our calculation for electrical conductivity and electronic thermal conductivity are based upon the assumption that relaxation time is energy independent constant equal to 6.4 × 10−15 [31]. Thermoelectric parameters were calculated along the XX (perpendicular) direction and along the ZZ (parallel) direction due to the tetragonal structure of the compound. Figures 4 and 5 gives the thermoelectric parameters of TiXSb with respect to the chemical potential (µ). The positive trend in the Seebeck coefficient represents p-type carriers, while the negative trend indicates the n-type carriers. Along both the perpendicular and parallel direction, the magnitude of the n-type trend is larger, hence making HfSiSb n-type material. In order to ensure high Seebeck coefficient, there should only be one type of carrier. Mixed conduction of n-type and p-type will cancel out the induced Seebeck voltage [32]. From figure 4, the Fermi energy of thermoelectric parameters are considered corresponding to each temperature. The Fermi energy (EF) calculated was about 0.632 Ry. From figure 4(b) we see that at around the Fermi energy, the electrical conductivity values increase for increases in temperature along both the parallel and perpendicular directions for about 400 K temperature, after that the value decreases slightly with the increase in temperature. In figure 4(c), for the perpendicular direction, the electronic thermal conductivity increases with increasing temperatures; this is expected. For the parallel direction, the situation is a bit complex but can be assumed to have the same trend as that of the perpendicular direction. The complexity along the parallel direction may be due to lattice imperfections. The lattice thermal conductivities were estimated by the RTA–BTE, as implemented in the code Phono3py [28]. The thermal conductivity above 100 K is due to both the electronic as well as phononic contribution. Below 100 K, electronic thermal conductivity is negligible [33].
Figure 4. Thermoelectric parameters as a function of chemical potential (µ) along the X and Z directions at different temperatures: (a) Seebeck coefficient, (b) electrical conductivity, and (c) electronic thermal conductivity.
Download figure:
Standard image High-resolution imageFigure 5. Thermoelectric parameters as a function of temperature: (a) Seebeck coefficient, (b) electrical conductivity, (c) Electron and Lattice thermal conductivity and (d) total thermal conductivity.
Download figure:
Standard image High-resolution imageA plot of thermoelectric parameters as a function of temperature is shown in figure 5. The calculated Seebeck coefficient is quiet low, only of the order of 10−4 at room temperature (300 K). The values being −2.12 × 10−4 (V K−1) and -3.26 × 10−4 (V K−1) for the XX and ZZ directions, respectively. The negative sign in the Seebeck coefficient predicts the majority charge carriers are n-type. It is seen from figure 5(a) that the S value almost becomes constant for higher temperatures. This is because as the temperature increases, more electrons get excited, and the electrons tend to undergo mixed carrier concentration, thus cancelling the induced Seebeck voltage (see figure 4(a)). The electrical conductivity increases initially with the increase in temperature and then gradually decreases for high temperature values. This is because of high electronic thermal conductivity at higher temperatures. The highest ZT value is achieved at room temperature (200–300 K). The calculated ZT values at temperature range 200 K–300 K are ~0.25 and ~0.39 along the XX and ZZ directions, respectively. The calculated thermoelectric parameters at room temperature are presented in table 2.
4. Conclusions
Tetragonal HfSiSb shows metallic characteristics within the GGA. Moreover, treating correlated electrons more effectively from local density approximation plus Coulomb potential may give better description about the electronic and magnetic properties. The material under our investigation shows a significant response to external temperature. However, the calculated ZT value is not up to the benchmark value, ~1, for practical application. However, the material's response to temperature gradient indicates that ZT value can be enhanced by applying structural modifications such as nanostructuring and doping. The linear increase in Seebeck coefficient with rise in temperature is key. If HfSiSb is doped with heavy elements having d/f obitals, there might exist d–d orbital hybridization to open a band gap, leading to enhancemenet of the Seebeck coefficient. The enhanced Seebeck coefficient will finally optimize the ZT value. Further, tuning the electronic and lattice properties through elemental addition in unfilled lattice sites may enhance the phonon scattering, reducing the lattice thermal conductivity. These compounds operate best at room temperature. The best thermoelectric materials known to date are either narrow gap semiconductors or semimetals, thus a deep profound study of these materials may lead us to metallic thermoelectric materials functionable at room temperature.
Acknowledgment
HJ and RKT acknowledge research project grant from SERB (Government of India) EMR /2015/001407. This work has been also partially supported by the Research Fund of the Aksaray University. Project Number: 2016-037. D. P. Rai acknowledges DST-RFBR, Project Ref. No. INT/ 312RUS/RFBR/P-264.