Abstract
Realizing effective manipulation and explicit identification of topological spin textures are two crucial ingredients to make them as information carrier in spintronic devices with high storage density, high data handling speed and low energy consumption. Electric-field manipulation of magnetism has been achieved as a dissipationless method compared with traditional regulations. However, the magnetization is normally insensitive to the electric field since it does not break time-reversal symmetry directly, and distribution of topological magnetic quasiparticles is difficult to maintain due to the drift arising from external fluctuation, which could result in ambiguous recognition between quasiparticles and uniform magnetic background. Here, we demonstrate that electric polarization-driven skyrmionic and uniform ferromagnetic states can be easily and explicitly distinguished by transverse voltage arising from anomalous valley Hall effect in the Janus magnet-based multiferroic heterostructure LaClBr/In2Se3. Our work provides an alternative approach for data encoding, in which data are encoded by combing topological spin textures with detectable electronic transport.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Controlling magnetism by electric field is the fundamental avenue for realizing high-efficiency and extremely low-power consumption memories and logic devices [1–5], such as electric field-tunable magnetoelectric random access memories with low writing energy [6]. Multiferroic materials, with both ferromagnetism and ferroelectricity, are prospective candidates that can achieve electric-field modulation of ferromagnetism, magnetic direction, and magnetic anisotropy via the magnetoelectric coupling effect [7–10]. The topological magnetic quasiparticles, consisting of skyrmion and bimeron, have attracted intensive attention. Due to possess many advantages such as nonvolatility, small-size, and high mobility, these quasiparticles hold huge potential in spintronic devices for information technologies [11–13]. In 2016, it was reported that the skyrmion can be transformed to uniform ferromagnetism by electric field Fe/Ir(111) film with a scanning tunneling microscope [14]. Then, ferroelectrically tunable magnetic skyrmions have been demonstrated in ultrathin oxide BaTiO3/SrRuO3 heterostructure (HS) [15]. Compared with bulk or multilayered multiferroic materials, the two-dimensional (2D) van der Waals (vdW) magnetic/ferroelectric HSs promote much miniaturization, simpler structure, better tunability, and highly interface quality for spintronic devices [16]. Recently, writing and erasing of skyrmion and bimeron also has achieved in 2D multiferroic HSs MnBi2Se2Te2/In2Se3, LaCl/In2Se3, WTe2/CrCl3/CuInP2S6, and Fe3GeTe2/In2Se3, where MnBi2Se2Te2, LaCl, WTe2/CrCl3 and Fe3GeTe2 are vdW magnets with Dzyaloshinskii–Moriya interaction (DMI), while In2Se3 is an atomic ferroelectric (FE) material easily altered by out-of-plane (OOP) electric field [17–20]. The topological magnetic quasiparticles and ferromagnetic (FM) states are potentially encoded and stored as '1' and '0' bit carriers, respectively. However, the location of these quasiparticles is susceptible to external fluctuations, making it difficult to distinguish from FM state. This problem has been mentioned in the skyrmion-based racetrack-type memories, which need to be maintained skyrmion/bimeron distribution in the operational time scales [21, 22]. Notably, the reversal of FE polarization induces different electronic states of 2D FE-based vdW HSs in reciprocal space. For example, the switchable topological edge states, valley polarization, and metal-to-semiconductor phase transition are found in bilayer-Bi(111)/In2Se3 and β-Sb/In2Se3, HfN2/CrI3/In2Se3, and CrI3/Sc2CO2, respectively [23–26]. The band structures of a large variety of FE-aided vdW HS can be obviously regulated because the two surface of FE layer is nonequivalent induced by built-in electric field [27]. The above results imply that the variation of band structures controlled by FE polarization is hopefully used in unambiguously distinguishing spin configurations.
Here, employing the first-principles calculations and atomistic spin model simulations, we propose a type of magnetoelectric effect which can be realized in 2D Janus-based multiferroic vdW HS, LaXY/In2Se3 (X/Y= Cl, Br, I, X≠ Y), where LaXY can be constructed by replacing one of halogen atom in 2H-LaX2 and considered as an ideal candidate to realize FE-controlled electronic states and topological magnetic quasiparticles since it combines long-range ferromagnetism, robust valley polarization and inversion symmetry breaking-allowed DMI [28]. Moreover, LaXY monolayer has small lattice mismatch with room-temperature ferroelectric materials In2Se3. For LaClBr/In2Se3 HS, skyrmions embedded in domain walls (DWs) with metal state are transformed into uniform ferromagnetism with anomalous valley Hall effect (AVHE) by switching the direction of FE polarization from −z (P↓) to +z (P↑) axis, implying the skyrmionic and uniform FM state can be distinguished by transverse voltage of sample. Furthermore, skyrmion (bimeron) solitons in LaXY/P↓ are obtained by applying external magnetic field. Further analysis indicates that the topological magnetic phase transition attributed to the change of DMI caused by FE polarization, and the polarization-dependent band alignments are influenced by charge transfer between layers. Our work thus propose that approach for realizing unambiguous recognition of FE-controlled topological spin configurations under the assistance of band structures, and provides specific systems for realizing it.
2. Calculation method
All first-principles calculations are performed using the density functional theory (DFT) as implemented in the Vienna ab initio simulation package code [29–31]. The exchange and correlation functionals are treated by the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof functional [32, 33]. The interaction between ions and electrons is described by projector-augmented wave method [34]. After compared the magnetic parameters under the different cut-off energies (see table S1 and section S4 in supplementary material), the plane-wave basis set in 420 eV. To avoid interaction between adjacent layers, the thickness of vacuum layer is set no less than 15 Å along the z direction. We employ the GGA + U method with U = 7 eV to treat the f electrons for La as reported in the previous studies [18]. Brillouin zone is sampled using Г-centered 24 × 24 × 1 Monkhorst-pack k-point mesh. The electronic convergence is performed with a tolerance of 10−7 eV. Optimized structures are fully relaxed until the force converged on each atom less than 10−3 eV Å−1. To check the stability of the Janus LaXY monolayer, Phonon dispersions are calculated with 4 × 4 × 1 and 5 × 5 × 1 supercell by using the PHONOPY code [35], and ab initio molecular dynamics are simulated with 4 × 4 × 1 supercell in the canonical NVT ensemble [36]. The vdW interaction between LaXY and In2Se3 monolayer are corrected by DFT-D3 [37]. To avoid the influence of external strain from sublattice (table S2 and section S3 of supplementary material), by using 1 × 1 cell of In2Se3 to match 1 × 1 cell of LaXY, the lattice mismatch is 0.51%, 1.85%, and 3.09% for LaClBr/P, LaClI/P, and LaBrI/P, respectively. The maximally location Wannier function are calculated using WANNIER90 package code to obtain the Berry curvature and anomalous Hall conductivity [38]. More computational details are demonstrated in supplementary material.
3. Results and discussions
Figure 1(a) displays the top and side views of Janus LaXY (X/Y= Cl, Br, I, X≠ Y), which contain two atomic planes with different halogen elements and form hexagonal network with point group C3v. Bulk LaBr2 is a hexagonal layered crystal with a space group of P63/mmc [39], and LaBr2 monolayer has been proposed as an ideal FM semiconductor with Tc > 200 K [40, 41], Which is higher than that of CrI3 monolayer (45 K) [42] and Cr2Ge2Te6 bilayer (28 K) [43]. The optimized lattice constant of LaClBr, LaClI, and LaBrI monolayer is listed in table 1, and corresponding magnetic moment of La atom is 0.385, 0.374, and 0.371 μB, respectively. The structural stability, including the phonon dispersions (figure S1 shows that the other two monolayers are dynamically stable except for LaClI with small imaginary frequency around Г point) and molecular dynamic simulations (figure S2 shows that LaXY monolayers are thermal stability), are demonstrated in sections S1 and S2 of supplementary material. In2Se3 is a 2D vdW room-temperature FE material [44–46] and figure 1(b) presents its crystal structure, which the lattice constant is 4.108 Å. The position of center-Se layer in In2Se3 gives rise to the different OOP polarization P↓ and P↑, leading to the variation of magnetic and electronic properties in LaXY when In2Se3 is used as substrate. The successful synthesis of Janus monolayers of transition metal dichalcogenides (MoSSe, MoSH) and FE-aided HSs (MoS2/In2Se3) illustrate the experimental feasibility of construction of LaXY/In2Se3 multiferroic HSs [47–50]. The LaXY monolayers perform in-plane (IP) anisotropy, FM state and clockwise chirality DMI (see table S2). As described in section S3 of Supplementary material, we consider twelve stacking configurations of LaXY/P↓ (figure S3) and calculate the corresponding total energy (figure S4). We find that the P↓ state is always energetically more stable than P↑ state, which is consistent with previously generic trend [27]. The magnetic properties can be regulated by changing the interfacial coupling, when revers the OOP polarization of In2Se3 in the LaXY/In2Se3 HS. In table 1, the equilibrium interlayer distance of LaXY/P↓ is lower than P↑ due to the stronger interfacial coupling between LaXY and In2Se3 in P↑. Top and side views of the most stable structure of LaClBr/P↓ and LaClBr/P↑ are shown in figure 1(c), where the electric polarization is −0.103 and 0.113 eÅ u.c.−1, respectively. The polarization of LaClBr/In2Se3 is very close to that of In2Se3 monolayer (0.1 eÅ u.c.−1), indicating that the ferroelectricity of HS mainly comes from In2Se3 layer. In experiment, an OOP electrical field around 1 V nm−1 can flip the perpendicular polarization direction [46], which implies that the reversal of polar orientation is achieved using a large enough electric field in LaXY/In2Se3 HS.
Figure 1. Top and side views of the 2D (a) Janus LaXY, (b) In2Se3 monolayer, and (c) LaXY/In2Se3 heterostructure with P↓ and P↑ states. The shadow areas indicate the unit cell. The green, orange, brown, red and blue balls represent X, Y, La, In and Se atoms, respectively. Red vectors in (c) indicate clockwise (anticlockwise) spin configurations used to extract the in-plane DMI.
Download figure:
Standard image High-resolution imageTable 1. Calculated lattice constants a (Å), magnetic moment of La atom mLa ( ), equilibrium interlayer distance d (Å), magnetic anisotropy energy K (meV), nearest-neighbor exchange coupling J (meV), and in-plane DMI component
), equilibrium interlayer distance d (Å), magnetic anisotropy energy K (meV), nearest-neighbor exchange coupling J (meV), and in-plane DMI component  (meV) of LaXY/P↓ and LaXY/P↑ (X, Y = Cl, Br, I).
(meV) of LaXY/P↓ and LaXY/P↑ (X, Y = Cl, Br, I).
| a | mLa | d | K |
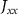
|

|

| J |
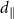
| |
|---|---|---|---|---|---|---|---|---|---|
| LaClBr/P↓ | 4.087 | 0.368 | 3.073 | 0.010 | 7.809 | 7.803 | 7.788 | 7.800 | 0.197 |
| LaClBr/P↑ | 4.087 | 0.381 | 3.101 | 0.009 | 6.757 | 6.754 | 6.739 | 6.750 | −0.008 |
| LaClI/P↓ | 4.184 | 0.351 | 3.172 | −0.050 | 8.141 | 8.124 | 8.073 | 8.113 | 0.597 |
| LaClI/P↑ | 4.184 | 0.364 | 3.224 | −0.090 | 7.071 | 7.069 | 7.013 | 7.051 | 0.167 |
| LaBrI/P↓ | 4.235 | 0.343 | 3.136 | −0.011 | 8.280 | 8.271 | 8.239 | 8.263 | 0.424 |
| LaBrI/P↑ | 4.235 | 0.358 | 3.195 | −0.073 | 7.281 | 7.277 | 7.222 | 7.260 | 0.158 |
In order to investigate the magnetic properties of LaXY/In2Se3, we adopt the following spin Hamiltonian:
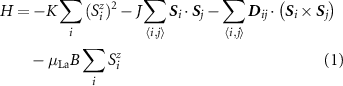
where  is a unit vector representing the orientation of the spin of the ith La atom, and
is a unit vector representing the orientation of the spin of the ith La atom, and  represents the nearest-neighbor (NN) La atom pairs. The magnetic parameters K, J, and
represents the nearest-neighbor (NN) La atom pairs. The magnetic parameters K, J, and  in the first three terms represent the magnetic anisotropy, exchange coupling, and interatomic DMI, respectively. And the
in the first three terms represent the magnetic anisotropy, exchange coupling, and interatomic DMI, respectively. And the  and
and  in the last term represent the magnetic moment of La and external magnetic field, respectively. Here we adopt the sign convention that K > 0 and K < 0 represent perpendicular magnetic anisotropy (PMA) and in-plane magnetic anisotropy (IMA), J > 0 and J < 0 indicates the FM and antiferromagnetic coupling, and the IP DMI component
in the last term represent the magnetic moment of La and external magnetic field, respectively. Here we adopt the sign convention that K > 0 and K < 0 represent perpendicular magnetic anisotropy (PMA) and in-plane magnetic anisotropy (IMA), J > 0 and J < 0 indicates the FM and antiferromagnetic coupling, and the IP DMI component  > 0 and
> 0 and  < 0 favor spin configuration with anticlockwise (ACW) and clockwise (CW) (as marked in figure 1(c) with red vectors), respectively. We first calculate the magnetic parameters of LaClBr/In2Se3 with Br–Se and Cl–Se interface contact, which constructed by switching LaClBr layer along z direction of the most stable structure (table S3 and section S3 of supplementary material). When the interface contacts between LaClBr and In2Se3 changes, i.e. LaClBr layer is switched along z direction, DMI chirality is consequently reversed according to Maryia rules. That indicates the interface contact has a great influence on these systems, then we use the most stable structure in the following calculations (figure S4). The calculated details about these parameters are explained in section S4 of supplementary material, and the results are shown in table 1. The magnetic moment of La atom of LaXY/In2Se3 is slightly smaller than that of pristine LaXY. Compared with pristine LaXY, LaXY/P↓(↑) except for LaClBr/P↑ HS possess weaker IP anisotropy, higher exchange coupling and larger DM interaction. The magnetic anisotropy energy (MAE) shows that LaClBr/In2Se3 has weak PMA whose amplitude reaches to 0.010 and 0.009 meV for P↓ and P↑, respectively. The LaClI/In2Se3 and LaBrI/In2Se3 both have an easy magnetization plane, i.e. they exhibit IMA. We then calculate the NN exchange coupling with magnetization along positive directions of x, y, z axis, Jxx, Jyy, Jzz
, and spin–orbit coupling (SOC) effects are also considered in calculations. We find that the NN exchange coupling of all systems remain FM state and are almost isotropic along different directions, indicating that the average of magnetic coupling parameter J can be defined to represents coefficient of the second term in the equation (1). The second-nearest- and third-NN exchange couplings are much smaller than J and thus can be neglected in these systems (see section S4 and figure S6 of supplementary material). For P↓ and P↑, the exchange coupling barely changes. For example, J is tuned from 7.80 to 6.75 meV in LaClBr/In2Se3 as the electric polarization reverses. Therefore, the electric polarization does not directly affect magnetic ordering of LaXY layer. In order to determine the transition temperature of the LaClBr/P↓(↑), we simulate the Curie temperature (Tc) using Monte Carlo method. As shown in figure S7, the Curie temperatures of LaXY/P↓ are around 100 K, and those of LaXY/P↑ are around 85K. For In2Se3, the ferroelectricity can sustain over room temperature which has been demonstrated in experimentally [46]. Remarkably, when direction of FE polarization reverses from down to up, the chirality of DMI of LaClBr/In2Se3 changes from ACW to CW, and the amplitude of DMI changes from 0.197 to 0.008 meV. Large variation of amplitude of DMI also emerges in LaClI/In2Se3 and LaBrI/In2Se3, while the chirality of DMI remains ACW. Ferroelectricity controllable DMI is expected to give rise the obvious variation of topological magnetic phases (see later discussions).
< 0 favor spin configuration with anticlockwise (ACW) and clockwise (CW) (as marked in figure 1(c) with red vectors), respectively. We first calculate the magnetic parameters of LaClBr/In2Se3 with Br–Se and Cl–Se interface contact, which constructed by switching LaClBr layer along z direction of the most stable structure (table S3 and section S3 of supplementary material). When the interface contacts between LaClBr and In2Se3 changes, i.e. LaClBr layer is switched along z direction, DMI chirality is consequently reversed according to Maryia rules. That indicates the interface contact has a great influence on these systems, then we use the most stable structure in the following calculations (figure S4). The calculated details about these parameters are explained in section S4 of supplementary material, and the results are shown in table 1. The magnetic moment of La atom of LaXY/In2Se3 is slightly smaller than that of pristine LaXY. Compared with pristine LaXY, LaXY/P↓(↑) except for LaClBr/P↑ HS possess weaker IP anisotropy, higher exchange coupling and larger DM interaction. The magnetic anisotropy energy (MAE) shows that LaClBr/In2Se3 has weak PMA whose amplitude reaches to 0.010 and 0.009 meV for P↓ and P↑, respectively. The LaClI/In2Se3 and LaBrI/In2Se3 both have an easy magnetization plane, i.e. they exhibit IMA. We then calculate the NN exchange coupling with magnetization along positive directions of x, y, z axis, Jxx, Jyy, Jzz
, and spin–orbit coupling (SOC) effects are also considered in calculations. We find that the NN exchange coupling of all systems remain FM state and are almost isotropic along different directions, indicating that the average of magnetic coupling parameter J can be defined to represents coefficient of the second term in the equation (1). The second-nearest- and third-NN exchange couplings are much smaller than J and thus can be neglected in these systems (see section S4 and figure S6 of supplementary material). For P↓ and P↑, the exchange coupling barely changes. For example, J is tuned from 7.80 to 6.75 meV in LaClBr/In2Se3 as the electric polarization reverses. Therefore, the electric polarization does not directly affect magnetic ordering of LaXY layer. In order to determine the transition temperature of the LaClBr/P↓(↑), we simulate the Curie temperature (Tc) using Monte Carlo method. As shown in figure S7, the Curie temperatures of LaXY/P↓ are around 100 K, and those of LaXY/P↑ are around 85K. For In2Se3, the ferroelectricity can sustain over room temperature which has been demonstrated in experimentally [46]. Remarkably, when direction of FE polarization reverses from down to up, the chirality of DMI of LaClBr/In2Se3 changes from ACW to CW, and the amplitude of DMI changes from 0.197 to 0.008 meV. Large variation of amplitude of DMI also emerges in LaClI/In2Se3 and LaBrI/In2Se3, while the chirality of DMI remains ACW. Ferroelectricity controllable DMI is expected to give rise the obvious variation of topological magnetic phases (see later discussions).
Once all the magnetic parameters J, K, and  in the spin Hamiltonian are calculated by first-principles calculations, we can perform the atomistic spin model simulations of LaXY/In2Se3 HS using the VAMPIRE package in a large enough space with a square length of 300 nm [51]. The initial spin direction is set to random states in the periodic boundary. Section S5 in supplementary material introduces more simulation details. The topological charge,
in the spin Hamiltonian are calculated by first-principles calculations, we can perform the atomistic spin model simulations of LaXY/In2Se3 HS using the VAMPIRE package in a large enough space with a square length of 300 nm [51]. The initial spin direction is set to random states in the periodic boundary. Section S5 in supplementary material introduces more simulation details. The topological charge,  , is adopted to quantify information of the skyrmion or bimeron, which all can be ascribed to Q = ±1. In the LaClBr/In2Se3 HS, skyrmions embedded in DWs transform into uniform OOP FM states are achieved by reversing the polarization from P↓ to P↑, as shown in figures 2(a) and (c), which origin from the significant difference of DMI strengths. Furthermore, in figure 2(b), we find the skyrmion solitons with Q = −1 is generated in LaClBr/P↓ by applying an OOP magnetic field along with the positive direction of the z axis (B↑). For P↓ state of LaClI/In2Se3 and LaBrI/In2Se3 HS, we obtain the chiral Néel DW arising from strong DMI (see figures S8(a) and (e)). It is worth noting that the DMI/exchange coupling ratio (|
, is adopted to quantify information of the skyrmion or bimeron, which all can be ascribed to Q = ±1. In the LaClBr/In2Se3 HS, skyrmions embedded in DWs transform into uniform OOP FM states are achieved by reversing the polarization from P↓ to P↑, as shown in figures 2(a) and (c), which origin from the significant difference of DMI strengths. Furthermore, in figure 2(b), we find the skyrmion solitons with Q = −1 is generated in LaClBr/P↓ by applying an OOP magnetic field along with the positive direction of the z axis (B↑). For P↓ state of LaClI/In2Se3 and LaBrI/In2Se3 HS, we obtain the chiral Néel DW arising from strong DMI (see figures S8(a) and (e)). It is worth noting that the DMI/exchange coupling ratio (| /J|) in LaClI/P↓ (0.074) is larger than in LaBrI/P↓ (0.051), which is consistent with the smaller width of the domain and DW energy in LaClI/P↓ compared with LaBrI/P↓ HS. Especially, isolated skyrmions are induced by using B↑ in LaClI (LaBrI)/P↓ (figures S8(b) and (f)), and bimerons consisted with a vortex and an anti-vortex appear in LaClI (LaBrI)/P↓ by applying an IP magnetic field along with +x axis (B→) (figures S8(c) and (g)). When the polarization is reversed to the P↑ state, the reduced DMI leads to small |
/J|) in LaClI/P↓ (0.074) is larger than in LaBrI/P↓ (0.051), which is consistent with the smaller width of the domain and DW energy in LaClI/P↓ compared with LaBrI/P↓ HS. Especially, isolated skyrmions are induced by using B↑ in LaClI (LaBrI)/P↓ (figures S8(b) and (f)), and bimerons consisted with a vortex and an anti-vortex appear in LaClI (LaBrI)/P↓ by applying an IP magnetic field along with +x axis (B→) (figures S8(c) and (g)). When the polarization is reversed to the P↑ state, the reduced DMI leads to small | /J| of 0.024 and 0.022 for LaClI/P↑ and LaBrI/P↑, respectively, accompanied by IP FM state (figures S8(d) and (h)). The chiral spin textures and FM states are used to '1' and '0' bit carriers by switching the FE polarization for encoding and storing information. However, the location of these spin textures is susceptible to thermal fluctuations or electric current, making it difficult to distinguish from FM state.
/J| of 0.024 and 0.022 for LaClI/P↑ and LaBrI/P↑, respectively, accompanied by IP FM state (figures S8(d) and (h)). The chiral spin textures and FM states are used to '1' and '0' bit carriers by switching the FE polarization for encoding and storing information. However, the location of these spin textures is susceptible to thermal fluctuations or electric current, making it difficult to distinguish from FM state.
Figure 2. The spin textures for (a) LaClBr/P↓ and (c) LaClBr/P↑ in real space. (b) The skyrmion solitons are created in LaClBr/P↓ at external field. The color map indicates the out-of-plane spin component of La atoms.
Download figure:
Standard image High-resolution imageNext, we focus on the electronic properties of LaXY/In2Se3 HS and use it to realize unambiguously recognition of different signal. Figures 3(a) and (b) show the spin-resolved band structures with SOC of LaClBr/In2Se3 HS, where the conduction bands and valence bands near the Fermi level consisting of carriers with the opposite spin. The LaClBr/P↓ performs metallic character while LaClBr/P↑ possesses an indirect band gap of 48 meV, and the nondegenerate valleys appear in the valence band maximum (VBM) at the −K and +K points. We also find that the metal state for LaClBr/P↓ preserves when the magnetic orientation rotates, as shown in figure S9. The easy magnetization orientation of LaClBr/In2Se3 is along +z and it can be turned form OOP to IP by overcoming an energy barrier of 10 and 9 meV for LaClBr/P↓ and P↑, respectively. When we rotate the magnetization from −z to +z axis, the valley polarization for P↓(P↑) defined as the energy different between VBM at +K and −K, ΔE = EVBM,+K
−EVBM,−K
, varies from −26.09 (−24.43) to 26.09 (24.43) meV (figure 3(c)). The quantitative relationship between magnetization orientation and valley polarization is consistent with previous conclusion, i.e. ΔE
 4cosθ, where the θ is the angle between the direction of spin and +z axis [17]. That means the valley splitting will gradually disappear as spin rotates from OOP to IP, which has been confirmed by first-principles calculations in figure 3(c). To demonstrate the AVHE which arises from the valley polarization, we calculate the Berry curvature of LaClBr/P↑ HS according to the Kubo formula as [52]:
4cosθ, where the θ is the angle between the direction of spin and +z axis [17]. That means the valley splitting will gradually disappear as spin rotates from OOP to IP, which has been confirmed by first-principles calculations in figure 3(c). To demonstrate the AVHE which arises from the valley polarization, we calculate the Berry curvature of LaClBr/P↑ HS according to the Kubo formula as [52]:
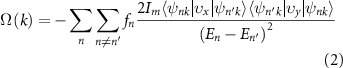
where  is Fermi–Dirac distribution function,
is Fermi–Dirac distribution function,  is velocity operator along x(y) direction, and
is velocity operator along x(y) direction, and  is Bloch wave function with eigenvalue En
. Figure 3(d) shows the Berry curvatures along the high-symmetry point in the whole 2D Brillouin zone, and the opposite signs and different absolute values are acquired at the −K and +K points while the values close to zero at other points. The anomalous valley Hall conductivity
is Bloch wave function with eigenvalue En
. Figure 3(d) shows the Berry curvatures along the high-symmetry point in the whole 2D Brillouin zone, and the opposite signs and different absolute values are acquired at the −K and +K points while the values close to zero at other points. The anomalous valley Hall conductivity  can be obtained by integrating the Berry curvature, which is expressed as [53]:
can be obtained by integrating the Berry curvature, which is expressed as [53]:
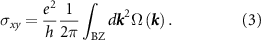
Figure 3. Spin-resolved band structures of (a) LaClBr/P↓ and (b) LaClBr/P↑. (c) The valley polarization ΔE as a function of magnetization orientation. The magnetization rotates from −z to +z. (d) For LaClBr/P↑, the distributions of Berry curvature in the whole Brillouin zone and the anomalous Hall conductivity as a function of EF.
Download figure:
Standard image High-resolution imageAs shown by labeled shadow in figure 3(d), when the EF is shifted between −K and +K valleys in the valence bands, a nonzero valley-polarized  is achieved, proving the existence of AVHE. However, for LaClI/In2Se3 and LaBrI/In2Se3, all band structures maintain metallic character under the influence of FE polarization even if the CBM lifts upward at P↑ state (figure S10). Generally speaking, we obtain the topological spin textures with metal state in P↓ and the trivial topological with valley polarization in P↑. Therefore, skyrmion state and uniform FM state with transverse voltage arising from AVHE can be used '1' and '0' bit carriers in data storage, which is modulated by switching the FE polarization in LaClBr/In2Se3 HS.
is achieved, proving the existence of AVHE. However, for LaClI/In2Se3 and LaBrI/In2Se3, all band structures maintain metallic character under the influence of FE polarization even if the CBM lifts upward at P↑ state (figure S10). Generally speaking, we obtain the topological spin textures with metal state in P↓ and the trivial topological with valley polarization in P↑. Therefore, skyrmion state and uniform FM state with transverse voltage arising from AVHE can be used '1' and '0' bit carriers in data storage, which is modulated by switching the FE polarization in LaClBr/In2Se3 HS.
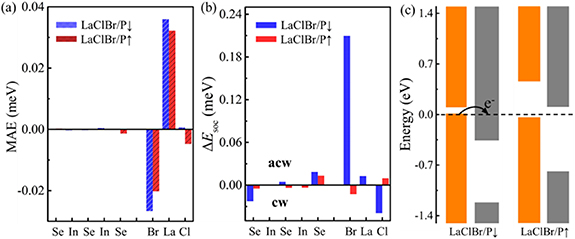
Then we analysis the physical mechanism of the FE-controlled magnetic phase and band structures transition of LaXY/In2Se3 HS. From the layer-resolved MAE of LaClBr/In2Se3 (figure 4(a)), LaClI/In2Se3 and LaBrI/In2Se3 (figure S11(a)), one can see that the MAE mainly comes from LaXY layer and the top-layer in LaXY basically does not contribute to the MAE. For LaClBr/In2Se3, the PMA of La is slightly larger than IMA of Br, while for LaClI(LaBrI)/In2Se3, both the La and X atoms contribute the IMA and the strength is enhanced significantly in P↑ compared with P↓. As shown in table S4, the DMI is reduced when the polarization of In2Se3 is changed to zero by placing all atoms at the local centrosymmetric positions, which means the electric field produced by polarization rather than the interfacial hybridization has the great importance in determining DMI. We further elucidate the layer-resolved SOC energy difference ΔESOC between the CW and ACW configurations for LaClBr/In2Se3 (figure 4(b)), LaClI/In2Se3 and LaBrI/In2Se3 (figure S11(b)). Strikingly, the sign and strength of DMI are mainly caused by the SOC from heavy elements, and the DMI of halogen atom which is close to the In2Se3 layer is increased obviously when the polarization of In2Se3 reverses from P↑ to P↓. The metal-to-semiconductor transition in LaClBr/In2Se3 HS based FE polarization is mainly due to the change of the band edge position of the In2Se3 layer. Figure 4(c) shows the band alignment of the LaClBr/P↓ and P↑ In the P↓ state, the conduction band minimum (CBM) of the In2Se3 layer becomes lower than the VBM of the LaClBr layer, exhibiting a type III band alignment with the vanishing of the band gap, whereas in the case of P↑ state, the system becomes type II semiconductor with the CBM and VBM derived from the In2Se3 and LaClBr layer, respectively. The fact that FE reversal-induced phase transition gives rise to the shift of electronic states of LaClBr/In2Se3 HS. Bader analysis exhibits that the charge transfer from LaClBr to In2Se3 decreases from 0.035 to 0.004e when FE polarization is changed from down to up [54]. We further calculate magnetic parameters of K, J, and  for LaClBr monolayer under 0.035e hole doping (table S2). These parameters are very close to that of LaClBr/P↓ HS, which indicate that the versatile properties in LaXY/In2Se3 is mainly derived from charge transfer between interface. Moreover, the planer-average charge-density difference shows that the charge is mainly transferred in In2Se3 layer of LaClBr/P↓ but restricted in the interface of LaClBr/P↑ (figure S12).
for LaClBr monolayer under 0.035e hole doping (table S2). These parameters are very close to that of LaClBr/P↓ HS, which indicate that the versatile properties in LaXY/In2Se3 is mainly derived from charge transfer between interface. Moreover, the planer-average charge-density difference shows that the charge is mainly transferred in In2Se3 layer of LaClBr/P↓ but restricted in the interface of LaClBr/P↑ (figure S12).
Figure 4. (a) Layer-resolved MAE of LaClBr/P↓ (black shaded bar) and LaClBr/P↑ (red shaded bar). (b) Layer-resolved localization of the associated SOC energy difference ΔESOC between clockwise and anticlockwise spin configurations in LaClBr/P↓ (black bar) and LaClBr/P↑ (red bar). (c) Band alignment of LaClBr/P↓ and LaClBr/P↑ heterostructures. The orange and grey bar represent the LaClBr and In2Se3 layer, respectively.
Download figure:
Standard image High-resolution image4. Conclusion
In summary, we systematically investigate the chiral spin configurations in real space and electronic band structures in reciprocal space by modulating FE polarization of 2D vdW multiferroic LaXY/In2Se3 HS via the first-principles calculations and atomistic simulation. The strength of DMI decrease apparently when the polar orientation is turned from P↓ to P↑, resulting in skyrmions in DWs are transformed into uniform ferromagnetism. By applying OOP or IP magnetic field, the skyrmion or bimeron solitons can be achieved in P↓, respectively. The generation of these topological magnetic quasiparticles could be used as a carrier of information transmission in spintronic devices. On the other hand, the electronic band structures are modulated easily by reversal of electrical polarization of LaXY/In2Se3 HS. Especially for LaClBr/In2Se3 HS, the metal-to-semiconductor phase transition is realized by flipping the polarization states from down to up, accompanied with valley polarization emergence. Detailed analysis demonstrates that charge transfers between LaClBr and In2Se3 layer play a crucial role in band alignments of HS: when P↓ is reversed to P↑ state, the conduction bands are lifted away from the Fermi level due to the reduce of the interlayer transferred charge. Therefore, the unambiguous recognition of different spin configurations is realized under the assistance of AVHE. Our work provides an alternative approach for data encoding, in which a data can be encoded by combing chiral spin configuration with untrivial electronic effects.
Acknowledgments
This work was supported by 'Pioneer' and 'Leading Goose' R&D Program of Zhejiang Province under Grant No. 2022C01053, the Key Research Program of Frontier Sciences, CAS (Grant No. ZDBS-LY-7021); National Natural Science Foundation of China (Grant Nos. 11874059 and 12174405); Zhejiang Provincial Natural Science Foundation (Grant No. LR19A040002) and Beijing National Laboratory for Condensed Matter Physics (Grant No. 2021000123).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Supplementary data (0.9 MB PDF)