Abstract
The cosine Gaussian beam (CGB) resulting from the coherent coaxial superposition of two Gaussian beams having the same width W and opposite radii of curvature R and − R is a ringed beam characterized by an M2 factor which can be very high, and adjustable by changing R. According to the paper by Hasnaoui et al(2011 Opt. Commun.284 1331–4) we expect that the CGB after 'rectification' by a binary diffractive optical element could be a good candidate for focal volume reduction, so useful to many laser applications. Unfortunately, this is not the case, and the physical factors responsible for this unexpected behaviour have been analysed. In particular, we have demonstrated that the three features (M2 factor, divergence and on-axis intensity) do not hold the same information about the spatial characteristics of rectified or unrectified CGBs.
Export citation and abstract BibTeX RIS
1. Introduction
Most laser applications need focusing of the laser beam, and the geometrical properties of the focal spot are of primary importance. These latter can be summarized through the following parameters.
- The focal spot size, determined on the basis of the second-order intensity moment [1] and denoted W0.
- The Rayleigh range or the depth of field, denoted zR, which corresponds to the longitudinal distance from the focus at which the beam width has been multiplied by a factor of
 .
. - The beam propagation factor [2], denoted M2, which becomes larger as the beam diverges more quickly after the focus. For a given value of W0, the beam is characterized by a Rayleigh range inversely proportional to the beam propagation factor:

- The on-axis intensity on both sides of the beam-waist plane.
- The focal volume Vf, i.e. the area where the intensity can be considered as high, plays an important role for the spatial resolution of the laser technique. It is defined by the following integral:

where W(z) is the beam width of the focused laser beam, which is expressed as [2]
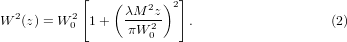
The origin z = 0 of the longitudinal coordinate is in the beam-waist plane of the focused beam. Let us consider the focal volume of the two following beams.
- Focal volume VG resulting from the focusing of a Gaussian beam (M2 = 1).
- Focal volume Vf resulting from the focusing of a beam having a beam propagation factor M2 > 1.
It is worthwhile to compare VG and Vf when the two beams have the same beam-waist size W0:

It is useful to recall that the focusing of a collimated Gaussian beam of width W incident on a converging lens of focal length f yields a Gaussian focal spot of width W0 given by

The associated focal volume VG is given by solving equations (1) and (2) for M2 = 1:

In order to reduce the focal volume given by equation (5) we can increase the incident beam width and reduce the focal length. However, due to the geometrical aberrations it is not indicated to increase excessively the beam width W. Indeed, the increase of the incident beam width on the focusing lens can yield a widening of the focal spot due to spherical aberration. Indeed, when light refracts through a lens with a spherical surface, the rays that pass through the outer diameters of the lens will focus at a different point from rays that pass through the centre. This causes the resulting intensity distribution in the focal plane to be widened, and this is why it is not indicated to increase excessively the beam width W for reducing the focal volume. In addition, for a given numerical aperture (NA) the ratio f/D is constant, where D is the lens diameter, and consequently reducing the focal length f is necessarily accompanied by a reduction of lens diameter. This is incompatible with an increase of W, due to aperturing effects, which could result from the reduction of D.
In a recent work [3, 4], we have proposed another approach for controlling the focal volume of a focused laser beam. The objective was to develop a new method based (figure 1) on reshaping of a particular laser beam for treating two fundamental issues.
Figure 1. Schematic optical layout for investigating the laser beam tailoring (rectification) ability of a binary diffractive optical element (BDOE) having a transmission alternately equal to + 1 and − 1 modelled on the zeros of intensity of the incident beam.
Download figure:
Standard image High-resolution image- (i)The generation of a special laser beam, having a beam propagation factor M2 > 1, which has the ability to give rise to a single-lobed beam in the focal plane of a converging lens and then to produce a focal volume smaller than the one resulting from an ordinary Gaussian beam as shown in equation (3).
- (ii)The decoupling between transversal and longitudinal resolutions within the focal volume. This is in contrast with the Gaussian beam whose depth of field is proportional to the square of its beam-waist radius W0.
The technique described in [3, 4] starts from a pure collimated high-radial-order Laguerre–Gaussian beam LGp0 which is made up of a central peak surrounded by p rings of light, and is characterized by a beam propagation factor M2 = (2p + 1). The electrical field Ein of the collimated LGp0 beam is given by
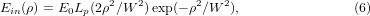
where Lp is the Laguerre polynomial of order p, and W the width of the Gaussian LG00 beam. The wavefront of the LGp0 can be viewed as alternately concentric out-of-phase rings. It is worthwhile to recall that the intensity profile in the focal plane is identical to that of the LGp0 beam incident on the lens. In contrast, the LGp0 beam can be transformed into a single-lobed beam [3, 4] in the focal plane provided that the incident beam is 'rectified' by an adequate diffractive optical element (DOE). The function of the latter is to convert the alternately out-of-phase rings of the incident LGp0 beam into a unified phase. This function corresponds to a 'rectification' of the wavefront. The rectifying DOE is simply a transparent phase plate made up of annular zones introducing a phase shift corresponding to alternatively to 0 or π. The phase discontinuities of the rectifying DOE coincide with the p intensity nulls of the incident LGp0 beam. The rectifying DOE is obviously a binary DOE, and as shown by Siegman [5] the rectified beam is found to have the same propagation factor M2 as the incident beam. It is important to note that the technique of in-phasing (rectification) of the light rings making up an LGp0 beam [3, 4] by using a phase plate including alternate zones introducing a phase difference of half-wavelength has been reported by Michelson in his book Studies in Optics published in 1927. This work concerned a 1D phase grating used to control the phase of the diffraction figure produced by a rectangular aperture. A more recent edition [6] of the book Studies in Optics was published in 1995, and deserves to be read because this experimental work of A A Michelson is not presented in most textbooks on optics.
We do not intend to present all the results given in [3, 4] but we will only make some comments about the property of transverse super-resolution that characterizes the focusing of a rectified LGp0 beam. We had found that, for a given W, the width of the focused rectified LGp0 beam is smaller than that of the Gaussian LG00 focused by the same lens and without any DOE. This effect has been improperly linked to a lateral super-resolution effect, and can be interpreted simply by the fact that an LGp0 beam is wider in the near-field ( ) than the Gaussian LG00 with the same value for W, hence resulting in a smaller spot size in the far-field, i.e. at the focal plane. The focused rectified LGp0 beam gives rise to a quasi-Gaussian pattern in the focal Plane, but the beam propagation factor remains almost unchanged [4] by the rectification, i.e. M2 = (2p + 1). As a consequence, the reduction of focal volume described in equation (3) can be achieved by the rectification of an LGp0 beam which creates a Gaussian intensity profile in the focal plane of a lens with a high value of M2, so that the beam diverges quickly on both sides of its focusing point. It is important to note that the operation of rectification achieves an efficient transfer of power from the rings constituting the LGp0 beam towards the central peak of the rectified beam in the focal plane [4].
) than the Gaussian LG00 with the same value for W, hence resulting in a smaller spot size in the far-field, i.e. at the focal plane. The focused rectified LGp0 beam gives rise to a quasi-Gaussian pattern in the focal Plane, but the beam propagation factor remains almost unchanged [4] by the rectification, i.e. M2 = (2p + 1). As a consequence, the reduction of focal volume described in equation (3) can be achieved by the rectification of an LGp0 beam which creates a Gaussian intensity profile in the focal plane of a lens with a high value of M2, so that the beam diverges quickly on both sides of its focusing point. It is important to note that the operation of rectification achieves an efficient transfer of power from the rings constituting the LGp0 beam towards the central peak of the rectified beam in the focal plane [4].
It could have been expected that any laser beam made up of rings and having a high beam propagation factor could be a good candidate, after rectification, for generating a reduced focal volume. However, in the following we will demonstrate that this is not always the case. By the way, it is important to note that the reduction of the focal volume can also sought by reducing the lateral size of the focal spot. For this, it is necessary to go beyond the diffraction limit, and this is possible for the family of vector beams, i.e. radially and azimuthally polarized laser beams [7–11].
To implement the method proposed in [3, 4] for reducing the focal volume, we need as a starting point an LGp0 beam, which can be obtained by forcing the laser oscillation on a single high-order transverse mode. This can be achieved for instance by inserting an amplitude mask inside the laser cavity [12], but sometimes it is inapplicable to some sealed lasers. Consequently, in this case the solution could be carried out in two steps. The first one should consist of transforming the Gaussian output beam of the laser into a ringed beam characterized by an M2 factor as high as possible, and which is in the following called a cosine Gaussian beam (CGB). The second step should achieve the rectification of the ringed beam and its focusing. These two steps are considered in section 2. In section 3 are considered the spatial characteristics of a focused unrectified CGB.
2. Rectification of a ringed beam
By means of the interference phenomenon it is easy to introduce rings of light in the cross section of a Gaussian beam. The coaxial superposition of two coherent Gaussian beams having the same width W and opposite radii of curvature (R and − R) gives rise to a modulated beam, a CGB, described by the following electrical field:
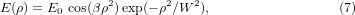
where β = π/(λR). As will be shown below, the ringed nature of the beam expressed by equation (7) is very sensitive to the radius of curvature R. The parameter β is a quantity inversely proportional to a squared length. For convenience, we introduce arbitrarily an undimensioned real parameter K defined as

All the numerical calculations are made with W = 1 mm and λ = 1064 nm. In contrast with the calculations presented in [3, 4] we will emphasize the variations of on-axis intensity after the couple (DOE + lens), because this gives a direct illustration of the efficiency of the beam transformation. In particular, this indicates the possible improvement of the focus intensity and especially the speed of decrease of on-axis intensity after the focal plane, which in principle should vary in the same way as the M2 factor. The intensity profile of the CGB, I(ρ) = |E(ρ)|2, is shown in figure 2 for K = 2. Note that the number of rings constituting the beam incident on the lens increases linearly with parameter K. It has been theoretically and experimentally recently shown that for K < 1 we have the possibility to transform a Gaussian beam into a bottle beam or top-hat beam in the focal plane of a converging lens [13]. Here, we consider the spatial properties of a rectified CGB. The rectification of the beam described by equation (7) is achieved by a binary diffractive optical element (BDOE) set before the focusing lens in order to convert the alternately out-of-phase rings of the CGB into a unified phase. The transmittance of the BDOE is + 1 or − 1, and the circles of phase discontinuities 0 − π and π − 0 are positioned on the zeros of cos(βρ2), which are given by
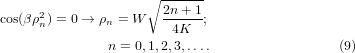
The transmittance of the BDOE is expressed as
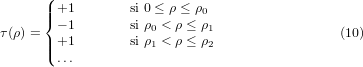
The electrical field ER associated with the rectified beam takes the following form:
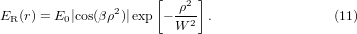
We will characterize the modulated beam and the rectified modulated beam after the lens by two quantities:
- the beam propagation factor M2;
- the on-axis intensity distribution which will give the information about the number of focal points, their position and their intensity.
Note that the spatial properties of the focused CGB have been treated in [13], except the beam propagation factor, which is considered below. By the way, one can notice that a few works have been published in the literature about the interferometric laser beam shaping techniques. Among them, some interesting features from laser beam shaping using coaxial superposition of laser beams concern the generation of optical singularities [10, 14, 15] or transverse and axial optical super-resolution [16].
Figure 2. Transverse intensity distribution I(ρ) = |E(ρ)|2 of the CGB E(ρ) defined by equations (7) and (8) for K = 2 and W = 1 mm.
Download figure:
Standard image High-resolution image2.1. Beam propagation factor
The calculation of the beam propagation factor  is based on the second-order moments 〈r2〉, 〈p2〉 in the spatial domain and spatial–frequency domain given by
is based on the second-order moments 〈r2〉, 〈p2〉 in the spatial domain and spatial–frequency domain given by
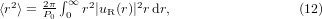
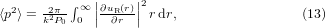
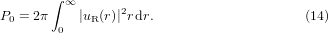
It is worth noting, according to Siegman [5], that the modulated Gaussian beam and the rectified Gaussian beam have the same M2 factor. If we apply equations (12)–(15) to the field u(r) = E0 cos(βr2)exp[−αr2], one finds easily using the software Mathematica
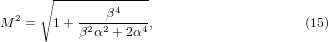
where we have set α = W−2. The variations of the M2 factor as a function of the number of rings follow a linear relationship as shown in figure 3. There is nothing surprising about this behaviour, since as the parameter K increases the number of rings also increases, and this contributes to introduce high spatial frequencies in the beam, making the M2 factor high. Note that to obtain a beam propagation factor of about 60 with an LGp0 beam the mode order has to be equal to p = 30, which cannot be envisaged from a practical point of view. At least, we have found a simple way of transforming a Gaussian beam into a ringed beam with an adjustable M2 factor. Now it remains to check if the rectified CGB can be a good candidate for yielding to a focal volume reduction.
Figure 3. Variations of the beam propagation factor M2 of the cosine Gaussian beam as a function of the number of rings.
Download figure:
Standard image High-resolution image2.2. On-axis intensity distribution of the rectified CGB
In the Fresnel approximation the diffraction field distribution uDR(r, z) associated with the rectified CGB after the lens of focal length f is given by the Fresnel–Kirchhoff formula
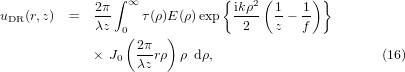
where ρ is the radial coordinate in the plane of the ensemble (DOE + lens), and r is the off-axis distance in the observation plane located at a distance z from the lens. The diffracted intensity distribution is defined as IDR(r, z) = |uDR(r, z)|2, and a quantity of importance giving an overview on the spatial properties of the diffracted field is the on-axis intensity distribution IDR(0, z). Since we are interested in on-axis points, we have then to evaluate the integral given by equation (16) for J0(0) = 1, which becomes
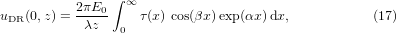
where we have set
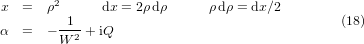


To solve equation (17) we will subdivide the integral depending on the transmittance τ being equal to + 1 or − 1:
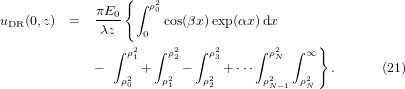
In equation (21), we have restricted the integration at the Nth circle of phase discontinuity of radius ρN so that the intensity of the Gaussian term is negligible. The radius ρN responds to


In summary we get
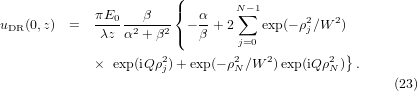
The on-axis intensity distribution of the rectified and unrectified beams, for K = 3, W = 1 mm, f = 50 mm and λ = 1064 nm, is shown with a logarithmic scale in figure 4. The CGB incident on the lens is made up of 14 rings.
Figure 4. Variation of the on-axis intensity as a function of the position z; the origin z = 0 is set in the plane of the couple (DOE + lens) for K = 3, f = 50 mm. The number of rings is 14. Dotted line, unrectified CGB; solid line, rectified CGB.
Download figure:
Standard image High-resolution imageThe following should be recognized.
- (i)The focused rectified modulated beam has two main focal points F1 andF2 which are laterally perfectly smooth (single lobed).
- (ii)The main focus F2 of the rectified CGB occurs in the focal plane of the lens whatever the value of K, and its width is very close to the beam waist fλ/(πW) = 16.9 μm and independent of the value of K.
- (iii)The second focus F1 is slightly less intense than F2 and occurs in a plane denoted zF1, which changes with K value. The fast decrease of the axial intensity is the signature of a sharper focal point. The latter has a width denoted WF1, which value together with zF1 is given in table 1. In the latter, also given for reference purposes, is the width
 and the position
and the position  of the focal point associated with the incident Gaussian beam having a radius of curvature − R. It is clearly seen that the focal point F1 is sharper than the beam waist of the Gaussian beam (W, −R) focused by the same lens of focal length f = 50 mm. Moreover, it is observed that
of the focal point associated with the incident Gaussian beam having a radius of curvature − R. It is clearly seen that the focal point F1 is sharper than the beam waist of the Gaussian beam (W, −R) focused by the same lens of focal length f = 50 mm. Moreover, it is observed that  , and in addition one notes that 1/zF1varies linearly with K. This can be interpreted in terms of a diffractive focusing effect associated with the binary DOE achieving the rectification of the CGB. Indeed, an ensemble of annular dephasing zones makes a zone plate having the property to focus light [18]. The refractive focusing effect of the lens competes with the diffracting lensing effect at the BDOE. Probably, the latter could be characterized by a focal length which should decrease with the number of rings as in a zone plate [19].
, and in addition one notes that 1/zF1varies linearly with K. This can be interpreted in terms of a diffractive focusing effect associated with the binary DOE achieving the rectification of the CGB. Indeed, an ensemble of annular dephasing zones makes a zone plate having the property to focus light [18]. The refractive focusing effect of the lens competes with the diffracting lensing effect at the BDOE. Probably, the latter could be characterized by a focal length which should decrease with the number of rings as in a zone plate [19]. - (iv)The key of this study is now to check if the two focal points F1 andF2 are characterized by a reduced depth of field, which could yield a focal volume reduction with regard to the possible large M2. The depth of field, at points F1 andF2, can be estimated by the distance over which the on-axis intensity decreases from its maximum by a factor of (2)−1/2. Unfortunately, it has been found that the depth of field around F1 (F2) is of order
 (
( ), as if the beam propagation factor M2 were equal to unity.
), as if the beam propagation factor M2 were equal to unity.
Table 1.
Parameters: W = 1 mm, f = 50 mm. Focus F1 of the rectified CGB: width WF1, position zF1. Focus of the Gaussian beam (W, −R): width  , position
, position  .
.
| K | WF1 (μm) | zF1 (mm) |  (μm) (μm) |
 (mm) (mm) |
|---|---|---|---|---|
| 0 | 16.9 | 50 | 16.9 | 50 |
| 1 | 14.6 | 41.2 | 15.3 | 45.2 |
| 2 | 11.8 | 35 | 13.9 | 41.2 |
| 3 | 10.2 | 30.5 | 12.8 | 37.9 |
| 4 | 9 | 27 | 11.8 | 35 |
| 5 | 8 | 24.2 | 11 | 32.6 |
| 6 | 7.3 | 22 | 20.3 | 30.5 |
| 7 | 6.8 | 20.1 | 9.7 | 28.6 |
| 8 | 6.1 | 18.5 | 9.1 | 27 |
| 9 | 5.7 | 17.2 | 8.6 | 25.5 |
| 10 | 5.3 | 16 | 8.2 | 24.2 |
| 11 | 5 | 15 | 7.8 | 23 |
| 12 | 4.7 | 14.1 | 7.4 | 22 |
| 13 | 4.5 | 13.3 | 7.1 | 21 |
| 14 | 4.2 | 12.6 | 6.8 | 20 |
| 15 | 4 | 11.9 | 6.5 | 19.2 |
| 16 | 3.9 | 11.3 | 6.3 | 18.5 |
| 17 | 3.7 | 10.8 | 6 | 17.8 |
The first conclusion that can be drawn is that a high value of the beam propagation factor M2 associated with the rectified CGB could implicate a high divergence, and then a rapid decrease of the on-axis intensity beyond the focal point. In other words, a high value of the M2 factor should signify a beam with a high divergence while the on-axis intensity variation of the rectified beam away from the two main focal planes seems to indicate that the divergence has the same order of magnitude as that of a Gaussian beam for which M2 = 1. In fact, the information held by the rate of variation of the on-axis intensity of the rectified beam contradicts that brought by the beam propagation factor M2. The quantities that are used for characterizing the lateral expansion of a laser beam are generally the M2 factor, the angular divergence θ and the Strehl factor. It has been recently shown that in some cases of particular laser beams or a Gaussian beam subject to amplitude or phase diffraction the Strehl ratio and the angular divergence are not correlated [20]. The CGB resulting from the coaxial superposition of two coherent Gaussian beams, and described by equation (11), is a particular beam, made up of a certain number of rings, characterized by a beam propagation factor M2, which can be large but even so characterized by an on-axis intensity varying as if the angular divergence is small. Although the beam given by equation (11) meets the conditions recalled in the introduction for achieving a focal volume reduction, we are forced to admit that this cannot be reached by resorting to the coaxial superposition of two coherent Gaussian laser beams. In this step, we have no choice but to doubt the accuracy on the M2 factor given by equation (15) and on the on-axis intensity deduced from equation (23). The determination of the on-axis intensity from a numerical calculation of the integral expressed by equation (16) gives the same results as those given by equation (23).
As regards M2 factor, we have used another approach close to the usual experimental technique for measuring the beam propagation factor of a laser beam. The intensity distribution IDR(r, z) = |uDR(r, z)|2 is calculated in 40 planes z after the lens by solving equation (16). For each plane z is deduced the width W2(z) based on the second moment order of the intensity distribution IDR(r, z):
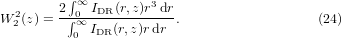
From the plot of W2 versus z, the longitudinal position, we get the waist spot size W0, the minimum value of W2(z) and its location z0. Then, the M2 factor is found from the fit with the following parabola:
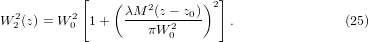
The M2 factor value obtained in this way is the same as the one given by equation (15), and confirms the linear variation shown in figure 3 with a difference which does not exceed 2%. Now, we have to understand why a laser beam having a beam propagation factor M2 ≫ 1 has an axial intensity decreasing with the longitudinal position as if its beam propagation factor should be close to unity. To answer this question it is necessary to consider the spatial properties of the unrectified CGB. This point is addressed in section 3.
3. Spatial properties of a cosine Gaussian beam
In the following we will use the notation introduced in [13]. Two Gaussian beams, beam 1 and beam 2, with radii of curvature R and − R, respectively, having the same width, W = 1 mm, and the same power, are incident on the focusing lens of focal length f = 50 mm. A critical value of K, denoted Kc is defined as follows [13]:

For all the calculations the critical value of K is Kc = 9.39. Following the value of K, the transformation of the two beams after the focusing lens takes different forms.
- (i)K < Kc: beam 1 focuses at a distance
 from the lens with a beam-waist radius
from the lens with a beam-waist radius  ; beam 2 focuses at a distance
; beam 2 focuses at a distance  from the lens with a beam-waist radius
from the lens with a beam-waist radius  .
. - (ii)K = Kc: beam 1 is collimated and beam 2 focuses somewhere after the lens.
- (iii)K > Kc: beam 1 diverges and beam 2 focuses somewhere after the lens.
The four quantities  ,
,  ,
,  and
and  are given in [13] but written here differently, as follows:
are given in [13] but written here differently, as follows:
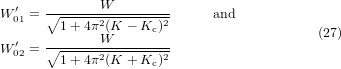
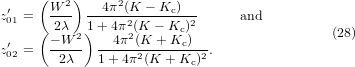
 and
and  means that the focal point is after (before) the position of the lens, meaning that the corresponding beam is focusing (diverging).
means that the focal point is after (before) the position of the lens, meaning that the corresponding beam is focusing (diverging).In the following, we will try to identify the reasons why the M2 factor of the beam resulting from the coaxial superposition of beams 1 and 2 is very large while its on-axis intensity has the properties of a beam having a beam propagation factor M2 ≈ 1. To do this, we will consider for sake of simplicity a rather incoherent coaxial superposition of beam 1 and beam 2. This means that the resulting intensity distribution is simply the sum of the intensity distribution associated with each beam, i.e. I(r) = I1(r) + I2(r).
It is important to note that the positions  and
and  correspond to the locations where on-axis intensity is maximum, as shown for instance in equation (4). Now, it is interesting to compare the values of
correspond to the locations where on-axis intensity is maximum, as shown for instance in equation (4). Now, it is interesting to compare the values of  and
and  with W0, the minimum of W2(z), the width of the beam resulting from the incoherent coaxial superposition of beam 1 and beam 2. Also, we will compare the distances
with W0, the minimum of W2(z), the width of the beam resulting from the incoherent coaxial superposition of beam 1 and beam 2. Also, we will compare the distances  and
and  with the distance z0. Before doing this, it is worthwhile to represent the longitudinal evolution of the widths Wp1 and Wp2 of the two Gaussian beams 1 and 2 after the lens. This is done in equation (5) for K = 5. Although in this case one observes two focal points, the caustic of the superposition of beam 1 and beam 2 represented by the variations of W2(z) in figure 6 shows only one minimum, while two could be expected. Moreover, the position z0 of the minimum of W2(z) is different from the two focal points located in planes
with the distance z0. Before doing this, it is worthwhile to represent the longitudinal evolution of the widths Wp1 and Wp2 of the two Gaussian beams 1 and 2 after the lens. This is done in equation (5) for K = 5. Although in this case one observes two focal points, the caustic of the superposition of beam 1 and beam 2 represented by the variations of W2(z) in figure 6 shows only one minimum, while two could be expected. Moreover, the position z0 of the minimum of W2(z) is different from the two focal points located in planes  and
and  , as shown in equation (6). Another important characteristic which can be deduced from the caustic of the coaxial superposition of beam 1 and beam 2 shown in figure 6(b) is the divergence θ. In table 2 are given the size and position of the different focal points associated with beam 1, beam 2 and (beam 1 + beam 2). In addition, table 2 gives for the case (beam 1 + beam 2) the value of the divergence θ together with the M2 factor deduced from the caustic as follows:
, as shown in equation (6). Another important characteristic which can be deduced from the caustic of the coaxial superposition of beam 1 and beam 2 shown in figure 6(b) is the divergence θ. In table 2 are given the size and position of the different focal points associated with beam 1, beam 2 and (beam 1 + beam 2). In addition, table 2 gives for the case (beam 1 + beam 2) the value of the divergence θ together with the M2 factor deduced from the caustic as follows:

It should be recognized that, although the number of rings (table 3) increases to N = 41 when K varies from 0 to 9, the divergence θ undergoes an increase of about 15% while the M2 factor is multiplied by a huge factor of about 47. The reason for this behaviour is the increase of the width W0 with K, which in turn is due to the surrounding pedestal of the beam resulting from the coaxial superposition of beam 1 and beam 2. To be convinced of the influence of the pedestal on the caustic of the beam, let us consider for instance in figure 5 the plane  where the beam 2 focuses into a spot of width
where the beam 2 focuses into a spot of width  , while beam 1 is very large, since its width is given by
, while beam 1 is very large, since its width is given by
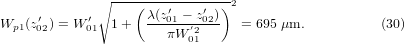
Since the two beams carry the same power, it turns out that the intensity associated with beam 2 is high but concentrated near the axis, while that of beam 1 is low and extends laterally far from the axis. This is the origin of the pedestal appearing in the intensity distribution of the beam resulting from the coaxial superposition of beam 1 and beam 2, as shown in figure 7.
Figure 5. Longitudinal variations of the widths Wp1 and Wp2 of beam 1 and beam 2, respectively, after a lens of focal length f = 50 mm for K = 5. The two Gaussian beams incident on the lens have the same width W = 1 mm. Note that beam 1 and beam 2 have the same width in the focal plane of the lens, z = f = 50 mm.
Download figure:
Standard image High-resolution imageFigure 6. W = 1 mm, f = 50 mm, K = 5. (a) Variations of the on-axis intensity of (beam 1 + beam 2). (b) Caustic of (beam 1 + beam 2).
Download figure:
Standard image High-resolution imageFigure 7. Transverse intensity distribution of beam 2 and (beam 1 + beam 2) showing the presence of a pedestal, in the plane  where beam 2 is focused. The parameters are W = 1 mm, K = 5 and f = 50 mm.
where beam 2 is focused. The parameters are W = 1 mm, K = 5 and f = 50 mm.
Download figure:
Standard image High-resolution imageTable 2. Characteristics of the three beams as a function of K: beam 1, beam 2 and (beam 1 + beam 2).
| Beam 1 | Beam 2 | Beam 1 + beam 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| K |  (μm) (μm) |
 (mm) (mm) |
 (μm) (μm) |
 (mm) (mm) |
W0 (μm) | z0 (mm) | θ (mrad) | M2 |
| 0 | 16.9 | 50 | 16.9 | 50 | 16.9 | 50 | 20 | 1 |
| 1 | 18.9 | 55.9 | 15.3 | 45.2 | 107 | 49.5 | 20.1 | 6.3 |
| 2 | 21.5 | 63.5 | 13.9 | 41.2 | 208 | 48 | 20.5 | 12.6 |
| 3 | 24.9 | 73.5 | 12.8 | 37.9 | 304 | 45.5 | 21 | 18.8 |
| 4 | 29.5 | 87.1 | 11.8 | 35 | 391 | 42.5 | 21.5 | 24.8 |
| 5 | 36.2 | 106.8 | 11 | 32.6 | 469 | 39 | 21.9 | 30.4 |
| 6 | 46.9 | 138.3 | 10.3 | 30.5 | 538 | 35.5 | 22.3 | 35.4 |
| 7 | 66.4 | 195.7 | 9.7 | 28.6 | 597 | 32 | 22.6 | 39.8 |
| 8 | 113.7 | 333.6 | 9.1 | 27 | 648 | 29 | 22.9 | 43.8 |
| 9 | 377.8 | 1032 | 8.6 | 25.5 | 691 | 26 | 23.1 | 47.2 |
Table 3. Correspondence between N the number of rings in the cosine Gaussian beam and the parameter K.
| K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| N | 5 | 9 | 14 | 18 | 23 | 28 | 33 | 37 | 41 |
In figure 8(b) is shown the influence of the pedestal in the numerical value of the integrand appearing in the numerator of equation (24), allowing the calculation of the caustic of (beam 1 + beam 2). For reference purposes the product I2(r)r3 for the focused beam 2 alone is given in figure 8(a). In fact, the presence of the cubic term r3 enhances dramatically the contribution of the wings of (beam 1 + beam 2), even though the intensity is weak. The presence of the pedestal justifies (i) why the caustic of (beam 1 + beam 2) shown in figure 6(b) displays only one minimum instead of two as suggested by figure 6(a), and (ii) why W0 is very large (table 2) in comparison with the smallest focal spot, i.e.  . All these conclusions are valid whether the coaxial superposition of beam 1 and beam 2 is coherent or incoherent.
. All these conclusions are valid whether the coaxial superposition of beam 1 and beam 2 is coherent or incoherent.
Figure 8. Variations of the integrand of the numerator of equation (24) allowing the calculation of the second moment order of the intensity distribution: (a) r3I2(r); (b) r3[I1(r) + I2(r)].
Download figure:
Standard image High-resolution imageBy the way, it is worthwhile to point out an unexpected behaviour which concerns the divergence angle of (beam 1 + beam 2). Although the presence of a pedestal in the region between planes  and
and  has the tendency to cause overestimation of the width W2 given by equation (24), one observes the contrary in the far-field region. Indeed, it is seen that for K = 9 the expected divergence of beam 2 alone is 30.3 mrad
has the tendency to cause overestimation of the width W2 given by equation (24), one observes the contrary in the far-field region. Indeed, it is seen that for K = 9 the expected divergence of beam 2 alone is 30.3 mrad  , while the divergence of (beam 1 + beam 2) is only 23.1 mrad (table 2), that is a decrease of about 70%.
, while the divergence of (beam 1 + beam 2) is only 23.1 mrad (table 2), that is a decrease of about 70%.
4. Conclusion
It is demonstrated that a coaxial superposition of two coherent Gaussian beams with axially offset beam-waists gives rise to a combined beam called a cosine Gaussian beam (CGB) characterized by a possible high M2 factor, which is adjustable by changing the radius of curvature of the two incident beams.
It could have been expected from the beginning that the rectified CGB described by equation (11) could be a good candidate for focal volume reduction. Indeed, its M2 factor can be high and easily adjusted, and is made up of many rings of light giving rise to a single-lobed intensity distribution in the focal plane. However, these conditions are not sufficient, since the rectified beam has to have also a very fast angular divergence to really achieve a focal volume reduction. The rectification of the CGB is achieved by a binary diffractive optical element (BDOE) in order to convert the alternately out-of-phase rings of the CGB into a unified phase. This ringed beam after being rectified and focused gives rise to a single lobe intensity distribution but without the expected focal volume reduction which has been observed with rectified Laguerre–Gauss beams [4].
As expected, this modulated beam is supposed to contain high spatial-frequency components, and effectively is characterized by a beam propagation factor M2, which has been found to be proportional to the number of rings. We can carefully conclude that the M2 factor has to be used with care when its value is high. Probably, we have also to admit that the M2 factor has an inherent limitation due to its definition based on the second moment order of the intensity distribution (equation (24)). Indeed, the cubic term r3, in the calculation of the second moment order of the intensity distribution, could enhance dramatically the contribution of the beam wings. It has been recently demonstrated [20] that amplitude and phase clippings that a laser beam suffers could disturb the information held by its main spatial characteristics (M2 factor, divergence, on-axis intensity). Contradictions between these parameters can also be found in the case of some free-propagation beams. One can cite the very well known example made up of the family of Bessel–Gauss beams called 'nondiffracting' beams, which are characterized by a large M2 factor together with a central lobe keeping its shape over a large distance [21]. This study shows that once again the description of the spatial properties of any laser beam has to be founded not only on a single parameter but on several, i.e. M2 factor, divergence and on-axis intensity.
Acknowledgments
The authors are grateful to Professor A Forbes of the National Laser Centre (Pretoria) for helpful discussions. The authors also acknowledge the financial support of the French Agence Nationale de la Recherche (ANR), through the programme 'Investissements d'avenir' (ANR-10-LABX-09-01), LabEx EMC3, and the Fond Européen de Développement Régional.




















