Second-harmonic generation in integrated nanosphere chains

In the past few decades, nonlinear optical harmonic generation [1] has been intensively studied because of its numerous applications in photonics [2–4], chemistry [5, 6], materials science [7], and biosensing [8, 9]. The increase of nonlinear conversion efficiency is a key factor for these applications. In the case of second-harmonic generation (SHG), different parameters must be considered in order to achieve high conversion efficiency. First, we should choose materials with large second-order nonlinear susceptibility such as Al_xGa_1−xAs semiconductor. However, the refractive index dispersion of the semiconductor makes it difficult to achieve the phase-matching condition which enables an optimal SHG. Thus, various methods have been proposed to overcome this difficulty. For example, the photon dispersion relations are tailored by periodic index modulations in photonic crystals, phase-matching resonant modes of frequencies close to the photonic band gap edge can be realized, and strong second-harmonic conversion processes can be achieved [10–12]. Another way is to embed the nonlinear material in an external resonant cavity by using resonance effects [13–16].

Recently, a subwavelength photonic circuit with dielectric particle arrays has been designed and guiding electromagnetic energy below the diffraction limit has been realized [17–21]. Based on such an investigation, highly efficient SHG in finite size dielectric nonlinear nanorod chains has been demonstrated [22]. However, the discussions only focus on the two-dimensional case. In our previous investigations [23], the SHG in three-dimensional structures consisting of arbitrary distributions of metallic spheres has also been discussed. In this work, we present a theoretical investigation of the SHG in a three-dimensional subwavelength photonic circuit consisting of spherical semiconductors with large second-order nonlinear susceptibility. The SHG in a single chain, around a corner, and split at forked structures will be analyzed.

We consider a chain composed of N spheres with radii r and separations d embedded in a background medium. The spheres are made of GaAs, whose permittivity has a real part ε = 12.25 and a negligible imaginary part in the frequency domain (3.6–34.0) × 10¹³ Hz [17, 24]. Recent investigations have shown that the contribution of surface susceptibility is not only detectable but can even give rise to a prominent feature in the bulk SHG spectrum of GaAs [25]. Therefore, to study the nonlinear scattering of spherical particles of GaAs, we consider the surface region to contribute through the tensor elements ${\chi }_{\mathrm{s},x y z}^{(2)}={\chi }_{\mathrm{s},x z y}^{(2)}={\chi }_{\mathrm{s},y x z}^{(2)}={\chi }_{\mathrm{s},y z x}^{(2)}=2 0 0~\mathrm{pm}~{\mathrm{V }}^{-1}$ [25]. Here the crystalline axis of GaAs (conventional (100) surface orientation) is arranged along the direction of the sphere chain (incident direction of the beam). We calculate the SHG of a single spherical particle according to [23, 26, 27].

In order to study the nonlinear response of the system, we employ the nonlinear multiple-scattering method [23]. Based on it, the second-harmonic (SH) field can be obtained exactly by numerical calculations. The main steps in the calculations are as follows. First, the fundamental frequency (FF) scattering field is determined by solving the linear multiple-scattering equation, which relates the scattering amplitude from each particle to the amplitude of the incoming wave by the scattering matrix. Such a field is used to compute the total nonlinear polarization at the SH. Once one knows the total nonlinear polarization at the FF one can determine the source field. Then, the scattering field at the SH is determined from the nonlinear multiple-scattering equations [23]. Finally, the SH field can be obtained from the sum of the source field and all the SH scattered field. The detailed description about the method has been given in [23].

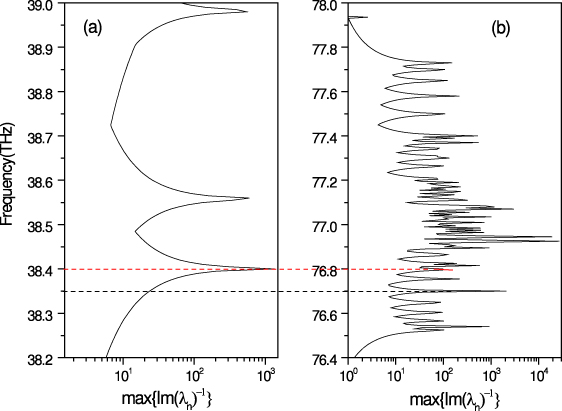
We first consider the waveguide modes of the FF field along the particle chain, which are characterized by the sharp peaks in max{|[Im(λ_n)]⁻¹|} versus the frequency [17]. Here λ_n is the nth eigenvalue of the FF scattering matrix. For a single particle, a peak in max{|[Im(λ_n)]⁻¹|} corresponds to a Mie resonance [28]. So the waveguide mode of the chain can be understood as a result of collective resonance due to the coupling among the Mie resonances of all constituent particles. Figure 1 shows the calculated results of max{|[Im(λ_n)]⁻¹|} as a function of the frequency for the chain with N = 20 spheres. Here GaAs spheres of radius r = 1.0 μm are placed at the x axis and separated by d = 3.0 μm. Figures 1(a) and (b) correspond to different frequency regions. At the low frequency region, Du et al have demonstrated [17] that transverse subwavelength confinement can occur for the guided mode (3.84 × 10¹³ Hz marked by the red dotted line in figure 1(a)) and the sphere chain supports the energy transfer below the diffraction limit. If the corresponding SH guide mode can be found, the SHG in the nanosphere chain is expected to be realized. Such a guide mode (7.68 × 10¹³ Hz) has been found at the present sphere chain as marked by the red dotted line in figure 1(b).

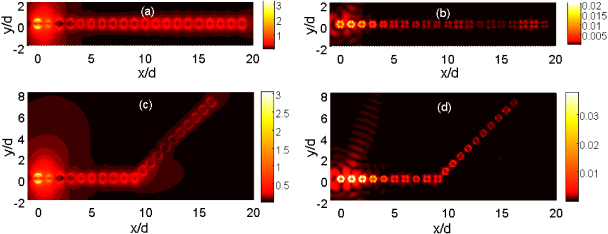
Zoom In Zoom Out Reset image size

To demonstrate such a phenomenon, we illuminate a chain of 20 spheres with an incident Gaussian beam of numerical aperture NA = 0.9 that propagates in the z direction with the E field polarized along y. The frequency of the beam is taken as 3.84 × 10¹³ Hz, corresponding to the peak marked by the red dotted line in figure 1(a). The beam is focused at the center of the first sphere in the chain. The distribution of the FF electric field intensity is displayed in figure 2(a). The propagation of the electromagnetic energy of the FF field below the diffraction limit over long distance is clearly seen and is similar to those in [17]. It is interesting that the corresponding propagating mode along the sphere chain for the SH field is also observed clearly, as shown in figure 2(b).

Zoom In Zoom Out Reset image size

The advantage of the SHG in the present system is that the high conversion efficiency can be obtained by taking advantage of subwavelength light confinement together with the resonant phase-matching condition [22]. From the analysis of the coupled mode model in the undepleted pump approximation, the conversion efficiency is a quadratic function of the photon lifetime [29]. This photon lifetime is related to the imaginary part of the scattering matrix's poles. The computation of the poles associated with the FF mode reveals that the lifetime increases with the cube of the numbers of spheres [18]. Therefore, the conversion efficiency increases theoretically at several powers of the chain length. For example, our simulation shows that the ratio of the SH field generated by the sphere chain with N = 20 and 10 is 18, and the corresponding result for the case with N = 30 and 10 becomes 63. In addition, we would like to point out that the conversion efficiency mainly depends on the transverse subwavelength confinement for the FF field, and the presence of the resonance at the SH frequency is not critical. For example, if we take the frequency 3.835 × 10¹³ Hz (marked by the dark dotted line in figures 1(a) and (b)), which deviates from the FF resonance, and only resonance at the SH frequency appears, the conversion efficiency in such a case reduces to half of the FF resonance case.

Another advantage of the SHG in the present system is that it is robust against disorder. We consider the case of site randomness. Such a disordered chain can be produced by randomizing the above ordered systems. Each sphere is moved randomly, but only within a range. Our calculated results show that the intensity of the SH field generated by the sphere chain with N = 20 decreases only 6% when the spheres are allowed to exhibit random displacements with a maximum amplitude equal to 15% of the spacing a₀.

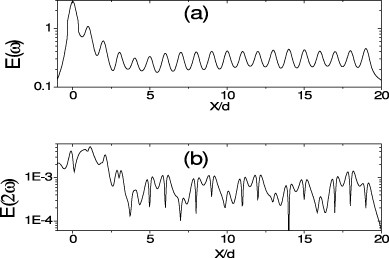
The advantage of the subwavelength dielectric waveguide is expected to have negligible loss in some spectral regions. Therefore, the SHG based on such a system is also expected to have less effect by the intrinsic absorption loss. Figure 3 shows distributions of the electric field intensity at a line parallel to the chain of 20 spheres and 1.1r above the chain axis subject to the beam excitation at 3.84 × 10¹³ Hz. Here the sphere's permittivity is taken as 12.25 + 0.02i, which represents a much bigger loss than the realistic case for GaAs at this frequency regime [24]. Figures 3(a) and (b) correspond to the cases of the FF and SH, respectively. The propagation of the FF electromagnetic energy is achieved with extremely small propagation loss, which is identical to the result in [17]. Comparing figure 3(b) with figure 3(a), we find that the effect of loss on the SHG is similar to that of the FF field.

Zoom In Zoom Out Reset image size

The energy transfer is not only along the linear sphere chain, it is also performed around corners. Figures 2(c) and (d) show the electromagnetic energy transfer in a corner structure composed of two linear arrays of spheres with a finite angle θ = 45° for the FF and SH fields, respectively. The other parameters are identical to those in figures 2(a) and (b). The incident Gaussian beam is also centered at the first sphere of the horizontal array. It is clearly seen from the field distributions that the electromagnetic energy for the FF field is guided around the corner, and this is also the case for the SH field. Similar to the FF case, the generation efficiency of the SH field is very high, for example, when θ = 30°, the maximum SH field intensity on the side arm can reach 85% of that on the main arm in the present case.

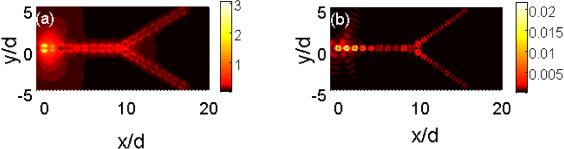
Sometimes integrated optics requires that information be transported efficiently at a bifurcate structure. Such a case can also be realized in the present sphere chain structures. Figures 4(a) and (b) show the energy splitting for the FF and SH field on a Y-type structure composed of three linear arrays, respectively. Each array consists of ten spheres, with two forked arrays forming an angle θ = 60°. When the horizontal main arm of the Y-shaped structure is illuminated by a Gaussian beam with 3.84 × 10¹³ Hz, the electromagnetic energy for the FF field is seen to transfer along the main arm and split into two parts on two side arms, and similar phenomena can also be observed for the SH field, as shown in figure 4(b). The field distributions on the two side arms bear close similarity to that on the horizontal main arm illuminated with the beam. Our calculations show that the maximum field intensity on each side arm reaches 80% of that on the horizontal main arm, indicating high SH conversion efficiency in energy splitting. With the increase of the angle between the two forked arrays, the SH conversion efficiency decreases. However, when θ ≤ 90°, the maximum field intensity on each side arm is also larger than 60% of that on the horizontal main arm. We would like to point out that the subwavelength waveguides serve to localize and guide electromagnetic energy in the subwavelength scale rather than acting as waveguides in the conventional sense, so the sum of the electromagnetic energy on the side arms may exceed that on the horizontal main arm due to the concentration effect of the near field. However, the sum of propagating powers in the split arms does not exceed the power of the input beam, as has been discussed in [17, 30].

Zoom In Zoom Out Reset image size

Based on the multiple-scattering method, we have investigated the SH generation process in a three-dimensional subwavelength photonic circuit consisting of semiconductors with large second-order nonlinear susceptibility. The SH fields along a single chain, around a corner, and split at forked structures have been demonstrated by using the three-dimensional confinement effects of subwavelength light. Our results open an interesting route for the design of integrated three-dimensional nonlinear devices.

This work was supported by the National Natural Science Foundation of China (Grant No. 10825416).