Abstract
In order to obtain the ground state of the biased quantum Rabi model in the ultrastrong coupling regime, a generalized squeezing rotating-wave approximation method including the displacement and the squeezing transformations is proposed in this work. While considering the deformation of the oscillator state, our method evidently improves the generalized variational method. The analyses of a few physical quantities show that our method works well especially in the ultrastrong coupling and large atomic frequency regime.
Export citation and abstract BibTeX RIS
1. Introduction
The quantum Rabi model (QRM) [1, 2] describes the coupling between a two-level atom and a bosonic field. Such model is of fundamental importance, since it has been widely applied in modern physics, such as in optical waveguides [3], superconducting circuits [4, 5], trapped ion [6] and so on. Given its great importance, there have been numerous theoretical studies on the Rabi model finding approximated solutions [7–9, 10–21]. Despite a great achievement of all those studies, the exact solution of QRM was only obtained recently [22–24]. This analytical solution, however, is in the form of composite transcendental function defined in power series, and it is not feasible to analyze the miscellaneous physical quantities of the QRM. Thus, theoretical research of finding the optimal analytical solution still attracts much attention.
In early days, the atom-field coupling strength of the Rabi model achieved in experiments is much smaller than the frequency of the field. Therefore, the QRM can be further simplified into the renowned Jaynes Cummings model (JCM) through rotating wave approximation (RWA), which ignores the counter-rotating-wave (CRW) terms [25]. With the tremendous development of experimental technologies, the strength of the light-matter coupling greatly increases. Recently one remarkable achievement is the realization of ultrastrong coupling [26–28]. To this end, the RWA breaks down [29, 30] since the effect of CRW terms is no longer negligible. In this respect, the generalized RWA (GRWA) [7] with a fixed displacement is proposed by considering the effect of CRW terms. However, the GRWA method does not perform well enough in the ultrastong coupling regime when the resonator frequency is small, and a more general variational method which relaxes the displacement is proposed [8, 9]. These approximation methods have been applied in the family of the QRM [8, 10–20].
The ultrastrong coupling of the QRM has been experimentally achieved in circuit quantum electrodynamics system due to operational conveniences [26–28, 30], and the so-called bias term is naturally involved. Compared to the standard form of the QRM, the additional bias term may bring in complication but more physics. For instance, the parity symmetry in the QRM is broken due to the presence of this bias. Given the interesting physics that come together with the bias term, it is therefore highly desirable to study the corresponding model analytically. Though there already exists some analytical discussions based on the GRWA and generalized variational method (GVM) for the biased QRM [9, 11], we find that there is still space to improve the accuracy in the ultrastrong coupling regime. The crucial idea to construct a close ground state in the widely used methods (e.g. GRWA, GVM) is to figure out the displacement of the oscillator. Since a quantum harmonic oscillator not only can be displaced but also can be squeezed, it is natural and necessary to consider the squeezing effect of the oscillator. The squeezing effect of the oscillator can be introduced in the same way with the displacement. The squeezing deformation of quantum state in the QRM can be naturally captured by an additional squeezing transformation applied onto the oscillator state, and thus substantial improvements may be anticipated. The squeezing plays an important role in high precision applications. For instance, it can be used to improve the sensitivity of gravity-wave detectors [31]. In quantum optics, the most common and useful way to create entangled states has been through squeezing [32–35], and it has been recognized that the intrinsic nonlinearities of atoms lead to quadrature squeezing [36–40]. With regard to this consideration, a generalized squeezing RWA (GSRWA) [15, 41] with an additional squeezing transformation was proposed to study the anisotropic QRM and shows high accuracy in large parameter regime. In this work, by taking both the displacement and squeezing transformations, we adopt the GSRWA by introducing a squeezing transformation to study the underlying physics of the biased QRM. The variational parameters in the GSRWA are determined by minimizing the ground-state energy. In order to show the improvement of our methods over the GVM, we also calculate several physical quantities by GVM and numerical method for comparison.
The paper is outlined as follows. In section 2, we give the Hamiltonian of the biased QRM and shows the details of our method. In section 3, we show the results of several physical quantities. In section 4, the applicable regime is discussed and a brief summary is finally given.
2. Model and analytical solution
Conventionally, the Hamiltonian of the biased QRM reads [42–45]
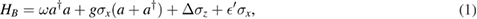
where 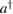
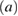 is the creation (annihilation) operator of the bosonic oscillator with frequency
is the creation (annihilation) operator of the bosonic oscillator with frequency  , Pauli matrix
, Pauli matrix 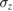 describes the two-level system with energy splitting
describes the two-level system with energy splitting 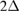 ,
,  is the biased term, and g is the coupling strength between the oscillator and the qubit. Taking a rotation of the spin along y -axis and replacing the parameters with
is the biased term, and g is the coupling strength between the oscillator and the qubit. Taking a rotation of the spin along y -axis and replacing the parameters with  and
and  , we can obtain
, we can obtain
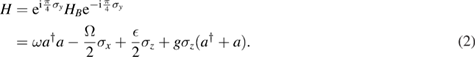
For convenience, the following discussions are focusing on Hamiltonian equation (2) by default.
The model Hamiltonian in equation (2) can be divided into the main part and the perturbation as

Here the displaced oscillator

is treated as the non-perturbed Hamiltonian, and

can be considered as the perturbation. The ground state of the unperturbed Hamiltonian in equation (4) is doubly degenerate, which can be expressed by the direct production of a spin eigenstate and a corresponding coherent state:

where 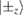 are the eigenstates of
are the eigenstates of  with eigenvalues
with eigenvalues 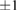 , and
, and  are the coherent states with
are the coherent states with  .
.
Taking the perturbation  into accounted, the ground state can be approximated by the linear combinations of equation (6) in the subspace of degenerate states:
into accounted, the ground state can be approximated by the linear combinations of equation (6) in the subspace of degenerate states:
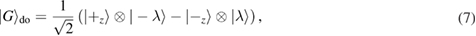
where  is unfixed, since
is unfixed, since 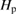 effectively reduces the distance of the displaced oscillator. The quantitative value of the
effectively reduces the distance of the displaced oscillator. The quantitative value of the  can be determined by a variational manner, namely, minimizing the ground-state energy function of the full Hamiltonian. The state in equation (7) is the starting point of the GVM, which has proven to perform better than the adiabatic approximation and the GRWA in a number of cases [8, 10, 12].
can be determined by a variational manner, namely, minimizing the ground-state energy function of the full Hamiltonian. The state in equation (7) is the starting point of the GVM, which has proven to perform better than the adiabatic approximation and the GRWA in a number of cases [8, 10, 12].
To proceed, the displacement in equation (7) can be understood through the unitary transformation on the vacuum state 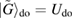
 , i.e.
, i.e.

where 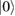 is the vacuum Fock state, and the incorporated displacement unitary operator is
is the vacuum Fock state, and the incorporated displacement unitary operator is

Correspondingly, the Hamiltonian in the transformed representation can be expressed as

Here  is introduced as a variational parameter rather than being fixed as
is introduced as a variational parameter rather than being fixed as 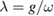 in GRWA, and this difference makes GVM obtain better accuracy. The transformed Hamiltonian reads
in GRWA, and this difference makes GVM obtain better accuracy. The transformed Hamiltonian reads

where
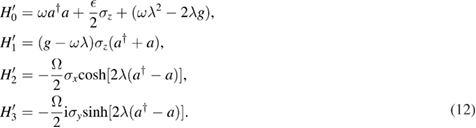
The hyperbolic cosine and sine terms can be further expanded as [46]
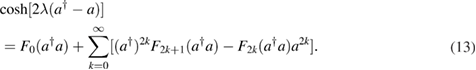
and
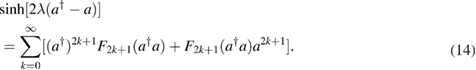
The function Fm is defined as
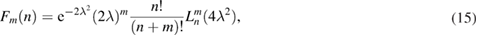
where m and n are integers, and

is the Laguerre polynomial. The detailed calculations see the appendix.
Similar to the displacement effect, the squeezing effect can be considered by a squeezing unitary operator

One can easily obtain the transformation of creation and annihilation bosonic operators as

Substitute equations (18) into (11) and the transformed Hamiltonian 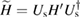 is rewritten as
is rewritten as

with

We note that in the bosonic Fock space  only has the diagonal terms, and
only has the diagonal terms, and 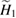 shows the off-diagonal terms with the first order of a (
shows the off-diagonal terms with the first order of a ( ). By comparison,
). By comparison,  and
and 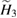 are more complicated. More precisely,
are more complicated. More precisely,  can be expanded as the sum of even power of a and
can be expanded as the sum of even power of a and 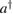 , while
, while 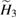 undertakes the sum of odd power of a and
undertakes the sum of odd power of a and  . It is noteworthy that the coefficients of diagonal terms in
. It is noteworthy that the coefficients of diagonal terms in 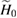 are evidently amplified through the squeezing transformation comparing with
are evidently amplified through the squeezing transformation comparing with 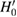 in (12), while the off-diagonal contributions in equation (20) are either unchanged or reduced. Especially for the variational parameter
in (12), while the off-diagonal contributions in equation (20) are either unchanged or reduced. Especially for the variational parameter 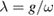 chosen in GRWA,
chosen in GRWA, 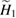 is vanishing. For the ultra-strong coupling regime we are interested in, we only consider diagonal terms of the Hamiltonian (19) in the following calculations, which leads to an effective adiabatic Hamiltonian:
is vanishing. For the ultra-strong coupling regime we are interested in, we only consider diagonal terms of the Hamiltonian (19) in the following calculations, which leads to an effective adiabatic Hamiltonian:
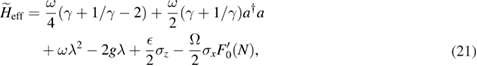
where  and
and 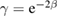 is defined for convenience. It is obvious that the Hamiltonian in equation (21) is analytically solvable. The basis can be chosen as
is defined for convenience. It is obvious that the Hamiltonian in equation (21) is analytically solvable. The basis can be chosen as 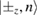 , where
, where  are the eigenstates of
are the eigenstates of 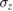 with eigenvalues
with eigenvalues  , and
, and 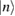 is the Fock state. The Hilbert space can be divided into different subspaces, in which the effective Hamiltonian equation (21) can be recast into the following form:
is the Fock state. The Hilbert space can be divided into different subspaces, in which the effective Hamiltonian equation (21) can be recast into the following form:

where  , and
, and  . From equation (22), the eigenstates and eigenvalues depending on the displacement variable
. From equation (22), the eigenstates and eigenvalues depending on the displacement variable  and the squeezing variable
and the squeezing variable 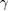 can be easily obtained as
can be easily obtained as
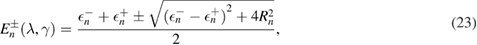
and
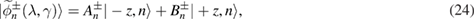
where
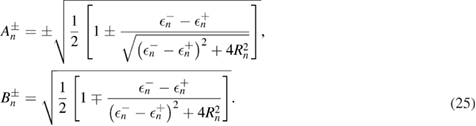
The ground-state energy reads
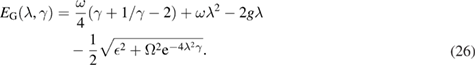
Taking  , the obtained energy spectra in equation (26) recover the GVM results [9]:
, the obtained energy spectra in equation (26) recover the GVM results [9]:
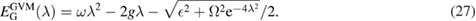
If one further set the variational parameter  , the GRWA result is recovered as
, the GRWA result is recovered as
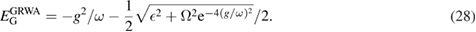
The variational parameters  and
and  in the GSRWA vary with
in the GSRWA vary with  ,
, 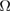 and
and  , and they can be determined by minimizing the
, and they can be determined by minimizing the  by solving
by solving  and
and 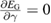 . These two nonlinear equations can not be easily solved in the analytical way. However, in the ultratrong coupling regime we interested in, the approximate solutions are
. These two nonlinear equations can not be easily solved in the analytical way. However, in the ultratrong coupling regime we interested in, the approximate solutions are
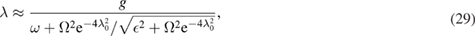
and

where  and
and  . With determined values of
. With determined values of  and
and 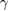 , we finally obtain the analytical formula of the ground-state wavefunction,
, we finally obtain the analytical formula of the ground-state wavefunction,
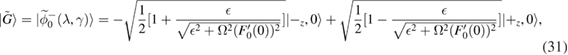
and the physical observables can thus be calculated.
Before going on, we would like to discuss the difference between our analytical method and the GVM. Equations (29) and (30) show that even if the parameter 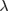 takes the same value as that in the GVM, another parameter
takes the same value as that in the GVM, another parameter 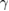 may play an essential role in lowering the ground-state energy. When g and
may play an essential role in lowering the ground-state energy. When g and  are small enough, the optimized
are small enough, the optimized 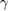 in our method approaches to 1, which is the exact value presumed in the GVM. However, when g and
in our method approaches to 1, which is the exact value presumed in the GVM. However, when g and 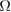 increase, the optimal value of
increase, the optimal value of  will no longer be 1. In other words, our method improves the precision of variational method when g and
will no longer be 1. In other words, our method improves the precision of variational method when g and  are sizeable.
are sizeable.
3. The observables and comparison with other methods
With the analytical ground-state wave function equation (31) in hand, in order to show the accuracy of the GSRWA quantitatively, we calculate several physical observables to compare with the results obtained by the GVM. The numerically exact diagonalized results are also involved as a benchmark. The quantum average of a physical observable Q is  , where
, where 
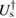
 . In this work, we take the ground-state energy
. In this work, we take the ground-state energy  , the mean photon number
, the mean photon number  , the spin orientation
, the spin orientation 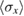 , and the correlation
, and the correlation 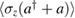 for illustration. For convenience, we set
for illustration. For convenience, we set 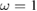 as an energy unit.
as an energy unit.
The ground-state energy obtained is given in equation (26). Figures 1(a) and (b) show the ground-state energy of the biased Rabi model as a function of g for different parameters. We see that both the results obtained by the GSRWA and the GVM agree well with the numerical ones for small coupling strength g. With the increase of g, the deviations between the GVM results and the numerical ones enlarges. In contrast, our results fit quite well with the exact ones. Figures 1(c) and (d) show the ground-state energy of the system as a function of  and
and  . It is obvious that our results are better than the GVM. From these comparisons, we find that the GSRWA works much better for large g and large
. It is obvious that our results are better than the GVM. From these comparisons, we find that the GSRWA works much better for large g and large  than the GVM. The precision has been greatly improved in a wide parameter regime.
than the GVM. The precision has been greatly improved in a wide parameter regime.
Figure 1. The ground-state energy  as a function of g,
as a function of g, 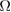 or
or  for different parameters. (a)
for different parameters. (a)  ,
, 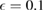 ; (b)
; (b) 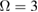 ,
,  ; (c) g = 0.7,
; (c) g = 0.7, 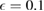 ; (d)
; (d) 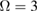 , g = 0.3.
, g = 0.3.
Download figure:
Standard image High-resolution imageNext we focus on the mean photon number

the spin orientation

and the qubit-cavity correlation

As is shown in figure 2, it is obvious that our results is quite close to the numerical results for large g, where there are clear deviations for the GVM results.
Figure 2. 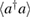 ,
, 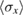 and
and  as a function of
as a function of 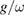 for different parameters. (a)
for different parameters. (a)  ,
, 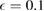 ; (b)
; (b)  ,
,  ; (c)
; (c)  ,
,  ; (d)
; (d) 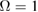 ,
,  .
.
Download figure:
Standard image High-resolution imageAnother interesting quantity characterizing the squeezing effect is the square of the squeezing strength

In figure 3, we make the comparison of  calculated by different methods. One observes the result obtained by GVM is a constant −1, but in our method,
calculated by different methods. One observes the result obtained by GVM is a constant −1, but in our method,  changes with other parameters. The result of
changes with other parameters. The result of  through our method is in good agreement with the numerical results when
through our method is in good agreement with the numerical results when 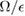 is large, which indicates that it is necessary to take the squeezing effect into account, and our GSRWA method is a convincing way to reveal the squeezing effect of the ground-state wave function.
is large, which indicates that it is necessary to take the squeezing effect into account, and our GSRWA method is a convincing way to reveal the squeezing effect of the ground-state wave function.
Figure 3. 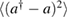 as a function of g,
as a function of g,  and
and  for different parameters. (a)
for different parameters. (a) 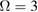 ,
, 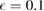 ; (b)
; (b)  ,
, 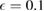 ; (c) g = 0.7,
; (c) g = 0.7, 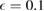 ; (d)
; (d)  , g = 0.3.
, g = 0.3.
Download figure:
Standard image High-resolution image4. Discussion and conclusion
As an approximation, it is necessary to discuss the applicable range of the method we proposed. It is shown that the GSRWA work quite satisfyingly for large g. According to the so-called polaron picture [47], in such ultrastrong coupling regime, the ground-state energy can be well approximated by a single oscillator. Although some numerical methods have already considered the squeezing effect [48], the analytical results are relatively rare for an intuitive picture The parameter 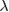 describes the displacement effect. From equation (29), we see that the optimal value of
describes the displacement effect. From equation (29), we see that the optimal value of  is independent of squeezing rate
is independent of squeezing rate  , while the squeezing effect is sensitive to the rate of
, while the squeezing effect is sensitive to the rate of 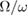 and
and 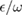 shown in equation (30). When
shown in equation (30). When  is large, the
is large, the  is nonnegligible. The difference between our method and the GVM is noticeable. In such a case, our method evidently improves the GVM. When
is nonnegligible. The difference between our method and the GVM is noticeable. In such a case, our method evidently improves the GVM. When 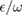 is large, the
is large, the 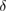 is small, and it implies that a large bias reduces the squeezing.
is small, and it implies that a large bias reduces the squeezing.
We would like to point out that the analytical method is challenged for large 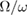 or large
or large 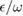 in the sense of perturbation in equation (5). In the large
in the sense of perturbation in equation (5). In the large  case, we limit our discussion to the ultrastrong coupling regime (
case, we limit our discussion to the ultrastrong coupling regime ( ). If the coupling strength becomes much larger, one oscillator approximation (single polaron picture) is not enough. In such a case, no matter how optimal the displacement and squeezing parameters are chosen, some important physics must be missed. In such a case, a novel critical regime meets. Plenty of interesting phenomena emerge [49–52].
). If the coupling strength becomes much larger, one oscillator approximation (single polaron picture) is not enough. In such a case, no matter how optimal the displacement and squeezing parameters are chosen, some important physics must be missed. In such a case, a novel critical regime meets. Plenty of interesting phenomena emerge [49–52].
In conclusion, in this paper we propose an approximation method to improve the GVM to study the biased QRM by introducing the squeezing transformation. Since the QRM is an oscillator-involved model, the wave packet of its ground state is naturally expected to be compressed. In the preceding literature, various transformations to the Hamiltonian are mainly limited to the displacement effect of the wave function. The comparison of several physical quantities with different parameters show that our method works well for larger coupling strength g and atom frequency  than the GVM. In these parameter regimes, the effect of deformation of the oscillator state can not be neglected. Thus the additional squeezing transformation brings a prominent improvement over the GVM. A natural question arises whether such approximation method considering both the displacement and the squeezing effects works well for the low-lying excited states. We hope our study is a starting point for further investigations and has potential applications in quantum thermodynamics and quantum computing, where a very accurate approximation for obtaining energy spectra is desired [53–56].
than the GVM. In these parameter regimes, the effect of deformation of the oscillator state can not be neglected. Thus the additional squeezing transformation brings a prominent improvement over the GVM. A natural question arises whether such approximation method considering both the displacement and the squeezing effects works well for the low-lying excited states. We hope our study is a starting point for further investigations and has potential applications in quantum thermodynamics and quantum computing, where a very accurate approximation for obtaining energy spectra is desired [53–56].
Acknowledgments
This work is supported by Ministry of Science and Technology of China (Grant No. 2016YFA0301300), National Science Foundation of China (Grant No. 11604009, 11474211). We also acknowledge the computational support in Beijing Computational Science Research Center (CSRC).
Appendix.: Calculation details of equations (13) and (14)
The associated Laguerre function defined by
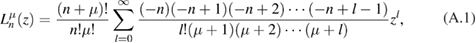
with its reduced form, namely the Laguerre function

For the operator production, we have
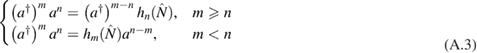
where
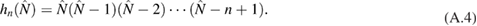
With the above equations in hand, we can obtain
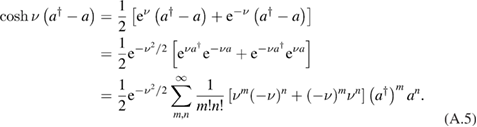
Here, we use the formula

For  , there is
, there is
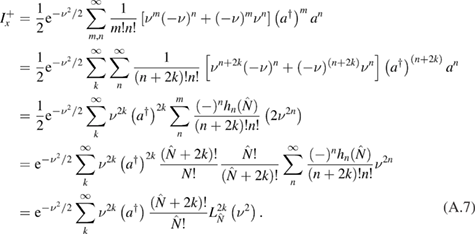
For  , there is
, there is
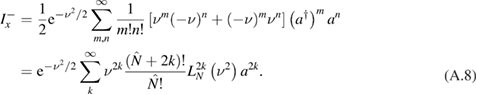
With the above all and the definition of Fm(n) in equation (15), the equation (13) can be obtained after some algebra. In the similar way, equation (14) can be obtained as well.




