H-mode plasmas in the pre-fusion power operation 1 phase of the ITER research plan

The ITER research plan (IRP) considers the option to investigate H-mode access and sustainment in the initial phase of pre-fusion power operation (PFPO-1) in hydrogen or helium plasmas to minimize scientific and operational risks for later operational phases in the IRP [1]. Specifically, H-mode operation in PFPO-1 would allow early determination of the required power to access and sustain H-modes in ITER, provide first evidence of the energy confinement level of H-mode plasmas in ITER, provide a first characterization of power fluxes to plasma facing components during edge localized modes (ELMs), and allow a first exploration of edge-core integration operational aspects in H-mode in ITER.

In this phase, the only heating and current drive scheme available in ITER is 20 MW of electron cyclotron heating (ECH) (170 GHz), and this poses specific restrictions to the H-mode scenario regimes that can be explored in this phase. An operational space for H-mode operation with 20 MW ECH has been identified for a toroidal field value of 1.8 T, taking into account the specificities of ECH for this value of the field (3rd harmonic) in ITER [2].

In this paper, we complement the studies in [2] with more detailed studies of H-mode access and plasma transport modelling and compare the predictions for ITER with experimental results. Edge-core compatibility issues and other H-mode aspects impacted by specificities of 1.8 T H-mode plasmas in ITER (e.g. impact of H-mode ripple) are discussed in order to identify the open issues that need to be addressed by further modelling and experimental R&D.

The paper is organized as follows: in section 2 we discuss the issues related to H-mode access at 1.8 T in ITER in PFPO-1, in section 3 we present the results of integrated transport modelling of 1.8 T H-mode plasmas in ITER with various first principle models, in section 4 we compare the results of the integrated transport modelling of 1.8 T ITER H-mode plasmas with relevant plasmas from present experiments, in section 5 we discuss edge-core and other integration issues in these plasmas and in section 6 we summarize our studies and draw conclusions.

The power required to access the H-mode (P_LH ) is evaluated for ITER on the basis of the ITPA 2008 scaling [3]:

$$\begin{equation}{P}_{LH,\mathrm{D}}=0.049{\times}{\bar{{n}_{e}}}^{0.72}{\times}{{B}_{t}}^{0.8}{\times}{S}^{0.94}\end{equation} \tag{ 1 }$$

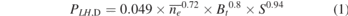
where S is the plasma surface (∼680 m² for ITER plasmas), $\bar{{n}_{\mathrm{e}}}$ is the line averaged density and B_t is the vacuum toroidal magnetic field at the geometric major radius. Note that this scaling is derived from a multi-machine database in deuterium plasmas dominated by devices with carbon plasma facing components. For devices without carbon plasma facing components, such as ASDEX Upgrade and JET–ILW, the H-mode threshold power is found to be lower [4, 5] by 30%–40%. However, we do not take advantage of this to estimate the H-mode power threshold because there are other unfavourable effects that may increase it with regards to the value given by equation (1), such as the large distance from the X-point to the divertor target in ITER [6, 7] and, possibly, the intrinsic level of plasma rotation [8], since the physics of the H-mode transition remains to be fully understood.

Equation (1) is derived for deuterium plasmas and thus needs to be adjusted to provide an evaluation of P_LH for other isotopes and ion species. For hydrogen plasmas the H-mode power threshold is found to be typically twice that of deuterium P_LH,H = 2 × P_LH,D, while for helium this is ${P}_{LH,\mathrm{H}\mathrm{e}}=\left[1\enspace \mathrm{t}\mathrm{o}\enspace 1.5\right]{\times}{P}_{LH,\mathrm{D}}$. The isotope scaling with ion mass (M) was originally identified in T, DT, D and H experiments at JET, P_LH ∝ M⁻¹ [9] and found to be a good guideline in other tokamaks and subsequent JET experiments with the precise value of the multiplier from H to D depending on plasma parameters [10].

He versus D has also been explored on DIII-D, ASDEX Upgrade, Alcator C-Mod and JET, most of the experiments in a C wall environment [11, 12]. When comparing He with D plasmas, either the power threshold is unchanged (ASDEX Upgrade), unchanged or somewhat increased depending on density (JET) or largely increased by up to factors of three at some densities (DIII-D and Alcator C-Mod). Experiments from JET show that the behaviour of the H-mode threshold in mixed H–D and H–He plasmas is non-linear [13]. The detrimental effect of H was identified already in ASDEX Upgrade for He plasmas [5]. However, the impact of a heavier species (He or D) in the H-mode threshold of H plasmas is more complex. The JET results indicate a significant effect reducing the H-mode power threshold when 10%–20% D or He are present in H plasmas, while in ASDEX Upgrade such effects do not take place [14]. It is important to clarify the physics process behind this different behaviour to understand whether the JET-like of ASDEX Upgrade-like behaviour should be considered for ITER, since such reduction of the H-mode threshold by a small amount of He could potentially be beneficially exploited to expand the range of ITER H-mode operation in hydrogen-dominant plasmas.

For individual machines it was found that the P_LH value provided by equation (1) is only applicable above a given density value (n_L,H,min), for densities under this value P_LH is found to increase with decreasing density, i.e. an opposite trend to that predicted by the scaling. The physics determining this minimum value is not yet fully understood. The basic physics picture for the minimum density for H-mode access includes changes to the nature of the turbulence with collisionality (which depends on density) and stabilization of the underlying turbulence by the radial electric field shear [15], which itself depends on gradients of electron and ion temperatures/densities and, thus, on the sharing of the edge power flux between ions and electrons [16]. The value of the turnover density as well as the power threshold in the vicinity of this density can depend on the divertor configuration [4, 13, 17], presence of impurities [18], ion species [10–12, 19] and plasma rotation [8].

To evaluate n_L,H,min in ITER we adopt the physics model put forward on the basis of ASDEX Upgrade [16] that showed that this minimum density is determined by the role of the edge ion power fluxes in triggering the L–H transition. Edge ion power fluxes depend on the plasma heating scheme (electron or ion heating) and equipartition. Equipartition is less efficient at low densities and thus increases the heating power required to achieve a given edge ion power flux at low densities for electron heated plasmas [16]. This is particularly relevant for H-mode plasmas in ITER, since all ITER plasmas are electron heating dominated and, in particular for PFPO-1 since only ECH will be available in this phase.

Based on these results, an expression for the density providing the minimum threshold L–H power has been derived for ITER. It should be noted that this physics picture describes well the values found in other tokamaks of different size such as Alcator C-Mod [20] but for other tokamaks such as JET its applicability is less clear and other physics mechanisms related to the presence of impurities may be at work [13, 19, 21] and further R&D is required. On the basis of the model in [16]:

$$\begin{equation}{n}_{LH,\mathrm{min}}^{\text{scal}}\left({10}^{20}\enspace {\mathrm{m}}^{-3}\right)\approx 0.07\;{I}_{\mathrm{p}}^{0.34}{B}_{t}^{0.62}{a}^{-0.95}{\left(R/a\right)}^{0.4}\end{equation} \tag{ 2 }$$

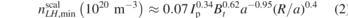
For ITER, this leads to,

$$\begin{equation}\frac{{n}_{LH,\mathrm{min}}^{\text{scal}}}{{n}_{\mathrm{G}\mathrm{W}}}\approx 0.71\frac{{I}_{\mathrm{p}}^{0.34}{B}_{t}^{0.62}}{{I}_{\mathrm{p}}}\end{equation} \tag{ 3 }$$

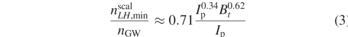
For q₉₅ = 3 conditions in ITER, for which B_t (T) = 0.35×I_p (MA), this corresponds to ${n}_{LH,\mathrm{min}}^{\text{scal}}$ ≈ 0.35 × n_GW.

In our further consideration we use the generally conservative assumptions P_LH,H = 2 × P_LH,D, and P_LH,He = 1.5 × P_LH,D for plasma densities above the minimum density predicted by equation (3).

Using the ASTRA code, the plausibility of applying equation (3) to the ITER H-mode, based on the hypothesis that it arises from maximizing the ion heat flux over variation in density, has been confirmed by modelling of 5 MA/1.8 T hydrogen and helium L-mode plasmas. Since the aim of the study was to confirm the basis of equation (3) for ITER application rather than a detailed quantitative comparison with the values of the coefficient and exponents in equation (3), the model for L-mode transport used in the simulations was kept simple. The transport model used assumes parabolic profiles for the heat diffusion coefficients with χ_i = χ_e and particle transport is modelled with D = 0.2 (χ_i + χ_e). The values of the heat diffusion coefficients are adjusted to achieve the plasma energy predicted by the ITER-97 L-mode scaling [22].

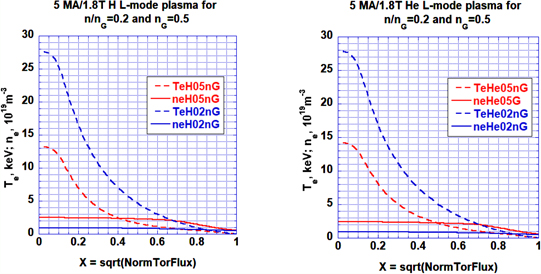
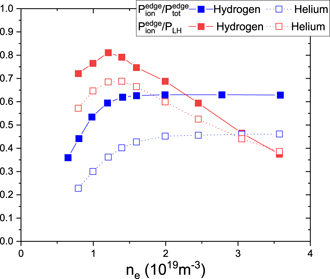
The modelled density and temperature profiles for hydrogen and helium L-mode plasmas are shown in figure 1, and the resulting normalized ion heat flux at the separatrix for a range of densities is shown in figure 2. The density which provides the minimum power for H-mode access, n_LH,min, has been evaluated on the basis of 1.5-D transport modelling as the density at which the edge ion power flux starts to saturate with increasing density following the physics picture in [16]. The value for n_LH,min derived from direct modelling appears to be close to the scaling predictions ${n}_{LH,\mathrm{min}}\approx {n}_{LH,\mathrm{min}}^{\text{scal}}\approx 0.35$ n_GW, which corresponds to 1.4 × 10¹⁹ m⁻³ at 5 MA in ITER (figure 2). The actual ratio at which the edge power flow saturates depends on assumptions regarding the electron and ion transport (ratio χ_i/χ_e), but the value of the density at which saturation takes place depends only weakly on this assumption, provided that the overall confinement is assumed to follow the L-mode scaling (this is the normalizing parameter for the actual values of χ_i and χ_e). It should be noted that these ASTRA simulations also show a clear difference on the maximum value of the edge ion heat flux for hydrogen and helium plasmas but a weak dependence of the minimum density at which this heat flux saturates on plasma species (H or He). Both these predictions are presently the topic of on-going experimental and modelling R&D [23].

Zoom In Zoom Out Reset image size

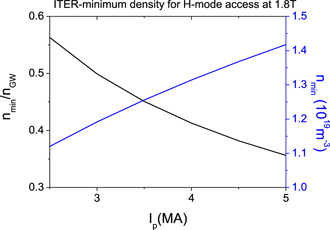
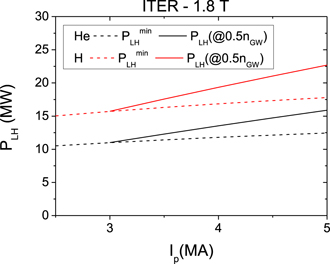
Zoom In Zoom Out Reset image size

The predicted value of n_LH,min with equation (3) for ITER plasmas at 1.8 T spanning a range of q₉₅ = 3–6 is shown in figure 3; as can be seen in this figure very low absolute values of plasma density 1.0–2.0 × 10¹⁹ m⁻³ are characteristic of these H-mode plasmas. The corresponding H-mode power threshold value at this minimum density and at n_e = 0.5 n_GW for hydrogen and helium plasmas (assuming the higher range of the power threshold for helium) is shown in figure 4. For sustained H-mode operation in ITER, it is likely that the plasma density will be higher than this minimum value due to the reduced transport in the pedestal. Thus, in order to estimate the power required for sustained H-mode operation of 1.8 T plasmas, a value of ⟨n_e⟩ = 0.5 n_GW has been used; this accounts for the potential increase of the plasma density from the minimum value after the L–H transition (⟨n_e⟩ = 0.35 n_GW) to stationary H-mode conditions. Integrated simulations of ITER plasmas find that the core plasma density increase after the L–H transition in ITER is moderate (⩽1.4) compared to present experiments (a factor of 2 or more) [24]. This is due to the inefficient fuelling of the core plasma by recycling neutrals in ITER, which are preferentially ionized in the SOL periphery as the H-mode pedestal builds-up. This is a specific feature of ITER edge/divertor plasmas associated with the large distance between the main recycling source (the divertor targets) and the confined plasma compared to the neutral ionization mean free path and also applies to the PFPO-1 plasmas considered here, as shown by detailed edge plasma modelling studies for these plasma conditions [25].

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

For 5 MA operation at 1.8 T sustained H-modes, operation in helium plasmas requires ${P}_{\text{sustained}}^{\mathrm{H}\mathrm{e}\mathrm{H}-\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}}$ ∼ 16 MW while for hydrogen plasmas ${P}_{\text{sustained}}^{\mathrm{H}\mathrm{H}-\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}}$ ∼ 23 MW is required. Given the baseline ECH installed power of 20 MW in this phase, sustained operation in He plasmas is expected to be viable, although with a reduced margin of power flow above the threshold P_tot/P_LH ∼ 1.3. For hydrogen plasmas the H-mode may be accessible since ${P}_{LH\mathrm{min}}^{\mathrm{H}}$ ∼ 17.5 MW but sustained H-mode operation would require densities below 0.5 n_GW. On this basis, the physics basis for an early upgrade of the ITER ECH system to provide 30 MW already in PFPO-1 has been investigated [2]. This increased ECH power would provide robust sustained helium plasma H-mode operation and the possibility to explore hydrogen plasma H-modes, and/or hydrogen-dominant plasmas (with 10% helium) if the H-mode threshold were reduced by the presence of helium, as found at JET [13] but not for ASDEX Upgrade [14]). Note that the margin for sustained H mode can be increased at 1.8 T by operating at lower current, e.g. at 3.3 MA with q₉₅ = 4.5. However, the increase in margin is very moderate since, from equations (1) and (3), ${P}_{LH}\left({n}_{LH,\mathrm{min}}^{\text{scal}}\right)\sim {I}_{\mathrm{p}}^{0.24}$, and, in addition, issues related to unabsorbed power due to the 3rd harmonic heating become more problematic due to the decrease in density and temperature of the plasmas. Therefore the approach to increase the H-mode operational space by I_p reduction under 5 MA for 1.8 T hydrogen and helium plasmas is not viable, in practice, in PFPO-1.

ITER is equipped with ferromagnetic inserts to reduce the value of the toroidal field (TF) ripple; the mass of these inserts is optimized to reduce the value of TF ripple from 1.0% down to 0.3% at the separatrix outer midplane in ITER for an axial vacuum toroidal field value of 5.3 T. Thus, the level of ripple at 1.8 T is sizeable for the nominal outer midplane separatrix position (1.3%) since the ferromagnetic inserts overcompensate the natural ripple of ITER determined by its 18 TF coils. This sizeable TF ripple value is not expected to have a significant effect on the power required to access the H-mode or if it has, it is most likely to be favourable (reducing power threshold) on the basis of present experimental evidence, assuming that this applies to ITER. The effect of TF ripple on H-mode threshold was found to be negligible at JET for values of the TF ripple spanning from 0.08% up to 1.1% [6]. On the other hand, in JT-60U, the H-mode power threshold was reduced when increasing the ripple [26]. The JT-60U behaviour could be associated with enhanced ion losses in the X-point region increasing the edge electric field shear with TF ripple, since the level of ripple at the X-point for a given separatrix ripple value is larger in JT-60U than in JET and ITER. This is due to the different TF coil shape design (circular coils for JT-60U versus D-shaped coils in JET and ITER) [27].

Modelling of 5 MA/1.8 T H-mode plasmas with 20 and 30 MW of ECH heating has been performed with the ASTRA integrated modelling suite [28] and a range of first-principles models for anomalous transport, namely GLF23 [29] and TGLF [30], the latter with two implementations (SAT-0 and SAT-1). The most up-to-date one (SAT-1) [31] that accounts for the effects of multi-scale physics on turbulent transport is implemented in ASTRA as described in [32, 33], but does not consider toroidal rotation effects on transport. Multi-scale physics transport described with the SAT-1 TGLF implementation can potentially play an important role in these ECH heated plasmas with low equipartition since streamer-like transport can significantly increase electron transport for plasmas in which the ion temperature gradient is low [31]. On the other hand the SAT-1 TGLF implementation includes the effect of zonal fluctuations that give rise to a nonlinear upshift in the effective critical gradient at which turbulent fluxes start to play a role (Dimits shift). As a result, the predicted electron and ion heat fluxes with the SAT-1 implementation may be lower than those predicted with SAT-0 in ITER-like plasma conditions for ion and electron temperature gradients with inverse temperature scale lengths 1.6 < R/L_T < 8, as already pointed out in [34].

These simulations have been performed to obtain an initial characterization of the plasma parameters expected in these first H-modes to be achieved in ITER, to determine the dominant physics processes in such plasmas and the associated edge-core integration challenges in order to guide further experimental and modelling R&D. Since early operation in H-mode is mainly considered for mitigation of risks in the IRP [1], it is important to ensure that the H-mode plasmas to be demonstrated at 5 MA/1.8 T are appropriate to this objective.

An issue identified in applying such first-principles models is that the saturation rules used to evaluate plasma transport in the quasilinear approximation are based on gyrokinetic simulations for deuterium plasmas. Therefore, in order to be consistent with the physics models used, the simulations have been performed for D plasmas while the corresponding plasmas in PFPO-1 will be performed in H and He. H and He H-mode plasmas are expected to have lower confinement than D plasmas in ITER typically by 20%–30%, if the results obtained in present experiments apply (e.g. [10, 12]). In this case, our predictions for PFPO-1 H-mode plasma parameters (e.g. temperature for a given density) are likely to be higher by 20%–30% than those that will actually be achieved in H and He H-modes in ITER. It is important to note that the lower confinement in H and He H-modes in present experiments results from differences in pedestal plasma behaviour, core plasma transport and are also impacted by the plasma heating scheme since electron–ion equipartition depends on the mass of the main plasma ion and its charge. Therefore, direct empirical extrapolation of overall confinement from present day D, H and He H-mode plasmas to ITER should only be used as a guideline whose physics basis should be consolidated. In this respect, the development of turbulent transport models that account for isotopic and plasma species effects remains an open R&D issue and further ITER modelling with turbulent transport models that include these effects are required to refine the ITER predictions. This is an area of open R&D where significant advances for ITER are expected from the upcoming H, T and DT experiments at JET [35].

The simulations have been performed by applying similar modelling assumptions to those in previous ITER studies for DT plasmas [36] regarding pedestal MHD stability and SOL conditions based on the EPED1 + SOLPS boundary condition approach. It should be noted that the EPED1 model does not account for isotopic effects on the pedestal plasma pressure and that we are thus applying here a scaling that is also valid only for deuterium plasmas. Similarly, the pedestal plasma is modelled in a time-averaged way, implicitly assuming that the time-averaged value of the pedestal pressure is close to its maximum value predicted by the EPED1 + SOLPS scaling.

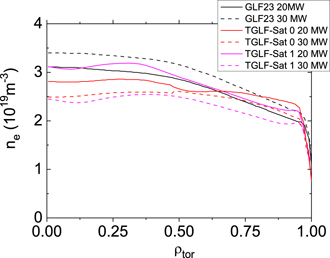
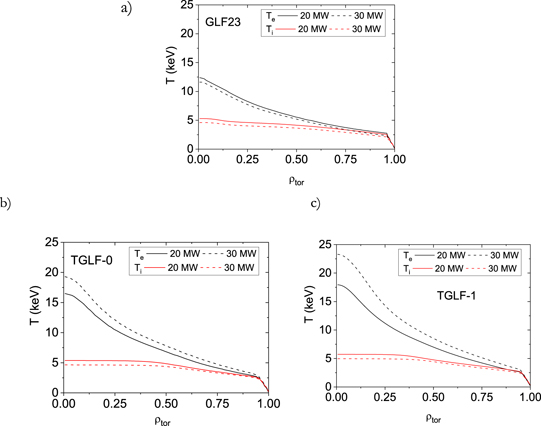
A simple model for the ECH deposited power has been taken with all radio-frequency power centrally deposited ρ_tor ⩽ 0.4 in the electrons, which is a reasonable approximation to the expected ECH power deposition profile for 3rd harmonic heating in these plasma conditions [2]. The density targeted for the simulated plasmas is n_e/n_GW ∼ 0.5. However, the level of density in the plasma is the result of transport and fuelling sources resulting from the application of SOLPS boundary conditions. The results obtained for the density and temperature profiles are shown in figures 5 and 6. The particle sources have not been fine-tuned to match the same density level in all simulations causing some variation of the line average density value across the simulations.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Note that sawteeth are not included in these simulations. The application of ECH/ECCD has been proven to have a significant effect on sawtooth frequency depending on the details of the deposition profile (e.g. [37–45]). The evaluation of these effects for 5 MA/1.8 T ITER plasmas and the resulting sawtooth frequencies requires a detailed assessment that will be the topic of future studies. In this respect, the temperatures modelled in these studies can be considered as an upper limit to those that will be observed in these ITER plasmas.

In general, for all transport models used, electrons and ions are not well coupled thermally in the central part of the plasma. For TGLF, the central ratios of T_e/T_i can be even larger than 3.0 for high heating ECH powers; this is accompanied by a large plasma transport that flattens the density and ion temperature profiles, which reinforces the large central T_e/T_i ratio. The exact magnitude of the ion temperature flattening is to some degree dependent of the implementation of the ion heat diffusivities derived from the TGLF modelled fluxes in the ASTRA transport equations, but the density profile resembles the experimental observations of density pump-out from the centre with strong ECH heating seen in some conditions for present tokamaks [46]. Modelling with TGLF-SAT-1 saturation rule produces a higher central electron temperature than with TGLF-SAT-0 and thus higher electron temperature gradients to support the same electron heat flux. This is consistent with previous evaluations for ITER-like plasmas [34], since the inverse electron temperature scale length in these plasmas is R/L_Te ∼ 6.5 (shown later in figure 8) [34].

To determine if the results obtained represent a well-founded physics-based extrapolation from present experimental results to ITER, we have compared the results of ITER modelling with results from present experiments both in a global and in a local way. In particular, we have compared the modelled density and temperature profiles to determine if the predicted density and temperature gradients as well as the total plasma energy match with existing experiments. For these comparisons, we have considered published results from JET high current/low collisionality H-modes for the global comparisons [47, 48] and from dominantly electron heated H-mode plasmas from ASDEX Upgrade [49] for the local comparisons.

The overall plasma density and temperature profiles predicted for ITER 5 MA/1.8 T ECH heated H-modes have been compared with those from JET H-mode plasmas at high current (I_p > 4 MA) from [47, 48]. These plasmas have high plasma energy (W_plasma,JET ∼ 11 MJ compared to W_{plasma, ITER} ∼ 30 MJ) and specific features that make them particularly relevant for comparison with ITER 5 MA/1.8 T H-modes, such as q₉₅ ⩽ 3, a low core particle source from the NBI heating and a low ITER-like plasma collisionality [50]. The latter characteristics are associated to operation at high current at JET (and high density but moderate ⟨n_e⟩/n_GW = 0.5–0.6) for which NBI penetration in the core plasma is low [50] together with the high edge and core plasma temperatures [48]. We note here that high current H-mode plasmas of this type (albeit not precisely the JET discharge considered here) have been successfully modelled by the JINTRAC integrated modelling suite, which includes the same models and assumptions as those used for ITER with ASTRA, namely GLF23 to describe core transport and peeling-ballooning ideal MHD limits to determine the pedestal pressure in addition to full edge-SOL-divertor modelling [51].

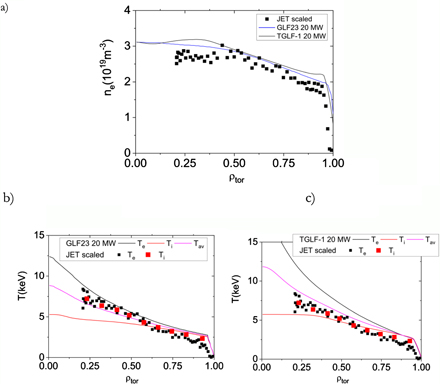
We have used a similar approach to scale the JET plasmas to ITER to that followed in pedestal similarity experiments [52]. We have assumed that β_ped will be the same for these JET and ITER plasmas and scaled first the whole density and temperature plasma profiles from JET to ITER accordingly ($n\sim {a}^{-1/3}{B}_{t}^{4/3}$ and $T\sim {a}^{-1/3}{B}_{t}^{2/3}$). As discussed in [52] this scaling approach does not maintain an approximately constant ⟨n_e⟩/n_GW across devices, which is required for the comparison with ITER. Therefore, we have rescaled the density profile to match the value of the pedestal density to that in ITER modelling results while maintaining the same plasma β_ped. This is a valid approach since the MHD-limited pedestal plasma pressure is weakly dependent on the pedestal density value for ITER plasmas [36]. The outcome of such a scaling comparison is shown in figure 7 for both GLF23 and TGLF-SAT-1 modelling results. Although the separate gradients of T_e and T_i are very different for the extrapolated JET plasma and those of the ITER plasmas, the average (T_e + T_i) profiles obtained from the ITER modelling results and those scaled from JET to ITER match rather well. The difference of the individual profiles can be understood because of the different heating systems in these two plasmas. The original JET plasma scaled to ITER (Pulse No. 79676 4.3 MA/3.4 T) is NBI heated (21 MW) [47] and with large electron–ion equipartition while the modelled ITER plasma is electron heated with low equipartition in the plasma core region. It is important to note that the scaling methodology applied could not be simpler; a single point in the whole plasma cross section is used to scale the JET plasmas to ITER. In addition, there are some differences regarding plasma shape between this JET plasma and that modelled for ITER; the plasma triangularity of the JET plasmas (δ ∼0.3) is lower than that of the ITER plasma (δ ∼ 0.5), which results in a lower pedestal pressure being extrapolated to ITER on the basis of the JET plasma.

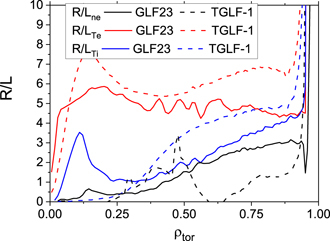
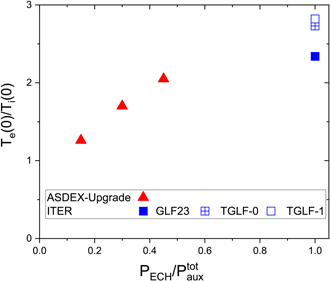
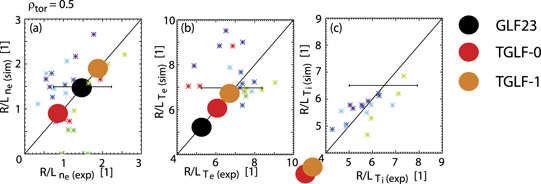
Zoom In Zoom Out Reset image size

To compare the core plasma density, ion and electron transport predictions for these ECH heated plasmas, experiments in ASDEX Upgrade with a significant fraction of ECH power in the total auxiliary heating have been selected [49]. The plasma density, electron and ion temperature scale lengths, shown in figure 8, and the ratio between the electron and ion temperatures for the modelled ITER 5 MA/1.8 T plasmas have been compared with ASDEX Upgrade measurements. For this purpose, the T_e/T_i ratio at the plasma centre and the radial scale lengths of plasma density and electron and ion temperatures at mid-radius in ASDEX Upgrade H-mode experiments [49] have been compared with the values modelled for ITER at the same normalized radial location. As shown in figures 9 and 10, the main difference between ITER modelling and the ASDEX Upgrade experiments corresponds to the results obtained with GLF23 that produces much flatter T_i profiles at mid-radius in ITER than in ASDEX Upgrade experiments and a lower T_e/T_i ratio at the plasma centre, while TGLF results are in better agreement with experimental results. The main difference between TGLF predictions for ITER and ASDEX-Upgrade experimental results concerns the ion temperature scale length which is somewhat lower in the ITER modelled plasmas than in ASDEX Upgrade. This is due to the fact that, while for ITER plasmas ECH provides 100% of the additional heating, in ASDEX Upgrade experiments the ECH contribution is in the range of 15%–45% of the total with the rest being provided by NBI heating; the other factor is the differences in turbulent transport between ASDEX-Upgrade and ITER. In ASDEX-Upgrade the transport is ITG dominated with the ion heat flux being dominant over most of the conditions explored [49] and with a ratio of ion to electron power flux at mid-radius in the range of q_i/q_e = 0.7–2.0. Even for the highest levels of ECH heating in ASDEX-Upgrade the ion heat flux is comparable to the electron one due to the destabilization of ITG turbulence with increasing T_e/T_i. In the ITER PFPO-1 plasma simulations electron transport is dominant and q_i/q_e ⩽ 0.35. Consistent with the lesser role of the ion channel to carry the power flux in ITER, a lower R/L_Ti is modelled for ITER plasmas than measured in ASDEX Upgrade for the highest ECH power fractions of 45%.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

As mentioned in the introduction, H-mode operation in the PFPO-1 phase of the IRP has as main objective the reduction of risks for latter phase of the IRP. This concerns aspects related to H-mode access, sustainment and determination of H-mode confinement in ITER as well as the development of control schemes to integrate core and edge plasma aspects. These are essential for later phases of the research plan with higher levels of plasma heating, in particular when high levels of alpha heating will be demonstrated in the fusion power operation phase (FPO). In this respect, it is important to evaluate specific aspects of 1.8 T operation in ITER that can affect H-mode confinement as well as the expected transient and stationary power fluxes to the plasma facing components. On one hand, in order to develop control schemes for these power fluxes, it is interesting that these fluxes are representative of later operational phases. On the other hand, it would be preferable that these loads do not exceed material limits (e.g. melting of tungsten divertor mono-blocks) while the required control schemes are being developed.

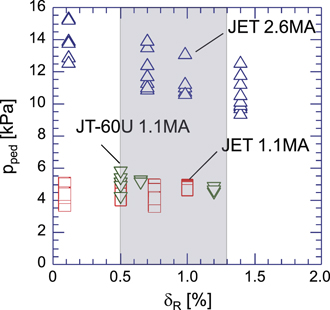
Regarding the achievable H-mode confinement, beyond the modelling assessment discussed in the previous two sections, there is a specific issue which is expected to affect H-mode confinement and that is the relatively high level of ripple at the nominal outer midplane separatrix of 1.3% for 1.8 T plasmas in ITER. An assessment of the effects of TF ripple on H-mode plasmas was jointly performed by coordinated experiments at JET and JT-60U [27, 53]. The outcome of these experiments was that the value of TF ripple at the level of ∼1.3% can have an effect on the pedestal pressure and maximum energy confinement that can be achieved in H-mode, with this effect being significant for low collisionality plasmas while for higher collisionalities this effect is negligible [27]. This corresponds to the JET 2.6 MA plasma for which the pedestal collisionality is ν^* _ped ∼ 0.04, as shown in figure 11 from [27]. Extrapolation of these findings requires a complete physics-based approach, which is not yet fully developed. To quantify the effect of ripple on H-mode pedestal behaviour and confinement in ITER we take as guiding parameter the pedestal collisionality following these experimental findings and assume that, for pedestal conditions in which the collisionality is equal or lower than ν^* _ped ∼ 0.04 in ITER, the experimentally observed pedestal degradation effects with TF ripple apply. We use the ITER predictions for the pedestal pressure derived from EPED1 + SOLPS [36], applied to the modelling in section 3, to evaluate the possible effects of increased TF ripple on the pedestal plasma and H-mode confinement for 5 MA/1.8 T plasmas in ITER. We first evaluate the expected characteristics of the pedestal parameters and H-mode confinement without ripple effects and then consider how they could be modified by the level of TF ripple expected in 5 MA/1.8 T plasmas in ITER.

Zoom In Zoom Out Reset image size

According to the EPED1 + SOLPS scaling ν^* _ped ≈ 0.16 (n_ped/n_GW)³B^−0.68 [54], the collisionality of 1.8 T plasmas with the same n_e/n_GW is about two times larger than that of B = 5.3 T plasmas. However, for the expected plasma conditions in ITER 5 MA/1.8 T plasmas, as discussed in sections 2 and 3, we require much lower n_e/n_GW values to access and sustain the H-mode (i.e. n_ped/n_GW|_5MA ∼ 0.5 n_ped/n_GW|_15MA-Q=10) with the available heating power level in PFPO-1. This reduces the pedestal plasma collisionality so that, for the foreseen ITER 5 MA/1.8 T H-mode plasmas to be explored in PFPO-1, is ν^* _ped |_5MA-PFPO-1 = 0.25 ν^* _ped |_{15MA-Q =10}, where ν^* _ped|_{15MA-Q =10} = 0.015, while ρ_ped |_5MA-PFPO-1 ∼ 2 ρ_ped |_{15MA-Q =10} (T_ped |_5MA-PFPO-1 ∼ 0.5 T_ped |_{15MA-Q =10}), with ρ_ped being the ion larmor at the pedestal, the latter being important for processes associated with drift losses in the TF ripple wells. On the basis of the JET experiments [27, 53] carried out to evaluate the effects TF ripple on ITER, whose results are included in figure 11, this implies a reduction of pedestal pressure and H-mode energy confinement by 20%–30% at 1.3% ripple level compared to the modelling in section 3, which intrinsically assumes no ripple effects. Since this is a significant reduction, alternative magnetic configurations have been developed for 5 MA/1.8 T plasmas in which the TF ripple at the outer separatrix midplane can be decreased to 0.5% by reducing the plasma minor radius and shifting the plasma inwards, away from the TF coils, while maintaining good vertical stability control [55].

Concerning other pedestal related issues, the TF ripple has been found to affect the ELM energy losses both in JET [53] as well as in JT-60U [27] independently of whether TF ripple affects pedestal pressure or not; for TF ripple levels of ∼1% the ELM energy loss is found to be reduced by a factor of 2 compared to low TF ripple levels. On this basis, it is expected that ELM energy losses for 5 MA/1.8 T plasmas for the nominal separatrix position with 1.3% ripple will be a factor of 2 lower than predicted from multi-machine scalings from experiments with low ripple values [56]. However, it should be noted that the reduction of ELM energy losses is also correlated with a decrease of edge toroidal rotation with increasing ripple and associated fast ion losses, which are seen at JET [27] and JT-60 U [57]. If fast ion loss is the dominant mechanism behind the ELM energy loss reduction with increasing ripple, then this reduction may not materialize for 5 MA/1.8 T H-mode plasmas in PFPO-1 since these are ECH heated and there are no fast ions.

Closely related to the ELM energy losses, one of the objectives of H-mode operation at 5 MA/1.8 T in PFPO-1 is to explore ELM control to refine the schemes applied for later operational phases [58]. During PFPO-1, active ELM control can be explored by pellet injection [59, 60] and vertical plasma oscillations [61]; in the present formulation of the ITER staged approach [62] the ELM control coils will not operate in this phase. Evaluations on the application of ELM control coils in the PFPO-1 phase have been performed [63] in the context of discussions that might eventually lead to the advanced installation of the power supplies (all or a partial set) for the ELM control coils to be operational for PFPO-1. Since it will not be possible to demonstrate ELM control from the first 5 MA/1.8 T H-mode discharges and the operational space in these conditions is very restricted in PFPO-1, it is important to ensure that uncontrolled ELM power fluxes to the divertor will not exceed material limits (melting of tungsten macro-brushes edges and top surface). This has been the subject of specific studies described in [64] which show that, even for the more conservative estimates of ELM power fluxes at the ITER divertor derived from experimental scalings [65], the ELM energy fluxes expected for 5 MA/1.8 T H-mode plasmas are a factor of 1.5 lower than those required to cause tungsten melting of the edge macro-brushes and a factor of 5 lower than those required to cause top macro-brush melting. Integrated simulations of ITER plasmas, considering tungsten production by ELMs and transport into the pedestal plasma in a simplified way, have shown that, although divertor melting is not expected to occur for these plasmas, a basic level of ELM control may be required to prevent H−L transitions due to excessive core tungsten radiation following the ELMs. This is the result of physical sputtering at the tungsten target by the high temperature pedestal ions released by the ELM and its propagation into the core plasma. These tungsten-caused H−L transitions are found to occur at values of ELM energy losses of ∼1.25 MJ [54], while the uncontrolled ELM energy is expected to be in the range of ∼1.5–3 MJ for 5 MA/1.8 T ITER plasmas on the basis of empirical scalings [56]. It should be noted that the evaluation of core tungsten radiation following ELMs is subject to large uncertainties, in particular related to the fraction of prompt tungsten re-deposition during the ELMs. The assumptions in [54] to derive the 1.25 MJ ELM energy limit are very conservative (zero prompt re-deposition during the ELM).

Similarly, control of divertor power fluxes by radiative divertor conditions will be explored in these plasmas with the purpose of initial testing of these schemes in H-mode plasmas, since divertor power flux control is particularly challenging for devices with tungsten divertors [66]. Initial integrated modelling of these plasmas has been performed with JINTRAC including [67]: core plasma transport with the EDMW transport model [68] for main ions and impurities and the interactions of the plasma with the beryllium first wall and tungsten divertor. EDWM predicts similar plasma parameters for ITER to those with GLF23 in figure 6. The reason for its use in these integrated modelling studies instead of GFL23 is because EDWM facilitates simulations that include discrete pellet fuelling, which is also part of the JINTRAC studies, although not reported here. The injection of pellets leads to transient peripheral local maxima of the density profiles at ρ ∼ 0.8 for ITER whose relaxation is difficult to model with GLF23 due to numerical instability issues. The effect of ELMs was simulated with a continuous ELM model by which the transport in the pedestal and near SOL regions is increased to keep the plasma pressure at MHD stability limit. This approach aims to describe the ELM-averaged behaviour of the pedestal plasma and strictly applies when ELM energy losses are very small. The simulations also include neon that allows the study of radiative divertor regimes.

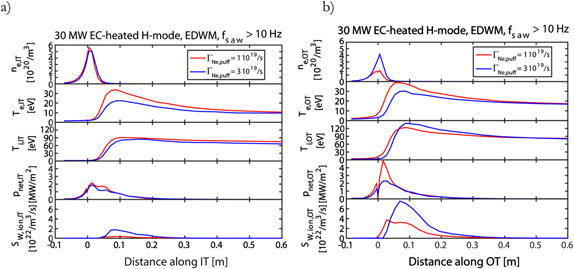
The results of the core and divertor plasma parameters obtained for two simulations of 5 MA/1.8 T hydrogen H-mode plasmas with 30 MW ECH and different Ne puffing levels (10¹⁹ s⁻¹ and 3 × 10¹⁹ s⁻¹) are shown for the core plasma profiles in figure 12 and for the inner and outer divertor profiles in figure 13. Ne has been chosen for these studies instead of N because the potential formation of large quantities of ammonia has consequences for several aspects of the ITER plant operation in terms of gas reprocessing and duty cycle [69] thus making Ne preferable for ITER. Ar, on the other hand, leads to larger core plasma radiative losses than Ne and thus reduces the margin for H-mode operation, which is not large neither in these H/He PFPO-1 scenarios nor for Q = 10 DT operation in ITER [70].

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

For the low Ne rate the effect of Ne on the plasma parameters is negligible, since Ne divertor radiation is 3 MW and less than 0.5 MW is radiated in the core plasma, while for the high Ne rate it is more significant (7 MW of divertor radiation and 1.5 MW of core radiation). In this respect, it should be noted that simulations with EDMW (and those with GLF23 shown in section 3) produce plasmas with lower electron temperatures than those performed with TGLF (typically central temperatures of ∼10–15 keV with EDWM/GLF23 versus ∼15–20 keV with TGLF SAT-0/SAT-1 saturation rules). For Ne radiation from the core plasma, this difference has a very small impact since Ne is fully ionized in both temperature ranges [71]. On the contrary, W is not fully ionized and its radiation efficiency decreases with increasing electron temperature in the range of 10–30 keV [71]. Therefore, regarding the impact of W radiation on core plasma performance, the EDWM simulations are conservative compared to those that could be performed with more advanced transport models such as TGLF. These simulations consider the effect of sawteeth in the central part of the plasma in a time-averaged way, which corresponds to sawtooth frequencies (f_saw) larger than 10 Hz, i.e. ∼10 sawteeth per energy confinement time, which is ∼1 s in these plasmas. This sawtooth repetition time of 0.1 s is also much shorter than the resistive diffusion time for the q = 1 radius of ∼1000 s in these ITER plasmas. Thus, the inclusion of sawteeth effects in these simulations provide conservative predictions of the central temperature values that can be achieved in these ITER plasmas.

The results of these studies in figure 13 show that the divertor power flux at the outer divertor for low Ne levels are modelled to be very peaked (λ_q ∼ 5 mm at the outer midplane) and its peak can reach values of ∼5 MWm⁻². The electron temperature at the outer divertor target has maximum values of ∼ 40 eV (this does not occur at the separatrix where the ion flux is the highest) for 30 MW ECH heated 5 MA/1.8 T hydrogen plasmas in ITER. These levels of power loads and the resulting plasma parameters are in agreement with detailed SOLPS–ITER simulations for similar plasma conditions [25]. Increasing the level of Ne is effective in reducing the divertor power flux by a factor of ∼2 in the simulations performed so far, which do not reach strongly detached divertor conditions at the outer divertor. The effective W sputtering yield for these plasmas is in the range of 0.0005 W-atom/H–ion (low Ne puffing rate case) to 0.001 W–atom/H–ion (high Ne puffing rate case) which is typical for W interacting with a hydrogenic plasma that contains a few % concentration of medium Z impurities and with a temperature of 10–20 eV [72]. The core W concentrations in these plasmas are very low (1.5–2.5 × 10⁻⁶), as shown in figure 12(b), despite the fact that no local re-deposition of W is assumed in the simulations; this assumption results in a very conservative upper estimate of the W divertor source. The low core W concentration is due to the very effective screening of impurities in the pedestal plasma shown in figure 12(b). The effective screening of impurities in the ITER pedestal is caused by the neoclassical temperature screening term being dominant in low edge density gradient/high edge temperature gradient conditions at the ITER pedestal leading to an outwards-directed neoclassical impurity pinch velocity [73]. Similar full-integrated simulations including ELM-resolved tungsten production and transport to core with JINTRAC are in progress and will be compared with those already performed with a simpler approach [54].

The results of the studies of 5 MA/1.8 T hydrogen H-mode stationary plasmas with 30 MW ECH heating show that, on the basis of present modelling results, there are no major operational physics-integration issues with respect to their practical feasibility in ITER. Many of the features of these H-mode plasmas will be similar to those of later phases in the IRP, i.e. narrow λ_q and high divertor power fluxes, impurity screening in the pedestal, etc. These H-mode scenarios are therefore expected to provide a good basis for the development of ITER H-mode operation thus minimizing the risks associated with H-mode operation in later phases of the research plan. Obviously, the confirmation of these predictions requires the validation of the models applied to ITER in H-mode plasmas with parameters as close to those of ITER in terms of core and edge plasma parameters and dominant transport mechanisms (including dominant electron heating).

The assessment detailed in this study identifies the plasma conditions for optimum H-mode access and sustainment in the PFPO-1 phase of the IRP in which 20 MW of ECH will be available for plasma heating. With this level of additional heating H-mode access and sustainment of 5 MA/1.8 T H-mode plasmas appears viable on the basis of the existing scalings and their physics-based extrapolation albeit only for helium plasmas and with a reduced operational space. Increase of the heating power level beyond the foreseen one in the baseline to 30 MW would open significantly the operational space of H-mode plasmas in helium and would allow the exploration of hydrogen or, possibly, hydrogen dominant plasmas (i.e. hydrogen + 10% helium) if the H-mode threshold were lowered by the presence of helium over a reduced operational space.

The H-mode plasma properties predicted by integrated modelling of deuterium plasma transport simulations with first principle models and pedestal-SOL parameters predicted by EPED1 + SOLPS scalings is extrapolated to hydrogen operation. The simulations indicate central electron temperatures in excess of 10 keV with ion temperatures typically a factor of 2–3 times lower for H-mode plasmas with n_e = 0.5 n_GW, for which H-mode sustainment is possible. Such difference between electron and ion temperatures is due to the central ECH heating of these plasmas depositing all additional heating power on the electrons and the inefficient equipartition in the central region of the plasma due to the low absolute value of the plasma density (2.0–3.0 × 10¹⁹ m⁻³).

The comparison with low collisionality JET H-mode plasmas with a level of plasma current and additional heating similar to these ITER H-mode plasmas, scaled from JET to ITER following a dimensionless similarity approach, reveals good agreement in terms of global plasma energy and density and temperature profiles although not on the separate electron and ion temperature profiles. This is caused by differences in the heating schemes (ECH in ITER versus NBI in JET) and dominance of equipartition (low in ITER due to low densities and high in JET due to high densities). The characteristic scale lengths of the electron density and electron and ion temperatures for H-mode experiments at half radius in ASDEX Upgrade with significant ECH heating are in line with those predicted for ITER, except the ion temperature profile predicted by GLF23. However, in contrast to ITER the NBI power still constitutes 55% of the total additional power level which heats mainly the ions in ASDEX Upgrade. These first principle model predictions for ITER satisfactorily match results in JET and ASDEX Upgrade experiments albeit at different plasma collisionalities and, thus, further experimental and modelling R&D is required to confirm the accuracy of the predictions with these models for ITER plasmas.

Integration issues related to specific aspects of 5 MA/1.8 T H-mode operation in ITER have also been evaluated beyond the aspect of 3rd harmonic ECH heating, which is discussed in detail in [2]. These concern the impact of increased ripple at 1.8 T on H-mode pedestal parameters, the consequences of uncontrolled ELMs on the tungsten divertor components and the magnitude of the divertor power fluxes and resulting core contamination by tungsten caused by plasma-wall interaction for these plasma conditions. It is estimated, from extrapolation of experiments, that TF ripple can have a significant effect on the achievable pedestal pressure decreasing the total plasma energy by 20–30%; this can be reduced by a factor of ∼2 by modifying the plasma configuration and shifting the plasma radially inwards. Divertor and ELM power fluxes, if uncontrolled, are significant but well away from the limits determined by material limits (divertor macro-brush melting) and divertor stationary power exhaust for the ITER divertor design. Similarly, tungsten divertor production for hydrogen plasmas is not negligible but the favourable transport in the pedestal region (neoclassical screening) leads to very small levels of tungsten concentration in the main plasma as required for good H-mode confinement.

The results of our studies of 5 MA/1.8 T hydrogen H-mode stationary plasmas with ECH heating show that these plasmas show many of the features of H-mode plasmas in later phases of the IRP including integration issues with respect to their practical feasibility in ITER. Therefore, these H-mode plasmas provide a good basis for the development of H-mode operation in ITER thus minimizing the risks associated with H-mode operation in later phases of the research plan. Some of the features of these plasmas are linked to the specific conditions of these operational scenarios in ITER such as the low density leading to low electron–ion equipartition and the increased level of ripple, and their impact on the plasma parameters and achievable confinement have been assessed on the basis of modelling results and comparison with experiments.

Further R&D is required to strengthen these initial results concerning H-mode access and sustainment, the plasma parameters and transport processes expected in these initial H-mode plasmas in ITER as well as edge-core integration issues. An important open issue to refine these quantitative evaluations concern the impact of the hydrogen isotope and/or plasma species (helium) on core plasma transport and overall confinement that can be achieved in H-mode. Many of the models used in our evaluations have been derived for deuterium plasmas (e.g. first principle transport models) and need to be refined to take into account different isotopes and/or different ion specifies since these are found to have non-negligible effects on H-mode access, pedestal stability and H-mode confinement in present experiments [10]. This is an area of open R&D where significant advances for ITER are expected from the upcoming H, T and DT experiments at JET.

ITER is the Nuclear Facility INB No. 174. The views and opinions expressed herein do not necessarily reflect those of the ITER Organization.

The authors are grateful to T Luce, C Angioni, C Bourdelle, H Urano, G Staebler, J Citrin, J Garcia, U Plank, T Pütterich and the members of the International Tokamak Physics Activities Transport and Confinement group for enlightening discussions and advice. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 and 2019–2020 under Grant Agreement No. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.