Abstract
This paper explains the considerations that were important in 1972, when the current leap second procedure was adopted, to maintain a close connection between UTC, the international reference time scale, and UT1—a time scale based on the rotation of the Earth. Although some of these considerations are still relevant, the procedure for adding leap seconds creates difficulties in many modern applications that require a continuous and monotonic time scale. We present the advantages and disadvantages of the leap second procedure, and some of the problems foreseen if it is not reconsidered. We suggest the general outline of a way forward, which addresses the deficiencies in the current leap second system, and which will ensure that UTC remains an international standard that is useful and appropriate for all time and frequency applications. Further discussion and evaluation of the impact of any changes is required.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
International standards of time and frequency play a central role in many applications around the world. These applications include synchronizing information and communication systems, providing a common time reference for commercial and financial transactions, and a common frequency reference for the distribution of electrical power. They support research programs in areas that depend on precision measurements involving the fundamental constants and are also essential for position and timing applications based on global navigation satellite systems (GNSS). The resilience of time synchronization has been recognized as crucial to many pieces of critical national infrastructures. A common requirement for all of these applications is that the reference time be monotonic, smoothly varying, and single valued, and that time intervals and frequencies be traceable to international standards.
The international reference time scale is coordinated universal time (UTC). It is computed by the BIPM using data from atomic clocks maintained in more than 80 institutions and is maintained in agreement with UT1, the angular rotation of the Earth, by the use of a procedure that inserts 'leap seconds' if the value of UT1–UTC exceeds 0.9 s. This procedure creates discontinuities in UTC at the time when they are inserted. Hence whilst UTC is intended to satisfy all the requirements for a single, universal reference for both time and frequency and to be a realisation of the definition of frequency in the SI system of units, it does not meet the requirement to be continuous when a leap second is inserted.
At its 26th meeting in 2018 [1], the CGPM stated that
'UTC is the only recommended time scale for international reference and is the basis of civil time in most countries'.
By the same resolution, the CGPM also recommended that
'all relevant unions and organizations work together to develop a common understanding on reference time scales, their realization and dissemination with a view to consider the present limitation on the maximum magnitude of UT1–UTC, so as to meet the needs of the current and future user communities'.
The number of applications that depend on a smooth and monotonic source of time and frequency data, which is traceable to the SI system of units, has increased significantly since the current version of UTC was developed in the 1970s. The current realisation of UTC with leap seconds does not satisfy these requirements, and the need to support these diverse applications has prompted discussions about possible changes to UTC to make it a continuous time scale. These discussions have also considered future requirements for increased accuracy and improved statistical characterization both for existing applications and for emerging technologies to the extent that they can be predicted. An important aspect of these discussions is the recognition that many current applications that depend on international standards of time and frequency either were not significant or did not exist when the current version of UTC was defined. This trend is likely to continue, and the definition and realization of UTC must be sufficiently flexible to support future applications that are not even imagined now.
As part of its work to advance the common understanding of both current and future requirements for reference time scales by the diverse time and frequency user community, the Consultative Committee for Time and Frequency (CCTF) carried out an online survey in 2021. The survey invited National Metrology Institutes (NMI), UTC laboratories, liaisons, and stakeholders to evaluate the current realization of UTC, and to suggest actions to be taken to ensure its continued usefulness, acceptability, and universality [2].
More than 200 responses were received, of which about 80% confirmed the need to take some action to address the problems that result from the insertion of leap seconds. The responses strongly supported a realization of UTC that would allow a more useable and universal international system for time tagging that would give improved access to the SI second.
In this paper we discuss these problems and possible ways to address them. Despite the fact that the discussion on the discontinuities of UTC started a long time ago (see for example [3]), we consider that the time has come to propose a modification to the correction of UTC, because there will be significant undesirable consequences of not making a change.
2. Atomic time and astronomical time
The basis of atomic time is the 'caesium second' which is defined with respect to the frequency of a hyperfine transition in the ground state of caesium 133 [4]. When coordinated universal time (UTC) was introduced, it was recognized that there should be a close agreement between the atomic time obtained by the accumulation of atomic seconds and the astronomical time scale (UT1), which is based on the rate of rotation of the Earth around its axis. It was understood that a procedure was needed to maintain this connection between UTC and the everyday notion of time, which has been linked to solar time since antiquity. The procedure was also designed to enable UTC to support simple celestial navigation, which used it as a proxy for UT1. The difference between UTC and UT1 was limited to ±0.9 s, which was adequate for the purpose of simple celestial navigation.
The length of the mean solar day has been increasing at an average rate of less than 1 s per year since the procedure for realizing UTC was begun in 1972. However, the rate of increase is variable, so that the difference between UTC and UT1 cannot be predicted with any useful level of accuracy far into the future.
When a code for the transmission of UTC was defined by the International Telecommunication Union Radiocommunication Sector (ITU-R) in 1972, the ITU-R also recognised the requirement to maintain the link between UT1 and UTC using a procedure to insert an extra second into UTC whenever the UTC time scale is predicted to differ from UT1 by ±0.9 s. The need for a leap second is determined by the International Earth Rotation and Reference Service Systems (IERS) and is published about 6 months before the leap event will take place. When a 'positive leap second' is needed, it is added at the end of a UTC day with first preference given to the last day of either June or December. The label for this leap second is 23:59:60, so that the last minute of the day has 61 s when the leap second is added. The ITU-R also considered the possibility that a 'negative' leap second might be needed if the UTC time scale was slow with respect to UT1. This negative leap second would be realized by skipping the time 23:59:59 UTC and advancing from 23:59:58 UTC to 00:00:00 of the next day. This possibility was included for completeness, although the need for negative leap seconds was not considered likely in 1972. Whilst this presumption has been true for almost 50 years, recent data suggest that the need for a negative leap second is no longer simply an academic possibility. We will discuss this point in more detail below.
The decision to maintain the agreement between UTC and UT1 at the level of 1 s allowed celestial navigation methods to use UTC as a proxy for UT1 with an accuracy corresponding to about 15'' of longitude, which is about 460 m at the equator. In addition, the ITU-R defined a transmission code for a coarse estimate of the difference UT1–UTC, named DUT1, with a resolution of a tenth of a second. The IERS calculates and publishes the value of DUT1, which is then broadcast by many radio services.
These tolerances are too large for more precise astronomical applications, which must use the predictions of UT1–UTC that are published by the IERS in Bulletin A. These data are based on observations made by very long baseline interferometry (VLBI), lunar ranging, satellite ranging, and by other methods. The IERS publishes weekly updates with ten-microsecond accuracy (corresponding to about 0.3 cm uncertainty in position) [5]. Other services are available to disseminate this information through the internet and from satellite systems. For example, some GNSS transmit an estimate of UT1–UTC in the navigation message.
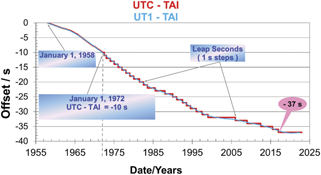
Since the beginning of the current version of UTC in 1972, an offset of 37 s has been accumulated with respect to UT1. Figure 1 illustrates the rate of accumulation of leap seconds. Starting from about 1 s every year at the beginning, they have become less frequent, and no leap seconds have been introduced in the six years since December 2016. Details on the computation of the International Atomic Time and UTC at the BIPM can be found in [6].
Figure 1. Offset of UTC and UT1 with respect to the International Atomic Time (TAI) since the beginning of atomic time. TAI and UTC were set in agreement with UT1 in 1958. The current method of adding only integer leap seconds was begun in 1972. Fractional adjustments in both the time and the frequency of UTC were used before that time.
Download figure:
Standard image High-resolution imageIn recent years, the practice of correcting UTC by inserting leap seconds has been questioned by users in several sectors. For example, most clocks, and especially digital clocks that keep time as the number of seconds that have elapsed since some epoch, cannot represent the time 23:59:60.
Conventional analogue clocks cannot display the time 23:59:60, and even simple digital clocks that display the time in the traditional hour:minute:second format cannot cope with a leap second event. Although it would be possible in principle for a simple digital clock to display the time value of 23:59:60, it is not possible to program these clocks to display this time when they are built because the occurrence of a leap event cannot be predicted far into the future, and simple digital clocks have no mechanism by which they can be informed about leap second events.
In addition to the difficulty of representing the time during a positive leap second, the discontinuity in the time interval measured across a leap second is not consistent with assigning monotonic and equally spaced time tags to real-time processes. As examples, this difficulty affects processes that estimate the speed of a moving object by dividing the distance travelled by the elapsed time or the execution speed of a computer program by dividing the number of instructions processed by the time needed for the computation. These and other difficulties have led some communities to devise 'ad hoc methods' that address their particular requirements but are not consistent with the internationally agreed procedure of inserting leap seconds into UTC. Since each one of these communities has devised its own unique method, the data from different sources are usually not consistent with each other. We will discuss this point further in the next section.
3. GNSS system times
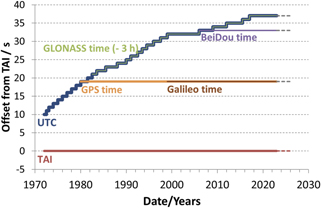
The issue of discontinuities in UTC was encountered by GNSS designers who decided, in most cases, to define a system time that would ignore leap seconds after the initial synchronization of the system time to UTC. This is not a surprising decision; the GNSS signals were designed to support navigation, and the insertion of leap seconds complicates the calculation of the speed of a moving object as we discussed above. Although it is possible to adjust the system time of the constellation to include a leap event in principle, future leap seconds were not incorporated into most of the GNSS system times in order to avoid any risk of failure in the system due to the difficulty of inserting leap seconds into the entire satellite constellation at the same instant. The GNSS system times differ among themselves by an integral number of seconds depending on when they were initialized. These differences are shown in table 1 and figure 2. Note that the Russian GLONASS system, conversely, includes leap seconds in the system time to maintain an agreement with the international standards (apart from a constant offset of 3 h).
Table 1. Offsets in use by different GNSS system times (2022).
| GNSS | Offset from UTC |
| GPS | +18 s |
| GALILEO | +18 s |
| BEIDOU | +4 s |
| GLONASS | Constant 3 h, and leap seconds are applied |
Figure 2. Offset between UTC, the GNSS system times, and International Atomic Time TAI.GLONASS time has a constant offset of 3 h with respect to UTC.
Download figure:
Standard image High-resolution imageAlthough the GNSS system times are intended to be only a parameter internal to the operation of their systems, they are often used as a reference time scale in other applications because they are easily accessible world-wide. The widespread use of GNSS system times introduces confusion amongst users and creates a risk of potential synchronization errors. For example, a recent recommendation by ITU-T explains the need for a continuous reference time scale for the telecommunication networks and recommends GPS time without leap seconds as an alternative to UTC [7]). The use of GPS system time as a proxy for UTC introduces an ambiguity because the current difference between UTC and GPS system time shown in table 1 will change each time a leap event occurs.
4. Synchronization of digital systems
The increasing importance of digital time systems and the possible disruption to national critical infrastructures caused by the insertion of leap seconds has led to the development of various ad hoc correction methods as alternatives to the insertion of the leap second. For example, some systems realize the extra positive leap second by repeating the time value corresponding to 23:59:59 a second time. Other systems use a similar method and realize the leap second by repeating the time value corresponding to 00:00:00 of the next day. Both of these methods have the correct long-term behaviour with respect to UTC, but both disagree with UTC during the leap-second event, and the method of repeating the time value corresponding to 00:00:00 inserts the extra second in the wrong day. Other methods replace the time step produced by the leap second by a frequency adjustment that amortizes the leap second over some interval. The details are listed in table 2. All of these frequency-adjustment methods have the correct long-term behaviour with respect to UTC, but all of them have an error on the order of ±0.5 s during the adjustment period. An error of this magnitude is much larger than the accuracy required in many commercial and financial applications, so that systems that realize a leap-second event using these methods cannot be used to apply time stamps to most commercial and financial transactions. To further complicate the problem, these providers generally do not indicate which method is being used to amortize the leap second or the details of the frequency adjustment that is applied, so that it is difficult to combine or compare data from different sources for about 24 h before and after the leap event. Since the methods are not transmitted with the data and since they may change from time to time, this incompatibility makes it difficult to estimate the traceability to UTC.
Table 2. Examples of ad hoc correction procedures used by major web service providers.
| Ad hoc correction procedure | User(s) |
|---|---|
| Frequency adjustment for 24 h before the leap second | |
| Frequency adjustment for 18 h after the leap second | |
| Symmetrical 'smear' from 12 h before to 12 h after the leap second | Alibaba |
| Frequency reduced to one-half for the second before the leap second | Microsoft |
The use of such ad hoc methods to realize the leap second is increasing and is even being recommended by major web service providers as the basis for future international standards [8]. (Each provider advocates for the adoption of its particular method of frequency adjustment.) The use of these different ad hoc correction methods presents a risk of failure of crucial national services. The monotonic and single valued time scales generated by the different frequency-adjustment methods threaten the choice of UTC for many contemporary applications, especially international financial, commercial, and telecommunication services. These methods have a particularly large impact in the western United States, where the leap second is inserted at 16 h (4 pm) during the working day, and in most parts of Asia and Australia, where the leap second event coincides with the opening of the stock markets the following morning.
5. The SI second and Earth rotation
The duration of the 'caesium second' was defined based on the measurements made by Markowitz, Hall, Essen and Parry in the 1950s [9]. The intent of the definition was to ensure the continuity of the duration of the caesium second with the previous definition of the second, which was based on Ephemeris Time. The duration of the ephemeris second, in turn, was based on astronomical data that averaged a century of observations that ended about the year 1900. The result of this work defined the duration of the caesium second as equal to 9192 631 770 cycles of the hyperfine transition frequency in the ground state of caesium 133. From the beginning, the duration of the atomic second was shorter than the experimentally determined duration of the second based on the Earth rotation in the 1950s because, the secular slowing down of the Earth rotation was not considered. Therefore, clocks that used the caesium frequency value gained time with respect to rotational time, UT1. A number of methods, based on fractional adjustments to atomic time both in time and in frequency, were tried to address this problem, but they were cumbersome and confusing. In particular, the frequency adjustments, which were of order 10−8 in fractional frequency, were not universally applied, and it was difficult to use a source of frequency data. The multiplicity of frequency sources and the ambiguity of whether a particular source did or did not apply the currently mandated frequency offset greatly complicated the frequency calibration methods of that period and provide an example of the problems with multiple incompatible sources of time and frequency transmissions. It would be wise not to forget this lesson.
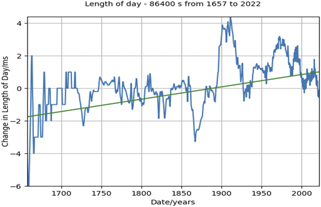
The current leap second procedure was defined in 1972 to address this problem. The fractional adjustments in time and in frequency, which were used up to that time and which were difficult to realize, were replaced by a single time step of exactly 1 s with no adjustment in the frequency of UTC relative to the atomic second. The implicit understanding was that the caesium second would continue to be shorter than the astronomical second because both historical data and simple models suggested that the length of the day, and the length of the astronomical second, would continue to increase. The basis for this understanding was the historical long-term increase in the length of the day as shown in figure 3.
Figure 3. The length of the day from 1657 to 2022 [10]. The slope line shows the long-term increase of 0.76 milliseconds per century in the length of the day. There are significant deviations from this trend that can last for several years.
Download figure:
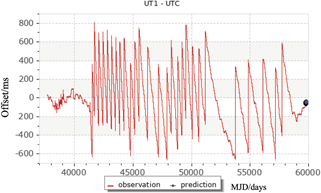
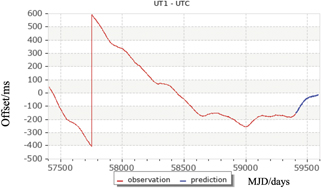
Standard image High-resolution imageFigure 4 presents the values of UT1–UTC since the beginning of UTC. The current system of inserting leap seconds into UTC started in 1972 (MJD 41317). Although it was not obvious at the time, we can see in retrospect that the length of the day started to decrease at almost the same time as the current leap second system was initialized, and the interval between leap seconds has gradually increased since then as a result. The acceleration became quite noticeable at MJD 51000 (1998-07-06), and has continued since the last leap second, which was inserted at the end of 2016 (MJD 57753). See figure 5, which shows the values of UT1–UTC since the most recent positive leap second.
Figure 4. The difference between UT1 and UTC as a function of modified Julian day number (MJD). The current leap second system was initialized at MJD 41317, and a positive step in UT1–UTC was introduced each time the difference approached approximately −600 ms. The civil dates corresponding to some of the MJD values are: 45 000 = 1982-01-31, 50 000 = 1995-10-10, 55 000 = 2009-06-18 (figure obtainable from https://eoc.obspm.fr/index.php? index=realtime&lang=en).
Download figure:
Standard image High-resolution imageFigure 5. Observed and predicted value of UT1–UTC since the last insertion of a leap second in 2016 (MJD 57753). The abscissa shows the modified Julian date (MJD). (Figure obtainable from https://eoc.obspm.fr/index.php? index=realtime&lang=en).
Download figure:
Standard image High-resolution imageThe IERS predicts that UT1–UTC will go through zero in January or February 2023 and will continue to increase at a rate of about 100 ms year−1 (Bulletin A, www.iers.org) If this rate continues, then UT1–UTC will approach +0.9 s within 7 or 8 years. An extrapolation of this length has a large uncertainty, and this is not a firm prediction. Instead, it is an indication of what might happen rather than a prediction of what will happen, but it illustrates the point that the original assumption, based on the long-term trend shown in figure 3, that negative leap seconds would never be required should be reconsidered.
We could be tempted to redefine the atomic second a bit longer to cope with the slowing down of the Earth, but this cumbersome approach would not help. First, the continuity in the definition of measurement units is fundamental to be able to maintain the traceability with respect to past measurements. In addition, with the observed irregularities in the rotation of Earth, it will never be possible to get a strict agreement with the atomic metrology, accurate at 10−18 in relative value, versus the Earth rotation, which shows changes at the level of 10−7 in relative value. Finally, any change in the definition of the length of the atomic second would have a significant impact on the entire SI system of units, since the standard of frequency explicitly defines other units, such as the standard of length. It is also implicitly linked to other SI units through various relationships such as the Josephson effect.
6. Use and dissemination of the value UT1–UTC
There is a long-standing connection between civil time and the rotation of the Earth that dates to antiquity. The everyday understanding of this relationship is closely linked to apparent solar time. Gabor refers to this as the principle of astronomical conformity [11]. In spite of this link, civilian time at almost all locations has a very significant offset relative to mean solar time, which is the basis for the time-zone system, and there is an additional difference of up to 16 min between mean solar time and apparent solar time that has an annual variation. All the locations in a single time zone have the same civil time, but the apparent solar time at locations in the same time zone can differ from each other by up to ±30 min. For example, China covers 5 time zones, but Beijing time is used everywhere in the country. Similarly, Russian time and Central European Time are used in three time zones. The application of daylight-saving time in some locations causes an additional seasonal offset of 1 h, and the dates when daylight saving time is effective vary from country to country and from year to year. The additional offset of UT1–UTC is objectively smaller than these offsets, and this would be true for a very long time even if no leap seconds had ever been added to UTC in the past and were never added in the future. But this is not the whole story for two reasons. In the first place, all of these offsets are algorithmic, and can be removed for any date in the recent past or in the future. On the other hand, the leap second events are not algorithmic and a separate adjustment must be applied for every event. This can be a difficult job because tables of previous leap seconds events are not widely available, and the dates of previous leap seconds are not stored with the time tags that were affected by them. In the second place, making any significant change to the link between UTC and astronomical time is likely to have a subjective impact on the public perception of time that far exceeds the objective impact of the change. This problem would be particularly troublesome if the link between UTC and UT1 was eliminated completely. This is why we do not question the importance of maintaining the link between UTC and the rotation of the Earth given by UT1.
The decision, in 1972, to insert leap seconds to maintain a close link between UT1 and UTC was driven by several technical considerations. Some of these considerations are less important now than they were then, but some are still important. Any proposal to change the procedure to correct UTC, for example by enlarging the tolerance UT1–UTC, must be considered in the light of these technical issues and their relative importance in 2022.
6.1. Celestial navigation and astronomical tables
Celestial navigation was important in 1972 and maintaining a close link between UT1 and UTC made it possible to use UTC as a proxy for UT1. A time error of 1 s (corresponding to 15 s of arc) did not result in a significant error in position in the open sea or when flying an airplane not close to busy airports. The difference between UT1 and UTC was not significant for navigation in rivers or in the approach to harbour entrances or airports, since celestial navigation was neither needed nor useful in those situations anyway. The widespread use of GNSS satellites for navigation has largely replaced celestial navigation, even for the smallest airplanes. In principle, celestial navigation remains an emergency backup method if GNSS data are not available, but the use of GNSS data is so common and widespread that many pilots may not know how to determine a position based on astronomy if they had to do so.
Astronomical tables and ephemerides can be published with both UT1 and UTC time as the independent variable. For example, the web pages of the US Naval Observatory [https://aa.usno.navy.mil/data/mrst] use time tags in UTC with a resolution of 1 min for some data. This presentation would not change if the offset UT1–UTC were small relative to 1 min. Anther web page for celestial navigation requires input time in UT1 with a resolution of seconds and fractions (https://aa.usno.navy.mil/data/celnav). Since all time services transmit UTC, the difference between UT1 and UTC must be known to use these web pages, or the difference must be kept small enough so that it can be ignored for many purposes.
Since a new leap second is generally announced only 6 months in advance because of uncertainties in predicting the long-term rotation rate of the Earth, it is not possible to make long-term predictions for ephemerides. For example, when the last leap second was announced in 2016, the French Bureau des Longitudes had already published the predicted ephemerides in its 'Annuaire' based on the previous number of leap seconds, leading to an error in the date of the predictions [12].
6.2. Radio time-service broadcasts
The difference between UT1 and UTC is broadcast by time-service radio stations in a format that was designed with the assumption that the difference between UT1 and UTC would be limited by the leap second process. The radio stations operated by the National Institute of Standards and Technology (NIST), WWV, WWVB, and WWVH, are typical examples, and conform to the method recommended by the ITU-R [13]. The stations transmit DUT1, a coarse estimate of UT1–UTC that is calculated by the International Earth Rotation and Reference Service and published in IERS Bulletin D [5]. The broadcast format assumes that the resolution of DUT1 is 0.1 s and that it will never exceed 0.9 s in magnitude. This transmission format would have to be modified (or the transmission of DUT1 would have to be discontinued) if the magnitude of UT1–UTC were to exceed 0.9 s.
6.3. Global navigation satellite systems
The GPS and BeiDou GNSS satellites transmit an estimate of UT1–UTC as part of the ephemeris messages of each system. The two systems partition the data bits differently. The GPS system transmits an estimate of UT1—GPS time in 31 bits (30 bits of data and 1 sign bit). The binary value must be scaled by 2−23, so that the transmission can accommodate a value of UT1—GPS time with a magnitude of up to 127 s. The BeiDou system also uses 31 bits (30 bits of data and 1 sign bit), but the scale factor is 2−24, so that the dynamic range is ±64 s. The transmission formats of both systems would eventually fail if the difference between UT1 and GPS time exceeded these limits, but both systems could accommodate an increase in the maximum magnitude of UT1—GPS time of order 1 min without any changes.
The GLONASS GNSS satellites uses a system time that is based on UTC with leap seconds. The leap second is inserted into GLONASS system time at the same instant when it is inserted into UTC (The system time is UTC(SU) + 3 h) The data message includes an estimate of UT1–UTC, and the magnitude of the transmitted difference is limited to 0.9 s. If the offset UT1–UTC should exceed 0.9 s, the GLONASS navigation message and the ground receivers must be updated. The modernization of the GLONASS system has taken this necessity into consideration [14] and the future navigation message will allow the magnitude of UT1–UTC to increase to 256 s. The complete update of the satellites and ground equipment was declared to need 15 years notice ( [15] and the CCTF UTC presentation in [2]).
7. Implementations of the leap second
Although the procedure for inserting positive leap seconds into UTC has been in use for more than 50 years, there are still occasional reports of failures of systems at every leap second event. A few examples are reported here [16]. Contrary to our expectations, the number of problem reports has increased with time. The increase in the number of problem reports may be a result of the increase in the interval between leap seconds. It is becoming increasingly likely that the software of an application will be deployed without ever having been tested by a real leap event, and many 'smart' devices have time software that cannot be upgraded once it has been released into the user community.
In principle, the problems and deficiencies of UTC should focus on the issues that are inherent in the definition of the UTC time scale—the ambiguity of how to represent a leap second, the discontinuity in the time interval across a leap event, and other issues, some of which we have discussed above. Problems with the software that realizes the insertion of leap seconds into UTC raise issues that must be addressed, but they point to inadequacies in the way software is developed, tested, and deployed, and should not be considered as problems with the definition of UTC itself. This strict perspective would suggest that no changes were needed to UTC to address these problems.
We think that this strict perspective is too narrow. It is certainly true that the process for developing, and testing application software can be improved, but it is also true that the increase in the interval between leap seconds and the lack of any algorithm that can correct for past leap seconds or predict future ones places a heavy burden on software implementations of UTC.
The irregular variation in the length of the UT1 day means that there is probably no way of realizing a leap second system that is completely algorithmic, and this issue could be totally removed only if we completely stopped adding leap seconds. However, just increasing the tolerance between UT1 and UTC without doing anything else, will increase the interval between leap events and is almost certain to make this problem worse. For example, if a leap event happened only a few times per century, a typical applications programmer might never see a leap event during an entire professional career.
The possibility of a negative leap second compounds this problem. These events have never happened, so that it is almost a certainty that there will be widespread errors in realizing the event, if it happens. The various 'smear' techniques do not include any discussion of how a negative leap second would be handled; this possibility has not even been considered in principle in the discussions of the various frequency-adjustment methods. The continued errors and mistakes in realizing positive leap seconds even after 27 leap events confirm these concerns.
8. Summary and conclusions
The procedure for maintaining a close link between UT1 and UTC by adding leap seconds to UTC has resulted in a UTC time scale that is not suitable for an increasing number of applications, especially applications that use a digital representation of time as the number of seconds and fractions that have elapsed since some time origin. The deficiency in UTC resulting from the addition of leap seconds has been addressed by a number of ad hoc methods, which are not consistent with UTC and are not even consistent with each other. These methods are defined by various third parties to satisfy their internal requirements, but the developers also advertise their solution as suitable for widespread, global adoption to replace the current internationally agreed upon definition of UTC.
The widespread availability of time from GNSS satellites and the excellent statistical characteristics of these time signals has resulted in these signals replacing UTC as a primary source of time in many applications. This trend is almost certain to continue. It will effectively transfer the practical definition of time from the BIPM and the timing laboratories in many countries to the GNSS operators, whose data are not sanctioned by any international agreement. The increasing use of signals from the GPS satellites effectively means that the US military controls a primary source of international time signals with almost no oversight nationally or internationally.
The problems and deficiencies of UTC could be addressed by discontinuing the process of adding leap seconds. The UTC time scale would then have the same statistical character as TAI. Although this approach would address the problems and deficiencies we have listed in the previous paragraphs, we think that it is important to maintain a link of some type between UTC and UT1, and we have listed some of the reasons why we consider this to be important and some of the problems and difficulties that would result if this link were completely removed.
If a link between UT1 and UTC is to be maintained, and if the current procedure of inserting leap seconds is not a suitable method for realizing this link, then we must consider other methods to do so. One possibility would be to increase the maximum difference between UT1 and UTC. For example, if the tolerance were increased from 1 s to 1 min, the interval between leap events would be on the order of a century, if the tolerance were increased to 1 h, then the interval between leap events would be a few thousand years, assuming the current change in the rate of UT1 were to continue at its current magnitude. A change in the tolerance of these magnitudes would have significant negative consequences, and we have presented some of these in the text. However, extrapolations of this length have a very large uncertainty. Since increasing the maximum tolerance between UT1 and UTC would make leap events much less common, it would also increase the impact of an event when the maximum tolerance was finally reached. Therefore, it will be necessary to place an increased emphasis on education and awareness ahead of such a step. (A time step of 1 min is a more significant than the current steps of 1 s; some other method would probably be used such as a method based on an international frequency adjustment would be a possibility).
If the tolerance between UT1 and UTC is increased, it will be increasingly important to provide near-real-time access to the UT1–UTC difference, especially for applications that now use UTC as a proxy for UT1. The access should be widely and easily available and should support the transmission of data in a reliable, secure, and machine-readable format. The role of the IERS will be fundamental in this.
If the current rate of change of UT1–UTC continues for 7 or 8 years, then a negative leap second will be needed by about the year 2030. Negative leap seconds have never been needed, and it is almost certain that the methods that are used to implement these events will have errors because the method has never been tested by a real event. The continued problems with the insertion of positive leap seconds even after 50 years are a measure of the difficulties in implementing software to support events that occur only rarely and unpredictably. This possibility emphasizes the need for making a decision now.
In conclusion, we do not consider that there is a 'perfect' solution to the problems discussed here. Defining a time scale that satisfies the needs of time and frequency users and is also in agreement with astronomical phenomena is not straightforward and a series of trade-offs is necessary [11]. We consider that enlarging the tolerance is a wise provisional solution, which should be reconsidered when new discoveries and deeper understanding could result in a better solution.
It is encouraging that the ITU, where the leap second format was initiated and recommended, and the BIPM, through its committees as the CCTF, are working together to understand the current and future needs of UTC and its users to agree on a way forward.