Abstract
RNAs carry out diverse biological functions, partly because different conformations of the same RNA sequence can play different roles in cellular activities. To fully understand the biological functions of RNAs requires a conceptual framework to investigate the folding kinetics of RNA molecules, instead of native structures alone. Over the past several decades, many experimental and theoretical methods have been developed to address RNA folding. The helix-based RNA folding theory is the one which uses helices as building blocks, to calculate folding kinetics of secondary structures with pseudoknots of long RNA in two different folding scenarios. Here, we will briefly review the helix-based RNA folding theory and its application in exploring regulation mechanisms of several riboswitches and self-cleavage activities of the hepatitis delta virus (HDV) ribozyme.
Export citation and abstract BibTeX RIS
1. Introduction
RNAs play a multitude of diverse cellular roles in many biological reactions, from catalysis,[1,2] gene regulation,[3–5] protein synthesis to bacterial immunity.[6–11] In order to exert functions, they have to fold into correct structures. As RNAs are quite dynamic and prone to forming multiple structures, they can be trapped readily in inactive, long-lived conformations during the folding process.[12–14] In many cases, the native structure may not be thermodynamically favored over other intermediate structures,[15,16] leading to the requirement for other factors (RNA chaperone or small ligands) that aid in RNA folding. On the other hand, these kinetically trapped intermediates or alternative metastable structures create a time window for RNAs to implement different cellular roles in vivo, such as regulating translation of gene,[17] controlling of plasmid R1 maintenance or acting as highly sensitive molecular switches.[18–21] An impressive example is riboswitches. Especially for the kinetically controlled switches, such as pbuE and metF riboswitches,[16,22] they need to stay in the non-native, kinetically trapped intermediates to make the relevant genetic decisions. Not just the structural information of native states, a thorough analysis of RNA folding kinetics is required inevitably to underlie RNA function.
RNA folding is one of the core issues to comprehensively understand the cellular activities of RNA. There are two kinds of folding manners:[13,20,23–25] (i) RNA folds with a random coil of a denatured transcript (free folding or refolding); (ii) RNA folds as it is transcribed with a growth length (co-transcriptional folding). The first scenario typically occurs in vitro while the later one is under a cellular environment. Due to the completely different folding conditions, even with the same sequence, the folding process in the two scenarios could be different for many RNA molecules.[23]
Under a transcription context, many naturally evolved RNA molecules can effectively avoid misfolded intermediates and form correct structures on a biologically reasonable timescale.[26–28] However, this sequential process with structure formation and transition on the μs timescale plus the extremely complex cellular environment, poses a severe challenge to visualize RNA intracellular folding events. By monitoring self-cleavages of transcripts with variable lengths, co-transcriptional folding was initially assayed for some catalytic RNAs through their splicing activities.[29–31] For example, group I and group II introns, which exhibited catalytic properties in vitro without proteins, were intensively used in previous RNA folding studies.[32,33] Recent researchers employed the optical-trapping assay to successfully observe distinct co-transcriptional folding transitions for an adenine riboswitch.[15] Besides these experimental approaches, several theoretical methods, such as the kinetic Monte Carlo simulation,[34–36] RNAkinetics,[37] CoFold,[37] BarMap, and Kinefold were developed to address RNA co-transcriptional folding.[38–40] By comparison with experimental results to fix the simulation timescale, the kinetic Monte Carlo can simulate dynamics of RNA secondary structure for both folding scenarios. Based on RNA secondary structures, BarMap models effects of environmental changes on RNA co-transcriptional folding as small and discrete changes in the landscape.[38] Other aforementioned methods, are inherently subject to length limitations or can not provide co-transcriptional folding pathways or transition rates.
The recently developed helix-based RNA folding theory are suitable to calculate folding kinetics of RNA secondary structure with pseudoknots for long RNA sequences.[16,41–44] This method has been used to study the target's effects on siRNA efficiency,[45] refolding behaviors of HDV ribozyme and its co-transcriptional folding pathways with different flanking regions.[46,47] In order to model the effect of external triggers, the theory further incorporated ligand binding kinetics and successfully investigated regulatory behaviors of several kinds of riboswitches, including kinetically and thermodynamically controlled representatives.[16,48] Here, we will provide a brief overview of this method and its application in revealing the action mechanisms of HDV and riboswitches.
2. Helix-based RNA folding kinetics
Due to the incredible complexity of the cellular environment, studying RNA folding almost exclusively starts in vitro, with a random, unfolded chain in an optimal condition (a suitable ionic concentration and temperature).[12,20,23] This folding scenario, which simulated the intracellular situation, provided an invaluable approach to initially explore the folding details and dissect effects of individual cellular factors. However, in vivo, most functional RNAs fold co-transcriptionally with varying chains because of the sequential nature of RNA. To address RNA co-transcriptional folding under such complex conditions, relevant knowledge and suitable methodologies are both limited till now. The theory of helix-based RNA folding kinetics becomes a useful tool to investigate RNA refolding and co-transcriptional folding processes. Directionality, speed, and pause of transcription, which strongly affect co-transcriptional folding, are taken into consideration in this theory.
2.1. Refolding kinetics
Opening/closing a base stack is the most elementary step in RNA folding, which has been studied by molecule dynamic simulations.[49,50] Recent results verified that opening/closing a base stack can be described by a two-state transition process by using proper reaction coordinates,[51–54] and kinetic rates for stack formation (k+) and disruption (k−) can be obtained:[51,55] k+ = k0eΔS / kBT, k− = k0eΔH / kBT. Where k0 equals 6.6 × 1012 s−1 and 6.6 × 1013 s−1 for an AU and GC base pairs respectively, kB is the Boltzmann constant, T is the temperature. ΔS and ΔH are entropic and enthalpic changes upon stack formation and disruption. If the stack closes a loop, the entropic change ΔS should also include the entropy change of the loop.
A basic process in RNA folding is helix formation, which includes closing several consecutive stacks. After the first few stacks are formed, closing the subsequent stacks in the helix could be fast, as the rate of stack formation is larger than that of stack disruption (except the first stack). It is reasonable and efficient to use helices as elementary units for studying the overall folding kinetics of RNAs.[56] In the case of RNA refolding, all possible helices are enumerated and then used to assemble RNA secondary structures and pseudoknots. According to the nearest-neighbor model,[57] the free energy of each structure in the conformation space equals the sum of free energies of all stacks and loops. The free energy of the loop within a pseudoknot is calculated as below:[46] Gps = 0.83Gss + 0.2nf + 0.1np (for nf ≤ 9), Gps = 0.83Gss + 0.2[9 + log (nf / 9)] + 0.1np (for nf > 9). Where Gps is the free energy of a pseudoknot loop, Gss is the free energy of loops before formation of the pseudoknot, nf and np are the numbers of free bases and paired bases in the pseudoknots respectively. Energy parameters of other loops and stacks are taken from the previous study.[57]
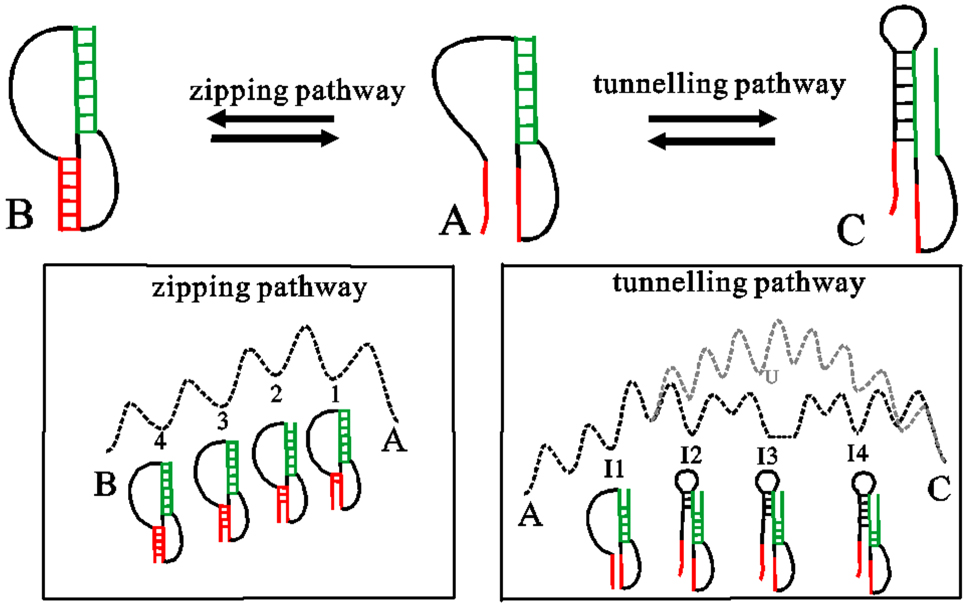
In the conformation space, an elementary kinetic move between two structures is forming, disrupting a helix or exchange between two helices. If two structures only have one different helix, they can directly transit to each other by formation or disruption of the helix via the zipping pathway. This kind of pathway is the most probable pathway for helix formation, because breaking an existing stack or forming another distant stack is much slower than formation of a neighboring stack. For example, by forming the red helix, structure A can fold to B through the zipping pathway in Fig. 1 with a rate of
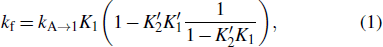
where Ki and  are the forward and reverse probabilities of state i,
are the forward and reverse probabilities of state i,
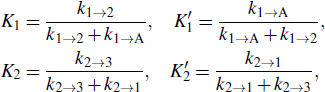
with ki → j being the transition rate from state i to j. kf in Eq. (1) only considers the formation of the first three stacks, since the energy landscape of a zipping pathway usually presents a downhill profile after that. In fact, there are several other zipping pathways which differ in the first formed stacks, and so kA → B is the sum of the rates along all possible zipping pathways.
Fig. 1. Transitions between states (A, B, C) through formation (A to B), disruption (B to A) of a helix (red), and exchange between two helices in A (green) and C (the left/right shoulder of the helix is colored black/green). The relevant pathways labeled along the arrow are shown in the bottom boxes, where the dotted dark lines denote the schematic energy landscape of zipping and tunneling pathways. The unfolding-refolding pathway are shown with gray color, U is the unfolded, open chain.
Download figure:
Standard imageWhen two helices overlap with each other, direct transition between them is helix exchange through the unfolding-refolding or tunneling pathways (see Fig. 1). Compared to completely unfolding the green helix and then refolding the other, the tunneling pathway where disrupting a stack in A is followed by concurrently forming a stack in C after breaking several stacks in A, returns a much lower transition barrier. The rate constants to disrupt (form) a stack in A (C) are supposed to be ki and  respectively. Hence, the rate through the tunneling pathway from A to C is calculated by the following equation:[56]
respectively. Hence, the rate through the tunneling pathway from A to C is calculated by the following equation:[56]
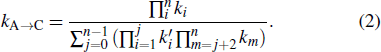
According to the detailed balance condition, all reverse transition rates are equal to the product of relevant forwards transition rates and e−ΔG / kBT, where ΔG is the free energy difference of the two states. After all transition rates are calculated, the population pi (t) of state i over time t can be obtained by solving the master equation ![${\rm{d}}{p}_{i}(t)/{\rm{d}}t=\displaystyle \sum _{j}[{k}_{i\to j}{p}_{i}(t)-{k}_{j\to i}{p}_{j}(t)]$](https://content.cld.iop.org/journals/1674-1056/29/10/108703/revision2/cpb_29_10_108703_ieqn3.gif) , whose matrix form is dp(t) / dt = M ⋅ p(t). Here, M is the rate matrix with elements
, whose matrix form is dp(t) / dt = M ⋅ p(t). Here, M is the rate matrix with elements  and
and  . p(t) denotes the vector of the population distribution. The solution of the equation is
. p(t) denotes the vector of the population distribution. The solution of the equation is  , where nm and −λm are the m-th eigenvector and eigenvalue of the rate matrix. The coefficient Cm is determined by the initial conditions. For refolding processes, the initial state is the unfolded chain.
, where nm and −λm are the m-th eigenvector and eigenvalue of the rate matrix. The coefficient Cm is determined by the initial conditions. For refolding processes, the initial state is the unfolded chain.
Based on the calculated population distribution, the detailed refolding pathway is identified as follows.[46] If two states (A, B) can transit to each other through one elementary move, the net flux FA → B (t) form state A to state B till time t will be given by ![${F}_{{\rm{A}}\to {\rm{B}}}(t)=\displaystyle {\int }_{t=0}^{t}[{k}_{{\rm{A}}\to {\rm{B}}}{p}_{{\rm{A}}}(t)-{k}_{{\rm{B}}\to {\rm{A}}}{p}_{{\rm{B}}}(t)]{\rm{d}}t$](https://content.cld.iop.org/journals/1674-1056/29/10/108703/revision2/cpb_29_10_108703_ieqn7.gif) . By calculating all the net flux flowing into the native state, we can find the states that directly fold into the native state and their population. These states can be considered as the first layer. The second, third, ... layers also can be obtained in the same manner. The overall transition pathway between the unfolded and naive state, can be identified by a recursive procedure.
. By calculating all the net flux flowing into the native state, we can find the states that directly fold into the native state and their population. These states can be considered as the first layer. The second, third, ... layers also can be obtained in the same manner. The overall transition pathway between the unfolded and naive state, can be identified by a recursive procedure.
2.2. Co-transcriptional folding kinetics and transition node approximation
The basic idea to deal with the co-transcriptional folding is dividing the whole transcription process into a series of transcription steps, each of which corresponds to synthesis one nucleotide.[43] The newly transcribed nucleotide could extend the 3' single-strand tail, pair with an upstream nucleotide to elongate a helix or form a new helix. Given a transcription rate of v nucleotides per second (nt/s), the folding time at each step is (1/v) s. If the transcription process pauses t s when transcribing one nucleotide, the folding time of the relevant step will be (1/v + t) s.
The folding kinetics of each step is calculated in a similar way to that in refolding. Here, we use a certain step M as an example to illustrate. At the M-th transcription step, the RNA chain has M nucleotides available to form structures. The newly transcribed nucleotide is the M-th nucleotide, which could extend the 3' single-strand tail, pair with an upstream nucleotide to elongate a helix or form a new helix. The conformation space for this M-nt chain, free energies of all possible states and transition rates are first obtained as described earlier. Then, the master equation is solved to get the population kinetics within this step, where the initial condition is determined by the structure relationship between the two adjacent steps (step M and M − 1). If a state has one or more newly formed helices, its initial population at this step will be zero. Otherwise, the initial population is equal to its end population of step M − 1.
When RNA molecule increases in size, it still generates a large conformation space, which could low the calculation efficiency. In general, when more nucleotides are released, the initial population of each following step mostly concentrated in several metastable states. If these states formed before the current step, are much more stable than the newly formed states, it will be impossible for RNA to fold the new states. By searching the possible transitions, we can therefore neglect these structures except those at the main folding pathways, which can contribute to population flow. The approximation can efficiently reduce the conformation space especially after around the 120-th transcription step. It makes predictions for long RNA sequences with large conformation ensembles become possible and computationally viable.
3. The application of the helix-based RNA folding kinetics
For a certain RNA molecule, its biological function relies heavily upon the folding process. To make a careful analysis of RNA folding process therefore becomes a core issue and prerequisite in exploring the cellular activities. The analysis on RNA folding process inevitably concerns the information of main folding pathways and associated structures. For functional mRNAs, such as riboswitches and HDV, all these mentioned information can be provided by using the helix-based RNA folding theory.
3.1. Refolding and co-transcriptional folding of HDV ribozyme
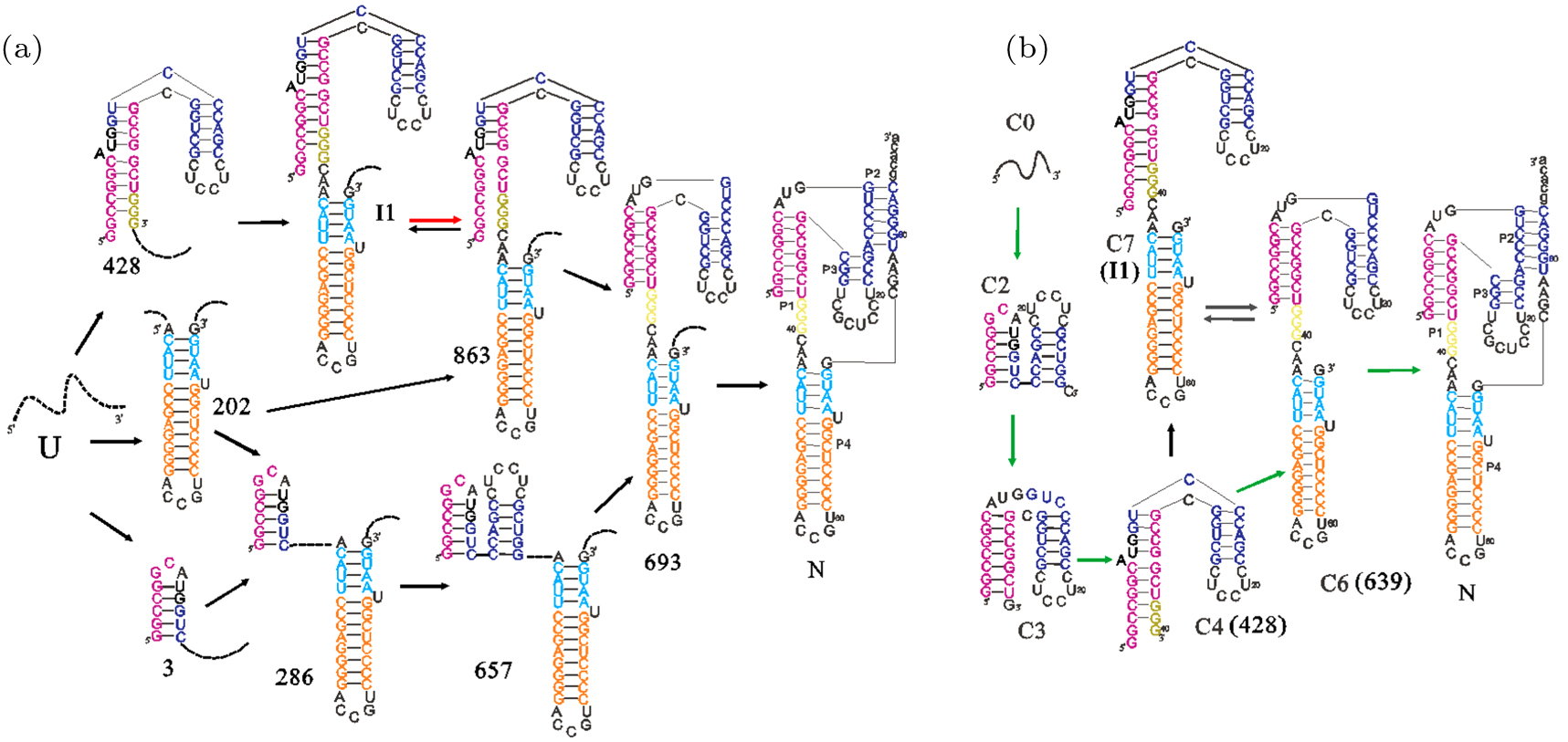
The virulence of hepatitis B virus infections could be accelerated and enhanced by co-infection or super-infection with HDV, a human pathogen.[58] It contains a small ribozyme with about 85 nt in its RNA genome. As self-cleaving catalytic RNA, the nascent HDV sequence undergoes self-cleavage during its rolling-circle replication process by forming a catalytic fold.[59–61] This native fold (state N in Fig. 2), which directly controls the self-cleaving activities, has a complex double-pseudoknot topology with several helices.
Fig. 2. The main pathways of HDV ribozyme under two different scenarios: refolding (a) and co-transcriptional folding (b). Upper and lowercase letters denote the ribozyme region and the flanking region. The unpaired nucleotides in the external loop are simply described by dotted lines in panel (a). The rate-limited transition in the slow refolding pathway panel (a) and the main co-transcriptional transition with net flux about 90% (b) are shown with red and green arrows respectively. Except the different RNA lengths in panels (a) and (b), structure model of states denoted inside and outside parentheses in panel (b) are the same.
Download figure:
Standard imageEarly experiment suggested that the self-cleavage of HDV in vitro is bi-phasic: about 30% RNAs fold into the native structure N in around 15 s and the rest slowly cleavages in the next 30 minute (min).[60] Refolding behaviors of the wild-type ribozyme show two distinguish stages as well, and these special features are further studied by recursive searching the states with high net flux-in (out) to identify the detailed folding pathway.[46] The results (see Fig. 2(a)) suggest that, the slow cleavages result from that part of the ribozymes trapped in the non-native state I1. Compared to state I1, state 863 is much more unstable and always has a little equilibrium population. Thus, even the rates from I1 to 863 and 863 to 639 are around 101 s−1 and 103 s−1, the overall slow folding pathway is still limited by the transition from state I1 to 863. The non-phasic feature observed in mutated HDV folding experiments,[60] is because the mutation breaks GC pair and destabilizes I1, thereby decreasing the population flowing through I1.
Different from the refolding behaviors, the main folding pathway is from C4 to C6 then to state N with flowing population of 90% under a transcription of 15 nt/s (see Fig. 2(b)).[47] The native state N is formed as soon as the nucleotides are transcribed, which facilitates its role of self-cleavage in rolling–circle replication process. Like other naturally evolved RNAs,[23,24] transcription can affect the HDV folding process positively by preventing non-native trapped intermediates.[59,62]
In vivo, ribozymes are often embedded in large molecules with flanking sequences. These sequences are not essential for catalysis, but their presence has a significant effect on the folding of HDV and other ribozymes.[63–65] The helix-based RNA folding theory combined with the transition node approximation is employed to address the effects of the flanking sequences and ulteriorly analyze the reason.[47] The existence of the 30-nt upstream flanking sequence inhibits formation of state N through folding an alternative helix with nucleotides 79–86 (see Fig. 2(b)). However, the 54-nt upstream flanking sequence directs the ribozyme folding in the same way as that without any flanking sequences, by forming a hairpin itself. That is, the longer upstream flanking sequence facilitates formation of the native state N. If the 55-nt downstream flanking sequence is present, the folded state N will be broken by a stable helix formed via base-pairing between nucleotides in the flanking region and P2 helix. This process involving a great conformation change yields a transition rate of 4 × 10−2 s−1, which is slower than the measured self-cleavage rate of 40 min−1.[59,60] Thus, most RNAs can cleave completely before unfolding of the native structure. These results suggested that the natural HDV sequence has evolved to function co-transcriptionally with the flanking sequences, from the point of its role in double rolling-circle replication.
3.2. The regulation mechanisms of riboswitches
As genetic control elements, riboswitches can regulate gene expression via a signal-dependent change in RNA structure.[66–72] Most of them are composed of two functional domains: an aptamer responsible for sensing ligands and an expression platform to control gene expression. Since the two domains often partly overlap with each other, ligand binding could induce structural changes, such as exposing/sequestering the Shine–Dalgarno (SD) sequence or alternative splice site in the second domain, which directly switch gene expression on/off.
To mimic the effect of external triggers, ligand binding kinetics is incorporated into the helix-based RNA folding theory.[16,41] If the ligand is present, the bound states will be added to the conformation space. Free energies of bound states are equal to the free energies of the corresponding ligand-free states plus the energy term ΔGbinding = kBT ln(kon[L] / koff). Where kon and koff are experimentally measured association and dissociation rates. Under a linear relation, the transition rates between the unbound states and the corresponding ligand-bound states are the effective binding rate keff = kon [L] and dissociation rate koff. Effects of different ligand concentrations on outcomes of riboswitch-mediated gene expression can be simulated by varying the value of ligand concentrations [L].
3.2.1. Kinetically controlled riboswitches
Among the more than 30 discovered riboswitch species, the yjdF riboswitch belongs to a new riboswitch class which senses natural azaaromatics that are toxic to the host cells.[73–75] The experimental and additional bioinformatic analyses suggests, this translational riboswitch regulates production of yjdF protein by controlling access to the ribosome binding site (RBS) through a pseudoknot (Pk).[75] As a newly validated riboswitch, all these findings had laid a foundation to reveal its activities, but there are still many unknowns, such as the precise type of its natural ligand and its regulation mechanism.
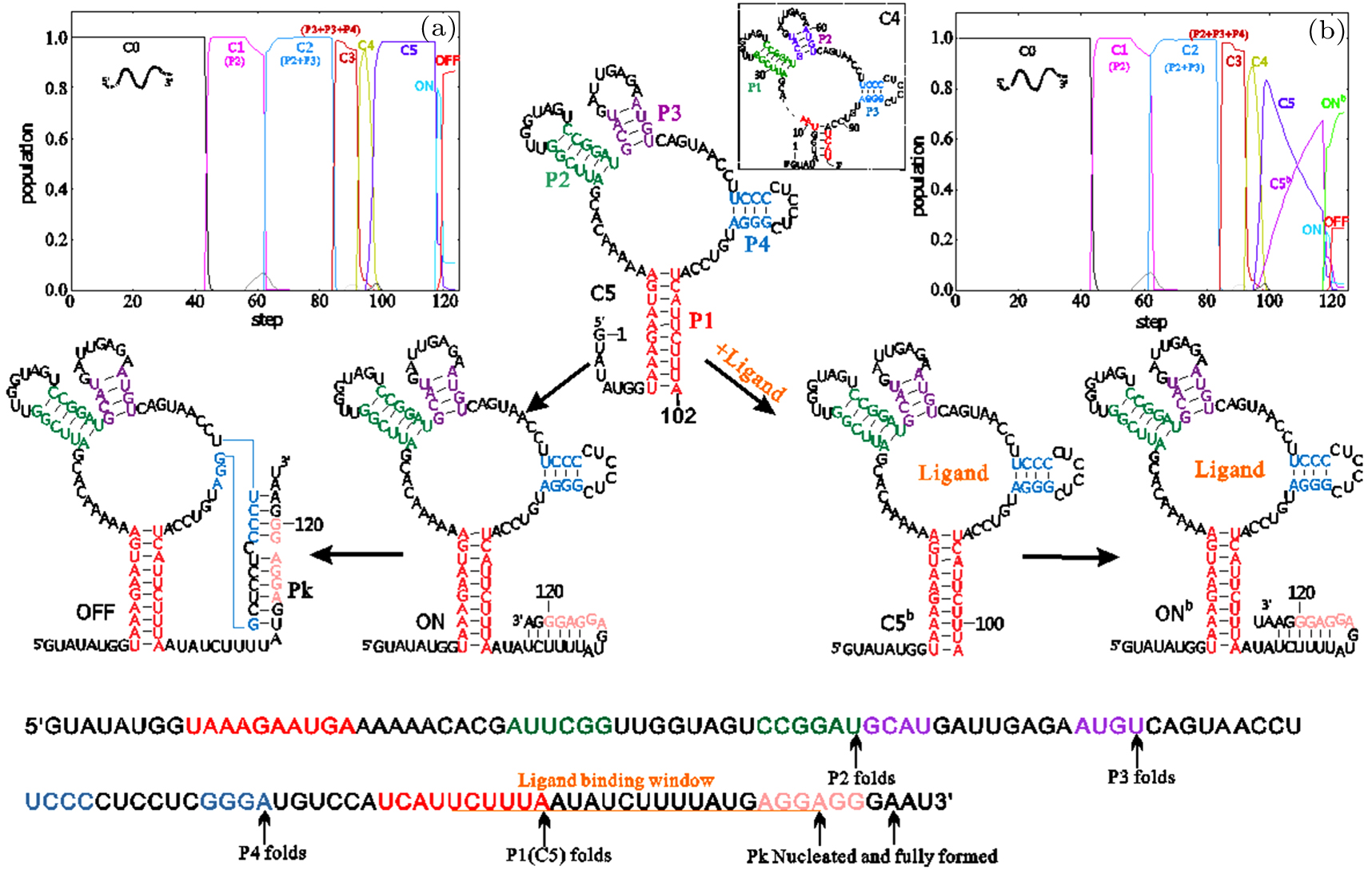
According to the predicted co-transcriptional folding behaviors,[44] the previously discovered pocket structure C5,[73] is formed as an intermediate and finally broken by the pseudoknot in OFF state without its ligand. The segment of this folding pathway, where helices P2, P3, P4, and P1 are sequentially formed, is the same to that with the ligand (see Fig. 3(b)). Once the aptamer structure C5 is folded, it will bind to the ligand and then quickly fold into ONb state by forming a small hairpin. As translation initiation correlates to the stability of the paired region near RBS,[76] this hairpin can promote translation initiation while the pseudoknot in OFF state has the opposite effect (ΔGHairpin = −2.20 kcal/mol, ΔGPk–helix = −21.40 kcal/mol), although both of them cover the RBS.
Fig. 3. The co-transcriptional folding behaviors of the yjdF riboswitch from B. subtilis. The population kinetics of main states and their structure at an elongation rate of 15 nt/s are shown in (a) with 0-μM and (b) with 10-μM ligand. Important folding events are mapped in the low panel. The superscript "b" denotes the corresponding state with ligand bound. C0 is the open chain and C4 is a four-way branch structure shown in box near C5. Structures C1, C2, and C3 composed of one or more hairpins labeled in the brackets nearby. The RBS region is colored pink.
Download figure:
Standard imageAs the transition rate from OFF state to the pocket structure closes to the mRNA decay rate (kdecay = 3 min−1),[77] along with the time delay of the ligand and ribosome binding, formation of OFF state will primarily be an irreversible event. The time window allowed for ligand binding is therefore limited from the point when the non-local helix P1 becomes stable to the point when OFF state begins to invade into the aptamer structure. Obviously, a high ligand level can increase the effective binding rate and a slow transcription elongation rate yields a long binding time period, both of which are in favor of the bound state.
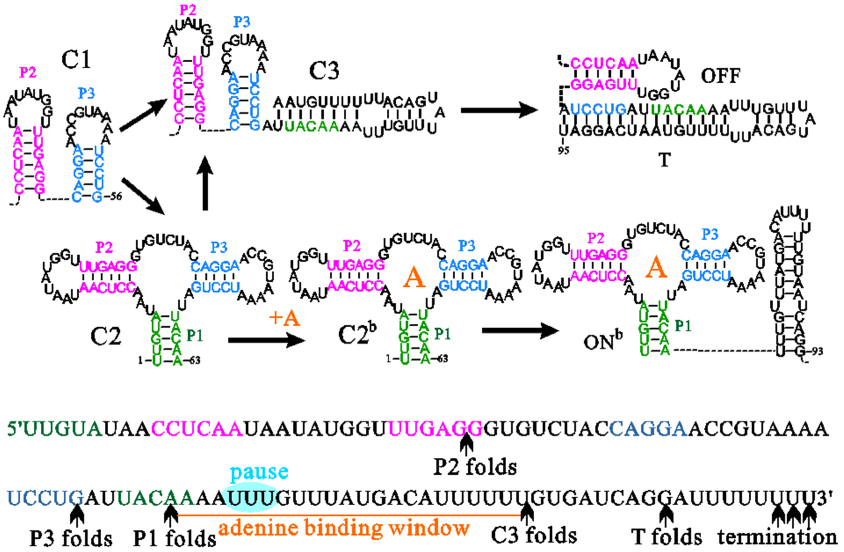
Unlike the translational addA riboswitch,[22,78] the yjdF riboswitch exerts its biological function of translation regulation under a combined action of transcription rates, ligand properties and concentrations, consisting with a kinetic model. Besides, transcription pausing can modulate activities of kinetically driven riboswitches, such as pbuE riboswitch as well, although it functions at the transcription level. Since the full-length pbuE riboswitch quickly refolds into a ligand incompetent OFF state without any trapped intermediates, the pocket structure with helices P1, P2, and P3 only can be formed in the transcription process (see Fig. 4). To switch on, adenine must bind to the pocket structure before formation of the most stable OFF state. Pausing at the U tract directly followed the aptamer domain can provide extra time for ligand binding. Especially at a low ligand concentration, enough pausing time will largely increase the efficiency of gene expression to reduce adenine levels.
Fig. 4. Structure transitions on main co-transcriptional folding pathways of the pbuE riboswitch. T is the terminator hairpin. Nucleotides within helix regions of the aptamer structure and the pause site are colored differently.
Download figure:
Standard image3.2.2. Thermodynamically driven riboswitches
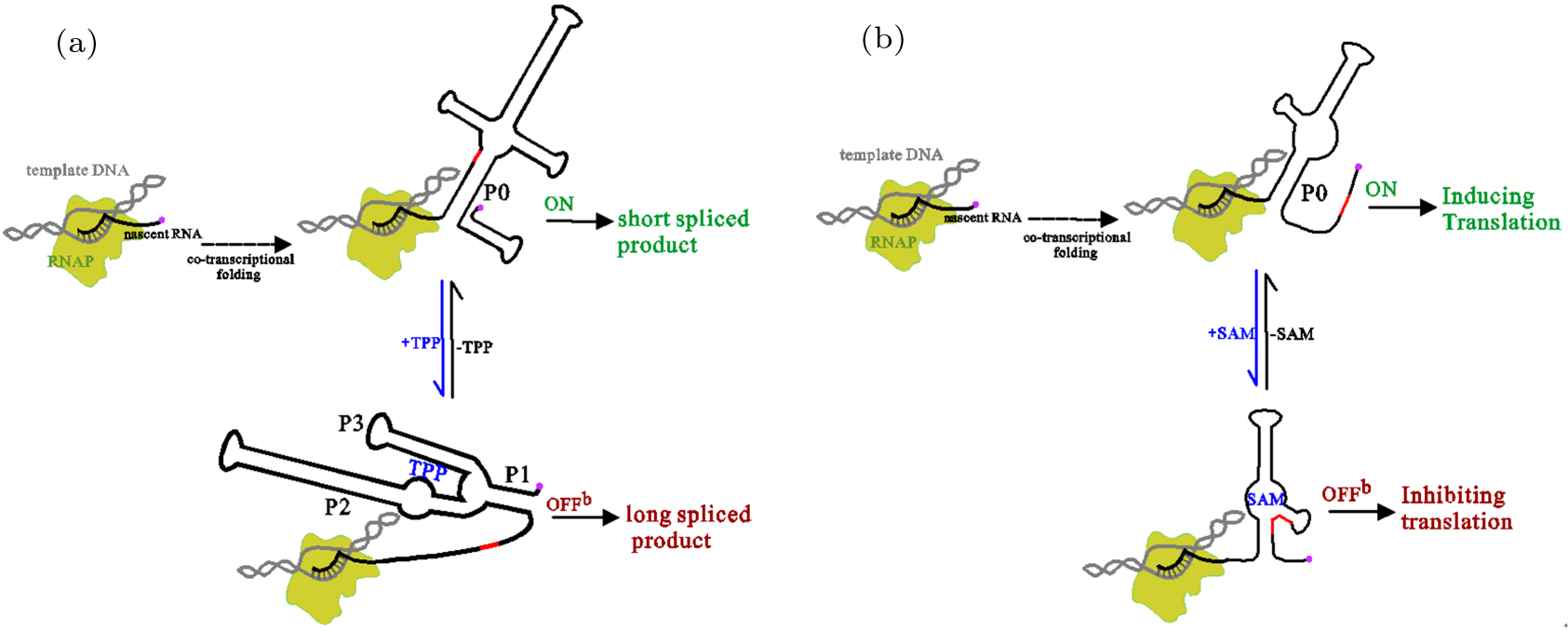
The thiamine pyrophosphate (TPP) riboswitch in NMT1 mRNA from N. crassa is a typical representative that regulates gene expression by controlling mRNA splicing.[79] It only utilizes a single domain to sense ligand and modulate gene expression.[79] The structural difference near the 5' splice site in two functional states, results in different spliced products, which can repress or induce NMT1 gene expression. Compared to the solved high-resolution bound state, that ligand-free functional state with a paired structure near the 5' splice site is the only structural information of ON state inferred from the experiments. The co-transcriptional folding behavior suggested that (see Fig. 5(a)),[44] its ON state was mainly organized by a four-stem junction with a structured 5' splice site in helix P0. During the transcription, this riboswitch predominately folds into lower-energy ON state without forming the pocket structure. As nucleotides in ON state (ΔGON = −73.07 kcal/mol) are synthesized prior to that in OFF state (ΔGOFF = −71.67 kcal/mol), there is only one main co-transcriptional folding pathway without any switch point regardless of the TPP levels. It implies that the ligand-induced conformation rearrangement should occur after the full-length chain has been transcribed.
Fig. 5. Regulatory behaviors of the TPP (a) and SMK riboswitch (b). The nature ligand of SMK riboswitch is S-adenosylmethionine (SAM). The arrows with dotted lines denote the co-transcriptional folding, where RNAs transit from a series of intermediate states (not shown) to ON state, which is formed near the end of transcription. The 5' splice site in the TPP riboswitch (a) and the SD in the SMK riboswitch are colored red. The 5' ends of nascent RNA are shown with red circles.
Download figure:
Standard imageAccording to the experimental observations, TPP and the mutation in helix P3 can switch genetic off separately.[80] This mutation, which exchanges nucleotides between two sides of three base pairs in helix P3, breaks the potential to form the bottom five stacks in helix P0. The mutated ON state with a shorten helix P0 co-transcriptionally folds and quickly equilibrates into other two states with a flexible splice site before the splice reaction initiates. All these results show that like addA and SMK riboswitches,[81,82] regulation of the TPP riboswitch is not sensitive to the transcription process. Instead of the transcription context, their switch efficiencies greatly depend on stabilities of the two functional structures.
In addition to these common features shared by thermodynamically controlled riboswitches, the TPP and E. faecalis SMK riboswitch own some unique characters because they only have one single domain.[48] For the two riboswitches, even under different ligand concentrations, the main folding pathway is the same (see Fig. 5). The external trigger has no effect until the transcription process closes to the end. What is more, the shorten SMK construct which breaks nonlocal helix P0, also loses most abilities of the ligand-dependent gene control. That is to say, the potential of fully forming the nonlocal helix is crucial for both riboswitches to restore switch functions.[48,83] These common characters shared by the two riboswitches, have not been found in two-domain riboswitches, which at least have one switchpoint during the transcription.[15,74,84]
4. Conclusion and perspectives
RNA folding process is a crucial step in functional characterization and structural biology. As intermediate structures formed and transited fast in this process, it mounts a great challenge to fully monitor folding pathways under different cellar conditions. Based on RNA secondary structure, the helix-based RNA folding theory has been developed to explore folding behaviors of several riboswitches and HDV. The good agreement with experiments suggests it becomes a reliable tool to simulate RNA folding directly in a variety of RNA structures, including structures with pseudoknot. Compared to the recently developed CRKR resampling algorithm which needs to run the master equation for the whole chain,[85] our method is quite suitable for longer RNA, especially for RNA molecules longer than 150 nt. But at the same time, it takes longer time when the chain grows to 250 nt or more. The current theory is mainly subject to RNA secondary structure and the energy parameters at this theory are of RNA at 1M NaCl solution condition. Although RNA secondary structure can provide sufficient structural information, biological functions of RNA depends critically on the tertiary structure, which is the key determinant of their interactions with ions and other molecules in cell.[86–88] For example, Mg2+ could significantly stabilize the tertiary interactions,[89] which may alter RNA folding pathway. More significant efforts are needed to make for further developing this theory by considering these intracellular factors.
Acknowledgment
The numerical calculations related to our work in this review were performed on the supercomputing system in the Supercomputing Center of Wuhan University.
Footnotes
- *
Project supported by the Science Fund from the Key Laboratory of Hubei Province, China (Grant No. 201932003) and the National Natural Science Foundation of China (Grant Nos. 1157324 and 31600592).