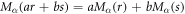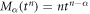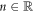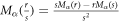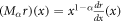Abstract
This paper deals with the new analytical solutions of conformable nonlinear Boussinesq equations. Boussinesq equation is one of the important equation in the field of applied mathematics and engineering, particularly in optical fibers, plasma physics, fluid dynamics, signal processing, and shallow water etc. The focus of this paper is to obtain the new explicit solutions of conformable Boussinesq equations. Exponential function technique is employed to solve the considered models. The conformable properties are utilized to obtain new analytical solutions for this type of nonlinear Boussinesq equations. The new analytical solutions are acquired especially for the space-time boussinesq equation. The results are shown graphically. The obtained solutions can be useful for engineers and physicists to further analyze the phenomena. The implemented technique is valuable for finding new analytical solutions of nonlinear partial differential equations (PDEs).
Export citation and abstract BibTeX RIS
List of abbreviations
| PDEs | Partial differential equations |
| ODEs | Ordinary differential equations |
1. Introduction
In recent decades, a large amount of work has been done in development of symbolic programming. Many researchers developed new techniques on computer-based platforms in order to solve complicated algebraic equations more quickly than manually. Numerous efficient techniques have been employed to solve various PDEs.
Many applied mathematicians are focused to solve PDEs. Thus, different techniques are developed to get the solutions of nonlinear PDEs. The first integral technique [1–4], 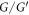 expansion technique [5, 6], the functional variable technique [7–9], the sub-equation technique [10–12], the exp
expansion technique [5, 6], the functional variable technique [7–9], the sub-equation technique [10–12], the exp 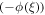 technique [13, 14], the improved tan
technique [13, 14], the improved tan  -expansion technique [15–17], the exponential and modified exponential function technique [18–21] are some of the recent effectual techniques for discovering the solution of nonlinear PDEs. This paper uses exp-function technique to get the analytical solutions of nonlinear Boussinesq equation.
-expansion technique [15–17], the exponential and modified exponential function technique [18–21] are some of the recent effectual techniques for discovering the solution of nonlinear PDEs. This paper uses exp-function technique to get the analytical solutions of nonlinear Boussinesq equation.
Hydrodynamics deals with the transmission of waves in dissipative and nonlinear medium is illustrated by the Boussinesq equation [22]. For example, the study of long waves in shallow water. Boussinesq equation is extensively used in ocean and coastal engineering [23, 24]. Most of the models based on Boussinesq equations are used to describe subsurface drainage problems and unconfined ground water flow. Moreover, Boussinesq equation with fractional order is preferable for water propagation in heterogeneous porous media. Boussinesq equations of fractional order is derived to model for unconfined groundwater [25].
The exact solutions are always imperative to study the physical phenomenon. Many researchers studied Boussinesq equations and various solutions were presented in the literature. Yildrim and Mohud-Din presented the solution of Boussinesq equation using the He's semi-inverse method [26]. Neyrame et al applied the 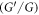 -expansion method to extract the traveling wave solutions [27]. In the literature, very few papers are available on the solution of conformable boussinesq equation with the help of different methods [28–30]. Hosseini et al obtained the solution of nonlinear time conformable Boussinesq equations using the exp(
-expansion method to extract the traveling wave solutions [27]. In the literature, very few papers are available on the solution of conformable boussinesq equation with the help of different methods [28–30]. Hosseini et al obtained the solution of nonlinear time conformable Boussinesq equations using the exp(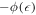 )-expansion method [28]. Hosseini and Ansari acquired the solutions of nonlinear time conformable Boussinesq equations using the modified Kudryashov method [29]. In the current study, the novel exponential function method is implemented and new analytic solutions are acquired, particularly, for the space-time conformable boussinesq equation. The results for conformable order 0 < α < 1 are new and results for α = 1 can be retrieved from already published work using other techniques.
)-expansion method [28]. Hosseini and Ansari acquired the solutions of nonlinear time conformable Boussinesq equations using the modified Kudryashov method [29]. In the current study, the novel exponential function method is implemented and new analytic solutions are acquired, particularly, for the space-time conformable boussinesq equation. The results for conformable order 0 < α < 1 are new and results for α = 1 can be retrieved from already published work using other techniques.
In 2006, He and Wu has introduced a reliable and effectual technique known as exponential function technique to extract the solutions of nonlinear PDEs which are travelling wave solutions [31, 32]. This technique depends on principle of homogeneous balance. The execution of our proposed technique is efficient and reliable for solving nonlinear PDEs. The focus of this study is to employ exponential function technique for acquiring the new analytical solutions of nonlinear time conformable Boussinesq equation and space-time conformable boussinesq equation.
The layout of the paper is as follows. Section 2 comprises of conformable derivative and its properties, section 3 consists of exponential function technique, section 4 presents the application of exponential function technique for nonlinear time conformable Boussinesq equation and space-time conformable Boussinesq equation and section 5 contains conclusions.
2. Preliminaries
2.1. Conformable derivative
Recently khalil et al introduced a simplest, most natural and efficient definition of local derivative of order ![$\alpha \in (0,1]$](https://content.cld.iop.org/journals/1402-4896/96/10/105209/revision2/psac0e01ieqn6.gif) , known as conformable derivative [33, 34]. For any value of α, we can generalize the definition.
, known as conformable derivative [33, 34]. For any value of α, we can generalize the definition.
Definition 2.1.1. Let 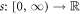 be a function. The conformable derivative having order α for function s is given as [33, 35, 36]:
be a function. The conformable derivative having order α for function s is given as [33, 35, 36]:
Here  and x > 0. If in some (0, a) with a > 0, the function s is α-differential and
and x > 0. If in some (0, a) with a > 0, the function s is α-differential and  exists, then definition becomes:
exists, then definition becomes:
Conformable derivative of constant function is zero. The conformable mean value theorem proves s(x) = 0 for 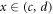 if we take
if we take 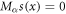 [33].
[33].
The conformable integral is represented as:
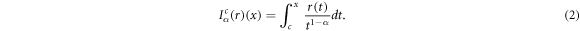
Here c ≥ 0 and ![$\alpha \in (0,1]$](https://content.cld.iop.org/journals/1402-4896/96/10/105209/revision2/psac0e01ieqn12.gif) . The above integral represents the usual Riemann improper integral.
. The above integral represents the usual Riemann improper integral.
By using the above definition of derivative, khalil presented the following theorem [33, 36–38].
Theorem. Let 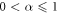 and r, s are α-differentiable functions at a point x > 0 then,
and r, s are α-differentiable functions at a point x > 0 then,
- 1.
 for all
for all  .
. - 2.
 for all
for all  .
. - 3.Mα (λ) = 0, for all constant functions r(λ) = 0.
- 4.
 .
. - 5.
 .
. - 6.If r is differentiable, then
 .
.
Theorem. Let us consider two (left) α-differentiable functions r, s such that 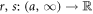 , with
, with ![$\alpha \in (0,1]$](https://content.cld.iop.org/journals/1402-4896/96/10/105209/revision2/psac0e01ieqn22.gif) . We have h(x) is left α-differentiable when
. We have h(x) is left α-differentiable when 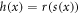 , ∀x except
, ∀x except 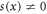 and
and 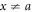 . Hence chain rule will be given as [35]:
. Hence chain rule will be given as [35]:
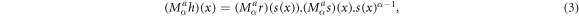
consider x = a, we get

This definition attracted many scientists and they worked more intensively for further investigations [33, 35]. Abdeljawad applied conformable derivative to describe rules for exponential functions, chain rule and integration by parts, Laplace transform and Taylor power series expansion [35]. Researchers worked incredibly on its applications for solving conformable models in mathematical physics [1–3, 39], quantum mechanics [40] and Newton mechanics [41, 42].
3. The exponential function technique
In 2006, He and Wu established exponential function technique [31] and systematically studied in [43–45]. The proposed technique is established on the basis of homogeneous balancing principle. Only those nonlinear conformable PDEs that satisfies homogeneous balancing principle can be solved by using exponential function method. Thus, we get analytical solutions for these equations. Exponential function technique is very compact and an easy technique to acquire solutions of nonlinear evolution equations arising in mathematical physics [46–48]. Firstly, we utilize the wave transformation to reduce nonlinear conformable PDEs to nonlinear ordinary differential equations (ODEs) for finding the analytical solutions of PDEs.
3.1. Demonstration of exponential function technique for nonlinear conformable PDEs
The general form of nonlinear conformable PDEs is described as follows:
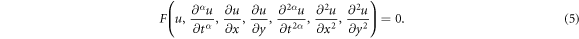
Now, consider a following transformation:
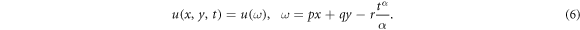
Here  ,
, 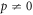 and
and 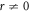 are constants, these constants are calculated later in process.
are constants, these constants are calculated later in process.
Utilizing equation (3), we have
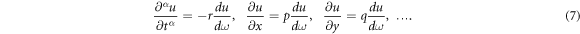
Using equations (7) into (5), we get a nonlinear ODE as

Assume the above ODE has solution of the following form
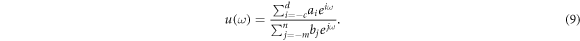
Here c, d, n and m are positive integers determined by homogeneous balancing principle, ai and bj are constants which are unknown. The next step is to balance the lowest order linear term in equation (8) with the lowest order non-linear term, in order to evaluate c and m. Similarly balance the highest order linear term in equation (8) with highest order nonlinear term, in order to calculate the value of d and n. As a result, we get the analytical solution of nonlinear PDEs.
4. Implementation of the proposed technique
4.1. Example 1
The nonlinear time conformable Boussinesq equation has the following form [22, 49, 50]:
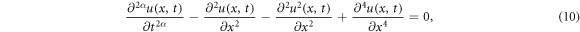
where  ,
, 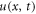 is a field function and
is a field function and 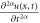 represents the conformable derivative of u(x, t).
represents the conformable derivative of u(x, t).
Equation (10) includes two competing effects i.e. (i) the linear dispersive term represented by 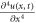 that explains the out spreads and (ii) the nonlinear term
that explains the out spreads and (ii) the nonlinear term 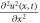 which describes the translation of wave. If both of these effects are presents then solitary wave can be determined. Hence Boussinesq equation gives rise to solitary waves because of the balance between the dissipative effects of
which describes the translation of wave. If both of these effects are presents then solitary wave can be determined. Hence Boussinesq equation gives rise to solitary waves because of the balance between the dissipative effects of 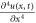 and nonlinearity effects of
and nonlinearity effects of 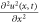 . These waves are confined as they travel with constant shapes and speeds. For large distances these waves are asymptotically zero. Solitary waves have special kind called solitons. Solitons possess a property which keeps its identity after interacting with other solitons. Now, using the wave transformation and chain rule, we get
. These waves are confined as they travel with constant shapes and speeds. For large distances these waves are asymptotically zero. Solitary waves have special kind called solitons. Solitons possess a property which keeps its identity after interacting with other solitons. Now, using the wave transformation and chain rule, we get
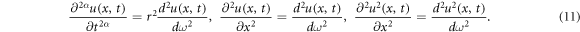
Using equations (11) into (10), we have
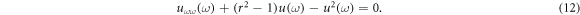
Assume a solution of the above ODE as follows:

In order to evaluate the constants c, d, n and m, here we apply homogeneous balancing principle. According to this principle, we have to compare 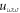 and
and 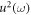 of equation (12). Now consider
of equation (12). Now consider
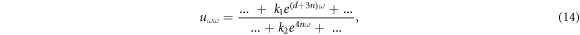
and
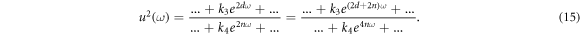
For unknowns d and n compare the highest order of exp-function in equations (14) and (15) which results
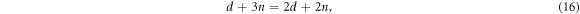
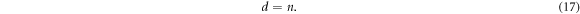
Similarly,
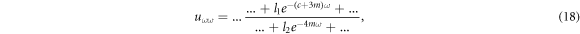
and

where li are coefficients. Comparing the lowest order of exp-function in equations (18) and (19) we get
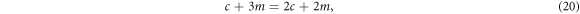
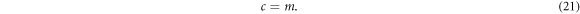
Setting d = c = 1, equation (13) becomes
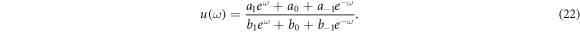
Substitute equations (22) into (12), then equating the coefficients of  , we obtain
, we obtain
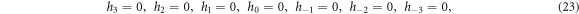
where  are algebraic equations evaluated by the help of Maple 13.
are algebraic equations evaluated by the help of Maple 13.
By inspection, we get
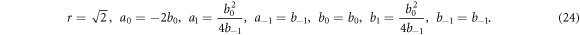
Using equations (24) into (22), it becomes
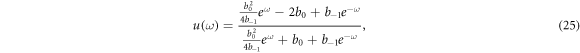
where 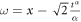 , after simplifying equation (25) we obtain
, after simplifying equation (25) we obtain
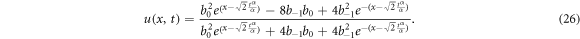
Setting 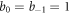 , equation (26) becomes
, equation (26) becomes
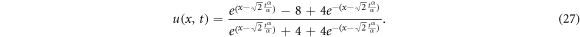
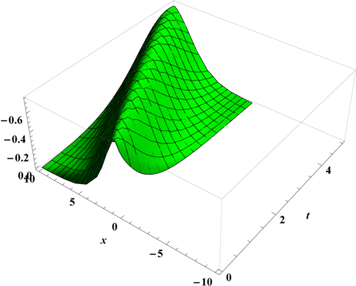
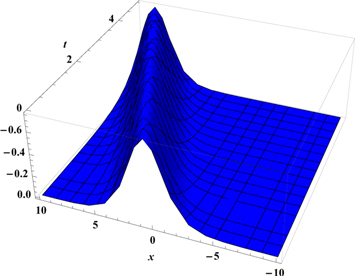
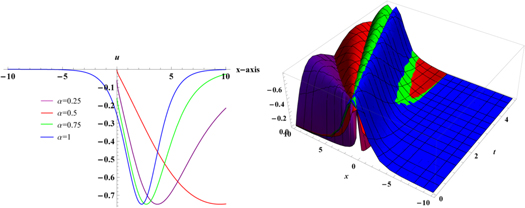
Equation (27) reveals that Boussinesq equation can exhibits explosive wave form. Figures 2–4 show the solution of time conformable Boussinesq equation for α = 0.25, α = 0.5, α = 0.75 and α = 1, respectively. Figure 5 represents the solution of time conformable Boussinesq equation by allocating various values to α. This solution describes an explosive solitons. For different values of α these solitons are moving with constant speed and shape. The solutions presented in figures 1–4 are the singular type of solitons. The similar type of solutions for α = 1 (c.f. figure 4) can be observed in the literature [50, 51].
Figure 1. Graph of u(x, t) for α = 0.25.
Download figure:
Standard image High-resolution imageFigure 2. Graph of u(x, t) for α = 0.5.
Download figure:
Standard image High-resolution imageFigure 3. Graph of u(x, t) for α = 0.75.
Download figure:
Standard image High-resolution imageFigure 4. Graph of u(x, t) for α = 1.
Download figure:
Standard image High-resolution imageFigure 5. 2D and 3D Graphs of u(x, t) for various values of α.
Download figure:
Standard image High-resolution image4.2. Example 2
The nonlinear space-time conformable Boussinesq equation is described as follows [25, 29, 52, 53]:
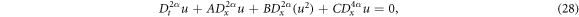
where t > 0, 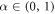 and the diffusion parameter C = constant where C > 0 depends on the hardness and compression properties of the substance, u(x, t) is the vertical diversion, B is the nonlinearity coefficient and the curvature of the bending beam is described by the quadratic nonlinearity
and the diffusion parameter C = constant where C > 0 depends on the hardness and compression properties of the substance, u(x, t) is the vertical diversion, B is the nonlinearity coefficient and the curvature of the bending beam is described by the quadratic nonlinearity 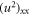 , α is a parameter which explains the conformable order of the space and time derivatives.
, α is a parameter which explains the conformable order of the space and time derivatives.
Introducing the transformation 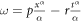 , equation (28) is converted into an ODE of the form:
, equation (28) is converted into an ODE of the form:
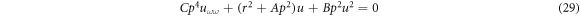
Assume a solution of the form,

Using the same approach in example 1, equating the highest order of exp-function in 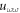 and
and 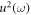 , we get the result
, we get the result
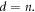
Similarly, equating lower order of exp-function in 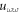 and
and 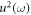 , we get
, we get
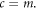
Taking d = c = 1, equation (30) becomes
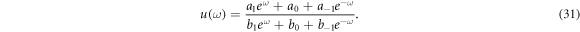
Putting equation (31) into equation (29), then equating coefficients of 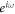 we obtain a system of algebraic equations. Then obtained algebraic system is solved by using Maple and we get the following results:
we obtain a system of algebraic equations. Then obtained algebraic system is solved by using Maple and we get the following results:

using equations (32) into (31), we have
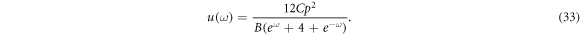
As 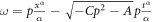 therefore, equation (33) becomes
therefore, equation (33) becomes

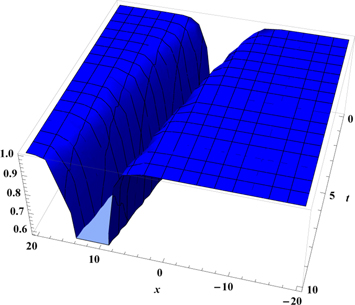
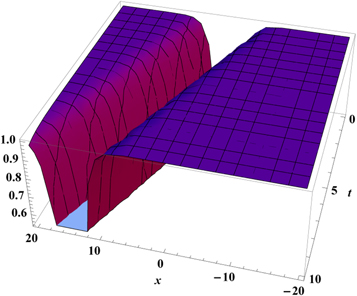
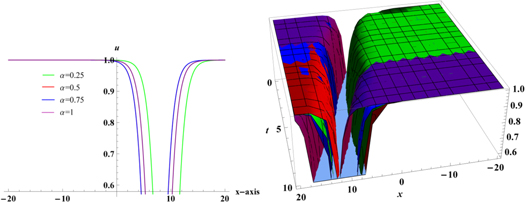
The real valued domain of u(x, t) is positive values of x. Figures 6–9 show the solution of space-time conformable Boussinesq equation for α = 0.25, α = 0.5, α = 0.75 and α = 1, respectively. Figure 10 represents the solution u(x, t) of space-time conformable Boussinesq equation by using different values of α. Figure 10 reveals that the flatten curves are observed for less values of α, and sharp curves for values of α near to 1. Figure 9 represents the bell-shaped solitary wave solution for α = 1 which is already presented in literature [50].
Figure 6. Figure of u(x, t) for B = −1, C = 0.5, A = −3, p = 1 and α = 0.25.
Download figure:
Standard image High-resolution imageFigure 7. Figure of u(x, t) for B = −1, C = 0.5, A = −3, p = 1 and α = 0.5.
Download figure:
Standard image High-resolution imageFigure 8. Figure of u(x, t) for B = −1, C = 0.5, A = −3, p = 1 and α = 0.75.
Download figure:
Standard image High-resolution imageFigure 9. Figure of u(x, t) for B = −1, C = 0.5, A = −3, p = 1 and α = 1.
Download figure:
Standard image High-resolution imageFigure 10. Graphs of u(x, t) for B = −1, C = 0.5, A = −3, p = 1 and for some specific values of α.
Download figure:
Standard image High-resolution image5. Conclusion
The exponential function technique with conformable derivative was successfully implemented to solve Boussinesq equations. New analytical solutions of nonlinear time conformable Boussinesq equation and nonlinear space-time conformable Boussinesq equation were obtained. The results for α = 1 can be retrieved from already published work. The obtained solutions can be utilized to further analyze by physicists or engineers on varied instances. The considered technique permitted to perform tedious and difficult algebraic calculations computationally. Exponential function technique proved encouraging and useful tool for solving nonlinear PDEs.
Acknowledgments
The first author acknowledges her mother, Mussarat Jabeen, with gratitude for her support to accomplish the research tasks.
Data availability statement
No new data were created or analysed in this study.
Data availability
The data used to support the findings of this study are included within the article.
Conflicts of interest
The authors declare that they have no conflicts of interest.
Authors contributions
Conceptualization, Shumaila Javeed; Formal analysis, Shumaila Javeed, Sidra Nawaz and Hadi Rezazadeh; Investigation, Shumaila Javeed and Sidra Nawaz; Methodology, Shumaila Javeed and Sidra Nawaz; Project administration, Dumitru Baleanu, Hadi Rezazadeh; Resources, Dumitru Baleanu; Software, Hadi Rezazadeh; Supervision, Shumaila Javeed, Dumitru Baleanu; Validation, Sidra Nawaz and Hadi Rezazadeh; Writing—original draft, Sidra Nawaz and Shumaila Javeed; Writing—review & editing, Shumaila Javeed.