Abstract
This paper investigates the generation of the ultra-broadwidth (0.1–30 THz) terahertz (THz) radiation carrying fractional/integer orbital angular momentums (OAMs) via the interaction of the two-color (ω0 and 2ω0) laser field carrying initial fractional topological charges (TCs) with air in a moderate pump intensity regime (20 TW cm−2 < Ipump < 50 TW cm−2). The two four-wave mixing (FWM) processes (i.e., ω0 + ω'0 − 2ω0 → ωTHz and 2ω0 − ω0 − ω'0 → ωTHz) are responsible for THz generation. The two processes can produce two THz pulses. They interfere with each other and THz interference vortex beams are obtained. More importantly, the generation probability from the first FWM process grows while that of the second process declines in the positive frequency region over distance. This is largely due to the combined action of phase mismatch and the blue shift of the THz center frequency. For a longer distance, THz fractional vortex beams (FVBs)/integer vortex beams (IVBs) are produced by the dominant FWM process (ω0 + ω'0 − 2ω0 → ωTHz). Therefore, via employing different combinations of the initial TCs of the ω0 and 2ω0 pulses, one can manipulate the generation of the THz vortex beams with arbitrary fractional-order or integer-order TCs at some specific propagation distances. What is even more interesting is that, when employing half-integer TCs, THz FVBs with varying TC over distance can be produced, companied with birth and annihilation of the alternative vortex pair. This is principally due to diffraction-related effects and the unstable nature of the fractional vortex structures. This simple manipulation for THz waves carrying arbitrary fractional or integer TCs in this scheme encourages the applications for optically rotation, manipulation of molecular or cell assays and image edge enhancement in the field of biomedicine.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Corrections were made to this article on 6 July 2023. Funding information in the Acknowledgments section was updated.
1. Introduction
Vortex beams like Laguerre–Gaussian (LG) modes and high-order Bessel modes with an azimuthal phase of exp(ilθ) carry an orbital angular momentum (OAM) of lℏ per photon, in which l, θ and ℏ indicate the topological charge (TC) and azimuthal coordinate and reduced Planck constant, respectively [1, 2]. For integer l values, the beams comprise l intertwined helical surfaces giving a screw dislocation along the beam axis and a doughnut intensity distribution [1, 2]. They can be used for micro-manipulation in biology [3], contrast enhancement and resolution improvement in phase contrast microscopy [4], fast data manipulation in quantum information processing [5], data encoding and multiplexing in ultrafast communications [6], and etc. For non-integer l values, the beams with a phase distribution of the form exp[i(lθ + α)], called non-integer vortex beams (non-IVBs) or fractional vortex beams (FVBs), have a low-intensity radial strip on the bright ring due to the radial phase discontinuity, where α is the angular position of the angular phase discontinuity [7, 8]. The radial opening width is strongly dependent on the value of l. The closer l towards half integer, the bigger the radial opening width. In essence, the FVBs can be regarded as light waves containing the mixed screw-edge dislocation, in analogy with the defeat in crystal [9]. Interestingly, the vortex structure within a half-integer FVB can acquire a chain of alternate-signed vortices which forms in a dark line associated with the edge dislocation of the phase and consequently has non-trivial propagation characteristics [7, 8, 10]. The characteristics of the FVBs endow them with unique advantages compared to the integer ones. For example, since a FVB has a radial opening, it can be used to guide and transport particles [11], study topologically structured darkness [12], improve the ability of optical sorting [13], and its asymmetric intensity distribution can be utilized to achieve anisotropic edge enhancement [14, 15]. In quantum information processing, it is more efficient to use FVBs to investigate quantum digital spiral imaging [16] and high dimensional entanglement states or fractional OAM entanglement of two photons than using integer ones [17–19]. In fact, such states, instead of the eigenstate of OAM in IVBs, are superposition states of the basis of integer OAM states [17, 20, 21]. Most previous studies on vortex beams refer to integer TCs. Recently, interest of FVBs has spread over different fields. Schemes of producing FVBs via spiral phase plates [7] or spatial light modulator [11, 21] have been proposed, however, are limited to visible and near-infrared domains.
The development of ultrafast vortex beams has opened new possibilities for the generation of filamentation [22, 23], supercontinuum [24], high-order harmonics [25–31], and even terahertz (THz) pulses [32–36] with complex structures. It has been demonstrated that the nonlinear phenomena are crucial during the interaction of laser with bulk media and atmospheric air [23, 25–31]. As for frequency up-conversion process of high-order harmonic generation via vortex laser-gas interaction, the OAMs of the high-order harmonics for both integer and fractional schemes, always scales with the harmonic orders due to OAM conservation [25–31]. In contrast, when it turns to the frequency down-conversion process of THz generation via vortex laser-induced gas plasma, the THz transverse spatial distributions and also physical mechanics are far more different, which depend on the pump intensity, the pump laser modes, the pump chirp parameter, the THz frequency, the filament length, and so on [32–36]. Particularly, for long filaments induced by integer-order vortex two-color field, three types of singular beams (i.e., THz necklace beams, THz azimuthal accelerating vortex beams (AAVBs), THz IVBs) can be produced at different filament lengths, which result from the coherent superposition of the two collinear THz vortex pulses with variable relative amplitudes and conjugated TCs [34]. What if two-color vortex pulses with initial fractional TCs are employed to interact with air? What will happen and what will we get? To our knowledge, this has not been considered in any previous work.
In this paper, we employ a fractional-order vortex two-color field (ω0 and 2ω0) at a moderate pump intensity level (20 TW cm−2 < Ipump < 50 TW cm−2) to interact with air to generate the ultra-broadband (0.1–30 THz) THz FVBs or IVBs. Here, four-wave mixing (FWM) mechanism is the dominant physical mechanism for THz generation. Generally, two simultaneous FWM processes of ω0 + ω'0 − 2ω0 → ωTHz and 2ω0 − ω0 − ω'0 → ωTHz occur with different generation probabilities in the positive frequency region, thereby generating the two THz pulses with conjugated average TCs due to OAM conservation. The THz radiation comes from their coherent superposition. At the beginning, the two FWM processes take place with almost the same generation probability in the positive frequency region. As the propagation distance increases, the generation probability of the second process starts to decrease until a minimum, which is smaller than that of the first process. Here the process of ω0 + ω'0 − 2ω0 → ωTHz can be regarded as the only FWM process for THz generation. Therefore, by controlling the initial TCs of the ω0 and 2ω0 pulses, THz FVBs or IVBs can be obtained at some specific propagation distances. For instance, when the ω0 and 2ω0 pulses have the initial TCs of l1 = l2 = 1.8, THz vortex beams with fractional TC of +1.8 can be obtained; while ω0 and 2ω0 pulses are with l1 = 1.8 and l2 = 1.6, respectively, THz vortex beams with integer TC of +2 can be produced. Both THz vortex beams with fractional and integer TCs can propagate steadily for several millimeters. More interestingly, when it comes to the half-integer case (for instance, l1 = l2 = 1.5), it presents totally different evolution characteristics. It is found that the average TC for the generated THz FVBs at a centimeter-scale distance decreases with the propagation distance, which is mainly due to diffraction-related effects and the unstable nature of the fractional vortex structures. At the same time, the birth and annihilation of the alternative vortex pair occur during propagation.
2. Physical model and parameters
In our numerical simulation, we consider a fractional-order vortex two-color field consisting of an 800 nm-fundamental pulse (ω0) and its second harmonics (2ω0) with initial TCs of l1 and l2, respectively. The ω0 and 2ω0 pulses are linearly polarized along x axis to excite the air. In practice, nitrogen (N2) gas, with the proportion of 78%, is the primary constituent gas of the atmospheric air. It is reasonable to consider the air to consist only of N2 gas under the standard atmospheric pressure, which has been widely adopted to study ionization dynamics in atomic and molecular physics [37]. Both ω0 and 2ω0 pulses are the FVBs and can be expanded in integer LG modes with the following expression of [1, 2]
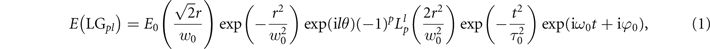
where r and θ are the radial and the azimuthal coordinates, respectively. A(r) is the radial amplitude in transverse plane. While E0, l, p, ω0, τ0, φ0 and i are the peak amplitude, azimuthal index, number of radial nodes, central frequency, pulse duration, initial phase, and imaginary unit, respectively.  is the associated Laguerre polynomial. A FVB has a phase distribution of the form exp[i(lθ + α)]. We set the wavefront cut angular position of both ω0 and 2ω0 radially along π/2 direction (i.e., α = π/2). The initial peak intensities of ω0 and 2ω0 are ∼20 TW cm−2 and ∼4 TW cm−2, respectively. The original phase difference of ω0 and 2ω0 is assumed as π/2.
is the associated Laguerre polynomial. A FVB has a phase distribution of the form exp[i(lθ + α)]. We set the wavefront cut angular position of both ω0 and 2ω0 radially along π/2 direction (i.e., α = π/2). The initial peak intensities of ω0 and 2ω0 are ∼20 TW cm−2 and ∼4 TW cm−2, respectively. The original phase difference of ω0 and 2ω0 is assumed as π/2.
In this paper, a numerical simulation of the laser-gas interaction based on the unidirectional pulse propagation equation (UPPE) [32–35] is carried out to simulate the laser nonlinear propagation. The spectral-domain UPPE in the group-velocity moving reference frame is performed, which can be expressed as [34, 38, 39]
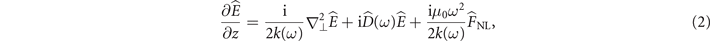
where  is the spectra of electric field.
is the spectra of electric field.  is the transverse Laplacian transformation. The dispersion is expressed by
is the transverse Laplacian transformation. The dispersion is expressed by  with k(0) = n0
ω0/c and k(n) = [dn
k(ω)/dωn
]ω=ω0, while μ0 is the vacuum permeability and n0 is linear refractive index of the laser.
with k(0) = n0
ω0/c and k(n) = [dn
k(ω)/dωn
]ω=ω0, while μ0 is the vacuum permeability and n0 is linear refractive index of the laser.  is the nonlinearity term including the third-order Kerr nonlinear polarization
is the nonlinearity term including the third-order Kerr nonlinear polarization  , the current density
, the current density  and the ionization energy loss term
and the ionization energy loss term  . For clarity, here we have dropped the (x, y, z, ω) dependence of
. For clarity, here we have dropped the (x, y, z, ω) dependence of  and the (x, y, z, t) dependence of (E, FNL, PNL, Je, Jloss, Ne). PNL = 2ε0
n0
n2|E|2
E, Je = (e2/me)[(vc + iω)/(vc
2 + ω2)]Ne
E, Jloss = R1(Nat − Ne)Ui/E, where ε0, n2
e, me and vc are the dielectric constant in vacuum, nonlinear refractive index of the laser, electron charge, electron mass, and electron-ion collision rate, respectively. In our simulation, the spot size (w0) and the pulse duration (τ0) for the ω0 and 2ω0 pulses are the same, and w0 is 200 μm and τ0 is 30 fs. We use 64 × 64 × 4096 grids for the spatial parameters x, y and time t with the steps of ∆x = ∆y ≈ 15.6 μm and ∆t ≈ 0.08 fs, respectively. We employed the intensity-dependent propagation step size ∆zn = ∆z0
I0/In
, where I0 and In
are the peak intensity of the initial and the nth step, respectively [34, 38]. It has been widely known that plasma-based THz sources induced by femtosecond laser with tens of TW cm−2 are characterized by an ultrabroad bandwidth [40, 41]. The THz bandwidth is strongly dependent on the pump pulse modes and plasma spatial distributions. The generated THz radiation produced by fractional-order vortex two-color scheme has a broadband of 0.1–30 THz. Therefore, the ultrabroad THz window of ν < 30 THz is selected in our numerical calculation. The alternating direction implicit Peaceman–Rachford finite difference scheme [38, 39] is used to solve numerically equation (2).
and the (x, y, z, t) dependence of (E, FNL, PNL, Je, Jloss, Ne). PNL = 2ε0
n0
n2|E|2
E, Je = (e2/me)[(vc + iω)/(vc
2 + ω2)]Ne
E, Jloss = R1(Nat − Ne)Ui/E, where ε0, n2
e, me and vc are the dielectric constant in vacuum, nonlinear refractive index of the laser, electron charge, electron mass, and electron-ion collision rate, respectively. In our simulation, the spot size (w0) and the pulse duration (τ0) for the ω0 and 2ω0 pulses are the same, and w0 is 200 μm and τ0 is 30 fs. We use 64 × 64 × 4096 grids for the spatial parameters x, y and time t with the steps of ∆x = ∆y ≈ 15.6 μm and ∆t ≈ 0.08 fs, respectively. We employed the intensity-dependent propagation step size ∆zn = ∆z0
I0/In
, where I0 and In
are the peak intensity of the initial and the nth step, respectively [34, 38]. It has been widely known that plasma-based THz sources induced by femtosecond laser with tens of TW cm−2 are characterized by an ultrabroad bandwidth [40, 41]. The THz bandwidth is strongly dependent on the pump pulse modes and plasma spatial distributions. The generated THz radiation produced by fractional-order vortex two-color scheme has a broadband of 0.1–30 THz. Therefore, the ultrabroad THz window of ν < 30 THz is selected in our numerical calculation. The alternating direction implicit Peaceman–Rachford finite difference scheme [38, 39] is used to solve numerically equation (2).
Besides, the transient plasma dynamics are described by free electron density Ne [42], i.e.,
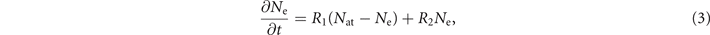
where Nat = 2.7 × 1019 cm−3 is the density of neutral atoms, while R1 or R2 is the laser field or the avalanche ionization rates. R1 can be obtained from Keldysh formula, and R2 = σ(ω0)E2/Ui. σ(ω0) = (e2/me)[vc/(vc 2 + ω0 2)] is the inverse Bremsstrahlung cross-section. Ui = 15.6 eV is the atomic ionization potential of N2 [37].
3. Simulation results and discussion
Note that the pump peak intensity in our scheme is kept in the range of 20–50 TW cm−2 during the nonlinear propagation. The physical reason for that is to manipulate the dominated physical mechanism to be the Kerr nonlinearity (i.e., FWM mechanism) instead of photocurrents (i.e., PC mechanism) in our fractional-order vortex two-color field scheme. When Kerr nonlinearity prevails, the two FWM processes of ω0 + ω'0 − 2ω0 → ωTHz and 2ω0 − ω0 − ω'0 → ωTHz occur. The corresponding OAM conservation can be easily expressed by l1 ħ + l1 ħ − l2 ħ = (2l1 −l2)ħ and l2 ħ − l1 ħ − l1 ħ = (l2 − 2l1)ħ, respectively. This helps to investigate the positive and negative OAM states in a desirable qualitative χ(3)-picture [40]. Beyond this range, photocurrents play a significant role and THz AAVBs are produced instead of THz FVBs or THz IVBs after centimeter-scale propagation. Specifically, it has been demonstrated theoretically and experimentally that both Kerr nonlinearity and plasma currents contribute to THz generation during filamentation since filamentation is the result of dynamical balance between the Kerr self-focusing and plasma defocusing [43, 44]. Basically, they dominate at different pump laser intensities and filament lengths, and contribute to different THz frequency ranges [32–36]. At the early stage of filament formation, self-focusing for Kerr effect always plays a leading role [43]. Also, when the pump intensity is at a moderate level and less than clamping intensity, Kerr nonlinearity is dominated over plasma currents [35, 45]. However, when the pump intensity reaches or even exceeds the clamping intensity, and filament length reaches several centimeters, photocurrents overwhelm the contribution from Kerr nonlinearity since plasma accumulates rapidly and defocusing occurs [35, 40, 43]. It is worth noting that the clamping intensity is different for different laser modes. For a Gaussian pulse, the clamping intensity in air is about 50 to 100 TW cm−2 depending on focusing conditions [23, 46]. Accordingly, the ionized electron density is on the order of 1017–1018 cm−3 [46], corresponding to the plasma frequency of several THz. While the clamping intensity for a LG mode is much bigger than that of a Gaussian one [23]. It is verified that when the pump intensity is at the range of 20–50 TW cm−2, Kerr nonlinearity dominates over plasma currents [34, 35].
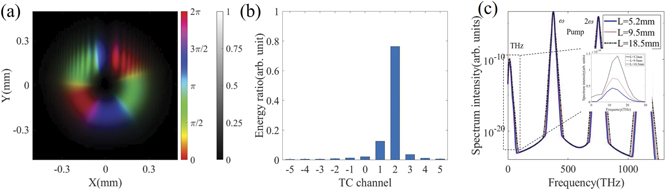
The fractional-order vortex two-color field with an identical initial TCs of l1 = l2 = 1.8 at t = 0.5T (T is the time cycle) is taken as an example to check the characteristics of the transverse spatial and OAM spectrum distributions. The transverse normalized intensity distribution with phase profile is shown in figure 1(a). The brightness of the picture indicates the normalized magnitude-squared amplitude (|E|2) of the field. The hsv color shows the phase (arg(E)) of the field. Its transverse intensity distribution shows a 'C' shape with the opening upward (i.e., α = π/2), which is a contrast to the circular symmetric distributions of the IVBs. The FVBs can be expanded into the superposition of eigenmodes with integer OAM states. The corresponding energy distribution over TC is shown in the OAM spectrum (see figure 1(b)). Besides, the phase distributions of the FVBs depend, to a greater extent, on the number of modes included in the superposition. The vortex structure is dominated by the one or two modes which contribute most to the superposition. For initial TC of +1.8, the expanded mode peaks around TC of +2. Figure 1(c) presents the calculated spectra of the output electric field at the propagation distances of ∼5.2, ∼9.5 and ∼18.5 mm. The THz radiation has an ultrabroad bandwidth ranging from 0.1 to 30 THz.
Figure 1. (a) Snapshot of the transverse normalized intensity |E|2 (gray) and phase arg(E) (hsv) distributions of the initial pump two-color field with l1 = l2 = 1.8 at t = 0.5 T; (b) OAM spectrum of the pump two-color field; (c) output electric field spectrum at the propagation distances of ∼5.2 mm (blue solid line), ∼9.5 mm (red dotted line) and 18.5 mm (black dash-dotted line) (inset: ultra-broadband THz spectrum ranging from 0.1 to 30 THz).
Download figure:
Standard image High-resolution imageIt has been experimentally verified that the two FWM processes occur and interfere with each other, whose generation probabilities in the positive frequency region vary with propagation distances [47, 48]. The generation of THz vortex beams is attributed to the domination of ω0 + ω'0 − 2ω0 → ωTHz over 2ω0 − ω0 − ω'0 → ωTHz. However, the physical explanation for the domination of the first FWM process was not shown in reference [34]. In this paper, we provide a detailed physical explanation of THz vortex beam generation. It is found that it is the combined action of the stronger phase mismatch for the second FWM process and the blue shift of the THz center frequency that enhances the generation probability of the first FWM process and declines that of the second one in the positive frequency region. Additionally, the generated THz radiation in reference [34] varies periodically from THz AAVBs to THz IVBs during propagation. While in the fractional scheme here, the THz AAVBs evolve to the THz FVBs or IVBs during a relative long-distance propagation. Then the THz FVBs or IVBs propagate for a few millimeters before collapse. This fractional scheme can generate THz vortex beams with not only integer but also fractional TCs, which is a more universal scheme. So far, the schemes for producing FVBs are quite limited, which are strongly dependent on device materials [7, 11, 21]. It is more challenging to produce FVBs in THz domain. While THz FVBs have more unique advantages and consequently a wide range of applications compared to THz IVBs [16–19]. The main aim of this paper is to propose a better scheme that can generate THz FVBs. Moreover, the characteristics of the THz FVBs generated in this paper are more desirable than that of the THz IVBs obtained in reference [34].
For a more complete description of evolution characteristics of the generated THz FVBs or IVBs, we proceed to investigate their spatial mode characteristics via two-color field scheme with different TC combinations (case 1: l1 = l2 = 1.8, case 2: l1 = 1.8 and l2 = 1.6, case 3: l1 = l2 = 1.5) for different propagation distances. Interestingly, the THz FVBs produced by the half-integer case (l1 = l2 = 1.5) with varying TC over distance are obtained, companied with birth and annihilation of the alternative vortex pair, which is quite distinct from that in reference [34].
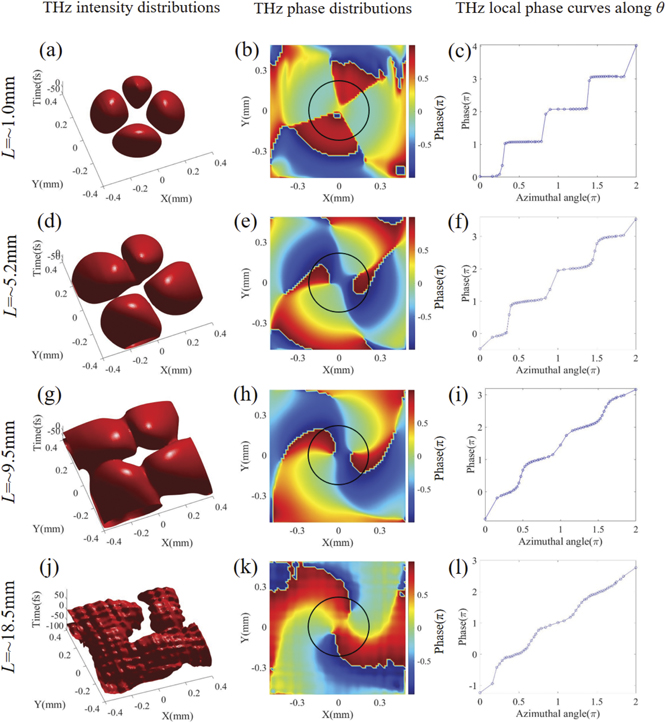
First, we check the fractional case with l1 = l2 = 1.8 to reveal the generation and evolution characteristics of THz radiation. The spatial intensity and phase distributions of the generated THz radiation for different propagation distances are shown in figure 2. For a very short distance (∼1 mm or short), the intensity distribution of the THz pulse is necklace-shape with four separate petals, where one of them is smaller than the others, shown in figure 2(a). This is a typical intensity characteristic of the interference between two FVBs with same amplitude and equal but opposite average TCs [49]. The phase distribution of the generated THz pulse (figure 2(b)) presents a π-stepwise variance. With the increase of the azimuthal angle θ, the phase has a ladder-type growth with four π jumps (see figure 2(c)). As the propagation distance increases, the THz intensity petals start to connect with each other slowly (see the upper two petals in figure 2(d)). Later, all petals grow to almost the same size and connect to each other (see figure 2(g)). Interestingly, upon further propagation, all petals merge to a 'C' shaped intensity distribution with a visible radial opening (see figure 2(j)), indicating that the interference vortex beam turns to a THz FVB. Meanwhile, the phase distribution can be marked by two color cycles, shown in figures 2(e), (h) and (k). Within every cycle, the color varies clockwise from red to green, then to blue, indicating a 4π increase along θ. The THz local phase curves along the black circles in figures 2(e), (h) and (k) show nonlinear variation over θ. The nonlinearity decreases with the propagation distance (see figures 2(f), (i) and (l)). At L = ∼18.5 mm, the nonlinearity of the former part has stronger nonlinearity than that of the latter part divided by θ = ∼1.3π, revealing the variation of nonlinearity with θ for large distances.
Figure 2. THz spatial intensity distributions (first column), THz phase distributions (second column) and THz local phase curves along θ (third column) at different nonlinear propagation distances (L = ∼1.0, ∼5.2, ∼9.5, ∼18.5 mm).
Download figure:
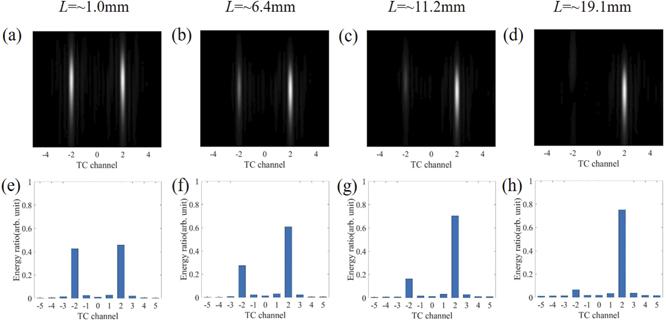
Standard image High-resolution imageThe above spatial characteristics indicate that the generated THz pulses result from the interference of two vortex beams with variable relative amplitudes and conjugated average TCs. To further prove this point, we give a quantitative analysis for the OAM spectra of the generated THz radiation. The THz OAM spectra can be calculated in OAM mode sorting systems based on optical coordinate transformation [50]. The principle of the OAM mode sorting is first to map vortex beams' helical phase to a transverse phase gradient. Then, the transformed OAM pulses are focused by a lens to a TC-related position. In this way, different OAM states are separated into corresponding TC channels on the modelled CCD detector plane [50]. The images in the first row are the intensity images mapped on the modelled CCD plane for different propagation distances. Only TCs of ±1 and ±2 can be resolved, and the intensity of the latter dominates over the former. The bar charts in the second row of figure 3 are the corresponding OAM spectrum distributions in which the energy ratios of every OAM state are presented. Most of the energy are fallen on the OAM states of +2 and −2.
Figure 3. THz intensity images mapped on the modelled CCD plane (first row) and the corresponding THz OAM spectra (second row) at different nonlinear propagation distances (L = ∼1.0, ∼5.2, ∼9.5, ∼18.5 mm).
Download figure:
Standard image High-resolution imageA quantitative analysis of the average TCs for the negative and positive components (donated by ltn and ltp) is shown in table 1. The values of ltn and ltp for all the cases are around −1.8 and +1.8, respectively when ignoring the errors from the OAM sorting algorithm [50]. As the propagation distance increases, the energy ratio of the negative OAM modes decreases and that of the positive ones increases. At L = ∼18.5 mm, the total energy ratio of positive components reaches to 85.0%, which is much higher than that of the negative components (12.8%). In consideration of the OAM spectra and the 'C' shaped intensity distributions, one can conclude that the generated THz radiation is roughly a THz FVB with TC of +1.8. Besides, the THz FVBs can propagate stably for about 2.8 mm (the propagation distance is from ∼17.3 to ∼20.1 mm). This is a little longer than the case excited by the integer-order two-color vortex field (∼2.3 mm) [34].
Table 1. Average TCs and total energy ratios for the negative and positive components.
| Nonlinear propagation distance (mm) | Negative | Positive | ||
|---|---|---|---|---|
| ltn | Energy ratio | ltp | Energy ratio | |
| ∼1.0 | −1.77 | 0.4869 | 1.81 | 0.4923 |
| ∼5.2 | −1.71 | 0.3848 | 1.87 | 0.5935 |
| ∼9.5 | −1.73 | 0.2338 | 1.90 | 0.7488 |
| ∼18.5 | −1.81 | 0.1281 | 1.85 | 0.8500 |
As for single-cycle THz vortex pulses, the properties of the amplitude distributions and the waveforms are very significant. According to the THz amplitude distributions (see the first column in figure 4), there are four consecutive negative and positive lobes, one of which has smaller magnitude than the others. Obviously, the amplitude distributions rotate with the propagation distance. This is related to the relative phase shift of ω0 and 2ω0 pulses upon the nonlinear propagation, i.e., ∆φ = ∆nω0 L/c [23, 35], where ∆n = ∆nKerr + ∆nplas is the total refractive index variance. From L = ∼1.0 to ∼18.5 mm, the THz amplitude pattern rotates by about 70° due to the analytical estimation ∆φ ∼ 82°. As for the THz waveforms at ∼0.5T at the propagation distances of ∼1.0 and ∼5.2 mm, the polarity of the THz waveforms along θ reverses, i.e., the THz amplitudes change but the phases do not (see figures 4(b) and (e)). Clearly, the four representative waveforms at different θ (marked as vertical red dashes and donated by A, B, C, and D in figures 4(b) and (e)) are plotted in figures 4(c) and (f), respectively. Upon further propagation, the minimum amplitudes of THz radiation do not go to zero, and their positive or negative electric field peaks start to exhibit downward inclined stripes (see figures 4(h) and (k)). From the representative waveforms plotted in figures 4(i) and (l), not only the amplitudes but also the phases of THz waveforms change.
Figure 4. THz amplitude distributions (first column), THz waveforms along θ (second column) and four THz typical waveforms vs time (third column) at different nonlinear propagation distances (L = ∼1.0, ∼5.2, ∼9.5, ∼18.5 mm).
Download figure:
Standard image High-resolution imageThe transverse spatial distributions and OAM spectrum analysis indicate that the characteristics of the generated THz radiation are determined by the interference of two vortex THz beams with average TC of ±1.8, which are associated with the two FWM processes (i.e., ω0 + ω'0 − 2ω0 → ωTHz and 2ω0 − ω0 − ω'0 → ωTHz). Since the weakening of the second FWM process with the increase of L, a THz FVB is roughly generated at a large L. Now here comes a question: why the total energy ratio of negative TC components declines and that of positive ones grows as the propagation distance increases? Generally speaking, it is the combined action of the stronger phase mismatch for the second FWM process and the blue shift of the THz center frequency that enhances the generation probability of the first FWM process and declines that of the second one in the positive frequency region. A concrete elaboration is given as follows.
On the one hand, for a certain THz frequency (ωTHz), the 2ω0 component in the second FWM process (i.e., 2ω0 − ω0 − ω'0 → ωTHz) shall be bigger than that in the first FWM process (i.e., ω0 + ω'0 − 2ω0 → ωTHz). The bigger the frequency, the greater the refractive index, thereby the larger the chromatic dispersion. That is, the second FWM process will experience larger chromatic dispersion. The FWM process is a quasi-phase matching process in two-color field regime. The phase-matching condition is not only influenced by chromatic dispersion but also by nonlinear phase shift [51]. The larger dispersion occurring in the second FWM process induces a stronger phase mismatch (∆k = (nTHz ωTHz + n1 ω1 + n'1 ω'1 − n2 ω2)/c), which will in turn suppressed the corresponding FWM process. This suppression effect accumulates over distance. Therefore, the first FWM process come into prominence.
On the other hand, the 2ω0 pulse is delayed relative to the ω0 pulse due to the resultant walk-off. This ω0 − 2ω0 time delay accumulates with propagation (see figure 5(a)). It has been verified that the generated THz intensity changes with the ω0 − 2ω0 time delay with a period of ∼0.67fs, corresponding to an optical distance of ∼200 nm [47, 48]. According to the Wigner–Ville distributions (WVDs) [52] of the generated THz radiation at different propagation distances (figures 5(b)–(e)), the center frequency position of the WVD shifts from ∼9.5 to ∼12.4 THz when the propagation distance increases from L = ∼1.0 to ∼18.5 mm. Generally, self-phase modulation (SPM) can induce the blue shift and broadening of the pump spectra during propagation, which are the key processes to generate higher frequency of THz radiation [48]. Therefore, the blue shift of the THz center frequency is the result of the blue shift and broadening of the pump spectra induced by SPM during propagation. Note that the white dash lines in WVDs denote the time-dependent instantaneous central frequency curves. Furthermore, the THz radiation is determined by the generation probabilities of the two FWM processes in the positive frequency region, which can be characterized by third-order nonlinear polarization  and
and  , respectively [47, 48], where ωTHz0 is the THz center frequency. When the bandwidth of
, respectively [47, 48], where ωTHz0 is the THz center frequency. When the bandwidth of  is comparable to ωTHz0, the nonlinear polarizations
is comparable to ωTHz0, the nonlinear polarizations  and
and  are partial overlapped in the positive frequency region (see figure 5(f)), and consequently interfere with each other [47, 48]. The THz interference vortex beams can be obtained at the beginning stage of the propagation. Upon further propagation, the spectrum curve of
are partial overlapped in the positive frequency region (see figure 5(f)), and consequently interfere with each other [47, 48]. The THz interference vortex beams can be obtained at the beginning stage of the propagation. Upon further propagation, the spectrum curve of  shifts to the right, while the curve of
shifts to the right, while the curve of  shifts to the left, resulting in the increase of the first FWM process and decrease of the second one in the positive frequency region. At a large L, the spectrum related to the first and second processes are roughly confined in the positive and negative frequency regions, respectively, which avoids interference and leads to the generation of a THz FVB with average TC of +1.8. Additionally, it is worth noting that, at the initial stage (L = ∼1.0 mm), the time-dependent instantaneous central frequency of the generated THz pulse shows a symmetric parabolic-like curve due to intrinsic chirp of single-cycle pulse [52], shown in figure 5(b). Upon further propagation, it becomes asymmetric since a negative chirp (figures 5(d) and (e)) is introduced into the THz pulse [52]. The chirp comes from SPM induced by Kerr effect [53, 54].
shifts to the left, resulting in the increase of the first FWM process and decrease of the second one in the positive frequency region. At a large L, the spectrum related to the first and second processes are roughly confined in the positive and negative frequency regions, respectively, which avoids interference and leads to the generation of a THz FVB with average TC of +1.8. Additionally, it is worth noting that, at the initial stage (L = ∼1.0 mm), the time-dependent instantaneous central frequency of the generated THz pulse shows a symmetric parabolic-like curve due to intrinsic chirp of single-cycle pulse [52], shown in figure 5(b). Upon further propagation, it becomes asymmetric since a negative chirp (figures 5(d) and (e)) is introduced into the THz pulse [52]. The chirp comes from SPM induced by Kerr effect [53, 54].
Figure 5. (a) ω0 − 2ω0 time delay vs propagation distance; (b)–(e) WVDs of the generated THz radiation at different propagation distances (L = ∼1.0, ∼5.2, ∼9.5, ∼18.5 mm); (f) spectra of the nonlinear polarizations from the two FWM processes at propagation distances of L = ∼1.0 and ∼18.5 mm.
Download figure:
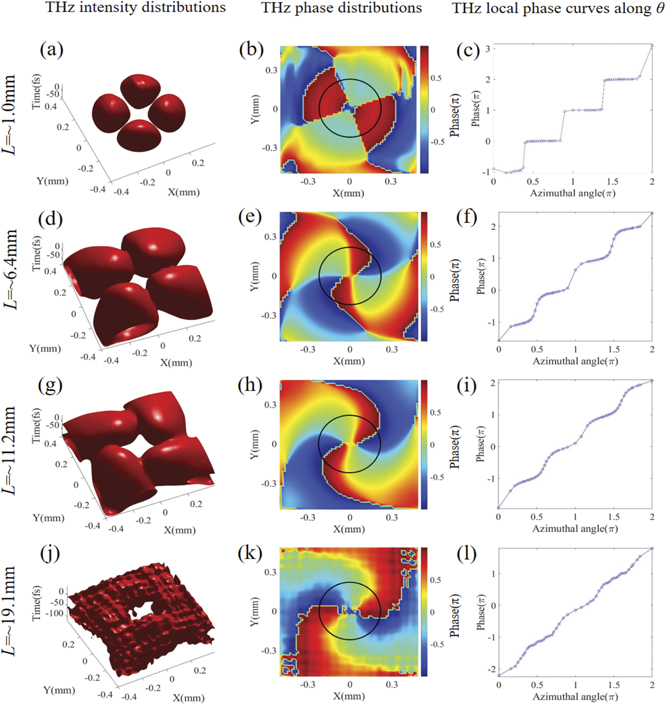
Standard image High-resolution imageSimilarly, THz IVBs can be generated when pump ω0 and 2ω0 pulses have the initial TCs of l1 = 1.8 and l2 = 1.6, respectively. In this case, the OAM conservation laws of the two FWM processes can be expressed by 1.8ħ + 1.8ħ − 1.6ħ = 2ħ and 1.6ħ–1.8ħ − 1.8ħ = −2ħ, respectively. The spatial intensity and phase distributions of the generated THz radiation, and the corresponding THz OAM spectra are presented in figures 6 and 7, respectively. There are several distinguished features from the first case mentioned above. For instance, the four petals in the THz intensity distributions are almost the same (see the first column in figure 6). The THz intensity distribution at ∼19.1 mm is ring-shaped without a radial gap (see figure 6(j)), and the corresponding phase can be considered as the nearly linear increase with a slope of 2 (see figure 6(l)). As for the THz OAM spectra (see figure 7), the intensity images mapped on the CCD plane are roughly concentrated at TCs of ±2, but those for other OAM states are invisible (see the first row in figure 7), which can be further verified by the energy ratio of each OAM state (see the second row in figure 7 and table 2). Additionally, the THz IVBs can propagate steadily for about 1.2 mm (the propagation distance is from ∼18.1 to ∼19.3 mm).
Figure 6. Same as figure 2, except for the pump ω0 and 2ω0 pulses with l1 = 1.8 and l2 = 1.6, respectively.
Download figure:
Standard image High-resolution imageFigure 7. Same as figure 3, except for the pump ω0 and 2ω0 pulses with l1 = 1.8 and l2 = 1.6, respectively.
Download figure:
Standard image High-resolution imageTable 2. Same as table 1, except for the pump ω0 and 2ω0 pulses with l1 = 1.8 and l2 = 1.6, respectively.
| Nonlinear propagation distance (mm) | Negative | Positive | ||
|---|---|---|---|---|
| ltn | Energy ratio | ltp | Energy ratio | |
| ∼1.0 | −1.97 | 0.4731 | 1.96 | 0.5150 |
| ∼6.4 | −1.91 | 0.3116 | 1.99 | 0.6750 |
| ∼11.2 | −2.00 | 0.2028 | 2.03 | 0.7841 |
| ∼19.1 | −2.13 | 0.1244 | 2.06 | 0.8570 |
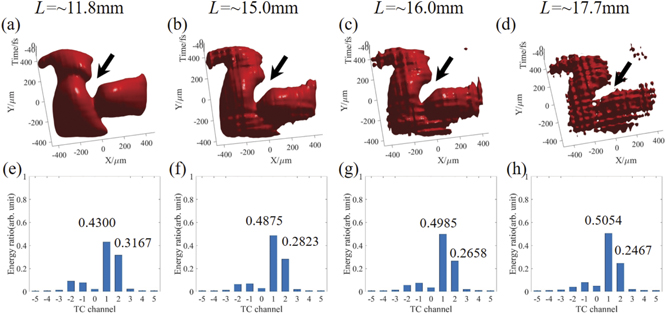
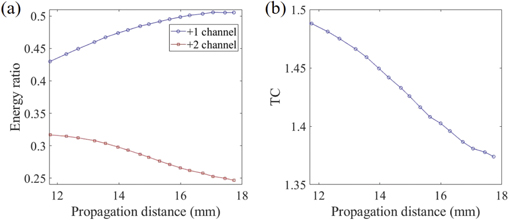
Next, we will elaborate the evolution characteristics of the THz FVBs from half-integer scheme (i.e., l1 = l2 = 1.5). The results are presented in figures 8–10. Figure 8 presents the intensity distributions (first row) and the corresponding OAM spectra (second row) at different nonlinear propagation distances (L = ∼11.8, ∼15.0, ∼16.0, ∼17.7 mm). When the THz FVBs are generated at ∼11.8 mm (see figure 8(a)), the calculated average TC is close to half integer (i.e., 1.5), at which the radial opening width reaches to its maximum. Upon further propagation, the radial opening width on the bright ring decreases as the distance increases (see the black arrows in the first row of the figure 8), indicating that its fractional TC is moving away from the half integer. Meanwhile, the variance of the TC can be also clearly seen in the OAM spectra (see the second row in figure 8). Note that the numbers marked on the subgraphs of OAM spectra are the energy ratios fallen on the TC channels of +1 and +2, respectively. Obviously, after THz FVBs are produced at ∼11.8 mm, the energy ratio of the TC channel of +1 grows with propagation distance L, while that of +2 declines, which can be observed from figure 9(a) more intuitively. More strikingly, the calculated average TC declines from ∼1.5 to ∼1.37 when THz pulses propagate from L = ∼11.8 to L = ∼17.7 mm (see figure 9(b)), indicating THz FVBs with decreasing TC over distance are obtained.
Figure 8. THz spatial intensity distributions (first row), corresponding OAM spectra (second row) from half-integer scheme (i.e., l1 = l2 = 1.5) at different propagation distances (L = ∼11.8, ∼15.0, ∼16.0, ∼17.7 mm).
Download figure:
Standard image High-resolution imageFigure 9. (a) Energy ratios of the TC channels of +1 and +2 and (b) calculated average TC over distance for half-integer scheme (i.e., l1 = l2 = 1.5).
Download figure:
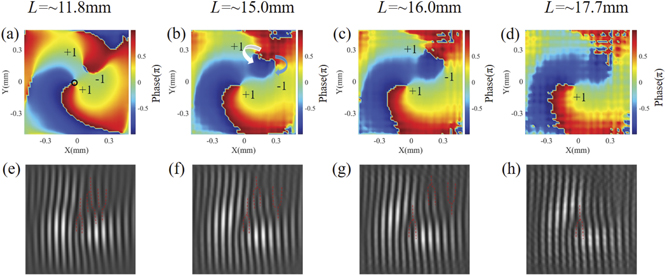
Standard image High-resolution imageFigure 10. THz phase distributions (first row), corresponding interference patterns (second row) from half-integer scheme (i.e., l1 = l2 = 1.5) at different propagation distances (L = ∼11.8, ∼15.0, ∼16.0, ∼17.7 mm).
Download figure:
Standard image High-resolution imageAccording to the phase profiles (see the first row in figure 10), a pair of alternating charge vortices is formed near the initial radial discontinuity, and moves away from the center phase singular point (marked with a black circle in figure 10(a)). In the simulated vortex phase structures, the arrows show the phase flip of alternating charge pair (see the markers in figure 10(b)). Before the annihilation of the alternating charge pair at L = ∼17.7 mm, the distance between the alternating positive and negative charge pair grows first and declines later. To investigate the birth and evolution of alternating charge pair, interferograms of the THz FVBs with plane waves are present (see the second row in figure 10), from which one can identify all vortices indicated by these fork-like interference patterns. The opening direction of the fork-like interference pattern determines the sign of charge. The downward and upward fork-like interference patterns indicate the +1 and −1 charges, respectively. The downward one-pronged fork near the axis shows the location of the center phase singular point in the beam with the charge of +1. It keeps stable during propagation. Apart from that, an extra pair of the connected fork with opposite opening directions appears (see figure 10(e)), indicating that a pair of +1 and −1 charges is born. Subsequently, the one-pronged forks forming a pair depart from each other (figure 10(f)) and then attract to each other (figure 10(g)). Finally, the fork pair disappears (see figure 10(h)). As has been well studied in optical vortices, the FVBs with half-integer TC can create new phase singularities through a Hilbert's Hotel mechanism [55]. When there are a number of pairs, the TC of the field is undefined, because, in principle, any number of unbalanced charges could be taken [55]. Moreover, the alternating charge pair tends to disappear or annihilate due to diffraction-related effects and the instability of the fractional vortex structures [56, 57]. Therefore, the calculated average TC of the generated THz FVBs is decreasing over distance.
4. Conclusion
In conclusion, THz FVBs or IVBs are obtained using a vortex two-color field with different combinations of initial fractional TCs with a moderate intensity (20 TW cm−2 < Ipump < 50 TW cm−2). In this regime, the THz radiation is produced by the two FWM processes of ω0 + ω'0 − 2ω0 → ωTHz and 2ω0 − ω0 − ω'0 → ωTHz. Although that the two FWM processes start with almost the same generation probability, upon further propagation, the former process becomes dominant in the positive frequency region due to the combined action of phase mismatch and blue shift of the THz center frequency. Therefore, by controlling the combinations of the initial TCs of the ω0 and 2ω0 pulses, THz FVBs or IVBs can be obtained at some specific propagation distances. More interestingly, when half-integer TCs are used, THz FVBs with varying TC over distance can be obtained, along with the birth and annihilation of the alternative vortex pair. This is mainly caused by diffraction-related effects and the unstable nature of the fractional vortex structures. We believe that this study will provide a theoretical support for the experimental generation of vortex THz radiation with fractional/integer TCs via laser-gas interaction.
Acknowledgments
We gratefully acknowledge the support of China Postdoctoral Science Foundation (2021M702201), Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, Shanghai Rising-Star Program, National Natural Science Foundation of China (92050203, 61775142 and 12074262). We also appreciate the help of the characterization of FVBs from Huangcheng Shangguan (from Delft University of Technology) and Shuiqin Zheng (from Great Bay University).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.