Abstract
While the spin of two-dimensional polarization states admits a simple representation, its physical interpretation for three-dimensional (3D) mixed polarization states requires a more involved analysis. In this work, we address the spin structure of the electric field of a general 3D polarization state by taking advantage of the characteristic decomposition and the recently introduced notion of nonregularity associated with 3D states. We show that a nonregular polarization state necessarily has an additional spin component due to the state's genuinely 3D nature, and both the orientation and magnitude of the spin are regulated by the degree of nonregularity. The results provide new physical insight into partially polarized evanescent and tightly focused light fields in which strong nonregular character has recently been demonstrated.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The advances in nanotechnologies and near-field phenomena, in which light-matter interactions involve exchanges of angular momentum mainly via electric transitions, require the best understanding of the spin of the electric field of three-dimensional (3D) mixed polarization states, beyond the usual two-dimensional (2D) representation of the spin of light. As usual in related works, we use the term genuine 3D polarization state to refer to those states whose electric field vector at the point considered fluctuates in three orthogonal spatial directions in any reference frame, while 2D polarization states are characterized by the fact that the polarization ellipse fluctuates in a fixed plane. From a quantum point of view, polarization states are necessarily genuine 3D states due to the uncertainties affecting the Stokes parameters [1]. For short time intervals, the polarization ellipse classically remains stable, but usually the measurement time exceeds the polarization time [2, 3] and the underlying randomness leads to fluctuations affecting, in general, both the orientation and the shape of the polarization ellipse. Thus, even from a classical point of view, a complete characterization and interpretation of polarization requires a 3D representation. This important area of physics has therefore received a great deal of attention in recent years [4–12].
When dealing with monochromatic light, the concept of spin of the electric field is conventionally derived from the helicity of photons, i.e. the projection of the intrinsic angular momentum on the propagation axis [13]. As suggested by Poynting [14] and experimentally observed by Beth [15], the intrinsic angular momentum of a fully polarized beam-like electromagnetic wave, at a given point in space, is determined by the amount of circular polarization associated with the polarization state. Such an intimate relation between intrinsic angular momentum and circular polarization is also known to hold in the case of random light, both in 2D and in 3D, for which the degree of circular polarization is obtained from the imaginary part of the corresponding polarization matrix [5].
In this work, we analyze the structure of the spin (intrinsic angular momentum density vector) of a quasimonochromatic electric field in a general 3D partially polarized state. We make use of the characteristic decomposition [7], which is the 3D analogue of the traditional (unique) division of the 2D polarization matrix into its polarized (pure) and unpolarized constituents. Besides the fully polarized and unpolarized contributions, the characteristic decomposition contains a 3D partially polarized component. We call it the discriminating component since it identifies whether the 3D polarization state is regular or nonregular [16]. Both spin and nonregularity are intrinsic properties of the polarization state, with nonregularity being a signature of the genuinely 3D character of the state [16–18]. We demonstrate that unlike with 2D states, for which the spin originates solely from the pure component, for 3D polarization states the spin may arise from the fully polarized component as well as from the discriminating component and the latter contribution is specified by the state's degree of nonregularity [17]. In other words, it is shown, for the first time, that nonregularity involves a precise way to measure the features of 3D states with respect to its spin.
While a number of works deal with the concept of spin of monochromatic fields and its transverse features linked to the change of the polarization ellipse plane from point to point over a spatial region [19–24], the present work is focused on the spin of the electric field of a 3D polarization state (thus corresponding to a fixed point in space) and its essential and fundamental link to the recently introduced notion of degree of nonregularity of such a state. The internal spin structure of nonregular polarization states provides new physical insight into complex light fields in modern photonics applications involving nonparaxial light fields. For instance, an evanescent wave created by a partially polarized or unpolarized plane-wave field in total internal reflection is necessarily in a nonregular 3D polarization state [18]. In addition, recent findings show that a tightly focused vectorial beam can exhibit strong nonregular character in the focal region [25]. We emphasize that while the 3D polarization matrix could be decomposed in several ways, the characteristic decomposition is unique for assessing the effect of nonregularity to the total spin of a genuine 3D polarization state.
2. Concept of spin of a 3D polarization state
The polarization matrix
R (also called coherency matrix) has the structure of a covariance matrix of the zero-mean electric field components and fully determines the second-order polarization properties of a random electromagnetic field at a fixed point in space [26]. Therefore, the electric spin of arbitrary polarized light should be stated in terms of the elements of R. The general expression of R in terms of the fluctuating analytic signals ɛ1(t), ɛ2(t), ɛ3(t) representing the quasimonochromatic electric field components (with respect to a given coordinate system XYZ) and defining the instantaneous 3D Jones vector
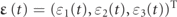 [7] (T indicates transpose) is given by
[7] (T indicates transpose) is given by
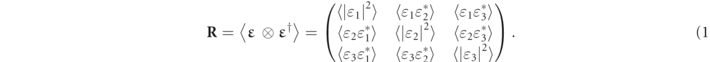
Above, ⊗ stands for the Kronecker product, superscript † represents conjugate transpose, and the brackets 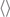 indicate time average over the measurement time [2, 3]. The intensity, defined as I = tr(R) with tr denoting matrix trace, is invariant under changes of the Cartesian reference system and provides a measure of the average power of the electric field of the electromagnetic wave at the point considered.
indicate time average over the measurement time [2, 3]. The intensity, defined as I = tr(R) with tr denoting matrix trace, is invariant under changes of the Cartesian reference system and provides a measure of the average power of the electric field of the electromagnetic wave at the point considered.
In the case of a pure (fully polarized) state, for which the field components are totally correlated, the spin angular momentum is determined from the Stokes parameter s3 describing circular polarization. Its intensity-normalized version,  , a dimensionless physical quantity, is precisely the degree of circular polarization [13, 26, 27]. For a pure state the spin vector is given by np
= Im(ɛ* × ɛ), where
ɛ
is the (time-independent) 3D Jones vector of the associated electric field. Examples of this are strictly monochromatic fields [19, 28, 29]. The magnitude of np
is the corresponding s3. For light in an arbitrary mixed state, the electric-field spin vector n is obtained by averaging over time, and the related spin density vector is given by
, a dimensionless physical quantity, is precisely the degree of circular polarization [13, 26, 27]. For a pure state the spin vector is given by np
= Im(ɛ* × ɛ), where
ɛ
is the (time-independent) 3D Jones vector of the associated electric field. Examples of this are strictly monochromatic fields [19, 28, 29]. The magnitude of np
is the corresponding s3. For light in an arbitrary mixed state, the electric-field spin vector n is obtained by averaging over time, and the related spin density vector is given by
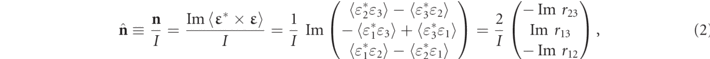
where rij
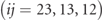 are the off-diagonal elements of the polarization matrix R. The characteristics of the pseudovector (or axial vector)
are the off-diagonal elements of the polarization matrix R. The characteristics of the pseudovector (or axial vector) 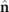 [5] follow from the fact that it is defined through a vector product.
[5] follow from the fact that it is defined through a vector product.
In this work we analyze the spin structure and its mathematical representation of such general 3D partially polarized states. For this purpose, let us first elaborate a pure state and its representation by means of the associated polarization matrix Rp
. The fact that the state is pure is fully characterized by the property 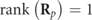 , so that the polarization ellipse related to Rp
is well defined and lies in a fixed plane Π.
, so that the polarization ellipse related to Rp
is well defined and lies in a fixed plane Π.
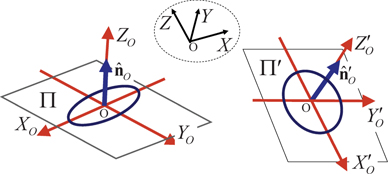
For the sake of clarity, let us now consider the simpler mathematical expression for Rp with respect to its intrinsic coordinate system XO YO ZO [26], which is defined such that the axes XO and YO determine the plane Π and they coincide with the directions of the major and minor axes of the polarization ellipse, respectively, while the axis ZO is orthogonal to plane Π, see figure 1. The most general form of the intrinsic polarization matrix of a pure state is [26]
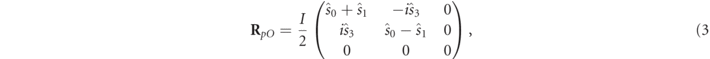
where 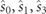 are the intensity-normalized 2D intrinsic Stokes parameters of the pure state [30]. Recall, in passing, that the 3D Stokes parameters also exist and are customarily defined as the (real) expansion coefficients when R is expressed in terms of the eight Gell–Mann matrices and the identity matrix [5, 6, 11, 31–35]. In addition, through a specific rotation of the reference system (the one that diagonalizes the real part of R) a complete set of six meaningful 3D intrinsic Stokes parameters emerge [26, 30]. These quantities have direct physical interpretations as the intensity of the state, the degree of linear polarization, the degree of directionality (a measure of the stability of the fluctuating plane containing the polarization ellipse), and the three components of the spin vector of the state with respect to its intrinsic reference frame.
are the intensity-normalized 2D intrinsic Stokes parameters of the pure state [30]. Recall, in passing, that the 3D Stokes parameters also exist and are customarily defined as the (real) expansion coefficients when R is expressed in terms of the eight Gell–Mann matrices and the identity matrix [5, 6, 11, 31–35]. In addition, through a specific rotation of the reference system (the one that diagonalizes the real part of R) a complete set of six meaningful 3D intrinsic Stokes parameters emerge [26, 30]. These quantities have direct physical interpretations as the intensity of the state, the degree of linear polarization, the degree of directionality (a measure of the stability of the fluctuating plane containing the polarization ellipse), and the three components of the spin vector of the state with respect to its intrinsic reference frame.
Figure 1. Representation of the polarization ellipse of a pure state with respect to its intrinsic coordinate system XO YO ZO and with respect to an arbitrary frame XYZ. The plane XO YO contains the polarization ellipse, while the spin density vector lies along the ZO axis.
Download figure:
Standard image High-resolution imageConcerning the intrinsic representation of a pure state in equation (3), note that since the axis XO
has been taken along the major axis of the polarization ellipse, the state RpO
exhibits zero azimuth and therefore 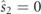 . We also remark that, in general,
. We also remark that, in general, 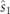 and
and 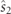 depend on the reference frame but the parameters
depend on the reference frame but the parameters 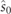 and
and 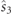 do not. Observe that the lack of symmetry of RpO
is due to its imaginary off-diagonal elements, which carry the entire information on the chirality of the pure polarization state. Therefore, the spin density vector
do not. Observe that the lack of symmetry of RpO
is due to its imaginary off-diagonal elements, which carry the entire information on the chirality of the pure polarization state. Therefore, the spin density vector  of the state RpO
is given by
of the state RpO
is given by 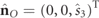 . As before, here the term density refers to the intensity-normalized spin vector of RpO
. The magnitude of
. As before, here the term density refers to the intensity-normalized spin vector of RpO
. The magnitude of 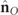 is
is 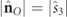 and its direction coincides with that of the ZO
axis, with positive s3 > 0 (negative s3 < 0) sign for right-handed (left-handed) polarization ellipses.
and its direction coincides with that of the ZO
axis, with positive s3 > 0 (negative s3 < 0) sign for right-handed (left-handed) polarization ellipses.
When an arbitrary reference coordinate system XYZ is considered, the polarization matrix Rp
of the pure state is given by a similarity orthogonal transformation Rp
= QRpO
QT, with QT = Q−1, det Q = +1 (see figure 1). The real and imaginary parts of the polarization density matrix
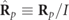 transform independently [5] in the following manner
transform independently [5] in the following manner
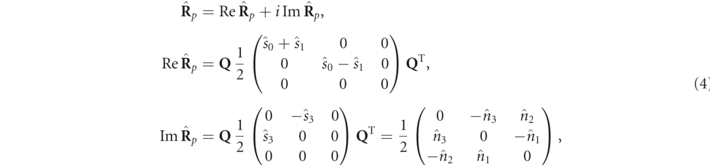
where 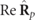 is a symmetric real valued matrix (thus with zero spin), while the skew-symmetric matrix
is a symmetric real valued matrix (thus with zero spin), while the skew-symmetric matrix 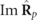 contains exclusively the information on the spin density vector of the state by means of its three components with respect to XYZ. Comparing with equation (2), the spin density vector of Rp
is found to be
contains exclusively the information on the spin density vector of the state by means of its three components with respect to XYZ. Comparing with equation (2), the spin density vector of Rp
is found to be 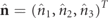 with magnitude
with magnitude 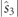 , while the spin vector is
, while the spin vector is 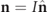 . The explicit expression for Q in terms of three angles that determine the corresponding rotation from XO
YO
ZO
to XYZ can be found in [36].
. The explicit expression for Q in terms of three angles that determine the corresponding rotation from XO
YO
ZO
to XYZ can be found in [36].
The incoherent composition, at a given point O in space, of a set of pure polarization states Rpi
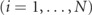 whose polarization ellipses lie in different respective planes (namely Π, Π',..., see figure 2), requires that all states are represented with respect to a common 3D reference frame XYZ. The resulting polarization matrix R (referenced with respect to XYZ) is given by the sum of the polarization matrices of the pure components, so that such a sum can be performed separately for the corresponding real and imaginary parts, that is,
whose polarization ellipses lie in different respective planes (namely Π, Π',..., see figure 2), requires that all states are represented with respect to a common 3D reference frame XYZ. The resulting polarization matrix R (referenced with respect to XYZ) is given by the sum of the polarization matrices of the pure components, so that such a sum can be performed separately for the corresponding real and imaginary parts, that is,
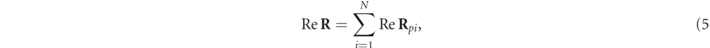
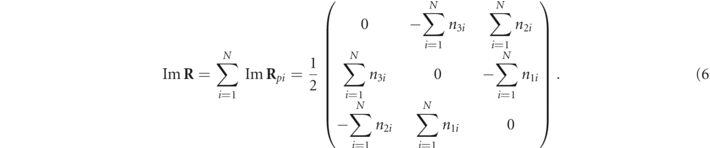
Figure 2. Two pure states that have their respective polarization ellipses lying in different planes Π and Π' are incoherently superposed at a point O. The calculation of the polarization matrix of the mixed state in an arbitrary Cartesian reference system XYZ is given by the sum of the polarization matrices of the components, all of them represented with respect to the common system XYZ.
Download figure:
Standard image High-resolution imageConsequently, 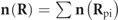 , showing that, from a classical point of view, the spin vector of a partially polarized 3D state is the vector sum of spin vectors of its pure polarization components. Note that, since the constituent states can have different intensities, we here add the spin vectors and not the spin density vectors. We also remark that Im R in equation (6) can at once be expressed in terms of the second-order moments of the fluctuating electric field components via equation (1).
, showing that, from a classical point of view, the spin vector of a partially polarized 3D state is the vector sum of spin vectors of its pure polarization components. Note that, since the constituent states can have different intensities, we here add the spin vectors and not the spin density vectors. We also remark that Im R in equation (6) can at once be expressed in terms of the second-order moments of the fluctuating electric field components via equation (1).
3. Characteristic components of a 3D polarization state
To gain insight into the structure of the spin of a general 3D partially polarized state and especially to connect the spin to the nonregularity of the state, let us next consider some useful properties of the polarization matrix R, which can always be expressed by means of its characteristic decomposition [7, 8]
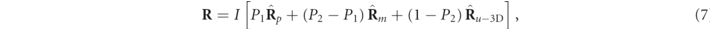
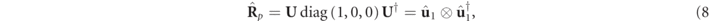
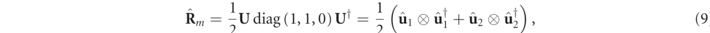
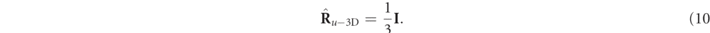
The notations in these expressions should be interpreted as follows: U is the unitary matrix that diagonalizes R, 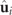 (the columns of U, taken in decreasing order of their respective eigenvalues) are the unit eigenvectors of
(the columns of U, taken in decreasing order of their respective eigenvalues) are the unit eigenvectors of  (i.e. the 3D Jones vectors of the polarization eigenstates), and I is the 3×3 identity matrix. In addition, P1 and P2 are the so-called indices of polarimetric purity (IPP) [4, 37], defined in terms of the eigenvalues of
(i.e. the 3D Jones vectors of the polarization eigenstates), and I is the 3×3 identity matrix. In addition, P1 and P2 are the so-called indices of polarimetric purity (IPP) [4, 37], defined in terms of the eigenvalues of 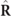 as
as
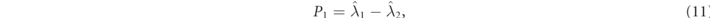
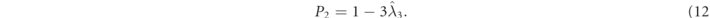
Because of the normalization, the eigenvalues add up to one, 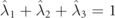 , and they are taken in decreasing order,
, and they are taken in decreasing order, 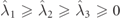 , whereby the IPP satisfy 0 ⩽ P1 ⩽ P2 ⩽ 1. The matrices
, whereby the IPP satisfy 0 ⩽ P1 ⩽ P2 ⩽ 1. The matrices 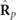 and
and 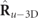 represent pure and 3D unpolarized states, respectively, whereas
represent pure and 3D unpolarized states, respectively, whereas 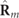 is the discriminating component (see below).
is the discriminating component (see below).
Concerning the physical parameters associated with 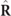 that are invariant under rotations of the coordinate system, the quantitative information on the structure of polarimetric randomness of
that are invariant under rotations of the coordinate system, the quantitative information on the structure of polarimetric randomness of 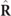 expressed by the IPP above is complemented by the qualitative information provided by the three components of purity of
expressed by the IPP above is complemented by the qualitative information provided by the three components of purity of  (hereafter CP), two of which are the degree of linear polarization
Pl
and the degree of directionality
Pd
. These are specified in terms of the nonnegative eigenvalues
(hereafter CP), two of which are the degree of linear polarization
Pl
and the degree of directionality
Pd
. These are specified in terms of the nonnegative eigenvalues  of
of  as [26]
as [26]

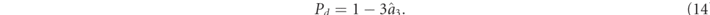
The third CP, the degree of circular polarization
Pc
, on the other hand is specified by 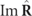 . It is explicitly given by the absolute value
. It is explicitly given by the absolute value  of the spin density vector
of the spin density vector 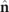 of the state
of the state 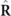 [26] [see also equations (2) and (4)], which is directly linked to the Frobenius norm
[26] [see also equations (2) and (4)], which is directly linked to the Frobenius norm 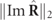 of
of 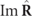 , i.e.
, i.e.
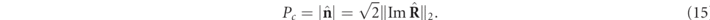
Although it may appear natural, it is quite remarkable that the physical equality of Pc
and  holds not only for the conventional 2D states but also for general 3D mixed polarization states.
holds not only for the conventional 2D states but also for general 3D mixed polarization states.
4. Discriminating component and nonregularity
A state R is said to be regular when P2 = P1 or when the discriminating component
 in equation (7) represents a 2D unpolarized state (i.e. a state whose electric field evolves fully randomly in a fixed plane) [16]. When P2 = P1 holds, the only characteristic components of R in equation (7) are
in equation (7) represents a 2D unpolarized state (i.e. a state whose electric field evolves fully randomly in a fixed plane) [16]. When P2 = P1 holds, the only characteristic components of R in equation (7) are  and
and 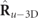 and all polarimetric anisotropies [38] are concentrated in the pure component
and all polarimetric anisotropies [38] are concentrated in the pure component 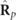 . In general, 3D states are nonregular and a measure of the distance to regularity is given by the degree of nonregularity
PN
of R [17]. This quantity can be defined in terms of the IPP of R and the absolute value
. In general, 3D states are nonregular and a measure of the distance to regularity is given by the degree of nonregularity
PN
of R [17]. This quantity can be defined in terms of the IPP of R and the absolute value 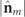 of the spin density vector
of the spin density vector 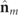 of
of  as [17]
as [17]
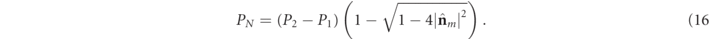
Observe that nonregularity  entails the simultaneous conditions P2 ≠ P1 and
entails the simultaneous conditions P2 ≠ P1 and  . In particular, the link in equation (16) between the degree of nonregularity of R and the spin of
. In particular, the link in equation (16) between the degree of nonregularity of R and the spin of 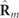 indicates that, provided P2 ≠ P1, a 3D polarization state is nonregular if the discriminating component has nonzero spin and vice versa. In addition, with fixed IPP PN
increases with increasing magnitude of the spin of
indicates that, provided P2 ≠ P1, a 3D polarization state is nonregular if the discriminating component has nonzero spin and vice versa. In addition, with fixed IPP PN
increases with increasing magnitude of the spin of  . Notice also that the degree of nonregularity PN
m
of the discriminating state is
. Notice also that the degree of nonregularity PN
m
of the discriminating state is 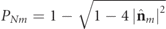 [17], so that
[17], so that  . The fact that the discriminating component of a nonregular polarization state necessarily carries spin is an important result of this work. The contribution of this spin to the total spin of the state will be analyzed in section 6.
. The fact that the discriminating component of a nonregular polarization state necessarily carries spin is an important result of this work. The contribution of this spin to the total spin of the state will be analyzed in section 6.
While  and
and  of the characteristic decomposition in equation (7) represent respectively a pure state and a fully random state, i.e. a 3D unpolarized state, the interpretation of the discriminating component
of the characteristic decomposition in equation (7) represent respectively a pure state and a fully random state, i.e. a 3D unpolarized state, the interpretation of the discriminating component 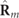 is more involved. In fact, in general, the planes containing the polarization ellipses of the eigenstates
is more involved. In fact, in general, the planes containing the polarization ellipses of the eigenstates 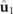 and
and 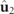 , which constitute
, which constitute 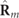 , do not coincide, and consequently
, do not coincide, and consequently 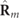 is not a real matrix and corresponds to a 3D partially polarized state [16, 17]. For the particular case that
is not a real matrix and corresponds to a 3D partially polarized state [16, 17]. For the particular case that  is real, necessarily
is real, necessarily 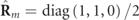 , whereupon
, whereupon 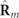 represents a 2D unpolarized state and therefore
represents a 2D unpolarized state and therefore 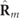 lacks spin.
lacks spin.
5. Spin of a nonregular polarization state
As indicated above, for regular states satisfying P2 > P1, the discriminating component takes the form of a 2D unpolarized state 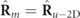 [16]. According to equation (9), the fixed plane where the polarization ellipse of
[16]. According to equation (9), the fixed plane where the polarization ellipse of 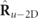 evolves fully randomly coincides with the plane of the polarization ellipse of the pure characteristic component
evolves fully randomly coincides with the plane of the polarization ellipse of the pure characteristic component 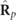 (it is easy to prove that otherwise the characteristic decomposition takes a different form where the discriminating component is nonregular). Since
(it is easy to prove that otherwise the characteristic decomposition takes a different form where the discriminating component is nonregular). Since 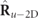 and
and 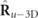 lack spin, the spin density vector
lack spin, the spin density vector 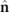 of a regular state is proportional to the spin density vector
of a regular state is proportional to the spin density vector 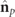 of the pure component
of the pure component 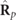 , i.e.
, i.e. 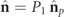 .
.
In the case of nonregular states, the discriminating component 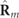 exhibits nonzero amounts of linear polarization and spin [17]. The spin density vector
exhibits nonzero amounts of linear polarization and spin [17]. The spin density vector 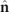 of the state R is thus composed as
of the state R is thus composed as
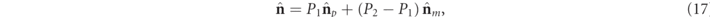
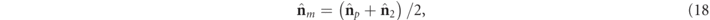
where 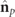 and
and 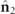 are the respective spin density vectors associated with the 3D Jones eigenvectors
are the respective spin density vectors associated with the 3D Jones eigenvectors 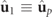 and
and 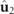 . It is remarkable that the overall spin is composed of only the spins of the two first spectral components
. It is remarkable that the overall spin is composed of only the spins of the two first spectral components 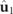 and
and 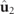 . Equation (17) expresses the main point of this work, i.e. that the total spin of a 3D polarization state, in general, has two contributions: one due to the pure polarization component and another due to the nonregular discriminating component. For regular polarization states, only the pure component may have spin.
. Equation (17) expresses the main point of this work, i.e. that the total spin of a 3D polarization state, in general, has two contributions: one due to the pure polarization component and another due to the nonregular discriminating component. For regular polarization states, only the pure component may have spin.
To analyze the possible physical configurations of the spin structure, we will first consider the case of an isolated discriminating state 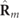 , and then we will compose the overall spin density vector from those of the components
, and then we will compose the overall spin density vector from those of the components 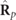 and
and  . For a discriminating state, the spin density vector equals one half of the sum of the spin density vectors of the two eigenstates
. For a discriminating state, the spin density vector equals one half of the sum of the spin density vectors of the two eigenstates 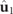 and
and 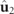 i.e.
i.e. 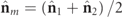 (with
(with 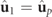 ). Note that since the vectors
). Note that since the vectors 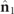 and
and 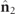 have a common origin, they determine a well defined plane. The relative geometric configuration of any pair of orthonormal polarization states has been studied in [39], showing that the magnitude of
have a common origin, they determine a well defined plane. The relative geometric configuration of any pair of orthonormal polarization states has been studied in [39], showing that the magnitude of 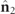 varies in a continuous manner from
varies in a continuous manner from 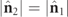 down to
down to 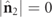 . In the former case,
. In the former case, 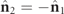 and the planes of the polarization ellipses of the Jones eigenstates
and the planes of the polarization ellipses of the Jones eigenstates 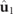 and
and 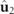 coincide, whereas in the latter situation
coincide, whereas in the latter situation 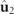 represents a linearly polarized state whose electric field vibrates along a direction normal to the plane of the polarization ellipse of
represents a linearly polarized state whose electric field vibrates along a direction normal to the plane of the polarization ellipse of 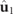 .
.
Thus, in general, the planes of the polarization ellipses of the eigenstates  and
and 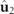 are different and only coincide in the case of regular states. Figure 3 illustrates this property by means of an example of a representative family of pairs
are different and only coincide in the case of regular states. Figure 3 illustrates this property by means of an example of a representative family of pairs 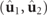 of orthogonal polarization states. The relative orientations of the planes containing the polarization ellipses are indicated, while the relative angle of the directions of the respective spin density vectors varies accordingly. For simplicity, the example case is represented with respect to the intrinsic reference frame of the eigenstate
of orthogonal polarization states. The relative orientations of the planes containing the polarization ellipses are indicated, while the relative angle of the directions of the respective spin density vectors varies accordingly. For simplicity, the example case is represented with respect to the intrinsic reference frame of the eigenstate 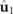 . As indicated above, if
. As indicated above, if 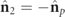 then
then 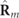 is regular, and the degree of nonregularity PN
increases for increasing values of the angle between
is regular, and the degree of nonregularity PN
increases for increasing values of the angle between 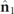 and
and 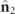 . Observe that, the smaller the ellipticity angle of
. Observe that, the smaller the ellipticity angle of 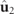 , the larger the angle between
, the larger the angle between 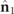 and
and 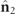 and the bigger the degree of nonregularity of
and the bigger the degree of nonregularity of  . Therefore, a state
. Therefore, a state 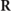 is nonregular if and only if
is nonregular if and only if 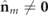 (that is
(that is 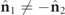 ), showing that the concept of nonregularity is intimately related to the spin properties as noted earlier.
), showing that the concept of nonregularity is intimately related to the spin properties as noted earlier.
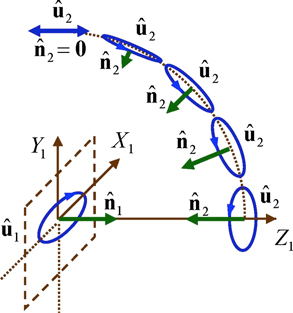
Figure 3. Representation of a family of pairs of orthogonal eigenstates 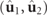 of a discriminating state, with respective spin density vectors
of a discriminating state, with respective spin density vectors 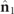 and
and 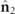 . All eigenstates are realized in a common point in space, but have been separated for the sake of clarity.
. All eigenstates are realized in a common point in space, but have been separated for the sake of clarity.
Download figure:
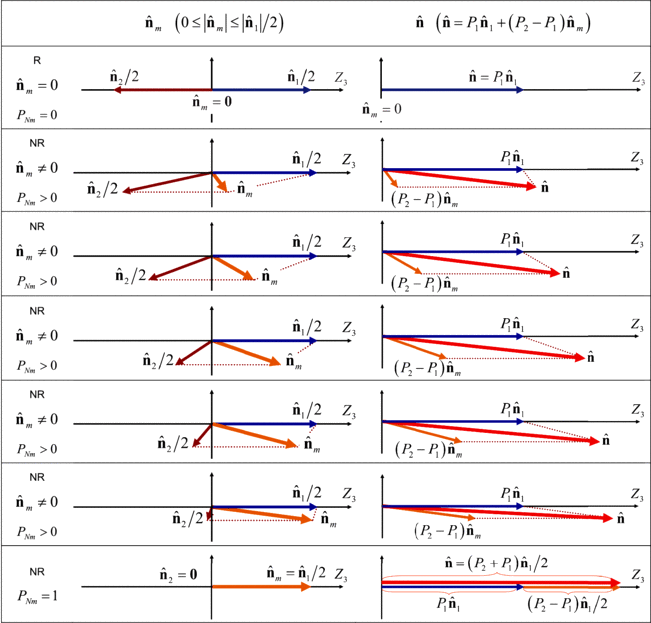
Standard image High-resolution imageIn accordance with the representations of figure 3, the spin density vector 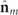 of a discriminating state is illustrated in the left column of table 1 as a composition of those of the two Jones eigenstates
of a discriminating state is illustrated in the left column of table 1 as a composition of those of the two Jones eigenstates 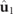 and
and 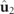 generating
generating 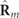 . The overall spin density vector
. The overall spin density vector  is composed of
is composed of 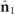 and
and 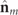 as indicated in equation (17) and it is represented in the right column of table 1 in accordance with the cases represented in the left column for
as indicated in equation (17) and it is represented in the right column of table 1 in accordance with the cases represented in the left column for 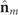 . For given values of the IPP (P1 and P2), the absolute value
. For given values of the IPP (P1 and P2), the absolute value 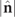 of the spin of the state R takes its minimal value
of the spin of the state R takes its minimal value 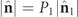 when R is regular (PN
= 0). The spin magnitude increases monotonically for increasing values of PN
(hence of PN
m
) up to a maximal value
when R is regular (PN
= 0). The spin magnitude increases monotonically for increasing values of PN
(hence of PN
m
) up to a maximal value  that is achieved when PN
m
= 1.
that is achieved when PN
m
= 1.
Table 1. Composition of the spin density vectors 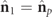 and
and 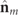 of the pure and discriminating characteristic components, respectively, for increasing values of the degree on nonregularity
of the pure and discriminating characteristic components, respectively, for increasing values of the degree on nonregularity 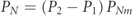 (R and NR stand for regular and nonregular states).
(R and NR stand for regular and nonregular states).
|
6. Conclusions
The spin of general 3D polarization states (i.e. states for which the local electric field fluctuates in three orthogonal spatial directions in any frame) was revisited and its nature and properties were analyzed on the basis of the characteristic decomposition and the degree of nonregularity. The characteristic decomposition of the polarization matrix expresses the state in terms of an incoherent combination of three specific states, namely the pure component, the discriminating component, and the 3D unpolarized component. The relevance of using such a decomposition for the present analysis derives from the fact that it provides a unique view to the structure of polarimetric purity of 3D polarization states [16]. More specifically, the degree of nonregularity, which is in essence determined by the physical nature of the discriminating component, affects the direction and magnitude of the spin of the entire state.
The 3D unpolarized component is fully isotropic from a polarimetric point of view and therefore lacks spin, while each of the two remaining components can exhibit nonzero spin. In the limiting case of regular states, the discriminating component vanishes or corresponds to a 2D unpolarized state, thus lacking spin, so that the overall spin is determined exclusively by that of the pure component. For the general case of nonregular states, the discriminating component necessarily exhibits nonzero spin, and therefore the spin of the whole state is given as a vector composition of those of the pure and discriminating components. Consequently, the direction of the overall spin generally does not coincide with that of the pure component, but it is influenced by the value of the degree of nonregularity. This peculiar feature shows that the discriminating component plays a key role for understanding the structure of the spin of 3D polarization states. In particular, the nonregularity determined by the discriminating component is intimately linked to spin, as emphasized by the finding that for fixed IPP the magnitude of spin is smallest for a regular state and largest for a maximally nonregular state (i.e. with the highest degree of nonregularity). The results can find applications in assessing the spin of nonparaxial light such as partially polarized evanescent and tightly focused fields where strong nonregular characteristics have recently been demonstrated.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Acknowledgments
Authors are supported by the Jane and Aatos Erkko Foundation; Academy of Finland (310511, 308393, 320166); Joensuu University Foundation; University of Eastern Finland (930350, 931726).