Abstract
A new method to diagnose extreme laser intensities through measurement of angular and spectral distributions of protons directly accelerated by the laser focused into a rarefied gas is proposed. We simulated a laser pulse focused by an off-axis parabolic mirror by Stratton–Chu integrals, that enables description of laser pulse with different spatial-temporal profiles focusing in a focal spot down to the diffraction limit, that makes our theoretical predictions be a basis for experimental realization. The relationship between characteristics of the proton distributions and parameters of the laser pulse have been analyzed. The analytical and numerical results obtained justify the new method of laser diagnostics. The proposed scheme should be valuable for the commissioning of new extreme intensity laser facilities.
Export citation and abstract BibTeX RIS
1. Introduction
Over the past two decades, significant progress in short-pulse high-power laser technology has resulted in the development of petawatt-class lasers [1–12], ten petawatt-class lasers [13–18]. Even higher power laser systems have been proposed [19]. Focusing of these high power laser beams to diffraction limited spots has led to laser intensities exceeding 1022 W cm−2 [20–22], with even higher intensities possible in the near future. Such intensities will enable the exploration of light-electron interactions at the limit where radiation-reaction effects dominate the electron dynamics. In addition, these intensities can elucidate effects of vacuum polarization, can trigger electron–positron pair production in photon–photon and electron–photon collisions, can initiate QED cascades, and also allow the study of nuclear quantum optics [23].
The direct measurement of such extreme intensities is challenging using conventional techniques, and so it is important to be able to accurately compare the results of different experiments with theoretical predictions and with each other. Therefore, the development of new methods for characterizing the laser intensity is crucial for the realization of experiments requiring extreme intensities and for the commissioning of new laser facilities. Moreover, by using optimization techniques [24], the intensity may be significantly increased for high repetition-rate systems, if the intensity is measured accurately.
Typically, intensity characterization is based on separately measured spatial (focal spot) and temporal (pulse duration) characteristics at low pulse energy, then extrapolating these results to full laser power. However, the laser intensity given by this approach may significantly differ from the actual value achieved in experiment because of wavefront and spectral phase distortions in the laser stretcher-amplifier-compressor chain which can degrade the focal spot and temporal pulse shape mainly due to chromatic aberrations and frequency chirp [25–27]. The other indirect approach, which measures a part of the beam that 'leaking-through' a mirror in the interaction chamber, will not account for the final focusing optic, which is the main source of aberrations, particularly for short-focal length parabolic mirrors.
Several methods have been proposed and implemented to characterize laser intensities, which include the use of multiple tunneling ionization of high Z atoms with high ionization potentials [28–30], nonlinear Compton scattering [31, 32], and temporally resolved intensity contouring based on a chirped probing scheme [33]. The first method involves the time-of-flight (TOF) detection of multiple ion species produced in the focus of a laser interacting with very low density gases. These ions are accelerated using a few static kV electric field in the direction perpendicular to the laser propagation direction. The ions are then detected with dual microchannel plates (MCPs). The major problem with this method at intensities above 1022 W cm−2 is the importance of ponderomotive acceleration of high Z ionsin the laser field which will complicate the TOF measurements. The second method involves a complicated experimental setup which uses the collision of the laser pulse with a laser wakefield accelerated electron beam. This requires perfect synchronization and spatial overlap of both beams, and the electron beam must be fully characterized. The latter approach is based on the diagnostics of the laser intensity distribution via the overdense plasma contour formed as a result of the laser-plasma interaction. The target is probed by the chirped laser pulse, which is replicated after that. A small unique frequency range is chosen from each copies by narrow bandpass filters, so that each residual part of the probing pulse contains information about the laser spatial distributions in the unique moments of time. It allows measure the pulse temporal profile on the picosecond scales, that is undoubtedly important.
At the same time, the highest intensities can be achieved only in the case of ultra-tight focusing close to the diffraction limit. Such a laser pulse, which has a complex electric field structure at the focus, will accelerate particles without needing subsidiary devices or electron beams. The effects of direct (vacuum) particle acceleration can then be used to diagnose the laser pulse. There have been some recent work, which considered ponderomotive electron acceleration [34–39]. Some of them are devoted to experiments in a limited range of laser intensities (1018− 1021 W cm−2) [37, 40], whereas theoretical studies cover a wider range of intensities (up to 1022 W cm−2) [36, 38, 39]. Such diagnostics are based on measurements of angular and spectral distribution of electrons accelerated from a rarefied gas. This allows for the omission of plasma fields, which are small in comparison with the amplitude of the laser field, so that electron dynamics are determined only by parameters of the measured pulse. This approach can also be supplemented by the measurement of the secondary radiation of electrons [41].
While the approach discussed above has a simple experimental realization with a low Z gas used as a target, the atoms of the gas will be fully ionized by the leading edge of the intense laser pulse and the ionized electrons will escape the focal region before the peak intensity is reached. Here, instead, we propose using protons accelerated from the rarified hydrogen gas for the laser intensity diagnostic. Laser intensities below 1024 W cm−2 are considered as the interaction of lasers with protons below the limit will result in particle velocities significantly smaller than the speed of light. Hence, the protons will stay within the focal volume during the full duration of their interaction with the femtosecond duration pulse, and the resulting energy of the proton will be directly related to the laser intensity.
This paper is dedicated to a detailed theoretical analysis of proton dynamics driven by high-intensity femtosecond laser pulses focused by an off-axis parabolic mirror. This work could become the basis of a new method to diagnose extreme laser intensities via measurement of angular and spectral distributions of accelerated protons. The work addresses a range of laser parameters with intensities from 1021 to 1024 W cm−2, pulse durations from 15 to 80 fs and focal spot diameters from 1λ to 4λ, where λ = 0.8 μm is a laser wavelength of Ti:Sapphire based laser systems. Stratton–Chu integrals are used to describe a laser pulse with different spatial-temporal parameters (this approach allows us to perform accurate calculations for the focal spots down to the diffraction limit), and a test particle method using a ponderomotive force is used to simulate laser-proton interactions. Both models and the conditions for their applicability are considered in section 2. In section 3, we discuss the spectral and angular characteristics of the proton distributions depending on the laser parameters, such as peak intensity, temporal-spatial profiles and the diameter of the focal spot, from the perspective of their use as a the diagnostic of the laser pulse.
2. Model of proton acceleration
The method for characterizing a laser pulse intensity profile presented in this paper is based on the analysis of the proton momentum distributions after direct acceleration by the laser field. For the proton distributions to be unambiguously related to the pulse parameters the main requirement is a negligible effect of Coulomb fields induced in the plasma on the proton dynamics. In this case, the dynamics of charged particles can be described as a solution of the equation of motion through the Lorentz force
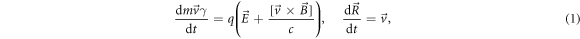
where q and m are the charge and mass of the particle; 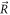 ,
, 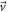 and γ are its position, velocity and Lorentz-factor;
and γ are its position, velocity and Lorentz-factor;  and
and 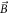 are the electric and magnetic fields of the laser pulse. Some trajectories have been integrated independently by the Adams method [42] and the Boris scheme [43]. A good agreement between the results confirmed the calculation accuracy, and subsequently a preference has been expressed for the first numerical scheme.
are the electric and magnetic fields of the laser pulse. Some trajectories have been integrated independently by the Adams method [42] and the Boris scheme [43]. A good agreement between the results confirmed the calculation accuracy, and subsequently a preference has been expressed for the first numerical scheme.
In this paper we use the solution of Helmholtz equation in the form of Stratton–Chu integrals [44] to describe all six components of the laser pulse focused by an off-axis parabolic mirror. The integrals with boundary conditions for incident and reflection laser fields give the following relation between the components of the incident and focused laser pulses [39]:
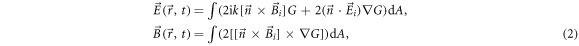
where k is a magnitude of the wave vector, 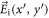 and
and 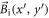 are the components of the incident laser pulse, A and
are the components of the incident laser pulse, A and 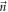 are the mirror surface and the unit vector normal to it,
are the mirror surface and the unit vector normal to it,  is the Green's function for the Helmholtz equation, and rS is the vector from the reflecting point on the mirror to the observed point. After the transformation from the surface integrals to the double integrals, taking into account the shape of the reflecting surface (
is the Green's function for the Helmholtz equation, and rS is the vector from the reflecting point on the mirror to the observed point. After the transformation from the surface integrals to the double integrals, taking into account the shape of the reflecting surface ( , where F is a focal length of the parent parabola, see figure 1), the diffraction integrals can be written in the following form:
, where F is a focal length of the parent parabola, see figure 1), the diffraction integrals can be written in the following form:
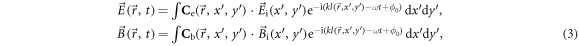
where 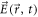 and
and 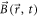 are the electric and magnetic components of the focused laser beam,
are the electric and magnetic components of the focused laser beam, 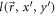 is a function describing a distance between the mirror
is a function describing a distance between the mirror 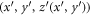 and the observation point (x, y, z), also taking account of additional phase for different points on the mirror;
and the observation point (x, y, z), also taking account of additional phase for different points on the mirror; 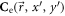 and
and 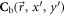 are tensors whose components depend on mirror characteristics, such as off-axis angle ψoff and effective focal length
are tensors whose components depend on mirror characteristics, such as off-axis angle ψoff and effective focal length 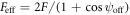 , ω is the carrier frequency. Here, to introduce relations between the mirror and laser characteristics, we review the main steps of the construction of the formulas describing the focused laser pulse, which are shown in detail in [39]. The integrated area corresponds to the projection of the mirror surface onto the plane X'Y' perpendicular to the direction of the propagation of the incident laser pulse:
, ω is the carrier frequency. Here, to introduce relations between the mirror and laser characteristics, we review the main steps of the construction of the formulas describing the focused laser pulse, which are shown in detail in [39]. The integrated area corresponds to the projection of the mirror surface onto the plane X'Y' perpendicular to the direction of the propagation of the incident laser pulse:  , if the y'-axis was a rotating axis. After reflection, the direction of laser propagation rotates to the angle ψoff such that a new coordinate system can be defined by the following expressions,
, if the y'-axis was a rotating axis. After reflection, the direction of laser propagation rotates to the angle ψoff such that a new coordinate system can be defined by the following expressions,  ,
,  and y = y'. In this system, the laser pulse will propagate along the z-axis, and the incident laser pulse linearly polarized along the x'-axis will be transformed to the reflected laser pulse linearly polarized along the x-axis. Both coordinate systems are shown in figure 1, their origin is coincident with the best focal position (the point O). The requirements for the discretization scheme have been discussed in [45], which has concluded that is necessary to resolve only the variations in the shape of the incident pulse. This enables us to use the straightforward Simpson method [46] to calculate laser fields from the formulas (3).
and y = y'. In this system, the laser pulse will propagate along the z-axis, and the incident laser pulse linearly polarized along the x'-axis will be transformed to the reflected laser pulse linearly polarized along the x-axis. Both coordinate systems are shown in figure 1, their origin is coincident with the best focal position (the point O). The requirements for the discretization scheme have been discussed in [45], which has concluded that is necessary to resolve only the variations in the shape of the incident pulse. This enables us to use the straightforward Simpson method [46] to calculate laser fields from the formulas (3).
Figure 1. Schematic of laser pulse focused by off-axis parabolic mirror. F, Feff are parent and effective focal lengths, ψoff is the off-axis angle, ρ is the mirror radius.
Download figure:
Standard image High-resolution imageUnless otherwise specified, we consider linearly polarized incident laser pulses with wavelength λ = 0.8 μm and a Gaussian spatial profile:  , where w0 is the Gaussian beam radius chosen so that 99% of the laser power would fall on the mirror, of dimensions ρ ≈ 5 cm, ψoff = 90°, as indicated in figure 1. We have not taken into account the effect of the temporal distribution on the spatial laser characteristics. The temporal envelope of the reflected laser pulse is described by the Gaussian function
, where w0 is the Gaussian beam radius chosen so that 99% of the laser power would fall on the mirror, of dimensions ρ ≈ 5 cm, ψoff = 90°, as indicated in figure 1. We have not taken into account the effect of the temporal distribution on the spatial laser characteristics. The temporal envelope of the reflected laser pulse is described by the Gaussian function  , the duration of the laser pulse at full-width-half-maximum (FWHM) is
, the duration of the laser pulse at full-width-half-maximum (FWHM) is 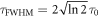 . Hence, this approach allows for modeling laser pulses with different spatial-temporal profiles focused to spots down to the diffraction limit, provided their durations are sufficiently long to neglect spatial-temporal correlations [47]. The reflected laser pulse is characterized by the focal spot size DF at FWHM, which is determined by the f-number of the focusing system,
. Hence, this approach allows for modeling laser pulses with different spatial-temporal profiles focused to spots down to the diffraction limit, provided their durations are sufficiently long to neglect spatial-temporal correlations [47]. The reflected laser pulse is characterized by the focal spot size DF at FWHM, which is determined by the f-number of the focusing system, 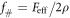 , and the spatial distribution of the laser pulse. For the parameters considered here, DF = 1.3λ for f# = 1, DF = 2λ for
, and the spatial distribution of the laser pulse. For the parameters considered here, DF = 1.3λ for f# = 1, DF = 2λ for  and DF = 3.9λ for f# = 3.
and DF = 3.9λ for f# = 3.
Analogous to the usual field strength parameter a0 for electrons, we introduce 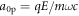 , which is the normalized amplitude of the laser field in terms of the proton mass m. For intensities,
, which is the normalized amplitude of the laser field in terms of the proton mass m. For intensities, 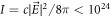 W cm−2, considered here,
W cm−2, considered here, 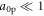 and the quiver energies of protons,
and the quiver energies of protons, 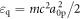 , are nonrelativistic, and therefore their Lorentz-factor is γ ≃ 1 throughout the interaction with the laser pulse. The amplitude of the proton oscillations,
, are nonrelativistic, and therefore their Lorentz-factor is γ ≃ 1 throughout the interaction with the laser pulse. The amplitude of the proton oscillations, 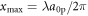 , is also substantially smaller than the characteristic size of the laser focal spot, which allows for averaging the particle motion over an optical period, which is described by the ponderomotive force [48]:
, is also substantially smaller than the characteristic size of the laser focal spot, which allows for averaging the particle motion over an optical period, which is described by the ponderomotive force [48]:
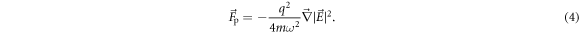
This force can therefore replace the Lorentz force (1) to give equations of motion for the averaged velocity (the so-called drift velocity) and particle position. This equation is also numerically integrated by the Adams method. We have compared the results obtained by this approach with those calculated by the full Lorentz force. Figure 2(a) shows net proton energies as a function of particle initial position for y = 0 and z = 0. The results are in a good agreement with each other. The same results were also received for distribution of proton positions. Proton energy as a function of time is shown in figure 2(b). The full Lorentz force allows calculated proton dynamics in the every moment of time, whereas the ponderomotive approximation gives the time-average characteristics of proton motion. However, the moving average of the proton energies calculated by the former approach show the same final energy gain as the ponderomotive approach. Thus, the ponderomotive approximation can be used for the description of the average and final characteristics of proton dynamics. Hence, below we use ponderomotive description in the proton equation of motion unless specified otherwise.
Figure 2. Comparison of results obtained by Lorentz force (red color) and ponderomotive force (blue color): (a) final energy as a function of initial proton position along x-axis (y = 0, z = 0) and the absolute value of intensity gradient of Gaussian laser beam (green line), (b) average energy (from the ponderomotive approximation) and its moving average (from Lorentz approach) as a function of time. Numerical calculations were performed for a Gaussian laser pulse with peak intensity Ip = 1022 W cm−2 and τFWHM = 36 fs, focused to a spot of size DF = 1.32λ.
Download figure:
Standard image High-resolution imageIn real experiments, the requirement of negligible plasma effects places limits on the proton density in the rarefied gas, which can be estimated in the following way. The interaction of the laser pulse with the gas results in the effective removal of electrons from the interaction area, leading to the formation of a volume of charge. The Coulomb interaction of an individual proton with the resulting charge volume should be negligible as compared with the ponderomotive force of the laser. The strength of the Coulomb interaction can be estimated as 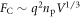 , where np is the concentration of protons and
, where np is the concentration of protons and 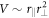 is the interaction volume.
is the interaction volume. 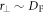 and
and  are the characteristic longitudinal and transverse sizes, respectively. By comparing it with the magnitude of the ponderomotive force results in the limit of the maximum proton concentration:
are the characteristic longitudinal and transverse sizes, respectively. By comparing it with the magnitude of the ponderomotive force results in the limit of the maximum proton concentration:  ,
,  is less than 1 for nonrelativistic interactions, for instance, I = 1021 W cm2 corresponds to
is less than 1 for nonrelativistic interactions, for instance, I = 1021 W cm2 corresponds to  . The limiting expression can be rewritten as
. The limiting expression can be rewritten as 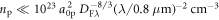 , where
, where  . In this article, the minimum value of the laser peak intensity considered is I = 1021 W cm−2 and the maximum focal spot diameter is approximately DF = 4λ. Therefore, in experiments the proton concentration should be less than 1017 cm−3 to meet this criterion.
. In this article, the minimum value of the laser peak intensity considered is I = 1021 W cm−2 and the maximum focal spot diameter is approximately DF = 4λ. Therefore, in experiments the proton concentration should be less than 1017 cm−3 to meet this criterion.
At the same time the laser pulse is affected by the ionized gas (hydrogen), being refracted. Since the refractive index depends on electron density, neglecting the shift of the focal spot position in comparison with the laser wavelength also limits the gas concentration n. It can be approximately estimated using geometrical optics by the expression: n ≪ λncr/l, where l is thickness of the ionized medium and 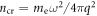 . If l ≈ 10 cm, the concentration should be less than 1016cm−3, that is a more restrictive condition in contrast with the one discussed before.
. If l ≈ 10 cm, the concentration should be less than 1016cm−3, that is a more restrictive condition in contrast with the one discussed before.
3. Diagnosing a laser pulse using the proton momentum distribution
Based on the model introduced in the previous section, we now consider the possibilities of using the measured proton momentum distributions as a diagnostic of ultraintense laser pulses. In this section we first discuss typical accelerated proton spectra, and then show the connection between its characteristics and different laser parameters, such as the peak laser intensity, pulse duration, and focal spot size as well as the spatial-temporal profile. The numerical calculations discussed in this section were performed for 10 125 test particles randomly uniformly distributed in a box of 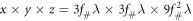 .
.
3.1. Angular-spectral proton distribution
Since the ponderomotive force (4) of the laser is in the opposite direction to the intensity gradient, in the field of a tightly focused laser pulse, protons are pushed predominantly in the direction perpendicular to the laser propagation. Figure 3(a) shows φ-integrated proton spectra as a function of ϑ-angle, which is the polar angle measured from the direction of laser propagation (the positive direction of the z-axis). The angle φ is the azimuthal angle in the plane perpendicular to the z-axis. It is measured from the direction of the laser polarization, i.e. the positive direction of the x-axis. The majority of the ponderomotively accelerated protons move in the 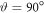 direction. This angle also refers to the emission direction of the most energetic particles (see figure 3(a)).
direction. This angle also refers to the emission direction of the most energetic particles (see figure 3(a)).
Figure 3. φ-integrated (a) and φ, ϑ-integrated (b) spectral distributions of protons accelerated by a Gaussian laser pulse with duration τFWHM = 36 fs and peak intensity Ip = 5 × 1022 W cm−2, focused by an off-axis parabolic mirror (ρ = 5.08 cm, ψoff = 90°) to a focal spot size DF = 1.3λ.
Download figure:
Standard image High-resolution imageHere we analyze the impact of laser parameters on the proton energies. For a proton initially at rest close to the laser focus where the phase fronts are approximately planar, the laser intensity may be separated into 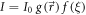 , where I0 is the peak laser intensity,
, where I0 is the peak laser intensity,  is the spatial distribution and f(ξ) is the pulse shape with respect to the coordinate ξ = t − z/c, which was introduced in the previous section. Assuming the proton moves a negligible distance during the laser pulse, which is valid provided
is the spatial distribution and f(ξ) is the pulse shape with respect to the coordinate ξ = t − z/c, which was introduced in the previous section. Assuming the proton moves a negligible distance during the laser pulse, which is valid provided 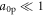 , the energy gain of the protons, εp, can be roughly estimated from ponderomotive approximation in the following way:
, the energy gain of the protons, εp, can be roughly estimated from ponderomotive approximation in the following way:
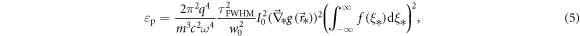
where 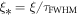 and
and  ,
,  are normalized variables. This formula shows that the particles with the highest energy, εmax, are initially located in the area of the maximum intensity gradient (
are normalized variables. This formula shows that the particles with the highest energy, εmax, are initially located in the area of the maximum intensity gradient (![${[\vec{{\rm{\nabla }}}g(\vec{r})]}_{\max })$](https://content.cld.iop.org/journals/1367-2630/22/2/023003/revision2/njpab6eacieqn48.gif) , which agrees with the results obtained from the numerical modeling of the interaction with a focused Gaussian laser pulse (see figure 2(a)). Thus, the proton spectra has a maximum value εmax of the achieved energies (see numerically calculated spectrum with εmax ≈ 350 keV in figure 3(b)) that hereinafter will be named the 'cutoff energy'.
, which agrees with the results obtained from the numerical modeling of the interaction with a focused Gaussian laser pulse (see figure 2(a)). Thus, the proton spectra has a maximum value εmax of the achieved energies (see numerically calculated spectrum with εmax ≈ 350 keV in figure 3(b)) that hereinafter will be named the 'cutoff energy'.
This formula allows comparing energies, εp, of protons accelerated by the ponderomotive force with energies, εC, gained through the 'Coulomb explosion', if the proton concentration would be rather high. The problem of ion acceleration by electrostatic field of a volume of charge has been studied in detailed in the paper [49], where linear dependence of the energy εC on the laser intensity has been demonstrated. Comparison of the formula (5) with the result of that paper gives the following relation: 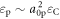 , where
, where 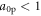 for the intensity range considered in this paper. It means that the regime of 'Coulomb explosion' results in higher proton energies.
for the intensity range considered in this paper. It means that the regime of 'Coulomb explosion' results in higher proton energies.
3.2. Estimation of the peak laser intensity
The formula (5) shows that energies of protons are proportional to the square of the peak intensity, if the other parameters introduced in the equation are fixed. Figure 4 illustrates the cutoff energies (dots in the form of circles, triangles and squares) obtained in numerical calculations as a functions of the peak intensity for different values of the focal spot size. The lines represent theoretical estimations based on the formula (5) and the assumption of the Gaussian spatial-temporal form of the laser pulse near the focal spot. For the laser intensities in the range from 1021 to 1023 W cm−2, the results obtained with theoretical and numerical approaches are in a good agreement with each other for different values of the focal spot size. Thus the cutoff energy of the proton spectra can be estimated by the following analytical formula: ![${\varepsilon }_{\max }\approx 1.7\times {10}^{-10}{I}_{{\rm{L}}18}^{2}{({\tau }_{\mathrm{FWHM}}[\mathrm{fs}]/{D}_{{\rm{F}}\lambda })}^{2}$](https://content.cld.iop.org/journals/1367-2630/22/2/023003/revision2/njpab6eacieqn51.gif) (keV), where
(keV), where 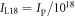 W cm−2 for the laser parameters (wavelength and spatial-temporal profile) similar to ones considered in this paper.
W cm−2 for the laser parameters (wavelength and spatial-temporal profile) similar to ones considered in this paper.
Figure 4. The cutoff energies as a function of the laser peak intensities for fixed value of the focal spot sizes (red, R, green, G, and blue, B, lines) and laser peak power (purple, P, line). Dots show results of numerical calculations, RGB lines are results of their estimations with the formula (5). The purple line is a result of fitting by the linear function y = kx + b on a logarithmic scale with kP ≈ 3 of dots for the same power of laser pulses. Calculations have been performed for a Gaussian laser pulse with τFWHM = 36 fs.
Download figure:
Standard image High-resolution imageThe formula (5) has been deduced under the assumption that the shift of protons during the interaction with the laser pulse is negligible as compared with the focal spot size, i.e. the intensity gradient retains its own value in the position of each particle. However, higher laser intensities leads to substantial shifting the particles, therefore the effect of the gradient variation through the interaction time changes the dependence of proton energies on the laser peak intensity. Figure 4 shows deviations of the results, that have been calculated for the laser diameters DF = 1.3λ and DF = 2λ, from the fitting lines. The smaller focal spot and the higher laser intensity requires proton shifting to be taken into account. Net proton energies also depend on the time τint of the interaction with the laser beam, which is equal to the pulse duration (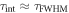 , see formula (5)) in the case of lower intensities. For higher intensities, the interaction time is determined by the dynamics of accelerated protons (so that
, see formula (5)) in the case of lower intensities. For higher intensities, the interaction time is determined by the dynamics of accelerated protons (so that  ). By using this ratio instead of τFWHM in formula (5) results in the net proton energies to be linearly proportional to the laser intensity and independent of the focal spot size. That is why, the points, corresponding to Ip = 1024 W cm−2 for DF = 1.3λ and 2.0λ, turn out to be close together.
). By using this ratio instead of τFWHM in formula (5) results in the net proton energies to be linearly proportional to the laser intensity and independent of the focal spot size. That is why, the points, corresponding to Ip = 1024 W cm−2 for DF = 1.3λ and 2.0λ, turn out to be close together.
The purple line in figure 4 shows the energies gained during proton acceleration by pulses with the same power but different values of the focal spot size and peak intensity. In this case, the expression 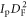 should be held constant, which results in the proton energy being proportional to the cube of the intensity. The slope coefficient of the purple line has been obtained after fitting the numerical results as 3, which is also in agreement with the theory. Thus, the cutoff energy of the protons and the laser intensity are connected and are a function of both the spot size and the laser pulse power. The proton cutoff energy differs from the electron energy characteristics, where expansion of the focal size at first leads to growth of their energies and then to their reduction [39].
should be held constant, which results in the proton energy being proportional to the cube of the intensity. The slope coefficient of the purple line has been obtained after fitting the numerical results as 3, which is also in agreement with the theory. Thus, the cutoff energy of the protons and the laser intensity are connected and are a function of both the spot size and the laser pulse power. The proton cutoff energy differs from the electron energy characteristics, where expansion of the focal size at first leads to growth of their energies and then to their reduction [39].
3.3. Effect of the laser pulse temporal profile
The estimation of the final energy shows its value to be proportional to the square of the laser duration. However this estimate is only valid when the drift of the protons is negligible compared with the spatial scale of the laser pulse throughout the interaction. This restricts the range of valid laser durations, which can be estimated by the following approximate relation: 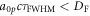 . Figure 5 shows the cutoff energy as a function of the laser duration on a double logarithmic scale. Results from numerical calculations are shown with red dots and a linear fit of the form y = kx + b on this scale is indicated by the blue line. The fit coefficient is k ≈ 2, which is in agreement with the theoretical hypothesis of squared dependence of the cutoff energy. It means that the simulation parameters indeed refer to a regime of proton dynamics with negligible spatial drift during the interaction time.
. Figure 5 shows the cutoff energy as a function of the laser duration on a double logarithmic scale. Results from numerical calculations are shown with red dots and a linear fit of the form y = kx + b on this scale is indicated by the blue line. The fit coefficient is k ≈ 2, which is in agreement with the theoretical hypothesis of squared dependence of the cutoff energy. It means that the simulation parameters indeed refer to a regime of proton dynamics with negligible spatial drift during the interaction time.
Figure 5. The cutoff energies as a function of the pulse duration τFWHM of the Gaussian laser pulse with Ip = 1022 W cm−2 and DF = 1.32λ. Dots show results of numerical calculations, line is a result of their fitting by the linear function y = kx + b in the logarithm scale, where k ≈ 2.
Download figure:
Standard image High-resolution imageIn this regime of the laser-particle interaction, the accelerated proton energy depends on the integral of the temporal distribution of the laser pulse (5). It results in the same energy distribution of protons for laser pulses with the same energy W and focal spot size DF, where the laser pulse energy is 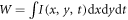 . This assumption refers to the negligible drift of protons as well as the case discussed above. We have carried out a number of numerical calculations for laser pulses with different temporal profiles (see in figure 6(a)) and equal energies, peak intensities and focal spot sizes. We have considered Gaussian, 6-order Gaussian distributions and their different configurations. The results show that the temporal form of a pulse with fixed pulse energy does not impact the cutoff energies of the proton spectra for the peak laser intensity 1022 W cm−2, and therefore this characteristic is not uniquely determined by the accelerated protons spectrum (figure 6(b)). A recent paper [39] shows that the electron distributions are sensitive to the temporal profile of the laser pulse, and so can be used as a complementary diagnostic in this case. Hence, if the laser pulse is free of femtosecond features and has a high level of energy contrast, the laser duration can be estimated with a good accuracy by the proposed method. Our calculations have shown that the protons gain 1% higher energy during the interaction with the laser pulse, which has additional 1% of its energy in picosecond prepulse. Therefore, this introduces an insignificant contribution to the results of the proposed diagnostic.
. This assumption refers to the negligible drift of protons as well as the case discussed above. We have carried out a number of numerical calculations for laser pulses with different temporal profiles (see in figure 6(a)) and equal energies, peak intensities and focal spot sizes. We have considered Gaussian, 6-order Gaussian distributions and their different configurations. The results show that the temporal form of a pulse with fixed pulse energy does not impact the cutoff energies of the proton spectra for the peak laser intensity 1022 W cm−2, and therefore this characteristic is not uniquely determined by the accelerated protons spectrum (figure 6(b)). A recent paper [39] shows that the electron distributions are sensitive to the temporal profile of the laser pulse, and so can be used as a complementary diagnostic in this case. Hence, if the laser pulse is free of femtosecond features and has a high level of energy contrast, the laser duration can be estimated with a good accuracy by the proposed method. Our calculations have shown that the protons gain 1% higher energy during the interaction with the laser pulse, which has additional 1% of its energy in picosecond prepulse. Therefore, this introduces an insignificant contribution to the results of the proposed diagnostic.
Figure 6. Temporal distributions of laser pulses (a) 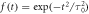 (Gaussian, purple),
(Gaussian, purple), 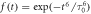 (blue),
(blue), ![$f(t)=\tfrac{1}{2}[\exp (-{t}^{2}{/\tau }_{0}^{2})+\exp (-{t}^{6}/{\tau }_{1}^{6})]$](https://content.cld.iop.org/journals/1367-2630/22/2/023003/revision2/njpab6eacieqn60.gif) (orange), double Gaussian laser pulses (green and red). The corresponding cutoff energies of the proton spectra for laser pulses with the same energies, focal spots and peak intensities: (b)
(orange), double Gaussian laser pulses (green and red). The corresponding cutoff energies of the proton spectra for laser pulses with the same energies, focal spots and peak intensities: (b)  and (c) Ip = 1024 W cm−2. The results were obtained by a series of numerical simulations.
and (c) Ip = 1024 W cm−2. The results were obtained by a series of numerical simulations.
Download figure:
Standard image High-resolution imageAs it was shown in section 3.2, the displacement of the protons becomes significant relative to the focal spot size for a laser intensity of 1024 W cm−2. We have performed a series of numerical calculations for the same laser profiles and given peak laser intensity. Similar to the case of the laser interaction with electrons, the temporal form of the laser pulse impacts the proton energies in this regime, as shown in figure 6(c). A laser pulse with a steeper leading edge results in greater values of the maximum proton energy: 32 MeV for  (blue) and 23 MeV for a double Gaussian laser pulse with a femtosecond prepulse (green).
(blue) and 23 MeV for a double Gaussian laser pulse with a femtosecond prepulse (green).
3.4. Diagnostics of cross beam spatial inhomogeneity in the laser focal spatial distribution
In the previous section we discussed the impact of the laser parameters on the proton energy characteristics. The ponderomotive approximation also allows us to analyze the angular distributions of accelerated particles. From the expression (4) introduced to the equation of motion, the relation between components of the proton momentum and laser intensity distribution is given by:

where the dummy index i indicates either the x, y or z coordinate. Because the emission angles (ϑ and φ) of the particle are determined by the values of the momentum projections, 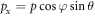 ,
, 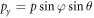 , pz = p cos θ, features of the laser focal distribution will correspond to properties of the angular distributions of protons.
, pz = p cos θ, features of the laser focal distribution will correspond to properties of the angular distributions of protons.
Let us consider two laser pulses with different spatial profiles in the focal plane (figure 7) and the same peak intensity, Ip = 5 × 1022 W cm−2, and duration, τFWHM = 36 fs. One of them is a laser beam with the Gaussian initial spatial profile studied in the previous sections,  , the other is a half-Gaussian with non-zero values for x' > 0 with initial profile proportional to
, the other is a half-Gaussian with non-zero values for x' > 0 with initial profile proportional to 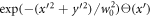 , where Θ(x') is the Heaviside step function. Thus, in the focal plane, the first pulse is axially symmetric while the second one turns into an ellipse with the major axis oriented along the x-axis with
, where Θ(x') is the Heaviside step function. Thus, in the focal plane, the first pulse is axially symmetric while the second one turns into an ellipse with the major axis oriented along the x-axis with  ,
, 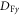 along the minor axis y is approximately equal to 1.57λ. Such change of the spatial distribution can be explained because the far-field distribution is related to the Fourier transform of the near-field distribution, so introducing an aperture in one dimension will increase the diameter in reciprocal space in that dimension.
along the minor axis y is approximately equal to 1.57λ. Such change of the spatial distribution can be explained because the far-field distribution is related to the Fourier transform of the near-field distribution, so introducing an aperture in one dimension will increase the diameter in reciprocal space in that dimension.
Figure 7. Focal profiles of focused laser pulses with different initial spatial distributions. The laser intensity is measured in W cm−2.
Download figure:
Standard image High-resolution imageThese laser beams allow us to analyze the effect of the spatial inhomogeneity on the angular-energy distributions of protons. Figure 8 illustrates ϑ-integrated spectral distributions of protons, the results were received by the numerical calculations. Although the f# of the focusing systems were the same, the smallest diameter of the elliptical focal spot is larger than one of the φ-symmetrical laser beam (1.57λ and 1.3λ, respectively). It leads to the smallest energies of protons accelerated by the half-Gaussian laser pulse for the same peak laser intensities, as shown in section 3.2. The formula (6) keeps a similar form in cylindrical coordinates for the radial component of proton momentum, which means the φ-energy distributions should be φ-symmetric for particles accelerated by a Gaussian beam, since the intensity does not depend on φ-angle. This assumption is in agreement with results obtained from our numerical calculations (see in figure 8(a)). For the elliptical laser beam, we consider two orthogonal directions, φ = 0° and φ = 90°, for particles propagating in the ϑ = 90° direction, which correspond to the momentum components px and py respectively. Since 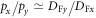 , which can be evaluated from formula (6), the ratio between maximum energies detected along the φ = 0° and 90° directions will be proportional to the square of this expression. Figure 8(b) shows the φ-angular spectral distribution of protons accelerated by the laser pulse pictured in figure 7(b). As predicted by the theoretical hypothesis, the maximum energy detected along the x-axis achieves lower values than the same characteristic of the particles propagating along y-axis. The ratio of εp(φ = 0°) to εp(φ = 90°) is equal to 0.3, which agrees with the estimate
, which can be evaluated from formula (6), the ratio between maximum energies detected along the φ = 0° and 90° directions will be proportional to the square of this expression. Figure 8(b) shows the φ-angular spectral distribution of protons accelerated by the laser pulse pictured in figure 7(b). As predicted by the theoretical hypothesis, the maximum energy detected along the x-axis achieves lower values than the same characteristic of the particles propagating along y-axis. The ratio of εp(φ = 0°) to εp(φ = 90°) is equal to 0.3, which agrees with the estimate  . Thus, this laser diagnostics method also enables us to evaluate the ratio of the beam focal widths. The ponderomotive force is independent of the laser polarization (see formula (4)). It means that replacing the x'-coordinate by y' in the function Θ(x') only leads to rotating the proton distribution in figure 8(b) to 90°, i.e. maximum energies will be detected along φ = 0°and 180°.
. Thus, this laser diagnostics method also enables us to evaluate the ratio of the beam focal widths. The ponderomotive force is independent of the laser polarization (see formula (4)). It means that replacing the x'-coordinate by y' in the function Θ(x') only leads to rotating the proton distribution in figure 8(b) to 90°, i.e. maximum energies will be detected along φ = 0°and 180°.
Figure 8. ϑ-integrated spectral distributions of protons accelerated by axial symmetric (a) and anisotropic (b) laser pulses, corresponding to the focal distributions shown in figures 7(a) and (b).
Download figure:
Standard image High-resolution imageThe diagnostic method considered in this paper is not limited to a Gaussian spatial form of the laser pulse. Based on formula (5), the maximum energy of protons can be calculated for the laser pulses with different focal distributions, including profiles with peripheral rings. In this case, the maximum energy of protons will be defined by the intensity at the main (central) peak of the spatial profile, whereas peripheral rings should lead an increase in the number of protons with intermediate energies, as it has been shown for electrons in [39]. At the same time our approach is restricted by the intensity gradient of the rings, which should be less than that of the main peak. Let consider a pathological example; the laser pulse has an on axis intensity minimum. In this case, the assumption that the proton energy is correlated with the diameter and intensity of the main peak, which does not exist, is erroneous. It means that we should know some a priori information about the focal spot distribution. However, this method can be supported by a similar method based on electrons [39].
3.5. Evaluation of the focal spot size
Figure 3(a) indicates an angular width,  , measured at the half-maximum level, in the angularly resolved energy spectrum. To estimate how the laser intensity profile relates to this characteristic, we start from formula (6) under the same assumption
, measured at the half-maximum level, in the angularly resolved energy spectrum. To estimate how the laser intensity profile relates to this characteristic, we start from formula (6) under the same assumption  as before, which results in the following relations in cylindrical coordinates,
as before, which results in the following relations in cylindrical coordinates, 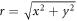 and z:
and z:
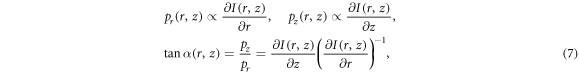
where α is the angle between the direction of particle emission and ϑ = 90°. The final energy of the protons is proportional to the sum of squared components of their momenta:
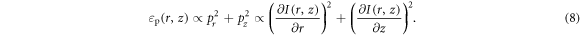
The results produced above show the highest-energy particles propagating along ϑ = 90° and that the longitudinal component of their momentum, pz, is zero. If the initial position of such particles is 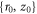 , then their energy can be expressed in the form:
, then their energy can be expressed in the form:
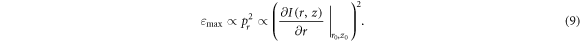
Hence, the initial position of protons with energy εmax/2 may be determined as an implicit function r of z:

Introducing the substitution of variables: Z = z/zR and R = r/DF, where zR corresponds to the FWHM intensity along the z-axis, i.e. the Rayleigh range, and using the expression for tanα, we can rewrite (10) in the following form:
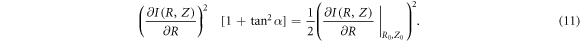
In our calculations, the squared tangent of the emission angle α of the protons with energies  was small, α ≪ 1, and so it can be neglected in formula (11). Thus, using normalized scales {R, Z} the initial positions of the particles, which gain approximately εp1/2 energies, have almost no dependence on the focal spot size (see figure 9(a)). Let this area be determined by the function R = Ri(Z).
was small, α ≪ 1, and so it can be neglected in formula (11). Thus, using normalized scales {R, Z} the initial positions of the particles, which gain approximately εp1/2 energies, have almost no dependence on the focal spot size (see figure 9(a)). Let this area be determined by the function R = Ri(Z).
Figure 9. (a) Matching R = r/DF to Z = z/zR for the initial positions of protons with final energies 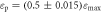 . (b) The graph of connection between the angular width of proton spectra, Δϑ, and the focal size, DF, for the laser pulse with Gaussian initial spatial profile: the red points are corresponding to the numerical simulations, the green squares are results of semi-theoretical predictions, the blue line presents the data approximation.
. (b) The graph of connection between the angular width of proton spectra, Δϑ, and the focal size, DF, for the laser pulse with Gaussian initial spatial profile: the red points are corresponding to the numerical simulations, the green squares are results of semi-theoretical predictions, the blue line presents the data approximation.
Download figure:
Standard image High-resolution imageBased on the introduced substitution, the formula (7) for 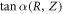 is represented in the following form:
is represented in the following form:
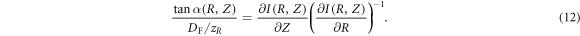
To find the value of Δϑ/2 for given focal spot size, which refers to the maximum α-value for particles initially located in the area R = Ri(Z), we should maximized the value attained by the right part of the equation (12) under the condition R = Ri(Z):
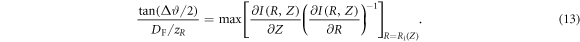
Since both the maximized function and the condition do not depend on the focal spot size, if the maximum value (i.e. the right-hand side of the equation) exists, that was observed in the numerical simulations, it also does not depend on the focal spot size. As a result, the left part of the equation (13) remaining fixed for different values of the focal diameter. Consequently, tan (Δϑ/2) is inversely proportional to zR/DF. Since zR is nonlinearly related with DF (e.g. the square dependence for paraxial approximation [50]), the ratio zR/DF takes on a different value for various focal spot sizes. The considered characteristic of proton spectra does not depend on the laser peak intensity in the ranges of the laser parameters discussed at the beginning of this section. This fact was verified by a series of numerical calculations. At the same time the results demonstrated here were received for Ip = 5 × 1022 W cm−2.
Table 1 contains the spatial characteristics of the laser pulse (DF, zR) and corresponding angular widths of the proton spectra. The numerical calculations show that the ratio of 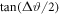 to the expression (DF/zR) is maintained for different spot sizes, being approximately equal to 0.8 in the case of the laser pulse with the Gaussian initial spatial profile. The points corresponding to these results are shown in figure 9(b) by the red dots. The green squares represent semi-theoretical results, that have been obtained by two sequential steps: (i) numerical calculation of the Rayleigh length for the different focal diameters and (ii) transition from the value of DF/zR to the angular width of proton spectra by formula (13). Figure 9(b) also illustrates with the blue line the result of data approximation, this curve is converted into the dashed line for
to the expression (DF/zR) is maintained for different spot sizes, being approximately equal to 0.8 in the case of the laser pulse with the Gaussian initial spatial profile. The points corresponding to these results are shown in figure 9(b) by the red dots. The green squares represent semi-theoretical results, that have been obtained by two sequential steps: (i) numerical calculation of the Rayleigh length for the different focal diameters and (ii) transition from the value of DF/zR to the angular width of proton spectra by formula (13). Figure 9(b) also illustrates with the blue line the result of data approximation, this curve is converted into the dashed line for  exceeding 0.14. It means that for the latter range of the angular widths the determination of the focal spot size by this plot should take into account error associated with no smallness of
exceeding 0.14. It means that for the latter range of the angular widths the determination of the focal spot size by this plot should take into account error associated with no smallness of 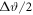 (or equivalently α). If the error has an unacceptably high value, the numerical calculations can be used to specify the result.
(or equivalently α). If the error has an unacceptably high value, the numerical calculations can be used to specify the result.
Table 1. Numerically calculated angular width of proton spectra for different values of the focal spot size for the Gaussian laser pulse.
| f# | DF | zR | Δϑ, deg. |
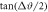
|

|
|---|---|---|---|---|---|
| 1 | 1.3λ | 7.8λ | 15.4 | 0.14 | 0.84 |
| 1.5 | 2.0λ | 18λ | 9.8 | 0.086 | 0.77 |
| 3 | 3.9λ | 73.6λ | 4.95 | 0.043 | 0.81 |
Therefore, the proposed method of the laser diagnostics allows estimating the focal spot size by means of corresponding calculations, based on the technique discussed above, or the graph in figure 9(b) (for Gaussian laser pulses). Using the angular widths of the proton spectra for the laser diagnostics requires minimizing the effect of multiple proton scattering due to collisions of protons with hydrogen nuclei (ion–ion collisions). It leads to both distortion of the proton angular distribution and energy losses. The effect of proton interactions with ambient gas is considerably weaker. With regard to the angular spreading, the limit of the gas thickness, l, (proton propagation distance) and density, n, can be roughly estimated by the following expression [51]: 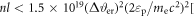 cm−2], where Δϑer is the acceptable angular error in degrees, that should be as low as the accuracy of the angular measurement, me is the electron mass. The energy losses of the accelerated protons can be also neglected for small angular widening. Thus for Δϑer = 1° and εp = 2 keV, the gas parameters are limited by nl < 1015 [cm−2]. It can be fulfilled in experiments, for instance, by using a gas jet of low concentration (<1016 cm−3) and 1 mm thickness. For more accurate estimations of the proton elastic scattering and energy losses, commonly used computer software [52, 53], which model ion propagation though matter using a Monte Carlo method can be used.
cm−2], where Δϑer is the acceptable angular error in degrees, that should be as low as the accuracy of the angular measurement, me is the electron mass. The energy losses of the accelerated protons can be also neglected for small angular widening. Thus for Δϑer = 1° and εp = 2 keV, the gas parameters are limited by nl < 1015 [cm−2]. It can be fulfilled in experiments, for instance, by using a gas jet of low concentration (<1016 cm−3) and 1 mm thickness. For more accurate estimations of the proton elastic scattering and energy losses, commonly used computer software [52, 53], which model ion propagation though matter using a Monte Carlo method can be used.
3.6. Principal scheme of diagnostics
Using the results discussed above, we propose the following scheme of laser pulse diagnostics (see figure 10). The laser pulse is focused by the off-axis parabolic mirror with an effective focal length Feff and an off-axis angle ψoff into a rarefied hydrogen gas. The concentration of the gas should be sufficiently low to satisfy three conditions: (i) the insignificance of plasma effects (section 2); (ii) stopping distance for protons with energy E ∼ εmax/10, where εmax corresponds to the peak laser intensity (figure 4), should be much larger than the distance to the detector (section 3.5); (iii) the laser power is below the critical power for the relativistic self-focusing PL < Pcrit = 17(ω/ωpe)2 [GW]. The most demanding restriction is related to proton scattering, it is overcome by using a gas jet [with centimeter-thickness and low concentration(<1016cm−3)]. The number of particles in the interaction area exceeds 104 for this gas density and the smallest focal spot considered in the paper.
Figure 10. Principal scheme of the laser pulse diagnostics via angular-spectral distributions of protons accelerated from the focus of measured laser pulse.
Download figure:
Standard image High-resolution imageFor the detection of the accelerated protons, the chevron type MCP detectors working in the TOF mode or nuclear track detectors CR-39 can be used. The MCPs have a detection efficiency of ∼10% for protons with E ∼ 0.1 keV and of ∼70% for protons with E ≥ 1 keV [54], providing intensity measurements above 1021 W cm−2 (figure 4). For the MCP operation, a vacuum better than 0.1 mTorr is required. If the pressure in the experimental chamber is above this value, differential pumping of the MCP can be used. The time of arrival to the detector situated at a distance Ldet and the proton energy are connected as 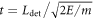 . By measuring the time of arrival of the accelerated protons, their spectrum can be reconstructed. Ideally, it is necessary to use several MCP detectors positioned at different ϑ-angles relative to the laser propagation direction as indicated on figure 10. This will enable collecting the information about the angular and spectral distribution of protons.
. By measuring the time of arrival of the accelerated protons, their spectrum can be reconstructed. Ideally, it is necessary to use several MCP detectors positioned at different ϑ-angles relative to the laser propagation direction as indicated on figure 10. This will enable collecting the information about the angular and spectral distribution of protons.
The CR-39 detectors have ∼100% detection efficiency for protons above 30 keV [55]. Such energy detection threshold for the CR-39 sets a lower boundary for a peak laser intensity of (2−5) × 1022 W cm−2, depending on the focal spot size. CR-39 detectors can work in an accumulation mode, collecting information for hundreds or even thousands of laser shots. Multiple CR-39 detectors can also be placed at the different ϑ-angles and at different φ-angles. The later will provide information about the axial asymmetry of the focal distribution (see section 3.4). This configuration of the experiment allows the laser focal spot size and a peak intensity to be inferred.
4. Conclusion
We have considered the impact of the laser pulse parameters on the characteristics of angular-spectral distributions of protons accelerated from a rarefied gas to analyze the possibility of ultra intense laser pulse diagnostics. The description of the laser pulse was based on diffraction integrals [44], which allows calculating laser pulses focused by off-axis parabolic mirror to focal spots with sizes down to the diffraction limit. In this paper the peak laser intensities were varied in the range from 1021 to 1024 W cm−2, which justifies the use of the ponderomotive force approximation in calculations of proton dynamics by the test particle method. This approach also helped us to construct analytical formulas estimating the angular-spectral characteristics of particles.
Using the results presented in the main part of the paper, we emphasize the central points of the proposed diagnostic method. First of all, it was found that the angular width of proton spectra is determined by the focal spot, which is uniquely related to the convergence angle of the laser beam (the angular measure of the decreasing of the beam diameter, when the laser pulse converges to the focal spot), and maintained during variation of the peak intensity. Thus measuring this characteristic breaks ambiguity about the laser focal spot size. Energy characteristics of the protons depend on the peak intensity, time duration and also focal spot size of the laser pulse. The next step of the diagnostics is a determination of cross spatial inhomogeneity of the laser beam, which consists in measuring the ratio of the maximum energy of protons emitted at the different φ-angles in the plane perpendicular to the direction of the laser propagation. After that, the product of laser peak intensity and pulse duration can be estimated, the square of which is proportional to the maximum energy of protons. It means that if there is no information about the duration and temporal form, the diagnostics will not be able to unambiguously determine the value of the peak intensity. However, in related recent work [39] we show that energy characteristics of electrons are sensitive to these parameters of the laser pulse, which could solve this ambiguity problem. Both approaches of the laser diagnostics could be realized at the same time. Instead of keV-protons mainly propagating perpendicular to the laser pulse, electrons are accelerated to MeV energies relativistically moving at small ϑ-angles to the laser propagation direction. This fact leads to possible complementary measurements using different detectors set in disjoint positions.
The analytical estimations were received in this paper under the assumption of a laser pulse representable by separation of the spatial and temporal profiles. Spatio-temporal coupling can, however, exist in the laser pulses [56]. This configuration of the laser-particle interaction is more complicated and is left as future work.
The proposed method allows measurement of the spatial features of the laser beam and its energy that is actually concentrated in the focal volume. Temporal characteristics should be known previously or determined by another method. At the same time, the method discussed here seems to be easy-to-handle, low cost and does not require significant calculation. This technique can be of high interest for the contemporary sub-petawatt/petawatt laser facilities, which have already been commissioned, and for large laser systems that will be developed in the future. The approach considers a wide range of laser intensities, only the low-intensity part of which has been achieved in experiments, which emphasizes the applicability of this diagnostic method.
Acknowledgments
The numerical simulations and analytical analysis have been carried out under the support of the Russian Science Foundation (Grant No. 17-12-01283). The formulation of the concept and design of the proposed experiment was supported by the Department of Energy through the Laser Network US under award number DE-SC0019255 and the National Science Foundation through the ZEUS project under cooperative agreement number 1935950. OEV is grateful to the foundation Basis for support of her work (18-1-5-102-1) on the numerical model used for the simulations performed.














