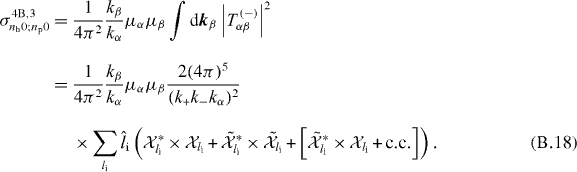Abstract
In the framework of the gravitational behaviour of antihydrogen at rest (GBAR) experiment, cross sections for the successive formation of  and
and 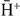 from collisions between positronium (Ps) and antiprotons (
from collisions between positronium (Ps) and antiprotons (  ) have been computed in the range 0–30 keV
) have been computed in the range 0–30 keV  energy, using the continuum distorted wave-final state theoretical model in its three-body and four-body formulations. The effect of the electronic correlations in
energy, using the continuum distorted wave-final state theoretical model in its three-body and four-body formulations. The effect of the electronic correlations in  on the total cross sections of
on the total cross sections of  production has been studied using three different wave functions for H− (the matter equivalent of
production has been studied using three different wave functions for H− (the matter equivalent of 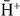 ). Ps excited states up to np = 3, as well as
). Ps excited states up to np = 3, as well as  excited states up to nh = 4, have been investigated. The results suggest that the production of
excited states up to nh = 4, have been investigated. The results suggest that the production of  can be efficiently enhanced by using either a fraction of Ps(2p) and a 2 keV (
can be efficiently enhanced by using either a fraction of Ps(2p) and a 2 keV (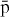 ) beam or a fraction Ps(3d) and antiprotons with kinetic energy below 1 keV.
) beam or a fraction Ps(3d) and antiprotons with kinetic energy below 1 keV.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The formation of positronium (Ps) in collisions between a positron and an atomic hydrogen target (equation (1)) has already been widely studied for it is the prototype of a three-body charge exchange reaction, where the three particles involved are distinguishable. However, even more than providing a testing ground for atomic collision theories, this reaction, and more precisely its charge conjugated inverse (equation (2)), stirred interest for antimatter experiment very early:
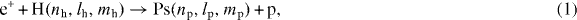
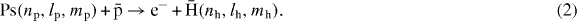
Indeed, in the 1980s, a sub-GeV beam of antiprotons was available at CERN's LEAR facility and the possibility of efficiently producing antihydrogen ( ) atoms using ground state Ps had already been discussed [1]. The importance of using low-energy antiprotons was stressed; a note added by the authors of [1] also suggested investigating the production of excited states of
) atoms using ground state Ps had already been discussed [1]. The importance of using low-energy antiprotons was stressed; a note added by the authors of [1] also suggested investigating the production of excited states of  . These cross sections were computed, for instance by Igarashi et al [2] using a hyperspherical coupled-channel calculation and by Mitroy [3] using the unitarized Born approximation. In the latter, the production of
. These cross sections were computed, for instance by Igarashi et al [2] using a hyperspherical coupled-channel calculation and by Mitroy [3] using the unitarized Born approximation. In the latter, the production of  states up to nh = 7 was considered for Ps energies between 0 and 4 eV and, furthermore, for Ps being itself excited (from np = 1 to 4). Mitroy thus showed that high-nh antihydrogen levels provide the main contribution to the total
states up to nh = 7 was considered for Ps energies between 0 and 4 eV and, furthermore, for Ps being itself excited (from np = 1 to 4). Mitroy thus showed that high-nh antihydrogen levels provide the main contribution to the total 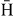 formation cross section. This was later confirmed by a more accurate close coupling (CC) calculation [4]. Mitroy also pointed out the interest of having the Ps excited to a state np = 3 or 4, since these states lead to the highest cross sections below 1 eV centre of mass energy.
formation cross section. This was later confirmed by a more accurate close coupling (CC) calculation [4]. Mitroy also pointed out the interest of having the Ps excited to a state np = 3 or 4, since these states lead to the highest cross sections below 1 eV centre of mass energy.
Around the same period, experimental values became available for both direct and reverse reactions of (1): (i) Weber et al [5] and Zhou et al [6] performed scattering experiments of positrons on, respectively, a mixture of H/H2 and H2; they deduced from their measurements the total cross section for Ps formation from ground state hydrogen (in the range 0 to ≃200 eV positron energy). Their experimental measurements are in good agreement with each other and with available two-centre CC calculations [7–9]. The maximum of the cross section is found to be about 3.5 πa20 around 1 Ryd positron energy; and (ii) three experimental values of hydrogen formation from protons and ground state Ps are also available in the range 11–16 keV (proton energy) [10]. The CC calculations of Mitroy and Ryzhikh [4] give lower values however, they are almost within the error bars.
More recent theoretical calculations include: a two-centre CC approach by Kadyrov and Bray [11] where the production of Ps(1s–2p) from ground state hydrogen is considered; modified Faddeev equations [12, 13] for Ps(1s) − H(1s–2p) and Ps(2s, 2p) − H(nh = 3); also the continuum distorted wave-eikonal final state (CDW-EFS) [14, 15] for H(1s) − Ps(nh = 1–5).
If reaction (1) is a fundamental three-body charge exchange reaction, then the reaction of Ps formation from collisions between positrons and H− ions (equation (3)) would be the four-body equivalent. However, the literature is much less abundant on that process, certainly because of its complexity and the extra care required to describe correctly the highly correlated system that is H−. Usually, the main motivation in studying equation (3) lies in astrophysics, where it is supposed to be a major contribution of the 511 keV annihilation line observed:
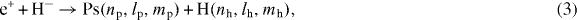
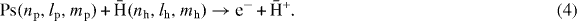
Straton and Drachman used the Coulomb Born approximation (CBA) with two wave functions for H− to compute the cross sections of equation (3) at four different positron energies (0.1, 0.5, 1 and 100 eV) when Ps and H are in their ground states [16]. Chaudhuri [17] highlighted the importance of the choice of the H− wave function and demonstrated the influence of the correlation description on the total cross section above 50 eV positron energy. Biswas [18] used the two-channel exchange coupled-channel theory to compute the cross section of the reverse process studied in [16], but took a plane wave for the exit channel and thus did not take into account the long range Coulomb interaction between e+ and H−. This resulted in a total cross section going to zero close to the threshold when a finite value is expected. The most complete studies currently available are those of McAlinden et al [19] and Roy and Sinha [20], who both considered the formation of H− from H(1s) + Ps(1s–2p), using respectively a coupled pseudo-states approach and a Coulomb modified eikonal approximation (CMEA). The both found the predominance of Ps(2p) at a low energy. Currently, no experimental result for this four-body reaction can be found in the literature.
So far, the two sets of equations have not been studied as an ensemble of two consecutive reactions. Taken as a whole, they describe the production of H− ions from protons interacting with a gas of Ps or, from the antimatter point of view, the formation of  from antiprotons and Ps. The GBAR experiment precisely relies on these two processes to obtain
from antiprotons and Ps. The GBAR experiment precisely relies on these two processes to obtain  ions.
ions.
GBAR, which stands for gravitational behaviour of antihydrogen at rest, will be a future experiment at CERN's antiproton decelerator [21, 22]. The aim of the experiment is to perform a free fall of an antihydrogen atom in order to make a direct measurement of  , the acceleration constant of antimatter on Earth. To observe this free fall and to reduce the uncertainty due to the initial velocity of the antiatom, the latter has to be cooled to a few neV (about 10 μK). The key idea of the GBAR experiment is to use
, the acceleration constant of antimatter on Earth. To observe this free fall and to reduce the uncertainty due to the initial velocity of the antiatom, the latter has to be cooled to a few neV (about 10 μK). The key idea of the GBAR experiment is to use 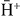 ions that can then be trapped and sympathetically cooled in an ultracold cloud of Be+. Using this regular technique of cold atoms science, the required energy can be reached. The production of the
ions that can then be trapped and sympathetically cooled in an ultracold cloud of Be+. Using this regular technique of cold atoms science, the required energy can be reached. The production of the  ions therefore has to be optimized. In particular, for equation (4), a classical energetic argument suggests that the reaction could be nearly resonant close to the threshold (which is 4 meV antihydrogen energy) in the case nh = 1 and np = 3. To our knowledge, cross sections for the four-body reaction are not available for Ps in a state np = 3.
ions therefore has to be optimized. In particular, for equation (4), a classical energetic argument suggests that the reaction could be nearly resonant close to the threshold (which is 4 meV antihydrogen energy) in the case nh = 1 and np = 3. To our knowledge, cross sections for the four-body reaction are not available for Ps in a state np = 3.
The main objective of this work is thus to provide a complete set of cross sections for the second reaction upon which an estimation of  production can be made for GBAR. Since both reactions (2) and (4) are of interest for the experiment, it was also decided to compute cross sections for the first reaction, with the same theoretical model, at the same level of approximation. The model chosen is called CDW-final state (CDW-FS) and has both a three-body and a four-body formulation. CDW-FS for light particles was first introduced by Fojón et al [23] to study Ps formation from positron capture by light hydrogen-like ions. Asymptotic states are described by Coulomb wave functions giving the exact boundary conditions (hence the relation to CDW methods). In the prior formulation of the theory, if the target is charged in the entrance channel, extra care must be taken so that the perturbative potential remains short ranged. The model also includes distortions in the final channel due to the Coulomb field of the residual target; this special treatment gives its name to the theory. On the same basis, this model has later been adapted to four-body reactions, in particular the case of positron capture by metastable helium [24]. More details on CDW-FS can be found in the mentioned publications [23, 24].
production can be made for GBAR. Since both reactions (2) and (4) are of interest for the experiment, it was also decided to compute cross sections for the first reaction, with the same theoretical model, at the same level of approximation. The model chosen is called CDW-final state (CDW-FS) and has both a three-body and a four-body formulation. CDW-FS for light particles was first introduced by Fojón et al [23] to study Ps formation from positron capture by light hydrogen-like ions. Asymptotic states are described by Coulomb wave functions giving the exact boundary conditions (hence the relation to CDW methods). In the prior formulation of the theory, if the target is charged in the entrance channel, extra care must be taken so that the perturbative potential remains short ranged. The model also includes distortions in the final channel due to the Coulomb field of the residual target; this special treatment gives its name to the theory. On the same basis, this model has later been adapted to four-body reactions, in particular the case of positron capture by metastable helium [24]. More details on CDW-FS can be found in the mentioned publications [23, 24].
However convenient CDW-FS is, it holds several drawbacks inherent to this family of perturbative theories. Firstly, its usual validity domain is at intermediate and high energies and it is probably not valid towards the threshold, energy region which is of primary importance for GBAR. Secondly, it has been demonstrated that the post/prior discrepancy of CDW theories increases towards low energies [25]. Despite the lack of reliability close to the threshold energies, useful informations can be extracted from the relative behaviours of the computed cross sections. Also, the use of this theoretical framework allows us to investigate in full detail, for the first time, the role played by the electron correlations of H− in four-body scattering processes (equation (4)). Furthermore, a comparison with available experimental (in the case of the three-body reaction) and theoretical results should give hints on the validity of CDW-FS at low energy.
In the following section, the analytical expressions of the cross sections calculated within the framework of CDW-FS theory and using a partial wave technique are detailed for very general cases (any state of hydrogen and Ps). Particular cases of lh = 0 and/or lp = 0 are included in appendices. In the next section, the results of the numerical computation are then presented and the importance of the correlations in H− is discussed. Differential cross sections are not considered. The cross sections have been computed for reactions (1) and (3) but, assuming invariance by charge conjugation and micro-reversibility, they are related to cross sections of reactions (2) and (4) by a simple kinetic factor. Throughout this paper, atomic units have been used, unless otherwise specified.
2. Theoretical methods
2.1. Three-body reaction
2.1.1. General case: lh,lp ⩾ 0
The capture of an electron with Ps formation in e+–H collisions is considered (reaction (1)). Figure 1 describes the coordinates used in this section; for further discussion and details about the CDW-FS model of this reaction and on the choice of the coordinates, see [23].
Figure 1. Coordinates used for reaction (1).
Download figure:
Standard image High-resolution imageThe wave function corresponding to the entrance channel is

where  is the wave function of the electron in the hydrogen atom in the (nhlhmh) state and
is the wave function of the electron in the hydrogen atom in the (nhlhmh) state and 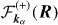 is the Coulomb wave function of the positron in the continuum of the hydrogen target. The final state is described by the wave function
is the Coulomb wave function of the positron in the continuum of the hydrogen target. The final state is described by the wave function

where  is the wave function of the electron bound in the Ps atom, formed in the (nplpmp) state,
is the wave function of the electron bound in the Ps atom, formed in the (nplpmp) state, 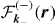 and
and  are, respectively, the Coulomb wave functions of the outgoing electron and the positron in the continuum of the residual proton of charge ZT = 1. The Coulomb wave functions write as
are, respectively, the Coulomb wave functions of the outgoing electron and the positron in the continuum of the residual proton of charge ZT = 1. The Coulomb wave functions write as
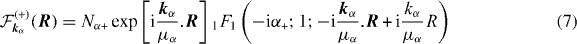
with  since the charge ZT − 1 of the hydrogen target is 0 (in which case, the Coulomb wave function actually reduces to a plane wave) and
since the charge ZT − 1 of the hydrogen target is 0 (in which case, the Coulomb wave function actually reduces to a plane wave) and  . kα is the wavevector of the reduced positron in the entrance channel and μα is the reduced mass of the positron–target system (
. kα is the wavevector of the reduced positron in the entrance channel and μα is the reduced mass of the positron–target system ( );
);
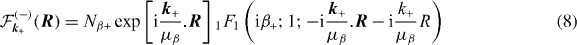
with  and
and  . k+ is the wavevector of the reduced positron in the exit channel and μβ is the reduced mass of the Ps–residual target system (
. k+ is the wavevector of the reduced positron in the exit channel and μβ is the reduced mass of the Ps–residual target system (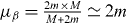 );
);

with 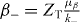 and
and 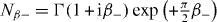 . k− is the wavevector of the reduced electron in the exit channel.
. k− is the wavevector of the reduced electron in the exit channel.  , where kβ is the wavevector of the reduced Ps in the exit channel. Even if the exit channel of the reaction (1) is not Coulombic as it contains two species with only one having the overall charge, the CDW-FS model includes distortions in the final channel which are related to the Coulomb continuum states of the positron and the electron (of the Ps atom) in the field of the residual target (the proton). Therefore, the continuum wave functions (8) and (9) do not reduce to plane waves. If no distortions are included in the final channel, the CBA is obtained. This situation is similar to the one described in [1, 26]. By artificially fixing the charges β− and β+ to zero, we have got back almost the same results, which are quoted in [1]. The latter will be discussed in section 3.1.2.
, where kβ is the wavevector of the reduced Ps in the exit channel. Even if the exit channel of the reaction (1) is not Coulombic as it contains two species with only one having the overall charge, the CDW-FS model includes distortions in the final channel which are related to the Coulomb continuum states of the positron and the electron (of the Ps atom) in the field of the residual target (the proton). Therefore, the continuum wave functions (8) and (9) do not reduce to plane waves. If no distortions are included in the final channel, the CBA is obtained. This situation is similar to the one described in [1, 26]. By artificially fixing the charges β− and β+ to zero, we have got back almost the same results, which are quoted in [1]. The latter will be discussed in section 3.1.2.
In order to compute the transition matrix element, the following partial wave expansion of the Coulomb wave functions has been used:
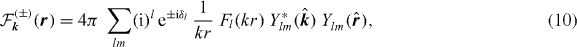
where the functions Fl(kr) are the Coulomb radial functions with the Sommerfeld parameters η = β± or α+ and δl are the usual Coulomb phase shifts 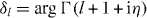 . The spherical harmonic function
. The spherical harmonic function  has been treated using the development [27]
has been treated using the development [27]
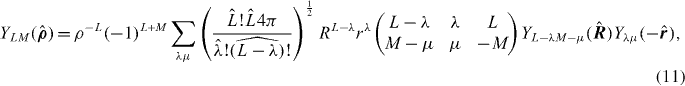
where 0 ⩽ λ ⩽ L and −λ ⩽ μ ⩽ λ.
The perturbative potential in the entrance channel (initial state) is

The transition matrix element is then
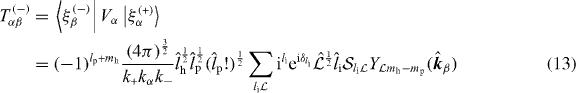
with
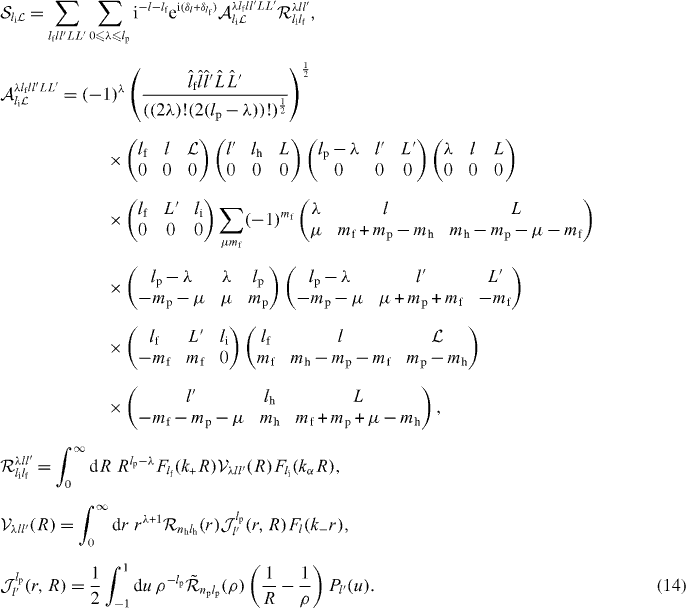
In the above expression, the variable u is defined as  and
and  indicates
indicates  . Pl' is the Legendre polynomial of degree l', coming from the multipole expansion
. Pl' is the Legendre polynomial of degree l', coming from the multipole expansion
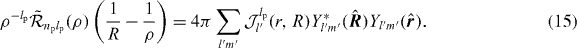
The CDW-FS total cross section for Ps(np,lp) formation from H(nh,lh) (reaction (1)) is given by
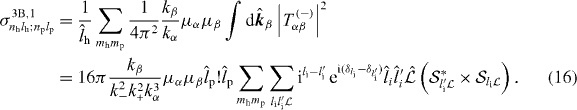
These expressions can be simplified in the cases when either lh or lp, or both, are taken to be 0; details can be found in appendix A.
2.2. Four-body reaction
2.2.1. General case: lp,lh ⩾ 0
We develop here the very general case where both lh and lp are different from 0 (the particular cases when lh = 0, lp = 0 and lh = lp = 0 are described in appendix B) and the wave function for H− is of the form

where r12 is defined as 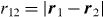 . This wave function has been treated using a partial wave expansion, which can be written as follows:
. This wave function has been treated using a partial wave expansion, which can be written as follows:

with

and
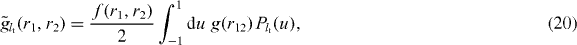
where 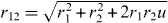 . Three different wave functions have been used for modelling H−. The first one is the 'uncorrelated' Chandrasekhar wave function (labelled UC in the following) [28]. This is a simple and convenient wave function which takes into account the radial correlations between the two electrons of H− but no angular correlations. It has been used in several papers already cited and is usually considered as a sufficient level of description for H−. ΦUCα(r1,r2) is given by
. Three different wave functions have been used for modelling H−. The first one is the 'uncorrelated' Chandrasekhar wave function (labelled UC in the following) [28]. This is a simple and convenient wave function which takes into account the radial correlations between the two electrons of H− but no angular correlations. It has been used in several papers already cited and is usually considered as a sufficient level of description for H−. ΦUCα(r1,r2) is given by
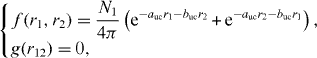
where auc = 1.0392,buc = 0.2831 and the normalization constant N1 = 0.3948. The binding energy of H− computed with this function is EH− = −0.5133, which has to be compared with the exact theoretical value, −0.5277 [29]. This wave function can be modified by introducing g ≠ 0, so that now it takes into account angular correlations. This 'correlated' Chandrasekhar wave function ΦCCα(r1,r2) is defined by [28]

where acc = 1.0748, bcc = 0.4776, D = 0.3121 and the normalization constant N2 = 0.3942. The binding energy is then EH− = −0.5259. Note that a misprint turned the sign of D into negative in several papers (in [17], for instance) whereas it is positive in the original Chandrasekhar paper, as it should be. The last wave function chosen to describe H− is the Le Sech wave function (labelled LS in the following) [30]. ΦLSα(r1,r2) decomposes as follows:
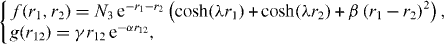
where α = 0.05, β = 0.04, γ = 0.50, λ = 0.57 and the normalization constant N3 = 0.03615 [31]. The binding energy calculated with the LS wave function is EH− = −0.5270. This wave function has been emphasized as a very accurate description of H− [32]. Table 1 shows the contribution of the different angular components in the H− wave function and the convergence of the normalization when using the partial wave expansion (18); in this table, alt is defined by  .
.
Table 1. Convergence of the H− partial wave expansion.
| alt | UC | CC | LS |
|---|---|---|---|
| a0 | 1 | 0.9955 | 0.9959 |
| a1 | 0 | 4.454×10−3 | 3.954×10−3 |
| a2 | 0 | 5.326×10−5 | 9.444×10−5 |
| a3 | 0 | 4.165×10−6 | 7.776×10−6 |
| a5 | 0 | 1.568×10−7 | 2.966×10−7 |
| a10 | 0 | 1.604×10−9 | 3.042×10−9 |
| a30 | 0 | 9.029×10−13 | 1.714×10−12 |
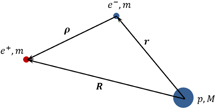
Figure 2 describes the coordinates used for the four-body reaction, similarly to [24] and derived from [33]. The wave function of the initial state is

with the Coulomb wave function 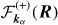 describing the positron in the continuum of H− (see equation (7)). kα is the wavevector of the reduced positron in the entrance channel with
describing the positron in the continuum of H− (see equation (7)). kα is the wavevector of the reduced positron in the entrance channel with 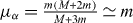 the reduced mass of the positron–H− target system. The wave function for the final state is
the reduced mass of the positron–H− target system. The wave function for the final state is
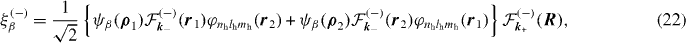
where 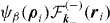 describes electron i captured in the outgoing Ps while electron j remains in the residual hydrogen atom (φnhlhmh(rj));
describes electron i captured in the outgoing Ps while electron j remains in the residual hydrogen atom (φnhlhmh(rj));  is the Coulomb wave function of the outgoing positron (see equation (8)). kβ is the wavevector of the reduced Ps in the exit channel; we also define
is the Coulomb wave function of the outgoing positron (see equation (8)). kβ is the wavevector of the reduced Ps in the exit channel; we also define  , the reduced mass of the Ps–residual target system. As defined in the previous section,
, the reduced mass of the Ps–residual target system. As defined in the previous section,  . Again, a partial wave expansion of the Coulomb wave functions has been used (see equation (10)). The Sommerfeld parameters are
. Again, a partial wave expansion of the Coulomb wave functions has been used (see equation (10)). The Sommerfeld parameters are  ,
,  and
and 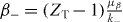 ; since the proton charge ZT = 1, we have β± = 0: therefore, it should be noted that the Coulomb wave functions for the electron and the positron in the exit channel are actually plane waves. The Coulomb phase shifts δl are defined as in the previous section. The 1S symmetry of the initial state of H− imposes the symmetry in the final state, hence the choice of expression (22) for ξ(−)β.
; since the proton charge ZT = 1, we have β± = 0: therefore, it should be noted that the Coulomb wave functions for the electron and the positron in the exit channel are actually plane waves. The Coulomb phase shifts δl are defined as in the previous section. The 1S symmetry of the initial state of H− imposes the symmetry in the final state, hence the choice of expression (22) for ξ(−)β.
Figure 2. Coordinates used for reaction (3).
Download figure:
Standard image High-resolution imageThe chosen short-range perturbative potential is

and the four-body CDW-FS matrix element T(−)αβ reads as
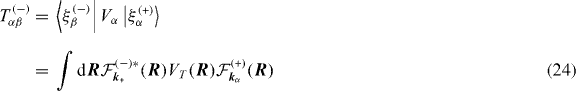
with
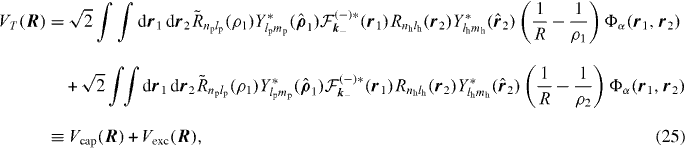
where 'cap' stands for capture and 'exc' for excitation, notations that are justified in the case of the uncorrelated Chandrasekhar wave function (see section 2.2.2). The transition matrix element T(−)αβ can be thus written as a sum of two terms, tcap and texc. After lengthy calculations, the former term may be expressed as
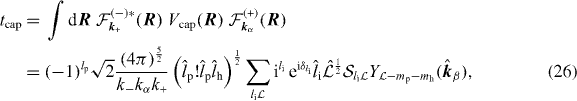
where
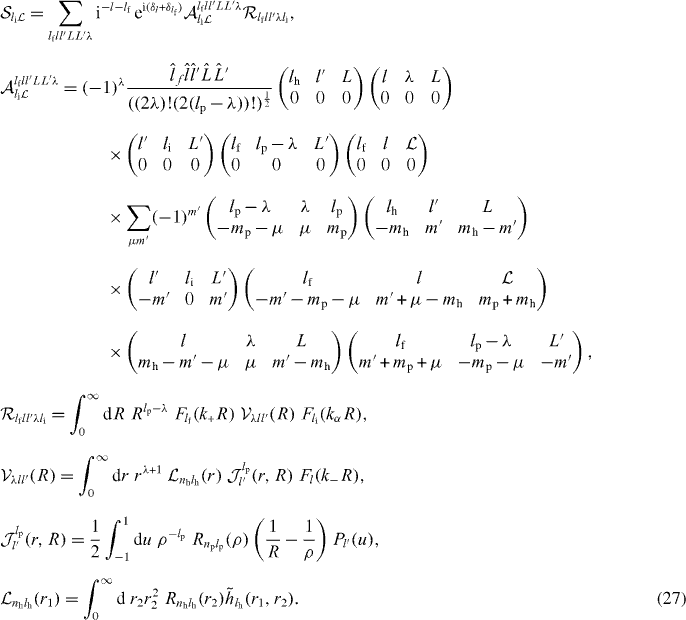
Similarly the excitation transition matrix element is given by

with
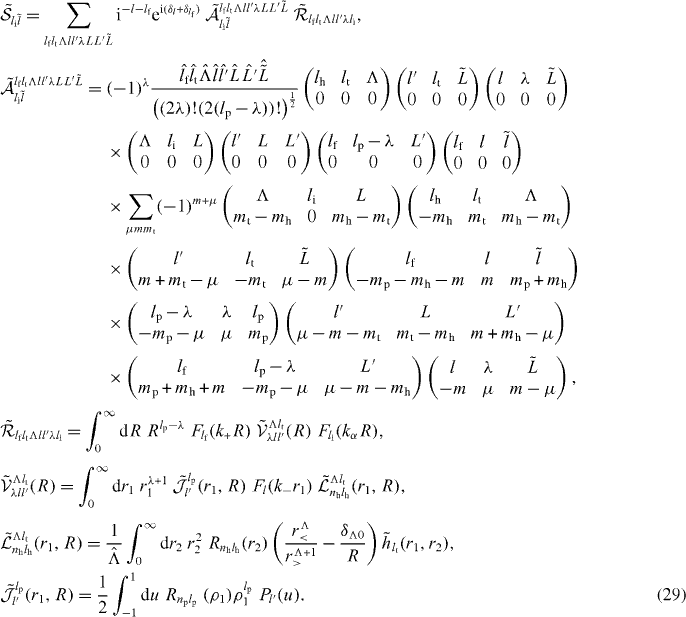
r< (respectively r>) is defined as min(r2,R) (respectively max(r2,R)). The total cross section for a given state (nh,lh) of H and a given state (np,lp) of Ps (reaction (3)) is given by
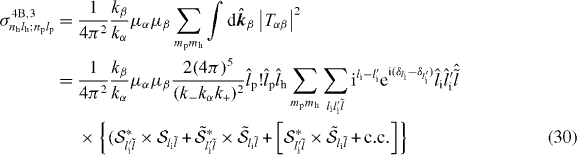
with
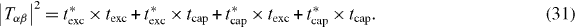
2.2.2. Uncorrelated Chandrasekhar wave function
Because of the absence of angular correlations in the uncorrelated Chandrasekhar wave function, further simplifications can be applied to the transition matrix element. The H− wave function can be treated slightly differently. Indeed, one notices that the UC wave function can also be written as
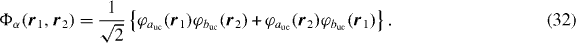
Now, in T−αβ, terms depending on r1 and r2 are fully separable and the transition matrix element can be written as

where auc is shortened into a and buc in b. tij describes the capture into the Ps of the electron initially in state i in H− while, simultaneously, the electron initially in state j is excited to a final state H(nh,lh,mh). Since both electrons in H− are indistinguishable, T−αβ is the coherent sum of two terms. We have

where
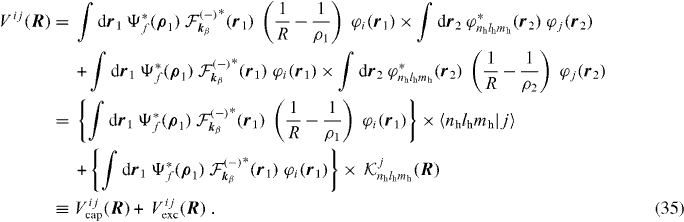
According to this, the matrix element tij may be expressed as

The matrix elements tijcap and tijexc may be obtained by replacing Vij in equation (34) with Vijcap and Vijexc, respectively. The term tijcap mostly describes the capture of the electron in state i in H− into the Ps; the process is pondered by the overlap between the wave function of the electron in the hydrogen atom and the wave function of the H− electron initially in state j. Due to the scalar product  , it is worthwhile noticing that the term of 'capture' is equal to zero for lh ≠ 0. The term tijexc encloses the excitation of the electron that remains bound to the proton, from state j in H− to state (nh,lh,mh) in the hydrogen atom. Indeed,
, it is worthwhile noticing that the term of 'capture' is equal to zero for lh ≠ 0. The term tijexc encloses the excitation of the electron that remains bound to the proton, from state j in H− to state (nh,lh,mh) in the hydrogen atom. Indeed, 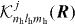 can be written as
can be written as

with
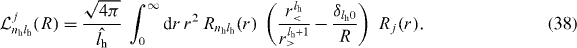
The total cross section with the uncorrelated Chandrasekhar wave function can be written as
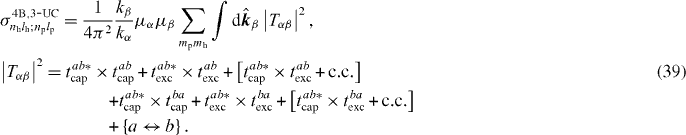
If mh or lh are different from zero, most of these terms are null. The expression of the pure capture terms is
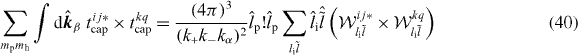
with
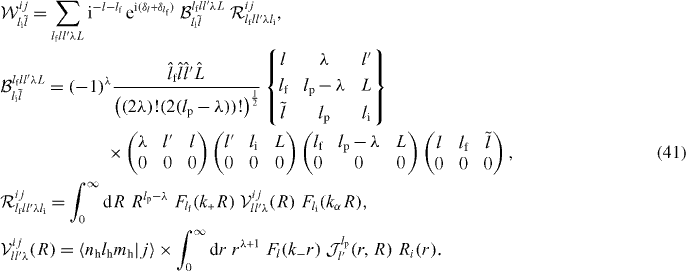
Pure excitation terms can be written as follows:
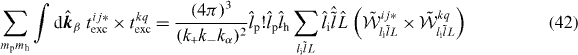
with
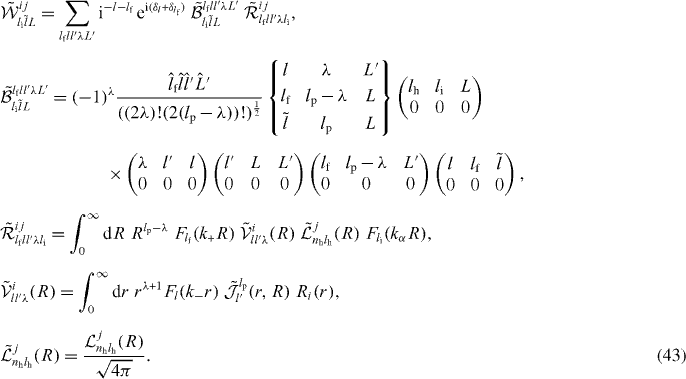
Finally, the cross terms can be expressed with the previously introduced quantities. For instance
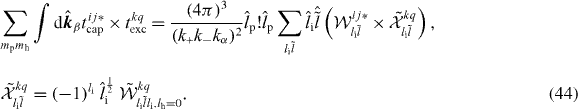
3. Results
3.1.  production (three-body reaction)
production (three-body reaction)
3.1.1. Three-body continuum distorted wave-final state (CDW-FS)
Cross sections for reaction (1) have been computed for 6 states of the Ps atom, from Ps(1s) to Ps(3d) and for 13 states of hydrogen, from H(1s) to H(5d) (and up to H(5g) for ground-state Ps). Higher states have not been investigated yet since the calculation for each (np, lp, mp)–(nh, lh, mh) pair is very time-consuming. To obtain the cross sections for the reverse reaction (2), the following kinetic transformation is applied, assuming microreversibility and invariance by charge conjugation [1]:

where 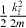 is almost the kinetic energy of the Ps atom in the centre of mass and
is almost the kinetic energy of the Ps atom in the centre of mass and 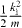 is almost the kinetic energy of the electron/positron in the centre of mass. The energy considered for reaction (1) ranges from 0 to 50 eV positron energy and the results presented here for reaction (2) focus on the 0 and 30 keV antiproton energy region.
is almost the kinetic energy of the electron/positron in the centre of mass. The energy considered for reaction (1) ranges from 0 to 50 eV positron energy and the results presented here for reaction (2) focus on the 0 and 30 keV antiproton energy region.
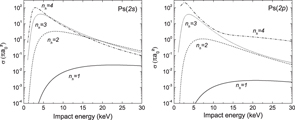
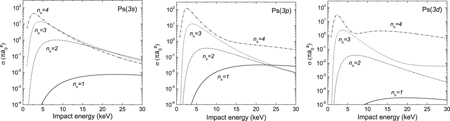
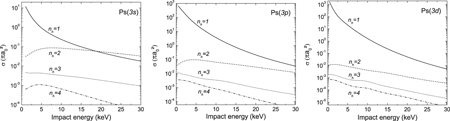
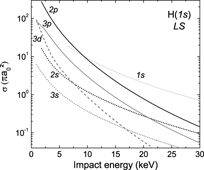
Figures 3–5 present, for Ps(1s)–Ps(3d), the cross sections of antihydrogen formation σ3B,2nhlh;nplp for nh = 1–4. They demonstrate the large production of the higher excited states of 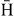 (this general behaviour is in agreement with other computations [3, 4]),
(this general behaviour is in agreement with other computations [3, 4]),  (1s) production being almost negligible at low energies in all cases. Figure 6 details, in the case of Ps(2p) and nh = 4, the different contributions of the lh states. The relative behaviour of the cross sections in this example are similar in any other (nh,lh)–(np,lp) case. It shows that, for a given nh, the production of s-state antihydrogen is always the lowest contribution, whereas the formation of states with non-zero angular momentum quantum numbers gets more and more favoured as lh increases. For the highest lh state, this hierarchy can be slightly perturbed towards the threshold and towards the intermediate energy region, as can be seen in figure 6 for the
(1s) production being almost negligible at low energies in all cases. Figure 6 details, in the case of Ps(2p) and nh = 4, the different contributions of the lh states. The relative behaviour of the cross sections in this example are similar in any other (nh,lh)–(np,lp) case. It shows that, for a given nh, the production of s-state antihydrogen is always the lowest contribution, whereas the formation of states with non-zero angular momentum quantum numbers gets more and more favoured as lh increases. For the highest lh state, this hierarchy can be slightly perturbed towards the threshold and towards the intermediate energy region, as can be seen in figure 6 for the  (4f).
(4f).
Figure 3. Antihydrogen production cross sections from ground state Ps as a function of the antiproton impact energy.
Download figure:
Standard image High-resolution imageFigure 4. Antihydrogen production cross sections from Ps excited in a state np = 2 as a function of the antiproton impact energy.
Download figure:
Standard image High-resolution imageFigure 5. Antihydrogen production cross sections from Ps excited in a state np = 3 as a function of the antiproton impact energy.
Download figure:
Standard image High-resolution imageFigure 6. Cross sections of antihydrogen production in the states nh = 4 for Ps(2p), as a function of the antiproton impact energy.
Download figure:
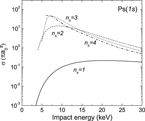
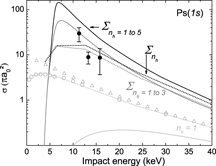
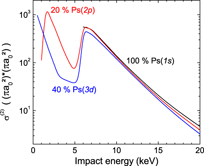
Standard image High-resolution imageIn the prospect of the GBAR experiment for which the highest production rate of antihydrogen atoms is sought, figure 7 compares the different states of Ps, when all the contributions of 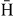 states are summed from (1s) to (5d). The maximum of
states are summed from (1s) to (5d). The maximum of  production occurs around 6 keV antiproton energy when the Ps is in its ground state and, because of the threshold constraints for nh > 1,
production occurs around 6 keV antiproton energy when the Ps is in its ground state and, because of the threshold constraints for nh > 1, 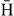 formation from Ps(1s) appears to be completely negligible below 5 keV. For excited states of Ps, the production of antihydrogen atoms peaks in the region between 2 and 3 keV. The highest cross section is obtained for Ps(2p) at 2 keV: this maximum dominates the others by at least a factor of 2.
formation from Ps(1s) appears to be completely negligible below 5 keV. For excited states of Ps, the production of antihydrogen atoms peaks in the region between 2 and 3 keV. The highest cross section is obtained for Ps(2p) at 2 keV: this maximum dominates the others by at least a factor of 2.
Figure 7. Cross sections of antihydrogen production up to  (5d) for Ps(1s)–Ps(3d), as a function of antiproton impact energy.
(5d) for Ps(1s)–Ps(3d), as a function of antiproton impact energy.
Download figure:
Standard image High-resolution image3.1.2. Comparison with experimental data
As already explained in the introduction, cross sections for reaction (2) can only be compared to one experiment performed by Merrison et al [10] for ground state Ps in the energy range 11–15 keV. In these inclusive measurements, no distinction between the hydrogen states produced could be done. The comparison, shown in figure 8 will thus take place between these experimental data and the sum of our cross sections over the (anti)hydrogen states. Despite a slight over-estimation from the summed cross sections, the theoretical calculations and the experimental data are in rather good agreement. To give another perspective, the CC(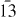 ,
,  ) and CC(
) and CC(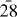 , 3) calculations by Mitroy and Ryzhikh [4] are also included in figure 8. As mentioned in the introduction, these calculations and the experimental data are in good agreement, except for the value at 11.3 keV. In that region, the CDW-FS results seem to better reproduce the behaviour of the total hydrogen production. On the other hand, CDW-FS largely underestimates the production of ground state hydrogen, which nonetheless remains small compared to the production of excited states. In the absence of other experimental results for reaction (2) (or its matter counterpart), in particular in the case of excited Ps, this positive comparison validates the use of CDW-FS to address the needs of the GBAR experiment.
, 3) calculations by Mitroy and Ryzhikh [4] are also included in figure 8. As mentioned in the introduction, these calculations and the experimental data are in good agreement, except for the value at 11.3 keV. In that region, the CDW-FS results seem to better reproduce the behaviour of the total hydrogen production. On the other hand, CDW-FS largely underestimates the production of ground state hydrogen, which nonetheless remains small compared to the production of excited states. In the absence of other experimental results for reaction (2) (or its matter counterpart), in particular in the case of excited Ps, this positive comparison validates the use of CDW-FS to address the needs of the GBAR experiment.
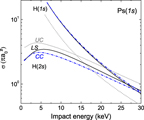
Figure 8. Comparison to the experimental values of Merrison et al [10]. The solid lines are our CDW-FS results and the dotted lines are the results from Mitroy and Ryzhikh [4]. In light grey, the production of hydrogen in its ground state; in darker grey, the sum of the hydrogen production cross sections up to state H(3d). The solid black line corresponds to the CDW-FS results taking into account the hydrogen states up to H(5d) whereas the dotted black line from [4] is an estimation of the total hydrogen production using the 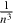 scaling for the states above (3d). Also represented: the CBA results for H(1s) production (light grey triangles) compared to the cross section given in [1] (light grey circles).
scaling for the states above (3d). Also represented: the CBA results for H(1s) production (light grey triangles) compared to the cross section given in [1] (light grey circles).
Download figure:
Standard image High-resolution imageThe predictions of the CBA model (obtained by setting β− = β+ = 0) are also depicted in figure 8, along with the cross section given in [1]. As expected, the two models exhibit very similar results.
3.2.  production (four-body reaction)
production (four-body reaction)
3.2.1. Four-body CDW-FS
Uncorrelated Chandrasekhar wave function
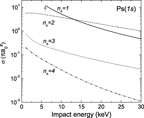
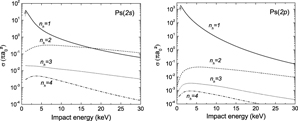
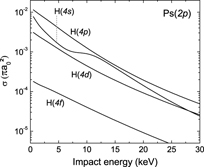
The cross sections for reaction (3) were first computed using the uncorrelated Chandrasekhar wave function. Ps in states (1s)–(3d) were investigated and excited states of hydrogen up to (4f) were considered. The results translated for reaction (4) (see equation (46) below): relations between the cross sections of reactions (3) and (4), assuming microreversibility and invariance by charge conjugation, are presented in figures 9–11, for energies between 0 and 30 keV antihydrogen energy and the contribution of the antihydrogen excited states have been summed over lh. As an example of the cross sections dependence in the orbital quantum number lh, more detailed results are shown in figure 13 for Ps(2p) and in a state nh = 4:

The general behaviour of the four-body reaction cross sections is a dramatic increase of the 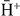 production towards the thresholds (see table 2) when the antihydrogen is in its ground state. This had already been noted by McAlinden et al (who gave a
production towards the thresholds (see table 2) when the antihydrogen is in its ground state. This had already been noted by McAlinden et al (who gave a  law to estimate the cross section of reaction (3) at very low energies) and Roy et al for Ps(1s) to (2p) [19, 20]; it is now also demonstrated for np = 3. The other tendency, over all the energy range considered, is a shift of the cross sections towards lower values when nh increases. This decrease of the cross sections with nh is amplified as lp goes up. Two cases can be distinguished: lp = 0 and lp ≠ 0. Indeed, for s-states of Ps, values of the cross sections for
law to estimate the cross section of reaction (3) at very low energies) and Roy et al for Ps(1s) to (2p) [19, 20]; it is now also demonstrated for np = 3. The other tendency, over all the energy range considered, is a shift of the cross sections towards lower values when nh increases. This decrease of the cross sections with nh is amplified as lp goes up. Two cases can be distinguished: lp = 0 and lp ≠ 0. Indeed, for s-states of Ps, values of the cross sections for  formation from
formation from 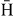 (1s) are very similar: they are all of the order of 10 πa20 at the threshold and decrease with the impact energy, until, around 10–15 keV, they become comparable to the cross sections when
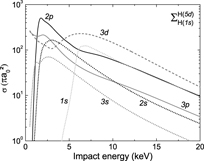
(1s) are very similar: they are all of the order of 10 πa20 at the threshold and decrease with the impact energy, until, around 10–15 keV, they become comparable to the cross sections when  is in the nh = 2 states in the entrance channel. For the lp ≠ 0 states of Ps, the channel where the antihydrogen is in its ground state is always dominant; below 5 keV, these cross sections are one or two orders of magnitude higher than the ones with s-state Ps, as can be seen in figure 12.
is in the nh = 2 states in the entrance channel. For the lp ≠ 0 states of Ps, the channel where the antihydrogen is in its ground state is always dominant; below 5 keV, these cross sections are one or two orders of magnitude higher than the ones with s-state Ps, as can be seen in figure 12.
Figure 9.  production cross sections from ground state Ps as a function of the antihydrogen impact energy; the arrow indicates the threshold of the
production cross sections from ground state Ps as a function of the antihydrogen impact energy; the arrow indicates the threshold of the  (1s) channel.
(1s) channel.
Download figure:
Standard image High-resolution imageFigure 10. 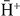 production cross sections from Ps excited in a state np = 2 as a function of the antihydrogen impact energy; the arrows mark the threshold of the
production cross sections from Ps excited in a state np = 2 as a function of the antihydrogen impact energy; the arrows mark the threshold of the  (1s) channel.
(1s) channel.
Download figure:
Standard image High-resolution imageFigure 11.  production cross sections from Ps excited in a state np = 3 as a function of the antihydrogen impact energy.
production cross sections from Ps excited in a state np = 3 as a function of the antihydrogen impact energy.
Download figure:
Standard image High-resolution imageFigure 12. Comparison between the different Ps states for reaction (4) when 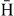 is in the ground state, in the case of the uncorrelated Chandrasekhar wave function.
is in the ground state, in the case of the uncorrelated Chandrasekhar wave function.
Download figure:
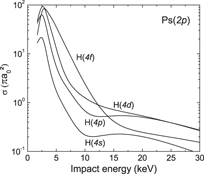
Standard image High-resolution imageFigure 13. 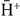 production cross sections from Ps(2p) and the different nh = 4 states of antihydrogen.
production cross sections from Ps(2p) and the different nh = 4 states of antihydrogen.
Download figure:
Standard image High-resolution imageTable 2. Thresholds (keV) for reaction (4) when  is in its ground state, given for each H− (
is in its ground state, given for each H− ( ) wave function used in this work.
) wave function used in this work.
| np | UC | CC | LS | exact |
|---|---|---|---|---|
| 1 | 5.887 | 5.590 | 5.562 | 5.545 |
| 2 | 1.205 | 0.908 | 0.880 | 0.863 |
| 3 | 0.346 | 48.6×10−3 | 20.6×10−3 | 3.67×10−3 |
The cross sections presented in figure 13 are representative of the behaviour for nh ⩾ 3 and lp > 0. The 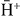 ions are preferentially produced from s-state and p-state antihydrogen atoms in close competition and then, to a lower extent, from d-states. For s-state antihydrogen atoms, the cross sections always exhibit the same structure with a maximum in the region between 10 and 15 keV. In the case of s-state Ps (lp = 0), not presented here,
ions are preferentially produced from s-state and p-state antihydrogen atoms in close competition and then, to a lower extent, from d-states. For s-state antihydrogen atoms, the cross sections always exhibit the same structure with a maximum in the region between 10 and 15 keV. In the case of s-state Ps (lp = 0), not presented here, 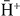 production will be favoured for lh = 0, but when nh = 4, it is now the p-state antihydrogen channel which dominates the one with s-state antihydrogen. For any state of Ps, when
production will be favoured for lh = 0, but when nh = 4, it is now the p-state antihydrogen channel which dominates the one with s-state antihydrogen. For any state of Ps, when  is in a state nh = 2 in the entrance channel, it is
is in a state nh = 2 in the entrance channel, it is  (2s) that leads preferentially to
(2s) that leads preferentially to 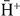 .
.
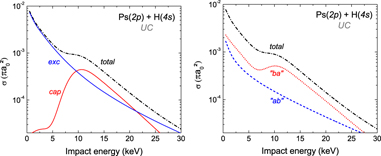
Using equation (39) given for the UC wave function, it is possible to investigate the respective contributions of the capture and the excitation terms to the total cross section by taking either the tijexc or tijcap terms equal to zero. This is shown in figure 14(a) in the case of Ps(2p) and 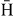 (4s). The maximum observed in the cross section is explained by the preponderance on the capture process at these energies. The behaviour of the capture cross section is typical and the energy value at the maximum (11 keV) corresponds, as expected, to a projectile velocity twice larger than the velocity of the positron in the np = 2 level of the Ps atom. The excitation is largely dominant below 5 keV. The cross terms, not presented here, are completely negligible above 10 keV. Similarly, the contributions of the processes 'ab' and 'ba' can be investigated by taking respectively tba or tab equal to zero. The results are presented in figure 14(b) and show that the major contribution to the total cross section of
(4s). The maximum observed in the cross section is explained by the preponderance on the capture process at these energies. The behaviour of the capture cross section is typical and the energy value at the maximum (11 keV) corresponds, as expected, to a projectile velocity twice larger than the velocity of the positron in the np = 2 level of the Ps atom. The excitation is largely dominant below 5 keV. The cross terms, not presented here, are completely negligible above 10 keV. Similarly, the contributions of the processes 'ab' and 'ba' can be investigated by taking respectively tba or tab equal to zero. The results are presented in figure 14(b) and show that the major contribution to the total cross section of 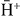 is the 'ba' process, which corresponds to the de-excitation of the positron initially in the antihydrogen atom towards the lower level a of
is the 'ba' process, which corresponds to the de-excitation of the positron initially in the antihydrogen atom towards the lower level a of 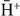 while, simultaneously, the positron in the Ps is captured in the outer level b of
while, simultaneously, the positron in the Ps is captured in the outer level b of 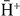 .
.
Figure 14. Contributions of the different processes involved in the formation of 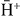 from Ps(2p) and
from Ps(2p) and  (4s). (a) Capture and excitation. (b) 'ab' and 'ba'.
(4s). (a) Capture and excitation. (b) 'ab' and 'ba'.
Download figure:
Standard image High-resolution imageCorrelated Chandrasekhar and Le Sech wave functions.
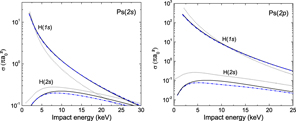
From the previous results with the uncorrelated Chandrasekhar wave function, cases of interest for GBAR have been selected to be investigated with the correlated Chandrasekhar wave function and the LS wave function. Since the formation of  ions from excited states of antihydrogen atoms is negligible, only
ions from excited states of antihydrogen atoms is negligible, only  (1s) and (2s) have been considered. Other cases can of course be calculated using the formulas given in section 2.2 and in appendix B but at the cost of a long computational time. The results are presented in figures 15–17, where they are also compared to the ones obtained with the uncorrelated Chandrasekhar wave function. In the case of the LS wave function, figure 18 compares, for each state of Ps investigated, the cross sections of
(1s) and (2s) have been considered. Other cases can of course be calculated using the formulas given in section 2.2 and in appendix B but at the cost of a long computational time. The results are presented in figures 15–17, where they are also compared to the ones obtained with the uncorrelated Chandrasekhar wave function. In the case of the LS wave function, figure 18 compares, for each state of Ps investigated, the cross sections of 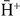 production when
production when 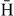 is in its ground state in the entrance channel.
is in its ground state in the entrance channel.
Figure 15.  production cross sections from ground state Ps (np = 1). Comparison between the three H− wave functions investigated: (grey) dotted lines for UC, (blue) dash-dot lines for CC and (black) solid lines for LS. The upper lines correspond to ground state antihydrogen in the entrance channel and the lines below are for the (2s) state of antihydrogen.
production cross sections from ground state Ps (np = 1). Comparison between the three H− wave functions investigated: (grey) dotted lines for UC, (blue) dash-dot lines for CC and (black) solid lines for LS. The upper lines correspond to ground state antihydrogen in the entrance channel and the lines below are for the (2s) state of antihydrogen.
Download figure:
Standard image High-resolution imageFigure 16. Same as for figure 15 but for np = 2.
Download figure:
Standard image High-resolution imageFigure 17. Same as for figure 15 but for np = 3.
Download figure:
Standard image High-resolution imageFigure 18. Comparison between the different Ps states for reaction (4) when 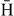 is in the ground state; the LS wave function has been used for H−.
is in the ground state; the LS wave function has been used for H−.
Download figure:
Standard image High-resolution imageThe first observation is that the angular correlations taken into account in the CC and LS wave functions have an important effect on the total cross sections in all the energy ranges investigated and thus cannot be overlooked as a small correction. However, there is little difference between the CC and the LS wave functions: for  (1s) in the entrance channel, the CC and LS wave functions give the same results within 1% below 10 keV. The most notable difference is observed for
(1s) in the entrance channel, the CC and LS wave functions give the same results within 1% below 10 keV. The most notable difference is observed for  (2s) above, roughly, 5 keV; below, the cross sections obtained with the CC and the LS wave functions converge towards the threshold. This means that the collisional model is not sensitive to the level of description of these angular correlations at low energy, close to the reaction thresholds. The observed effect of the angular correlations is, when
(2s) above, roughly, 5 keV; below, the cross sections obtained with the CC and the LS wave functions converge towards the threshold. This means that the collisional model is not sensitive to the level of description of these angular correlations at low energy, close to the reaction thresholds. The observed effect of the angular correlations is, when 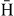 is in its ground state, to increase the cross section for ground state Ps by almost a factor of 2, to slightly increase the cross section above 3 keV for Ps(2s) and (3s) (and slightly decrease them below 3 keV), to decrease it for Ps(2p) and (3p) below, roughly, 10 keV and finally to largely decrease that cross section for Ps(3d), losing up to one order of magnitude close to the threshold. For
is in its ground state, to increase the cross section for ground state Ps by almost a factor of 2, to slightly increase the cross section above 3 keV for Ps(2s) and (3s) (and slightly decrease them below 3 keV), to decrease it for Ps(2p) and (3p) below, roughly, 10 keV and finally to largely decrease that cross section for Ps(3d), losing up to one order of magnitude close to the threshold. For  (2s) in the entrance channel, the use of the correlated wave functions leads to a decrease of the total cross sections compared to the UC results. The predominance of the
(2s) in the entrance channel, the use of the correlated wave functions leads to a decrease of the total cross sections compared to the UC results. The predominance of the 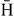 (1s) channel below 20 keV is confirmed. The expected nearly resonant behaviour for np = 3 is indeed observed, but, in the prospect of the GBAR experiment, does not lead to a very sharp increase of the
(1s) channel below 20 keV is confirmed. The expected nearly resonant behaviour for np = 3 is indeed observed, but, in the prospect of the GBAR experiment, does not lead to a very sharp increase of the  production, unless using Ps(3p) or (3d) well below 2 keV antiproton energy. However, as can be remarked in figure 18,
production, unless using Ps(3p) or (3d) well below 2 keV antiproton energy. However, as can be remarked in figure 18, 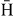 (1s) with the (3p) or, above all, the (2p) states of Ps dominate all the other processes below 6 keV. Above 10 keV, Ps(1s) is the dominant channel.
(1s) with the (3p) or, above all, the (2p) states of Ps dominate all the other processes below 6 keV. Above 10 keV, Ps(1s) is the dominant channel.
3.2.2. Comparison with available theoretical results
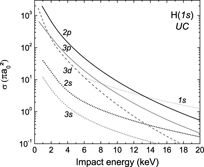
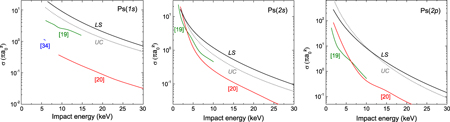
Since no experimental results are yet available for the four-body reaction, only a comparison with other theoretical models can be undertaken. The coupled pseudo-states computations of McAlinden et al, using an approached wave function for H−, and the CMEA calculations of Roy and Sinha, who chose the uncorrelated Chandrasekhar wave function, are thus compared to our four-body CDW-FS results with both uncorrelated Chandrasekhar and LS wave functions. So far, others authors kept the hydrogen atom in its ground state. The CC calculation at the threshold for the Ps(1s) + H(1s) channel performed by Blackwood et al [34] is also included. Figure 19 details the cases of Ps(1s), Ps(2s) and Ps(2p).
Figure 19.  production cross sections from ground state antihydrogen computed with different models. Our CDW-FS calculations are represented by the (black) solid line labelled LS for the LS wave function and the (grey) dotted line with label UC for the uncorrelated Chandrasekhar wave function. The (red) line labelled [20] is for the CMEA results of Roy and Sinha [20] and the pseudo-state approach results of McAlinden et al [19] correspond to the (green) line labelled [19]; the (blue) line with label [34] for Ps(1s) is the calculation at the threshold done by Blackwood et al [34].
production cross sections from ground state antihydrogen computed with different models. Our CDW-FS calculations are represented by the (black) solid line labelled LS for the LS wave function and the (grey) dotted line with label UC for the uncorrelated Chandrasekhar wave function. The (red) line labelled [20] is for the CMEA results of Roy and Sinha [20] and the pseudo-state approach results of McAlinden et al [19] correspond to the (green) line labelled [19]; the (blue) line with label [34] for Ps(1s) is the calculation at the threshold done by Blackwood et al [34].
Download figure:
Standard image High-resolution imageIn most of the cases, although the general behaviour of the cross sections is similar, the CDW-FS results are in disagreement with the other theories' calculations, giving a much higher cross section. The notable exception is for Ps(2s) below 5 keV, where all the models seem to agree towards the threshold. Otherwise, the discrepancy can be higher than one order of magnitude. It could be expected, since CDW-FS, like the CMEA model used by Roy and Sinha, is not a low energy theory and is subdued to the post/prior discrepancy (which is emphasized towards the low energy region). In the medium energy region above 20 keV, both CDW-FS and CMEA should be valid but still disagree. The main difference between the two models is the treatment of the asymptotic states, which is exact in the case of CDW-FS and could be a reasonable explanation. However, the latter argument cannot be used when comparing to the CC calculation, which is intended to be accurate in the low energy region. Nonetheless, the model developed by McAlinden et al is itself not free from approximations: in particular, the wave function they used for H− (a split shell function involving one electron in the H(1s) state and the other in a linear combination of s-orbitals) gives a binding energy of −0.513, similar to the uncorrelated Chandrasekhar wave function. These observations stress that our results should be handled with particular care when used to predict experimental behaviours, either for GBAR or for other future projects.
3.3. Consequences for GBAR
As has been already underlined, no quantitative conclusions should be drawn. Concerning the energy of the antiprotons, two regions have been identified: below 2 keV and between 6 and 7 keV. In the 6 keV region, the use of Ps(1s) only (and this is the state in which Ps is produced) appears to be sufficient to produce sequentially  and
and 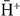 ; the
; the  production can be enhanced using a fraction of Ps excited in the (3d) state, whereas the second reaction can be slightly enhanced by a fraction of Ps(2p). Below 2 keV, Ps(1s) is almost of no use (below thresholds or too low cross sections), with the exception of the case when
production can be enhanced using a fraction of Ps excited in the (3d) state, whereas the second reaction can be slightly enhanced by a fraction of Ps(2p). Below 2 keV, Ps(1s) is almost of no use (below thresholds or too low cross sections), with the exception of the case when  is in the (2s) state. Then, the best solution is to excite as much as possible the Ps to the (2p) state; the alternative is Ps(3p) or (3d) around 1 keV. Ps(3d) has the advantage to be a longer-lived state compared to Ps(2p) and (3p). To illustrate this discussion, figure 20 presents a rough approximation of the cross sections for the two reactions combined (using the cross sections obtained with the LS wave function). They have been calculated using equation (47). It is assumed that the proportions of Ps in the ground state (1 − f) and in the (np, lp) excited state (f) are fixed during the whole process and that 20% (ε) of the excited
is in the (2s) state. Then, the best solution is to excite as much as possible the Ps to the (2p) state; the alternative is Ps(3p) or (3d) around 1 keV. Ps(3d) has the advantage to be a longer-lived state compared to Ps(2p) and (3p). To illustrate this discussion, figure 20 presents a rough approximation of the cross sections for the two reactions combined (using the cross sections obtained with the LS wave function). They have been calculated using equation (47). It is assumed that the proportions of Ps in the ground state (1 − f) and in the (np, lp) excited state (f) are fixed during the whole process and that 20% (ε) of the excited  produced in the first reaction had time to de-excite to the ground state before undergoing the second reaction. These cross sections are given for 100% Ps(1s) (f = 0), 20% Ps(2p) (f = 0.2; np = 2, lp = 1) and 40% Ps(3d) (f = 0.4; np = 3, lp = 2), values that are thought to be experimentally feasible:
produced in the first reaction had time to de-excite to the ground state before undergoing the second reaction. These cross sections are given for 100% Ps(1s) (f = 0), 20% Ps(2p) (f = 0.2; np = 2, lp = 1) and 40% Ps(3d) (f = 0.4; np = 3, lp = 2), values that are thought to be experimentally feasible:
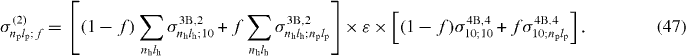
Figure 20. Comparison between the global (i.e. both reactions combined)  production cross sections for different simple solutions of Ps excitation.
production cross sections for different simple solutions of Ps excitation.
Download figure:
Standard image High-resolution imageAs suggested above, the interaction region of the GBAR experiment will also have to take into account the constraints on the  states. Indeed, the first reaction will mainly, if not exclusively produce excited states of antihydrogen, while the second reaction requires ground-state antihydrogen. Some time must be given to the antihydrogen atoms for them to de-excite towards the ground state or the (2s) state, which will give a small contribution, and still be able to interact with (excited) Ps atoms. This implies that one needs to have a long but still dense enough Ps cloud (or, ideally, two separated Ps clouds, which can be excited into different states at different times).
states. Indeed, the first reaction will mainly, if not exclusively produce excited states of antihydrogen, while the second reaction requires ground-state antihydrogen. Some time must be given to the antihydrogen atoms for them to de-excite towards the ground state or the (2s) state, which will give a small contribution, and still be able to interact with (excited) Ps atoms. This implies that one needs to have a long but still dense enough Ps cloud (or, ideally, two separated Ps clouds, which can be excited into different states at different times).
A simulation taking into account these different options is currently being developed.
4. Conclusions
In the framework of the GBAR experiment, three-body and four-body CDW-FS models have been adapted to compute the cross sections of positronium (Ps) formation by charge exchange reactions between a positron and, firstly, a hydrogen atom (equation (1)) and secondly, a negatively charged hydrogen ion (equation (3)). From the results, total cross sections for antihydrogen and antihydrogen ion production using Ps have been deduced (equations (2) and (4)). The different contributions of the lower excited states of both 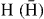 and Ps have been systematically investigated (up to nh = 4–5 in the case of the (anti)hydrogen atom and up to np = 3 for the Ps). Three approximated wave functions have been used to describe H− (
and Ps have been systematically investigated (up to nh = 4–5 in the case of the (anti)hydrogen atom and up to np = 3 for the Ps). Three approximated wave functions have been used to describe H− (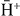 ), from the simple and useful uncorrelated Chandrasekhar wave function, to the more refined, with respect to the angular correlations, correlated Chandrasekhar and LS wave functions. To our knowledge, this is the largest study available concerning reactions (3) and (4).
), from the simple and useful uncorrelated Chandrasekhar wave function, to the more refined, with respect to the angular correlations, correlated Chandrasekhar and LS wave functions. To our knowledge, this is the largest study available concerning reactions (3) and (4).
Results on the three-body reaction draw the same conclusions as previous studies (production of excited (anti)hydrogen; gain with Ps excitation) and compares quite well to the experiment of Merrison et al in the range 10–15 keV. Three-body CDW-FS has thus been proven a good tool to estimate the cross sections of antihydrogen formation from antiprotons and Ps. In the absence of experimental data and due to the few works available on the four-body reaction, it is more difficult to put this model to the test. Despite the discrepancy between CDS-FS and the other two theories that were used for the reaction (3), it is worth noticing that, when the comparison is available, the relative behaviour of the cross sections is the same. This represents the information that can be extracted from these results, which can be used to guide experimental choices. It has been thus demonstrated that ground state antihydrogen is required in the entrance channel to have high cross sections, that Ps(2p) is the most interesting Ps state to enhance the  production and that antiproton energy close to the reaction threshold should be aimed at. The expected nearly-resonant behaviour for Ps in a state np = 3 has been observed, but would require ultra-low energy antiprotons (a few hundred eV) to be competitive with Ps(2p). Finally, it has also been shown that the
production and that antiproton energy close to the reaction threshold should be aimed at. The expected nearly-resonant behaviour for Ps in a state np = 3 has been observed, but would require ultra-low energy antiprotons (a few hundred eV) to be competitive with Ps(2p). Finally, it has also been shown that the  formation from
formation from  (2s) and Ps(1s) is a non-negligible channel.
(2s) and Ps(1s) is a non-negligible channel.
Acknowledgments
The authors thank their collaborators from GBAR and acknowledge C Le Sech for useful discussion. This work was partially funded by the Agence Nationale de la Recherche (contract no. ANR-10-BLAN-0420).
Appendix A.: Complements on three-body continuum distorted wave-final state (CDW-FS)
A.1. lp = 0 and lh ≠ 0
In this particular case, the transition matrix element reads
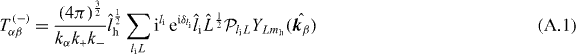
with
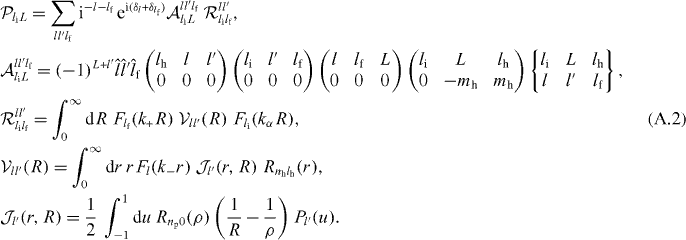
The differential and total cross sections are given by

and

with
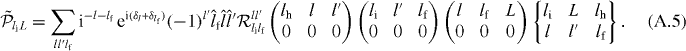
A.2. lh = 0 and lp ≠ 0
We have
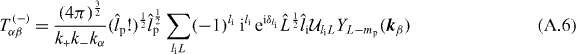
with
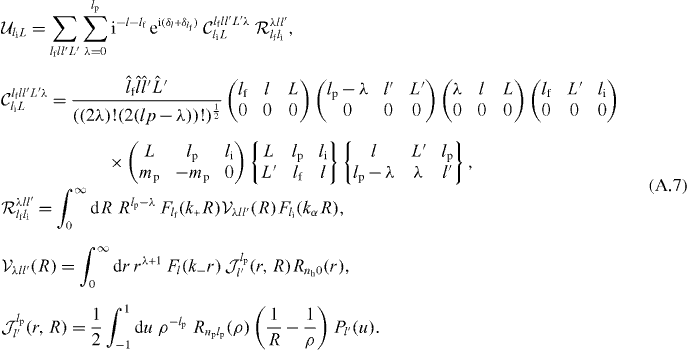
This gives a total cross section summed over the degenerated states of the Ps atom
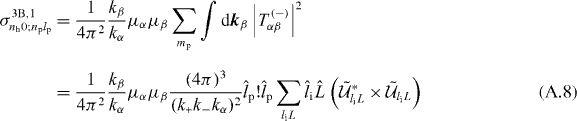
with
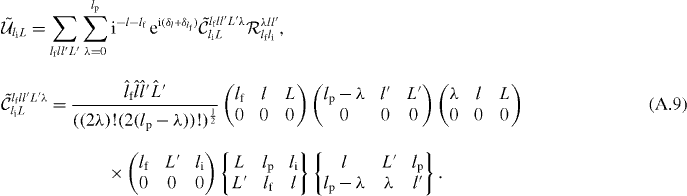
A.3. lp = lh = 0
In this case we have
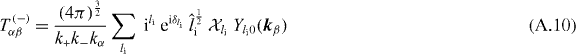
with
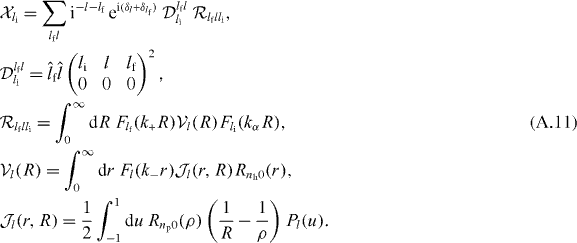
The total cross section is then given by
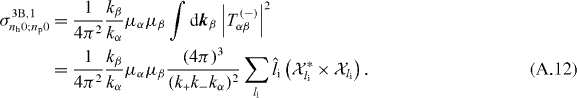
Appendix B.: Complements on four-body CDW-FS
B.1. lh = 0 and lp ≠ 0
This case is especially useful when only the production of H(1s) is considered (or, equivalently, only the production of  from
from  in its ground state). The different terms in the total cross section now write (for any value of nh)
in its ground state). The different terms in the total cross section now write (for any value of nh)
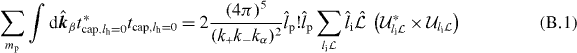
with
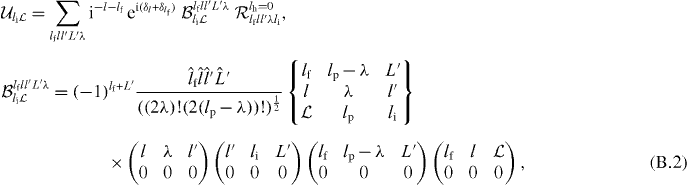
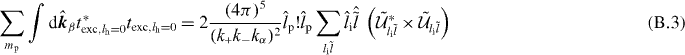
with
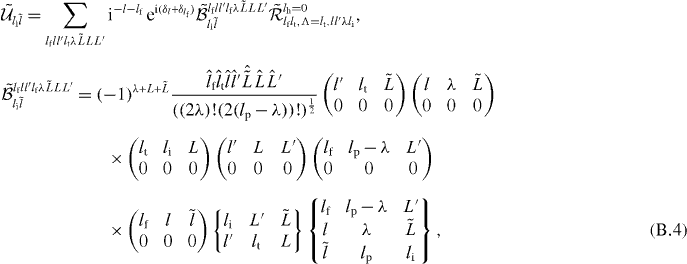
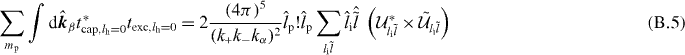
and thus
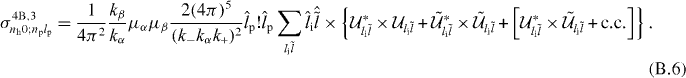
B.2. lp = 0 and lh ≠ 0
In the case of lp = 0, the different terms of the four-body reaction can also be simplified. The pure capture term reads
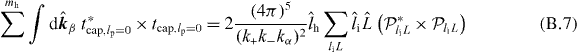
with
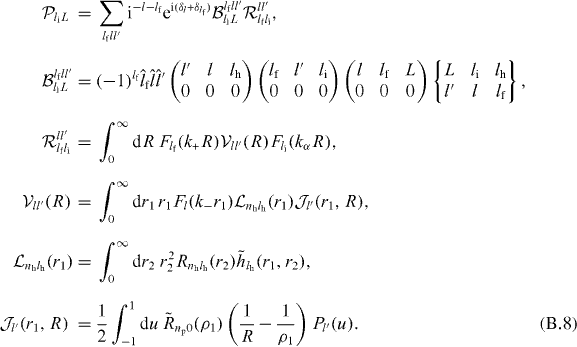
The pure excitation term is given by
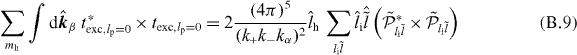
with
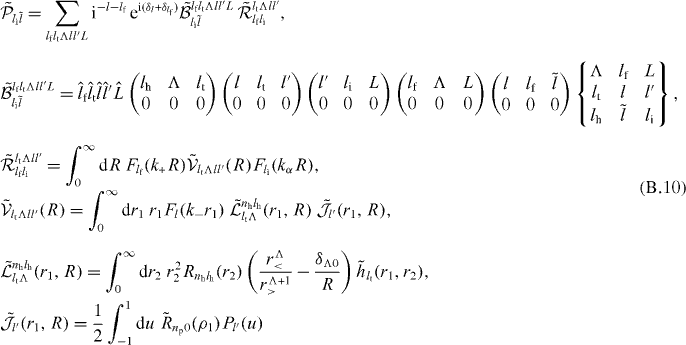
and the cross terms are of the form
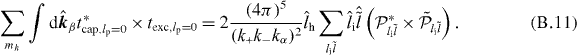
The cross section is thus
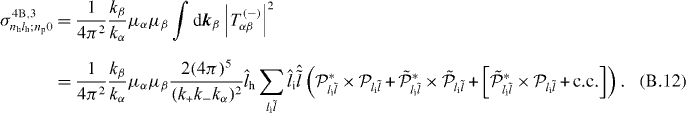
B.3. lp = lh = 0
When both lp and lh are equal to zero, further simplifications can be found for the different terms of the four-body reaction. The pure capture term reads
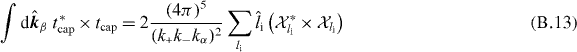
with
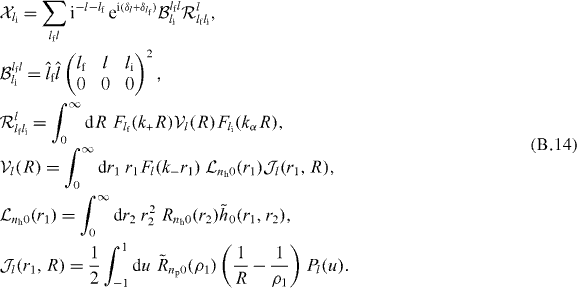
The pure excitation term is given by
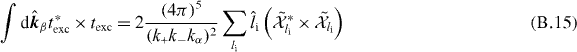
with
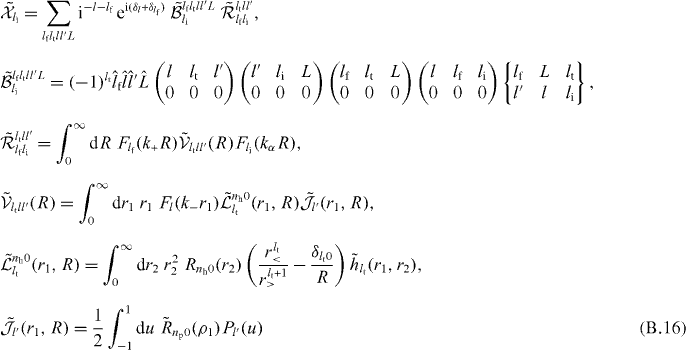
and the cross terms are of the form
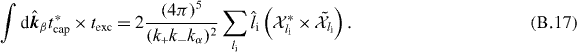
This leads to the cross section