Abstract
We discuss the connection between strong-field ionization, saturation of the Kerr response and the formation of the Kramers–Henneberger (KH) atom and long-living excitations in intense infrared (IR) external fields. We present a generalized model for the intensity-dependent response of atoms in strong IR laser fields, describing deviations in the nonlinear response at the frequency of the driving field from the standard model. We show that shaping the driving laser pulse allows one to reveal signatures of the excited KH states in the Kerr response of an individual atom.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The physical reality of bound states of a nearly free electron has been recently demonstrated experimentally by Eichmann et al [1]. They have observed acceleration of neutral helium atoms at a rate of 1014 times the Earth gravity g, expelled from the focus of the 800 nm, 100 fs laser pulse with intensities approaching 1016 W cm−2. The high kinetic energies of the neutrals expelled from the laser focus prove that the atoms have remained neutral throughout the whole duration of the laser pulse. The ponderomotive force responsible for the acceleration could have only come from laser-induced oscillations of the nearly free electron, still managing to pull the heavy atomic core after itself during the laser pulse.
Theoretically, the existence and relevance of such 'almost-free' states for weakly bound systems such as the potassium atom and modest IR laser intensities I ∼ 1013 W cm−2 has recently been verified in [2]. Detailed ab initio theoretical study of the emergence of these states for well-bound systems with an ionization potential Ip around 10–14 eV in the relevant frequency regime (near-infrared (IR) light) has recently been done by Popov et al [3] and Kapoor and Bauer [4].
The 'bound states of a free electron' are associated with the formation of the Kramers–Henneberger (KH) atom: the stable system of 'atom + strong laser field' [3, 5, 6]. In such states the electron motion is a combination of nearly free oscillations and a slow drift around the atomic core. The potential of the KH atom is described in the frame of reference attached to the moving electron. It is defined as the laser-period averaged part of the 'laser-dressed' oscillating ionic potential. For high frequencies in the extreme ultraviolet range it appears to be natural that the harmonics of the oscillating ionic potential become negligible and thus the stable KH states physically relevant. However, ab initio theoretical analysis [2, 3, 7, 8] has confirmed the analytical prediction [7, 9] and Floquet analysis [10, 11] that for laser field strengths F ≫ FBS the KH states are also formed even for relatively small laser frequencies ℏω ≪ Ip. Here FBS is the so-called barrier suppression field at which the potential barrier, created by the Coulomb field together with the laser field, is suppressed below the binding energy of the field-free state.
It is generally assumed that for the KH picture to hold, all atomic states must enter the KH regime. Here, we analyse the situation where all excited atomic states are in the regime of F ≫ FBS while the ground state is still well bound. Importantly, this condition is fulfilled for all excited states of noble gas atoms already at laser intensities I ∼ 1013 W cm−2.
We show that even when the ground state of the atom is well bound, the excited states entering the KH regime show clear signatures in the system's response, including the Kerr effect: the (linear) growth of the refractive index at the driving field frequency with the field intensity. We show that while ionization does indeed play a very important role in the reversal of the linear Kerr effect with increasing intensity in standard experimental conditions (see e.g. [12–18] for experimental evidence), the 'bound states of a free electron' are equally, if not even more, important for the onset of this behaviour, corroborating recent ab initio results of Béjot et al [19]. Thus, our results show that the suggestions made in [19–25] are not entirely without merit.
For standard laser pulses, separating the contribution of ionization from other possible mechanisms leading to the saturation of the Kerr effect is very challenging. In particular, the importance of Rydberg states in the Kerr response has been extensively discussed in ab initio simulations by Volkova et al [26, 27], concluding that while such states are important, the numerical evidence does not prompt the revision of the existing filamentation paradigm. Similar conclusion is reached by Köhler et al [28], using the method for analysis proposed by Nurhuda et al [29]. This method separates the induced dipole into bound–bound, bound–continuum and continuum–continuum contributions by projecting the exact time-dependent wavefunction on the field-free states and associating the first two with (instantaneous) polarization of the ground state while the third is associated with ionization. However, using the field-free states in the presence of an intense laser field is not adequate, especially for identifying the role of the KH states which, while bound, are dominated by the free electron motion. Interestingly, Nurhuda et al have reached a somewhat different conclusion using the same approach, especially regarding the ground state polarization via continuum states (compare figure 2(d) of [29] versus figure 2(c) of [28]). The complexity in the analysis of the contribution of the nearly free states is confirmed by results of Kano et al [30], who find that bound states alone can provide saturation of the Kerr response.
Here we show that shaped laser pulses offer additional opportunities for addressing this difficult question: they emphasize the role of the restructured spectrum of the dressed atom compared to the field-free system and allow us to identify the origin of resonance structures appearing in the Kerr response (also found but not discussed by e.g. Köhler et al [28] and Kano et al [30]). We show that these resonances are associated with the KH states.
The 'bound states of a free electron' are relevant for the Kerr response in two complementary ways. Firstly, their polarizability is largely the same as that of the genuinely free electrons. Thus, once these states get populated, their response to the propagating light pulse will be very similar to that of a plasma. Trapping of classical trajectories launched at the exit from the tunnelling barrier, simulating ionization, has been documented and discussed in [31]. It has now been analysed in detail, both experimentally and theoretically in [32–36], and is called 'frustrated tunnelling'. The bound nature of these trapped states can show up after the end of the laser pulse, possibly in the anisotropic response of the excited medium to the delayed probe pulse as recently shown in [37] using full ab initio treatment of the problem and solving coupled Schrödinger and Maxwell equations.
Secondly, the laser-induced restructuring of the excited states should also have implications for the instantaneous response of the ground state, i.e. non-resonant polarization associated with virtual (rather than real) excitations. Consider the standard perturbative expression describing the linear response of a ground-state atom to a weak laser field, linearly polarized along the z-axis:

Here ω is the light frequency, Eg denotes the energy of the initial ground state |g〉, En is the energy of the intermediate virtual state |n〉 and 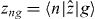 is the corresponding transition matrix element. Assuming for a second that a similar expression applies to the dressed atom, except that the energies En(F) and the matrix elements zng(F) are those of the dressed states, the restructuring of the spectrum should alter the susceptibility. One obvious effect is the growth of the resonance denominators due to the ponderomotive shift Up of the excited states, En → En(F) ∼ En + Up, where Up = F2/4ω2. Clearly, if the substitutions En → En(F) and zng → zng(F) were legitimate under certain conditions, one would expect the atomic susceptibility to decrease with increasing intensity.
is the corresponding transition matrix element. Assuming for a second that a similar expression applies to the dressed atom, except that the energies En(F) and the matrix elements zng(F) are those of the dressed states, the restructuring of the spectrum should alter the susceptibility. One obvious effect is the growth of the resonance denominators due to the ponderomotive shift Up of the excited states, En → En(F) ∼ En + Up, where Up = F2/4ω2. Clearly, if the substitutions En → En(F) and zng → zng(F) were legitimate under certain conditions, one would expect the atomic susceptibility to decrease with increasing intensity.
Below we discuss the generalization of (1) and show that such substitutions are indeed justified in a field with frequency ω ≪ En − Eg. For noble gases with a large gap between the ground and the excited states this corresponds to IR frequencies. Then we discuss numerical simulations for the hydrogen atom, both in one dimension (1D) and in three dimensions (3D), and show how the field-dressed states influence the response of a single atom.
2. Preliminary analytical analysis
Due to the large gap between the ground and the excited states in noble gas atoms, or in air molecules, it is useful to break the full Hilbert space of the field-free system into two subspaces, one containing the lone ground state |g〉, another all other states |n〉, both excited bound and continuum. Writing the wavefunction as

where ag(t) is the ground state amplitude and Ψ(2)(t) belongs to the second subspace, we find the exact formal expression for Ψ(2)(t) [38]:
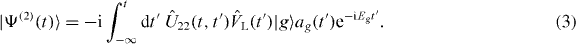
Here 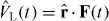 describes the interaction with the linearly polarized laser field F(t) = F(t)cos(ωt) ez ( ez denotes the unit vector along the z-axis), which couples the two subspaces.
describes the interaction with the linearly polarized laser field F(t) = F(t)cos(ωt) ez ( ez denotes the unit vector along the z-axis), which couples the two subspaces. 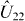 is the exact propagator in the second subspace, which includes fully the interaction with the laser field that couples the field-free states of this subspace.
is the exact propagator in the second subspace, which includes fully the interaction with the laser field that couples the field-free states of this subspace.
For time-periodic Hamiltonians, we can introduce the exact Floquet states

in the second subspace, where both the energy Ek(t) and the wavefunction ϕk(t) are periodic functions of time with period Tω = 2π/ω. These states form a complete basis set in the second subspace, and hence the decomposition of identity 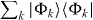 can be inserted into (3) between
can be inserted into (3) between  and
and  :
:
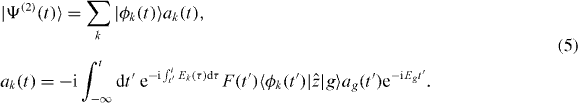
Using (2), one can see that the dipole induced by the laser field contains two components
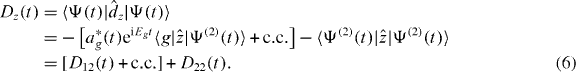
In the strong-field limit, keeping in mind that F(t') is a slow function of time compared to the t'-dependent phases, the amplitudes ak(t) are given by integrals of fast-oscillating functions, see (5). Such integrals always have two types of contributions. The first main contribution comes from the saddle points inside the integration contour and signify real transitions from the ground state into the excited and continuum states, which, in turn, contribute to the induced dipole. Deviations from the usual linear Kerr effect due to real ionization and real excitation are associated with these transitions.
The second contribution to the integral in (5) comes from the end point of the integral, t' = t, and is equally standard. This contribution is derived using integration by parts and assuming that the laser field Fcos(ωt) is slow compared to the oscillations of the exponents. Writing out explicitly the ground-state Stark shift in the low-frequency field as
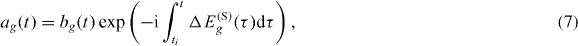
we find for the second contribution
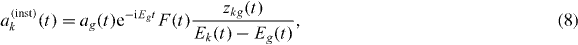
where Eg(t) = Eg + ΔE(S)g(t) and  . This contribution describes virtual transitions from the ground state to the excited states, i.e. the instantaneous polarization of the ground state driven by the low-frequency field. At the intensities of interest, a(inst)k ≪ 1 since Fzkg ≪ Ek − Eg. Substituting this expression into (6) for the leading term D12(t), we obtain the contribution to the ground-state atom response from the instantaneous polarization following the driving laser field:
. This contribution describes virtual transitions from the ground state to the excited states, i.e. the instantaneous polarization of the ground state driven by the low-frequency field. At the intensities of interest, a(inst)k ≪ 1 since Fzkg ≪ Ek − Eg. Substituting this expression into (6) for the leading term D12(t), we obtain the contribution to the ground-state atom response from the instantaneous polarization following the driving laser field:
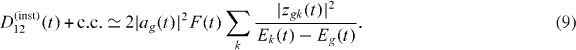
There are several obvious restrictions on the applicability of this expression. Firstly, it is only valid in the low-frequency field, when the photon energy is small compared to the energy gap between the ground and the excited states. Secondly, the virtual amplitudes ak must be small, i.e. 1 − |ag(t)|2 ≪ 1, otherwise the D22(t) term becomes equally important.
Expression (9) is remarkably similar to the lowest-order perturbation theory result, except that the field-free states and their energies are replaced by the dressed Floquet states and the associated energies Ek(t).
Knowing the structure of the states ϕk(t) and the energies Ek(t), one can analyse the field dependence of the instantaneous response. In particular, one can apply the first-order perturbation theory to the field-free states ϕk, Ek to find corrections introduced by the field. In this approximation, one immediately obtains the standard Kerr effect, i.e. α = α0 + κF2. As the application of the first-order perturbation theory to the excited states becomes insufficient, one should not be surprised to see deviations from the linear intensity dependence. From this perspective, the recent experimental results for near-IR laser fields [39] showing that this does not happen until close to the onset of ionization, are counter-intuitive. We will return to this point later in the paper, when discussing our numerical results.
Consider now non-perturbative IR fields with intensities in the range of 1013 W cm−2, and noble gases such as Ne, Ar or Kr. The ground state, with Ip ∼ 14 eV or even larger, remains strongly bound at these intensities, and its Stark shift ΔE(S)g is negative. All excited states are, however, deeply in the barrier suppression regime. The dressed states associated with them are the quasi-bound KH states [3, 5, 6]. In the so-called KH reference frame, which oscillates with the free electron r = rKH + (F/ω2)cos(ωt) ez, they are well approximated [2, 4] by stationary eigenstates ϕ(KH)k( rKH) of the laser-cycle averaged binding potential
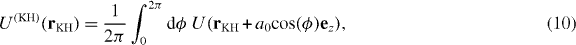
where a0 = F/ω2 is the quiver amplitude of the free electron. For a0 ≫ 1 the potential acquires the characteristic double-well structure, with the two wells separated by 2a0, becoming shallower as a0 increases. As a consequence the spectrum changes. Transforming back to the laboratory frame, the states ϕ(KH)k( rKH) (i) begin to oscillate and (ii) acquire the associated phase,
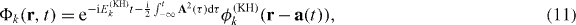
where A(t) = −(F/ω)sin (ωt) ez and a(t) = a0cos (ϕ) ez. Thus, the instantaneous contribution to the induced dipole reads
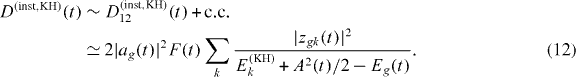
The ponderomotive term A2(t)/2 is large and positive. Consequently, the denominator grows. Simultaneously, the ϕ(KH)k become progressively more delocalized with increasing a0, leading to the reduction of the transition matrix elements. Hence, it is reasonable to expect that the instantaneous response decreases with intensity as the excited states enter the KH regime, i.e. for laser field strengths F ≫ FBS. For states with binding energies of a few eV this implies I ⩾ 1013 W cm−2.
3. Numerical simulations
To gauge the importance of light-induced restructuring of the atom for its nonlinear response, we have calculated the full nonlinear response of a 1D model hydrogenic system and the real 3D hydrogen atom by solving the time-dependant Schrödinger equation (TDSE) numerically on a grid. We have computed the induced dipole d(t) and its Fourier transform at the fundamental driving frequency dω for a broad range of peak laser field strengths F0 and frequencies ω ranging from UV to mid-IR. In all 1D and 3D simulations a reflection-free absorbing boundary [40] is used.
Numerical analysis of the importance and the relative contribution of the KH states is challenging for two conceptual reasons. Firstly, there is a well-known difficulty of unambiguously distinguishing bound versus continuum states when the laser pulse is still present. Secondly, it is also difficult to separate virtual from real excitations while the field is turned on, and such analysis is even sensitive to the gauge [19]. Moreover, given the very large negative polarizability of both continuum and KH states, even small transfer of real population to these states (at the few 10−3 level) will dominate the negative contribution to the Kerr response for IR laser frequencies.
The strategy we have adopted to deal with these challenges is as follows. For each set of laser parameters, we have performed our calculations for different sizes of the simulation volume. For small volumes, all or most of the free electrons are absorbed, suppressing their contribution (the plasma response) to dω. For very large simulation volumes, all continuum electrons are retained in the calculation until the end of the laser pulse. Thus, following the dependence (or independence) of the response on the size of the simulation volume, we can quantify the contribution of the free electrons.
Moreover, changing the size of the simulation volume also allows us to gauge the role of the KH states. Indeed, for high laser intensities their size is ∼ ± 2a0, where a0 = F/ω2 is the electron oscillation amplitude. As soon as the size of the simulation volume, including the width of the absorbing potential (33 au in our case) becomes less than ±2a0, the KH states will be effectively destroyed and their contribution to dω suppressed. This turns the system into an analogue of a short-range potential with a sole bound (ground) state left. The short-range system has been analysed by Kolesik and collaborators [41, 42], showing that in this case the linear Kerr effect persists until ionization. Our calculations shown in figure 1(c) are fully in line with their results for small box sizes.
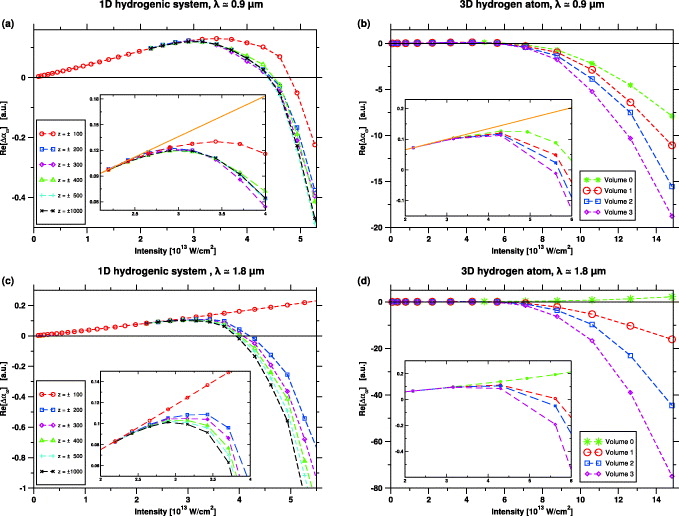
Figure 1. Dependence of the Kerr response on the size of the simulation grid for the short (4-0-4)-pulse. Plotted is the real part of the nonlinear contribution to the polarizability (with the low-field limit subtracted) as a function of intensity for (a) the 1D hydrogenic system and a central frequency of the driving pulse of ω = 0.050 au, (b) the 3D hydrogen atom and a central frequency of the driving pulse of ω = 0.050 au, (c) same as (a), but for ω = 0.025 au, (d) same as (b), but for ω = 0.025 au. 1D results are shown for different grid sizes ranging from z∈[ − 100,100] au to z∈[ − 1000,1000] au. 3D results are computed in cylindrical coordinates for the simulation volume 0 with radius ρ∈[0,100] au and z∈[ − 100,100] au, simulation volume 1 with radius ρ∈[0,100] au and z∈[ − 200,200] au, simulation volume 2 with radius ρ∈[0,100] au and z∈[ − 400,400] au, and simulation volume 3 with radius ρ∈[0,200] au and z∈[ − 800,800] au. The horizontal black solid line indicates Re[Δαω] = 0. The insets show a zoom of the intensity regions, in which the Kerr response saturates. The solid orange lines are the extrapolations of the linear response at small intensities towards higher intensities.
Download figure:
Standard image High-resolution imageImportantly, the laser pulse envelope will have significant effect on the relative role, existence and stability of the KH states. Indeed, the formation of stable 'bound states of the free electron' requires that the intensity of the laser field remains constant during many laser cycles. In the case of short bell-shaped laser pulses the positions of these states, and their lifetimes, change from cycle to cycle, making their identification much more difficult and smearing distinct features that they might produce in the nonlinear response. Moreover, the KH states suffer fast decay during the transition between the perturbative and the KH regime. Therefore our analysis was done for two different laser pulse shapes: (i) a short eight-cycle pulse with a smooth bell-shaped envelope ((4-0-4)-pulse) and (ii) a long flat-top pulse that turns on in four cycles until the peak intensity is reached, which then remains constant during the next 40 cycles until the pulse smoothly turns off in four cycles ((4-40-4)-pulse). In both cases the leading edge and the trailing edge of the two pulses are described by a sin2-envelope. The flat-top pulse is favourable for the existence, stability and efficient population of the KH states.
In figure 1 we present the intensity-dependent response of the hydrogen atom, both 1D and 3D, for two selected frequencies and the short (4-0-4)-pulse. In all calculations the applied electric field has linear polarization along the z axis. We plot the real part of the nonlinear contribution to the frequency-dependent polarizability, calculated as Δαω(F) = dω(F)/F0 − limF0 → 0dω(F)/F0, where ω is the central frequency of the driving field and F0 is the peak value of the electric field.
Panels (a) and (c) show the results for a 0.9 μm and a 1.8 μm laser pulse acting on a model 1D system with soft-core Coulomb potential 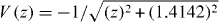 and ground state energy Eg = −0.5 au. The response is calculated by solving the TDSE for different grid sizes ranging from z∈[ − 100,100] au to z∈[ − 1000,1000] au, with a time-step of Δt = 0.125 au, and a grid step-size of Δz = 0.05 au. The orange lines in the insets of figure 1 are the extrapolations of the linear response at small intensities towards higher intensities. For λ ≃ 0.9 μm, the polarizability increases linearly until I ≃ 2.4 × 1013 W cm−2. Beyond this intensity the Kerr response first saturates and subsequently reverses its sign.
and ground state energy Eg = −0.5 au. The response is calculated by solving the TDSE for different grid sizes ranging from z∈[ − 100,100] au to z∈[ − 1000,1000] au, with a time-step of Δt = 0.125 au, and a grid step-size of Δz = 0.05 au. The orange lines in the insets of figure 1 are the extrapolations of the linear response at small intensities towards higher intensities. For λ ≃ 0.9 μm, the polarizability increases linearly until I ≃ 2.4 × 1013 W cm−2. Beyond this intensity the Kerr response first saturates and subsequently reverses its sign.
Firstly, we note that saturation starts just before the results begin to depend on the simulation volume. Thus, it is not yet dominated by the free electrons.
Secondly, there is a very peculiar dependence on the volume size beyond I = 2.9 × 1013 W cm−2. For grid sizes above ±200 au, there is no size-dependence of the response. Thus, all electrons responsible for the saturation of the Kerr response are within the ± (200 − 33) au = ± 167 au distance from the origin.
Thirdly, comparing with the results for the smallest simulation volume ±100 au, we see that about half of them are much closer, within ±(100 − 33) au = ± 67 au for the intensity range shown in the inset. They are either trapped into Rydberg states or have a positive energy below 0.5 eV (our absorbing potential absorbs virtually all electrons above this energy).
The physics becomes much clearer for the mid-IR wavelength of 1.8 μm. Here we can see a clear dependence of the saturation effect on the grid size.
First, let us consider all grids larger than ±200 au. The saturation occurs universally at the same intensity and starts just before the onset of the grid-size dependence. For higher intensities, the clear dependence on the grid size demonstrates the contribution of free electrons.
Now, we bring the reader's attention to the dramatic change for the ±(100 − 33) au = ± 67 au grid: the linear dependence of the Kerr response is perfectly restored. To interpret this result, we note that the size of the KH states is 2a0 ≈ 90 au at the intensity I = 2.7 × 1013 W cm−2. Thus, in this regime the saturation and the reversal of the Kerr effect are dominated by the response of the KH states, which are not supported by the ±100 au grid.
Figures 1(b) and (d) show similar calculations for the 3D hydrogen atom. A spatial resolution of 0.2 au and a time-step of Δt = 0.005 au is used. For λ ≃ 0.9 μm, the Kerr response is saturated around I = 4.3 × 1013 W cm−2, however, the results do not depend on the size of the simulation volume. Virtually all states that contribute to the atom's response are confined within the smallest simulation volume (ρmax = 100 au, −100 < z < 100 au).
At I = 5.6 × 1013 W cm−2 the Kerr effect is reversed and the polarizability shows a dependence on the simulation volume meaning that the free electrons contribute. However, the overall decrease relative to the linear Kerr response is noticeably larger than the variation between the bigger simulation volumes, suggesting that the physics is similar to that in the 1D case: substantial contribution of the Rydberg states.
Also for λ ≃ 1.8 μm, the 3D simulations are in line with the 1D results. For the smallest simulation volume, the KH states are absorbed by the absorbing boundary, preventing the saturation and reversal of the Kerr response at higher intensities. For the larger simulation volumes, the Kerr effect is saturated at the same intensity I = 4.3 × 1013 W cm−2 as for λ ≃ 0.9 μm. However, the grid size dependence is more pronounced: the deviation from the linear response is twice as big for the largest simulation volume compared to that of volume 1 and that of volume 2, for which the response is virtually the same. The grid size dependence demonstrates bi-modal distribution of electrons: at this intensity half of the contributing electrons are located within the volume 1 with |z| < 200 au while the rest are outside volume 2, i.e. at |z| > 400 au.
How does the Kerr response change for the longer (4-40-4)-pulse? Good convergence of the results in 3D requires very large simulation volumes, with |zmax| = 1600 au and ρmax = 400 au, making reliable computations for long laser pulses prohibitively expensive. Figure 2 shows our results for the 1D hydrogenic system and several values of the laser wavelength. A spatial resolution of 0.1 au and a time-step of Δt = 0.125 au is used.
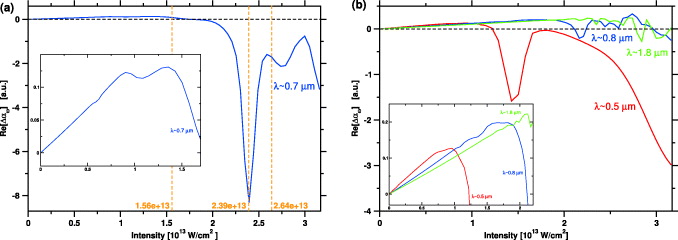
Figure 2. Kerr response for the long (4-40-4)-pulse. Plotted is the real part of the nonlinear contribution to the polarizability (with the low-field limit subtracted) as a function of intensity for the 1D hydrogenic system and a central frequency of the driving pulse of (a) ω = 0.0675 au, (b) ω = 0.090 au (red), ω = 0.055 au (blue) and ω = 0.025 au (green). The insets show the low-intensity regions. The horizontal black dashed line indicates Re[Δαω] = 0. The vertical orange dashed lines in (a) indicate the intensity values for which the Floquet spectra shown in figure 3(c) are computed.
Download figure:
Standard image High-resolution imageFirst of all, we note that there are clear resonances in the response at the driving frequency, especially well pronounced for shorter laser wavelengths (λ ≃ 0.5 μm and λ ≃ 0.7 μm), where they are accompanied by a dramatic drop in the Kerr response due to population transfer into excited states with large negative polarizability.
Complementary calculations monitoring ionization (not depicted here) show that these resonances are accompanied by very little ionization and that the population stays bound after the end of the laser pulse. For λ ≃ 0.8 μm, the drop in the Kerr response due to a multiphoton resonance just precedes the onset of ionization. For longer wavelengths, the onset of ionization is essentially frequency-independent, with ionization probability reaching 0.5% around I = 3.2 × 1013 W cm−2. Importantly, for the longest wavelengths, resonances persist in the tunnelling regime of the Keldysh parameter γ2 = Ip/2Up = 2Ipω2/F2 < 1 and even well in the barrier suppression regime for all excited states.
What is the origin of these resonance structures? We stress that we are looking at the response at the fundamental frequency, ω, with the ground state well separated from the rest of the spectrum. Let us focus on the prominent resonance for λ ≃ 0.7 μm, centred at the intensity I = 2.39 × 1013 W cm−2. Figure 3(a) shows the intensity-dependent energy structure of the 1D hydrogenic system. The dashed lines represent the energies of its excited states shifted by Up. The Stark shift of the ground state of only ∼ − 0.08 eV at 3 × 1013 W cm−2 is negligible.
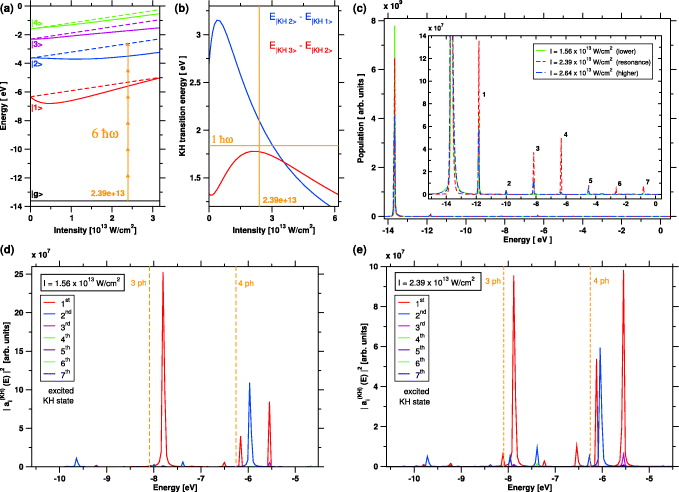
Figure 3. Analysis of the origin of the resonance in the response for λ ≃ 0.7 μm at I = 2.39 × 1013 W cm−2, see figure 2(a). (a) Energy structure of the 1D hydrogenic system versus intensity. Dashed lines represent the energies of its excited states shifted by Up. The solid black line represents the ground state energy, which is assumed to remain constant for all intensities. The six-photon Freeman resonance between the ground state and the second excited state at I = 2.39 × 1013 W cm−2 is indicated. Non-black solid lines represent the energies of the excited states of the associated KH atom. (b) Transition energies between the third and the second excited KH state, E|KH3〉 − E|KH2〉, and between the second and the first excited KH state, E|KH2〉 − E|KH1〉, versus intensity. The horizontal orange line denotes the one-photon energy of the λ ≃ 0.7 μm laser field. The vertical orange line indicates I = 2.39 × 1013 W cm−2. (c) Quasi-energy spectra for I = 1.56 × 1013 W cm−2 (green solid line), I = 2.39 × 1013 W cm−2 (red dashed line) and I = 2.64 × 1013 W cm−2 (blue dashed line). The energies corresponding to a n-photon (n = 1,...,7) transition starting from the unperturbed ground state are indicated. Panels (d) and (e) show the partial quasi-energy spectra calculated for a subsystem consisting of the seven lowest excited KH states for I = 1.56 × 1013 W cm−2 and I = 2.39 × 1013 W cm−2, respectively. The orange dashed lines indicate the energies corresponding to the three-photon and the four-photon transition starting from the unperturbed ground state.
Download figure:
Standard image High-resolution imageFirst thing to note is the six-photon Freeman resonance [43] between the ground state |g〉 and the second excited state |2〉 at I = 2.39 × 1013 W cm−2. Figure 3(c) shows the Floquet analysis of the energy-amplitude structure of the populated field-dressed states for I = 2.39 × 1013 W cm−2, as well as for a lower intensity, I = 1.56 × 1013 W cm−2 and for a higher intensity, I = 2.64 × 1013 W cm−2, both outside the resonance region, cf figure 2(a). The Floquet analysis was carried out as described in [4]. Surprisingly, the six-photon peak is negligible. However, the three-photon peak and the four-photon peak are distinct for I = 2.39 × 1013 W cm−2 and drop considerably for I = 2.64 × 1013 W cm−2. The solid lines in figure 3(a) show the intensity-dependent energies of the excited states of the associated KH atom. In the KH picture no six-photon Freeman resonance occurs, explaining why the six-photon peak is negligible.
However, the transition energies between the third and the second excited KH state, E|KH3〉 − E|KH2〉, and between the second and the first excited KH state, E|KH2〉 − E|KH1〉, become nearly resonant with the λ ≃ 0.7 μm laser field, see figure 3(b). Hence, for I = 2.39 × 1013 W cm−2, these excited KH states are strongly coupled by the field, potentially forming a Floquet ladder which can be felt by the ground state.
To check this idea we have considered a subsystem consisting of the seven lowest excited KH states, 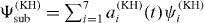 , which are coupled by the first and second harmonic of the KH potential, see (10). Starting from the first excited KH state, we have solved the (truncated) TDSE in the KH frame
, which are coupled by the first and second harmonic of the KH potential, see (10). Starting from the first excited KH state, we have solved the (truncated) TDSE in the KH frame
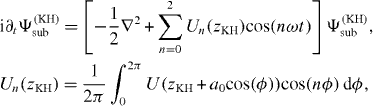
where U is the binding potential, thereby obtaining the time-dependent partial amplitudes a(KH)i(t) and their Fourier transforms a(KH)i(ω).
Panels (d) and (e) show the partial quasi-energy spectra |a(KH)i(ℏω)|2 for I = 1.56 × 1013 W cm−2 and I = 2.39 × 1013 W cm−2, respectively. The energies corresponding to the three-photon transition and to the four-photon transition starting from the unperturbed ground state are indicated. For I = 1.56 × 1013 W cm−2 no resonance is present. For I = 2.39 × 1013 W cm−2 two quasi-energy peaks appear at the three-photon and four-photon resonance, consistent with the full calculation. We note that the relative amplitudes of the quasi-energy peaks are not reliable due to the limited number of states included in the calculation, especially due to the absence of the ground state. Thus, our analysis suggests an interplay of quasi-static tunnelling from the ground state, trapping of the tunnelled population in the KH states, and the modifications of the 'instantaneous' response of the dressed ground state associated with the establishment of the KH regime for the excited states (which requires several laser cycle with constant intensity).
4. Conclusions
We have shown that our numerical analysis supports our analytical prediction that the restructuring of a 'laser-dressed' atom, in particular the formation of KH states, does play an important role in the nonlinear Kerr effect, even for mid-IR wavelengths. This is an unusual regime since the KH atom is only formed for the excited states but not for the ground state, which remains only weakly perturbed. The significance of the KH states for the Kerr response is strongly pulse-shape dependent. For the short bell-shaped pulse our numerical results indicate that the saturation of the Kerr response happens just before ionization sets in. The higher-order Kerr effect appears to be real, but it is important only in a very narrow intensity window. As soon as ionization occurs, the free electrons start to dominate. The deviations from the standard model are much more prominent for the flat-top pulse, for which our calculations reveal clear resonances in the response at the driving frequency. Our Floquet analysis suggests that these resonances can be explained by population transfer into excited KH states. While clear observation of these effects in laser filamentation is challenging and requires the use of shaped laser pulses, their signatures could be visible due to the presence of resonance structures in the Kerr response, possibly leading to unusual self-focusing and propagation dynamics. From the perspective of attosecond and intense-field physics, finding such signatures outside the traditional setup employing high-resolution photo-electron spectroscopy, velocity map imaging and COLTRIMS, would be extremely exciting.
Acknowledgments
We thank A M Popov, M Kolesik, P Polynkin, C Köhler, L Bergé, J-P Wolf, J Kasparian, H M Milchberg, R J Levis, G Steinmeyer and J V Moloney for stimulating and insightful discussions. This research was supported in part by the EPSRC Programme grant no. EP/I032517/1, the Marie Curie ITN Network CORINF and the ERA-Chemistry Project PIM2010EEC-00751.