Abstract
In a recent work, we have shown that the plasma flow around the magnetic island can excite the beta-induced Alfvén eigenmode (BAE) (Marchenko et al 2016 Nucl. Fusion 56 106021). In the present communication, it is shown that coupling of this primary BAE and magnetic island generates secondary geodesic acoustic mode (GAM), which has the frequency and mode structure identical to those of the primary BAE. The fixed GAM/BAE amplitude ratio, determined by the plasma neutrality, is comparable with the plasma/magnetic pressure ratio. This nonlinear coupling can be responsible for axis-symmetric modes, which accompany island-driven Alfvénic modes observed on HL-2A tokamak (Chen et al 2013 Nucl. Fusion 53 113010).
Export citation and abstract BibTeX RIS
The geodesic acoustic mode (GAM) is a high frequency (few tens kHz) zonal flow induced by the component of the field line curvature tangential to the magnetic surface [1]. The GAM has attracted much attention during last decades due to the ability to regulate anomalous transport via turbulence suppression [2]. It can be excited parametrically by plasma turbulence [3] as well as by energetic ions [4] (in the latter case, there exists also a specific GAM branch, so called EGAM, induced by energetic ions itself [5]). It is possible to excite the GAM by an external antenna [6].
Recently, axis-symmetric (i.e. with zero toroidal mode number, n = 0) modes identified as GAM, which accompanied standing beta-induced Alfvén eigenmodes (BAE) [11, 12] driven by magnetic islands, have been observed on HL-2A tokamak [9]. This observation motivated present communication. Below we demonstrate that this GAM has frequency (in the island frame) and mode structure identical to those of BAE, and calculate the GAM/BAE amplitude ratio.
We proceed introducing the toroidal sidebands of the axis-symmetric (A) and helical (B) electron response
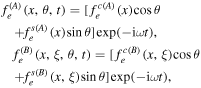
where x is the distance from the rational surface, θ is the poloidal angle, 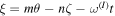 is the island phase, and upper index c(s) denotes amplitude of the up-down symmetric (asymmetric) toroidal sideband. Note that the choice of the island phase in the BAE response is natural, since island-driven BAE observed in experiments [7–10] have the same helicity as magnetic island, and form standing wave in the island frame. For this reason, up-down symmetric part of the electron response to BAE generates up-down asymmetric, axis-symmetric perturbation of the electron distribution via magnetic flutter in the dominant parallel streaming term of the kinetic equation
is the island phase, and upper index c(s) denotes amplitude of the up-down symmetric (asymmetric) toroidal sideband. Note that the choice of the island phase in the BAE response is natural, since island-driven BAE observed in experiments [7–10] have the same helicity as magnetic island, and form standing wave in the island frame. For this reason, up-down symmetric part of the electron response to BAE generates up-down asymmetric, axis-symmetric perturbation of the electron distribution via magnetic flutter in the dominant parallel streaming term of the kinetic equation
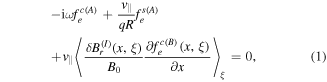
where 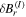 is the perturbation of the radial magnetic field induced by the island, and
is the perturbation of the radial magnetic field induced by the island, and
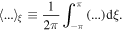
Under the condition 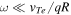 , with vTe the electron thermal velocity, the solution of equation (1) is given by
, with vTe the electron thermal velocity, the solution of equation (1) is given by
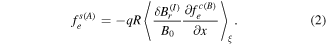
In the previous work [13], we have neglected 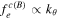 assuming that
assuming that 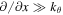 in the inertial layer around the rational surface, a reasonable assumption for the almost 'zonal' BAE with
in the inertial layer around the rational surface, a reasonable assumption for the almost 'zonal' BAE with 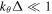 , where Δ is the BAE half-width defined shortly. Below we calculate this sideband, which contributes to equation (2) and to the corresponding flux-surface averaged radial current
, where Δ is the BAE half-width defined shortly. Below we calculate this sideband, which contributes to equation (2) and to the corresponding flux-surface averaged radial current  .
.
The sideband 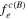 satisfies the kinetic equation
satisfies the kinetic equation
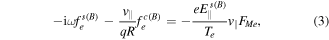
where 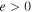 is the elementary charge,
is the elementary charge, 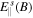 is the sideband of the parallel electric field, and FMe is the equilibrium (Maxwellian) distribution function. In the limit
is the sideband of the parallel electric field, and FMe is the equilibrium (Maxwellian) distribution function. In the limit 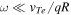 , equation (3) yields
, equation (3) yields
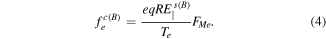
Note that neglect of the 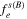 in equation (3) is justified provided
in equation (3) is justified provided  .
.
The sideband 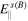 can be found from the neutrality condition for the sideband density perturbations. For the ions we have
can be found from the neutrality condition for the sideband density perturbations. For the ions we have
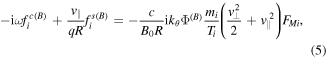
where 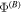 is the BAE electric potential. In the limit
is the BAE electric potential. In the limit 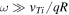 , equation (5) yields
, equation (5) yields
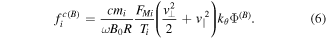
Equations (4) and (6), and neutrality condition 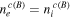 yield
yield
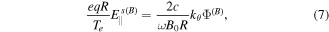
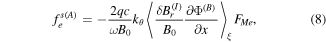
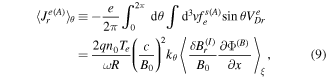
where 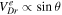 is the radial component of the electron magnetic drift.
is the radial component of the electron magnetic drift.
To keep the charge neutrality, the plasma responds to the current (9) by generation of a geodesic acoustic mode (G). Corresponding expressions for the flux-surface averaged radial currents are well known (e.g. see [14–16]) and given by

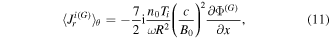
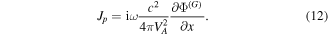
Equations (10) and (11) represent radial currents of electrons and ions, respectively, both induced by the geodesic plasma compressibility, whereas equation (12) is the radial polarization current. Balance of the all radial currents, 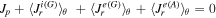 , yields
, yields
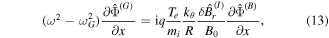
where hats denote the mode amplitude. In the 'constant Ψ' approximation,  , where
, where 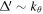 is the tearing mode stability index and w is the magnetic island half-width, we have
is the tearing mode stability index and w is the magnetic island half-width, we have 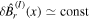 . Then it follows from equation (13) that the generated secondary GAM has a mode structure identical to that of the primary BAE. When the ion and electron Landau damping are neglected, the latter is determined by the BAE eigenmode equation [13]
. Then it follows from equation (13) that the generated secondary GAM has a mode structure identical to that of the primary BAE. When the ion and electron Landau damping are neglected, the latter is determined by the BAE eigenmode equation [13]
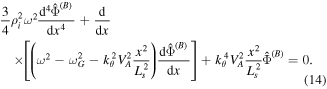
The eigenvalues of this kinetic, tearing parity BAE versus the poloidal mode number are shown in figure 1(a), and corresponding mode structures are shown in figure 1(b). Here, 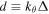 with the BAE half-width Δ given by
with the BAE half-width Δ given by
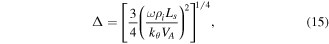
where 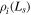 is the ion gyro-radius (magnetic shear length). Furthermore,
is the ion gyro-radius (magnetic shear length). Furthermore,
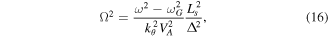
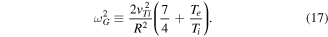
Figure 1. (a) The eigenvalues of the primary BAE versus d for l = 1 (blue), l = 2 (green), and l = 3 (red). Here l is the number of radial nodes of the radial electric field eigenfunction shown in (b) for d = 0.1.
Download figure:
Standard image High-resolution imageFrom figure 1 and equation (16), we have for 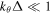 and for the lowest frequency mode (shown in blue in figure 1)
and for the lowest frequency mode (shown in blue in figure 1)
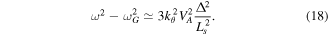
The perturbation of the radial magnetic field induced by the island is given by
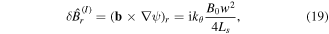
where ψ is the helical flux, and we have used the fact that the island and the primary BAE have the same mode number. Combining equations (13)–(19), we arrive at the final expression for the GAM/BAE radial electric field amplitude ratio necessary to compensate the flux-surface averaged radial current (9) induced by the island-BAE coupling
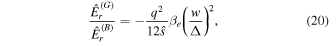
where  is the magnetic shear and
is the magnetic shear and 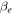 is the electron beta. As expected, to keep the plasma neutrality, the phase of the secondary GAM is shifted by π with respect to the primary BAE phase. It is difficult to infer about the actual value of
is the electron beta. As expected, to keep the plasma neutrality, the phase of the secondary GAM is shifted by π with respect to the primary BAE phase. It is difficult to infer about the actual value of 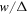 in the experiment [9]. However, the color code in figure 3 of [9] implies that intensity of the secondary GAM is about two orders of magnitude smaller than that of the primary BAE, qualitatively consistent with equation (20).
in the experiment [9]. However, the color code in figure 3 of [9] implies that intensity of the secondary GAM is about two orders of magnitude smaller than that of the primary BAE, qualitatively consistent with equation (20).
In summary, coupling of the magnetic island with its 'daughter' BAE generates axis-symmetric, up-down asymmetric electron response. As a result, finite flux-surface averaged radial current is generated. To keep the neutrality, plasma responds to this current by GAM generation. This secondary GAM has the same frequency and mode structure as the primary BAE. The GAM/BAE amplitude ratio given by equation (20) can be comparable to the plasma/magnetic pressure ratio.
Acknowledgments
VM and SR are supported by the project No. 0114U000678 of the National Academy of Science of Ukraine. AP and CMR are supported by the grants from IBS (IBS-R012-D1-2015-a03) and also by the National R&D Program through the NRF funded by the Ministry of Science, ICT & Future Planning (2015M1A7A1A02050238) in Korea.


