Abstract
Magnetic resonance-guided high intensity focused ultrasound (MR-HIFU) is a noninvasive thermal technique that enables rapid heating of a specific area in the human body. Its clinical relevance has been proven for the treatments of soft tissue tumors, like uterine fibroids, and for the treatments of solid tumors in bone. In MR-HIFU treatment, MR-thermometry is used to monitor the temperature evolution in soft tissue. However, this technique is currently unavailable for bone tissue. Computer models can play a key role in the accurate prediction and monitoring of temperature. Here, we present a computer ray tracing model that calculates the heat production density in the focal region. This model accounts for both the propagation of shear waves and the interference between longitudinal and shear waves. The model was first compared with a finite element approach which solves the Helmholtz equation in soft tissue and the frequency-domain wave equation in bone. To obtain the temperature evolution in the focal region, the heat equation was solved using the heat production density generated by the raytracer as a heat source. Then, we investigated the role of the interaction between shear and longitudinal waves in terms of dissipated power and temperature output. The results of our model were in agreement with the results obtained by solving the Helmholtz equation and the frequency-domain wave equation, both in soft tissue and bone. Our results suggest that it is imperative to include both shear waves and their interference with longitudinal waves in the model when simulating high intensity focused ultrasound propagation in solids. In fact, when modeling HIFU treatments, omitting the interference between shear and longitudinal waves leads to an over-estimation of the temperature increase in the tissues.
Export citation and abstract BibTeX RIS
1. Introduction
High intensity focused ultrasound (HIFU) is a thermal technique emerged over the last years (ter Haar 2001). One important HIFU application is the treatment of various types of benign or malignant tumors (ter Haar 2001, Kim 2015). During HIFU cancers' therapy, the ultrasound (US) beam is focused on target tissues, such as the tumors, in the body (focal region), leading to rapid heating and subsequent coagulative necrosis (ter Haar and Coussios 2007, ter Haar 2011). HIFU treatments are usually performed under image-guidance using magnetic resonance imaging (MRI) or Ultrasound for planning and guidance. MRI-guidance has the advantage of measuring nearly real-time temperatures using MR-thermometry techniques such as the proton resonance frequency shift (PRFS) (McDannold 2005, Senneville et al 2005, Rieke and Pauly 2008, Köhler et al 2009). This method is suitable for water-rich tissues with a long transversal relaxation time (T2), and therefore works well for monitoring HIFU ablations of soft tissue tumors, such as uterine fibroids (Stewart et al 2003) and other emerging applications such as liver cancer (Al-Bataineh et al 2012, Leslie et al 2012, Aubry et al 2013). HIFU treatment of uterine fibroids focuses on alleviating the pain by reducing the tumor size (Vaezy et al 2000, Stewart et al 2006), in a safe and effective manner (Fischer et al 2015, Lee et al 2015), with acceptable adverse events (Wang et al 2014). MR-guided HIFU (MR-HIFU) has also been used as an alternative treatment strategy for palliative treatment of bone metastases (Li et al 2010, Hurwitz et al 2014, Huisman et al 2014, 2015, Chan et al 2016, Harding et al 2018). Bone metastases are associated with pain and reduced quality of life (Coleman 2006). General treatments focus on alleviating the pain, and aim at improving the patients' life conditions. MR-HIFU procedures have been shown to be technically feasible (Huisman et al 2014, Chan et al 2016), effective (Li et al 2010, Harding et al 2018) and safe with promising results (Huisman et al 2014). Clinical therapies with MR-HIFU have also been used recently for the treatment of osteoid osteoma (Napoli et al 2017, Sharma et al 2017, Yarmolenko et al 2018). Osteoid osteoma is a benign but painful neoplasm (Motamedi et al 2009) which occurs commonly in children and adolescents (Sharma et al 2017). MR-HIFU has been shown to be a valid alternative to the standard radiofrequency ablation techniques (Sharma et al 2017), while remaining feasible (Yarmolenko et al 2018), safe, and effective (Napoli et al 2017). Studies also state that HIFU treatments are a safe and feasible method for the treatment of malignant neoplasm osteosarcoma (Li et al 2009, 2010) and local unresectable recurrence of osteosarcoma (Yu et al 2015). However, the number of current treatments is small, and large-scale randomized control clinical studies are yet to be implemented (Yang et al 2018). MR-Thermometry (PRFS) is used during HIFU treatments to monitor whether a high enough temperature for ablation is achieved in the target region, while avoiding undesired heating of the surrounding healthy tissues. However, PRFS does not give the temperature information in bone due to low T2. Monitoring the temperature in bone is of utmost importance, given that the high ultrasound absorption in the cortex leads to an extremely rapid heating. Such rapid heating is undesired because it can cause unwanted side effects. Although innovative MR-based thermometry techniques for bone are already being investigated (Ramsay et al 2015a, 2015b), computer models can play a key role in the accurate prediction and monitoring of temperature. Modeling HIFU propagation in bone poses several challenges, due to the acoustic and thermal properties of the cortex (Goss et al 1979, Nell and Myers 2010). Moreover, at the interface of muscle and bone, all the reflected and transmitted ultrasound waves have to be considered. Particular attention must be paid to the shear wave mode conversion in bone. Since bone is a solid material (while muscle behaves as a liquid for ultrasound waves), both longitudinal and shear waves play a role in the heating process. Also, shear wave propagation cannot be neglected if the US waves hit the muscle-bone interface at an oblique incidence angle (Chan et al 1974, Fujii et al 1999, White et al 2006). Various studies including the shear waves HIFU propagation in bone have been performed (Fujii et al 1999, Lin et al 2000, Nell and Myers 2010, Treeby and Saratoon 2015, ten Eikelder et al 2016). Nevertheless, these methods tend to neglect the interference between longitudinal and shear waves or use simple transducer geometries. The latter enables the use of 2D-axisymmetric models. The use of 2D-axisymmetric models is sometimes necessary to avoid computer memory problems. However, it reduces the flexibility to adapt the model to transducers composed of multiple elements and to complex shaped propagation media (e.g. real bone CT data). In this paper, we present a computer ray tracing model for HIFU propagation, valid in soft tissues and bone. The model calculates the heat production density (in W cm−3) in the focal region and takes the interaction between longitudinal and shear waves into account. The model is able to deal with complex transducer geometries, and it can potentially handle propagation media with complex shapes, which makes it suitable for diverse medical applications. To investigate if our raytracer describes the HIFU propagation correctly, we compared the pressure in soft tissue and the displacement in bone computed by the raytracer with those obtained by solving the Helmholtz equation and the frequency-domain wave equation, in the case of one transducer element. Then, using a more realistic and complex configuration with multiple transducer elements (Philips Sonalleve system (Köhler et al 2009)) we investigated the role of the interference between longitudinal and shear waves, comparing the results given by two versions of the raytracer approach: one including the interference and the other neglecting it. In particular, we used two setups: the first one with only flat interfaces (lossless oil—soft tissue—bone) and the second one, more realistic, considering the bone as a cylinder with fat and marrow layers.
2. Materials and methods
2.1. Modeling approach
The computation of the temperature trend for tissues under HIFU consists of two stages. First, the ultrasound propagation has to be modeled, to compute the heat production density in the given geometry due to HIFU. To calculate the heat production density, a raytracer approach implemented in MATLAB (Version 2015a, MathWorks, Natick, MA, 2015) has been used. To investigate if the raytracer approach describes the US propagation correctly, it has been compared with the solution of the Helmholtz equation in soft tissue and the frequency-domain wave equation in bone, using a finite element method. Second, the temperature evolution is obtained by solving the heat equation, using a finite element approach, with the computed heat production density as the heat source. In this paper, spatial derivatives of any vectorfield  are indicated by a number, i.e.
are indicated by a number, i.e.  and differentiation with respect to the time
and differentiation with respect to the time  is indicated by dots, like
is indicated by dots, like  .
.
2.2. Computation of the heat source: raytracer approach
In the raytracer approach, ultrasound waves are modeled as rays leaving the transducer element(s), with a certain frequency (harmonic oscillations are assumed). The orientation of the rays leaving each transducer element is given by a probability density calculated according to the far field approximation formula (Morse and Ingard 1968), which describes the pressure pattern in the far field zone generated by a circular transducer element (see figure 1). Each ray carries a power, a phase, a wave vector (parallel to the propagation direction of the rays) and, in case of shear rays in bone, also a polarization direction. The spatial distribution of the rays emitted from each transducer element is chosen such that the average intensity emitted by the rays corresponds to the far field distribution of the transducer element. The power of the ray  , after a distance
, after a distance  in a material with an attenuation coefficient for pressure
in a material with an attenuation coefficient for pressure  , is computed as
, is computed as  . At each interface, the transmission and reflection coefficients are computed, and all the reflected/refracted rays are generated, taking a possible phase shift into account. Rays showing the same pattern (i.e. which are generated by the same transducer element, and with almost the same physical path to an observation point
. At each interface, the transmission and reflection coefficients are computed, and all the reflected/refracted rays are generated, taking a possible phase shift into account. Rays showing the same pattern (i.e. which are generated by the same transducer element, and with almost the same physical path to an observation point  ) describe waves propagating from the transducer element to the observation point. Rays with the same pattern have the same reflection/refraction sequence. To find the contribution of the waves with this pattern to the total pressure or displacement, the intensity and phase from the rays in the pattern have been computed. That results in an expression for the pressure or displacement generated by the considered pattern. Since the considered wave equations are linear, the pressures (in soft tissue) and displacements (in solids) corresponding to the various patterns can be added to obtain the total pressure or displacement. Finally, the total pressure or total displacement is used to compute the total power loss due to attenuation, which results in heat production. In the following subsections more details of the various steps are given.
) describe waves propagating from the transducer element to the observation point. Rays with the same pattern have the same reflection/refraction sequence. To find the contribution of the waves with this pattern to the total pressure or displacement, the intensity and phase from the rays in the pattern have been computed. That results in an expression for the pressure or displacement generated by the considered pattern. Since the considered wave equations are linear, the pressures (in soft tissue) and displacements (in solids) corresponding to the various patterns can be added to obtain the total pressure or displacement. Finally, the total pressure or total displacement is used to compute the total power loss due to attenuation, which results in heat production. In the following subsections more details of the various steps are given.
Figure 1. The rays (in blue) leave each transducer element with a direction given by the far field approximation formula.
Download figure:
Standard image High-resolution image2.2.1. Intensity for soft tissue and bone
Consider a point  in soft tissue or in bone, and a volume (cube) around it. When a ray of a given pattern
in soft tissue or in bone, and a volume (cube) around it. When a ray of a given pattern  intersects the cube, the part of the ray inside the cube is described as an infinitesimally small cylinder with a circular base area
intersects the cube, the part of the ray inside the cube is described as an infinitesimally small cylinder with a circular base area  and a height
and a height  (see figure 2). The intensity associated to the ray in the cylinder is given by:
(see figure 2). The intensity associated to the ray in the cylinder is given by:

where  is the power of the ray. Equation (1) holds only in the cylinder with circular base area
is the power of the ray. Equation (1) holds only in the cylinder with circular base area  . Considering that the volume of the cylinder enveloping the ray is given by
. Considering that the volume of the cylinder enveloping the ray is given by  , the contribution of a ray to the total average intensity in the cube is:
, the contribution of a ray to the total average intensity in the cube is:
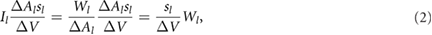
where  is the volume of the cube. The total intensity in the cube around
is the volume of the cube. The total intensity in the cube around  , for all the incoming rays with the same pattern, is:
, for all the incoming rays with the same pattern, is:

where  is the total number of rays of pattern
is the total number of rays of pattern  intersecting the small cube around
intersecting the small cube around  .
.
Figure 2. Cube representing a portion of the focal region.
Download figure:
Standard image High-resolution image2.2.2. Pressure in soft tissue
For soft tissue, the (complex) pressure  in a point
in a point  is related to intensity given in formula (3) as:
is related to intensity given in formula (3) as:
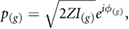
where  is the acoustic impedance and
is the acoustic impedance and  is the averaged phase in the small cube around
is the averaged phase in the small cube around  calculated as:
calculated as:
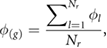
where  is the phase associated to the longitudinal
is the phase associated to the longitudinal  th ray.
th ray.
2.2.3. Displacement in bone
The intensity  for longitudinal waves of the same pattern
for longitudinal waves of the same pattern  in bone is related to the absolute amplitude
in bone is related to the absolute amplitude  of the displacement associated to longitudinal waves by:
of the displacement associated to longitudinal waves by:

where  is the angular frequency.
is the angular frequency.  ,
,  and
and  are the plane wave parameters related to the the Lamé coefficients
are the plane wave parameters related to the the Lamé coefficients  and
and  , to the first and second viscosities
, to the first and second viscosities  and
and  and to the material density
and to the material density  (see section 1 in supplementary information (stacks.iop.org/PMB/63/235024/mmedia)).
(see section 1 in supplementary information (stacks.iop.org/PMB/63/235024/mmedia)).
In the same fashion, the intensity  for shear waves of the same pattern
for shear waves of the same pattern  in bone is related to the absolute amplitude
in bone is related to the absolute amplitude  of the displacement associated to shear waves by:
of the displacement associated to shear waves by:

where  ,
,  and
and  are the plane wave parameters related to
are the plane wave parameters related to  ,
,  ,
,  ,
,  and
and  (see section 2 in the supplementary information). An explicit derivation of relations (4) and (5) can be found in sections 4 and 5 of the supplementary information. The absolute amplitudes
(see section 2 in the supplementary information). An explicit derivation of relations (4) and (5) can be found in sections 4 and 5 of the supplementary information. The absolute amplitudes  and
and  can be easily found from equations (4) and (5), respectively.
can be easily found from equations (4) and (5), respectively.
Then, using the averaged phases for longitudinal  and shear waves
and shear waves  that are also obtained from the rays in the considered pattern, the complex displacements around
that are also obtained from the rays in the considered pattern, the complex displacements around  can be written as:
can be written as:

where  is the averaged and normalized wave vector for longitudinal waves with the same pattern
is the averaged and normalized wave vector for longitudinal waves with the same pattern  and
and  is the averaged and normalized polarization vector for shear rays with the same pattern
is the averaged and normalized polarization vector for shear rays with the same pattern  .
.
2.2.4. Calculation of the total heat production density
The total pressure  (in soft tissue) and the total displacement
(in soft tissue) and the total displacement  (in bone) are obtained by adding the complex pressures and displacements of the various patterns. Adding complex values ensures that the interference is included.
(in bone) are obtained by adding the complex pressures and displacements of the various patterns. Adding complex values ensures that the interference is included.
Finally, the total power loss can be computed using:
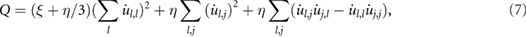
where  represents the differentiation of the
represents the differentiation of the  th component of the velocity with respect to coordinate
th component of the velocity with respect to coordinate  . Formula (7) is still time-dependent, and therefore its time average
. Formula (7) is still time-dependent, and therefore its time average  has been computed. More information about the derivation of formula (7) can be found in section 3 of the supplementary information. The spatial derivatives of the displacements in expression (7) are explained in sections 6 and 7 of the supplementary information. It is worth mentioning that the time average of equation (7) for soft tissue is reduced to the standard formula:
has been computed. More information about the derivation of formula (7) can be found in section 3 of the supplementary information. The spatial derivatives of the displacements in expression (7) are explained in sections 6 and 7 of the supplementary information. It is worth mentioning that the time average of equation (7) for soft tissue is reduced to the standard formula:
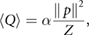
where  is the attenuation coefficient for soft tissue. The heat production density, which gives rise to heat production, is found as:
is the attenuation coefficient for soft tissue. The heat production density, which gives rise to heat production, is found as:
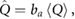
where  is the absorption fraction, defined as the actual fraction of power loss converted into heat, which depends on the tissue type. In fact, not all the power loss is responsible for the temperature increase, but also other effects like scattering take place. Typical values of
is the absorption fraction, defined as the actual fraction of power loss converted into heat, which depends on the tissue type. In fact, not all the power loss is responsible for the temperature increase, but also other effects like scattering take place. Typical values of  for soft tissue and bone can be found in table 1.
for soft tissue and bone can be found in table 1.
Table 1. Parameters used in simulations.
| Material |  (m s−1) (m s−1) |
 (kg m−3) (kg m−3) |
 (Np cm−1) (Np cm−1) |
 (—) (—) |
 (J (Kg K)) (J (Kg K)) |
 (W (m K) (W (m K) ) ) |
|---|---|---|---|---|---|---|
| Soft tissue—muscle—marrow | 1500 | 1050 | 0.07 | 0.35 |
3720 | 0.537 |
| Fat | 1450 | 909 | 0.034 | 0.35 |
— | — |
| Bone longit |
3736 | 2025 | 1.9 | 0.3 |
1300 | 0.487 |
| Bone shear |
1995 | 2025 | 2.8 | 0.3 |
1300 | 0.487 |
| Lossless oil | 1380 | 1030 | 0 | — | — | — |
aAverage of different values in Goss et al (1979). bNell and Myers (2010). cPinton et al (2012).
2.3. Comparison with a finite element approach with only flat interfaces
To investigate if the raytracer approach describes the US propagation in the correct way, a comparison between the raytracer and the solutions of the Helmholtz equation in soft tissue and the frequency-domain wave equation in bone has been done. In the soft tissue portion, the Helmholtz equation with the total pressure  as unknown is written as:
as unknown is written as:

where  is the (complex) wave number for soft tissue defined as
is the (complex) wave number for soft tissue defined as  , where
, where  and
and  are the speed of sound and attenuation for the soft tissue. In bone, the equations to solve are:
are the speed of sound and attenuation for the soft tissue. In bone, the equations to solve are:

where  is the strain tensor,
is the strain tensor,  is the density,
is the density,  are the components of the stress measure at each point,
are the components of the stress measure at each point,  is the displacement vector, and
is the displacement vector, and  are the component of the fourth-order stiffness or elasticity tensor, which are dependent on the Young modulus
are the component of the fourth-order stiffness or elasticity tensor, which are dependent on the Young modulus  and the second Lamé coefficient
and the second Lamé coefficient  , also known as shear modulus. In bone, the attenuation is taken into account by including damping:
, also known as shear modulus. In bone, the attenuation is taken into account by including damping:
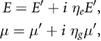
where  is the loss factor for Young modulus
is the loss factor for Young modulus  ,
,  is the real part of
is the real part of  ,
,  is the loss factor for shear modulus
is the loss factor for shear modulus  and
and  is the real part of
is the real part of  .
.
To define the same attenuation for the raytracer model and for the solution of equation (9), a relation between the attenuation coeffients  and
and  and the two loss factors
and the two loss factors  and
and  has been derived (see section 8 in the supplementary information).
has been derived (see section 8 in the supplementary information).
Equation (9) have been implemented for one circular transducer element with radius  mm, using a 2D-axisymmetric model in COMSOL Multiphysics (Version 5.0, Burlington, MA, 2014). The transducer element is immersed in soft tissue, and its center is in (0,0,0) cm. The ultrasound propagation is along the
mm, using a 2D-axisymmetric model in COMSOL Multiphysics (Version 5.0, Burlington, MA, 2014). The transducer element is immersed in soft tissue, and its center is in (0,0,0) cm. The ultrasound propagation is along the  -axis and the flat interface with bone is located at
-axis and the flat interface with bone is located at  cm. A schematic representation of the simulation setup and of the boundary conditions used is given in figure 3. The comparison with the raytracer has been done in terms of the pressure in the soft tissue and in terms of the displacement field in the bone. The frequency used is 1.2 MHz and the initial power is 1 W. The soft tissue and bone parameters are shown in table 1. A comparison between the raytracer and the solution of the frequency-domain wave equation has also been implemented by modeling the bone as a cylinder (see section 9 in the supplementary information).
cm. A schematic representation of the simulation setup and of the boundary conditions used is given in figure 3. The comparison with the raytracer has been done in terms of the pressure in the soft tissue and in terms of the displacement field in the bone. The frequency used is 1.2 MHz and the initial power is 1 W. The soft tissue and bone parameters are shown in table 1. A comparison between the raytracer and the solution of the frequency-domain wave equation has also been implemented by modeling the bone as a cylinder (see section 9 in the supplementary information).
Figure 3. Simulation setup for the comparison between the raytracer and the solutions of the Helmholtz equation and the frequency-domain wave equation. The transducer element is immersed in soft tissue and the interface with bone is located at (1.6,0,0) cm. The boundary conditions used are hard boundary conditions for pressure and displacement. A perfect matching layer (PML) of 1 cm thick is used to avoid US reflection from the wall at  .
.
Download figure:
Standard image High-resolution image2.4. Computation of the temperature evolution
When the total heat production density is known, the heat equation can be solved to find the temperature evolution in the desired volume. The heat equation is formulated as:

where  is the temperature at position
is the temperature at position  and time
and time  ,
,  is the diffusion coefficient defined as
is the diffusion coefficient defined as  with
with  the thermal conductivity,
the thermal conductivity,  the density and
the density and  the specific heat at a constant pressure. The value of
the specific heat at a constant pressure. The value of  has been modeled by a step function, i.e. it is equal to the heat production density computed by the raytracer in the point
has been modeled by a step function, i.e. it is equal to the heat production density computed by the raytracer in the point  under sonication, and zero otherwise. We assumed that there is no heat flux through the boundaries of the system (Von Neumann boundary conditions) both in soft tissue and in bone. To obtain the temperature rise during HIFU, a finite-element software package has been used (COMSOL Multiphysics, Version 5.0, Burlington, MA, 2014).
under sonication, and zero otherwise. We assumed that there is no heat flux through the boundaries of the system (Von Neumann boundary conditions) both in soft tissue and in bone. To obtain the temperature rise during HIFU, a finite-element software package has been used (COMSOL Multiphysics, Version 5.0, Burlington, MA, 2014).
2.5. Contribution of shear and longitudinal waves interference
To investigate the role of the interference between longitudinal and shear waves during a HIFU procedure, the geometry of the phased array transducer in the Philips Sonalleve system has been reproduced by the raytracer model. The system is composed of 256 transducer elements, positioned in a spherical shell and immersed in a lossless material. Each circular element has a radius of 3.5 mm. The system operates at 1.2 MHz, and it creates a cigar-shaped focal region with a dimension of approximately 2 mm width and 7 mm length. Two numerical simulations for two different setups have been performed (see figure 4). The first setup considers flat interfaces only, while the second one models a more realistic case, including a fat and a muscle layer, as well as a cylindrical bone. The used working frequency is 1.2 MHz, the initial total power is set at 25 W for the first setup and 40 W for the second one. The material parameters are given in table 1. In the first simulation, the total heat production density is computed in bone as a sum of  and
and  , where
, where  is the total power loss when only longitudinal waves are present and
is the total power loss when only longitudinal waves are present and  is the total power loss calculated when only shear waves are present. In this case, the interference between longitudinal-longitudinal and shear-shear and the contribution of shear waves are still taken into account, while the interference between shear and longitudinal waves is neglected. In the second simulation, the total power loss in bone is computed using the time averaged version of formula (7), containing the interference information. A comparison of the total power loss integrated over different volumes (in W) has been done using the first setup for the two simulations. Each volume is represented by a 3D half ellipsoid with semi-axes in
is the total power loss calculated when only shear waves are present. In this case, the interference between longitudinal-longitudinal and shear-shear and the contribution of shear waves are still taken into account, while the interference between shear and longitudinal waves is neglected. In the second simulation, the total power loss in bone is computed using the time averaged version of formula (7), containing the interference information. A comparison of the total power loss integrated over different volumes (in W) has been done using the first setup for the two simulations. Each volume is represented by a 3D half ellipsoid with semi-axes in  - and
- and  -direction (
-direction ( cm), and a length of the remaining semi-axis (
cm), and a length of the remaining semi-axis ( in the
in the  -direction) between 0 cm and 0.7 cm (see figure 5). Further, the temperature rise has been computed for both setups, with the heat source applied for 10 s. Both the total power loss and the temperature rise are computed on a grid with a maximum spacing of 0.29 mm.
-direction) between 0 cm and 0.7 cm (see figure 5). Further, the temperature rise has been computed for both setups, with the heat source applied for 10 s. Both the total power loss and the temperature rise are computed on a grid with a maximum spacing of 0.29 mm.
Figure 4. (a) Simulation setup with flat interfaces. The US waves travel in the lossless oil for around 6 cm and in the soft tissue for 7 cm, before reaching the bone. The natural focal point is in (0,0,0) cm. (b) Simulation setup representing the bone and the marrow using two cylinders with center in (0.5,0,0) cm. The central axis of the cylinders is parallel to the  -axis. The radius of the bone is 1.5 cm and the radius of the marrow is 0.4 cm. The US waves travel in the lossless oil for around 6 cm, in the fat for 7 cm, and in the muscle for around 5 cm before reaching the bone. The natural focal point is in (0,0,0) cm, inside the bone.
-axis. The radius of the bone is 1.5 cm and the radius of the marrow is 0.4 cm. The US waves travel in the lossless oil for around 6 cm, in the fat for 7 cm, and in the muscle for around 5 cm before reaching the bone. The natural focal point is in (0,0,0) cm, inside the bone.
Download figure:
Standard image High-resolution imageFigure 5. Half ellipsoid in which the total power loss is integrated. The semi-axes  and
and  are fixed, while
are fixed, while  can assume a value from 0 cm to 0.7 cm.
can assume a value from 0 cm to 0.7 cm.
Download figure:
Standard image High-resolution image3. Results
3.1. Comparison with a finite element approach
Figure 6 shows the pressure trends computed by solving the Helmholtz equation for soft tissue and the raytracer approach for the configuration in figure 3. The pressure was computed along the central line from the centre of the transducer element in the  -direction. As the raytracer model was based on the far field approximation approach, it is considered to give a correct description of the ultrasound propagation only in the far field zone. The near field distance in the US propagation direction, for a circular transducer element of diameter
-direction. As the raytracer model was based on the far field approximation approach, it is considered to give a correct description of the ultrasound propagation only in the far field zone. The near field distance in the US propagation direction, for a circular transducer element of diameter  , was calculated as
, was calculated as  , where
, where  is the wavelength. The near field distance with
is the wavelength. The near field distance with  mm and
mm and  mm was found to be at 3.2 mm. For
mm was found to be at 3.2 mm. For  -values smaller than 3.2 mm, the behavior of the pressure is not shown. In the far field zone, the two models described an output with a virtually identical oscillation and similar pressure values.
-values smaller than 3.2 mm, the behavior of the pressure is not shown. In the far field zone, the two models described an output with a virtually identical oscillation and similar pressure values.
Figure 6. Pressure in the soft tissue from the raytracer output (orange line) and from the Helmholtz equation solution (blue line). The behavior of the pressure, within the near field distance, is not taken into account, due to the applicability of the raytracer only in the far field zone.
Download figure:
Standard image High-resolution imageIn figure 7, the  - and
- and  -components (
-components ( and
and  ) of the absolute value of the displacement in the
) of the absolute value of the displacement in the  -plane of bone given by the raytracer and by solving equation (9) for the configuration in figure 3 are shown. The displacement in the
-plane of bone given by the raytracer and by solving equation (9) for the configuration in figure 3 are shown. The displacement in the  -direction has been omitted because it was zero everywhere for both the methods. The peak values for
-direction has been omitted because it was zero everywhere for both the methods. The peak values for  were 8.74 · 10−7 cm and 9.02 · 10−7 cm, and for
were 8.74 · 10−7 cm and 9.02 · 10−7 cm, and for  were 2.98 · 10−7 cm and 3.02 · 10−7 cm for equation (9) and the raytracer respectively. The two models predicted comparable displacements with regard to the peak values and to the field distribution in the planes, e.g. the low values assumed by
were 2.98 · 10−7 cm and 3.02 · 10−7 cm for equation (9) and the raytracer respectively. The two models predicted comparable displacements with regard to the peak values and to the field distribution in the planes, e.g. the low values assumed by  in the central region of the
in the central region of the  -plane were visible in both the methods.
-plane were visible in both the methods.
Figure 7. Component d1 computed by the raytracer (a) and by solving equation (9) (c), and d2 for the the raytracer (b) and by solving equation (9) (d) with only flat interfaces (the used configuration is shown in figure 3).
Download figure:
Standard image High-resolution image3.2. Contribution of shear and longitudinal waves interference
In figure 8,  , the total predicted power loss integrated over different volumes for the raytracer with (
, the total predicted power loss integrated over different volumes for the raytracer with ( ) and without (
) and without ( ) interference between longitudinal and shear waves, is shown. Computing
) interference between longitudinal and shear waves, is shown. Computing  with
with  led to an over-estimation of the integrated power loss of about 75%.
led to an over-estimation of the integrated power loss of about 75%.
Figure 8. First setup: the blue line represents the total integrated power loss predicted by  , while the orange line represents the values of
, while the orange line represents the values of  given by
given by  .
.
Download figure:
Standard image High-resolution imageIn figures 9 and 11, the predicted temperatures in the  -plane at time 11 s for
-plane at time 11 s for  and
and  for the two setups are shown. When using the first setup, the maximum temperature increase in bone predicted by
for the two setups are shown. When using the first setup, the maximum temperature increase in bone predicted by  was approximately 3.4 times higher than the one given by
was approximately 3.4 times higher than the one given by  . The over-estimation of
. The over-estimation of  was also visible when using the second setup, where the temperature predicted by
was also visible when using the second setup, where the temperature predicted by  was around 4.1 times higher than the one given by
was around 4.1 times higher than the one given by  . Higher values of temperature for
. Higher values of temperature for  were also observed when investigating the temperature trend over time at point (
were also observed when investigating the temperature trend over time at point ( ,0,0) cm (see figures 10 and 12) for the two setups.
,0,0) cm (see figures 10 and 12) for the two setups.
Figure 9. First setup: temperature values in the  -plane at time 11 s for the models
-plane at time 11 s for the models  (a) and
(a) and  (b). Note that the colorbars do not show the same range.
(b). Note that the colorbars do not show the same range.
Download figure:
Standard image High-resolution imageFigure 10. First setup: temperature evolution over time in the point ( ,0,0) cm. The point is located in the bone, at the interface with the soft tissue. The blue line represents the temperature predicted by
,0,0) cm. The point is located in the bone, at the interface with the soft tissue. The blue line represents the temperature predicted by  , while the orange line is the temperature trend given by
, while the orange line is the temperature trend given by  .
.
Download figure:
Standard image High-resolution imageFigure 11. Second setup: temperature values in the  -plane at time 11 s for the models
-plane at time 11 s for the models  (a) and
(a) and  (b). Note that the colorbars do not show the same range.
(b). Note that the colorbars do not show the same range.
Download figure:
Standard image High-resolution imageFigure 12. Second setup: temperature evolution over time in the point( ,0,0) cm. The point is located in the bone, at the interface with the soft tissue. The blue line represents the temperature predicted by
,0,0) cm. The point is located in the bone, at the interface with the soft tissue. The blue line represents the temperature predicted by  , while the orange line is the temperature trend given by
, while the orange line is the temperature trend given by  .
.
Download figure:
Standard image High-resolution image4. Discussion
We presented a raytracer model that describes the HIFU propagation in soft tissue and bone. Our aim was to investigate the interaction between longitudinal and shear waves in bone. The method was compared with the solution of the Helmholtz equation and the frequency-domain wave equation, in the case of one transducer element. Figure 6 shows that the pressure field predicted by the raytracer and by solving the Helmholtz equation agree well in the far field zone. At a distance within the near field length, the raytracer method is not applicable, because the rays are generated according to the far field approximation pattern. As our model assumes systems that focus on tumors in the far field area, e.g. the Philips Sonnalleve, it is logical to focus on the correct description of the US propagation only in the far field zone. Figure 7 shows a pattern in the displacement field inside the bone, both for the raytracer and the wave equation (e.g. higher displacement in the  - direction close to the interface in the central portion, and in the
- direction close to the interface in the central portion, and in the  - direction close to the interface in the upper and lower portions). The results compare very well with only minor differences in the values of the displacement in the
- direction close to the interface in the upper and lower portions). The results compare very well with only minor differences in the values of the displacement in the  -direction (see figures 7(a) and (b)). These minor differences could be due to the small approximation error inherent to the discrete nature of the raytracer approach (i.e. the finite number of rays used in the simulations).
-direction (see figures 7(a) and (b)). These minor differences could be due to the small approximation error inherent to the discrete nature of the raytracer approach (i.e. the finite number of rays used in the simulations).
The inclusion of shear propagation is crucial when the angle of incidence ( ) of US waves on the interface is oblique (Chan et al 1974, Fujii et al 1999, White et al 2006). Moreover, when
) of US waves on the interface is oblique (Chan et al 1974, Fujii et al 1999, White et al 2006). Moreover, when  is between 21° and 52°, the energy transferred to the bone by shear waves is more than the energy transferred by the longitudinal waves in the same interval (ten Eikelder et al 2016). In the Philips Sonalleve system, the angle between the normal to the outermost transducer elements and the normal to the coronal plane is more than 32°. Therefore, in our system, the shear wave propagation cannot be neglected. Furthermore, figures 8–12 show that it is important to include in the model both shear wave propagation and interference (constructive/destructive) between shear and longitudinal waves. Figure 8 in particular shows that not including the interference between the two waves leads to an over-estimation of the integrated power loss, causing an over-estimation of the temperature increase (figures 9–12). Not including the interference between shear and longitudinal waves gives an over-estimation of the temperature increase of about 3.4 times when using the first setup and of about 4.1 times when using the second setup. This slight difference can be due to the presence of the curved surface in the second setup, which increases the presence of shear waves and consequently the interference between shear and longitudinal waves grows in importance. The general over-estimation given by not considering the interaction between shear and longitudinal waves may be explained by the different phases of longitudinal and shear waves, which give rise to destructive interference. For US waves originating from the very same transducer element, the interference between longitudinal and shear waves is partially caused by the different sound velocities that these two kinds of waves have. At the interface of soft tissue and bone, the generated refracted shear waves show a phase shift with respect to the incoming wave, which is not observed for longitudinal waves. When the US waves originate from different transducer element, also the relative position of both transducer elements plays a role. For shear waves, the interference also occurs because of a difference in polarization directions. Hence, for HIFU propagation in bone, the interaction between shear and longitudinal waves plays an important role for the temperature evaluation in the focal region.
is between 21° and 52°, the energy transferred to the bone by shear waves is more than the energy transferred by the longitudinal waves in the same interval (ten Eikelder et al 2016). In the Philips Sonalleve system, the angle between the normal to the outermost transducer elements and the normal to the coronal plane is more than 32°. Therefore, in our system, the shear wave propagation cannot be neglected. Furthermore, figures 8–12 show that it is important to include in the model both shear wave propagation and interference (constructive/destructive) between shear and longitudinal waves. Figure 8 in particular shows that not including the interference between the two waves leads to an over-estimation of the integrated power loss, causing an over-estimation of the temperature increase (figures 9–12). Not including the interference between shear and longitudinal waves gives an over-estimation of the temperature increase of about 3.4 times when using the first setup and of about 4.1 times when using the second setup. This slight difference can be due to the presence of the curved surface in the second setup, which increases the presence of shear waves and consequently the interference between shear and longitudinal waves grows in importance. The general over-estimation given by not considering the interaction between shear and longitudinal waves may be explained by the different phases of longitudinal and shear waves, which give rise to destructive interference. For US waves originating from the very same transducer element, the interference between longitudinal and shear waves is partially caused by the different sound velocities that these two kinds of waves have. At the interface of soft tissue and bone, the generated refracted shear waves show a phase shift with respect to the incoming wave, which is not observed for longitudinal waves. When the US waves originate from different transducer element, also the relative position of both transducer elements plays a role. For shear waves, the interference also occurs because of a difference in polarization directions. Hence, for HIFU propagation in bone, the interaction between shear and longitudinal waves plays an important role for the temperature evaluation in the focal region.
Several studies about the role of shear waves in HIFU propagation on the temperature output for bone have been performed (Fujii et al 1999, Lin et al 2000, Nell and Myers 2010, Treeby and Saratoon 2015, ten Eikelder et al 2016). Fujii et al (1999) did not include longitudinal and shear waves interaction in bone, as they focused on the temperature evolution in the portion of muscle close to the interface with bone. Lin et al (2000), Treeby and Saratoon (2015) and ten Eikelder et al (2016) calculated the total heat production density in bone by summing the contribution of longitudinal waves and shear waves without including interference between the two waves. Nell and Myers (2010) considered bone as a solid-elastic material and they used a finite-element commercial software to calculate the temperature, including the interference between longitudinal and shear waves. However, the used transducer geometry is far less complex than more realistic transducer geometries, like the Philips Sonalleve transducer geometry that we used in this study. In fact, it is composed of one spherically focused transducer with a diameter of 8 cm, while the Philips Sonalleve system comprises 256 transducer elements (with 12 cm radius of curvature, 13 cm aperture). Nell and Myers (2010) used a 2D-axisymmetric model, not suitable for realistic transducer geometries, which aim to have as little geometric symmetry as possible to avoid overheating in the near-field (Ramaekers et al 2017) as well as to reduce the presence of grating lobes (Pompei and Wooh 2002). This type of models is also not adequate for complex shaped propagation media (such as real bone). In summary, the raytracer approach is flexible and it can easily deal with various transducer configurations. Moreover, it can handle 3D propagation geometries composed of multiples material layers, without becoming dramatically more memory intensive. This makes the use of the raytracer preferable to software packages for US propagation (e.g. COMSOL), as they often show a high memory consumption when treating 3D geometries. Our method has also the potential of handling more complex shapes (e.g. CT data, complex geometry described by meshes), which are able to describe real bones. In the future, the experimental validation of the raytracer approach using CT data should be implemented. Currently, considering the configuration with 256 transducer elements, the MATLAB version of the code takes around 50 min to generate the power production (in 56 000 points) when a cylindrical bone is present, and around 20 min when only soft tissues are considered. Therefore, we are currently working on the optimisation of the code, to reduce the computation time. This may lead to the application of the model for real bone lesions of patients, extending its usage to a clinical environment (i.e. treatment planning).














