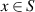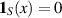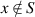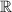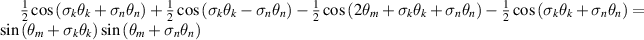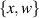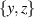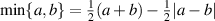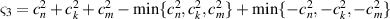Abstract
We formalise the concept of near resonance for the rotating Navier–Stokes equations, based on which we propose a novel way to approximate the original partial differential equation (PDE). The spatial domain is a three-dimensional flat torus of arbitrary aspect ratios. We prove that the family of proposed PDEs are globally well-posed for any rotation rate and initial datum of any size in any Hs space with 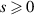 . Such approximations retain many more 3-mode interactions, and are thus more accurate, than the conventional exact-resonance approach. Our approach is free from any limiting argument that requires physical parameters to tend to zero or infinity, and is free from any use of small divisors (so that all estimates depend smoothly on the torus's aspect ratios). The key estimate hinges on the counting of integer solutions of Diophantine inequalities rather than Diophantine equations. Using a range of novel ideas, we handle rigorously and optimally challenges arising from the non-trivial irrational functions in these inequalities. The main results and ingredients of the proofs can form part of the mathematical foundation of a non-asymptotic approach to nonlinear, oscillatory dynamics in real-world applications.
. Such approximations retain many more 3-mode interactions, and are thus more accurate, than the conventional exact-resonance approach. Our approach is free from any limiting argument that requires physical parameters to tend to zero or infinity, and is free from any use of small divisors (so that all estimates depend smoothly on the torus's aspect ratios). The key estimate hinges on the counting of integer solutions of Diophantine inequalities rather than Diophantine equations. Using a range of novel ideas, we handle rigorously and optimally challenges arising from the non-trivial irrational functions in these inequalities. The main results and ingredients of the proofs can form part of the mathematical foundation of a non-asymptotic approach to nonlinear, oscillatory dynamics in real-world applications.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Footnotes
- 1
Evident from dispersion relation (2.10), the Coriolis term does not generate (linear) oscillatory dynamics in horizontal modes. Such a large set of non-oscillatory modes is a common feature that separates many fluid models (even in the inviscid case) from classically known dispersive PDEs.
- 2
For set S, the associated indicator function is defined as
 if
if  and
and  if
if  .
. - 3
The zero-mean assumption is imposed WLOG and this property propagates in time—see the start of section 2.
- 4
Such study can appear in literature concerning the van der Corput lemma.
- 5
A simple curve is a curve that does not cross itself.
- 6
In fact, it suffices to know that
 has zero Lebesgue measure in
has zero Lebesgue measure in  by Sard's theorem.
by Sard's theorem. - 7
Rewrite the numerator of (5.14) as:
 , and the denominator as
, and the denominator as  .
. - 8
Together with identity, they are the only self-inverse, parity-preserving members of the 4-permutation group, and form a subgroup. Then, necessarily, they are commutative and the three non-identity elements are cyclic under the group operation. This subgroup is isomorphic to the Klein 4-group and to
 .
. - 9
if the largest and smallest elements of
 form set
form set  or set
or set  , then
, then  .
. - 10
e.g.
 and
and  .
. - 11
Consider summability and
 .
.