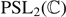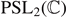On families of constrictions in model of overdamped Josephson junction and Painlevé 3 equation^*

The tunnelling effect predicted by Josephson (Nobel Prize, 1973) concerns the Josephson junction: two superconductors separated by a narrow dielectric. It states existence of a supercurrent through it and equations governing it. The overdamped Josephson junction is modelled by a family of differential equations on two-torus depending on three parameters: B (abscissa), A (ordinate), ω (frequency). We study its rotation number ρ(B, A; ω) as a function of (B, A) with fixed ω. The phase-lock areas are the level sets L_r := {ρ = r} with non-empty interiors; they exist for 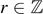$r\in \mathbb{Z}$ (Buchstaber, Karpov, Tertychnyi). Each L_r is an infinite chain of domains going vertically to infinity and separated by points. Those separating points for which A ≠ 0 are called constrictions. We show that: (1) all the constrictions in L_r lie on the axis {B = ωr}; (2) each constriction is positive: this means that some its punctured neighbourhood on the axis {B = ωr} lies in Int(L_r). These results confirm experiments by physicists (1970ths) and two mathematical conjectures. We first prove deformability of each constriction to another one, with arbitrarily small ω and the same 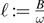$\ell {:=}\frac{B}{\omega }$, using equivalent description of model by linear systems of differential equations on $\bar{\mathbb{C}}$ (Buchstaber, Karpov, Tertychnyi) and studying their isomonodromic deformations described by Painlevé 3 equations. Then non-existence of ghost constrictions (i.e., constrictions either with 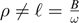$\rho \ne \ell =\frac{B}{\omega }$, or of non-positive type) with a given ℓ for small ω is proved by slow-fast methods.