Abstract
Symmetry indicates that low energy spectra of materials could be richer than well-known Dirac, semi-Dirac, or quadratic, hosting some unusual quasiparticles. Performing the systematic study of exact forms of low energy effective Hamiltonians and dispersions in high-symmetry points with fourfold degeneracy of bands, we found new, previously unreported dispersion, which we named poppy flower (PF) after its shape. This massless fermion exists in non-magnetic two-dimensional (2D) crystals with spin–orbit coupling (SOC), which are invariant under one of the proposed ten noncentrosymmetric layer groups. We suggest real three-dimensional (3D) layered materials suitable for exfoliation, having layers that belong to these symmetry groups as candidates for realization of PF fermions. In 2D systems without spin–orbit interaction, fortune teller (FT)-like fermions were theoretically predicted, and afterward experimentally verified in the electronic structure of surface layer of silicon. Herein, we show that such fermions can also be hosted in 2D crystals with SOC, invariant under additional two noncentrosymmetric layer groups. This prediction is confirmed by density functional based calculation: layered BiIO4, which has been synthesized already as a 3D crystal, exfoliates to stable monolayer with symmetry pb21a, and FT fermion is observed in the band structure. Analytically calculated density of states (DOS) of the PF shows semimetallic characteristic, in contrast to metallic nature of FT having non-zero DOS at the bands contact energy. We indicate possibilities for symmetry breaking patterns which correspond to the robustness of the proposed dispersions as well as to the transition from Dirac centrosymmetric semimetal to PF.
Export citation and abstract BibTeX RIS
1. Introduction
Electronic dispersion essentially determines crystal properties and it is well known that it is assigned by quantum numbers of the underlying symmetry group. These are space, layer (including wallpaper) or line groups, referring respectively to dimensionality of crystals: 3D, quasi-2D (Q2D), or quasi-1D. Probably the most famous example of a low-dimensional material is graphene (there are also related single layers, such as borophene [1], borophosphene [2], graphynes [3], etc), which hosts Dirac like (linear in quasi-momentum) dispersion in the vicinity of high symmetry Dirac points. Such shape of energy bands, besides being responsible for some intriguing phenomena, provides material realization of relativistic electron. This triggered numerous investigations of the connection between symmetry of materials and appearance of Dirac and Weyl points in their band structures. These points are attributed to existence of rotational [4], nonsymmorphic [5], mirror [6], space-time inversion [7, 8], time-reversal plus fractional translation [9], and generalized chiral symmetry [10]. There are also results on the search for Weyl and Dirac points according to group theoretical criteria in Brillouin zones (BZs) of all space [11], layer [12–14] or wallpaper groups [15].
In addition, geometrical symmetries impose conditions that lead to the emergence of unconventional quasiparticles in condensed matter systems. In 3D materials, enforced by space groups, double Dirac points [16], three-component [17, 18] or hourglass fermions [19] are found, inspiring further theoretical and experimental research [20–25]. Concerning Q2D systems, besides Dirac (as in graphene [26]), there are also semi-Dirac (Dirac-like in one direction, and quadratic in the orthogonal one, as in black phosphorus [27]), quadratic (as in molybdenum disulphide [28]), and fortune teller (FT) dispersions [29], which corresponds to the coexistence of a nodal point and lines. Namely, symmetry analysis of the possible completely linear dispersions in non-magnetic, Q2D materials with negligible spin–orbit coupling (SOC) has shown that only completely massless fermions appearing in layers are Dirac and FT [29]. Recently, FT dispersion has been experimentally confirmed in a surface layer of silicon [30].
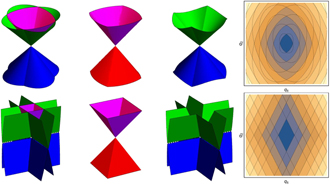
A question arises whether new types of fermions are possible in Q2D materials by inclusion of SOC? With help of layer double groups (LDGs) and time-reversal symmetry (TRS) (i.e. gray LDG), we made a quite general search for linear dispersions in the vicinity of high symmetry points (HSPs); since no reference to nonsymmorphic symmetries is made, the topological (hour-glass like) band crossing mechanisms are not a priori assumed, as it is usual. Indeed, it turns out that there are two peculiar types (figure 1) featuring twelve nonsymmorphic and noncentrosymmetric groups: two groups support previously predicted FT, and the remaining ones poppy flower (PF) dispersion (generalizing both FT and Dirac types).
Figure 1. PF (up) and FT (bottom) dispersions (given by equations (3.1)): from left to right are all bands, bands E±1,+1, bands E±1,−1 and horizontal sections of the bands (iso-energetic lines).
Download figure:
Standard image High-resolution imageAfter a brief overview of necessary group-theoretical methods, the obtained results are discussed on the basis of effective low-energy model, calculated densities of states and symmetry breaking patterns. Also, a list of material candidates supporting the new dispersions is provided. The predicted effect is justified by density functional based relaxation and band structure calculation in BiIO4 monolayer. Synthesis of this layered 3D material was reported around a decade ago [31]. Numerical band structure confirms our group theoretical prediction, which may be the motivation for future laboratory synthesis of this material as monolayer.
2. Method
Symmetry determines Bloch Hamiltonian in the vicinity of high-symmetry BZ wave vector through the allowed irreducible representations (IRs) of the little group [32]. Allowed IRs of LDGs are subduced from the corresponding space groups IRs (found on Bilbao Crystallographic Server [33]), and also independently constructed by POLSym code [34]. Concerning LDGs with TRS, the dimensions [33, 35] of the allowed IRs (actually co-representations) are 1, 2 or 4, and for generic ones, giving bands degeneracy, this is 1 or 2. Here we focus on the band structures near quadruple points at high-symmetry momenta. Further, we do not consider generically degenerate bands, giving double degenerate Dirac dispersion (precisely, it consists of two double spinfull degenerate cones meeting at one fourfold degenerate point); this automatically excludes centrosymmetric crystals, as Kramers degeneracy in them forbids non-degenerate bands [36]. Among the remaining groups, only twelve are with special points with four-dimensional allowed (co)representation.
Analysis of all allowed IRs R of little groups 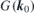 of HSPs k0 in LDG lacking the inversion symmetry gives the following conditions for quadruple point: k0 is time-reversal invariant momentum, R is two-dimensional, either real or complex IR. Therefore, we consider Ĥ(k) being Hamiltonian of the system Ĥ0 (including spin–orbit) in the basis
of HSPs k0 in LDG lacking the inversion symmetry gives the following conditions for quadruple point: k0 is time-reversal invariant momentum, R is two-dimensional, either real or complex IR. Therefore, we consider Ĥ(k) being Hamiltonian of the system Ĥ0 (including spin–orbit) in the basis 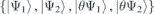 , where the spinors
, where the spinors  (i = 1, 2 counts two bands touching each other at k0 also in the absence of TRS) belong to R at k0 and θ is an anti-unitary operator of TRS, for which we used
(i = 1, 2 counts two bands touching each other at k0 also in the absence of TRS) belong to R at k0 and θ is an anti-unitary operator of TRS, for which we used 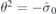 , since spinfull case is considered. Throughout the text
, since spinfull case is considered. Throughout the text 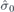 is two-by-two unit matrix, and
is two-by-two unit matrix, and 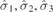 are Pauli matrices. Denoting the little group elements by ℓ = (h|r
are Pauli matrices. Denoting the little group elements by ℓ = (h|r + b), where h is crystallographic double point group element, while r
+ b), where h is crystallographic double point group element, while r and b are fractional and lattice translation, respectively, one gets the conditions imposed by time-reversal and geometrical symmetries on Ĥ(k0 + q) in the vicinity of k0 (therefore, the wavevector q is small):
and b are fractional and lattice translation, respectively, one gets the conditions imposed by time-reversal and geometrical symmetries on Ĥ(k0 + q) in the vicinity of k0 (therefore, the wavevector q is small):
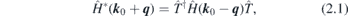
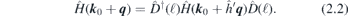
Here,  , and
, and  ' is an operator reduction of vector representation
' is an operator reduction of vector representation  to 2D BZ, while
to 2D BZ, while  represents the action of θ on the basis of spinors.
represents the action of θ on the basis of spinors.
To focus on the terms linear in q, Hamiltonian is expanded in the form 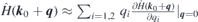 (energy scale is conveniently shifted such that Ĥ(k0) = 0). To incorporate symmetry, the matrix elements of the Hamiltonian gradient are arranged into the four-by-eight matrix Ŵ, which entries
(energy scale is conveniently shifted such that Ĥ(k0) = 0). To incorporate symmetry, the matrix elements of the Hamiltonian gradient are arranged into the four-by-eight matrix Ŵ, which entries 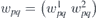 are pairs
are pairs 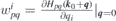 . The form
. The form
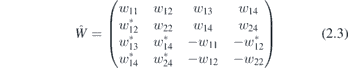
follows from the relation (2.1), together with  corresponding to the requirement that Hamiltonian Ĥ is a Hermitian operator. Note that the form (2.3) of Ŵ leads to the traceless Hamiltonian: it excludes the scalar term (which imposes the tilt of the bands). The geometrical symmetries are incorporated by (2.2), which is rewritten [11, 29] as an efficient fixed point condition
corresponding to the requirement that Hamiltonian Ĥ is a Hermitian operator. Note that the form (2.3) of Ŵ leads to the traceless Hamiltonian: it excludes the scalar term (which imposes the tilt of the bands). The geometrical symmetries are incorporated by (2.2), which is rewritten [11, 29] as an efficient fixed point condition
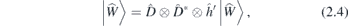
on the column vector (32 × 1) form 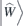 of Ŵ. The equation (2.4) is solved with help of the group projection operators for all of the twelve noncentrosymmetric groups hosting quadruple points at high symmetry momenta; in this way, the symmetry determines form of Ŵ. To explicate this, it is more convenient to use another general expansion of the effective low energy Hamiltonian,
of Ŵ. The equation (2.4) is solved with help of the group projection operators for all of the twelve noncentrosymmetric groups hosting quadruple points at high symmetry momenta; in this way, the symmetry determines form of Ŵ. To explicate this, it is more convenient to use another general expansion of the effective low energy Hamiltonian,
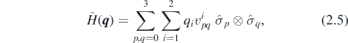
and find the constraints imposed by symmetry on the real coefficients 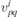 (simply interrelated with
(simply interrelated with 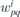 ).
).
3. Results and discussion
3.1. Symmetry adapted Hamiltonians and dispersions
Groups hosting new dispersions are listed in table 1. Besides intrinsic layer group notation (the first part), the space group of the system obtained by periodic repetition of the layer along axis perpendicular to it (column plane) according to Bilbao Crystallographic Server is also given (second part), where the directions x, y and z are along axes of orthorombic/tetragonal 3D primitive unit cell. On the other hand, in POLSym approach we used convention that layers are in xy-plane. Orthogonal lattice vectors a1 and a2 span primitive rectangular/square 2D unit cell, while reciprocal lattice vectors k1 and k2 satisfy aj⋅kl = 2πδj,l and q1, q2 are projections of q along k1 and k2. Relevant BZs are in figure 2.
Table 1. Groups providing dispersions (3.1). Notations for layer (columns 1 and 2) and space groups (columns 4, 5 and 6) are according to [37, 38] respectively. IR notation in the eighth column is as in Bilbao Crystallographic Server [33]. Effective Hamiltonian is indicated in the last column by the nonzero parameters (and their interrelations) of (2.5). For the last four groups a = c while 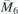 and
and 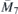 are conjugated pair of IRs.
are conjugated pair of IRs.
| Layer double group | Corresponding space double group | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Group | IR | Group | Plane | IR | Dispersion | Nonzero  | |||
| 21 | p21212 |  | 18 | P21212 | 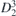 | z = 0 | 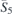 | (3.1a) | 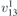 , , 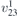 , , 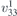 , , 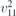 , , 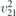 , , 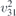 |
| 25 | pba2 |  | 32 | Pba2 | 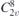 | z = 0 | 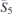 | (3.1a) |  , ,  , , 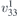 , , 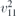 , , 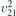 , , 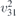 |
| 28 | pm21b | 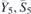 | 26 | Pmc21 | 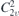 | y = 0 |  , Ū5 , Ū5 | (3.1a) | 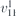 , , 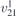 , , 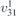 , , 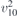 , , 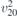 , , 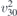 |
| 29 | pb21m | 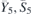 | 26 | Pmc21 | 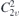 | x = 0 | 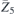 , , 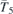 | (3.1b) | 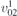 , , 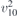 , , 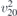 , , 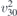 |
| 30 | pb2b | 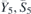 | 27 | Pcc2 | 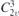 | x = 0 | 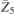 , , 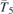 | (3.1a) | 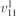 , , 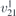 , , 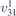 , , 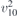 , , 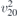 , , 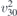 |
| 32 | pm21n |  5 5 | 31 | Pmn21 | 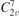 | y = 0 | 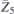 | (3.1a) | 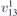 , , 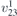 , ,  , ,  , , 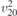 , , 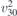 |
| 33 | pb21a |  5 5 | 29 | Pca21 |  | y = 0 | 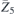 | (3.1b) | 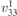 , ,  , , 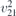 , , 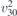 |
| 34 | pb2n |  5 5 | 30 | Pnc2 |  | x = 0 | 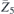 | (3.1a) | 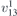 , ,  , , 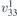 , , 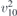 , , 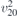 , , 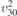 |
| 54 | p4212 | (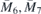 ) ) | 90 | P4212 | 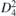 | z = 0 | ( ) ) | (3.1a) |  |
| 56 | p4bm | ( ) ) | 100 | P4bm | 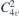 | z = 0 | (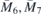 ) ) | (3.1a) | |
| 58 | 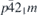 | (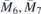 ) ) | 113 | 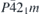 | 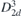 | z = 0 | (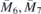 ) ) | (3.1a) | |
| 60 | 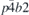 | ( ) ) | 117 | 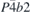 |  | z = 0 | (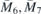 ) ) | (3.1a) | |
Figure 2. BZs of the groups (listed in table 1) supporting dispersions (3.1). For layer groups 28, 29, 30, 32, 33 and 34 vector k2 is along (screw) axis of order two.
Download figure:
Standard image High-resolution imageEffective Hamiltonians allowed by symmetry group in the special points of Brillouin's zone are presented in the last column of the table 1: the nonzero real coefficients 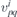 in the expansion (2.5) are specified, together with the constraints among them. The listed forms correspond to the group settings (lattice vectors and coordinate origin) and double valued irreducible co-representations obtained by POLSym code. In fact, this enabled flexibility in the choice of generators (coordinate system and translational periods), which finally results in the form of irreducible co-representations. These are chosen such to get the same form of the effective Hamiltonian whenever it is possible (for different groups). Equivalent (but different) settings (and co-representations) produce different (still equivalent with respect to dispersions) Hamiltonian forms. Clearly, the exact values of the nonzero coefficients
in the expansion (2.5) are specified, together with the constraints among them. The listed forms correspond to the group settings (lattice vectors and coordinate origin) and double valued irreducible co-representations obtained by POLSym code. In fact, this enabled flexibility in the choice of generators (coordinate system and translational periods), which finally results in the form of irreducible co-representations. These are chosen such to get the same form of the effective Hamiltonian whenever it is possible (for different groups). Equivalent (but different) settings (and co-representations) produce different (still equivalent with respect to dispersions) Hamiltonian forms. Clearly, the exact values of the nonzero coefficients  (listed in the last column of the table 1) are material dependent. The groups' generators and their representative matrices in the allowed co-representations associated to the specified high-symmetry points are in the table 2. It should be remarked that in all the considered cases this point is fixed by the whole gray group, i.e. the little group is the gray (double) group, and the allowed co-representations of the little group are simultaneously the irreducible co-representations of the gray group. The matrices of the relevant co-representations are four-dimensional. In all the cases time-reversal corresponds to the matrix
(listed in the last column of the table 1) are material dependent. The groups' generators and their representative matrices in the allowed co-representations associated to the specified high-symmetry points are in the table 2. It should be remarked that in all the considered cases this point is fixed by the whole gray group, i.e. the little group is the gray (double) group, and the allowed co-representations of the little group are simultaneously the irreducible co-representations of the gray group. The matrices of the relevant co-representations are four-dimensional. In all the cases time-reversal corresponds to the matrix 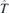 ; all other generators are represented by the block-diagonal matrices
; all other generators are represented by the block-diagonal matrices 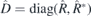 , with mutually conjugated 2 × 2 blocks. Therefore, only this block,
, with mutually conjugated 2 × 2 blocks. Therefore, only this block,  , is given in the table 2.
, is given in the table 2.
Table 2. Allowed irreducible co-representations: for each group and corresponding HSP, the generators are listed, and the block-diagonal part 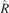 of double valued co-representation
of double valued co-representation 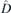 representing these generators (in the same order). Here,
representing these generators (in the same order). Here, 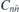 is rotation for 2π/n around axis
is rotation for 2π/n around axis 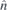 (which is
(which is 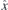 ,
,  ,
,  , or
, or  ),
), 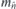 is vertical mirror plane which contains
is vertical mirror plane which contains 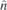 axis, mh is horizontal mirror plane, and Sn = Cn
axis, mh is horizontal mirror plane, and Sn = Cn mh.
mh.
| Group | HSP | Generators | 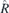 | ||||
|---|---|---|---|---|---|---|---|
| 21 | S | 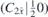 | 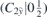 | 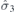 | 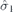 | ||
| 25 | S |  | 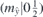 | 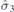 | 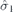 | ||
| 28 | Y | (I|10) |  | m | 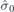 |  | 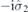 |
| 28 | S | (I|10) | 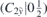 | m |  | 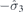 | 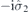 |
| 29 | Y | (I|10) | 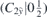 | mh |  | 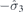 | 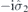 |
| 29 | S | (I|10) |  | mh | 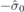 | 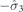 | 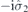 |
| 30 | Y | (I|10) | 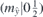 | C2 |  | 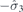 | 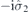 |
| 30 | S | (I|10) | 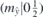 | C2 | 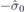 | 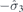 | 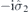 |
| 32 | Y | (I|10) | 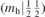 | m | 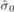 | 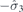 | 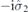 |
| 33 | Y | 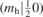 | 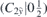 |  | 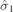 | ||
| 34 | Y | (I|10) | 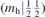 | C2 | 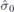 | 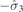 | 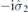 |
| 54 | M | (I|10) |  | C4 |  | 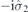 | 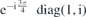 |
| 56 | M | (I|10) | 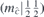 | C4 | 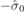 | 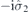 | 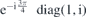 |
| 58 | M | (I|10) | 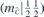 | S4 |  | 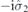 | 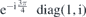 |
| 60 | M | (I|10) |  | S4 |  | 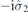 |  |
The described technique leads to two new types of dispersions (figure 1; crossings are taken at E = 0). The first one is PF, with four bands (obtained for u, v = ±1):
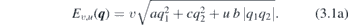
The expression under the square root is non-negative since a, b and c are positive quantities (functions of 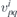 ) such that b2 − 4ac < 0. For quadratic layer groups (54, 56, 58, 60) c = a, and above dispersion degenerates to the isotropic one
) such that b2 − 4ac < 0. For quadratic layer groups (54, 56, 58, 60) c = a, and above dispersion degenerates to the isotropic one  . Two groups, 29 and 33, enforce b2 − 4ac = 0, hosting thus FT dispersions (with bands counted by u, v = ±1):
. Two groups, 29 and 33, enforce b2 − 4ac = 0, hosting thus FT dispersions (with bands counted by u, v = ±1):
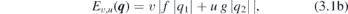
with f, g positive quantities, also functions of 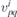 . Note that on the other side, the limit b → 0+ gives Dirac dispersion.
. Note that on the other side, the limit b → 0+ gives Dirac dispersion.
3.2. Density of states
Dispersions (3.1), differing from the well-known Dirac, semi-Dirac or quadratic, impose specific physical properties. In this context, one must take into account the range of validity of these forms, describing the realistic band structures only in the vicinity of high-symmetry point. In particular, corresponding density of states (DOS) near E = 0 are:
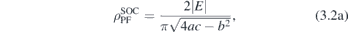
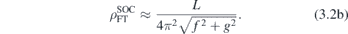
Unlike to PF, but similarly to 3D nodal semimetals [39], exact calculation of DOS of FT is prevented due to the non-circular iso-energetic lines (figure 1). Thus, the last expression corresponds to realistic situations where the horizontal parts of band crossing lines are of the length L (this is an effective range of approximation). In non-SOC case calculation of DOS gives doubled results (3.2), since each energy is spin degenerate, which is then decoupled from the orbital one. Non zero DOS of FT near E = 0 is in contrast to DOS of Dirac or PF dispersions being proportional to 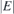 , as well as to semi-Dirac which is proportional to
, as well as to semi-Dirac which is proportional to 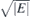 . This affects many properties, to mention only charge and spin transport. Further, it can be shown that the electron effective mass, obtained from band curvatures, for all dispersions (3.1) vanishes. Let us emphasize that the higher order terms, neglected in derivation cannot change the obtained band topology (figure 1), though may distort bands slightly.
. This affects many properties, to mention only charge and spin transport. Further, it can be shown that the electron effective mass, obtained from band curvatures, for all dispersions (3.1) vanishes. Let us emphasize that the higher order terms, neglected in derivation cannot change the obtained band topology (figure 1), though may distort bands slightly.
3.3. Symmetry breaking
Despite the obtained dispersions are essential, i.e. resistant to symmetry preserving perturbation, an interesting additional insight is gained by considering symmetry breaking. Herein, taking into account group–subgroup relations, we discuss the possibilities of robustness or switching between various dispersions at the same BZ-point by lowering the symmetry, e.g. due to strain. It is expected that decreasing the number of symmetry elements leads to relaxing the constraints imposed on Hamiltonians, and consequently increasing (or preserving) the number of independent parameters. In this context, taking into account the number of non-zero parameters 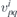 of (2.5) given in table 1, it is meaningful to consider the transitions from FT to anisotropic PF, as well as from isotropic PF to FT, when the symmetry is lowered. Precisely, the allowed four-band model Hamiltonian diagonalizing in PF dispersion have six real independent parameters, which are reduced to three for quadratic groups; similarly, there are 4 real independent Hamiltonian parameters for FT. Before proceeding, let us take a brief look into the robustness of FT and PF.
of (2.5) given in table 1, it is meaningful to consider the transitions from FT to anisotropic PF, as well as from isotropic PF to FT, when the symmetry is lowered. Precisely, the allowed four-band model Hamiltonian diagonalizing in PF dispersion have six real independent parameters, which are reduced to three for quadratic groups; similarly, there are 4 real independent Hamiltonian parameters for FT. Before proceeding, let us take a brief look into the robustness of FT and PF.
Regarding groups 29 and 33 supporting FT dispersion, symmetry reduction in which either nonsymmorphic glide plane or screw axis (but not both) is retained causes that FT at the Y point splits into two non-degenerate conical dispersions. Opposite out-of-plane shifts of the adjacent nuclei positioned in the mirror plane, transforms mirror into a glide plane, while doubling the lattice constant; this in turn halves primitive vector k1 of the reciprocal lattice. Group 29 reduces to 33 and the S point in 29 becomes Y point in 33. Consequently, FT in Y and S points in 29 are robust against lowering the symmetry to group 33. Similarly, concerning the PF, any homogenous stretching along a1 or a2 axis deforms square primitive cell to rectangular, reducing the symmetries of layer groups 54 and 58 (56 and 60) to the group 21 (25) and causes PF to change from isotropic to anisotropic form, which implies direction-dependent electronic and related properties.
Since PF is a generalized form of FT, one could expect that the parameters of these dispersions can be interrelated by tuning. However, continuous transformation from FT to PF at the same point of the BZ is not possible, since neither of groups supporting FT is a subgroup of any of groups allowing PF, nor vice-versa. The expression (3.2a) for DOS of PF shows that the changing parameters such that PF approaches to FT results in a singularity at zero energy. In the other words, if opposite would hold, arbitrarily small displacements of nuclei, being sufficient to lower the symmetry, would cause a jump of (graphene-like) negligible DOS of PF to a finite and constant DOS of FT, which we found unlikely. At the same time, such obstruction from DOS does not forbid the transition between Dirac (double degenerate cones with four-fold degenerate point) and PF, nor it forbids splitting of FT and PF into two non-degenerate conical dispersions (with double degenerate point).
Following the above arguments, it is expected that transition from Dirac cone to PF may be realized by lowering the symmetry, since Dirac dispersions has less independent parameters than PF. According to [5] Dirac semimetals in time-reversal invariant two-dimensional systems with strong SOC are possible in nonsymmorphic groups with inversion symmetry. E.g. let us consider the layer group 46 (pmmn), hosting Dirac cones at X, Y and S HSPs (the BZ is the same as this one given on the left panel in figure 2). It is expected that the violation of the inversion symmetry leads to Weyl points or node [5]. However, listing all subgroups, it turns out that the two of the subgroups, 32 and 21, actually host PF in the points Y and S, respectively. Indeed, in [46], using spinfull tight-binding model with four sites (with s-orbitals) per unit cell, authors show that at fillings 2, 6, system invariant under double layer group 21 is semimetal, which hosts one fourfold degenerate and four Weyl points. A plethora of such cases, where groups allowing PF from the table 1 are subgroups of symmetry groups of Dirac semimetals, indicates candidates for transitions between centrosymmetric and noncentrosymmetric crystals with protected four-fold band crossing point. Moreover, the existence of such essential fourfold degenerate point simultaneously with double degenerate Weyl points in the same system, makes that the layers from our list represent possible two-dimensional materials suitable for the study of their interplay.
3.4. Material realization
Despite the fabrication of freestanding layers is not always feasible, the above theoretical predictions required material realizations, or at least numerical simulations. To find realistic material with layer groups from table 1 we searched the list [41] of 3D layered materials, synthesis of which has been reported in the literature. In the table 3 we listed potential material candidates with symmetry groups allowing the predicted peculiar dispersions. These are laboratory fabricated 3D crystals with layered structures, which could be easily or potentially exfoliated into layers.
Table 3. Material candidates: layered systems with symmetry groups hosting the dispersions (3.1). Layer and corresponding space groups are listed for materials given by a formula and materials project ID. Abbreviations EE and PE stand for easily and potentially exfoliable, respectively, according to [41].
| Layer group | Space group | Formula | ID | EE/PE | ||
|---|---|---|---|---|---|---|
| 21 | p21212 | 18 | P21212 | As2SO6 | mp-27230 | EE |
| MgMoTeO6 | mp-1210722 | EE | ||||
| 25 | pba2 | 32 | Pba2 | Au2Se2O7 | mp-28095 | EE |
| Re2S2O13–I | mp-974650 | EE | ||||
| 28 | pm21b | 26 | Pmc21 | TlP5 | mp-27411 | EE |
| KO2H4F | mp-983327 | PE | ||||
| NaGe3P3 | mp-1104707 | PE | ||||
| 29 | pb21m | 26 | Pmc21 | WO2Cl2 | mp-32539 | EE |
| 32 | pm21n | 31 | Pmn21 | CuCOCl | mp-562090 | EE |
| 33 | pb21a | 29 | Pca21 | BiIO4 | mp-1191266 | PE |
| KPSe6 | mp-18625 | EE | ||||
| 58 | 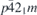 | 113 | 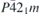 | LiReO2F4 | mp-554108 | EE |
It is interesting to single out our group-theoretical findings indicated that dispersions (3.1) are not preserved when SOC is neglected, except for the LDG 33, which supports FT dispersion also in that case [29]. Inclusion of SOC moves FT from BZ corners to the Y-point. The material BiIO4 belongs to corresponding space group 29 and has layers parallel to the y = 0 plane. Consequently, it should exfoliate to layer group 33 so we choose it for further DFT investigations, as an example of achievements of our theory. Since IRs from table 1 are the only extra IRs in these BZ points, the dispersions (3.1) are unavoidable for crystals with symmetry of these groups. On the other hand, the position of Fermi level cannot be determined solely by symmetry arguments, nor it can be guaranteed that no other bands cross or touch the Fermi level.
We determined crystal (figure 3) and band structure (figure 4) of BiIO4 mono-layer configuration using DFT calculations: full relaxation and bands calculations were performed by QUANTUM ESPRESSO software package [42], full relativistic PAW pseudopotentials [43, 44], with the Perdew–Burke–Ernzerhof exchange–correlation functional [45]. The energy cutoff for electron wavefunction and charge density of 47 Ry and 476 Ry were chosen, respectively. The band structures were found in 500 k-points on selected path, and 2500 k-points for 2D band structure plots in the vicinity of HSPs.
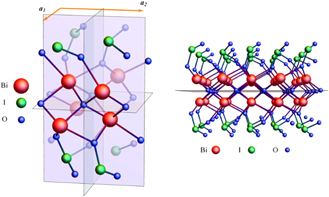
Figure 3. Crystal structure of BiIO4 mono-layer: elementary cell (left) and a part of layer (right).
Download figure:
Standard image High-resolution imageFigure 4. Band structure of BiIO4 mono-layer without SOC (top) and with SOC (bottom), with insets showing magnified FT and split FT dispersions. The Fermi level is set to zero eV.
Download figure:
Standard image High-resolution imageCrystal structure of mono-layer is shown in figure 3. It belongs to rectangular lattice of the group 33, with nearly equal a1 = 0.566 nm and a2 = 0.575 nm. Band structure of BiIO4 mono-layer with and without SOC is shown in figure 4. It turns out that the system is insulating in undoped and ungated regime. The closest to Fermi level FT state is at −0.9 eV. When SOC is neglected energy at the point S is eightfold degenerate (including spin), which gives electron filling of 8n that is necessary for insulating systems [40]. With inclusion of SOC the eightfold spinfull degeneracy at S is lifted, but sets of eight non-degenerate bands each, form cat's cradle structure along ΓX line, as predicted in reference [46]. This gives again electron filling of 8n [46, 47]. Our electron filling of 184, derived from DFT calculations, is indeed divisible by 8. Electron filling for DLG 33 prevents FT to be the only dispersion at the Fermi level, while for remaining groups in table 1 the filling condition necessary for Fermi surface consisting of isolated points is ν = 4n + 2.
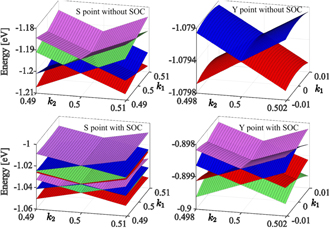
Behavior of FT states with inclusion of SOC is shown in figure 5. In non-SOC case, two pairs of Dirac lines meet at the point S and form the FT states. SOC splits eightfold degenerate band at S into four double degenerate ones. Near point Y, SOC splits fourfold spinfull degenerate Dirac line into one FT state. Since SOC strength is proportional to the fourth power of the atomic number [48], heavy elements in the material induced observable splitting.
Figure 5. Band structures of BiIO4 mono-layer without and with SOC near points S and Y. Inclusion of SOC turns FT dispersion into nodal lines in S, and degenerate Dirac line into FT in Y.
Download figure:
Standard image High-resolution image4. Conclusions
Characterized by band crossings (touching) points (lines) at Fermi level from which energies disperse linearly, nodal metals/semimetals take an important role in investigations of various topological properties of crystals. Among them, symmetry-enforced ones represent a class of materials hosting such dispersions in HSPs due to increased degeneracy. In the language of group theory, while the spinless case is described by the ordinary group of geometrical transformations, the spinfull situation, when system is robust on spin–orbit perturbation, needs double groups. Additional inclusion of TRS leads to gray magnetic ordinary or double group. The increased degeneracy of energy is enabled by higher dimensional allowed irreducible (co)representations of the corresponding underlying crystal symmetry.
New fermions in 2D materials revealed by application of full gray double layer group symmetry contribute to the interesting physical phenomena of layered systems: two new types of dispersions beyond Dirac, PF and FT, accompany the fourfold degeneracy of bands in high-symmetry points. Our findings single out list of twelve nonsymmorphic and noncentrosymmetric layer groups that support such unusual linear electronic dispersions. As the method is not based on the topological mechanism (invoking nonsymmorphic symmetry), the result is general, verifying a posteriori the necessity of nonsymmorphic elements for the considered dispersions. Providing this list, numerical simulations aimed to find material realizations of the peculiar dispersions are facilitated, which is of a great importance to achieve corresponding physical properties. PF dispersion occurs in ten groups; in particular, there are single isolated HSP hosting it in the groups p21212, pba2 (point S), pm21n, pb2n (Y), and p4212, p4bm,  ,
, 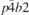 (M), while the groups pm21b and pb2b have two such points (Y, S). On the other hand, the FT type of dispersion in the group pb21a is hosted in single (Y), and in the group pb21m in two HSPs (Y, S).
(M), while the groups pm21b and pb2b have two such points (Y, S). On the other hand, the FT type of dispersion in the group pb21a is hosted in single (Y), and in the group pb21m in two HSPs (Y, S).
Particularly interesting are groups pb21a, supporting FT dispersion both with and without SOC, as well as pba2 and p4bm, which are also wallpaper groups, preserved even when perpendicular, homogenous electric field is applied (e.g. due to gating). Moreover, coexistence of degenerate point and lines at the same energy in FT dispersion may lead to some new phenomena. FT dispersion has constant contribution to DOS, manifested as a plateau nearby zero energy in FT. This may be important in technological applications, especially when electron and/or spin transport are looked for, like materials for solar cells [49], spintronic etc. On the contrary, PF dispersion, similarly to Dirac ones, contributes by linear DOS with no states on zero energy. It has both isotropic and anisotropic forms which may be continuously transformed into each other by crystal deformations.
Our numerical calculations show that layered BiIO4 3D crystal, exfoliates to stable mono-layer having a symmetry group from our list. Band structure of BiIO4 mono-layer confirms theoretical prediction, but further efforts are necessary in order to place the Fermi level at right energy.
Acknowledgments
Authors VD, AŠ and JP acknowledge funding provided by the Institute of Physics Belgrade, through the Grant by the Ministry of Education, Science and Technological Development of the Republic of Serbia. NL, BN and MD were supported by the Serbian Ministry of Education, Science and Technological Development under Project Number OI171035. DFT calculations were performed using computational resources at Johannes Kepler University, Linz, Austria.