Abstract
In this research, the decay of  is studied in two stages. In the first step, the QCD factorization (QCDF) approach is considered in the initial evaluation, the result of calculation is
is studied in two stages. In the first step, the QCD factorization (QCDF) approach is considered in the initial evaluation, the result of calculation is  . While the available experimental result for this decay is
. While the available experimental result for this decay is  , by applying the theoretical value of the
, by applying the theoretical value of the  that span the range of [0.9, 8.0]%, the result for QCDF approach becomes
that span the range of [0.9, 8.0]%, the result for QCDF approach becomes  ) **
) **  →
→  =
=  and the branching ratio in the experimental observation is obtained in the range of 2.57%–29.76% which is a large range. Therefore, it is decided to calculate the theoretical branch ratio by applying the effects of the final state interaction (FSI) through only possible cross section channel. In this process, before the meson
and the branching ratio in the experimental observation is obtained in the range of 2.57%–29.76% which is a large range. Therefore, it is decided to calculate the theoretical branch ratio by applying the effects of the final state interaction (FSI) through only possible cross section channel. In this process, before the meson  decays into two final mesons,
decays into two final mesons,  , first, it decays into two intermediate mesons (as
, first, it decays into two intermediate mesons (as  ), then these two intermediate mesons are converted into two final mesons by the exchange of another meson, (such as K+ corresponding to
), then these two intermediate mesons are converted into two final mesons by the exchange of another meson, (such as K+ corresponding to  ). The FSI effects are highly sensitive to the phenomenological parameters that appear in the form factor relationship, so that in most calculations, change the three units in the numeric value of this parameter changes the final result ten times. Therefore, the decision to use FSI is not unexpected. In this study, there are four intermediate states in the cross section channel in which the amplitude of each of them are calculated separately and included in the final amplitude. Considering
). The FSI effects are highly sensitive to the phenomenological parameters that appear in the form factor relationship, so that in most calculations, change the three units in the numeric value of this parameter changes the final result ten times. Therefore, the decision to use FSI is not unexpected. In this study, there are four intermediate states in the cross section channel in which the amplitude of each of them are calculated separately and included in the final amplitude. Considering  , the numerical value of the
, the numerical value of the  is from (1.54 ± 0.20) × 10−3 to (2.89 ± 0.41) × 10−3 for which obtained by entering the QCDF approach and FSI effects (η = 0.5–1.5). It should be noted that by choosing the value of the η according to the mass of the exchange meson, as η = 1.5 for exchange meson of B* (or B) and η = 0.5 for exchange meson of K* (or K) the obtained result is
is from (1.54 ± 0.20) × 10−3 to (2.89 ± 0.41) × 10−3 for which obtained by entering the QCDF approach and FSI effects (η = 0.5–1.5). It should be noted that by choosing the value of the η according to the mass of the exchange meson, as η = 1.5 for exchange meson of B* (or B) and η = 0.5 for exchange meson of K* (or K) the obtained result is  , that is in very good agreement with the experimental result.
, that is in very good agreement with the experimental result.
Export citation and abstract BibTeX RIS
1. Introduction
The weak decay channels of  meson can occur in three classes: (1) c weak decay modes:
meson can occur in three classes: (1) c weak decay modes:  , in these transitions b-quark plays the role of the spectator, more than 70% of the
, in these transitions b-quark plays the role of the spectator, more than 70% of the  width is due to c-quark decays, in which
width is due to c-quark decays, in which  transition has been observed with
transition has been observed with  decays [1]. (2)
decays [1]. (2)  weak decay modes:
weak decay modes:  , with c-quark as a spectator, around 20% of
, with c-quark as a spectator, around 20% of  meson decay width is due to the b-quark decays [2]. (3) Pure weak annihilation channels, the
meson decay width is due to the b-quark decays [2]. (3) Pure weak annihilation channels, the  annihilation amplitudes account for only 10% of the
annihilation amplitudes account for only 10% of the  . In the study of the
. In the study of the  decay, all three classes are important.
decay, all three classes are important.
The  decay has been observed by LHCb collaboration with a statistical significance of 5.1 standard deviations. They have been obtained a measurement of the branching fraction multiplied by the production rates for
decay has been observed by LHCb collaboration with a statistical significance of 5.1 standard deviations. They have been obtained a measurement of the branching fraction multiplied by the production rates for  relative to
relative to  mesons in the LHCb acceptance as [1]:
mesons in the LHCb acceptance as [1]:

The ratio of the production cross-sections of the  and B+ mesons,
and B+ mesons,  , can be get from the measurement involving another charmonium mode,
, can be get from the measurement involving another charmonium mode,  obtained from [3]. Although there is no experimental result for the
obtained from [3]. Although there is no experimental result for the  decay, but acceptable values have been calculated for it [4, 5]. So that the CMS [6] and LHCb [7, 8] collaborations have been used these theoretical values in their experimental estimates. Using the predictions listed in [4] for
decay, but acceptable values have been calculated for it [4, 5]. So that the CMS [6] and LHCb [7, 8] collaborations have been used these theoretical values in their experimental estimates. Using the predictions listed in [4] for  , which span the range (0.34–2.91) × 10−3,
, which span the range (0.34–2.91) × 10−3, ![$\sigma ({B}_{c}^{+})/\sigma ({B}^{+})\sim [0.23,2.15] \% $](https://content.cld.iop.org/journals/0954-3899/47/4/045003/revision1/jpgab6af6ieqn35.gif) is obtained [8]. Using the additional relation
is obtained [8]. Using the additional relation  quoted also in [8], it follows that the ratio of interest
quoted also in [8], it follows that the ratio of interest  lies in the range [0.9, 8.0]%. So the branching fraction in the experimental observation becomes:
lies in the range [0.9, 8.0]%. So the branching fraction in the experimental observation becomes:
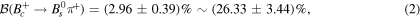
in this case its width will be from 2.57% to 29.76%. In the present work we calculate the branching fraction of the  decay by using the QCD factorization approach and effects of the FSI, the amount obtained from the first method is (16.52 ± 2.21)% in which located in the middle of the above range. Entering the FSI effects the values are obtained in the range of (16.92 ± 2.26)% to (32.07 ± 4.54)%, which are in good agreement with the range obtained in the equation (2). On the hand, for direct comparison with the experimental value, we multiply our predicted branching fraction by the estimates for
decay by using the QCD factorization approach and effects of the FSI, the amount obtained from the first method is (16.52 ± 2.21)% in which located in the middle of the above range. Entering the FSI effects the values are obtained in the range of (16.92 ± 2.26)% to (32.07 ± 4.54)%, which are in good agreement with the range obtained in the equation (2). On the hand, for direct comparison with the experimental value, we multiply our predicted branching fraction by the estimates for ![$\sigma ({B}_{c}^{+})/\sigma ({B}_{s}^{0})\sim [0.9,8.0] \% $](https://content.cld.iop.org/journals/0954-3899/47/4/045003/revision1/jpgab6af6ieqn39.gif) and get comparable result.
and get comparable result.
2. Short-distance contributions
In the QCD factorization (QCDF) approach, the  meson decays to
meson decays to  mesons via
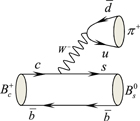
mesons via  transition, in this case there is a tree level a1 Wilson coefficient that has the dominant contribution. Feynman diagram in figure 1 clearly shows this process. So the amplitude reads
transition, in this case there is a tree level a1 Wilson coefficient that has the dominant contribution. Feynman diagram in figure 1 clearly shows this process. So the amplitude reads

where a1 = c1 + c2/3, fπ is the decay constant of the pion and  is the
is the  transition form factor which has been obtained in the
transition form factor which has been obtained in the  region. The form factors for
region. The form factors for  and s transitions are calculated via [9]
and s transitions are calculated via [9]

where F(0) = 0.73 ± 0.03, mfit = 1.77 ± 0.22 and δ = 0.60 ± 0.18 for  form factor. The branching fraction of
form factor. The branching fraction of  in
in  meson rest frame can be written as
meson rest frame can be written as

in which  is the absolute value of the 3-momentum of the
is the absolute value of the 3-momentum of the  or π+ mesons that can be calculated via:
or π+ mesons that can be calculated via:  and
and  is the lifetime of the
is the lifetime of the  meson. We obtain the following value for the branching ratio
meson. We obtain the following value for the branching ratio
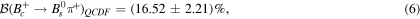
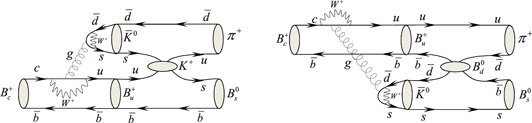
which is located in the middle of the branching fraction value in the experimental observation. It seems that, this decay mode requires a stronger model, a newer method or the effect of natural truth, which can compensate for this major difference. This is the effects of the FSI. Effect of FSI is a natural effect that has a significant contribution to some decays, especially in the  decay. This effect states that, before the final mesons are produced, other mesons may be produced along the way in the intermediate modes. In this case, two mesons produced in the middle state exchange another meson then they become the final two mesons. The Feynman graphs determine the type of intermediate and exchange mesons. These diagrams are presented in three different types for the quark model in FSI, (I) s-channel (II) t-channel (III) cross section channel. In B decays, in contrast to D decays, the resonant FSI will be expected to be suppressed relative to the rescattering effect arising from quark exchange owing to the lack of the existence of resonances at energies close to the B meson mass, this means that one can neglect the s-channel contribution. In the t-channel, two final mesons,
decay. This effect states that, before the final mesons are produced, other mesons may be produced along the way in the intermediate modes. In this case, two mesons produced in the middle state exchange another meson then they become the final two mesons. The Feynman graphs determine the type of intermediate and exchange mesons. These diagrams are presented in three different types for the quark model in FSI, (I) s-channel (II) t-channel (III) cross section channel. In B decays, in contrast to D decays, the resonant FSI will be expected to be suppressed relative to the rescattering effect arising from quark exchange owing to the lack of the existence of resonances at energies close to the B meson mass, this means that one can neglect the s-channel contribution. In the t-channel, two final mesons,  and
and  should share their similar quark that have the same flavor, but they do not have the same quark. In fact this process is only done with the cross section channel. In the cross section channel, each of the two final mesons exchanges a quark (these quarks do not have the same flavors) crosswise with the intermediate mesons. For the
should share their similar quark that have the same flavor, but they do not have the same quark. In fact this process is only done with the cross section channel. In the cross section channel, each of the two final mesons exchanges a quark (these quarks do not have the same flavors) crosswise with the intermediate mesons. For the  decay, final state mesons of
decay, final state mesons of  and π+ exchange the s and u quarks with the
and π+ exchange the s and u quarks with the  and B+ mesons in the intermediate states, respectively. In this case the K+ meson can participate as a meson of exchange. In the another process the final state mesons of
and B+ mesons in the intermediate states, respectively. In this case the K+ meson can participate as a meson of exchange. In the another process the final state mesons of  and π+ can be exchanged the
and π+ can be exchanged the  and
and  anti-quarks, respectively. Wherever the intermediate state mesons are the same as before (
anti-quarks, respectively. Wherever the intermediate state mesons are the same as before ( and B+) and the exchange meson become B0. These processes are shown in figure 2. In general, the amplitude of the
and B+) and the exchange meson become B0. These processes are shown in figure 2. In general, the amplitude of the  decay, using the FSI effects in cross section channel, is obtained from calculating the following four decay amplitudes:
decay, using the FSI effects in cross section channel, is obtained from calculating the following four decay amplitudes:

Figure 1. The Feynman diagram contributing to the  decay.
decay.
Download figure:
Standard image High-resolution imageFigure 2. Contributions to  from the color-allowed weak decay
from the color-allowed weak decay  followed by quark exchange.
followed by quark exchange.
Download figure:
Standard image High-resolution image3. Long-distance contributions
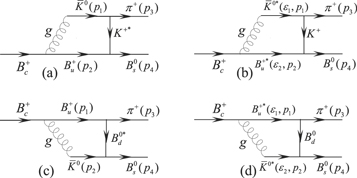
The diagrams which determine the long-distance FSI contributions on the rate of  decay are depicted in figure 3. The amplitude of the mode
decay are depicted in figure 3. The amplitude of the mode  with the exchange of the
with the exchange of the  , it follows that the absorptive part of figure 3(a) is given by
, it follows that the absorptive part of figure 3(a) is given by
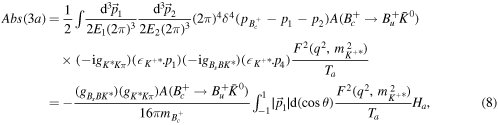
where
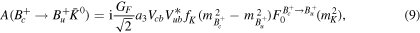
the form factor of the  is calculated via equation (4) by applying the values of the F(0) = 0.63 ± 0.04, mfit = 1.52 ± 0.20 and δ = 0.52 ± 0.13. In equation (8) θ is the angle between
is calculated via equation (4) by applying the values of the F(0) = 0.63 ± 0.04, mfit = 1.52 ± 0.20 and δ = 0.52 ± 0.13. In equation (8) θ is the angle between  and
and  , q and mi are the momentum and mass of the exchange
, q and mi are the momentum and mass of the exchange  meson, respectively, and
meson, respectively, and

and  is the form factor defined to take care of the off-shell character of the exchange particles, defined as [10, 11]
is the form factor defined to take care of the off-shell character of the exchange particles, defined as [10, 11]

The form factor (i.e. n = 1) normalized to unity at  . mi and q are the physical parameters of the exchange particle and Λ is a phenomenological parameter. It is obvious that for
. mi and q are the physical parameters of the exchange particle and Λ is a phenomenological parameter. It is obvious that for  ,
,  becomes a number. If Λ ≫ mi then
becomes a number. If Λ ≫ mi then  turns to be unity, whereas, as
turns to be unity, whereas, as  the form factor approaches to zero and the distance becomes small and the hadron interaction is no longer valid. Since Λ should not be far from the mi and q, we choose
the form factor approaches to zero and the distance becomes small and the hadron interaction is no longer valid. Since Λ should not be far from the mi and q, we choose

where η is the phenomenological parameter that its value in the form factor is expected to be of the order of unity and can be determined from the measured rates. According to the exchanged mesons, variable used values from 0.5 to 5 can be found for it. In [12] the exchanged mesons are D and D*, so the authors have chosen η = 0.5–3.0. However, the authors of [13] with the same exchanged mesons have fixed η ∼ 5. In this regard, in the [14], the value of the 4 has been fixed for this phenomenological parameter. In this work since the exchanged mesons in figure 2 are  and K+ (heavy and light mesons), to select the values of η from 0.5 until 1.5, we follow the [15] in which their exchanged mesons are both heavy and light. On the other hand, in the [10] the value of the η is selected corresponding to the mass of the meson exchanged: η = 2.2 for the exchanged particle D* (or D) and η = 1.1 for ρ (or π). This type of choice is also applied in this work, as η = 1.5 is selected for exchange meson B (or B*) and η = 0.5 for K (or K*). The result of this selection is presented separately. Likewise, for diagram 3(b), the amplitude of the
and K+ (heavy and light mesons), to select the values of η from 0.5 until 1.5, we follow the [15] in which their exchanged mesons are both heavy and light. On the other hand, in the [10] the value of the η is selected corresponding to the mass of the meson exchanged: η = 2.2 for the exchanged particle D* (or D) and η = 1.1 for ρ (or π). This type of choice is also applied in this work, as η = 1.5 is selected for exchange meson B (or B*) and η = 0.5 for K (or K*). The result of this selection is presented separately. Likewise, for diagram 3(b), the amplitude of the  (where K+ is exchanged particle) is given by
(where K+ is exchanged particle) is given by
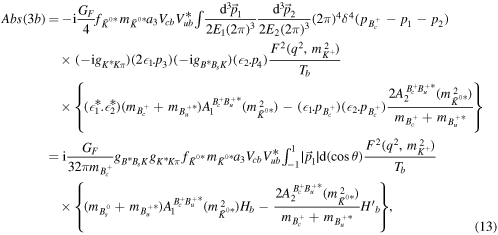
where the form factor of the  is calculated via equation (4) by applying the values of the F(0) = 0.43 ± 0.01, mfit = 1.16 ± 0.07 and δ = 0.27 ± 0.03. The form factors of
is calculated via equation (4) by applying the values of the F(0) = 0.43 ± 0.01, mfit = 1.16 ± 0.07 and δ = 0.27 ± 0.03. The form factors of  and
and  are related to each other via:
are related to each other via:
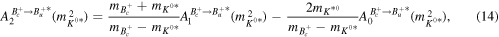
where the values of the F(0) = 0.47 ± 0.01, mfit = 0.99 ± 0.04 and δ = 0.31 ± 0.03 are used for  form factor, and
form factor, and
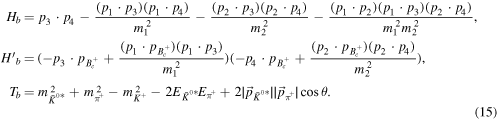
Figure 3. The long-distance cross section channel contributions to the color-allowed penguin amplitude in  .
.
Download figure:
Standard image High-resolution imageThe amplitude of the mode  with the exchange of the
with the exchange of the  is given by
is given by

where
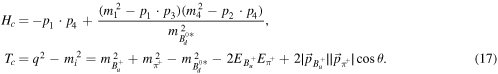
The amplitude of the  (where
(where  is exchanged particle) is given by
is exchanged particle) is given by

where

The dispersive part of the rescattering amplitude can be obtained from the absorptive parts via the dispersion relation [10, 16]
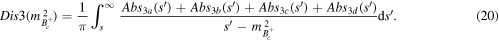
where s is the threshold of intermediate states, in this case  . The decay amplitude of
. The decay amplitude of  via the FSI corrections is
via the FSI corrections is
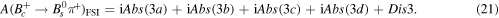
Then the decay amplitude for the  decay by using the QCDF approach considering the effects of FSI turn to
decay by using the QCDF approach considering the effects of FSI turn to
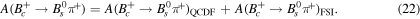
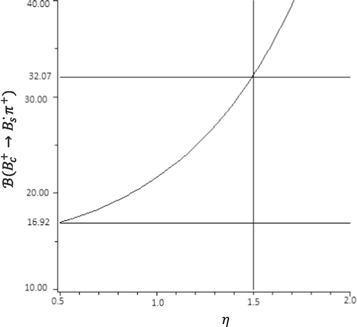
The numerical values of the absorptive and dispersive parts used in the calculation are given separately in table 1. Finally, using the above amplitude in the equation (5) and the input parameters of table 2, we are able to calculate the branching ratio of  decay with different values of η. The results are shown in table 3 and figure 4. In figure 4, we present the dependence of the branching ratio of
decay with different values of η. The results are shown in table 3 and figure 4. In figure 4, we present the dependence of the branching ratio of  decay on η. In this work the absorptive and dispersive parts of the four diagrams in figure 3 are calculated using the same value of η (for example η = 1 for all four diagrams) and contributed to the FSI amplitude. Then the amplitude resulting from the FSI effects with amplitude of the QCDF method are considered as the total amplitude. Note that, in addition to the conventional selection of η, we choose its value according to the mass of the exchange meson, as η = 1.5 for exchange meson of B* (or B) and η = 0.5 for exchange meson of K* (or K). The result is as follow:
decay on η. In this work the absorptive and dispersive parts of the four diagrams in figure 3 are calculated using the same value of η (for example η = 1 for all four diagrams) and contributed to the FSI amplitude. Then the amplitude resulting from the FSI effects with amplitude of the QCDF method are considered as the total amplitude. Note that, in addition to the conventional selection of η, we choose its value according to the mass of the exchange meson, as η = 1.5 for exchange meson of B* (or B) and η = 0.5 for exchange meson of K* (or K). The result is as follow:
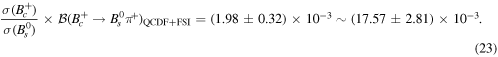
In this work we find that the best choice for η is proportional to the mass of the intermediate mesons and besides choosing  guide us to the closet answer to the experience. In addition to the changes of η from 0.5 to 1.5, in many cases of input parameters, there are uncertainties arising from the variation of CKM parameters, meson masses, form factors and decay constants. The uncertainties in table 2 are due to these uncertainties.
guide us to the closet answer to the experience. In addition to the changes of η from 0.5 to 1.5, in many cases of input parameters, there are uncertainties arising from the variation of CKM parameters, meson masses, form factors and decay constants. The uncertainties in table 2 are due to these uncertainties.
Figure 4. The dependence of the branching ratio of  on η.
on η.
Download figure:
Standard image High-resolution imageTable 1. Absorptive and dispersive parts of the FSI amplitude (in units of 10−6).
| η | Absorptive | Dispersive |
|---|---|---|
| 0.50 | 1.05 ± 0.07 | 0.23 ± 0.02 |
| 0.75 | 2.18 ± 0.15 | 0.49 ± 0.03 |
| 1.00 | 3.26 ± 0.23 | 0.74 ± 0.05 |
| 1.25 | 4.46 ± 0.31 | 1.01 ± 0.07 |
| 1.5 | 6.42 ± 0.46 | 1.51 ± 0.11 |
Table 2. Default values of the input parameters.
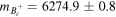 , , 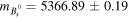 , , 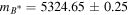 , , 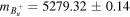 , , |
 , , 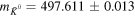 , ,  , , |
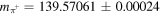 (MeV) [17] (MeV) [17] |
fK = 159.80 ± 1.84, 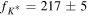 , fπ = 130.70 ± 0.46 (MeV) [17] , fπ = 130.70 ± 0.46 (MeV) [17] |
Vub = 0.003 94 ± 0.000 36, Vcb = 0.0422 ± 0.0008,  , Vud = 0.974 20 ± 0.000 21 [17] , Vud = 0.974 20 ± 0.000 21 [17] |
ΛQCD = 0.225 GeV, 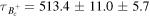 fs [18, 19] fs [18, 19] |
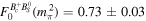 , , 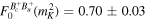 , , |
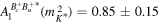 , ,  [9] [9] |
| c1 = 1.081, c2 = −0.190, c3 = 0.014, c4 = −0.036 [20] |
 , ,  , , 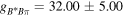 [21, 22], [21, 22], 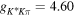 [11] [11] |
Table 3.
The branching ratio of  decay with
decay with ![$\sigma ({B}_{c}^{+})/\sigma ({B}_{s}^{0})=[0.9,8.0] \% $](https://content.cld.iop.org/journals/0954-3899/47/4/045003/revision1/jpgab6af6ieqn120.gif) , η = 0.5–1.5 and experimental data (BR in EXP is the branch ratio present in the experimental observation).
, η = 0.5–1.5 and experimental data (BR in EXP is the branch ratio present in the experimental observation).
| Contributions | η |
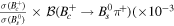 ) ) |
 (×10−2) (×10−2) |
|---|---|---|---|
| QCDF | — | (1.49 ± 0.20) ∼ (13.22 ± 1.77) | 16.52 ± 2.21 |
| 0.50 | (1.54 ± 0.20) ∼ (13.53 ± 1.78) | 16.92 ± 2.26 | |
| 0.75 | (1.64 ± 0.22) ∼ (14.62 ± 1.94) | 18.28 ± 2.48 | |
| QCDF+FSI | 1.00 | (1.84 ± 0.25) ∼ (16.38 ± 2.23) | 20.47 ± 2.79 |
| 1.25 | (2.16 ± 0.31) ∼ (19.45 ± 2.94) | 23.93 ± 3.33 | |
| 1.5 | (2.89 ± 0.41) ∼ (25.66 ± 3.63) | 32.07 ± 4.54 | |
| EXP [1] | — | 2.37 ± 0.31 ± 0.11 | — |
| BR in EXP | — | — | (2.96 ± 0.39) ∼ (26.33 ± 3.44) |
4. Conclusion
The decay of  has been observed by the LHCb collaboration with the measurement of the branching fraction multiplied by the production rates for
has been observed by the LHCb collaboration with the measurement of the branching fraction multiplied by the production rates for  relative to
relative to  mesons as
mesons as  . In this paper we have calculated the branching ratio of the
. In this paper we have calculated the branching ratio of the  decay using the QCDF theorem. The numerical value of this calculation is
decay using the QCDF theorem. The numerical value of this calculation is  . For direct comparison with the experimental result we have multiplied this value by
. For direct comparison with the experimental result we have multiplied this value by ![$\sigma ({B}_{c}^{+})/\sigma ({B}_{s}^{0})=[0.9,8.0] \% $](https://content.cld.iop.org/journals/0954-3899/47/4/045003/revision1/jpgab6af6ieqn129.gif) which is theoretically obtained, and got
which is theoretically obtained, and got  . On the other hand, by applying theoretical number of production rates (
. On the other hand, by applying theoretical number of production rates ( ), we have obtained the branch ratio value that exists within the experimental observation and got (2.96 ± 0.39) ∼ (26.33 ± 3.44)% in which our predicted value using the QCDF approach is located in the middle of the branching fraction value in the experimental observation. We investigated then the FSI effects, in which such decays are highly dependent on the phenomenology parameter which appear in the form factors of the long distance distributions. By applying these effects and considering that the decay in this work is done only through the cross section processes, four intermediate states have been created. The contribution of all these intermediate decays have been included in the final amplitude. Finally, we have calculated the branching ratio by using the QCDF approach and FSI effects together for various values of the phenomenological parameter, η = 0.5–1.5. The obtained results have covered the branch ratio that exists inside the experimental view. In another selection of η, we have fixed η = 0.5 and η = 1.5 for light and heavy intermediate mesons, respectively, with this selection and fixing
), we have obtained the branch ratio value that exists within the experimental observation and got (2.96 ± 0.39) ∼ (26.33 ± 3.44)% in which our predicted value using the QCDF approach is located in the middle of the branching fraction value in the experimental observation. We investigated then the FSI effects, in which such decays are highly dependent on the phenomenology parameter which appear in the form factors of the long distance distributions. By applying these effects and considering that the decay in this work is done only through the cross section processes, four intermediate states have been created. The contribution of all these intermediate decays have been included in the final amplitude. Finally, we have calculated the branching ratio by using the QCDF approach and FSI effects together for various values of the phenomenological parameter, η = 0.5–1.5. The obtained results have covered the branch ratio that exists inside the experimental view. In another selection of η, we have fixed η = 0.5 and η = 1.5 for light and heavy intermediate mesons, respectively, with this selection and fixing  where a more acceptable result of 0.9% has been obtained.
where a more acceptable result of 0.9% has been obtained.