Comment on 'AdS nonlinear instability: moving beyond spherical symmetry' (2016 Class. Quantum Grav. 33 23LT01)

In a recent paper [1], Dias and Santos considered gravitational perturbations of four dimensional anti-de Sitter spacetime and argued that only in special cases (listed in section 6 in [1]) do linear eigenmodes admit a nonlinear extension to a regular time-periodic solution (geon). The reason is that at the third order of the perturbation expansion around most eigenmodes there appear resonant terms that, in contrast to spherically symmetric scalar perturbations studied in [2, 3], cannot be removed by a frequency correction. The aim of this comment is to point out that this is a purely technical obstruction in constructing geons, due to the degeneracy of the spectrum and, when this degeneracy is properly taken into account, one can construct perturbatively one-parameter families of geons bifurcating from each linear eigenfrequency.

To illustrate our point, we restrict to the simplest case of axially symmetric scalar-type perturbations, for which the eigenfrequencies are (we set the AdS radius to one)

$$\begin{align}\label{spectrum} \omega_{\ell,p}=1+\ell+2p, \nonumber \end{align} \tag{ 1 }$$

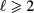where $\ell\geqslant 2$ is the angular momentum index and a non-negative integer p is the nodal number for radial mode functions

$$\begin{align}\label{radial} e_{\ell,p}(r) = \frac{r^{\ell + 1}} {\left(r^2+1\right)^{\frac{\ell + 1}{2}}} \, {\hspace{0pt}}_2F_1\left(-p,1+\ell+p;\frac{1}{2};\frac{1}{r^2+1}\right). \nonumber \end{align} \tag{ 2 }$$

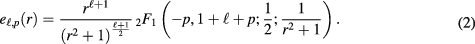
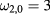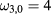It follows from (1) that (restricting to axial symmetry and to scalar-type perturbations only) all eigenfrequencies but $\omega_{2, 0}=3$ and $\omega_{3, 0}=4$ are degenerate. According to the first three rows in table 1 in [1], the eigenmode with the single eigenfrequency 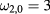$\omega_{2, 0}=3$ (the first row in table 1) can be extended to a geon (the same happens for the eigenmode with frequency 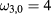$\omega_{3, 0}=4$). To see that the double eigenfrequency 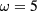$\omega=5$ (listed in the second and third row in table 1) also gives rise to a geon, consider a master gauge invariant variable for scalar-type perturbations

$$\begin{align} \Phi(t,r,\theta) = \epsilon \, \Phi^{(1)}(t,r,\theta) + \epsilon^2 \, \Phi^{(2)}(t,r,\theta) + \epsilon^3 \, \Phi^{(3)}(t,r,\theta) + \mathcal{O}\left( \epsilon^4 \right) \nonumber \end{align} \tag{ 3 }$$

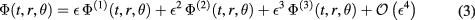
with a linear combination of two eigenmodes with 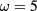$\omega=5$ as the seed:

$$\begin{align} \label{seed} \Phi^{(1)}(t,r,\theta) = \left(\eta \, e_{2,1}(r) P_2(\cos \theta) + (1-\eta) \, e_{4,0}(r) P_4(\cos \theta) \right) \cos\left((5 + \epsilon^2 \omega_2)t \right), \nonumber \end{align} \tag{ 4 }$$

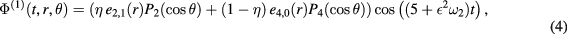
where 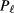$P_{\ell}$ are Legendre polynomials. At the third order we get two resonant terms (for the modes e_2,1 and e_4,0) that can be removed by a suitable choice of the frequency correction 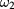$\omega_2$ and the mixing parameter η in (4). More precisely, the resonant terms will be absent if 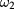$\omega_2$ and η satisfy the following system

$$\begin{align} \label{eq:l2} -651\,980\,329\, \eta^3 +673\,396\,185\,\eta^2 -358\,711\,575\,\eta + 22\,494\,375 = 49\,201\,152 \, \eta \,\omega_2 \nonumber \end{align} \tag{ 5 }$$

$$\begin{align} \label{eq:l4} 16\,847\,182\,891\, \eta^3 - 38\,330\,631\,185\, \eta^2 + 31\,825\,994\,625\, \eta - 10\,200\,766\,875 = 4182\,097\,920 \, (1-\eta) \,\omega_2. \nonumber \end{align} \tag{ 6 }$$

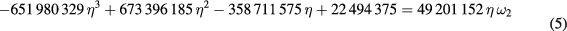
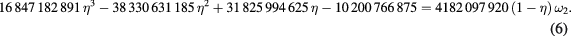
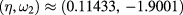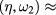
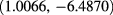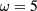This system has two real solutions: $(\eta, \omega_2) \approx (0.11433, \, -1.9001)$ and $(\eta, \omega_2) \approx$$(1.0066, \, -6.4870)$, thus we expect two one-parameter () families of geons to bifurcate from the eigenfrequency $\omega=5$. Note that setting 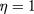$\eta=1$ in (5), we get 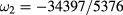$\omega_2 = -34397/5376$, while setting 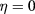$\eta=0$ in (6), we get 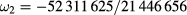$\omega_2 = -52\, 311\, 625/21\, 446\, 656$, in agreement with the values given by Dias and Santos in table 1.

In general, for the eigenfrequency with geometric multiplicity k we need to take a linear combination of k corresponding eigenmodes as the seed, and to remove the resonances at the third order we have to fulfill the system of k equations that are cubic in the mixing parameters 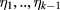$\eta_1,.., \eta_{k-1}$ and linear in 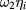$\omega_2 \eta_i$ terms (with 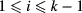$1 \leqslant i \leqslant k-1$). Each real root of this system gives rise to a one parameter family of geons bifurcating from the given eigenfrequency (the number of all (complex) roots is expected to grow exponentially with k, as after eliminating 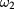$\omega_2$, we are left with the system of k  −  1 equations that are quartic in $\eta_1,.., \eta_{k-1}$). Interestingly, in all cases that we have studied so far (in axial symmetry, both for scalar and vector seeds), the number of bifurcating one-parameter families of time-periodic solutions is equal to the multiplicity of the eigenfrequency. This intriguing coincidence deserves further studies. Finally, we remark that in a parallel work Maliborski constructed axially symmetric time-periodic solutions for the cubic wave equation on the fixed AdS background [4], and in that model there is no such coincidence.

This research was supported in part by the Polish National Science Centre grant no. DEC-2012/06/A/ST2/00397. The author is indebted to Piotr Bizoń and Maciej Maliborski for many valuable discussions. The author acknowledges the six months scientific associate contract at CERN TH department that allowed him for the detailed studies of gravitational perturbations of AdS, and is particularly grateful to Luis Álvarez-Gaumé for providing propitious atmosphere for the research.