Cylinder stress in nanostructures: effect on domains in nanowires, nanotubes, and nano-disks

The relationship between domain width w and film thickness d in ferromagnets [1, 2] or ferroelectrics and ferroelastics [3–5] is derived by minimizing strain; creating more domain walls reduces depolarization or demagnetization field but costs strain energy for each wall created. This idea was extended by Arlt [6] to the case of domains in ceramic ferroelectrics, where the domain diameter d is now the characteristic length, replacing film thickness. In each case a square root relationship results with w² = bd where b is a constant related to domain wall thickness. Generally speaking, the stresses calculated in these models are only axial stresses—tensile or compressive—and are inversely proportional to the cross-sectional area of the film or domain.

Many experiments agree with this simple Landau–Lifshiftz-Kittel Law. Indeed Scott [5] shows agreement over eight orders of magnitude in film thickness, a remarkable result. However, growing evidence exists for a strong deviation of this model for domains: At small domain size, <1 micron, a linear relationship is found for a variety of materials. This has an obvious impact on the physics and engineering of nano-devices, including nanotubes, nanowires, and nano-disks. The purpose of the present paper is to suggest a simple explanation for all these data by including cylinder stress (often termed 'hoop stress') in the model.

When an object is compressed from opposite ends it develops an axial strain along the axis of compression and a radial strain outward, normal to that axis. Less obvious but familiar to engineers and architects is the hoop stress that develops azimuthally around the circumference. Hoop stress can be large, and its minimization was key in building the dome of the Florence Cathedral in 1436 by Filippo Brunelleschi. Most important in the present context is that hoop stress is given for a cylindrical or dome-shaped object by (Wikipedia):

$$\begin{equation}S\left(\text{hoop}\right)\quad =\quad F/\left[L\left({{r}_{2}}-{{r}_{1}}\right)\right],\end{equation} \tag{ 1a }$$

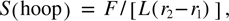
where F is the applied force; r₂ and r₁, the inner and outer radii of the cylinder, which for a very thick or solid cylinder is approximately the radius d; and L, the axial length. Note that for thick cylinders, S varies therefore as 1/d, in contrast with ordinary axial strain, which varies as the cross-sectional area, proportional to d²:

$$\begin{equation}S\left(\text{hoop}\right)\quad =\quad F/\left(Ld\right).\end{equation} \tag{ 1b }$$

In the present work we consider this stress as applied to a narrow domain wall approximately parallel to the edge of a nanowire, nanotube, or nano-disk (figure 1). We want to know what the width w of this domain will be, and how it relates to d. To get a hoop stress energy E we integrate the scalar product S·dx around an area bounded by an outer perimeter of d and an inner perimeter d − w, noting that S·dx is zero for hoop stress on the radial sides of width w, yielding

$$\begin{equation}E\left(\text{hoop}\right)\quad =\quad c\text{}\text{ log} \text{}d\quad c\text{}\text{ log}\text{}\left(d-w\right).\end{equation} \tag{ 2 }$$

Where c = F/L. Note that the magnitude c of this effect will be different for domains oriented in-plane compared with those out-of-plane. In cathedral domes c is positive and arises from gravity and weight, but in thin films or nano-domains c can arise from differential thermal expansion of film and substrate or electrodes, and can be of either sign. Hoop stress can therefore cause flopping from out-of-plane to in-plane or vice versa, as reported by Ng and Aluwalia [7] theoretically and Kumar and Scott [8] experimentally.

Zoom In Zoom Out Reset image size

The Landau–Lifshitz-Kittel Law balances axial stresses to obtain a free energy G

$$\begin{equation}G\quad =\quad Uw\quad +Bd/w\end{equation} \tag{ 3 }$$

where the first term comes from a domain axial stress F/(πr²) integrated over volume, and the second from domain walls (note that the number of walls is proportional to d/w). Minimizing the free energy with respect to w, 0 = dG/dw, immediately leads to w proportional to the square root of d, which in Arlt's model is the grain diameter.

Adding the hoop stress energy, we now get

$$\begin{equation}G\quad =\quad -c\text{}\text{ log}\text{}\left(d-w\right)\quad +\quad Uw\quad +\quad Bd/w\text{}\text{ +} \text{}c\text{}\text{ log}\text{}d\end{equation} \tag{ 4 }$$

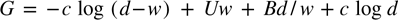
and minimizing this with respect to w yields 0 = dG/dw and hence

$$\begin{equation}U{{w}^{2}}=\quad Bd\quad -\quad c{{w}^{2}}/\left(d-w\right),\end{equation} \tag{ 5a }$$

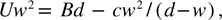
or

$$\begin{equation}U{{w}^{2}}=\quad Bd\quad -\quad cw/\left[\left(d/w\right)-1\right],\end{equation} \tag{ 5b }$$

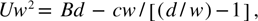
for large-radius disks, tubes, or cylinders with d >> w this gives the original Landau–Lifshitz-Kittel law; but for small-radius nano-geometries, it gives

$$\begin{equation}U{{w}^{2}}=\quad Bd\quad -\quad c{{w}^{2}}/d,\end{equation} \tag{ 6a }$$

and

$$\begin{equation}{{w}^{2}}=\quad B{{d}^{2}}/\left(Ud+c\right),\end{equation} \tag{ 6b }$$

which is a linear relation between w and d for large hoop stress (large c), but Arlt's Law for small hoop stress. For small d and large hoop stress (large c), from equation (4), G = c log [d/(d-w)], and dG/dw = 0 implies that w does not really go to zero, but reaches a constant w = d (single domain), in agreement with experiment.

This seems to be in accord with experimental data discussed below, where for example in bismuth titanate w is never less than w = 90 nm (and 40 nm for BaTiO₃ or PZT); for smaller values of d, a single domain always results.

Parenthetically we note that the domains along the perimeter need not themselves be curved. In a cathedral dome the building units are bricks. They are not curved either, and architects since Filippo Brunelleschi have found that laying the bricks in herringbone geometries stabilized them against hoop stress. This is reminiscent of the ac-domains considered by Pertsev and Zembilgotov [9]. Their result is only for thick films and 90 degree domains. But this linear dependence of w upon d has been observed in thinner films and for 180 degree domains in many materials—and always with a limit of d < 1 micron.

The work relating domain with w with grain diameter d began with a seminal paper by Arlt [6]. Although for large grains his data agreed with the predicted square-root dependence, below a micron or so he got a remarkably linear relationship, which he did not quantitatively explain. Subsequently the same result was obtained [10] by Cao and Randall for lead zirconate-titanate (PZT), by Eriksson et al for Na_0.5K_0.5NbO₃ [11, 12], and by Viola et al [13] for bismuth titanate. The presence of equivalent results on four materials from three different countries suggests that they all have the same explanation. They always find that the Kittel Law breaks down below diameters d = 2.0 micron, and the w(d) data are linear below that.

This is summarized in the double-logarithmic graph in figure 2, which combines data from [6] and [10–12]. These data are mostly from electron micrographs, except for the largest grains, which were measured optically; the uncertainties are typically 20%. In figure 3 similar data are plotted on a linear scale to emphasize the agreement of w(d) for submicron d with equation (7).

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In addition, the domain width w never really goes to zero, as predicted by the Landau–Lifshitz-Kittel Law and by Arlt; instead there is a finite minimum w as d becomes small (d < 90 nm in Bi₄Ti₃O₁₂); below that, there is always a single domain.

This also agrees with the hoop algebra above.

There is another way to include stress terms linear in diameter d rather than cross-sectional area. For the case of ferroelectric films, the effect of fringing fields causes a correction to the force of a capacitor that changes its effective area. This effect is large for nano-capacitors [14]. The fringing field correction is known to be made, to a good approximation, from Feynman et al [15] by replacing the area of a square of side r by an effective area

$$\begin{equation}A\quad =\quad {{\left( r-3\quad L/4 \right)}^{2}}.\end{equation}$$

which for thin films of thickness L < r is approximately

$$\begin{equation}A\quad =\quad {{r}^{2}}-3rL/2.\end{equation}$$

and as with the hoop stress equations in the preceding section, this introduces a stress that is linear in radius and not area.

Many studies of nanodomains in small ferroelectrics have revealed phenomena that are incompletely explained: These include unusual switching dynamics along the perimeter of nano-disks [16–18], faceting [8, 19] and geometrically driven phase transitions [20]. Because these phenomena all seem surprisingly sensitive to boundary conditions, it might be useful to incorporate hoop stress into their modeling. In the special case of the geometrically driven phase transitions [20], the origin of the stress is unknown, but it could be hoop stress. Similarly, very recent results on vertex–vertex domain collisions [21] are modeled using a lateral stress that is not applied but could result from thermal contraction of substrate if hoop stresses are included. The two-step process of domain reorientation of 90 degree walls reported [7] by Ng et al seems pertinent, as do the domain wall data parallel to grain boundaries reported by Bhattacharaya and Higgins [22]. The work of Baudry et al [23] shows that the shape of the nano-structure domains will differ according to boundary conditions, e.g. from J₀ to J₁-type Bessel function patterns.

Thanks are due to Professor G Catalan for helpful discussions.