Abstract
Recently, superconductivity was found in one atomic layer of Pb film, promising a new field of research where superconductors can be studied on the atomic level. In the presented paper, we report a theoretical study of the superconductivity in ultrathin Pb films consisting of five to ten monolayers. Using the strong coupling Eliashberg formalism we reproduced the experimental values of critical temperature (TC) and we estimated the superconducting energy gap (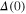 ), thermodynamic critical field (HC) and the specific heat jump at critical temperature (
), thermodynamic critical field (HC) and the specific heat jump at critical temperature (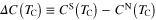 ) for a wide range of film thicknesses. In these systems, we found an oscillatory behaviour of the above thermodynamic properties modulated by quantum size effects. Moreover, the large values of
) for a wide range of film thicknesses. In these systems, we found an oscillatory behaviour of the above thermodynamic properties modulated by quantum size effects. Moreover, the large values of 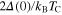 and
and 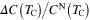 , and the small values of
, and the small values of  prove that the thermodynamic properties of Pb films cannot be correctly described using the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity due to the strong coupling and retardation effects.
prove that the thermodynamic properties of Pb films cannot be correctly described using the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity due to the strong coupling and retardation effects.
Export citation and abstract BibTeX RIS
1. Introduction
The effect of film thickness on the properties of superconducting states has been widely investigated in two-dimensional (2D) systems for several decades [1–3]. Those conducting research are motivated by the unique properties [4–7] and prospects for the potential technological application of these materials, for example in modern electronic and opto-electronic devices [8]. It has been found that a few intriguing aspects and novel physical phenomena exist in 2D superconductors. One of them is a transition from a superconducting to an insulating state with increasing disorder or magnetic field [9–13]. Additionally, quantum size effects such as oscillations of the critical temperature (TC) and other superconducting parameters with the thickness have stimulated considerable theoretical and experimental interest [14–21].
Recently, using scanning tunnelling microscopy measurements, superconductivity with a TC up to 1.83 K has been observed in one atomic layer of Pb film grown on a bulk-terminated Si(111) substrate [22]. Moreover, the transition temperature as a function of the film thickness shows oscillations; in particular with the film thickness decrease, an increase in the quantum oscillations of TC was observed. Systematic studies also found that TC decreases rapidly to very low values at the limit of 2 monolayers (ML) [23]. It is worth emphasizing that lead attracts more attention in superconductivity studies, because bulk Pb is a prototypical strong coupling electron–phonon elemental superconductor with a relatively high critical temperature of 7.19 K, energy gap ( ) of 1.4 meV [24] and a ratio
) of 1.4 meV [24] and a ratio 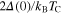 of 4.52 [25], well above the canonical BCS value of 3.53 [26].
of 4.52 [25], well above the canonical BCS value of 3.53 [26].
Motivated by the recent experimental progress in this area, we have carried out calculations to explore the thermodynamic properties of the superconducting state of Pb films in the ultrathin regime (5–10 ML). It is interesting to compare the superconducting properties of lead thin films with a bulk lead sample. In this paper we present the results of our calculations performed within the framework of the strong coupling approach.
The paper is organized as follows. Section 2 contains a short outline of the Eliashberg formalism and computational methods. In section 3, we discuss the thermodynamic properties of superconducting Pb(111) films consisting of five to ten monolayers. section 4 summarizes the obtained results.
2. Theoretical model and computational methods
The Eliashberg theory of superconductivity [27] allows prediction of the thermodynamic properties of conventional superconductors on the quantitative level. This is possible due to the fact that strong electron–phonon coupling and retardation effects implied by the time dependence of the pairing interaction are not omitted unlike in the case of BCS theory [26, 28].
The Eliashberg theory is based on the electron–phonon interaction Hamiltonian predicted by Fröhlich [29]:

Here 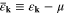 , where
, where  denotes the electronic band dispersion and μ is the chemical potential. Symbols
denotes the electronic band dispersion and μ is the chemical potential. Symbols 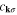 and
and  denote the electron annihilation and creation operators of momentum
denote the electron annihilation and creation operators of momentum 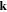 and spin σ =
and spin σ = 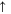 or
or  . Symbol
. Symbol  stands for the phonon frequencies,
stands for the phonon frequencies, 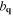 and
and 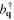 are the phonon annihilation and creation operators of modes
are the phonon annihilation and creation operators of modes 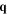 . The electron–phonon matrix element is given by
. The electron–phonon matrix element is given by 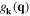 and
and 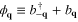 [29]. Nonlinear phonon–phonon and quadratic electron–phonon coupling can be included in this model by using anharmonic oscillators [30–37].
[29]. Nonlinear phonon–phonon and quadratic electron–phonon coupling can be included in this model by using anharmonic oscillators [30–37].
The Nambu formalism [38] and Greenʼs function theory [39] allow us to determine, directly from the Fröhlich Hamiltonian, the set of two coupled non-linear integral Eliashberg equations for the superconducting order parameter function  and the mass renormalization function
and the mass renormalization function 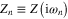 [40]. The one-band equations defined on the imaginary frequency axis take the following form:
[40]. The one-band equations defined on the imaginary frequency axis take the following form:
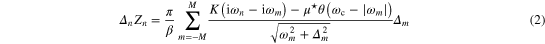
and
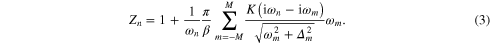
Here  , with
, with 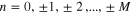 are Matsubara frequencies, where M = 1100. The inverse temperature is given by
are Matsubara frequencies, where M = 1100. The inverse temperature is given by 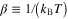 , where kB represents the Boltzmann constant. Symbols θ and
, where kB represents the Boltzmann constant. Symbols θ and  denote the Heaviside function and the cut-off frequency which is set to ten times the maximum phonon frequency (
denote the Heaviside function and the cut-off frequency which is set to ten times the maximum phonon frequency (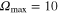 meV). The electron–phonon pairing kernel is defined as:
meV). The electron–phonon pairing kernel is defined as:
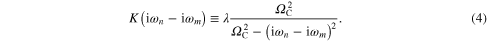
The symbol 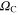 represents the characteristic phonon frequency, which is commonly used to reproduce, in the framework of the Eliashberg formalism, the critical temperature observed in experimental measurements [41]. At this point it should be noted, that the electron–phonon interaction in metals is generally considered to be isotropic. However, the necessity of an anisotropic theory has clearly been demonstrated in two important cases, magnesium diboride MgB2, and the graphite intercalation compound CaC6 [42, 43]. It has also been confirmed that bulk Pb is a two-gap superconductor [44–46]. The anisotropic properties of the superconducting state can be examined in the framework of the multi-band Eliashberg formalism [47, 48]. However, in the case of free-standing Pb(111) films the one-band Eliashberg formalism with very good accuracy reproduces the experimental results obtained using scanning tunneling spectroscopy [49]. A central quantity in the Eliashberg theory is the effective electron–phonon spectral function
represents the characteristic phonon frequency, which is commonly used to reproduce, in the framework of the Eliashberg formalism, the critical temperature observed in experimental measurements [41]. At this point it should be noted, that the electron–phonon interaction in metals is generally considered to be isotropic. However, the necessity of an anisotropic theory has clearly been demonstrated in two important cases, magnesium diboride MgB2, and the graphite intercalation compound CaC6 [42, 43]. It has also been confirmed that bulk Pb is a two-gap superconductor [44–46]. The anisotropic properties of the superconducting state can be examined in the framework of the multi-band Eliashberg formalism [47, 48]. However, in the case of free-standing Pb(111) films the one-band Eliashberg formalism with very good accuracy reproduces the experimental results obtained using scanning tunneling spectroscopy [49]. A central quantity in the Eliashberg theory is the effective electron–phonon spectral function 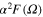 which delivers a description of the electron–phonon interaction by means of a spectral density. This function contains all the information about an investigated system needed to determine the thermodynamic properties of a superconducting state. The expression used to Scalculate the Eliashberg functions for free-standing Pb(111) films is given by
which delivers a description of the electron–phonon interaction by means of a spectral density. This function contains all the information about an investigated system needed to determine the thermodynamic properties of a superconducting state. The expression used to Scalculate the Eliashberg functions for free-standing Pb(111) films is given by

where, 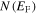 is the electronic density of states at the Fermi level,
is the electronic density of states at the Fermi level, 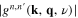 is an electron–phonon matrix element, and
is an electron–phonon matrix element, and 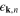 and
and 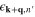 are electronic energies [50]. The calculation for each film thickness was carried out using first-principles calculations in the density functional perturbation formalism, where the free-standing films are modelled by a supercell with N-layer Pb(111) films separated by a vacuum gap of
are electronic energies [50]. The calculation for each film thickness was carried out using first-principles calculations in the density functional perturbation formalism, where the free-standing films are modelled by a supercell with N-layer Pb(111) films separated by a vacuum gap of 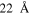 [50].
[50].
The information about the layer thickness is contained in the shape of the Eliashberg spectral function, therefore, the number of layers directly influences the value of the electron–phonon coupling constant which is given by the integration of the 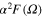 function:
function:
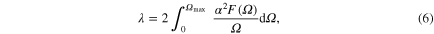
If  , the compound is classified in the group of strong coupling superconductors and should be described using the strong coupling Eliashberg approach. In the case of free-standing Pb(111) films consisting of five to ten atomic layers we have
, the compound is classified in the group of strong coupling superconductors and should be described using the strong coupling Eliashberg approach. In the case of free-standing Pb(111) films consisting of five to ten atomic layers we have 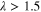 [50]. For conventional superconductors the electron–phonon coupling is counteracted by Coulomb repulsion. The depairing Coulomb interactions are modelled by the semiempirical screened Coulomb pseudopotential parameter
[50]. For conventional superconductors the electron–phonon coupling is counteracted by Coulomb repulsion. The depairing Coulomb interactions are modelled by the semiempirical screened Coulomb pseudopotential parameter 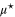 . In the presented paper the values of λ are taken from paper [50] and
. In the presented paper the values of λ are taken from paper [50] and 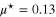 (the value obtained for bulk Pb) [24].
(the value obtained for bulk Pb) [24].
The Eliashberg theory allows us to calculate the properties of all conventional superconductors once λ and 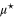 are known [51]. To be able to calculate the real physical quantities, the imaginary frequency axis solutions, computed from equations (2) and (3), should be implemented as input parameters to the Eliashberg equations in the mixed representation (defined both on the real and imaginary frequency axes) [52, 53]. In order to determine all of the significant thermodynamic properties of ultrathin Pb films, we conducted numerical calculations based on a self-consistent iteration method [54], which has been used successfully in our previous papers [55–58].
are known [51]. To be able to calculate the real physical quantities, the imaginary frequency axis solutions, computed from equations (2) and (3), should be implemented as input parameters to the Eliashberg equations in the mixed representation (defined both on the real and imaginary frequency axes) [52, 53]. In order to determine all of the significant thermodynamic properties of ultrathin Pb films, we conducted numerical calculations based on a self-consistent iteration method [54], which has been used successfully in our previous papers [55–58].
3. Results and discussion
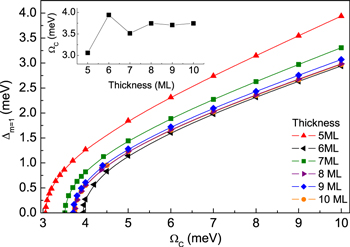
The critical temperatures of ultrathin Pb films have been determined from temperature-dependent gap measurements in paper [49]. On this basis, we were able to calculate the values of 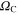 for each investigated thin film layer thickness (5-10 ML). In particular, in the Eliashberg equations we have assumed that
for each investigated thin film layer thickness (5-10 ML). In particular, in the Eliashberg equations we have assumed that 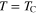 and then we have decreased the value of the parameter
and then we have decreased the value of the parameter  until we have reached the equality
until we have reached the equality 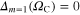 . The full dependence of
. The full dependence of 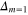 on
on 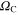 is presented in the main part of figure 1. The inset presents
is presented in the main part of figure 1. The inset presents 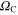 as a function of the layer thickness. It is easy to observe that the critical value of
as a function of the layer thickness. It is easy to observe that the critical value of 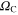 oscillations is in the range of 3.06 to 3.94 meV.
oscillations is in the range of 3.06 to 3.94 meV.
Figure 1. The order parameters as a function of the characteristic phonon frequency at TC. The inset presents the critical value of  as a function of the layer thickness.
as a function of the layer thickness.
Download figure:
Standard image High-resolution imageIn figure 2, the dependence of the order parameter on the temperature is presented for film layer thicknesses in the range of 5 to 10 ML. Moreover, the above results are supplemented by the results obtained for bulk Pb [59]. It can be observed that the value of 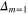 strongly decreases with the growth of the temperature and varies depending on the thickness. This fact can be exactly parameterized using the following formula:
strongly decreases with the growth of the temperature and varies depending on the thickness. This fact can be exactly parameterized using the following formula:

where the parameter Γ, in all cases is equal to 3.7. The values of TC and 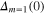 are shown in the insets (A) and (B) of figure 2. We notice that the order parameter function allows us to determine the physical value of the energy gap at the Fermi level
are shown in the insets (A) and (B) of figure 2. We notice that the order parameter function allows us to determine the physical value of the energy gap at the Fermi level  . For this purpose, we have numerically solved the Eliashberg equations in the mixed representation by using the solutions from the imaginary axis as input parameters. As a result we obtained 1.32, 1.26, 1.26, 1.21, 1.23 and 1.20 meV for 5, 6, 7, 8, 9, and 10 ML. It should be emphasized that a very good consistency of the experimental results [49] with the presented theoretical ones for
. For this purpose, we have numerically solved the Eliashberg equations in the mixed representation by using the solutions from the imaginary axis as input parameters. As a result we obtained 1.32, 1.26, 1.26, 1.21, 1.23 and 1.20 meV for 5, 6, 7, 8, 9, and 10 ML. It should be emphasized that a very good consistency of the experimental results [49] with the presented theoretical ones for 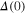 is observed. This proves the correctness of the theoretical model and numerical methods used in this paper. Let us note that in the case of bulk Pb, the above value is much higher:
is observed. This proves the correctness of the theoretical model and numerical methods used in this paper. Let us note that in the case of bulk Pb, the above value is much higher: ![$[\Delta (0){]}_{\mathrm{bulk}}^{\mathrm{Pb}}=1.40$](https://content.cld.iop.org/journals/0953-2048/28/9/095011/revision1/sust517121ieqn54.gif) [24, 25].
[24, 25].
Figure 2. Upper panel: the dependence of the order parameter on the temperature. Inset (A): critical temperature as a function of thickness [49]. Inset (B): zeroth temperature order parameter as a function of thickness. Lower panel: the dependence of the total normalized density of states on the frequency for T = 0 K.
Download figure:
Standard image High-resolution imageThe energy gap function also allows us to calculate the total normalized density of states [40]:

where the symbols  and
and 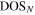 denote the density of states of the superconducting and normal state, respectively. The plot of the total normalized density of states is presented in the lower panel of figure 2.
denote the density of states of the superconducting and normal state, respectively. The plot of the total normalized density of states is presented in the lower panel of figure 2.
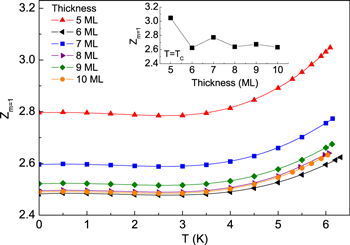
In contrast to the order parameter, the value of the mass renormalization function ( ) grows with increasing temperature and the maximum of this function is at TC, as presented in figure 3. The inset shows the dependence of
) grows with increasing temperature and the maximum of this function is at TC, as presented in figure 3. The inset shows the dependence of 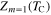 as a function of the layer thickness. We can observe the saturation effect of oscillations for higher values of thickness. From the physical point of view, the
as a function of the layer thickness. We can observe the saturation effect of oscillations for higher values of thickness. From the physical point of view, the 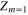 function with a very good approximation reproduces the value of the electron effective mass:
function with a very good approximation reproduces the value of the electron effective mass: 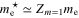 , where the symbol me denotes the electron band mass.
, where the symbol me denotes the electron band mass.
Figure 3. The dependence of the mass renormalization function on the temperature for selected thickness of Pb film. Inset presents the maximum values of 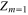 as a function of the layer thickness in an ultrathin regime.
as a function of the layer thickness in an ultrathin regime.
Download figure:
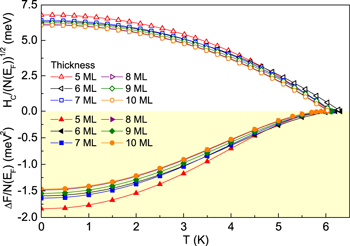
Standard image High-resolution imageTo explore the influence of film thickness on the thermodynamic properties of the investigated systems, in the first step we calculated the free energy difference between the superconducting and the normal state (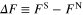 ) [40]:
) [40]:
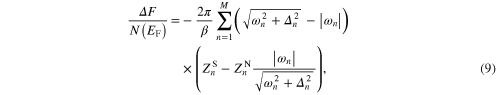
where symbols 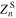 and
and  denote the mass renormalization functions for the superconducting and for the normal state, respectively. Then, on the basis of equation (9), the thermodynamic critical field HC was determined:
denote the mass renormalization functions for the superconducting and for the normal state, respectively. Then, on the basis of equation (9), the thermodynamic critical field HC was determined:

In figure 4, the detailed dependence of the thermodynamic critical field and free energy difference on the temperature for selected values of film layer thickness is plotted.
Figure 4. The free energy difference and the thermodynamic critical field as a function of temperature for selected film thickness.
Download figure:
Standard image High-resolution imageFrom the second derivative of the 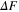 function the specific heat difference between the superconducting and the normal state (
function the specific heat difference between the superconducting and the normal state (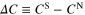 ) was calculated:
) was calculated:
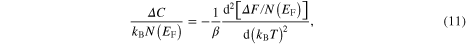
where the specific heat in the normal state is defined as:  . Symbol γ denotes the Sommerfeld constant:
. Symbol γ denotes the Sommerfeld constant: 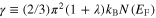 . In figure 5 we can trace the course of the specific heat function in the superconducting and normal states.
. In figure 5 we can trace the course of the specific heat function in the superconducting and normal states.
Figure 5. The specific heat for the superconducting and normal states as a function of temperature for selected layer thicknesses. At TC the characteristic specific heat jump is marked by the vertical line.
Download figure:
Standard image High-resolution imageThe thermodynamic functions determined in this paper allow us to estimate the dimensionless ratios: 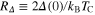 ,
, 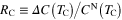 and
and 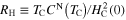 which play a very important role in the theory of superconductivity because they can be determined in experimental measurements and compared with theoretical predictions. In the framework of the BCS theory,
which play a very important role in the theory of superconductivity because they can be determined in experimental measurements and compared with theoretical predictions. In the framework of the BCS theory, 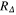 , RC and RH are universal and equal to 3.35, 1.43 and 0.168, respectively [26, 28, 40]. The results obtained for ultrathin Pb(111) films are presented in table 1. We can see that the values computed in the framework of the Eliashberg theory strongly differ from the predictions of the BCS theory. This situation is caused by the strong coupling and retardation effects which can be written approximately as the ratio
, RC and RH are universal and equal to 3.35, 1.43 and 0.168, respectively [26, 28, 40]. The results obtained for ultrathin Pb(111) films are presented in table 1. We can see that the values computed in the framework of the Eliashberg theory strongly differ from the predictions of the BCS theory. This situation is caused by the strong coupling and retardation effects which can be written approximately as the ratio 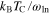 , where
, where 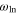 denotes the average phonon frequency which relates to the dynamics of the superconducting state [60]. For lead
denotes the average phonon frequency which relates to the dynamics of the superconducting state [60]. For lead  is no the order of 5.5 meV [61]. In the weak coupling BCS limit
is no the order of 5.5 meV [61]. In the weak coupling BCS limit 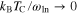 , while in the case of the Pb superconductor this parameter exceeds the value of 0.1. It should be noted that the results obtained for thin films are generally higher than the corresponding bulk values; in particular for bulk Pb we have
, while in the case of the Pb superconductor this parameter exceeds the value of 0.1. It should be noted that the results obtained for thin films are generally higher than the corresponding bulk values; in particular for bulk Pb we have ![${[{R}_{\Delta }]}_{\mathrm{bulk}}^{\mathrm{Pb}}=4.53$](https://content.cld.iop.org/journals/0953-2048/28/9/095011/revision1/sust517121ieqn77.gif) ,
, ![${[{R}_{{\rm{C}}}]}_{\mathrm{bulk}}^{\mathrm{Pb}}=2.63$](https://content.cld.iop.org/journals/0953-2048/28/9/095011/revision1/sust517121ieqn78.gif) and
and ![${[{R}_{{\rm{H}}}]}_{\mathrm{bulk}}^{\mathrm{Pb}}=0.129$](https://content.cld.iop.org/journals/0953-2048/28/9/095011/revision1/sust517121ieqn79.gif) [24, 59].
[24, 59].
Table 1.
The values of the dimensionless parameters: 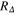 , RC and RH for selected values of film thickness in ML.
, RC and RH for selected values of film thickness in ML.
| Thickness | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|
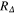
|
5.02 | 4.62 | 4.76 | 4.63 | 4.66 | 4.62 |
| RC | 3.76 | 3.21 | 3.46 | 3.27 | 3.32 | 3.24 |
| RH | 0.126 | 0.134 | 0.131 | 0.134 | 0.133 | 0.134 |
4. Conclusions
The Eliashberg theory has been used with great success to calculate the thermodynamic properties of ultrathin Pb films in the superconducting state. In particular, the measured superconducting critical temperature was reconstructed by using the matching parameter 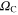 . Then the energy gap, free energy difference between the superconducting and normal state, thermodynamic critical field and the specific heat were determined for a wide range of film thicknesses (5–10 ML). We observed that for thin films, the thermodynamic parameter exhibits an oscillatory behaviour connected with a quantum size effect. Next, on the basis of the above thermodynamic functions determined for Pb films, it was proven that the values of the dimensionless ratios
. Then the energy gap, free energy difference between the superconducting and normal state, thermodynamic critical field and the specific heat were determined for a wide range of film thicknesses (5–10 ML). We observed that for thin films, the thermodynamic parameter exhibits an oscillatory behaviour connected with a quantum size effect. Next, on the basis of the above thermodynamic functions determined for Pb films, it was proven that the values of the dimensionless ratios 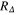 , RC and RH differ significantly from the predictions of the BCS theory and are generally higher than the corresponding bulk values. This is connected with the existence of strong coupling and retardation effects in the investigated systems.
, RC and RH differ significantly from the predictions of the BCS theory and are generally higher than the corresponding bulk values. This is connected with the existence of strong coupling and retardation effects in the investigated systems.
The results, presented in this paper are expected to stimulate further experimental and theoretical exploration or discovery of new 2D superconductors.
Acknowledgments
The author acknowledges financial support from the Czȩstochowa University of Technology under Grant No. BS/MN-203-303/2015.