Electron spin rephasing in n-type (0 0 1) GaAs quantum wells

In the past decade, the electron spin degree of freedom in semiconductors has been extensively investigated for the purpose of realizing spintronic devices [1–6]. To guarantee the information storage and manipulation in such devices, controllable spin lifetimes are required. In the localized systems, the interference due to the inhomogeneous broadening, which corresponds to the distinct spin precession of different electrons under the local hyperfine nuclear field [1] and/or exchange field due to the electron–electron interaction [7], can contribute to the decay of the total spin polarization [8]. This interference can be removed via rephasing schemes, which allows us to significantly extend the ensemble spin lifetime [8–16]. For the itinerant electrons in n-type semiconductors, the inhomogeneous broadening is mainly from the momentum-dependent spin–orbit coupling [5] and the electron spin relaxation is dominated by the D'yakonov–Perel' mechanism [17], where the spin lifetime is limited by the interplay between the inhomogeneous broadening and scattering. In the strong scattering limit (the average scattering time is much shorter than the average period of the spin precession due to the effective magnetic field from the spin–orbit coupling), the inhomogeneous broadening in such systems can be suppressed by the scattering and the spin relaxation time increases with increasing scattering strength [1, 5]. This leads to the motional narrowing relation [1] and reveals the way to manipulate the spin lifetime by tuning the scattering strength in semiconductors.

Recently, Pershin [18] introduced a spin rephasing scheme based on a serried periodic π-pulse sequence to attenuate the inhomogeneous broadening in two-dimensional electron gas. He modeled the isotropic elastic scattering and found a pronounced increase of the spin lifetime with an inter-pulse spacing shorter than the momentum scattering time. Moreover, he showed that the motional narrowing relation of the D'yakonov–Perel' spin relaxation mechanism [17] can be violated by the spin rephasing manipulation. It was suggested that the π-pulse sequence could be realized in the experiment by the optical Stark effect [19–22]. Although the basic properties under the rephasing sequence have been discussed in that work, it is still of critical importance to understand the following problems for the real implementation. First of all, the influence of the spin rephasing sequence in different temperature and density regimes is unclear, especially for the high density case at low temperature, where the motional narrowing relation itself is unsatisfied. Secondly, since only the elastic scattering was considered in Pershin's paper, the discussion there is reasonable for the low mobility system at low temperature, where the inelastic scatterings are irrelevant. However, in various cases, the inelastic scatterings, e.g. the electron–phonon scattering at high temperatures and the electron–electron scattering at moderate temperatures, can be more important than the elastic electron–impurity scattering, especially in high mobility samples. Therefore, all the relevant scatterings should be included and explicitly calculated by considering the critical role of the momentum scattering time on the proposed phenomena.

In this paper, we study the spin dynamics under a serried π-pulse sequence in n-type (0 0 1) GaAs quantum wells (QWs) in a wide range of temperature and density regimes. Our numerical simulation is based on the microscopic kinetic spin Bloch equations [5, 23] with all relevant scatterings, such as the electron–electron, electron–optical-phonon, electron–acoustic-phonon and electron–impurity scatterings, explicitly included. In a high mobility sample where the electron–impurity scattering is irrelevant, we find that the rephasing process results in a considerable increase in the spin lifetime only for the inter-pulse spacing of the order of several picoseconds. We explicitly study the density and temperature dependences of the spin lifetime with the inter-pulse spacing taken to be 2 ps, where the features are found to be quite different from those in the absence of the rephasing sequence. We show that these dependences in both strong and weak scattering limits can be well understood from the variation of the momentum relaxation time due to the electron–electron and electron–phonon scatterings. In addition, we also discuss the effect of the electron–impurity scattering in low mobility samples.

The Hamiltonian of the two-dimensional electron gas in semiconductor QWs can be written as

$$\begin{equation} H={\bf k}^2/(2m)+H_{\rm soc}({\bf k}), \end{equation} \tag{ 1 }$$

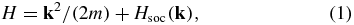
with k representing the momentum of the electron. The spin–orbit coupling H_soc is introduced to describe the Dresselhaus [24] and/or Rashba [25] terms between spin-up and -down states. In a (0 0 1) symmetric GaAs QW with a small well-width, only the lowest subband is relevant and the Dresselhaus term is dominant, i.e.

$$\begin{eqnarray} &&H_{\rm soc}=\case{1}{2}\gamma _D\left[k_x\big(k_y^2-\big\langle k_z^2\big\rangle\big)\sigma _x+k_y\big(\big\langle k_z^2\big\rangle -k_x^2\big)\sigma _y \right], \end{eqnarray} \tag{ 2 }$$

with σ_x and σ_y being the Pauli matrices and γ_D = 11.4 eV Å³ is the Dresselhaus spin–orbit coefficient [26].

The temporal evolution of the spin polarization can then be explicitly calculated by numerically solving the kinetic spin Bloch equations of the density matrices [5, 23]

$$\begin{equation} \partial _t\rho _{\bf k}=\partial _t\rho _{\bf k}|_{\rm coh}+\partial _t\rho _{\bf k}|_{\rm scat}. \end{equation} \tag{ 3 }$$

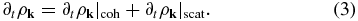
The first and second terms on the right-hand side of the equation represent the coherent and scattering terms, respectively. The detailed expressions of equation (3) can be found in [26] and [27].

Our calculation starts from the initial distribution produced by circularly polarized spin-pumping process, i.e. the Fermi distribution with a small spin polarization along the growth direction. We first choose remotely doped n-type (0 0 1) GaAs QWs to exclude the impurities. The well-width is taken to be 15 nm, where only the lowest subband is relevant. Following the previous work by Pershin [18], we apply a uniformly spaced π-pulse sequence with the inter-pulse spacing being Δt. We assume that each π-pulse generated by the optical Stark effect [19–22] rotates the spins of all electrons instantaneously along the growth direction by 180°. The numerical error is much smaller than 10%.

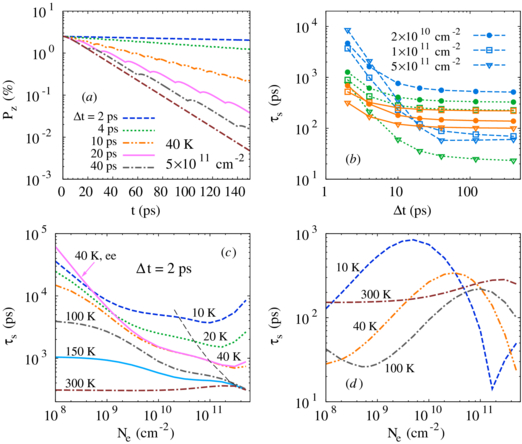
In figure 1, the temporal evolution of the spin polarization along the growth direction is plotted for N_e = 5 × 10¹¹ cm⁻² at different temperatures. The blue solid curves show the effect of the interference without any scattering and rephasing pulse. In the presence of the electron–electron and electron–phonon scatterings, the spin polarizations vary as shown by the pink chain curves. It is seen that the oscillation at 10 K is still visible, revealing that the system lies in the weak scattering limit. However, since the electron gas is in the degenerate limit (T ≪ T_F with the Fermi temperature T_F ≈ 208 K for 5 × 10¹¹ cm⁻³) in figure 1, the electron–electron scattering strength as well as the electron–phonon scattering strength increases with increasing temperature [28]. As a result, the system is pushed into the strong scattering limit at higher temperatures, e.g. at 40 and 100 K, where the oscillations are suppressed.

Zoom In Zoom Out Reset image size

To show the rephasing effect of the π-pulse sequence, we first take a large inter-pulse spacing, Δt = 40 ps. The results at different temperatures are shown in figure 1. In the absence of scattering, the spin polarization can be completely recovered as shown by the red dashed curves, because no spin relaxation mechanism exists in this case. When all the relevant scatterings are switched on, the spin polarization decays due to the D'yakonov–Perel' mechanism (shown as the khaki solid curves). By comparing the results without the rephasing sequence (pink chain curves), one finds that the pulses only have a marginal influence on the spin dynamics in both the weak and strong scattering limits. This is because the momentum scattering time is shorter than the inter-pulse spacing; therefore, the scattering is the dominant mechanism to suppress the inhomogeneous broadening. It is noted that the conclusion in the strong scattering limit is in agreement with the Monte Carlo simulation [18]. The green dotted curves in figure 1 show the results from the calculation solely with the electron–phonon scattering under the rephasing manipulation. By comparing with the corresponding ones with both the electron–electron and electron–phonon scatterings, one finds that the electron–electron scattering is very important in all the cases [27, 29–31].

We then gradually decrease the inter-pulse spacing and study the inter-pulse spacing dependence of the spin lifetime in the presence of both the electron–electron and electron–phonon scatterings. The temporal evolution of the spin polarization for different inter-pulse spacings at 40 K is plotted in figure 2(a). As expected, the spin polarization decays more slowly as the inter-pulse spacing decreases [18]. We plot the spin lifetime as a function of inter-pulse spacing in figure 2(b) for three densities. In this figure, three typical temperatures, i.e. 10 K (blue dashed curves), 40 K (green dotted ones) and 100 K (orange solid ones), are chosen. In all these cases, the spin lifetime for Δt > 40 ps is found to be insensitive to the inter-pulse spacing. When Δt reduces to 2 ps, the spin lifetime can even be increased by two orders of magnitude.

Zoom In Zoom Out Reset image size

We further focus on the short inter-pulse spacing case. In figure 2(c), we plot the density dependence under the serried π-pulse sequence with Δt = 2 ps. At low temperatures, e.g. at 10 K, one finds that the spin lifetime decreases (increases) with increasing density in the low (high) density regime, resulting in a valley in the density dependence of the spin lifetime. This is in contrast to that at high temperatures, e.g. at 300 K. As a comparison, we also show the density dependence of the spin lifetime in the absence of the rephasing sequence in figure 2(d), where the peaks are from the crossover between the degenerate and non-degenerate limits in the strong scattering limit [32, 33] and the dip (valley) at N_e = 1.7 × 10¹¹ cm⁻² (N_e = 10⁹ cm⁻²) for 10 K (100 K) is due to the crossover between the strong and weak scattering limits. It is seen that the density dependences of the spin lifetime with and without the rephasing sequence at low temperatures are quite different. This is due to the different mechanisms of the suppression of the inhomogeneous broadening. In the absence of the rephasing sequence, the inhomogeneous broadening is suppressed only by scatterings. However, when the serried rephasing sequence with inter-pulse spacing being shorter than the average momentum scattering time (Δt < τ*_p) is applied, the suppression of the inhomogeneous broadening is mainly from the serried π-pulse sequence. In such a case, the scatterings only introduce relaxation channels and one has τ_s∝τ*_p [18], suggesting that the spin lifetime varies by following the momentum scattering time. Below 100 K, the electron–electron scattering is the dominant scattering mechanism. Therefore, on has τ*_p ∼ τ_p^ee∝N_e/T² [28, 34] in the degenerate limit, which reveals an increase of the spin lifetime as the density increases in the high density regime. However, in the non-degenerate limit, τ*_p∝T/N_e [28, 34] leads to a decrease of the spin lifetime with increasing density in the low density regime. This picture is supported by the gray dashed curve in figure 2(c), which illustrates the crossover between the degenerate and non-degenerate limits according to the condition T_F = T. One may notice that the results at 300 K between figure 2(c) and (d) show good agreement. This is because that the enhanced electron–phonon scattering leads to τ*_p < Δt. Hence the scattering becomes the dominant mechanism of the suppression of the inhomogeneous broadening and the π-pulses are irrelevant to the spin relaxation as discussed above.

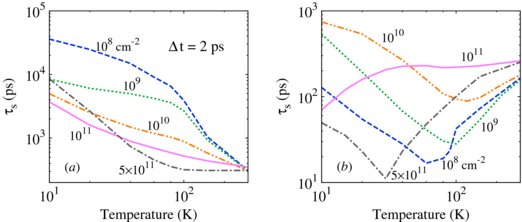
The temperature dependence of the spin lifetime with the π-pulse sequence for different densities is shown in figure 3(a), with Δ = 2 ps. Since τ*_p > Δt in the low temperature regime, the spin lifetime for the high densities, e.g. 5 × 10¹¹ cm⁻², decreases with increasing temperature as suggested by the relation τ_s∝τ^ee_p∝N_e/T² in the degenerate case. For the low densities, the system can be in the non-degenerate limit (T_F ≪ T) even in the low temperature regime. However, one notices that the spin lifetime still decreases with increasing temperature, violating the relation τ_s∝τ^ee_p∝T/N_e. This is due to the enhancement of the electron–acoustic-phonon scattering as the temperature increases. In figure 2(c), we plot the spin lifetime from the calculation only with the electron–electron scattering at 40 K, which is labeled by '40 K, ee'. One finds that the spin lifetime in this case can exceed the one at 10 K in the low density regime (the electron–phonon scattering at 10 K is negligible in this regime), which supports the relation τ_s∝T/N_e solely due to the electron–electron scattering in the non-degenerate limit. In figure 3(b), we plot the temperature dependence of the spin lifetime from the calculation without the rephasing sequence to show the role of the rephasing pulses more clearly. The valleys for 10⁸–10¹⁰ cm⁻² are mainly due to the competition between the inhomogeneous broadening and scattering strength, while the dip at 5 × 10¹¹ cm⁻² is related to the crossover between the strong and weak scattering limits. These features can be understood by comparing with figure 2(d).

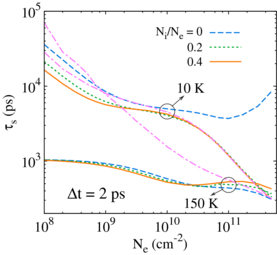
Zoom In Zoom Out Reset image size

To illuminate the role of the impurity scattering, we introduce impurities with the impurity densities N_i/N_e = 0, 0.2 and 0.4. The results are plotted as a function of electron density in figure 4. Since one has τ*_p > Δt at 10 K, the increase of the scattering strength by the electron–impurity scattering reduces the spin lifetime. This is also the situation in the low density regime at 150 K. However, the scattering at 150 K in the high density regime is too strong to keep the relation τ*_p > Δt. Therefore, the motional narrowing relation takes over, resulting in an increase of the spin lifetime as the scattering strength is enhanced by the impurity. In figure 4, we also plot the spin lifetime from the calculation with only the electron–impurity scattering for N_i/N_e = 0.4 at 10 and 150 K (shown by the pink chain curves). By comparing with the corresponding results from the full calculation, one finds that, at 10 K, the electron–impurity scattering is dominant in the high density regime, while the inelastic scattering is also important in the low density regime. At 150 K, the enhancement of the electron–phonon scattering makes the inelastic scattering even more dominant.

Zoom In Zoom Out Reset image size

In summary, we have calculated the spin lifetime due to the D'yakonov–Perel' mechanism in two-dimensional electron gas in (0 0 1) GaAs QWs in a wide range of temperature and density regimes under a serried π-pulse rephasing sequence. We show that the spin lifetime is insensitive to the rephasing sequence with a long inter-pulse spacing in both the weak and strong scattering limits. As the inter-pulse spacing decreases, the spin lifetime shows a pronounced increase. In the meantime, the temperature and density dependences of the spin lifetime can become quite different from those without the π-pulse sequence due to the different roles of scatterings. Since the suppression of the inhomogeneous broadening is mainly from the serried π-pulse sequence in the short inter-pulse spacing case, the scattering only performs as the source of the relaxation channel. We show that both in the strong and weak scattering limits, the density and temperature dependences of the spin lifetime under a serried π-pulse sequence are consistent with those of the momentum scattering time. Moreover, we show that the inelastic scattering mechanism can present an important contribution even in the presence of impurities, especially in the low density regime at high temperatures. According to our results, the efficient manipulation of the spin lifetime through the π-pulse rephasing sequence requires high mobility samples with very low (or high) electron densities and low temperatures. Finally, we should point out that the extension of the spin relaxation time beyond 100 ns can be limited by other spin relaxation mechanisms, e.g. the Elliott–Yafet mechanism [31, 32, 35] and/or the fluctuation of the hyperfine interaction [36].

Acknowledgments