ABSTRACT
We investigate the fate of disks around brown dwarfs in the ejection scenario and the implications on their observable properties. For that purpose, a parameter study of close triple approaches leading to escape is carried out where the ejected body is surrounded by a low-mass disk. We analyze the recircularized radial surface density profile of the post-encounter disk in dependence of the minimum two-body distances between the escaper and the perturbing bodies. Our results show that the general appearance of the disks is rather similar to disks after two-body encounters in as much as there is also an exponential drop in surface density for the outer disk regions as well as an enhancement of surface density for the innermost region relative to the initial disk profile. However, the disks after close triple approaches are mostly less massive, have generally flatter recircularized surface density disk profiles, and have radii that are similar or larger compared to disks after two-body encounters. From our results, we construct a simple scale-free model only depending on the minimum encounter distances of the two perturbers. Such a model is especially useful for statistical studies of disk collisions in triple systems that must cover a large range of encounter distances.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Dynamical interactions between pre-stellar objects are thought to play an important role during the earliest stages of star formation. As has been shown by simulations of bound, non-hierarchical, small-N multiple systems, the formation of binaries after the decay of these systems is able to explain the reduction of the mean distances between pre-stellar objects from a few 100 AU, the typical size of pre-stellar cloud cores, down to the typical distances of pre-stellar and stellar binaries of a few 10 AU (Sterzik & Durisen 1998; van Albada 1968). From an observational point of view, it has been argued that stars frequently form in clusters which then disperse within a few dynamical timescales (Zinnecker et al. 1993). This is also supported by direct detections of very young and dense small-N clusters (Lada & Lada 1991) and by the fact that in star-forming regions the fraction of binaries and bound multiple systems decreases rapidly with time, implying significant orbital evolution during the formation process (Zinnecker et al. 1993). On the theoretical side, it has been demonstrated that the fragmentation of a turbulent cloud core leads almost always to the formation of multiple fragments in a non-hierarchical, unstable configuration that decays after some crossing times, confirming these assumptions (see, e.g., Mac Low & Klessen 2004 for a recent review).
As forming stars are usually surrounded by circumstellar disks, dynamical interactions can also, through star–disk and disk–disk encounters, significantly modify the appearance of such disks (Hall 1997; Clarke & Pringle 1993; Hall et al. 1996; Pfalzner et al. 2005). The gravitational interaction in dense small-N cluster may also significantly influence, if not completely determine, the final stellar and substellar mass spectrum (Klessen 2001; Bonnell et al. 1997, 2001). This idea has been discussed in the context of brown dwarf formation in the past few years (Reipurth & Clarke 2001; Bate et al. 2002, 2003; Delgado-Donate et al. 2004; Umbreit et al. 2005). The formation of brown dwarfs is now generally seen as the continuation of star formation to lower masses, as observations have shown that young brown dwarfs possess properties rather similar to stars (see Luhman et al. 2007 for a recent review). However, which physical processes determine the low-mass cutoff of the stellar initial mass function (IMF), and, thus, might have a significant influence on the properties of brown dwarfs, is still unclear (see Whitworth et al. 2007 for a recent review). Reipurth & Clarke (2001) suggest that the ejection of cluster members out of their surrounding cloud core, caused by the decay of their non-hierarchical multiple host system, reduces, if not inhibits, the further accretion onto these objects, thereby limiting their mass. In this picture, the final mass of an object is correlated with the time it is bound to its parent cluster, a correlation that was also found by Bate & Bonnell (2005) in their simulation of large fragmenting molecular clouds. This implies that brown dwarfs must be ejected early in order to stop the accretion process at the right time.
Umbreit et al. (2005) have shown that such a scenario can also account for the close brown dwarf binaries observed in the galactic field, as ongoing accretion is able to reduce the initial separations of a triple system by a factor of up to 50 as opposed to a factor of 5 without accretion. Therefore, the initial separations of the multiple systems do not need to be very small in order to produce close brown dwarf binaries, but can have values as large as a few 100 AU.
However, brown dwarfs formed via ejection must have suffered at least one very close encounter with other cluster members in order to be ejected early. First, this follows from the fact that an encounter leading to escape is usually a close one compared to the initial size of the multiple system (Aarseth et al. 1994). Second, in order for the decay to happen early in time, the crossing time of the multiple system has to be short, which in turn requires the initial system to be rather compact. As mentioned above, such encounters strongly influence the properties of disks around pre-stellar objects. From simulations of star–disk encounters by Hall (1997) it became clear that the resulting perturbed disks are truncated down to radii half the closest encounter distance. Consequently, the disks around ejected brown dwarfs should be very small and therefore their lifetimes short (Reipurth & Clarke 2001).
So far, truncated sizes of disks were determined after close two-body encounters by Hall et al. (1996) and Hall (1997) for the case where the encounter orbits were usually parabolic ones. For large-N clusters, this type of encounter orbit is assumed to be the most likely one (Ostriker 1994; Larson 1990). For close encounters in bound small-N clusters, however, we will typically have more than two bodies approaching at the same time with the result that these encounter orbits deviate significantly from simple two-body ones. As another consequence, the resulting disk profile should depend on the closest encounter distances of each of the approaching bodies. Although close triple approaches have been investigated extensively in the literature (e.g., Aarseth et al. 1994; Agekian & Anosova 1990, 1991; Anosova & Zavalov 1981), the closest two-body encounter distances were unfortunately not determined.
The aim of our study is to investigate disk collisions in decaying triple systems that produce brown dwarfs by ejection and to characterize these strongly perturbed disks around the ejected brown dwarfs. Our investigation is conducted in two steps: first, we carry out a parameter study of disk collisions in triple systems, considering only the last close encounter that finally leads to decay. Although, at that time, the disk might already have suffered some close triple encounters, this is less of a concern for accreting triple systems, as the last encounter is in this case, on average, the closest and most violent one due to the decreasing total system size. As the outcome of such a collision depends on many parameters we will first simulate disk collisions in non-accreting triple systems, while we model the disk similar to Hall et al. (1996), i.e., we neglect the influence of gas pressure, viscosity, and self-gravity which implies low disk masses relative to its central object. This way the results are scale-free, which allows to apply them to accreting triple systems under a variety of initial conditions without the need for further simulations. Viscous effects are only included after the collision, when we recircularize the remaining disk material, i.e., orbital energy is removed while keeping the angular momentum constant until the orbit is circular. This treatment corresponds to the assumption that the disk can radiate the viscously generated internal energy efficiently perpendicular to its mid-plane and the timescale of any viscous process that redistributes angular momentum is much longer than both the radiative and the orbital timescales. Under these circumstances energy is lost more efficiently than angular momentum and each gas element settles down on a circular orbit, which is the orbit of least energy for a given angular momentum (Pringle 1981). To recircularize the disk after the collision also simplifies our investigation, as we now do not need to explicitly consider the post-encounter velocity profiles of the disk. Instead, we discuss only the resulting recircularized radial surface density profiles.
As a second step, in an accompanying paper, we will apply our disk model to the accreting triple systems we previously investigated in Umbreit et al. (2005) and consider the further viscous evolution of disks around ejected brown dwarfs. There we will compare the size and lifetime of disks around brown dwarfs and TTauri stars, focusing on the question to what extent one might expect to find signatures of the ejection process in the properties of brown dwarf disks.
In Section 2, we will investigate the encounter parameters of triple approaches leading to escape. In Section 3, we will describe our simulations of disk collisions in close triple encounters, and construct a model of the radial surface density profile that only depends on two encounter parameters. Finally, in Section 4 we will summarize our results.
2. CLOSE TRIPLE ENCOUNTERS LEADING TO ESCAPE
2.1. Classification of Close Triple Approaches
Most of the work that has been done on disk collisions only dealt with the case of two-body encounter orbits characterized by periastron distance and eccentricity. As already mentioned in Section 1, disk collisions in close triple approaches are characterized by at least two encounter distances and the encounter orbits deviate significantly from orbits in the two-body problem.
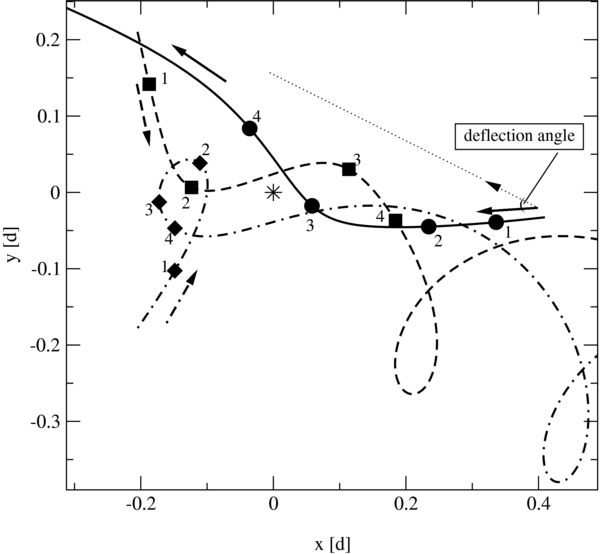
A classification of encounter orbits in close triple approaches for the general three-body problem with negative total gravitational energy is given in Anosova & Zavalov (1981) and Anosova & Orlov (1992). In these studies two basic types of orbits during close triple approaches, named "fly-by" and "exchange," have been found. Orbits of the "fly-by" type are characterized by a close passage of one of the components to the center of mass of the system while the other two bodies form a binary that moves into the opposite direction. Figures 1 and 2 show some typical examples. Close triple approaches of the "exchange" type, on the other hand, can be best described as a sequence of two close two-body collisions between the escaper and one body of the final binary, illustrated in Figure 3.
Figure 1. Typical example of a "fly-by" triple approach leading to escape. The solid line shows the escaper orbit, while the dashed and dot-dashed lines show the orbits of the bodies that form the binary. All orbits are shown with respect to the center of mass (star) and are given in units of the mean harmonic size d. The different filled symbols show the positions of the bodies at certain times, with the numbers reflecting their time sequence. This particular plot shows an example of a "fly-by" of type 1a* according to the classification in Anosova & Orlov (1992), with a value of the deflection angle (the angle between the velocity vector at the beginning and the end of the collision) of the escaper orbit much lower than 20°.
Download figure:
Standard image High-resolution imageFigure 2. Typical example of a "fly-by" triple approach leading to escape. The solid line shows the escaper orbit, while the dashed and dot-dashed lines show the orbits of the bodies that form the binary. All orbits are shown with respect to the center of mass (star) and are given in units of the mean harmonic size d. The different filled symbols show the positions of the bodies at certain times, with the numbers reflecting the time sequence. This particular plot shows an example of a "fly-by" of type 1b* according to the classification in Anosova & Orlov (1992), with a value of the deflection angle (indicated by the angle between the bold solid and dotted arrow) of the escaper orbit larger than 20°.
Download figure:
Standard image High-resolution imageFigure 3. Typical example of an "exchange" triple approach leading to escape. The solid line shows the escaper orbit, while the dashed and dot-dashed lines show the orbits of the bodies that form the binary. All orbits are shown with respect to the center of mass (star) and are given in units of the mean harmonic size d. The different filled symbols show the positions of the bodies at certain times, with the numbers reflecting the time sequence.
Download figure:
Standard image High-resolution imageAs we will restrict ourselves to disk collisions in triple encounters leading to escape of one of the bodies, we want to outline the relative importance of these two encounter types for this case. The results of Anosova & Orlov (1992) show that the "fly-by" encounter is the most probable one to lead to escape, with a probability of 84%, while the escape probability of "exchange" encounters is, with 16%, rather low. The authors further introduced four subtypes of "fly-by" approach based on the deflection angle, defined as the angle between the velocity vectors of the ejected body before and after the triple encounter (see Figure 2 for an example). They found that the probability of escape decreases with increasing deflection angle and more than half of these close approaches have deflection angles lower than 45°. From this study one can easily see that triple collisions leading to escape are mainly "fly-by" encounters where the escaping body is only little deflected.
Another important way to classify triple approaches is based on how close they are. In the literature different definitions for the minimum size of a triple system have been used. Agekian & Anosova (1990) defined this quantity as the minimum separation of the most distant body with respect to the center of mass, while Aarseth et al. (1994) determined several geometrical parameters, like the triangular perimeter, at the time when the moment of inertia is at minimum. Although the so obtained minimum sizes were defined at different times of the triple interaction, the average distance between the bodies at those times was always less than the virial system size, confirming that a triple approach leading to escape is always a close one. From these minimum triple sizes and geometrical configurations at those minima, there is, however, no simple quantitative relation to the minimum two-body distances due to the complex orbits of the three bodies, so the minimum two-body distances need to be determined by numerical simulations.
Qualitatively, one can already infer some basic properties of disk collisions in triple encounters from the general classification scheme. For simplicity, we assume that the disk mid-plane is in the orbital plane of the triple system for the rest of this discussion. From the orbits shown in Figures 1–3 it becomes clear that a disk around the escaper suffers at least two collisions, a prograde and a retrograde one. Depending on the encounter distances between the escaper and each of the two other bodies, either the prograde or the retrograde is the closer one and hence dominates the interaction. This is most prominent for "exchange" encounters, where one of the close two-body encounter distances is much smaller than the other, by usually much more than a factor of 20. Agekian & Anosova (1990) found that the minimum separation of the most distant body is always less than 0.65d for all types of triple encounter leading to escape, with d being the virial system size or the mean harmonic distance of the triple. As a direct consequence, the closest two-body encounter distance in an exchange encounter is, on average, extremely small compared to the virial size of the system. Therefore, the wider one of the two two-body encounters can be neglected in this case and the outcome of a disk collision in an exchange encounter will be almost completely determined by the two very close consecutive encounters the escaper experiences with one of the other two bodies. In addition, both of these encounters are either prograde or retrograde.
However, the situation is different for encounters of the "fly-by" type. In this case, the closest two-body encounter distances of the escaping body are comparable to each other in most of the cases and we expect that the resulting disk properties will be significantly different from the two-body disk collision results.
2.2. Encounter Parameters for Disk Collisions
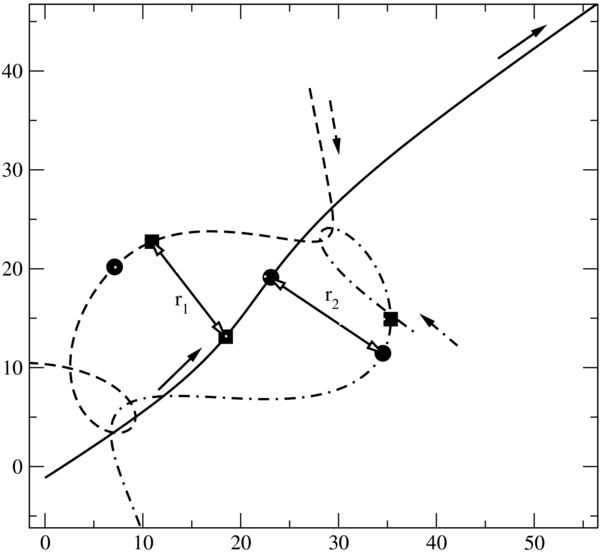
As we know from the previous discussion, disk collisions in "fly-by" encounters should deviate the most from pure two-body disk collisions because of a prograde and retrograde disk encounter happening nearly at the same time with comparable strength. This deviation should be largest if these two encounter distances are equal and should get smaller once their difference gets larger. Therefore, we parameterize disk collisions in close triple approaches by the ratio of r1/r2 and rmin, with rmin = r1 < r2, where r1, r2 are the closest two-body encounter distances between the escaper and the other two bodies. Figure 4 shows an example of three-body configurations at the times of the closest two-body distances. For our simulations of disk collisions, we do not consider the dependence of our results on the particular shape of an orbit as well as other parameters that influence the outcome of disk collisions. This is mainly because including other parameter would not only increase the parameter space significantly but is also very difficult to do in a systematic way. For example, the eccentricity of the perturber orbit cannot be easily accounted for as it constantly changes during the encounter and its time dependence differs significantly for different encounters with similar values of r1/r2 and rmin. For our post-encounter disk models we average over these additional parameters and should, therefore, expect that the scatter around the average disk model is intrinsic to our parameterization.
Figure 4. Parameterization of close triple approaches suitable for our investigation of disk collisions. r1, r2 are the closest two-body encounter distances. The different symbols show the triple configurations at the time a minimum of the distance between the escaper and one of the other bodies is reached.
Download figure:
Standard image High-resolution imageIn order to get a statistically representative sample of encounter orbits of close triple approaches leading to escape, we generate the triple positions following Anosova (1986, their Figure 1) where all three bodies are initially in the x–y-plane and two bodies are always placed at x = −0.5, y = 0 and x = 0.5, y = 0. The position of the third body is randomly chosen within a region lying in the positive quadrant and embraced by a unit circle around the point x = −0.5, y = 0. This arrangement of the bodies has been proven to be a representative sample for statistical studies of unstable triple systems by Anosova & Orlov (1994) and should, therefore, lead to a representative sample of close triple approaches leading to escape. We set the velocities of the bodies to zero initially, as we later, in an accompanying paper, want to apply our scale-free results to the ejected brown dwarfs obtained in Umbreit et al. (2005), where we chose the same initial conditions in the simulations of accreting triple systems. The integration of the equation of motion is carried out with the CHAIN code of Mikkola & Aarseth (1993) and is stopped if a binary and a single body are separated by more than 7d while they are gravitationally unbound to each other. In total we integrated 1000 triple systems and determined the minimum two-body distances and their ratios at the last triple approach.
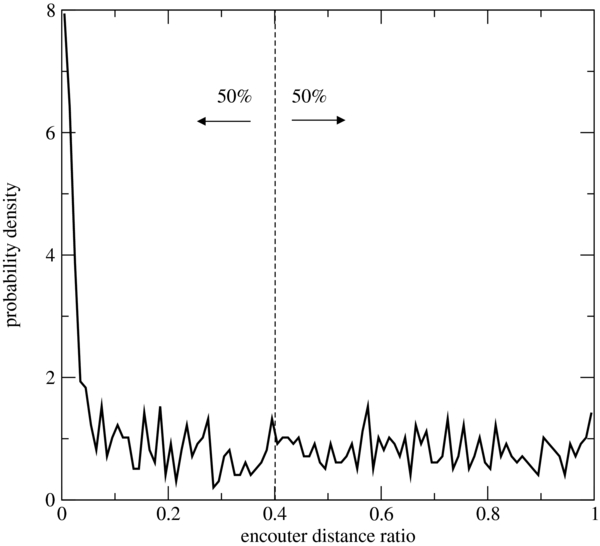
Figure 5 shows the distribution of r1/r2 of the last triple encounter before the triple system decays obtained from our simulations. As can be clearly seen, r1/r2 is uniformly distributed in the range (0.05, 1) and has a strong peak for values below 0.05. This strong peak was to be expected because all the close triple encounters of the "exchange" type have very small minimum two-body distance ratios and exchange encounters make up 16% of all close triple encounters leading to escape (Anosova & Orlov 1992). Taking this into account, the distance ratios of the "fly-by" encounters can then be assumed to be uniformly distributed in the whole range, which is also consistent with a median value of 0.4 for the entire distribution.
Figure 5. Distribution of the ratio of the closest two-body encounter distances r1/r2. The dotted line indicates the position of the median, which is at r1/r2 ≈ 0.4.
Download figure:
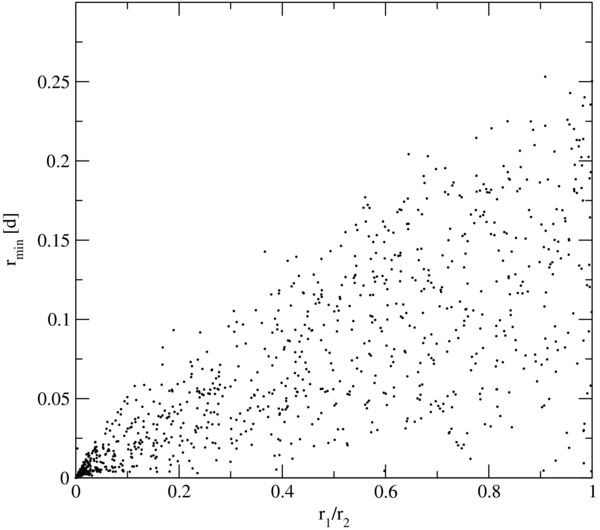
Standard image High-resolution imageFinally, in Figure 6 we plotted the closest two-body encounter distance rmin over the ratio r1/r2 for each close triple encounter that led to escape in our simulation. As can bee seen, for a given ratio of r1/r2 the minimum two-body distance is almost uniformly distributed between some maximum value and nearly zero. As mentioned earlier, due to the fact that there is a maximum size of a close triple encounter above which the triple system does not break up, there is roughly a correlation between the maximum value of rmin and the ratio r1/r2. The lower limit of rmin does not seem to depend on r1/r2 and can get close to zero.
Figure 6. Minimum distance rmin in units of the mean harmonic distance (virial size) over the ratio r1/r2.
Download figure:
Standard image High-resolution image3. DISK COLLISIONS IN CLOSE TRIPLE ENCOUNTERS
3.1. Initial Conditions
After determining the encounter parameter of close triple approaches suitable for the investigation of disk collisions, we now want to study the properties of the highly perturbed disks as a function of rmin and r1/r2. We considered six different values of r1/r2: 0.9, 0.8, 0.6, 0.5, 0.3, and 0.2. For each of these values we carried out between 12 and 32 realizations of disk collisions in triple systems with varying rmin.
For our disks we choose a thin disk model, neglecting pressure forces, which implies a short timescale of the event, and self-gravity which implies a low disk mass compared to the central mass, with Mdisk/Mcentral < 0.1. For our disks this inequality roughly corresponds to the modified Toomre criterion (see, e.g., Klahr & Brandner 2006):
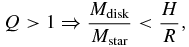
where Q is the Toomre parameter, H is the disk scale height, R is the disk radius, and Mdisk and Mstar are the masses of the disk and central star, respectively.
Even for a mass ratio as high as Mdisk/Mcentral = 0.1, the angular momentum and mass transfer is in principle very similar to lower-mass disks apart from a pronounced "self-evolution" of the disk after the collision which is due to its self-gravity. However, in our case we do not expect this self-evolution to be a dominant effect because our disks are much less massive after the encounter, owing to the much stronger interaction in a close triple encounter compared to the much wider encounters in Pfalzner et al. (2005).
The disk is composed of 10, 000 test particles, initially placed on circular orbits and distributed axial-symmetrically according to a given radial surface density distribution. For Σ we choose Σ = Σ0 (r0/r), with Σ0 being the surface density at r0. The choice of such a rather flat disk profile is motivated by hydrodynamical simulations of collapsing molecular clouds (see, e.g., Lin & Pringle 1990 and Yorke & Bodenheimer 1999) where the structure of disks around the forming central, deeply embedded object is still significantly influenced by the infall of matter from their accretion envelope. Therefore, choosing Σ∝r−1 for our disk profile seems reasonable, especially compared to the profile Σ∝r−1.25 obtained by Lin & Pringle (1990). In addition, choosing a flat profile increases the amount of material that gets stripped off the disk as more particles are initially in the outer disk compared to steeper disk profiles.
In our simulations we only consider cases where the disk mid-plane coincides with the orbital plane of the triple system, making the disk collisions coplanar. As this type of collision is probably most destructive to the disk, we overestimate the amount of material that gets stripped off the disk and consequently underestimate the final disk mass. However, the results of Hall et al. (1996) indicate that this effect should be rather small, as the amount of material that remained bound in their simulations hardly changed with inclination. The effect of the inclination on the disk profile, however, should be larger because of the larger differences in the energy and angular momentum transport compared to the coplanar cases, and needs to be quantified for disk collisions in triple systems in a future study.
In absence of detailed hydrodynamical calculations of triple systems in collapsing molecular clouds, we can only speculate about the initial size of the disk before the last encounter. It seems plausible to us that it should be less than the mean harmonic distance d of the triple system and choose, therefore, an initial radius of d/3 for our calculations. Although it is likely that the escaping body already suffered a two-body collision that was closer than the one at the last triple encounter, we restrict ourselves to those cases where the last encounter dominates the resulting disk profile. If the disk is much smaller due to a previous encounter, the effect of the last encounter on the disk is rather low, so the properties of the disk in that case are mainly determined by triple encounters that do not lead to escape. The systematic investigation of the much larger parameter space of these encounter types is, however, beyond the scope of the present work. Apart from that, we might expect that due to the infall of material in a collapsing cloud core, the disk should constantly gain mass as long as it resides in the core, which should partly compensate the mass loss due to previous close encounters.
For all of our calculations, we choose a fixed initial radial extent of the disk, ranging from 0.1 to 20 AU, covering more than two orders of magnitude in radius. We then adjust d, the mean harmonic size of the triple system, so that the outer radius of the disk corresponds to 1/3 d. In order to reduce the effect of the artificially chosen inner radius we only carry out disk collisions with rmin > 1.5 AU. We start our calculations at a time when the maximum separation between two bodies is 1d and stop if it is more than 4d. Although we found that varying the initial separation influences our results significantly, there was no systematic change. This is mainly because of the rather chaotic motion of the triple systems before the last encounter, resulting in very different initial orbital configurations for a given maximum separation of the bodies. This is the case even when the triple encounters have very similar values of r1/r2 and rmin. Together with the neglect of all the other parameters mentioned in Section 2.2 this should reduce the direct correlation between the post-encounter disk profiles and our set of encounter parameters. As we will show later, the correlation is still strong enough to allow for a scale-free model.
3.2. Numerical Integration Scheme
In order to integrate 10, 000 test particles efficiently, one has to make a compromise between accuracy and runtime. While the motion of the triple system can be integrated with a median accuracy of 10−12 in total energy within a very short time using the CHAIN algorithm (Mikkola & Aarseth 1993), to maintain such an accuracy level during the whole disk collision calculation for the motion of the test particles would require a huge amount of CPU time. The main reason for this is the rather large radial extent of our disk and the extremely small timescale of the motion of particles with small disk radii compared to the crossing time of the triple system. We therefore decided to integrate the test particle motion with the fifth-order Runge–Kutta Cash–Karp scheme (see Press 1993) with adaptive time-step control, which conserved the total energy of an undisturbed disk with an accuracy of 10−6 over 10 orbital periods of the outer edge of the disk. This makes it possible to integrate many realizations of disk collisions in triple encounters while still ensuring a reasonable accuracy of the particle motion over the time of integration, which was on average between 10 and 20 outer orbital periods in our simulation runs.
Thus, in our code, we use two integration schemes to advance the entire system in time, the CHAIN algorithm for the triple system and the Runge–Kutta scheme for the massless disk particles. Because of the smaller timescale of the particle motion around the ejected body, the particles are advanced on smaller time steps compared to the much larger time steps of the triple system. To couple the particle motion to the motion of the triple system, the force of the triple system acting on the massless particles is treated as a time-varying external force in the Runge–Kutta scheme. In order to obtain this force at a time required by the Runge–Kutta scheme, the triple system is integrated from a previous configuration of a regular CHAIN step up to this particular point. The triple configurations obtained at those times are, however, not used to advance the triple system further. This is to reduce the influence of accumulating round-off errors caused by having a much larger number of CHAIN steps than actually required by the corresponding accuracy criterion.
At the end of the simulation we recircularize each disk particle that remained bound to the perturber by calculating its specific angular momentum and calculate the corresponding radius the particle would have, if it was on a circular orbit. This way, we obtain for each particle its recircularized radius and can calculate the corresponding surface density profile of the post-encounter disk.
3.3. Disk Profiles
3.3.1. General Disk Structure
Figure 7 shows a typical example of a recircularized radial surface density disk profile after a close triple encounter, together with its initial profile. Many features of the radial disk profile seen in this diagram are similar to the results for parabolic two-body encounters investigated by Hall (1997), e.g., the disks are severely truncated and the surface density drops by orders of magnitudes in the outer disk regions. Also as in Hall (1997), the inclusion of the approximate viscous evolution of the strongly perturbed disk by recircularizing the disk material, further depletes the outer disk regions, because at larger radii the disk material loses much angular momentum and, therefore, ends up at smaller radii (Hall 1997; Hall et al. 1996). This has also the effect that in the inner regions of the disk the surface density is enhanced relative to the initial density. We also find, as in Hall (1997), that the surface density of the outer parts of the disk can be described by an exponential function. However, Hall (1997) gave no detailed description of the radial structure of the inner disk, where most of the disk mass resides.
Figure 7. Typical example of a truncated accretion disk surface density profile after a triple collision together with our fitted model. Shown is the initial (thin dashed line) as well as the truncated, recircularized profile (thin solid line). The bold solid lines represent the initial r−1 power law and our fitted model on a log–log scale (left) and on a semi-log scale (right). The recircularized profile can be divided into three different regions. Below 0.2 rmin it has the same power-law shape as the initial profile, but with Σ increased by a factor of ≈1.7 (bold dashed line). For larger disk radii there are two regions, between 0.2 rmin and 0.7 rmin (bold dot-dashed line) and above 0.7 rmin (bold dotted line), that can be fitted with an exponential profile, Σ∝exp (log (1/2) r/τ), having different slopes, τ1 and τ2 (here τ1 ≈ 0.064rmin and τ2 ≈ 0.2rmin).
Download figure:
Standard image High-resolution imageFrom our simulations we found that most of our disk profiles can be divided into three distinct regions, a power-law region with Σ∝r−1 for disk radii below 0.2rmin and two regions, located between 0.2 and 0.7rmin and above 0.7rmin, where the surface density decreases exponentially as Σ∝exp (log (1/2) r/τ), with the outer region being flatter, i.e., having a larger full-width-half-value τ, than the inner one. At 0.2rmin Kobayashi & Ida (2001) also found that the structure of the disk is changing by investigating the eccentricity change of the disk material after a prograde encounter. Inside that radius the disk is only weakly perturbed, whereas further out, resonances lead to strong perturbations. Although only strictly valid for parabolic encounters, they also found that this boundary is only weakly dependent on the eccentricity of the perturber. In our simulations the eccentricity of the perturber with the closest encounter distance was always below 2.5 at the time of closest approach and, therefore, the region was at most shifted to 0.24rmin which can be neglected given the uncertainties of our fits.
As already mentioned, inside the inner power-law region the surface density is enhanced relative to the initial surface density. As can bee seen from Figure 7 it is increased by a constant factor, which varied in our simulations between 1.4 and 2. This factor is similar to the surface density enhancement for the parabolic, retrograde encounters of Hall (1997) at r = 0.4rmin, although in all our runs we observed this increase at somewhat lower radii. This might be partly due to the influence of the prograde encounter, as Hall (1997) observes the enhancement at 0.25rmin for this case, but also because of the, on average, higher eccentricity at the time of closest approach. Another consequence of the higher eccentricity of the orbits might be that the density enhancement never exceeded a factor of two, in contrast to the prograde, parabolic encounters in Hall (1997), where the surface density was five times higher than its initial value. However, as we will see in Section 3.4, even if the eccentricities are close to the parabolic case, the disks' surface densities are not as strongly enhanced in the inner region as in that case, which indicates that the higher eccentricities have a rather limited influence on the disk structure. The reason for the lower surface density enhancement might have rather something to do with the dynamics of the triple encounters that cannot be sufficiently described in terms of two-body encounters, as we will discuss in Section 3.4.
3.3.2. Disk Profile as a Function of Encounter Parameters
In order to find out how the surface density profile is related to the encounter parameters rmin and r1/r2, we fitted for each of our obtained post-encounter disk profiles two exponential functions to the outer two regions and determined the full-width-half values τ1, for the region between 0.2 and 0.7rmin, and τ2, for the region outside 0.7rmin. We then plotted these values over rmin for each r1/r2 separately. We found that, while the uncertainties of the fitted values for τ1 were mostly between 2% and 10%, they were much larger for τ2, mainly because of the much lower number of particles left in the outer regions of the disk. In those regions many particles are stripped off the disk and the remaining ones are recircularized to smaller radii, due to their much smaller angular momentum. Therefore, we can give for most of the r1/r2 values we investigated only upper limits for τ2.
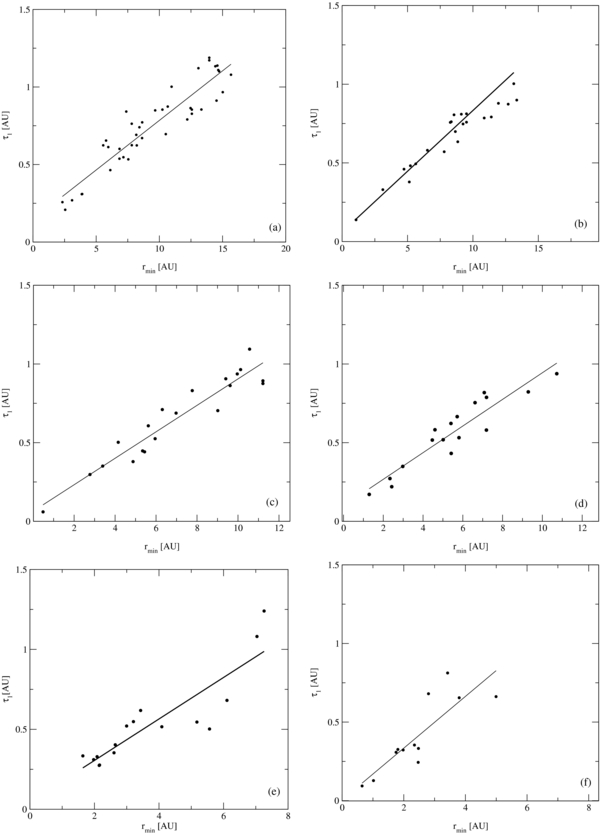
Figure 8 shows τ1 as a function of rmin for different values of r1/r2. In all cases τ1 increases with increasing rmin which means that for larger rmin the radial surface density disk profile gets flatter in this region. Furthermore, τ1 seems to depend linearly on rmin. However, we find that the values of τ1 scatter much more around this linear relation than one would expect from their individual errors, which come from the quality of the fit. As already mentioned in Sections 2.2 and 3.1 the reason for the large scatter is mainly intrinsic to our parameterization. Furthermore, we find no significant difference between triple collisions, where the disk suffered a retrograde or a prograde encounter at the time the ejected body reached the closest encounter distance rmin. This indicates that the orientation of the disk plays only a minor role and most of the large scatter comes from the rather large variety of initial conditions at the chosen maximum distance between the bodies. Also, we did not find that the deviations of τ1 correlate with any other parameter we investigated, like the eccentricity of the perturber orbit and the escape velocity of the ejected body. We therefore come to the conclusion that the value of τ1 must depend on many parameters in a rather complex way, which, in order to investigate further, would require to investigate a much larger parameter space than we can currently study.
Figure 8. Full-width-half-value τ1 over the smallest encounter distance rmin for r1/r2 ≈ 0.95 (a), 0.8 (b), 0.6 (c), 0.5 (d), 0.3 (e), and 0.2 (f). The behavior can be approximately described by a linear function, with a slope of 0.064 ± 0.005 (a), 0.076 ± 0.006 (b), 0.084 ± 0.005 (c), 0.085 ± 0.008 (d), 0.13 ± 0.02 (e), and 0.16 ± 0.03 (f). However, the deviations from this linear function cannot be explained by the errors of τ1.
Download figure:
Standard image High-resolution imageFor each of the values of r1/r2 we determined the slope of the linear fit of the τ1 values with the corresponding error and plotted these values over r1/r2 in Figure 9.
Figure 9. Slope of the linear change of τ1 with rmin over r1/r2. The error bars of the slope represent the errors of the linear fit which were always larger than the errors of the individual τ1. The horizontal error bars represent the r1/r2 intervals from which we have chosen the individual triple collisions. The solid lines are linear fits to the data in the intervals below and above r1/r2 = 0.5.
Download figure:
Standard image High-resolution imageAs can be readily seen, for values of r1/r2 greater than 0.5 there is only a weak increase in the slope of τ1(rmin) and, considering the errors, it is not absolutely certain if the slope at r1/r2 = 0.5 is really larger than the one at r1/r2 = 0.95 or if this is an effect of the limited number of points available for the fit. For encounters with r1/r2 < 0.5 we find that the slope of τ1(rmin) increases much stronger and nearly all values of τ1 for r1/r2 = 0.2 were larger than the corresponding values for r1/r2 ⩾ 0.5. This clearly shows that at least in this regime the radial surface density distribution depends strongly on the parameter r1/r2 and leads to disk profiles which are generally much flatter for lower values of r1/r2.
As mentioned earlier, the uncertainties in the values of τ2 are much larger than they are for τ1 because of the lower number of particles left in the outer disk regions for the fit. Only for the cases r1/r2 = 0.2 and r1/r2 = 0.3 we could determine τ2 with comparable accuracy as τ1, and found a value of ≈0.2 with an uncertainty of 15% for both. In all other cases we can only say that a2 must be between 0.1 and 0.2. As we cannot constrain how a2 changes with r1/r2 we, therefore, assume for simplicity a constant value of a2 = 0.2 for our study. Although this value is an overestimate for most of our disks after triple encounters with r1/r2 ⩾ 0.5, the error we introduce into our model is only minor. This is because, as we will also show later, the mass contained in the outermost part of the disk is, for these cases, always less than 6%.
3.3.3. Fitted Model for the Surface Density
From our results we are now able to construct a scale-free model for the recircularized post-encounter surface density disk profile as a function of the encounter parameters rmin and r1/r2. For its general form we can write
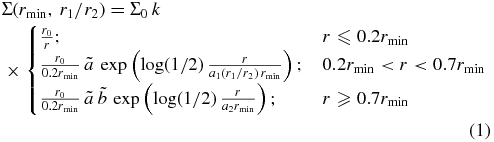
with
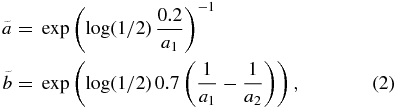
where we replaced the exponential slopes τ1, 2 with a1, 2 rmin.
In this equation, the density enhancement for the region below 0.2rmin is accounted for by a constant factor k while Σ0 is the initial value of the surface density at radius r0. The constants 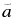 and
and 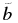 are coefficients to ensure continuity for Σ. The parameter a1 is given by our fits in Section 3.3.2, while a2 = 0.2, as we mentioned earlier. However, as a1 is only given for a limited number of r1/r2 values, we need to fit these data points with a simple function in order to be able to apply our results to different encounter parameters. Given the error bars, it is certainly legitimate to represent a1(r1/r2) by two linear fits, one for r1/r2 ⩾ 0.5 and another one for r1/r2 ⩽ 0.5, modifying the a1 intercept of each of them slightly to guarantee continuity at r1/r2 = 0.5. The parameters a1 and a2 are then given by
are coefficients to ensure continuity for Σ. The parameter a1 is given by our fits in Section 3.3.2, while a2 = 0.2, as we mentioned earlier. However, as a1 is only given for a limited number of r1/r2 values, we need to fit these data points with a simple function in order to be able to apply our results to different encounter parameters. Given the error bars, it is certainly legitimate to represent a1(r1/r2) by two linear fits, one for r1/r2 ⩾ 0.5 and another one for r1/r2 ⩽ 0.5, modifying the a1 intercept of each of them slightly to guarantee continuity at r1/r2 = 0.5. The parameters a1 and a2 are then given by
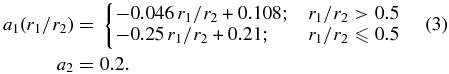
Thus, Equations (1)–(3) completely define the resulting post-encounter disk profile in terms of rmin and r1/r2, apart from the constants k and Σ0(r0). While the latter is related to the initial disk and, therefore, to the specific problem one wants to apply our model to, the constant k can be determined by considering the relative mass loss of the disk, which will be done in the next section.
3.4. Relative Disk Masses
3.4.1. Mass Distribution
From our model surface density profile we can now determine how the total disk mass changes with rmin for a given value of r1/r2. In addition, it allows us to measure the extent of the disks based on their mass distribution. There is, however, no unique definition of disk radius. In the literature the half-mass radius is frequently used for that purpose, which has the advantage that this radius is roughly consistent with the apparent 2.7 mm flux sizes of disks around T Tauri stars (Hartmann et al. 1998). However, the apparent disk size depends crucially on the optical depth of the disk and hence on the absolute value of the surface density. Therefore, it is not clear, a priori, that this relation will hold for disks around brown dwarfs, because if we assume roughly the same ratio of disk to central mass for the observed brown dwarfs as for T Tauri stars, which is also supported by observations of Klein et al. (2003) and Scholz et al. (2006), brown dwarf disks will have much lower surface densities than T Tauri disk and consequently very different optical depths. In absence of detailed radiative transfer modeling of low surface density disks there is no practical disk size definition which can be directly compared to observations.
For our investigation, we use the radius  , within which 90% of the disk mass is contained, as a measure of the size of the disk. We can then compare it with the result from parabolic two-body disk encounters of Hall et al. (1996), who found
, within which 90% of the disk mass is contained, as a measure of the size of the disk. We can then compare it with the result from parabolic two-body disk encounters of Hall et al. (1996), who found 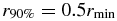 .7
.7
In order to obtain the disk mass MD from our model we integrate Equation (1) over the radius r:
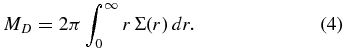
The general solution can then be written in the form
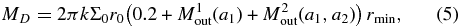
where M1, 2out are coefficients which are proportional to the mass of the disk contained in the corresponding region. As can be seen, in our model the disk mass is directly proportional to rmin for given values of a1, 2, which is also consistent with the disk masses we get from our simulations, shown in Figure 10.
Figure 10. Disk mass in units of the initial disk mass over the smallest encounter distance rmin for r1/r2 = 0.95 (a), 0.8 (b), 0.6 (c), 0.5 (d), 0.3 (e), and 0.2 (f). The solid line is the linear fit to the data, with a slope of 0.0296 ± 0.0007 (a), 0.031 ± 0.001 (b), 0.034 ± 0.002 (c), 0.036 ± 0.002 (d), 0.052 ± 0.005 (e), and 0.065 ± 0.005 (f).
Download figure:
Standard image High-resolution imageIn these figures, we plotted for each value of r1/r2 the masses of the disks in units of the initial disk mass over rmin and found that the values are linearly correlated with a correlation factor larger than 95%. The values of M1, 2out together with 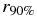 for each value of r1/r2 we investigated are shown in Table 1. Also shown is the fraction of the total post-encounter disk mass that is contained within the three different disk regions.
for each value of r1/r2 we investigated are shown in Table 1. Also shown is the fraction of the total post-encounter disk mass that is contained within the three different disk regions.
Table 1. Disk Mass Coefficients Minn, M1, 2out and the 90%-mass-radii 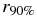 in Units of rmin for Our Disk Models with Different Values of r1/r2
in Units of rmin for Our Disk Models with Different Values of r1/r2
| r1/r2 | Minn | M1out | M2out |  (rmin) (rmin) |
|---|---|---|---|---|
| 0.95 | 0.2 (60%) | 0.13 (38%) | <0.006 (2%) | 0.38 |
| 0.8 | 0.2 (52%) | 0.17 (44%) | <0.015 (4%) | 0.49 |
| 0.6 | 0.2 (49%) | 0.19 (46%) | <0.02 (5%) | 0.52 |
| 0.5 | 0.2 (49%) | 0.19 (46%) | <0.02 (5%) | 0.52 |
| 0.3 | 0.2 (29%) | 0.35 (51%) | 0.14 (20%) | 0.9 |
| 0.2 | 0.2 (27%) | 0.37 (51%) | 0.16 (22%) | 1.0 |
Notes. Minn and M1, 2out are proportional to the mass contained in the respective region. In parenthesis the mass fraction with respect to the total post-encounter disk mass is given.
Download table as: ASCIITypeset image
This table clearly shows that for r1/r2 ⩾ 0.5 there is only a very small amount of mass contained in the outer region of the disk with r ⩾ 0.7rmin and more than 95% of the disk mass is within 0.7rmin, making the post-encounter disk very compact. Therefore, the rather large uncertainty of the disk profile and mass in the outermost region, which is of the order of 50%, does not have a significant influence on the overall mass distribution of the disk. Furthermore, we find only a weak increase in mass in the region between 0.2rmin and 0.7rmin for decreasing r1/r2 ⩾ 0.5, as it was to be expected from the results of τ1(rmin). Comparing this mass with the mass that is contained within 0.2rmin we find that they are nearly equal, given the errors of about 10% for M1out. Only in the case with r1/r2 = 0.95 there seems to be more mass contained in the innermost region, with about 60% of the total disk mass.
Because of the strong increase of τ1, 2 for r1/r2 ⩽ 0.5, as shown in Section 3.3, we also have a strong increase in mass contained in the outer disk regions for this case. As a consequence, these disks are no longer strongly concentrated and appear to be much flatter, as now there are only about 78% of the total disk mass contained within 0.7rmin as opposed to more than 95% for r1/r2 ⩾ 0.5. In contrast to disk encounters with r1/r2 ⩾ 0.5 the outermost part of the disk now contains almost a quarter of the total mass of the disk and most of its mass is contained in the region between 0.2rmin and 0.7rmin. This comes close to the corresponding values for a disk with Σ∝1/r truncated at a radius 1rmin.
3.4.2. Determination of k
So far, we completely specified the disk profile as shown in Equations (1)–(3) apart from a constant k, which specifies how much the surface density in the inner disk region below 0.2rmin is enhanced relative to the initial surface density. As in that region we are severely limited by noise, fitting each single profile for that region in order to determine k is rather problematic. This is because the power-law indices of the fits will also scatter around the mean value of −1, which in turn adds much to the error of k. We, therefore, determined k by assuming that the inner profile follows strictly a power law with index −1 and use the linearly fitted disk masses from Figure 10 together with Equation (5). This gives a statistically more robust value for k because the determination of the masses are based on a larger number of particles than that of the inner disk profile. For the determination of k, we expressed Equation (5) in terms of the initial disk mass Minit = 2π Σ0r0(rout − rin), where rout is the outer and rin is the inner initial disk radius. We then inserted the values from Table 1 for each r1/r2 and set the numeric value of the slope of M(rmin) equal to the corresponding slope of the fits, thus obtaining k. In all cases, we found that k = 1.7 ± 0.2, which lies also in the range we roughly expected from the disk profiles in Section 3.3. Since this factor does not seem to depend on r1/r2, it follows that a flatter disk profile implies a larger total disk mass. From this it follows further that in general the masses of the post-encounter disks increase with decreasing r1/r2, which also agrees with our results shown in Figure 10.
3.5. Comparison to Two-body Disk Encounters
3.5.1. Disk Masses
Since we noticed that disks after triple encounters are qualitatively similar to the ones after two-body encounters, we now want to find out to what extent this similarity holds, and compare these two cases in a more quantitative manner. Here we are only concerned with a comparison of disk masses and, in Section 3.5.2, of disk radii, as the only study that was concerned with recircularized surface density profiles (Hall 1997) did not have a sufficient resolution for the inner disk to compare our results with quantitatively.
For two-body disk collisions, Hall et al. (1996) found that the post-encounter disk has only one-third of the initial mass if the disk has a radius of 4rmin, which has also been found in a more recent study of Olczak et al. (2006). As our disk radius is always 20 AU this means that, in order to compare to our results, the corresponding disk mass in our case is the one at rmin = 5 AU for each r1/r2. From our calculations we find values ranging from 15% to 18% of the initial disk mass for r1/r2 ⩾ 0.5, while for r1/r2 < 0.5 we find values of up to ≈33%. This reflects the trend we intuitively would expect, as for larger values of r1/r2 we have roughly speaking two two-body encounters with similar strength and consequently more stripping of disk material, whereas for lower values of r1/r2 we are getting closer to a single two-body encounter. In addition, we also find that this trend is strongly nonlinear and not a simple function of r1/r2. The fact that in a triple encounter we only find the same disk mass for r1/r2 ⩽ 0.2 has the direct consequence, together with the distribution of r1/r2 shown in Figure 5, that the majority of close triple encounters is more destructive than the corresponding two-body ones and only in one-third of the cases we should get at least comparable disk masses.
However, the convergence of the disk masses for smaller r1/r2 is not as trivial as it might sound, because we also find that the influence of the third body in the case of r1/r2 = 0.2 is still significant. In order to demonstrate this effect, we carried out a calculation for one particular triple encounter where the disk is only affected by the escaper and the body with the closest encounter distance rmin, but otherwise leave the orbits of the bodies unchanged. In that example, we find that the post-encounter disk mass is increased by almost 10% of the initial disk mass which makes the post-encounter disk mass 33% larger compared to the case, where the disk is affected by all three bodies. As we find that for the r1/r2 = 0.2 case the disk masses are comparable to the two-body case, it directly follows that the particular motion of the escaping body in a triple encounter tend to increase the mass of the disk while the presence of the third body reduces it. We therefore expect that for ratios r1/r2 ⩽ 0.2 the trend for higher disk masses compared to two-body collisions for a given rmin is continued.
3.5.2. Disk Mass Transfer and Disk Radii after Triple Encounters
From our simulation, we suggest that the trend of higher disk masses for lower r1/r2 is closely related to the formation of the final binary after the triple encounter. To demonstrate this, we compared in Figure 11 the distance between the escaper and the body of the binary with the smallest encounter distance rmin and the distance these bodies would have if they moved on a hyperbolic orbit with the same eccentricity at r = rmin. As can be clearly seen, the distance between the bodies in the triple system is almost always lower than in the two-body case, leading to an enhanced interaction time which is much larger than five dynamical times found for the parabolic two-body case by Hall et al. (1996; one dynamical time is the ratio of rmin over the velocity vmin at that point). Before the encounter, the distances are lower because the bodies do not approach each other from an infinite distance, but are part of a bound system with finite size. The lower distances after the encounter are due to the formation of a binary where one of the two bodies is slowed down relative to the escaper because of the presence of the third body. For the disk around the escaper this means, on the one hand, that the disk starts losing material earlier in the encounter than it would do in a hyperbolic encounter. On the other hand, due to the lower distances after the encounter, particles that became unbound after the closest collision are slowed down again and could be re-captured by the escaper or the other two bodies depending on the direction of their ejection. Since much of the disk material is initially on smaller radii around the ejected body than after the encounter, the initial deviation from the hyperbolic encounter should only play a minor role, while the deviations after the closest encounter are more effective, because much of the disk material is distributed over a much larger area. Figure 12 shows a snapshot of a disk after the final binary has formed and where the disk is only affected by the perturber with the closest encounter distance rmin. Although, at this time, after more than 20 dynamical times, the particle states, i.e., whether they are gravitationally bound or unbound to any of the three bodies, would have been long evident in a two-body encounter (Hall et al. 1996), in a triple encounter there is a substantial amount of unbound material that gets captured later because of the perturber getting drastically slower when it forms a binary. The increased effect of the perturber on the disk can bee seen by looking on the strong spiral arm that develops during the encounter, which, in a two-body encounter, is always pointing away from the perturber. In this figure, however, it is bent toward the binary because of the much lower velocity of the perturber after binary formation relative to the escaping body, making it possible that this otherwise unbound material gets captured by the escaper or by the perturber. Here we want to stress that the effect is solely because of the deceleration of the closest perturber and not because of the mass of the third body, which has been artificially set to zero while retaining the orbit of the ejected body in this particular simulation. The re-capture of disk material can also be seen in Figure 13 where we plotted the change of mass of the disk around the ejected body. Here it is clearly shown that first, the time required for the particle states to settle is much longer than in the two-body case and, second, that just after the encounter and after the formation of a binary much of the disk material lost is re-captured by the ejected body. From this figure it is also evident that the change of disk mass in an orbit of a triple system is no longer a simple function over time and a substantial amount of disk material changes its gravitational state more than once. Without the rather abrupt deceleration the disks would have masses very close to the corresponding minimum shown in Figure 13. Therefore, the loss caused by the presence of the third body is in that case compensated by approximately 10% of the initial disk mass, leading to the mass expected for only two masses in a nearly parabolic two-body encounter.
Figure 11. Distance of the escaping body to the body of the binary with the smallest encounter distance rmin over the time in units of rmin/vmin for one particular triple system, where vmin is the relative velocity of the two bodies at the time of rmin (solid line). The dashed line represents the corresponding distance if the bodies would strictly move on a hyperbolic orbit with an eccentricity of ≈1.4. The dotted line marks the time when the final binary forms from the triple system.
Download figure:
Standard image High-resolution imageFigure 12. Snapshot of a disk after a triple encounter. Shown are the orbits of the escaper (solid line) and the binary (dashed and dot-dashed lines) as well as the particles representing the disk material (dots).
Download figure:
Standard image High-resolution imageFigure 13. Mass of the disk around the ejected body in units of the initial disk mass over time in dynamical time units for one particular triple system. Shown are the results for a triple collision where the disk is only affected by the escaper and its closest perturber (filled squares) and for a triple collision where the disk is affected by all three bodies (filled circles). Briefly after the time of the formation of the final binary (≈ + 15 dynamical times) the disk mass rises significantly due to the abrupt slow down of the perturber during binary formation. Due to this deceleration of the perturber motion the disks gained about 10% of the total disk mass.
Download figure:
Standard image High-resolution imageIn contrast to the behavior of the disk masses for lower r1/r2, the case r1/r2 = 0.2 does not converge toward the expected two-body result for the 90%-mass-radii  . Here we find that the disks after triple encounters are comparable or much larger than after slightly parabolic two-body ones. As shown in Table 1 we also find the tendency for the post-encounter disks to become flatter with decreasing r1/r2 in the value of
. Here we find that the disks after triple encounters are comparable or much larger than after slightly parabolic two-body ones. As shown in Table 1 we also find the tendency for the post-encounter disks to become flatter with decreasing r1/r2 in the value of  . The dependence on r1/r2 is nearly the same as for the slope of τ1(rmin), i.e., only a weak increase for r1/r2 ⩾ 0.5 and a much stronger one for values below. As a consequence of the high-mass concentration in the inner disk regions for r1/r2 ⩾ 0.5, the 90%-mass-radius has rather low values. However, compared to the results of Hall (1997), where
. The dependence on r1/r2 is nearly the same as for the slope of τ1(rmin), i.e., only a weak increase for r1/r2 ⩾ 0.5 and a much stronger one for values below. As a consequence of the high-mass concentration in the inner disk regions for r1/r2 ⩾ 0.5, the 90%-mass-radius has rather low values. However, compared to the results of Hall (1997), where 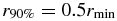 , our values are not much different in the cases with r1/r2 ⩾ 0.5, although here we would expect to have a much stronger deviation. As already mentioned, for r1/r2 < 0.5 we do not get similar 90%-mass-radii and find that
, our values are not much different in the cases with r1/r2 ⩾ 0.5, although here we would expect to have a much stronger deviation. As already mentioned, for r1/r2 < 0.5 we do not get similar 90%-mass-radii and find that 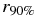 is around 1rmin, that is, twice as large as in the parabolic two-body case. Considering that for the r1/r2 = 0.2 case we have about the same disk mass as for the corresponding two-body case, we come to the conclusion that parabolic two-body collisions produce disks with a much higher mass concentration in the inner regions and, therefore, with a significantly increased average surface density.
is around 1rmin, that is, twice as large as in the parabolic two-body case. Considering that for the r1/r2 = 0.2 case we have about the same disk mass as for the corresponding two-body case, we come to the conclusion that parabolic two-body collisions produce disks with a much higher mass concentration in the inner regions and, therefore, with a significantly increased average surface density.
The generally flatter mass distribution of disks after triple encounters is presumably caused by the capture process of unbound material after the final binary has formed, as we described in the previous few paragraphs. Since it is known that the unbound material carries most of the angular momentum away from the disk (Hall et al. 1996), the re-capture process brings some of this high-angular-momentum material back to the disk, which recircularizes after the collision to larger radii, producing a flatter disk profile. In our example (Figure 13), one-third of the final disk material was re-captured for the case where all three bodies affect the disk, and should have a larger angular momentum thus ending up at larger radii.
3.6. Overview of the Disk Model
Table 2 summarizes all the numerical results of our post-encounter disk model in dependence of the encounter parameters rmin and r1/r2. These values are then used to construct the recircularized surface density profile of a post-encounter disk for a given set of encounter parameters by using Equations (1)–(3). The only free parameter that remains to be specified is Σ0, the value of the surface density of the initial disk at a radius of r0, which must be provided by the specific problem at hand. For instance, if we consider marginally stable disks (Mdisk ≈ 0.1MBD) around brown dwarfs and assume a disk radius of about 20 AU, typical for disks still deeply embedded in their molecular cloud core, we obtain values ranging from 70 to 570 g cm−2 for brown dwarfs with masses between 0.01 and 0.08 M☉.
Table 2. Summary of All Numerical Results for the Half-width-values a1, a2, the Constant k, the Disk Mass Coefficients Minn,, M1, 2out, and the 90%-mass-radii 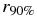 for Our Disk Models with Different Values of r1/r2
for Our Disk Models with Different Values of r1/r2
| r1/r2 | k | a1 | a2 | Minn | M1out | M2out | 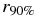 (rmin) (rmin) |
|---|---|---|---|---|---|---|---|
| 0.95 | 1.7 ± 0.1 | 0.064 ± 0.005 | 0.1–0.2 | 0.2 | 0.13 | <0.006 | 0.38 |
| 0.8 | 1.6 ± 0.1 | 0.076 ± 0.006 | 0.1–0.2 | 0.2 | 0.17 | <0.015 | 0.49 |
| 0.6 | 1.7 ± 0.1 | 0.084 ± 0.005 | 0.1–0.2 | 0.2 | 0.19 | <0.02 | 0.52 |
| 0.5 | 1.7 ± 0.1 | 0.085 ± 0.008 | 0.1–0.2 | 0.2 | 0.19 | <0.02 | 0.52 |
| 0.3 | 1.7 ± 0.2 | 0.13 ± 0.02 | 0.20 ± 0.03 | 0.2 | 0.35 | 0.14 | 0.9 |
| 0.2 | 1.7 ± 0.2 | 0.16 ± 0.03 | 0.20 ± 0.03 | 0.2 | 0.37 | 0.16 | 1.0 |
Notes. Minn is proportional to the mass contained in the inner region below 0.2rmin and M1, 2out are proportional to the masses in the outer two regions.
Download table as: ASCIITypeset image
4. SUMMARY AND DISCUSSION
We carried out the first systematic investigation of disk collisions in close triple approaches leading to escape of the body surrounded by a disk. Different from two-body disk encounters, we find that the outcome of disk encounters in close triple approaches can no longer be sufficiently described in dependence of minimum encounter distance and eccentricity of the perturber orbit. Instead, the ratio of the minimum two-body encounter distances r1 and r2, as well as the minimum of these two distances, rmin, provides a better set of parameters to describe the outcome of such disk encounters.
Our results show that most of the recircularized post-encounter disk profiles can be divided into three distinct regions, a power-law region for the innermost disk and two regions further outside where the surface density drops off exponentially with different half-width values. In the innermost region the surface density is enhanced compared to the initial disk profile, while it nearly follows the same power law as the initial disk. The extent of all three regions is directly proportional to rmin, while only the middle region, between 0.2 and 0.7rmin, depends also significantly on r1/r2. We find for this particular region that the lower the value of r1/r2 is, the flatter becomes the exponential drop, which means that the half-width value τ1 increases for decreasing r1/r2. The same trend as for τ1 can be found for the total disk mass and the disk radius, defined as the radius where 90% of the total disk mass is contained within. Thus, it follows that, for a given rmin, the truncated disks are flatter, more massive, and have a larger radii for lower values of r1/r2.
The general appearance of the recircularized post-encounter disk profiles is not much different from the ones after two-body encounters in Hall (1997) in as much as he also finds an exponential drop in surface density for the outer disk as well as an enhancement of surface density for the innermost region relative to the initial disk profile. However, we found that disks after close triple encounters are flatter and much less concentrated for a given periastron distance or rmin. The reason for the much flatter profile is the dramatic slow-down of the ejected body after the close triple approach when the two perturbers form the final binary. This causes much of the material that was unbound just after the closest passage to be re-captured by the ejected body. Because this material has also a larger specific angular momentum its recircularized radius will also be larger, causing the flatter disk profile. Here we want to note that this process is not specific to disk collisions in triple encounters but also applies to encounters in higher order multiple systems.
Although the re-capturing of unbound material compensates the disk mass loss to some degree, the total mass of the disk is still lower compared to the disk after a two-body encounter for the same rmin in most of the cases. This is because, in a close triple approach, there are two two-body encounters taking place at nearly the same time. Only when the effect of the third body becomes less important, as for r1/r2 < 0.2, the disk mass after the triple encounter might be larger than in a two-body encounter.
From our results we are able to construct a simple scale-free model for the recircularized surface density disk profile after the last close triple approach as a function of r1/r2 and rmin. Such a model is especially useful for statistical studies of disk collisions in triple systems that must cover a large range of encounter distances. This especially applies to the case of decaying accreting triple systems because, as was found previously, accreting triple systems rapidly shrink in size during their mutual interactions (Umbreit et al. 2005), with the result that the overall system size, and hence the average encounter distance, at breakup differs significantly for different decay times. Our disk model makes it possible to study the properties of a large number of disks around brown dwarfs that are the result of such a triple decay, without the computationally expensive task to carry out disk collision simulations that cover such a large parameter space. This way one can find out if the very close collisions required to eject the brown dwarfs early lead to properties of their disks that are generally inconsistent with observations as previously assumed. This study will be presented in an accompanying paper.
We also want to stress that our disk model is only an approximate model which reproduces the trends we found from our parameter study, while being roughly consistent with the general appearance of the individual post-encounter disk profiles. For instance, it also might be possible that there is a slight dependence of the density enhancement of the inner disk, k, on our encounter parameters. Because of the considerable scatter in our data and the limited resolution of our particle disk, we are not able to uniquely identify a trend. In addition, the choice to fit the outer disk regions with exponential functions has been mainly made for simplicity and because it fitted the surface density profile reasonably well in the respective radial range. Certainly, the disk profile has to be studied not only with higher resolution but also as a function of more than two encounter parameters in order to construct a more detailed post-encounter disk model.
We also want to point out that because of the initial radius of the disk we chose, the perturbers were always penetrating the disk. It is clear that smaller disks will not be as strongly affected by the last close triple approach as our disks. Instead, their properties are increasingly dependent on the details of their previous evolution within the unstable triple system, which we did not investigate here. Our disk model shows only the imprints of the last close triple encounter on the properties of the disk around the ejected body.
In summary we can conclude that disks after close triple approaches are mostly less massive, have generally flatter recircularized surface density disk profiles, and have radii that are similar or larger compared to disks after two-body encounters.
We thank all the people we enjoyed having inspiring and helpful discussions with on various occasions. Special thanks go to Cathy Clarke, who motivated the comparison of disk collisions in triple encounters to two-body disk encounters. R.S. is funded by the Chinese Academy of Sciences Visiting Professorship for Senior International Scientists, Grant Number 2009S1-5.
Footnotes
- 7
Here, rmin corresponds to the periastron distance.