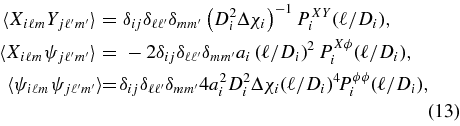ABSTRACT
We present a framework for analyzing weak gravitational lensing survey data, including lensing and source-density observables, plus spectroscopic redshift calibration data. All two-point observables are predicted in terms of parameters of a perturbed Robertson–Walker metric, making the framework independent of the models for gravity, dark energy, or galaxy properties. For Gaussian fluctuations, the two-point model determines the survey likelihood function and allows Fisher matrix forecasting. The framework includes nuisance terms for the major systematic errors: shear measurement errors, magnification bias and redshift calibration errors, intrinsic galaxy alignments, and inaccurate theoretical predictions. We propose flexible parameterizations of the many nuisance parameters related to galaxy bias and intrinsic alignment. For the first time, we can integrate many different observables and systematic errors into a single analysis. As a first application of this framework, we demonstrate that: uncertainties in power-spectrum theory cause very minor degradation to cosmological information content; nearly all useful information (excepting baryon oscillations) is extracted with ≈3 bins per decade of angular scale; and the rate at which galaxy bias varies with redshift, substantially influences the strength of cosmological inference. The framework will permit careful study of the interplay between numerous observables, systematic errors, and spectroscopic calibration data for large weak lensing surveys.
Export citation and abstract BibTeX RIS
1. INTRODUCTION
Weak gravitational lensing of background sources can produce exceptionally strong constraints on cosmological parameters and tests of general relativity. Initial analyses considered the two-point correlation function (or, equivalently, power spectrum) of the shear pattern induced on a single population of background galaxies (Miralda-Escudé 1991; Kaiser 1992; Blandford et al. 1991). A wealth of new statistics, however, have been suggested as more powerful means to extract information from weak lensing (WL): cross-power spectra of multiple source populations with distinct redshift distributions (also known as "tomography"; Hu 1999); the correlation of shear with foreground galaxy clusters (Jain & Taylor 2003), or more generally the cross-correlation of lensing shear with the galaxy distribution (Bernstein & Jain 2004; Zhang et al. 2005); joint analyses of density–density, density–shear, and shear–shear correlations in an imaging survey (Hu & Jain 2004); cross-correlation of magnification as well as shear (Jain 2002); use of the cosmic microwave background (CMB; Hu & Okamoto 2002; Hirata & Seljak 2003) or recombination era 21 cm signals (Metcalf & White 2007; Pen 2004; Zahn & Zaldarriaga 2006) as source planes; cross-correlation of source density or shear with a distinct spectroscopic galaxy survey population (Newman 2008; Schneider et al. 2006); and the use of three-point statistics (Takada & Jain 2004) or statistics such as peak counts (Hennawi & Spergel 2005; Wang et al. 2004; Marian & Bernstein 2006) to move beyond two-point information. Each of these potential innovations has been individually analyzed and shown to improve cosmological constraints. The first goal of this paper is to consider the simultaneous use of all of these observable statistics: can we forecast the cosmological information that they will yield collectively in future surveys? Can we start to develop a framework in which all these signals could be analyzed simultaneously in a real experiment?
In parallel with the increasing variety of proposed WL signals, the community has identified a series of potential astrophysical and instrumental nonidealities in WL data which, if ignored, would lead to substantial systematic errors in the inferred cosmology. These include: finite accuracy in our ability to predict the deflecting mass power spectrum due to nonlinearities (Jain & Seljak 1997) and baryonic physics (Zhan 2006; Jing et al. 2006); intrinsic alignments (IA) between galaxy shapes (Croft & Metzler 2000) and between galaxy shapes and the local mass distribution (Hirata & Seljak 2004) that are not induced by lensing; multiplicative "shear calibration" errors in the derivation of lensing shear from galaxy images (Ishak et al. 2004; Huterer et al. 2006); additive "spurious shear" due to uncorrected point-spread function (PSF) ellipticity or other imaging systematics (Huterer et al. 2006; Amara & Refregier 2007); and errors in the assignment of redshifts to the source populations (Ma et al. 2006). The impact of these systematic error sources on cosmological inferences has been analyzed by different means, but a second goal of this paper is to produce a comprehensive forecast that considers their presence simultaneously.
Previous work has shown that these multiple sources of information and systematic error in WL surveys can interact in interesting ways. For example, in the presence of tomographic data, many systematics are readily distinguishable from cosmological signals and can hence be diagnosed and corrected internally to a survey; this approach is called self-calibration (Huterer et al. 2006). It has also been shown that combining galaxy density and lensing correlations can lead to self-calibration of shear calibration errors (Bernstein & Jain 2004) and the uncertainties in galaxy biasing (Hu & Jain 2004; Zhan 2006). Intrinsic alignments of galaxies can be diagnosed and corrected if tomographic information is available (King & Schneider 2003); however, this places substantially greater demands on the precision and accuracy of redshift assignment than would otherwise be needed (Bridle & King 2007). These investigations raise important practical questions: will the self-calibration techniques continue to succeed when we attempt to simultaneously self-calibrate several different systematic errors? Do cross-correlation techniques reduce uncertainties in redshift distributions to negligible levels, or is it necessary to make a complete spectroscopic redshift survey of some size to measure redshift distributions directly (Ma & Bernstein 2008)? This paper presents a formalism through which all these questions can be answered, but we defer to later papers the application of the framework to these issues.
The third goal of this work is to describe the constraints by WL in a language that is not tied to a specific cosmological model. Most forecasts for WL survey constraints are done within the context of a universe that has homogeneous dark energy with equation of state w = w0 + wa(1 − a). Projecting the WL experiment onto this model gives concrete predictions, but obscures what the WL is really measuring. So the analysis framework presented here will be dark-energy agnostic, meaning that no specific model is assumed. We will be very explicit about the assumptions made in the analysis and try to keep them to a minimum. In fact, a great strength of WL experiments is their ability to test general relativity itself, so we seek an analysis method that is general enough to incorporate such tests. Similar to the approach of Knox et al. (2006), our analysis results in constraints on the distance and growth functions D(z) and gϕ(z) without reference to the particular dark-energy or gravity modifications that might cause deviations from ΛCDM.
In the following section, we describe a "kitchen-sink" formalism for WL survey observables that allows the incorporation of all suggested two-point statistics and very general treatments of nearly all proposed systematic errors. In Section 3, we give a likelihood function and Fisher matrix for an unbiased spectroscopic redshift survey of source galaxies. Then we briefly describe a software implementation of the lensing and spectroscopy likelihood calculations. We describe our model for the evolution of the lensing potential power spectrum in Section 5, and in Section 6 we describe generic models used for the nuisance functions required in the lensing survey analysis. In Section 7, we use the implementation of these methods to investigate the proper choices for the bin sizes and grid spacings needed to turn the lensing analysis into a tractable finite-dimensional problem. Further application of the framework to survey forecasting will be done in future papers.
An earlier version of this WL analysis formalism was used to generate forecasts for the Dark Energy Task Force (Albrecht et al. 2006) and is described in an appendix to that report.
2. THE WEAK LENSING TWO-POINT LIKELIHOOD
2.1. Observables
We make the assumption that the universe has only weak scalar perturbations to a homogeneous and isotropic four-dimensional metric. In this case, the metric can be written in the Newtonian gauge as a perturbed Robertson–Walker metric
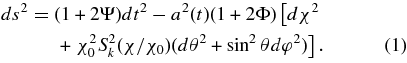
We assign all mass and sources in the universe to a series of narrow spherical shells centered at redshifts ai = (1 + zi)−1 for i ∈ {1, ..., Nz}. There is a comoving angular diameter distance Di to each shell, and the comoving radial extent of each shell is Δχi. Note that the Robertson–Walker metric formula for angular-diameter distance is D = χ0Sk(χ/χ0), where χ0 is the comoving radius of curvature of the universe. For small values of the curvature ωk ≡ −k/χ20, we have
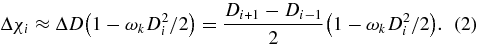
The Robertson–Walker metric also requires Δχi = Δzi/h(zi) = Δai/a2ih(ai). In this paper the Hubble parameter will be written as H(z) = h(z)H100, H100 = 100 km s−1 Mpc−1, and all distances will be in units of c/H100 = 2998 Mpc.
We assume that the photon sources in a survey will be divided into a series of sets α ∈ {1, 2, ..., Ns}. Note the use of latin indices for redshift shells and greek for source sets. We follow Hu & Jain (2004) by assigning each source set up to two observables: first its sky-plane density fluctuations gα(θ, φ), and second a lensing convergence κα(θ, φ). The convergence κ might be inferred from the shear or flexion (Goldberg & Bacon 2005) of galaxies, by a quadratic estimator on the CMB or 21 cm radiation fluctuations, or by any other observable except the source density. The sources can be assigned to sets by photometric or spectroscopic redshift, or even cruder color criteria (Jain et al. 2007), but there could be other criteria such as galaxy type, or perhaps observation by different instruments. We demand only that the criteria for division of the sources be spatially homogeneous, and that the division be invariant under application of gravitational lensing distortion. For notational convenience, we assign each set a nominal redshift zα, but a set can span a broad redshift range. If the sources are discrete objects such as galaxies, then the mean density on the sky of members of each set is denoted nα.
A source in set α has a probability pαi of lying on redshift shell i. The collection of galaxies in set α on shell i will be called the subset αi. The survey is assumed to tell us only which set any individual galaxy belongs to, but not which subset. The pαi are parameters which must be constrained by the lensing survey data or by additional observations, e.g., a spectroscopic redshift survey.
When the lensing sources are drawn from a spectroscopic survey (or when the source is the CMB), then the redshift probability is known a priori, and in particular the sets are probably divided by redshift so that pαi is essentially the identity matrix. The formalism can obviously accommodate the simultaneous analysis of WL samples with varying modes of redshift assignment.
Both the source-density fluctuation gα and convergence κα have a component due to intrinsic fluctuations plus a component due to gravitational lensing. Both are also measured as weighted sums over their respective subsets. We have
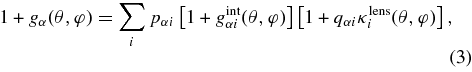
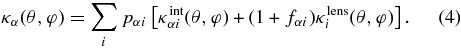
Here, we have assigned each subset a magnification bias factor qαi and a shear calibration factor fαi. In a simple flux-limited selection, the magnification bias factor will be determined by the logarithmic slope of the counts versus flux, and is typically of order unity. The shear calibration factor allows for the possibility that the inferred lensing convergence is mismeasured by some factor 1 + fαi due to multiplicative errors in the lensing methodology, e.g., as investigated by Heymans et al. (2006).
In the limit gint ≪ 1 and κlens ≪ 1, we can drop the second-order term in Equation (3) and write
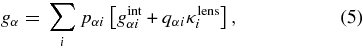
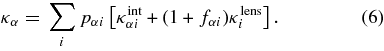
In this case the equations are linear in all the angular functions g and κ, so we can decompose them into spherical harmonic coefficient gαℓm, κlensiℓm, etc, and Equations (5) and (6) hold independently for every harmonic ℓm. We henceforth assume that the spherical-harmonic decomposition has been executed for all the angular functions g, κ, and suppress the ℓm indices for brevity.
We note that while κlens ≪ 1 is a good approximation over most of the sky, gint ≪ 1 is a poor approximation for thin density slices on smaller angular scales. We will forge ahead nonetheless with the assumption that lensing magnification simply adds to the intrinsic density fluctuations, recognizing that a real analysis of data with magnification bias may require inclusion of the nonlinear coupling between spherical harmonics that is induced by magnification bias on highly structured density fields.
The lensing convergence is determined entirely by the metric if we make the assumption that light rays are following its null geodesics. The paths of null geodesics are determined by the lensing potential

For each of our redshift shells, we derive a field ψ from the projected lensing potential via
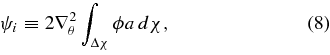
where the derivatives are taken with respect to angles on the sky. We will generally assume that ψ, like the observables, has been decomposed into spherical harmonics, and we will take the flat-sky approximation.
With the definition in Equation (8), and the adoption of the weak-lensing limit and Born approximation, the lensing convergence is
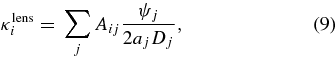
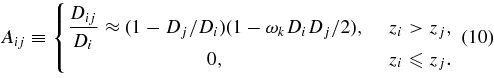
Here, Dij is the comoving angular diameter distance to zi as viewed from zj. In summary, the observables from the survey are, for each spherical harmonic,
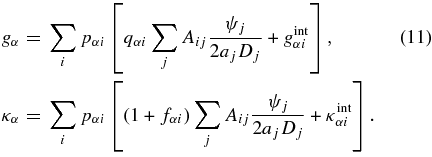
We reiterate that these equations depend only upon the assumption of a Robertson–Walker metric with scalar perturbations plus the approximation that magnification bias and intrinsic density fluctuations are additive.
The equations for the two observables are symmetric under the interchange of g ↔ κ and q ↔ (1 + f). Since q ∼ 1 + f, the lensing effects are similar. However, the intrinsic density fluctuations gint are ≈300 times stronger than κint, breaking the symmetry. Density-field observations are dominated by the intrinsic signal, while convergence (shear) observations are dominated by lensing effects.
2.2. Degeneracies
Equations (9)–(11) reveal a family of degeneracies present in lensing observations as described in Bernstein (2006). The transformations
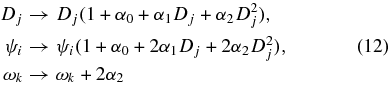
leave the observables unchanged to first order in {α0, α1D, α2D2, ωkD2}. It will hence be impossible for lensing+density surveys to constrain ωk or any quadratic (in D) deviations to ln D unless there are prior constraints on these variables or on ψ, gint, or κint. Constraint on these three degeneracies is unlikely to arise from models of intrinsic clustering or alignment since it is unlikely that a priori models of the redshift dependence of galaxy bias could reach high precision. We hence expect that these degeneracies are going to be broken by theoretical models of the potential fluctuation power spectrum or by other distance indicators such as supernovae or BAO.
2.3. Limber Approximation
To forecast the constraints on the parameters of this model, we require a likelihood expression for the observables. The two fundamental assumptions we make are the following.
- 1.The distributions of the lensing potential, intrinsic galaxy density fluctuations, and intrinsic shape correlations ψi, gintαi, and κintαi are described by a multivariate Gaussian with zero mean.
- 2.The Limber approximation is valid, and there is no correlation between these variables on distinct redshift shells or between different spherical harmonics,

where X, Y ∈ {gint, κint}, and PXYi(k) is the three-dimensional cross-spectrum of variables X and Y at epoch ai.
The first assumption ensures that the likelihood of an observation is fully specified by the expected covariance matrix of the observables. The second assumption implies that this covariance matrix can be expressed in terms of the three-dimensional cross-power spectra of the lensing potential, subset densities, and subset intrinsic correlations {ϕi, gintαi, κintαi} at each redshift shell.
2.4. Biases and Correlations
A typical convention is to express the galaxy density power Pgg as a bias-scaled version of the mass spectrum Pm, plus a Poisson shot-noise contribution, and then describe the mass-galaxy covariance Pmg with a correlation coefficient
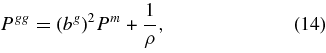

The comoving volume number density ρ of the sources determines the shot noise for a Poisson process, but there is no guarantee that the galaxies are distributed in the mass distribution by a Poisson process. Even when the galaxies do not have Poissonian shot noise, we can still usually write the power in this way for some bias parameter b; we just might keep in mind that rg > 1 is formally allowed if the sources are not Poisson distributed.
Most generally, both the bias and correlation coefficients are different for each source subset as well as being functions of comoving wavenumber k. Each set α has a nominal redshift zα, and each subset has a redshift deviation Δzαi = zi − zα. Galaxies with bad photo-z errors could easily have different bias from those with good photo-zs; for example, highly biased early types tend to have better photo-zs. So our analysis methods should allow for this complication.
We will adopt the bias/correlation notation for the intrinsic galaxy density fluctuations and for the intrinsic convergence κint, except that we will parameterize the bias and covariance with respect to the lensing potential rather than mass distribution. If Pggiαβ is the three-dimensional cross-power between density fluctuations in subsets αi and βi at wavenumber k, and we write Pϕi for the lensing potential three-dimensional power spectrum, then we express
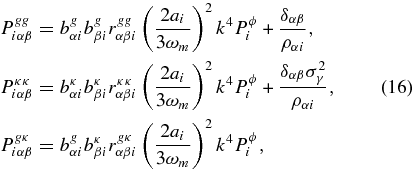
where ραi is a comoving volume density of the galaxy subset in the shell, and σγ is a measure of the shear noise per galaxy. These describe the normal "shape noise" term in the shear power spectrum and the shot noise in the density field. If flexions or other observables are used to infer the convergence, then the shape noise term may have a different form.
Moreover, if Pgϕiα is the cross-power between the density of subset iα and lensing potential, we express
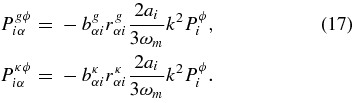
Note that specifying the bias and correlation bκ and rκ of the intrinsic convergence with the lensing potential is equivalent to giving the "GI" and "II" intrinsic alignment information, in the notation of Hirata & Seljak (2004).
The lensing power Pϕ is a function of z and k. The biases and correlation coefficients bκαi, rκαi, bgαi, and rgαi are functions of k, the nominal redshift zα of the source set, and Δzαi, the difference between the subset redshift and the nominal set redshift.
Most complicated are the cross-correlation coefficients such as rggαβi, which are, most generally, functions of k, zi, and both redshift errors Δzαi and Δzβi. In order for the covariance matrix of all these fields to be symmetric, we require rggααi = rκκααi = 1 and the symmetry rXYαβi = rYXβαi. Otherwise, the correlation coefficients are free to vary subject to the constraint that the overall correlation matrix of the potential and all fluctuations must remain nonnegative.
This parameterization of the fluctuations of the potential and the intrinsic fluctuations is completely general—we have not introduced any further assumptions into the model as long as all the bs, rs, and Pϕs are free parameters (non-negative in the last case).
2.5. The Two-point Statistics
Combining the formula for observables in Equation (11), the Limber formulae in Equation (13), and the bias notations in Equations (16) and (17), the covariance matrix for the observables {gα, κα} at a given multipole can be broken into three submatrices,
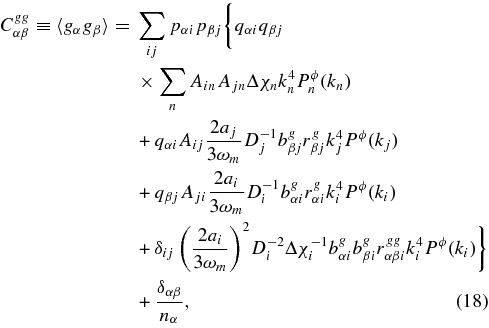
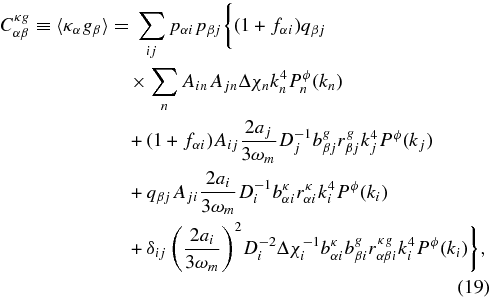

The comoving wavevector is ki = ℓ/Di. In each equation, note that only one of the last three terms is nonzero depending on whether j < i, j > i, or j = i, respectively. For the shear–shear correlation Cκκ, the i = j term is recognizable as the "II" intrinsic-correlation effect of Hirata & Seljak (2004), while the i < j and j > i terms are their "GI" effect.
Note that the last term in the density–shear expression Cκg is an additional intrinsic-correlation term between the galaxy density and the intrinsic shapes, which is distinct from the covariance between the lensing potential and shear. This galaxy–shear correlation has been constrained in the context of systematic errors to "galaxy–galaxy" lensing, e.g., Bernstein & Norberg (2002); Faltenbacher et al. (2007); Hirata et al. (2004).
Examining the density–density correlation Cgg, we find the final term has the normal expected form, but the first three terms describe correlations induced by lensing magnification.
Finally, we note that the covariance matrix manifests the same symmetries for g ↔ κ that were discussed at the end of Section 2.1.
2.6. Likelihood and Fisher Matrix
Under our Gaussian assumption, the likelihood functions for the observables are independent at each multipole ℓm. We define a data vector dℓm to be the union of the gα and κα observables at each multipole, and Cℓ to be the covariance matrix derived above. Under our Gaussian assumption, the total likelihood for the survey is
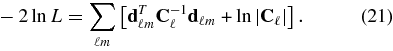
Forecasts of survey performance are made using the Fisher matrix. The usual formula for zero-mean Gaussian distributions applies (Tegmark et al. 1997). We reduce the mode sum to a series of Nℓ bins centered on multipoles ℓi, then the Fisher matrix element for parameters p and q is
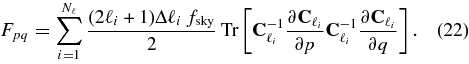
Examination of Equations (18)–(20) shows that all derivatives of C with respect to parameters are very simple. The calculation of the Fisher matrix is reduced to rapid linear algebra, significantly accelerated by exploiting the very sparse nature of most of the derivative matrices.
We have thus succeeded in producing a likelihood function for the most general joint lensing+density survey for the case of Gaussian likelihoods limited to two-point statistics. Given a likelihood we can, of course, form a Fisher matrix for forecasting, or we can execute a maximum-likelihood analysis of real data. Since this likelihood function makes no mention of a particular dark-energy theory, we see that the parameterization chosen here permits a highly flexible analysis. Indeed, no theory of gravity or initial conditions of the universe has been assumed either, just the existence of a Newtonian gauge metric on an RW background cosmology. The lensing potential power spectrum Pϕ(k, z) appears as a series of free parameters, as do the bias and correlation coefficients of the galaxy density and intrinsic alignments.
We have variables that describe in the most general possible fashion the important systematic errors, excepting additive shear contamination.
- 1.Uncertainty in power-spectrum theory will be expressed through prior distributions on the Pϕi parameters.
- 2.Shear calibration errors arise through finite prior uncertainty on the fαi.
- 3.Magnification bias calibration errors arise through finite prior uncertainty on the qαi.
- 4.Intrinsic alignments are embodied through the bκ, rκ, rgκ, and rκκ coefficients.
- 5.Redshift distribution errors are manifested through the uncertainties in the pαi probabilities.
The cost of this great generality is that there are a huge number of nuisance parameters, enough to make us doubt whether the maximum-likelihood analysis—or even the Fisher matrix analysis—is feasible.
2.7. Parameter Inventory
The WL survey covariance matrix has a horrendously large number of parameters. The cosmological treasure lies in the following:
- 1.the two global cosmological parameters ωm and ωk;
- 2.the distances Di, which encode the expansion history of the universe in Nz steps. The Δχi and the Hubble parameters h(zi) can be expressed in terms of these and ωk.
- 3.the metric-potential power spectra Pϕi, which describe the growth of dark-matter structure. For Nℓ bins in ℓ, there will be NℓNz distinct matter-power parameters in the model. A prediction for the growth of potential fluctuations will typically be an important element of any cosmological scenario under test, so the Pϕi can be replaced as parameters by a much smaller number of cosmological parameters.
There are then a large number of nuisance parameters. If there are Nss nonempty source subsets, the nuisance parameters are the following:
- 1.the redshift distribution parameters pαi with Nss − Ns degrees of freedom;
- 2.the shear-calibration errors fαi, another Nss degrees of freedom;
- 3.the magnification bias coefficients qαi, another Nss degrees of freedom;
- 4.the source-density biases bgαi and correlation coefficients rgαi with respect to ϕ, which may be scale dependent, yielding 2NℓNss degrees of freedom;
- 5.the intrinsic alignment power and correlations with the mass, bκαi and rκαi, another 2NℓNss parameters; and
- 6.the correlation coefficients rggαβi, rκgαβi, and rκκαβi, which may also be scale dependent. The number of such parameters is ≈3NℓN2ss/2Nz.
The number of nuisance parameters for a nonparametric analysis is enormous. If we are analyzing a photo-z survey with typical errors Δz ≈ 0.05(1 + z), then we would typically want to space the redshift shells logarithmically in 1 + z with Δln a ≈ 0.02 so that we resolve the redshift distribution of each photo-z bin. In this case, Nz ≈ 100 bins span 0 < z < 5, and we will require Nss ≳ 1000 if we track all subsets out to ±3σ of the photo-z distribution.
To reduce the dimensionality of the likelihood function, we can replace many of the discrete nuisance parameters by the values of parameterized functions for the nuisance variables. Table 1 lists the variables in the WL likelihood function that can be replaced by parametric functions. The nuisance variables are functions of: wavevector k; redshift z; and redshift difference Δz = zα − zi between the nominal and true redshifts of a source subset. In later sections, we will describe the parametric functions that we have implemented to reduce the number of degrees of freedom in the model. Each time we introduce a parametric function, we need to choose a fiducial parameter set and a prior distribution for the parameters.
Table 1. Nuisance Variables that can be Replaced by Functions
| Description | Discrete Variables | Parametric Function |
|---|---|---|
| Lensing potential power spectrum | Pϕi | Pϕ(k, z) |
| Shear calibration error | fαi | f(z, Δz) |
| Magnification bias | qαi | q(z, Δz) |
| Redshift distribution | pαi | p(z, Δz) |
| Source-density bias | bgαi | bg(k, z, Δz) |
| Density–mass correlation | rgαi | rg(k, z, Δz) |
| Intrinsic alignment bias | bκαi | bκ(k, z, Δz) |
| IA–density correlation | rκαi | rκ(k, z, Δz) |
| Density–density x-correlation | rggαβi | rgg(k, z, Δzα, Δzβ) |
| Density–IA x-correlation | rgκαβi | rgκ(k, z, Δzα, Δzβ) |
| IA–IA x-correlation | rκκαβi | rκκ(k, z, Δzα, Δzβ) |
Download table as: ASCIITypeset image
3. SPECTROSCOPIC REDSHIFT LIKELIHOOD
If we draw a single member from source set α and measure its spectroscopic redshift in an unbiased fashion, then by definition the likelihood of the spectroscopic redshift being on shell i is pαi. If we measure Nspecα redshifts, and find that Nspecαi are on shell i, then the likelihood is
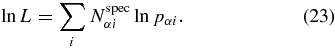
This is true if the redshifts are statistically independent, which requires that they be dispersed across the sky to eliminate source correlations. We assume this limit.
Following Ma & Bernstein (2008), the Fisher matrix for the parameters {pαi} resulting from the unbiased spectroscopic observations is
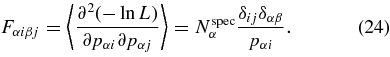
We add this Fisher information to the density–lensing Fisher matrix in Equation (22) when considering the constraints offered by a WL survey that is combined with an unbiased spectroscopic redshift survey drawn from one or more of the source population sets.
We do not, in general, presume any functional form for the pαi redshift distributions when the sets are assigned from photo-z's. We adopt fiducial values either from an analytic form or from a simulation of photo-z performance. Then we leave all the pαi as free parameters in the Fisher matrix, adding the spectroscopic survey Fisher matrix in Equation (24) if appropriate to the planned experiment. Note that the cross-correlations in the WL survey data offer constraints on the redshift distribution even if there is no unbiased spectroscopic survey (Nspecα = 0).
4. AN IMPLEMENTATION
A package of C++ classes implements the Fisher matrix calculation for Gaussian lensing+density observations, the spectroscopic survey Fisher matrix, plus the models for lensing potential power and nuisance functions described below. From these classes, we can construct numerous applications, the most obvious being a Fisher matrix forecast of cosmological constraints from the combination of a photometric galaxy lensing/density survey, plus a redshift survey to constrain the photo-z distribution. We list in Table 2 input fields for this forecasting implementation. Further program inputs are listed in later sections which detail the models for the lensing power spectrum and nuisance parameters that we describe below and adopt for this implementation.
Table 2. Controlling Inputs to Fisher Forecast
| Parameter Name | Description | Default |
|---|---|---|
| fsky | fsky, imaging sky coverage | 0.5 |
| minLogL | log10ℓmin, minimum multipole | 1.0 |
| maxLogL | log10ℓmax, maximum multipole | 3.5 |
| logLStep | Δlog10ℓ, multipole bin width in dex | 0.3 |
| zmax | zmax, redshift of most distant shell | 3.5 |
| dlna | Δln a, width of distance shells | 0.03 |
| coreDLna | Maximum |ln(1 + zi)/(1 + zα)| of subsets | 0.15 |
| sigGamma | σγ, shape noise per source galaxy | 0.24 |
| zdist | String specifying fiducial source nα and pαi | ⋅⋅⋅ |
| logNSpec | log10Nspec | 5.0 |
| outfile | Root name for output files | ⋅⋅⋅ |
Download table as: ASCIITypeset image
In the current implementation, we assume the source galaxies to be binned solely by photo-z, but generalizations are possible, e.g., including a second population of source galaxies sets that are observed spectroscopically. Note that when additional galaxy populations are introduced, we need a new set of nuisance functions to describe them. Furthermore, we need to model the cross-correlations between all galaxy populations.
The calculation of the Fisher matrix takes <1 minute per multipole bin using a single core of a typical current epoch desktop CPU. Total execution time for a forecast is 10–20 minutes with the default parameters, with the most time-consuming operation being the marginalization over bias model parameters. The execution time is very sensitive to the redshift shell width Δln a and to the photo-z error distribution width as these control the number of subsets and the parameter count.
5. POWER SPECTRUM MODELS
In most cosmological models, theory will offer strong guidance to the form of the lensing potential power spectrum Pϕ(k, z). In most forecasting or data-reduction codes, this is a fully deterministic function of a small number of cosmological parameters. In our analysis, however, the theoretical prediction is taken as the mean Pϕ value of a prior distribution of finite uncertainty.
5.1. Central Model
The WL likelihood given above can be calculated for any model that predicts Pϕ. We have chosen to implement a model that allows for failure of general relativity in describing growth of structure; but other models are possible if one wishes to test other tenets of general relativity. Under the following conditions:
- 1.the potential and the mass-energy density are related by the Newtonian Poisson equation, i.e., the field equation for nonrelativistic matter in general relativity;
- 2.nonrelativistic matter is the only significant inhomogeneous component of the universe, i.e., there is no dark energy clustering;
- 3.matter is conserved,
 ; and
; and - 4.Φ = −Ψ, as in the absence of anisotropic stress for general relativity,
then the potential power spectrum is related to the matter-density fluctuation spectrum Pm via
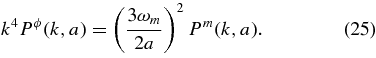
Under these conditions, the linearized perturbations to the metric grow in a scale-free manner, so we can write
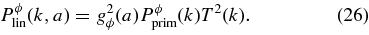
In our current code, the primordial power spectrum is a power law
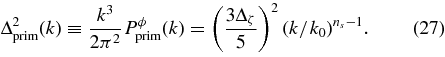
The curvature variation Δζ and spectral index ns are free parameters. A running of the slope could easily be added. The normalization wavenumber k0 must be set by some convention. We typically adopt the five-year WMAP parameters as fiducial values (Komatsu et al. 2009).
The transfer function T(k) is taken from Eisenstein & Hu (1999). It is a function of the matter and baryon densities ωm and ωb. The impact of massive neutrinos could be added to the transfer function if desired. We ignore the baryon acoustic oscillations; experiments that try to exploit them will generate a distinct Fisher matrix for them.
The map from Pϕlin to the nonlinear Pϕnl is derived using the prescription of Smith et al. (2003) for nonlinear Pm combined with the Poisson equation (25). The Smith et al. (2003) formula also requires knowledge of Ωm at the desired epoch, but it can be expressed in terms of other quantities that are already in our model: Ωm(zi) = ωma−3ih−2(zi). We do not expect the Smith et al. (2003) formula to describe nonlinear growth to high accuracy for all (or any) cosmologies. It does, however, capture the dependence of nonlinear power on cosmological parameters to a level that suffices for forecasting purposes.
In general relativity, the growth function gϕ(a) is determined by the expansion history H(z). Defining F = ln(agϕ), the growth equation is
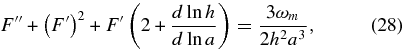
where a prime denotes differentiation with respect to ln a. Note that F' is the quantity dln gm/dln a that appears in the peculiar velocity power spectrum for a tracer of mass.
If GR holds, then the above relations fully specify the model for Pϕ given {ωm, ωb, ns, ln Δζ} plus the expansion history, which in turn is given by {Di, ωk}. As a test of GR, we allow the growth function arbitrary deviations from the Ffid that solves the GR growth equation for the fiducial expansion history,
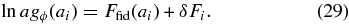
The δFi become parameters of the likelihood function.
5.2. Model Errors
An important WL systematic is the expected finite accuracy in theoretical modeling of the power spectrum. We hence introduce an error function to describe the (logarithmic) difference between the power Pϕ and the value predicted by the parametric model described in the previous paragraphs:
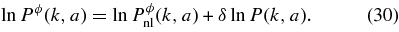
The nuisance function δln P will be modeled by the "kz" parametric form described in the
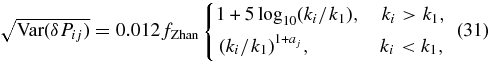

This function is a fit to an estimate supplied by Hu Zhan of the impact of baryonic physics on the mass power spectrum (Zhan & Knox 2004; Jing et al. 2006). We scale the overall size of the theory-error systematic with the control scalar fZhan. We can also adjust the density Δln k and Δln a at which the δPij grid points are spaced. This corresponds to setting some coherence length for theory errors in this space. In Section 7, we investigate the choice of these grid spacings. The procedure above means that we replace the Pϕi as parameters in our likelihood with a new (and hopefully smaller) set as below:
- 1.the small set {ωm, ωb, Δ2ζ, ns} that controls the linear power spectrum;
- 2.the {δFi} which defines the growth function versus redshift; and
- 3.a grid of theory error values δP, which are nuisance parameters to marginalize after construction of a Fisher matrix or likelihood. We have physically based priors to apply to these before marginalization.
Table 3 lists the input fields for the part of our forecasting code which constructs the power-spectrum model. The WMAP5 ΛCDM cosmology provides the fiducial values of all lensing power values; the program inputs define the behavior of the deviations from the theoretical model and the prior expectations on the size of such deviations.
Table 3. Power Spectrum Inputs to Fisher Forecast
| Parameter Name | Description | Default |
|---|---|---|
| zhan | fZhan, power-spectrum theory uncertainty relative to baryonic effects | 0.5 |
| psDlnk | Δln k, node spacing of power-spectrum theory errors in k | 1.0 |
| psDlna | Δln a, node spacing of power-spectrum theory errors in a | 0.5 |
Download table as: ASCIITypeset image
6. NONPARAMETRIC NUISANCE MODELING
6.1. General Comments on Nuisance Functions
The WL likelihood contains many nuisance parameters that are discretized representations of nuisance functions. It is common in the literature to assign some parametric form to a nuisance function, then marginalize over the parameters of the nuisance function to recover a purely cosmological likelihood. This can be a very dangerous approach: if the nuisance function does not in actuality follow the assumed form, then the process is invalid, and we may have greatly overestimated the power of the experiment to remove the systematic error from the signal. When marginalizing over a systematic, we must be sure that the assumed parametric form is sufficiently flexible to include any expected manifestation of the systematic. For example, we should not assume that systematics scale linearly with redshift unless there is a physical reason to expect this.
It is unfortunately not possible to model a completely free function with a finite number of free parameters. This becomes possible, however, if we limit the bandwidth of variation in the function. As an example, consider our power-spectrum theory error function δln P(k, z). We could decompose δln P into Fourier modes or polynomial terms over its finite (k, z) domain. Retaining a finite number of modes or terms leads to a tractable parameterization, albeit with a maximum frequency or polynomial order that defines a coherence length for the reconstructed function. For δln P, we choose to limit the bandwidth using linear interpolation between a two-dimensional grid of specified values. In the
These models of nuisance functions are nonparametric in the sense of being able to reproduce very general types of behavior once the bandwidth is specified. The question remains: what is the proper choice of bandwidth to allow the nuisance function? Our approach is to find the bandwidth which causes the most damage to cosmological constraints under a prior that specifies the expected RMS fluctuations in the nuisance function. This is the most conservative approach. Typically, one finds the following: if the nuisance function is given a highly coherent, low-order functional form, then it is easily distinguished from cosmological signals and can be marginalized away with little damage to cosmological constraints. On the other hand, if the nuisance-function bandwidth is very high, then the broad WL kernel tends to average away the nuisance signal, leaving little trace in the cosmology. There is an intermediate point where the systematic error is most easily confused with cosmology. The conservative approach is to find this regime and use it for modeling the systematic error. In Section 7, we will find coherence lengths in z and k at which our systematics are most damaging.
6.2. Redshift Distributions
We specify the fiducial values of the photo-z distribution nα and error probabilities pαi either with analytic formulae (e.g., photo-z errors Gaussian in ln a) or by taking the output of a simulation of galaxy detection and photo-z assignment for the chosen survey. For spectroscopic samples or the CMB source plane, there are no photo-z errors at all.
We do not place any parametric form or prior assumption on the pαi. All redshift constraints arise either from the lensing survey data itself or from additional spectroscopic data. The likelihood arising from spectroscopic redshift samples is described in Section 3.
6.3. Shear Calibration and Magnification Bias
The shear calibration factors fαi and magnification bias coefficients qαi are, most generally, distinct in every subset. We use the "zΔz" functional form described in the
We set the fiducial functions to be fαi = 0, and qαi = qfid independent of (k, z). The priors on the polynomial coefficients are chosen to yield a chosen RMS variation of f or of q. As detailed in the
Table 4 lists the program inputs necessary to specify the model for f or q: their functional form, fiducial values, and priors on deviations from the fiducial.
Table 4. Shear Calibration and Magnification Bias Inputs to Fisher Forecast
| Parameter Name | Description | Default |
|---|---|---|
| fRMS | fRMS, RMS variation of f allowed under prior | 0.01 |
| qFid | qfid, fiducial value for all qαi | 1.0 |
| qRMS | qRMS, RMS variation of q allowed under prior | 0.1 |
| fqDlna | Δln a, node spacing for f and q models | 0.5 |
| fqDzOrder | Order of polynomial used to model Δz dependence of f, q | 2 |
| fqVarFracDZ | Fraction of f, q variance due to Δz dependence | 0.5 |
Download table as: ASCIITypeset image
6.4. Galaxy Correlation Coefficients
The correlation coefficient rgαi is, most generally, different at each subset and at each multipole ℓ. We model rg using the "kzΔz" function form described in the
For the fiducial correlation coefficient, we interpolate smoothly between a linear and nonlinear limit according to the value of Δ2lin(k, z) = k3Pmlin(k, z)/2π2,

The constant W sets the width of the transition from the linear to nonlinear regime. We set W = 1 unless otherwise noted.
Each polynomial coefficient at each grid point is assigned an independent Gaussian prior. These are chosen to yield a preselected RMS variation rgRMS. The RMS prior uncertainties are interpolated in (k, z) space between linear and nonlinear limiting values rgRMS,L and rgRMS,NL using the same functional form as in Equation (33).
Table 5 lists the program inputs needed to specify the galaxy bias and correlation models.
Table 5. Galaxy Bias Inputs to Fisher Forecast
| Parameter Name | Description | Default |
|---|---|---|
| bg | bgfid, fiducial galaxy bias | 1.5 |
| rgL | rgL, fiducial galaxy correlation coefficients at linear limit | 0.9 |
| rgNL | rgNL, fiducial galaxy correlation coefficients at nonlinear limit | 0.6 |
| biasDlnk | Δln k, interpolation grid step for bias models | 1.0 |
| biasDlna | Δln a, interpolation grid step for bias models | 0.1 |
| brgRMSL | bgRMS,L and rgRMS,L, RMS prior variation for bias and correlation, linear limit | 0.05 |
| brgRMSNL | bgRMS,NL and rgRMS,NL, RMS prior variation, nonlinear limit | 0.10 |
| brVarFracDZ | Fraction of bg, rg variance due to Δz dependence | 0.2 |
| bgCoarseDlna | Δln a, node grid spacing for bgcoarse | 0.5 |
| bgCoarseZRMS | RMS prior variation of bgcoarse at Δz = 0 | 0.5 |
| bgCoarseDZRMS | RMS prior variation of bgcoarse at fixed z | 0.3 |
| kgg | Kggfid, fiducial value of Kgg(k, z) cross-correlation spectrum | 2.0 |
| kggRMS | KggRMS, prior variation on Kgg(k, z) | 1.0 |
Download table as: ASCIITypeset image
6.5. Galaxy Bias
We expect bg to vary quite strongly with z as the more distant source galaxies are likely intrinsically very bright and highly biased. There may also be a strong dependence of bg on Δz because both Δz and the bias may couple strongly to galaxy spectral type. Variation with k should be weaker. We hence define bg to be the sum of two functions,
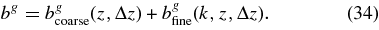
The fiducial values are bgcoarse = bgfid, bgfine = 0.
The coarse contribution is given a very weak prior, but can only vary slowly with z: Δln a = 0.5 by default for the bgcoarse grid nodes.
The bgfine function is interpolated between the same (ln k, ln a) grid points as the correlation coefficient rg. The prior on each bgfine node is arranged to give RMS uncertainty that is interpolated between linear and nonlinear limits bgRMS,L and bgRMS,NL, just as for rg.
6.6. Intrinsic Alignments
The strength of intrinsic alignments is specified by the bκαi and rκαi values at each multipole ℓ. As for the galaxy density, the free-parameter count can be reduced by specifying parametric functions bκ, rκ of (k, z, Δz) instead. Each of these two functions is modeled using the "kzΔz" form described in the
Table 6 lists the program inputs needed to specify the functional form for intrinsic alignments, the fiducial values, and the prior constraints. Note that we assume the intrinsic alignment functions to be defined on the same (ln k, ln a) grid as the galaxy bias and covariance functions.
Table 6. Intrinsic Alignment Inputs to Fisher Forecast
| Parameter Name | Description | Default |
|---|---|---|
| bk | bκfid, fiducial intrinsic alignment | −0.003 |
| rk | rκfid, fiducial correlation between mass and intrinsic alignment | 0.7 |
| rkRMS | rκRMS, RMS prior variation in rκ | 0.2 |
| kkk | Kκκfid, fiducial value of Kκκ(k, z) | 1.0 |
| kkkRMS | KκκRMS, RMS prior variance of Kκκ | 1.0 |
| skg | sgκfid, fiducial IA–bias cross-correlation | 0 |
| skgRMS | sgκRMS, RMS prior on IA–bias cross-correlation | 0.3 |
Download table as: ASCIITypeset image
6.7. Cross-correlation Coefficients
The cross-correlation coefficients rggαβi, rgκαβi, and rκκαβi are even more complex because each depends on k, z, plus two subsets Δzαi and Δzβi. We find it infeasible to construct nuisance-function templates spanning four dimensions. We, therefore, simplify by first writing
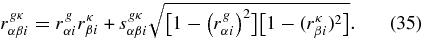
A value |sgκαβi| ⩽ 1 is necessary (but not sufficient) to keep the mass-galaxy covariance matrix from acquiring nonphysical negative eigenvalues. In principle, the functional form of sgκ must vary over four dimensions, but we make the gross simplification that it is constant for the survey since we expect this type of cross-correlation to have minimal effect on cosmological constraints. The program thus requires simply a fiducial scalar sgκ and an RMS for its Gaussian prior.
The density–density cross-correlation rgg may have substantial impact on cosmological constraints, so we model it with more freedom, though not full four-dimensional behavior. We set
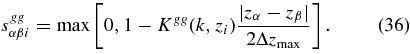
This functional form for s gives the most closely related subsets the highest covariance. Here, Δzmax is the width of the redshift distribution within a set. The function Kgg(k, z) adjusts how quickly the subsets decorrelate as their photo-zs diverge. The Kgg(k, z) is implemented as the "kz" functional form described in the
The cross-correlation parameters rκκαβi are similarly reduced from four-dimensional behavior by defining values sκκαβi that are set by the nodal values of a two-dimensional function Kκκ(k, z) in complete analogy with Equation (36).
6.8. An Apology
This section on nuisance functions is obscure and lengthy, especially regarding the cross-correlations of galaxies and intrinsic alignments. It is, unfortunately, impossible to fully describe the likelihood of lensing survey data without invoking some model for all of these functions.
Previous work has avoided these messy details and functions by making many simplifications. Most have implicitly assumed that all the correlation coefficients are unity, while most have ignored the intrinsic alignment signal entirely, i.e., taking bκ = 0. All previous analyses have considered the galaxy bias to be constant within a set, and if the multiplicative error has been considered, it has also been constant within a galaxy set. Only a few analyses have allowed galaxy bias to vary with redshift (Zhan 2006; Bernstein & Jain 2004). The most sophisticated treatment to date is that of Hu & Jain (2004), who take all bias and correlation coefficients to derive from a halo model of galaxies. The redshift distribution parameters pαi have, in the most ambitious analyses to date, been reduced to two-parameter (Gaussian) functions. Ma & Bernstein (2008) consider sum-of-Gaussian models. These assumptions can all be implemented in the present formalism if desired, but can also be relaxed to assess their impact on the cosmological constraints.
7. TUNING THE FORECAST PARAMETERS
In this section, we determine the values of bin widths and nuisance-function bandwidths that are needed for reliable extraction of maximum information from lensing surveys. Unless otherwise noted, we will derive these parameters for a canonical survey with fsky = 0.5; an effective source density of 60 galaxies per arcmin2 with median redshift of 1.2; σγ = 0.24; and Gaussian-distributed fiducial photo-z errors of σz = 0.04(1 + z). Except as noted, we assume Nspec = 107 so that photo-z calibration errors are negligible, and reduce the shear calibration RMS uncertainty to 10−4 to be negligible as well. Other inputs assume the default values given in Tables 2–6.
The information content of a survey will be gauged using the DETF figure of merit (Albrecht et al. 2006): the Fisher matrix will be marginalized over all nuisance parameters, then the Di and δFi variables are projected onto a model obeying general relativity with homogeneous dark energy of equation of state w = w0 + wa(1 − a). A prior representing expected Planck results is added (also from the DETF report), and we marginalize over {ωm, ωb, ωk, ωDE, ns, Δζ} to yield the Fisher matrix Fw over {wo, wa}. The DETF FoM is defined as |Fw|1/2.
7.1. Multipole Bin Size
Since we have excluded baryon oscillations from our transfer function, we expect to find little information in the detailed shape of the lensing or density power spectra. The broad lensing kernel in redshift also smoothes away fine structure in the convergence. So we expect the information content in the Fisher matrix to be independent of the multipole bin width Δlog10ℓ below some modest value. Larger values of Δlog10ℓ reduce the complexity and execution time of the calculations, so we seek the maximum Δlog10ℓ at which nearly all the lensing information is present.
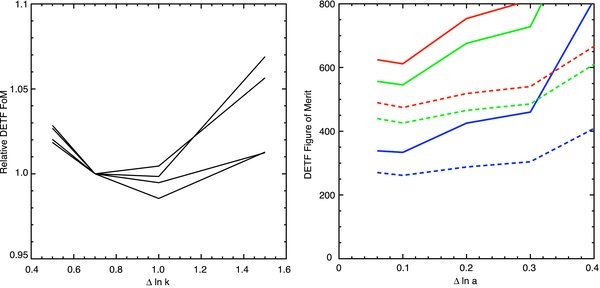
Figure 1 plots the DETF FoM of the lensing+density survey (plus spectroscopic redshift survey and Planck prior) versus Δlog10ℓ for several candidate surveys. The top line is for a very optimistic survey: neff = 100 arcmin−2, Nspec = 107, qRMS = 10−3, fRMS = 10−4, bgRMS = rgRMS = 0.01, and bκfid = 10−3. By reducing the systematics and the shot noise to (unrealistically) low levels, we give the lensing survey the chance to extract maximal information. We find that the FoM gains only 2% for Δlog10ℓ < 0.3.
Figure 1. Left: DETF figure of merit resulting from Fisher analyses of several weak lensing surveys plotted against multipole bin width Δlog10ℓ of the analysis. Each solid line plots a particular survey scenario (see text for details). The dashed lines are horizontal to help the eye judge the information degradation as we increase Δlog10ℓ. We conclude that Δlog10ℓ ⩽ 0.3 retains >97% of the information for surveys of any quality level. Right: value of DETF FoM for the default survey vs. range of multipole used. Choice of upper bound is more critical than choice of lower bound on ℓ.
Download figure:
Standard image High-resolution imageOther lines in the plot are FoM versus Δlog10ℓ for weaker surveys with Nspec = 104.5 and/or neff = 60 arcmin−2, qRMS = 0.1, bgRMS = rgRMS = 0.1, bκfid = −0.003. In these cases, we also find that the DETF FoM increases by <2%–3% for Δlog10ℓ < 0.3. We adopt Δlog10ℓ = 0.3 for all future use.
7.2. Multipole Range
On the right-hand side of Figure 1 we plot the DETF FoM for various ranges of ℓ. In this study, we assume a space-based survey obtaining neff = 60 arcmin−2 over fsky = 0.5. The photo-z and shear calibration systematics are held negligible with priors, but other systematics (intrinsic alignment, etc.) have default priors.
We see that the choice of ℓmax has a strong influence as moving from 103 to 104 changes the FoM by 1.7 times. We note this is true even though we have included uncertainty in the theoretical power spectrum at high k values, showing that there is still information to be gained when the theory is incomplete. We find, in fact, that our default power-spectrum theory uncertainty of fZhan = 0.5 leads to only 6% degradation of the DETF FoM, relative to an assumption of zero uncertainty in the theory even when ℓmax = 104.
Unfortunately, our assumption of Gaussian statistics will fail by ℓ = 104 (Cooray & Hu 2001; Lee & Pen 2008), rendering the Fisher calculation less reliable. We will restrict our analysis to ℓ < 103.5, but additional study of the effect of non-Gaussian statistics is clearly needed.
The flat-sky and Limber approximations will fail at low ℓ, but the choice of ℓmin appears less critical to the w0/wa information content; so we will retain the ℓ>10 bound in our analyses.
7.3. Scale Resolution for Nuisance Functions
We require choice of node spacing Δln k in the nuisance functions for the power-spectrum theory errors, the calibration errors f and q, and the bias/correlation parameters bgfine, rg, bκ, rκ, Kgg, and Kκκ. We set Δln k to be equal for all nuisance functions, and find the value which minimizes the DETF FoM as the "most damaging" scale of variation. We examine the default case described above for several values of the shear calibration prior fRMS and photo-z calibration size Nspec.
Figure 2 shows Δln k ≈ 0.7–1 yields minimum information for fixed RMS priors, but the dependence is very weak. The FoM varies by only 7% over the range 0.5 < Δln k < 1.5. We henceforth adopt Δln k = 1. Perhaps not surprisingly, this makes the nuisance functions have ≈1 independent node in each multipole bin of Δlog10ℓ = 0.3.
Figure 2. Left: DETF FoM vs. Δln k, the spacing of nuisance-function nodes in the length-scale axis. We examine surveys with varying strengths of priors on shear calibration and photo-z calibration. For this plot, each is normalized to the value at Δln k = 0.7 in order to show the (weak) dependence of FoM on Δln k when the priors on RMS nuisance-function fluctuations are held fixed. We adopt Δln k = 1 as the most conservative bandwidth for nuisance-function variation with scale. Right: DETF FoM vs. Δln a, the spacing of nodes in redshift for the bias, correlation, and intrinsic alignment nuisance functions. The FoM is quite sensitive to this choice, and allowing the bias/IA to vary on Δln a = 0.1 scales is most damaging to cosmological inference.
Download figure:
Standard image High-resolution image7.4. Redshift Resolution for Nuisance Functions
All of the nuisance functions are dependent on z. We next investigate the redshift node spacing Δln a at which the nuisance functions are most damaging to the DETF FoM. We find that the FoM is insensitive to the Δln a of the power-spectrum theory errors. The value of Δln a for the calibration functions f and q that minimizes the FoM depends upon the strength of the prior. The choice Δln a = 0.5 produces an FoM that is within 2% of the minimum, so we fix this value for the theory-error and calibration nuisance functions.
The redshift freedom given to the bias and intrinsic alignment nuisance functions has a strong impact on the DETF information content. Figure 2 illustrates that, at fixed RMS prior variation, models with freedom to vary on rather fine scales Δln a = 0.1 are most damaging to cosmological information.
8. CONCLUSION
The core of this paper are Equations (18)–(20) for the two-point correlation matrix of the lensing and density observable multipoles produced by a typical lensing survey. This was derived under a very limited set of assumptions: a homogeneous and isotropic four-dimensional metric universe with scalar perturbations; plus the weak lensing limit, the Limber and Born approximations, and an approximation that lensing magnification bias and intrinsic density fluctuations are additive. The last four assumptions could be relaxed at the expense of computational complexity. We thus hope that data analyses based on this framework could be used to constrain a wide variety of potential explanations for the acceleration phenomenon, including gravity modifications as well as new fields in the universe. In the limit of Gaussian fluctuation fields, the two-point information is a complete description of the likelihood, and hence can be used to construct Fisher matrices or analyze data. Currently configured, the analysis yields the survey's ability to constrain the distance function D(z) and linear growth function gϕ(z) without reference to particular dark-energy models. It would be straightforward to implement scale-dependent linear-growth functions.
This framework subsumes all of the information (up to two-point level) that is likely to be obtained from lensing observations: density–density, lensing–density, and lensing–lensing correlations, plus redshift distributions from unbiased spectroscopic surveys (Section 3). Furthermore, it allows for the most important expected forms of systematic error: photo-z calibration errors, shear and magnification-bias calibration errors, intrinsic alignments, and inaccuracies in power-spectrum theory. Systematics that are additive to shear (e.g., uncorrected PSF ellipticity) or to density (e.g., uncorrected foreground extinction) have not been included. We have not done so since the additive errors could, in principle, exhibit almost any arbitrary signature in the covariance matrix of the observables. Hence, a completely general model for additive errors would be degenerate with almost all other signals. For the additive systematics, it is better to determine the level at which they would bias the cosmological results than to attempt to fit a model. Amara & Refregier (2007) is a good example of this approach.
Since the analysis framework is independent of models for dark energy, gravity, power-spectrum evolution, or galaxy bias, we get a stripped-down look at what parameters are truly constrained by the data, and what nuisance functions must be modeled in order to extract the cosmological information. There is a substantial suite of biases and correlation functions involved in understanding the full survey data. In other work, these have been ignored or have been quantified by reference to halo occupation models (Hu & Jain 2004; Cacciato et al. 2009). Here, we introduce generic functions for bias and calibration nuisance functions that are not based on any particular physical model.
We implement one possible model for the evolution of the lensing potential power spectrum based on general relativity but allowing for failure of the growth equation. It is straightforward to implement other potential deviations from general relativity. In the current implementation, the result of the Fisher analysis is a forecast of the ability to constrain the functions DA(z) and gϕ(z).
Since the analysis must be discretized in redshift and angular scale in order to be feasible, we investigated the bin sizes or bandwidths of nuisance functions that should be chosen. We find that ≈3 bins per decade of angular scale suffice to extract all information (apart from baryon acoustic oscillations), and that nuisance functions should be specified no finer than this. Nuisance functions for power-spectrum theory errors and shear and magnification-bias calibration errors can be specified coarsely in redshift space (Δln a ≈ 1), but the galaxy biases, correlations, and intrinsic alignments must be modeled with potentially finer structure in redshift (Δln a ≈ 0.1) to immunize against potential astrophysical systematics.
In future papers, we will use this framework and its implementation to investigate the requirements for spectroscopic calibration of photo-zs in large lensing surveys and other practical issues. As a simple first application of our framework, we have shown here that power-spectrum theory uncertainty does not significantly degrade the cosmological power of a nominal lensing survey at 10 < ℓ < 104. Non-Gaussian statistics are a much more important factor to consider.
The C++ code to implement Fisher forecasting using this framework runs quickly on desktop computers despite the large number of free parameters in these general models. Interested parties should contact the author for access to the code.
This work is supported by National Science Foundation grant AST-0607667, Department of Energy grant DOE-DE-FG02-95ER40893, and NASA grant BEFS-04-0014-0018. I thank Bhuvnesh Jain, Zhaoming Ma, Chris Hirata, Ravi Sheth, Hu Zhan, and the members of the Dark Energy Task Force for helpful conversations during the long gestation of this work.
APPENDIX: PARAMETRIC FUNCTIONAL FORMS FOR NUISANCE VARIABLES
In modeling an experiment, we often encounter some systematic error associated with a nuisance variable f about which we have little a priori knowledge. We would like to fit some parametric form to this variable, but would like a form that is flexible enough to describe any "reasonable" behavior the function might exhibit. We also want to conveniently relate the number and prior probabilities for the parameters to the kind of variation that f might exhibit. A parametric description of some nuisance function f defined over a variable x ∈ [ − 1, 1] would ideally have the following properties.
- 1.f(x) has a variable number N of controlling parameters {a0, a2, ..., aN−1} such that any continuous differentiable function F(x) can be approximated to any desired accuracy with a sufficiently large choice of N.
- 2.We can draw {aj} from independent Gaussian distributions of zero mean and widths {σj} with the result that Var[f(x)] is independent of x. In other words, the nuisance value f has a uniform and well determined variance when we apply a simple diagonal Gaussian prior to the parameter set {aj}.
A Fourier decomposition, f = ∑(ajsin jπx + bjcos j πx), exhibits these qualities, but converges poorly when f(−1) ≠ f(+1).
A.1. Linearly Interpolated Functions
Another approach is linear interpolation: choosing a spacing Δx = 2/(N − 1), we define ai as the value of f at xi = iΔx − 1. At some other xi < x < xi+1, we define
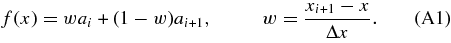
If we assign an independent Gaussian prior of width σa to each ai, then by definition we have Var[f(x)] = σ2a if x coincides with a node. But, the variance of f is not quite homogeneous: it drops to Var[f(x)] = σ2a/2 when x is halfway between two nodes. If we want the mean variance of f(x) over the interval x ∈ [ − 1, 1] to equal σ2f, then the variance of the prior on each node needs to be σ2a = 3σ2f/2.
A.2. Legendre Polynomials
Polynomial expansions are also commonly used to model nuisance functions. The simplistic form f(x) = ∑aixi results in extremely nonuniform variance for f with diagonal prior on {ai}, and hence is inappropriate for our purpose. A better choice is to expand in Legendre polynomials Pn(x), which are orthogonal over [ − 1, 1]. We define
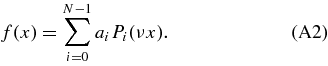
Recall that the Legendre polynomials satisfy P0 = 1, P1 = x, (n + 1)Pn+1 = (2n + 1)xPn − nPn−1.
We wish to choose priors {σi} on {ai} that cause the variance of f(x) be as uniform as possible for x ∈ [ − 1, 1]. We have not found a way to attain perfect uniformity in x with polynomial interpolation; however, the following scheme gets usefully close. We discover numerically that

This implies that if we set  , then in the limit of large N we will obtain Var[f(x)] = (1 − ν2x2)−1/2. For ν = 1, this would diverge at the ends of our nuisance function's interval. If, however, we choose ν = 0.9, the RMS is only ≈1.5 times larger at the endpoints than at x = 0. Over the [ − 1, 1] interval, the mean variance is (sin−1ν)/ν. Hence, if we wish to have a function with 〈Varf(x)〉x = σ2f, we set the priors on the Legendre coefficients to be
, then in the limit of large N we will obtain Var[f(x)] = (1 − ν2x2)−1/2. For ν = 1, this would diverge at the ends of our nuisance function's interval. If, however, we choose ν = 0.9, the RMS is only ≈1.5 times larger at the endpoints than at x = 0. Over the [ − 1, 1] interval, the mean variance is (sin−1ν)/ν. Hence, if we wish to have a function with 〈Varf(x)〉x = σ2f, we set the priors on the Legendre coefficients to be
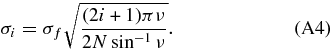
A.3. Standard Multidimensional Functions
The Fourier, linear interpolation, and Legendre polynomial functional forms can each be extended to >1 dimensions in a straightforward fashion. In the lens modeling, we need functions of the following dimensions:
- 1.comoving wavenumber or physical scale: x1 = ln k;
- 2.redshift z: more precisely, we will use the variable x2 = ln(1 + z); and
- 3.photometric redshift error Δz: more precisely, our code uses the variable x3 = Δln(1 + z) = ln [(1 + zα)/(1 + zi)] for subset αi.
A.3.1. The kz Form
For functions over the (x1, x2) space, we use a simple two-dimensional version of interpolation between values on a rectangular grid. The power-spectrum theory error δln P uses this form as do the Kgg(k, z) and Kκκ(k, z) nuisance functions. The only complication of note is that the nodal point aij should have a prior with variance σ2a = (3/2)2σ2f if the output function is to have variance σ2f. The factor of (3/2)2 is needed to counteract the reduced variance when interpolating between grid points.
The kz nuisance function is specified by the following:
- 1.the spacing Δx1 = Δln k of the nodes for linear interpolation in x1;
- 2.the spacing Δx2 = Δln(1 + z) of the nodes for linear interpolation in x2;
- 3.the RMS variation σf of the function allowed under the prior, which can depend on x1 and x2; and
- 4.the fiducial dependence of f on x1 and x2.
A.3.2. The zΔz Form
For nuisance variables over the (x2, x3) space (z and Δz), we adopt the following strategy: we choose to have variation over x3 be described by polynomials since we usually define the range of noncatastrophic photo-z errors to be bounded to some range |x3| ⩽ Δmax. We define the "zΔz" functional form as follows:
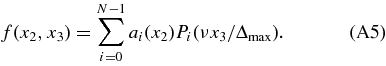
The Legendre coefficients are in turn defined to be linearly interpolated between a series of values aij at redshift nodes {ln(1 + zj)}. The aij become parameters of the model.
The fiducial and prior values for the i = 0 terms (constant in x3) are treated differently than the i > 0 terms. We might, for example, expect some nuisance functions to vary strongly with x2 (nominal redshift) but only slightly with x3 (photo-z error) at fixed x2.
We specify the total RMS fluctuation in f allowed by the prior to be σf. But, we also specify the fraction VarFracDZ of the variance that is due to dependence on x3. If we define
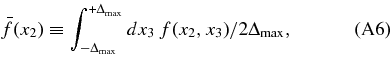
then we aim to achieve

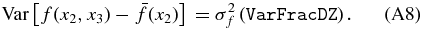
This is achieved approximately by setting the priors on the constant terms as

and the x3 dependent terms (i > 0) as
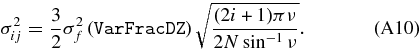
The RMS prior variation σf can be made a function of x2 without loss of generality. We typically take fiducial values of aij = 0 for i > 0 in our nuisance functions, i.e., no fiducial dependence upon Δz.
To summarize, the zΔz nuisance function is specified by
- 1.the order N of the polynomial in x3;
- 2.the maximum range Δmax of applicability in the x3 axis;
- 3.the spacing Δx2 = Δln(1 + z) of the nodes for linearly interpolation in x2;
- 4.the RMS variation σf of the function allowed under the prior, which can depend on x2;
- 5.the fraction VarFracDZ of this variance that is due to x3 (Δz) dependence; and
- 6.the fiducial dependence of f on x2.
A.3.3. The kzΔz Form
The bias and correlation coefficients can, most generally, depend on scale (x1) as well as subset (x2, x3), so we generalize to the "kzΔz" functional form
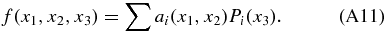
The coefficients ai are linearly interpolated between nodes in the two-dimensional space (x1, x2). Thus, the free parameters of this model become the Legendre coefficients aijk. As for the zΔz function, we specify the prior by the overall mean RMS variation σf (which can be a function of x2 and x3), plus the VarFracDZ specifying how much of the variance is manifested as dependence on Δz. The formulae for the priors σijk on the nodal coefficients are derived exactly as in Equations (A9) and (A10), except that we now need factors of (3/2)2 to account for the reduced variance when interpolating in two dimensions.
The kzΔz function thus requires all of the specifications as the zΔz function plus a spacing Δln k for nodes in the x1 axis.
Footnotes
- 1
In practice, we use ln a and Δln a to specify each subset's nominal redshift and redshift error, but in the text we will stick with (z, Δz) to reduce the clutter.