Abstract
We demonstrate the possibility of producing Au/SiO2 core–shell nanoparticles by nanosecond laser irradiation of thin (5 and 20 nm) Au films on Si. The Au/Si eutectic reaction and dewetting process caused by the fast melting and solidification dynamics induced by the nanosecond laser irradiations are investigated as the origin of the formation of core–shell nanoparticles. Using several microscopic techniques (Rutherford backscattering spectrometry, scanning electron microscopy, atomic force microscopy, transmission electron microscopy, and energy filtered transmission electron microscopy) the formation and evolution of the core–shell structures are investigated as a function of the laser fluence in the 500–1500 mJ cm−2 range for both film thicknesses. In particular, the mean height and diameter and surface density evolution of the core–shell structures are quantified and correlated to the laser fluence and Au film thickness.
Export citation and abstract BibTeX RIS
1. Introduction
Core–shell nanoparticles (NPs) constitute a novel class of materials with important technological applications [1–3]. In particular, metal–SiO2 core–shell NPs consisting of a noble metal core and silica shell or, conversely, a SiO2 core and a noble metal shell are attracting a lot of attention because of their unique properties relevant for many applications [1–16]. In this context, Au/SiO2 core–shell NPs are of great interest for their size-dependent optical properties [4–10, 14–16]. Au NPs exhibit extraordinary optical resonances: when excited by electromagnetic radiation they exhibit localized surface plasmon resonance (LSPR) due to the collective oscillations of their conduction electrons [17]. The resonant excitation of LSPR leads to selective photon absorption and enhancement of local electromagnetic fields near the NPs by orders of magnitude. The possibility of controllably tuning the LSPR wavelength through the visible to near infrared region makes Au NPs very important and promising for a wide range of applications in chemical and biological sensors [9, 12, 13], optical filters, optical tweezers, ultrafast optical switching, and surface enhanced Raman spectroscopy [14, 17]. Au NPs can be coated with a uniform thickness of amorphous silica or, conversely, SiO2 NPs can be coated with a Au shell exploiting chemical reduction routines [4–13, 16]. Such core–shell nanostructures have been used in photonic crystals and plasmonic waveguides, biosensors (in particular cellular imaging, exploiting unique fluorescent properties), and drug delivery systems. However, the critical point for the technological applications is the control of the Au/SiO2 NP size and shape to tune the LSPR wavelength. In the existing literature, a very small number of physical, low-cost methods have been successfully exploited to form or manipulate Au/SiO2 core–shell NPs: Mohapatra et al [14] reported a simple method for the synthesis of Au-core/SiOx-shell NPs embedded in a SiO2 matrix based on Au and SiO2 atom beam co-sputtering and subsequent annealings; Akchurin et al [15] reported a method based on nanosecond laser irradiation of chemically prepared silica-core/Au-shell NPs suspended in solution to induce a progressive Au-shell fragmentation, changing, as a consequence, the optical response of the entire solution. This last example is an impressive demonstration of the powerful exploitation of laser–matter interaction to form and manipulate an entirely new class of nanostructures. In general, recently, rapid progress in the development of ultrafast lasers has opened up new possibilities for material nano-processing because of the wide variety of nanostructures which can be obtained due to laser-induced melt and solidification dynamics [18–32]. The main advantages of laser-based approaches include local processing down to the micrometer and even sub-micrometer range, minimized thermal damage to the substrate and neighboring regions, non-contact nature, non-planar processing, and the possibility of combine it with other types of processing such as surface chemical treatment and film depositions steps [33]. In addition, the extraordinary interest in laser-based structuring approaches arises from the wide variety of metallic and composite nano- and microstructures that can be obtained (NPs, nanoholes, nano- and micro-bumps, nanojets, and nanofibers) when thin (1–200 nm) metal films, deposited on insulating or semiconducting substrates, are irradiated by nano- and femtosecond lasers [18–32]. The nature of the metal nano- and microstructures that can be produced depends, first of all, on the laser type: while under nanosecond laser irradiation material melt dynamics is the dominant process, femtosecond irradiation induces more complicated dynamics including film deformation [24, 25, 31]. It depends on the nature of the metal: for example, in transition metals (like Cr, Mo, W, Fe) sub-micron structures can be fabricated by direct laser ablation [18]. These metals are characterized by rapid electron–phonon relaxation which is responsible for the fast energy transfer to the lattice and material removal. In noble metals (like Au, Ag), the electron–phonon relaxation is much slower. For example, the parameter g (in 1016 W m−3 K−1 units) characterizing the electron–phonon coupling is equal to 42 for Cr while it is 2.3 for Au [24, 34, 35]. Due to the slower energy transfer from the electron sub-system, the lattice becomes melted and the molten phase in noble metals exists for much longer. In Au, characterized by a very low electron–phonon coupling, the energy is transferred to the lattice within 15 ps. Equilibrium between hot electrons and the lattice takes place with a time limit of up 50 ps [24, 32, 34, 35]. Obviously, also the film thickness, its optical properties (e.g. reflectance), and thermo-elastic properties play a key role in the structuring processes. Finally, the role of the substrate in the formation of these structures is also significant due to its substantial effect on the propagation of the laser-generated heat in this layered system.
In the present work, we exploit a novel physical approach to form Au-core/SiO2-shell NPs taking advantage of the laser–matter interaction properties. We demonstrate, for the first time, the possibility of producing Au/SiO2 core–shell NPs by nanosecond laser irradiation of thin Au film sputter-deposited on Si. Laser-based techniques have been used for decades to produce metallic nanoparticles on surfaces [18–32]; however, to our knowledge, no report on the formation of Au/SiO2 core–shell NPs using laser-based techniques is available today. While most of the literature deals with the formation of pure metals (Au, Ag, Ni, Co, Ti, Mo ...) or composed (Co–Si) nano- and microstructures on semiconductor and dielectric substrates using laser-based methods [18–32], in the present work we demonstrate, for the first time, the possibility of producing core–shell nanostructures, formed, in particular, by a Au core and a SiO2 shell on a Si substrate. Furthermore, we demonstrate the possibility of controlling both the size of the core–shell NPs and the shell thickness by changing the laser fluence and starting thickness of the Au film deposited on Si.
A thin Au film deposited onto Si constitutes a very important and well studied system [36–40]. In fact, the physical and chemical properties of Au/Si compounds have been studied for many decades because of their technical relevance in microelectronics. The growth of Au on Si substrates as well as possible silicide formation have been discussed extensively in the literature. In particular, the Au/Si phase diagram has a eutectic point at TE = 636 K (18.6 at.% of Au) [40], and upon solidification of Au/Si droplets under the eutectic temperature, phase separation occurs between Au and Si. Such a characteristic of the Au/Si system is exploited in the experiments presented in this work, to produce the Au/SiO2 core–shell NPs. We deposited 5 or 20 nm of Au on a Si substrate, and then nanosecond laser irradiation was performed, increasing the laser fluence from 500 to 1500 mJ cm−2. Several analytical techniques, such as Rutherford backscattering spectrometry (RBS), scanning electron microscopy (SEM), atomic force microscopy (AFM), and transmission electron microscopy (TEM) were used to study the structural and morphological evolution of the Au film as a function of laser fluence. In particular, the formation of Au NPs surrounded by a SiO2 shell was observed. The previous analytical techniques allowed a quantitative evaluation of the evolution of the NP size, surface density, and shape as a function of the starting Au thickness and laser fluence.
2. Experimental details
The samples were prepared using a CZ-〈111〉 silicon wafer as substrate. The Au depositions were carried out on the Si slides using a RF (60 Hz) Emitech K550x sputter coater apparatus, clamping the substrates against the cathode located straight opposite the Au source (99.999% purity target). The electrodes were laid at a distance of 40 mm under Ar flow keeping a pressure of 0.02 mbar in the chamber. For a set of samples, the deposition time was fixed at 240 s with a working current of 10 mA, obtaining an average Au film thickness of 5 nm (as probed by RBS analyses). For another set of samples, the deposition time was fixed at 120 s with a working current of 50 mA, obtaining an average Au film thickness of 20 nm (figure 1).
Figure 1. Picture of the analyzed samples (Au film thickness 5 and 20 nm) and the main characteristics of the performed laser irradiation.
Download figure:
Standard imageLaser irradiation was performed with a pulsed (12 ns) Nd:yttrium aluminum garnet (YAG) laser operating at 532 nm (Quanta-Ray PRO-Series pulsed Nd:YAG laser), as pictured in figure 1. The spot laser has a circular shape of 4 mm diameter. The laser intensity profile is Gaussian, characterized by a full width at half maximum of 1 mm. 97% of the maximum laser intensity is maintained within a circular area of 600 µm diameter centered at the maximum of the laser intensity. The error in the fluence measurement is 25 mJ cm−2.
AFM analyses were performed using a Veeco-Innova microscope operating in high amplitude mode; ultra-sharpened Si tips were used (MSNL-10 from Veeco Instruments, with anisotropic geometry, radius of curvature ∼2 nm, tip height ∼2.5 µm, front angle ∼15°, back angle ∼25°, side angle 22.5°) and substituted as soon as a loss of resolution was observed during the acquisition. The AFM images were analyzed using the SPMLabAnalyses version 7.00 software.
SEM analyses were performed using a Zeiss FEG-SEM Supra 25 microscope operating at 6 kV acceleration. The SEM images were analyzed using Gatan Digital Micrograph software.
TEM analyses were performed (after mechanical polishing and final Ar ion milling) using a Jeol 2010F energy filtered transmission microscope. The SEM images were analyzed using Gatan Digital Micrograph software.
The RBS analyses were performed using 2 MeV 4He+ backscattered ions at 165°. The RBS spectra were simulated by the RUMP program [41] to calculate the Au surface density Q (atoms cm−2). The statistical error in the measurement of Q is 5%.
3. Results and discussions
Figure 1 presents a schematic diagram of the investigated sample: on the Au film of thickness d = 5 or 20 nm on Si(111), one-pulse laser irradiation of duration τ = 12 ns and wavelength λ = 532 nm was performed. The Au reflection coefficient at λ = 532 nm is about R = 0.76 [43, 44], so that we expect that 24% of the laser intensity is transmitted to the Au film. Furthermore, at the same wavelength, the Si reflection coefficient is about 0.83 [43, 44], so that we expect that 17% of the laser intensity transmitted to the Au film will be transmitted to the Si substrate. In bulk Au, moreover, the optical absorption length is α−1 = 18 nm, while the thermal diffusion length is LT = 1237 nm [44]. So, we are in an experimental condition for which λh ≫ α−1 > d. We can also note that in Au the electron–phonon coupling constant is low, g = 2.3 × 106 W m−3 K−1 [42]. This fact implies that equilibrium between hot electrons and the lattice occurs with a time limit of up t* = 50 ps [42]. So, our experimental condition is also characterized by τ ≫ t*. As a consequence, we expect that the Au melt dynamics is the dominant process in the Au nanostructuring under nanosecond laser irradiation, considering that 200 mJ cm−2 is the threshold fluence for melting thin Au film on Si [32], whereas in the present experiments we use fluence in the range 500–1500 mJ cm−2.
First of all, we performed RBS analyses on the 5 and 20 nm Au on Si as-deposited samples and on the same samples subjected to laser irradiation with increasing fluence E (500, 750, 1000, 1250, 1500 mJ cm−2) to evaluate the amount Q of Au in each sample. As examples, figures 2(a) and (b) report the Au RBS peaks for the as-deposited sample and for the as-deposited sample irradiated by 1000 and 1500 mJ cm−2, respectively. The areas of such peaks quantify the amount Q (in atoms cm−2) of Au in the samples (i.e. Au cm−2). Regarding the 5 nm thick Au sample (figure 2(a)) we can observe that in the as-deposited sample Q = 2.95 × 1016 Au cm−2. When we perform laser irradiation on this sample, a lowering and broadening of the Au peak occurs. This phenomenon is a clear signature of a clustering process of the Au film in NPs, leaving exposed regions of Si. Furthermore, increasing E from 500 to 1500 mJ cm−2 the area of the Au peak remains constant to Q = 2.95 × 1016 Au cm−2, as can be seen in the plot in figure 2(c). This fact is a clear sign of the fact that the melting of the Au film is the dominant process without Au evaporation in this sample. On the contrary, in the 20 nm thick Au sample (figure 2(b)) we can observe a lowering and broadening of the Au peak and a decrease of Q from the as-deposited sample to the 1500 mJ cm−2 irradiated sample (figure 2(c)). In this sample Q decreases from 1.36 × 1017 Au cm−2 in the as-deposited sample to 3.7 × 1016 Au cm−2 in the 1500 mJ cm−2 irradiated sample. Obviously, a certain amount of Au is lost by evaporation since no significant Au diffusion in the Si substrate is indicated by the RBS analyses. From figure 2(c) the notable feature is the tendency of the remaining Au to a constant value of 2.95 × 1016 Au cm−2 characteristic of the 5 nm thick sample. This fact is a clear signature of the key role played by the Au/Si eutectic reaction as a consequence of the laser irradiation. In fact [45–47], melting at the eutectic temperature, once started, can proceed only if diffusion processes are fast enough to maintain the eutectic composition at the liquid–solid Au/Si interface (inset in figure 2(c)). Its propagation towards the surface is limited by mass transport of Si atoms. The thickness which can be melted at the eutectic temperature is then of the order of λ = √DSτ, where DS is the atomic diffusion coefficient in the liquid and τ is the time the liquid remains at the interface. Assuming DS ∼ 10−4 cm2 s−1 and τ = 10 ns the interfacial molten layer should not exceed λ = 10 nm (inset in figure 2(c)). In this regime the increase in the energy density of the laser pulse above the threshold for eutectic melting would not drive the molten layer up to the surface but results in an overall increase of the temperature in the layer. The surface temperature can then reach the Au/Si melting point while the internal melt is still propagating towards the surface. In the 5 nm thick Au sample we have d < λ, so that the entire Au film is involved in the eutectic reaction with Si and melting at 673 K. In the 20 nm thick Au sample we have d > λ, so that only about 10 nm near the Au/Si interface takes part in the eutectic reaction and melting with Si. The excess Au that does not take part in the eutectic reaction reaches the evaporation temperature and is lost by evaporation.
Figure 2. (a) RBS Au peak for a 5 nm thick Au as-deposited sample, and an as-deposited sample irradiated by 1000 and 1500 mJ cm−2. (b) RBS Au peak for a 20 nm thick Au as-deposited sample, and an as-deposited sample irradiated by 1000 and 1500 mJ cm−2. (c) Amount Q of Au in the 5 and 20 nm thick Au samples as a function of the laser fluence E.
Download figure:
Standard imageAfter the RBS analyses, morphological studies based on TEM, SEM, and AFM analyses were performed to evaluate the nanostructuring effect of the laser irradiation on the Au/Si system. We note that the laser intensity profile is Gaussian, characterized by a full width at half maximum of 1 mm (figure 3(a)). 97% of the maximum of the laser intensity is maintained within a circular area of 600 µm diameter centered at the maximum of the laser intensity. So, we have to perform the structural analyses within 300 µm of the center of the laser spot. This fact is clear from figures 3(b)–(d). We show plan-view TEM images recorded in the 5 nm thick Au/Si sample irradiated by 1000 mJ cm−2 at three different distances from the laser center spot, i.e. changing the laser fluence along the same sample: (b) more than 300 µm outside the center of the laser spot; (c) at about 300 µm from the center of the laser spot; and (d) within 300 µmof the center of the laser spot. The 1000 mJ cm−2laser fluence is effectively reached within 300 µm of the center of the laser spot. This sequence of images is particularly significant in showing the nanostructuring effect of laser irradiation on the system: at sufficiently high E the Au film is clearly observed to melt and break up into discrete nanometer-scale islands (NPs) of circular section. A dewetting process can be clearly identified: figure 3(b) is probably taken below the break-up fluence threshold. In this region, the Au film perforates and the molten film around these perforations is observed to have drawn away from the center of the hole. These perforations are likely to occur at thickness inhomogeneities in the film, as the fluence required for melting is predicted to be lower for thicker films. This will be discussed in more detail later. When the density of perforations is high, the retreating molten film between two holes can coalesce into filaments, as in the image in figure 3(c), taken in a transition region from the partially broken up film to the completely dewetted film, corresponding to the threshold fluence for break up. At fluences slightly higher than the threshold (figure 3(d)) the filaments can then split into droplets, possibly due to the Rayleigh instability [48] which has been recently observed experimentally for thermally annealed Cu nanowires on SiO2 surfaces [49] and for Au, Ag, Ni films on SiO2 irradiated by an excimer laser [20, 22, 23]. This phenomenon can be clearly observed in the magnification shown in figure 3(e).
Figure 3. (a) Spatial intensity profile of the laser. (b)–(d) Plan-view TEM images taken in the 5 nm Au/Si sample irradiated by 1000 mJ cm−2 at increasing distances from the center of the laser spot: (b) >300 μm, (c)= 300 µm, (d) <300 μm. (e) Magnification of (c).
Download figure:
Standard imageBefore break-up into NPs is possible, the film must first be brought to its melting point. It is important, therefore, to consider the heat transfer that occurs during the pulsed laser melting of thin films. With a pulse duration of 12 ns, we can describe the temperature changes that occur in the system using the heat conduction equation by introducing a source term. As the power density is uniform within 300 µm, which is large compared to the film thickness d, the heat conduction can be considered in only one spatial dimension. Hence, the heat conduction equation takes the form
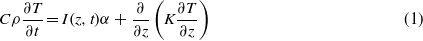
where C is the heat capacity (2.5 × 106 J m−3 K−1 for Au), ρ is the mass density (19.32 × 103 kg m−3 for Au), T(z,t) is the temperature at depth z and time t, I is the laser power density, α is the absorption coefficient (α−1 = 18 nm for Au), and K is the thermal conductivity (318 W m−1 K−1 for Au). z is taken to be zero at the surface of the metal film. A simple model to examine the general properties of the melting of thin film is the following [22]: the total heat S, per unit area, deposited in a thin film modeled as a single layer of thickness d, irradiated by a single laser pulse of duration Δt with a top-hat temporal profile is given by
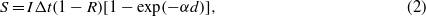
where R is the reflectivity of the film material at the laser wavelength. In a thin film of thickness d, the increase in temperature ΔT is ∝S/d, where S is the supplied energy. Then, in the limit of small d, we have

Thus, in the limit of small d and ignoring heat conduction, the temperature increase is ∝IΔt(1 − R)α/d. So the temperature increase is expected to be significant if α is large, and thicker films should require higher laser fluencies to melt. However, by observing the terms in equation (1), we can see that the rate of heat diffusion into the substrate for a thin film heated from the top surface will become greater as the film thickness decreases due to the temperature gradient across the film increasing. When heat conduction is considered, for thin films where d < 1/α a region of the substrate determined by the thermal diffusion depth of Si (4148 nm) will also be heated. The heat S absorbed in the metal will also have to heat this region. Thus, the fluence required to melt the film will increase with decreasing d. For thicker films (d > 1/α), heat conduction into the substrate will be significantly slower, and lower melting fluences would be expected. When d ≫ 1/α partial melting of the top surface of the film should occur.
Definitively, we can expect that once a thin metal film is molten, instability driven break-up into droplets may be expected if the liquid phase poorly wets the substrate [22]. Effectively, the Au/Si system has a non-wetting nature and the cohesion between Au atoms is larger than the adhesion between Au and the Si substrate [38], possibly promoting the break-up of the metallic films into droplets. Effectively, our starting Au films present roughness σ which justifies the thickness inhomogeneities where the melting and dewetting of the film start. The roughness σ of a film is a computed value of the root-mean-square variation (i.e. standard deviation) of the surface height profile from the mean height, and is given by [50]

where M is number of data points of the profile, yi are the data points that describe the relative vertical height of the surface, and  is the mean height of the surface. So it is a quantitative description of the film thickness inhomogeneity. It can be directly extracted by the AFM images (shown later) from section profile analyses. Following this procedure, we obtain for the 5 nm and 20 nm thick Au films, respectively, σ (5 nm) = 1.7 nm, and σ (20 nm) = 2.4 nm.
is the mean height of the surface. So it is a quantitative description of the film thickness inhomogeneity. It can be directly extracted by the AFM images (shown later) from section profile analyses. Following this procedure, we obtain for the 5 nm and 20 nm thick Au films, respectively, σ (5 nm) = 1.7 nm, and σ (20 nm) = 2.4 nm.
Concerning the dewetting phenomenon, it is well accepted that dewetting morphology can progress via three pathways [51]. (a) Homogeneous nucleation and growth, where holes appear spontaneously at random locations and times on the surface. Because of the inherent randomness, no characteristic length is present in this type of dewetting. (b) Heterogeneous nucleation and growth due to defects, impurities or other heterogeneities. In this type of dewetting, a characteristic length scale could appear at the early stage of dewetting due to ordered nucleation sites. (c) Thin film hydrodynamic instabilities such as the one associated with the dewetting of spinoidally unstable systems. The resulting patterns are characterized by a well-defined length scale in the hole spacing and/or size. Since our morphological analyses do not evidence any spatial order in the arrangement of the islands, the process in (a) seems to be the dominant one, as often observed for thin metallic films (Ni, Ag, Mo, Au, Ti and Zn) on SiO2 under nanosecond laser irradiation [20].
To analyze quantitatively the morphological evolution of the NPs as a function of E, we focus our analyses within 300 µm of the center of the laser spot for each sample irradiated by different fluences. As an example, figure 4(a) shows a plan-view TEM image of the 5 nm thick Au/Si sample irradiated by 1000 mJ cm−2, while figure 4(b) shows a magnification of (a). Furthermore, figure 4(c) shows a cross-view TEM image of the same sample, while figure 4(d) is a magnification of (c). The cross-view analyses clearly show the strong non-wetting nature of the formed NPs: they appear as almost spherical particles characterized by a well-defined height H and diameter D (figure 4(d)) dewetted from the starting quasi-continuous film. Further information on the structure of the NPs formed as a consequence of the laser irradiation of the Au/Si system can be obtained by high-resolution-TEM (HR-TEM) analyses: the dewetted NPs appears in the HR-TEM images as formed by a crystalline core surrounded by an amorphous shell. For example, figure 5(a) shows a plan-view HR-TEM image of a selected NP in the 5 nm thick Au/Si system irradiated by 1000 mJ cm−2: it appears to be formed by a crystalline core surrounded by a 1 nm amorphous shell. On the other hand, figure 5(b) reports a plan-view HR-TEM image of a selected NP in the 20 nm thick Au/Si system irradiated by 1000 mJ cm−2: it appears to be formed by a crystalline core surrounded by a 5 nm amorphous shell. The crystalline nature of the core is confirmed by the electron diffraction pattern shown in figure 5(c): it is identical to the electron diffraction pattern of 1 µm Au deposited on Si, and typical of the crystalline FCC structure of Au. Finally, to clarify the chemical nature of the amorphous shell, energy filtered TEM (EFTEM) analyses were performed. EFTEM allows mapping of the elemental composition of the analyzed sample with spatial resolution typical of TEM analyses, by selecting electrons with a well-defined energy from the transmitted beam. In particular, in our present case, a SiO2 EFTEM map obtained by recording electrons that lost 26 eV in the film (figure 5(d)) reveals that the amorphous shell of this core–shell structure is just SiO2. In fact, in this map the bright regions are those rich in SiO2, and by comparing figures 5(b) and (d) we can conclude that those regions are just the amorphous shells surrounding the crystalline Au core (note the perfect correspondence between the amorphous regions in figure 5(b) and the bright regions in figure 5(d)). So, we can conclude that the overall result of the nanosecond laser irradiation of thin Au film on Si is the formation of Au/SiO2 core–shell NPs of well-defined diameter D and height H. Taking into in account the considerations about Au/Si eutectic reaction and melting dynamics, we can sketch the steps of the process leading to the formation of such structures as a consequence of the laser irradiation, as follows: the laser irradiation determines the melting of the Au film in the regions where it is thinner. If the temperature reached in this region is T ≥ TE = 673 K, the Au film and Si substrate react, with melting starting from the interface, forming the Au/Si alloy. Furthermore, in these regions the dewetting process of the Au/Si film occurs, generating a retreating molten film. The dewetting process leads to the formation of Au/Si alloy liquid NPs. During the cooling phase, below the eutectic temperature TE, phase separation occurs between Au and Si. In particular, Si is segregated at the edge of the NP and reacts with the environmental O2, its solidification in SiO2 occurs, giving rise to the SiO2 shell. After solidification of the Au, the solid crystalline Au core is generated.
Figure 4. (a) Plan-view TEM image of the 5 nm thick Au sample irradiated by 1000 mJ cm−2. (b) Magnification of (a). (c) Cross-view TEM image of the 5 nm thick Au sample irradiated by 1000 mJ cm−2. (d) Magnification of (c): the characteristic height H and diameter D are indicated.
Download figure:
Standard imageFigure 5. (a) Plan-view HR-TEM of the 5 nm thick Au sample irradiated by 1000 mJ cm−2: the nanostructure appears clearly formed by a crystalline core surrounded by a 1 nm thick amorphous shell. (b) Plan-view HR-TEM of the 20 nm thick Au sample irradiated by 1000 mJ cm−2: the nanostructure appears clearly formed by a crystalline core surrounded by a 5 nm thick amorphous shell. (c) Electron diffraction pattern of the crystalline core: it is identical to the bulk Au electron diffraction pattern. (d) Plan-view EFTEM image of the core–shell nanostructures in (c). It is obtained by recording electrons with an energetic loss of 26 eV (SiO2 plasmonic peak) so that the bright regions indicate the zone in which the SiO2 is present. (e) Picture of the Au/SiO2 core–shell NP.
Download figure:
Standard imageTo obtain quantitative information on the evolution of the sizes H (height) and D (diameter) of the Au/SiO2 core–shell NPs as a function of E and d, we combined the TEM analyses with SEM and AFM analyses. As examples, figures 6(a)–(e) show SEM images of the 5 nm thick Au/Si sample unirradiated (a) and irradiated by 500 (b), 750 (c), 1000 (d), and 1500 mJ cm2 (e). Similarly, figures 6(f)–(l) are SEM images of the 20 nm thick Au/Si sample unirradiated (f) and irradiated by 500 (g), 750 (h), 1000 (i), and 1500 mJ cm−2 (l). Furthermore, figures 7(a)–(d) show, as examples, AFM images of the 5 nm thick Au/Si sample unirradiated (a) and irradiated by 750 (b), 1250 (c), and 1500 mJ cm−2 (d). Similarly, figures 7(e)–(h) show, as examples, AFM images of the 20 nm thick Au/Si sample unirradiated (e) and irradiated by 750 (f), 1250 (g), and 1500 mJ cm2 (h). By the simple visual inspection of the SEM and AFM images some conclusion can be derived: (1) the as-deposited 5 nm Au thick film shows a typical quasi-continuous and percolative morphology (figure 6(a)). After exposure to the laser fluence of 500 mJ cm−2 the Au/Si film is clearly observed to melt and break up into the Au/SiO2 NPs of circular section (figure 6(b)). Increasing the fluence E until 1500 mJ cm−2 only small changes seem to occur, mainly the appearance of a subpopulation of small islands (figures 6(c)–(e)). (2) The as-deposited 20 nm Au thick film shows a typical quasi-continuous morphology (figure 6(f)). After exposure to the laser fluence of 500 mJ cm−2 the continuous morphology evolves into a percolative morphology but such a fluence is too low to promote the clustering process (figure 6(g)). After 750 mJ cm−2 irradiation the Au/Si film is observed to perforate and break up into the Au/SiO2 NPS (figure 6(h)), even if the clustering process is incomplete. In this stage, coexistence of the percolative structure and the islands occurs (as already observed by TEM analyses in figure 3(b)). Increasing the fluence E to 1000 and 1500 mJ cm−2 the clustering process of the percolative film is complete (figures 6(i)–(l)).
Figure 6. (a)–(e) SEM images of the 5 nm thick Au/Si sample unirradiated (a) and irradiated by 500 (b), 750 (c), 1000 (d), 1500 mJ cm−2 (e). (f)–(l) SEM images of the 20 nm thick Au/Si sample unirradiated (f) and irradiated by 500 (g), 750 (h), 1000 (i), 1500 mJ cm−2 (l).
Download figure:
Standard imageFigure 7. (a)–(d) AFM images of the 5 nm thick Au/Si sample unirradiated (a) and irradiated by 750 (b), 1250 (c), and 1500 mJ cm−2 (d). (e)–(h) AFM images of the 20 nm thick Au/Si sample unirradiated (e) and irradiated by 750 (f), 1250 (g), and 1500 mJ cm−2 (h).
Download figure:
Standard image
From the AFM images we can obtain the distributions of the diameter D and height H of the Au/SiO2 NPs using the SPMLabAnalyses version 7.00 software that define each nanocluster area by the surface image sectioning of a plane that was positioned at half cluster height. From the plan-view TEM and SEM analyses we can also obtain the distributions of D. From the cross-view TEM analyses we can also obtain the distributions of H. Moreover, the surface density N (NPs per unit area) can be derived at each E by direct inspection of the AFM, SEM, and plan-view TEM analyses and counting. However, the results obtained by AFM, SEM, and TEM analyses are in good agreement (the respective results are identical within the statistical error). So, AFM, SEM, and TEM analyses were combined to derive the size distributions of Au/SiO2 NPs. As an example, figure 8 reports the distributions of D and H for the Au/SiO2 NPs in the 5 nm thick Au/Si system (a) and (b) and 20 nm thick Au/Si system (c) and (d) irradiated by 1500 mJ cm−2. These distributions were calculated on a statistic population of 200 islands and fitted (continuous lines in figure 8) by the log-normal function [52]
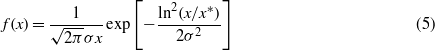
x being, respectively, D or H, with σ the standard deviation on x. The fits parameters were x* and σ. The mean value of x was obtained by 〈x〉 = x*exp(σ2/2). In this way, we obtain the evolution of the mean Au/SiO2 NP diameter 〈D〉 and height 〈H〉 (with the respective errors) as a function of E. Figure 9 reports the evolution of 〈D〉 and 〈H〉 as a function of E for (a) the 5 nm thick Au/Si system, and (b) the 20 nm thick Au/Si system. On the basis of the evolution of 〈D〉 and 〈H〉, in figures 9(c) and (d) we can schematize the evolution, with E, of the 'mean' shape of the Au/SiO2 NPs. So, for the 5 and 20 nm Au samples, changing E from 500 to 1500 mJ cm−2 we can control 〈H〉 and 〈D〉 to change in a controlled way the ratio 〈H〉/〈D〉 as reported in table 1. Finally, some control on the surface density N of the Au/SiO2 NPs can be obtained varying E, as reported in figures 10(a) and (b) for the 5 and 20 nm thick Au samples, respectively. N is obtained by direct inspection of the AFM, SEM, and TEM analyses, averaging on several images. From the averaging procedure the error bars for N are obtained. In the 5 nm thick Au sample, N changes from 1.6 × 1010 cm−2 at E = 500 mJ cm−2 to 1.77 × 1010 cm−2 at E = 1250 mJ cm−2. In the 20 nm thick Au sample, N changes from 4 × 109 cm−2 at E = 750 mJ cm−2 to 4.5 × 1010 cm−2 at E = 1250 mJ cm−2. Such a control on size, shape, and surface density of the Au/SiO2 core–shell NPs could be important, for example, for any plasmonics [53], optical [5, 10], or sensing [11–13] application.
Figure 8. Distributions of the Au/SiO2 NP diameter (a) and height (b) in the 5 nm Au thick/Si system irradiated by 1500 mJ cm−2 (the full lines are the fits). Distribution of the Au/SiO2 NP diameter (a) and height (b) in the 20 nm Au thick/Si system irradiated by 1500 mJ cm−2 (the full lines are the fits).
Download figure:
Standard imageFigure 9. Evolution of the mean height 〈H〉 and diameter 〈D〉 of the Au/SiO2 NPs as a function of the laser fluence for the 5 nm thick Au/Si (a) and 20 nm thick Au/Si (b) systems. Evolution of 〈H〉/〈D〉 and schematic of the mean shape evolution of the Au NPs as a function of E for the 5 nm thick Au/Si (c) and 20 nm thick Au/Si (d) systems.
Download figure:
Standard imageFigure 10. Evolution of surface density N of the Au/SiO2 NPs as a function of E for the 5 nm thick Au/Si (a) and 20 nm thick Au/Si (b) systems.
Download figure:
Standard imageTable 1. Synthesis of the mean height 〈H〉, mean diameter 〈D〉, and ratio 〈H〉/〈D〉 of the nanoparticles as a function of the laser fluence E for each fixed thickness d of the Au film.
| d = 5 nm | d = 20 nm | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| E (mJ cm−2) | 500 | 750 | 1000 | 1250 | 1500 | 750 | 1000 | 1250 | 1500 |
| 〈H〉 (nm) | 40.2 | 37.6 | 29.9 | 29.8 | 21.8 | 66.9 | 62.6 | 52.1 | 43.7 |
| 〈D〉 (nm) | 60.1 | 58.0 | 50.7 | 40.3 | 51.2 | 91.9 | 43.7 | 39.0 | 62.0 |
| 〈H〉/〈D〉 | 0.67 | 0.65 | 0.59 | 0.74 | 0.43 | 0.73 | 1.43 | 1.34 | 0.70 |
4. Conclusions
In this work, a novel physical, low-cost, and simple method to generate Au/SiO2 core–shell NPs was investigated. It is based on the nanosecond laser irradiation of a thin Au film deposited on Si. We demonstrated, with respect to previous works [18–32], that such irradiation promotes the eutectic Au/Si reaction, the dewetting of the Au/Si eutectic film, and the oxidation of Si to produce Au/SiO2 core–shell NPs. In particular, the following results were reached:
- 1.For 5 nm thick Au film on Si irradiated by500–1500 mJ cm−2 nanosecond laser fluence: Au/SiO2 core/shell NPs were obtained formed by a crystalline Au core surrounded by 1 nm amorphous SiO2 shell. The mean NP height and diameter decrease from, respectively, 40.2 nm and 60.1 nm for 500 mJ cm−2 to 21.8 nm and 51.2 nm for 1500 mJ cm−2. Respectively, the height to diameter ratio changes from 0.43 for 1500 mJ cm−2 to 0.74 at 1250 mJ cm−2. The NP surface density changes from 1.6 × 1010 cm−2 for E = 500 mJ cm−2 to 1.77 × 1010 cm−2 at E = 1250 mJ cm−2.
- 2.For 20 nm thick Au film on Si irradiated by500–1500 mJ cm−2 nanosecond laser fluence: Au/SiO2 core/shell NPs were obtained formed by a crystalline Au core surrounded by 5 nm amorphous SiO2 shell. The mean NP height and diameter decrease from, respectively, 66.9 and 91.9 nm for 500 mJ cm−2 to 43.7 nm and 62 nm for 1500 mJ cm−2. Respectively, the height to diameter ratio changes from 0.70 for 1500 mJ cm−2 to 1.43 for 1000 mJ cm−2. The NP surface density changes from 4 × 109 cm−2 for E = 750 mJ cm−2 to 4.5 × 1010 cm−2 for E = 1250 mJ cm−2.
While several previous works have analyzed the formation of pure metallic nanostructures on surfaces by laser irradiation of thin metal films, with this work we introduce a novel methodology taking advantage of the laser-based techniques to produce and manipulate metal-core/dielectric-shell nanostructures.










