Pump depletion in Raman lasing in a graded index multimode fibre

Offering a compact design, reliability, stability, and a high beam quality, fibre lasers have long been widely and successfully used in a variety of applications. Even though the technology of cw and pulsed fibre lasers is, on the whole, sufficiently well developed and many such sources are commercially available, classic fibre lasers present a number of problems. In particular, nonlinear properties of optical fibre, responsible for stimulated Raman scattering (SRS), self-phase modulation, and other effects, are in general undesirable and limit laser power characteristics. Besides, the working spectral range of fibre lasers, determined by doping with rare-earth elements, remains insufficiently wide, even though the list of active dopants used (Er, Yb, Tm, and others) is constantly expanding [1 – 3]. Moreover, in some wavelength ranges lasing efficiency is extremely low.

At the same time, the use of the nonlinear properties of silica fibre makes it possible to obtain fundamentally new fibre laser operation modes. For example, the SRS effect is successfully used to make lasers emitting at wavelengths unattainable with classic rare-earth-doped fibre lasers in continuous [4, 5] or pulsed [6, 7] mode. With the use of a single-mode laser pump source (typically an Yb or Er – Yb doped fibre laser), such lasers generate a Stokes line with a corresponding spectral shift. It is easy to see that such lasers have a more complex design and that nevertheless there are serious limitations on their output power and working spectral range, which is determined by the pump fibre laser output. Recently, a radically different approach to Raman lasing has been proposed, in which high-power multimode (MM) laser diodes (LDs) are used as pump sources and their radiation is launched into a graded index fibre supporting propagation of many modes, in which a high-quality stimulated Raman beam is generated (see a review by Babin et al. [8] and references therein). This approach has great potential for practical application, largely owing to the wide range of emission wavelengths of commercially available MM laser diodes. In particular, MM Raman lasers with an emission wavelength of 954 nm and a beam cleanup effect (beam quality factor M² = 2.3) [9] and an emission wavelength of 976 nm (M² = 1.9) [10] and a laser emitting at a second Stokes wavelength of 996 nm (M² = 1.6) [11] have been demonstrated to date. These lasers offer near-diffraction-limited beam quality in combination with a relatively high output power (∼50 W) and a high differential MM (M² = 30) pump conversion efficiency (∼70 %). Since the lasing wavelength 976 nm is much needed in laser engineering, e.g. for pumping fibre lasers and amplifiers, this makes such lasers rather promising. Moreover, such lasers were used to demonstrate efficient second harmonic generation at wavelengths of 477 and 488 nm [12].

This work is a logical continuation of our previous research concerned with diode-pumped MM fibre Raman lasers. We consider intermodal interaction processes that involve a multimode pump wave and few-mode signal wave in a linear cavity formed by fibre Bragg gratings (FBGs) and lead to a radially nonuniform pump beam depletion.

The Raman fibre laser configuration was similar to that described previously [10]. Figure 1 shows a schematic of the laser. Three fibre-pigtailed (105/125 μm, NA = 0.22) high-power MM laser diodes with an emission wavelength λ_p = 938 nm were connected to the corresponding inputs of a 3 × 1 pump combiner, whose output port was fusion-spliced to an ∼1 km length of GRIN 100/140 μm fibre with a graded index core and a numerical aperture of 0.29. The loss in the pump combiner was about 2 dB. The laser cavity was formed by a high-density FBG with reflectivity R ≈ 90 %, UV written by the phase mask technique, and a low-reflectivity output FBG (R ≈ 4 %) written by femtosecond pulses using a point-by-point process (see Ref. [10] for details). FBG writing by femtosecond pulses allows one to select the fundamental mode and suppress higher order modes by about 10 dB. The output fibre end was cleaved at an angle above 10° to rule out Fresnel reflection. The dichroic mirrors M1 and M2 were used to attenuate the pump beam at λ_p = 938 nm and the Stokes wave at λ_S = 976 nm, respectively. To further attenuate the light, an interference filter (IF) was placed in front of the beam profiler. To measure the Stokes beam and transmitted pump beam profiles, we used two distinct IFs: with a centre transmission wavelength of 976 nm (Δλ = 25 nm) or a transmission wavelength of 950 nm (Δλ = 25 nm). This allowed us to separate the spectral component of interest. The pump and Stokes wave powers were measured in the same way as previously [10].

Zoom In Zoom Out Reset image size

First, we measured the pump laser beam profile at the output of the SI 105/125 step index multimode fibre of one of the MM LDs. Figure 2 shows the resultant beam waist profiles, which proved to approach a step profile similar to the refractive index profile of the fibre. To adjust to the focus, we used an artificial defect on the fibre end face. Defocusing blurred spatial details of the beam (Fig. 2c).

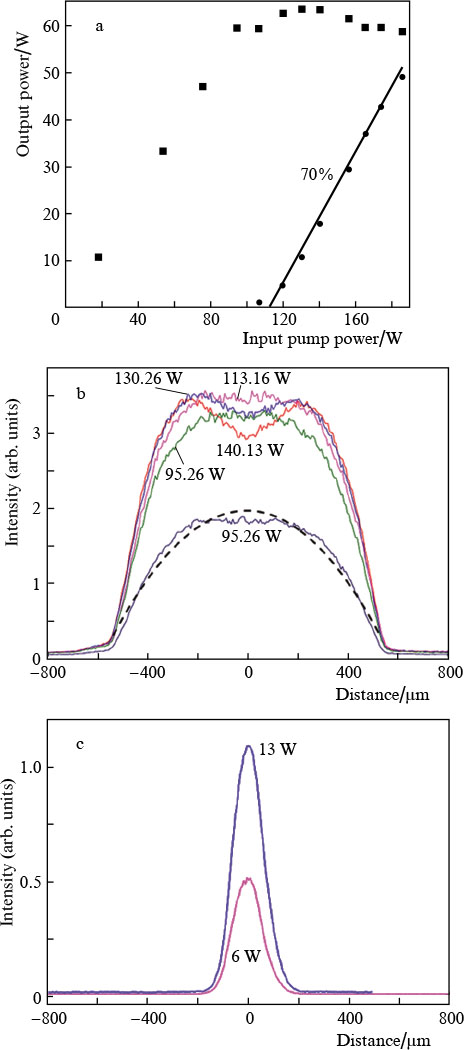
Zoom In Zoom Out Reset image size

Next, we studied characteristics of the beam leaving the multimode Raman laser based on GRIN graded index fibre. A pump power of ∼105 W (at the GRIN fibre input) led to Stokes generation at a wavelength of 976 nm (Fig. 3a), whereas a pump power of 185.5 W initiated second-Stokes generation at a wavelength of 1018.2 nm.

Zoom In Zoom Out Reset image size

At the fibre laser output, the quality factor M² of the pump beam from the three LDs below the SRS threshold was 34 – 36. The output profile of the transmitted pump beam resembled a parabola which to some extent reproduced the refractive index profile of the GRIN fibre used. After the onset of SRS generation of a Stokes beam, which had M² ≈ 1.9 – 2 as a consequence of the Raman beam cleanup effect and the selective properties of the FBGs, the transmitted MM pump beam had a well-defined central dip due to pump depletion. Figure 3b illustrates the effect of input pump power on the transmitted pump beam profile, and Fig. 3c shows profiles of the generated Stokes beam.

Consider, in the geometric optics approximation, the propagation of a pump wave filling the entire fibre core of radius R. Let us pick out an optical ray (narrow beam) of area dS that propagates along the trajectory r_j (z) = r_j cos[Δ(z – z⁰)], oscillating with a maximum deflection | r_j | < R and a period L_B = 2π/Δ. Averaging the field intensity of the jth beam, I_j ( r ) = AdSδ{ r – r_j cos[Δ(z – z₀)]}, over the peak position and summing it over all the beams filling the core, we obtain the average intensity of the random pump field in the form

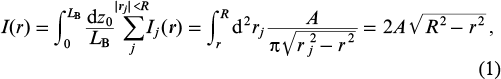
where A = 3P/(4π R³) can be determined through the total pump power P, i.e. near the maximum of the distribution

For comparison with the experimentally measured pump beam profile, the dashed line in Fig. 3b shows the parabolic profile corresponding to the equilibrium power distribution over all transverse modes of the core (Gauss – Laguerre functions) in the absence of interference between the modes.

Note that, in the case of a step index fibre, a ray propagates along a sawtooth trajectory with | r | < R. Because of this, the average intensity profile in this case is independent of r within the core and drops sharply to zero outside it (Fig. 2b).

Raising the pump power increases the Stokes wave power, which is additionally selected by the output FBG, inscribed in the region of the fundamental mode and having a spatial reflection profile approaching a Gaussian function of the radial coordinate. The high-intensity Stokes wave causes pump depletion, which appears as hole burning with the fundamental mode radius in the centre of the transverse pump beam intensity distribution, I_p( r ).

In the case of GRIN fibre, we can derive approximate equations for the pump and Stokes wave field intensities, I_S and I_p, taking into account their radial dependences and assuming a large number of transverse modes:

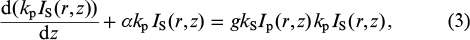
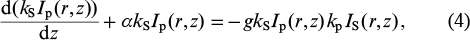
Here, k_p and k_S are the pump and Stokes wavenumbers; α is the absorption coefficient of the fibre; f is the ratio of the Raman constant to the Kerr constant; and n⁽²⁾ and n₀ are the linear and nonlinear refractive indices.

These equations have analytical solutions:

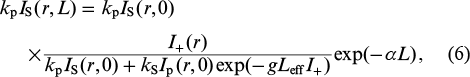
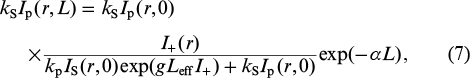
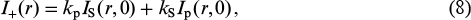
where the effective length is given by L_eff = [1 – exp(–α L)]/α.

The boundary conditions at point z = 0 correspond to total reflection of the Stokes wave, i.e. , where is the backward Stokes intensity, and . If a filter in the form of a Bragg reflector with reflectivity ρ(r) is placed at point L at the fibre output, we have . Thus, we obtain

The pump beam distribution at the fibre input is determined by the source light radial distribution: .

Substituting these relations into the solution, we obtain

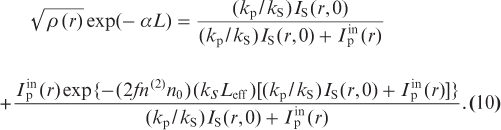
Since I_S → 0 at the lasing threshold, the expression for the threshold intensity at the maximum gain-to-loss ratio and r = 0 takes the form

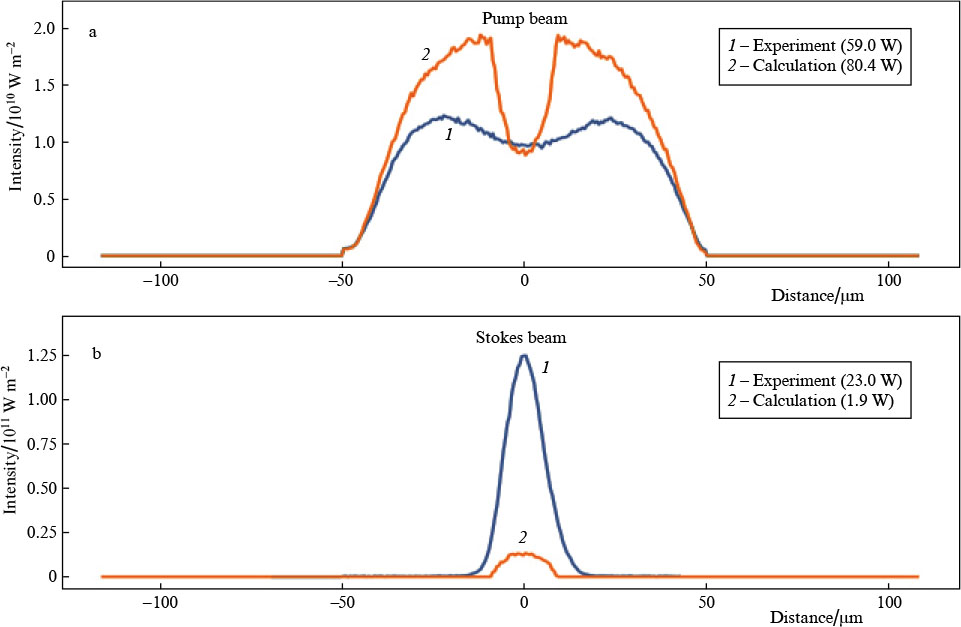
Figure 4 presents numerical calculation results obtained using relations (6) – (9) for pump depletion at an input pump power of 153 W and experimental data. In simulation, we used the FBG reflectivity ρ(r) in the form of a Gaussian with a maximum value of 4 % and a width of 12 μm (axial mode diameter). Even though the balance model constructed under the assumption that there is a large number of modes is rather rough (which is responsible for the sharp boundaries of the Stokes beam and the dip in the pump beam), it provides a qualitative explanation for spatial hole burning. At the same time, there are considerable quantitative discrepancies between the calculation results and experimental data. For example, the dip in the experimentally determined pump beam profile is markedly broader than that in the calculated profile, even though the Stokes wave propagates predominantly in the fundamental mode even at a high pump power. As a consequence, the experimentally determined SRS efficiency turns out to be higher because the dip in the pump beam becomes flatter on account of the peripheral parts of the beam. This increases SRS efficiency compared to numerical calculation results.

Zoom In Zoom Out Reset image size

Measurements of the output profile of a multimode pump beam and the generated Stokes wave have shown that, below the SRS threshold, the transmitted pump beam (with a quality factor M² ≈ 34) has a nearly parabolic profile. Such a profile corresponds to a uniform distribution of transverse modes due to possible mode mixing during beam propagation through a 1 km length of spooled graded index fibre. The generation of a high-intensity Stokes wave with M² ≈ 2 is accompanied by spatial hole burning in the transmitted pump beam. We have constructed a balance model for interaction of a low-quality pump wave and a high-quality Stokes beam in an MM Raman laser, which provides a qualitative explanation for the hole burning effect. Unfortunately, there are considerable quantitative discrepancies between the experimental data and calculation results: the dip in the experimentally determined pump beam profile is markedly flattened (it is broader and shallower than the calculated one), which also seems to be due to transverse mode mixing during pump wave propagation. At the same time, the Stokes wave, propagating predominantly in the fundamental mode, spreads out negligibly, which can be interpreted as evidence that it is significantly influenced by nonlinear effects, e.g. by Kerr beam self-cleaning, whose impact strongly depends on the initial mode composition of the beam and is strongest at a small fraction of higher order transverse modes [13]. Note that further research is needed to gain detailed insight into the mechanism of the observed effect.

This work was supported in part by the Russian Foundation for Basic Research (Grant No. 19-52-53021). E.V. Podivilov (the balance model) acknowledges the support from the RF Ministry of Science and Higher Education (14.Y26.31.0017).