Coherent beam combining in optically coupled laser arrays

A priority issue in laser engineering is the ability to minimise the far-field intensity distribution width, so a natural way of selecting supermodes is by filtering the field distribution in the focal plane of a lens or mirror in the output section of the system. To minimise the beam divergence of a large-aperture solid-state laser in their experiments, Gerasimov et al. [51, 52] used a limiting circular diaphragm in the focal plane of one of its mirrors, which selected out the laser mode with the smallest far-field divergence, suppressing all other supermodes. He et al. [53] demonstrated phase locking of radiation from two fibre lasers with a 88 % efficiency with the use of a focal filter. Wan et al. [54] presented a detailed numerical analysis of how parameters of a focal filter influence supermode separation selectivity in systems of two and three lasers. In such geometry, however, the edge of the diaphragm is exposed to high-power radiation and one loses the field in side diffraction orders in the focal plane. These drawbacks were partially overcome in experiments reported by Aleksandrov et al. [55], where the radiation from a CO₂ laser array was phase locked by passing it through a diaphragm with a system of holes corresponding to maxima in the far-field intensity distribution of the in-phase mode. An analogous spatial filter was used by Rediker et al. [56] to phase-lock the radiation from an array of five semiconductor lasers.

Fridman et al. [57] studied a 5 × 5 array of fibre amplifiers differing in length and coupled through a system of mirrors in the focal plane. At the output in the far field, they observed radiation with a rapidly varying brightness. In addition, at the instants corresponding to the average axial brightness the far-field intensity distribution corresponded to the output of one laser, whereas at the instants corresponding to maximum brightness they observed the structure of a combination of supermodes of the array. In the case of a 2D square array, the time-averaged efficiency decreased from 90 % for 3 lasers to 29 % for 25 lasers, but 90 % locking efficiency was reached for some time even at a larger number of lasers (N): 0.1% of the time at N = 12, 0.012 % at N = 16, 0.004 % at N = 20 and 0.001 % at N = 25. In addition, Fridman et al. [30] showed that, under the experimental conditions of their study, the average size of a cluster of locked lasers had a Gaussian probability distribution with a mean size of ∼7.

For a fibre laser array, single-mode fibre can be used as a spatial filter, with a small part of the output beam of a system of fibre amplifiers focused onto its input end [58]. The field produced in the single-mode fibre is delivered to the input of the amplifier system to form a common ring cavity (Fig. 2). Separating the in-phase mode in such a laser configuration, Shalaby et al. [59] achieved the phase locking of fields in an active 19-core fibre. To demonstrate the feasibility of the phase locking of two multicore lasers in a ring cavity configuration, Shalaby et al. [60] imitated lasers by two parallel passive seven-core structures and a common amplifier based on single-mode fibre, which served as a spatial filter as well. In those experiments, the in-phase mode separation efficiency was above 95 %, but the fraction of the power coupled into the single-mode fibre was far below 1 %.

Zoom In Zoom Out Reset image size

To improve the efficiency of common supermode separation in ring geometry, Yang et al. [61] proposed placing a diffraction grating between a focusing lens and single-mode fibre, so that the beams from three separate amplifiers propagated in diffraction order directions of the grating. Even though the efficiency of beam combining on the grating was relatively low, 61 %, they demonstrated phase locking with 20 W of output power. In this process, 1.5 mW of power was coupled into the fibre.

At high output powers, most of the light leaves the ring cavity. Since the optical fields in the individual amplifiers are phased, output beams can be combined on a diffraction grating. Using such a configuration with three fibre amplifiers, Liu et al. [62] obtained 206 W of output power at a beam quality factor M² = 1.38.

A natural development of the far-field filtering method is the use of the output end faces of a laser array as a selecting aperture in the Fourier plane (Fig. 3). The image at the focus of a lens coincides with the structure of the emitting laser end faces under the condition that Λ² = λF, where F is the focal length of the lens. Such a compound cavity with Fourier coupling was first used by Corcoran and Rediker [63] to phase-lock five fibre-coupled semiconductor lasers. Later, an analogous configuration was used to phase-lock seven fibre lasers [64]. The theory of phase locking of a Fourier-coupled laser array is discussed in Section 5.

Zoom In Zoom Out Reset image size

Field coupling of two lasers in four-wave scattering processes in nonlinear cells was first considered theoretically by Likhanskii et al. [65] and demonstrated experimentally in gas lasers with different nonlinear cells by Baranov et al. [66] and Bondarenko et al. [67]. Beams counterpropagating in an active medium produce gain gratings, which allows gain elements to be used as coupling cells based on the four-wave scattering effect [68, 69]. Basiev et al. [70, 71] demonstrated coupling of two and three Nd : YAG lasers in such geometry. In the latter case, they obtained pulses with an energy of 0.94 J at a wavelength of 1.34 μm and a repetition rate of 10 Hz.

If two fibre lasers are coupled by a 2 × 2 coupler and reflection from the fibre end face is eliminated in one of the coupler ports, such a compound cavity, equivalent to a Michelson interferometer, will ensure frequency tuning of the lasers to a common lasing frequency at which the loss due to emission through the open port will be zero [72]. Theoretically, sequential pairwise coupling with couplers allows any number of lasers to be coupled to each other. In experiments, stable coupling of seven or eight fibre lasers with a relatively low power was demonstrated [73, 74]. The drawbacks to this approach are that the output of the entire array is coupled into single-mode fibre and that lasing is unstable in time [75]. Bruesselbach et al. [76] experimentally studied a system of ten lasers, each with an output power of ∼100 W in the case of independent lasing. According to their results, eight lasers can be successfully phase-locked at a low output power, whereas increasing the array to nine or ten lasers leads to a reduction in phase locking efficiency (η), determined as the fraction of the power outcoupled through output fibre. At an increased power, the efficiency drops sharply as the number of coupled lasers increases.

Wang et al. [77] studied coherent combining of two large mode area fibre laser beams in a configuration with interference coupling. At an individual laser power of ∼27 W, an output power of 50.1 W was reached (η = 92.8 %). Reducing the active core size led to a more rapid decrease in efficiency with increasing power. As the difference in optical length between the lasers was increased, η became independent of pump power. Kabeya et al. [78] studied in detail the reduction in η with increasing pump power in a two-arm ring fibre laser system. It was shown that η decreased to 90 % and that the emission spectrum at the loss port followed the phase-locked emission spectrum except in narrow regions near peak positions in the latter spectrum. To interpret this effect, it was assumed that, at a high pump power, the width of the mode spectrum was determined by the gain band and the fraction cut from the emission spectrum by the external coupling system gradually decreased.

Multiple-beam interferometer geometry with a system of semi-transparent mirrors was successfully used by Ishaaya et al. [79] to couple 16 solid-state amplifiers. Zhao et al. [80] coupled three Nd : YAG lasers in an interferometer with additional far-field filters. As a result, a single beam with M² = 1.35, containing 76 % of the energy (124 W) in the central maximum, was obtained instead of three output beams with M² = 5.5. For semiconductor lasers, interference coupling was ensured by rotating the plane of polarisation of half of the beams and then bringing them together using a birefringent plate. Phase-coupling four lasers in this way, Purnawirman and Phua [81] reduced their output power from 10.2 to 7.2 W and their lateral M² factor by 20 times.

Early work on the phase locking of diode laser arrays was reviewed by Goldobin et al. [16] and Botez [41], and that on lasing dynamics, by Winful and Defreez [82]. It became clear as early as the 1980s that diode laser bars, consisting of active waveguides separated by passive regions with a lower refractive index (RI), were unsuitable for the stable phase locking of the in-phase mode [41]. As a result of the optical loss in interelement gaps, weak optical coupling due to the rapid decrease in the field tunnelling from active fibres and variations in RI due to heating of the contact and changes in carrier concentration in quantum wells, the out-of-phase mode prevails or single-mode lasing becomes unstable with increasing pump current.

Advances in single-mode diode bar scaling were made after a transition to antiguided structures with gain regions separated by passive waveguides. Optical coupling in such structures is ensured by travelling waves and, provided there is resonance wave propagation through interelement gaps, is similar in properties to global coupling [41]. In an antiguided 20-element laser bar, stable in-phase mode lasing was obtained with 500 mW of power in continuous mode [83] and 2 W in pulsed mode [84]. In a 40-element laser bar, Yang et al. obtained 10 W of power in pulsed mode [85] and 1.6 W in continuous mode [86] at a beam divergence exceeding the diffraction limit by a factor of 2 and 1.8, respectively.

In vertical-cavity surface-emitting lasers (VCSELs), stable phase locking was obtained in square antiguided arrays consisting of 100 [87] and 400 [88] elements. In recent years, the advent of quantum cascade lasers has revived interest in antiguided laser bars. Kirch et al. [89] demonstrated a five-element bar with 5.5 W of output power at a wavelength λ = 8.35 μm in pulsed mode. Note that the central peak, with a divergence exceeding the diffraction limit by a factor of 1.65, accounted for 4.5 W of power. At λ = 4.7 μm, Sigler et al. [90] obtained 3.6 W of peak output power in a five-element laser bar with diffraction-limited beam divergence.

One way of increasing the fundamental mode area in fibre lasers is by using multicore structures. In pioneering work by Glas et al. [91], to raise the pump absorption coefficient the centres of 38 circular active cores 6.9 μm in diameter were arranged on a 115-μm-diameter circle near the outer fibre cladding. According to calculation of core coupling constants in this configuration [92], diffractive field exchange between neighbouring cores will occur over a propagation distance of ∼1.3 mm. Experimental data demonstrate that, nevertheless, such coupling is insufficient for phase-locking the fields in the cores.

Huo et al. [93, 94] demonstrated the operation of fibre lasers with hexagonal arrays formed by 7 and 19 active cores, respectively, with a diameter of 7 μm and a period of 10.5 μm. They observed spontaneous phase locking of the fields in the cores as the pump power was raised.

A hexagonal structure of active cores was also studied in photonic crystal fibres with an ordered array of air holes, which formed a 2D photonic crystal with defects containing active components. The technology and properties of microstructured fibres were discussed in a review by Russel [95]. In a photonic crystal fibre laser [96] having six ytterbium-doped active cores, single-mode generation of pulses 26 ns in duration and 2.2 mJ in energy was achieved at a mode area of 4200 μm². Using such fibre, with seven cores, as a final amplifier in a standard pulse stretching – amplification – compression scheme, Fang et al. [97] obtained 110-fs pulses with a peak power of 150 MW and mode area of 5000 μm². Fang et al. [98] utilised a photonic crystal fibre with 18 active cores as an amplifier in a passively Q-switched laser. Its output had a relatively high optical quality (M² = 1.52). Next, the pulses were compressed by an external system to a duration of 690 fs. These results suggest that multicore fibre is promising for the generation of microjoule pulses shorter than 100 fs at a repetition rate of 50 MHz [99].

Beach et al. [100] proposed a ribbon fibre structure comprising a periodic sequence of active and passive segments (Fig. 4a), embedded in a reduced-index cladding region. According to calculations for a five-element structure with a varied index difference between the active and passive regions, such a structure is most effective at an index modulation under 0.001. The theoretical predictions were confirmed by experimental data [101] for a waveguide amplifier with five Nd-doped active cores, in which an in-phase mode with a uniform intensity distribution was realised.

Zoom In Zoom Out Reset image size

The structure analysed by Beach et al. [100] is similar to that of antiguided semiconductor laser bars [41], differing only in that there is no absorption in the passive sections and that the edges of the structure have high reflectivity. Theoretical analysis by Vysotsky et al. [102] generalised the results presented in Ref. [100] and included the case of a large index difference between the active and passive regions. The latter is important for practical applications because the index difference determines the acceptable processing-induced scatter in RI. They derived explicit expressions for the maximum higher mode discrimination level and the largest number of phase-locked cores. For a resonant antiguided ribbon fibre laser structure, higher mode discrimination was independent of the number of elements up to ∼1000 elements.

Dawson et al. [103] proposed increasing the ribbon structure thickness by adding thin increased-index layers, which would allow a mode with a flat intensity profile across the ribbon to be produced in each element. Mode profile flattening raises the threshold power for nonlinear processes and allows the single-mode lasing output power to be increased.

Drachenberg et al. [104] demonstrated multimode operation of a ribbon waveguide laser with an output power of 40 W and beam spot area of 600 μm². To achieve single-mode operation, the fibre was used as an amplifier with single-mode light injection [105]. An alternative approach is to place an external filter in the far field. As demonstrated by Anderson et al. [106], the use of a bulk Bragg grating with an angular reflection bandwidth of 4.7 mrad as an external mirror allows the output beam quality to be improved to M² = 1.45. This is accompanied by a drop in the optical efficiency of the laser from 76 % to 53 %.

A further development of the ribbon fibre laser concept is the structure represented in Fig. 4b [107]. Here, the active structure has the form of a ribbon waveguide rolled around the fibre axis and having alternating increased- and reduced-index regions. The reduced-index regions contain active dopants (Er, Yb and others). This design allows one to sharply increase the optical mode area, while maintaining a high degree of fundamental mode selection. Calculations [108] show that, in the case of a ring waveguide (RW) having seven active sectors, an inner radius of 18.5 μm and outer radius of 34.5 μm, the in-phase mode can be reliably selected at index differences in the range 0.0015 < Δn < 0.0025. The addition of circular passive layers with an RI exceeding that of the active elements will lead to the same advantageous effects as were predicted by Dawson et al. [103] for a ribbon laser.

The sliced slab CO₂ laser design reported by Sha et al. [109], with a laterally modulated RF pumping and weak index modulation, is in effect of the same type as the ribbon fibre laser design. Sha et al. [109] demonstrated the phase locking of ten overlapping laser beams, so that the far-field intensity distribution had one peak, without sidelobes.

5.1.1. T-matrix method

Characteristics of multielement linear arrays of semiconductor lasers are usually calculated using Maxwell's equations or the wave equation [82, 143]. Along with numerical calculations using Maxwell's equations, an analytical approach based on simplified models of structures was developed. The effective RI (ERI) approximation (see e.g. Ref. [143]) relies on the large difference between the length scales of structures in transverse and lateral directions and reduces to averaging the product of the RI and optical mode profile over the transverse coordinate in the plane of the laser diode at a constant lateral coordinate. As a result of averaging and the use of approximate expressions relating the gain coefficient (GC) to the population inversion in a quantum well (QW), calculation of laser structures reduces to solving a system of 1D equations for the field and inversion density.

In the ERI approximation, the problem of finding a supermode of an antiguided diode laser bar consists in finding eigenfunctions in a planar waveguide with periodic step profiles of the ERI (n_eff) and Γ-factor, which characterises the overlap between the transverse mode and gain profiles. Γ-factor modulation can be accounted for by field pulling from the active layer to passive waveguides responsible for ERI modulation. The lateral amplitude profile of a U(x)exp(iβz) field is determined by the equation [41]

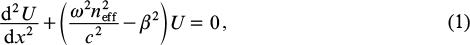
where β is the propagation constant; ω is the emission frequency; and c is the speed of light in vacuum.

Within each period of the structure, the field can be represented as the sum of two linearly independent solutions to Eqn (1): where the x_l coordinate is determined within the lth cell. The field distributions in the extreme cells of the structure are taken as basis solutions. At the boundaries of the laser bar, the amplitude of the field reflected from the boundary should be zero. The coupling of fields in neighbouring cells is determined by the joining of fields at each index step, which leads to linear recurrent relations for the coefficients of expansion of the field in terms of the basis functions and :

where the components of the unimodular transfer matrix T can be expressed through the basis functions and their derivatives on cell boundaries [144].

Since any matrix satisfies its secular equation, we can derive an equation relating the amplitudes of the -wave in three neighbouring cells:

where SpT = T₁₁ + T₂₂ is the trace of the matrix. A similar equation is valid for the amplitudes of the -wave. The general solution to Eqn (3) has the form a_l = c₁exp(ilQΛ) + c₂exp(–ilQΛ), where Q is the Bloch vector, playing the role of an eigenvalue, and the constants c₁ and c₂ can be determined from boundary conditions. At SpT = 2, the equation for exp(iQΛ), following from (3), has the doubly degenerate solution exp(iQΛ) = 1, whereas at SpT = – 2 we have exp(iQΛ) = – 1. These two limits correspond to the in-phase and out-of-phase modes. Side waves resonantly travel through such a periodic structure with a phase shift of 2sπ or (2s + 1)π per cell (where s is an integer). In terms of Bloch waves in a periodic crystal, solution degeneracy corresponds to the disappearance of the gap in the spectrum of the waves. Near both resonances, it is convenient to represent Eqn (3) in the form

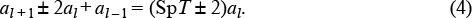
Even though, formally, diffractive exchange occurs between nearest neighbours, it plays a decisive role at |SpT± 2| << 1, because the right-hand side of (4) is small, and leads to effective phase locking of the elements, which is referred to as parallel coupling [41].

The described procedure was brought to analytical expressions [144, 145] for eigenvalues of the in-phase and neighbouring modes of an antiguided linear array as functions of the detuning of parameters of the structure from resonance. In the case of a resonance configuration, the fundamental mode and the neighbouring one turned out to have the same lasing threshold. To ensure discrimination of the neighbouring mode, it is necessary to move away from the resonance structure or introduce absorption in waveguide gaps.

A semiconductor amplifier was analysed in the limit of an infinite lateral size of an array of elements near resonance [146]. In such a case, after the field in the structure passes some distance, dependent on the input profile, the change in field per period of the structure becomes small, which allows the discrete equation (4) to be replaced by a differential equation for the lateral smooth field envelope. As shown earlier [146], in the case of a linear medium without absorption the type of this differential equation in x and z variables changes from elliptic to hyperbolic as resonance is approached. Because of this, an optical field in a resonance array propagates along straight lines at an angle to the optic axis, which depends on the geometric parameters of the structure, in agreement with experimental data [147] on light propagation in a 21-element resonant antiguided array.

In the general case, gain saturation and the associated positive change in RI can lead to field filamentation. It was found [146] that, at relatively low intensities of a field being amplified, self-focusing occurred if the following constraint on the difference Δ between the ERI step on the waveguide boundary and that corresponding to a resonance structure was fulfilled:

where α is the line broadening factor; I is the local intensity of the overall field; I_sat is the saturation intensity; g₀ is the small-signal GC; and α_T is the absorption coefficient of the waveguide gaps. In the absence of loss modulation, self-focusing develops as the index step on the waveguide boundary rises to above the resonance values, in agreement with calculation results [148].

In numerical simulation of an antiguided diode laser bar, Nabiev et al. [149] found soliton-like solutions in a lateral direction. In Ref. [146], the equation for a smooth envelope was reduced to a generalised Ginzburg – Landau equation, which has solutions in the form of spatially localised structures. The formation of a soliton is due to the fact that the field propagation constant spectrum has forbidden bands at Δ > 0. The dependence of the gain and refractive index on field intensity leads to a shift of the boundaries of the band gap, so that, at a certain combination of parameters, the propagation constant can fall in an allowed band at high intensities. Thus, there is a gap- or Bragg-soliton-like solution (see e.g. Ref. [150] and references therein), which was previously presented in explicit form for near-threshold lasing conditions [146].

5.1.2. Transfer equations for single-frequency light

In modelling double-cladding fibre lasers, use is typically made of transfer equations for mode powers. In doing so, radial intensity profiles of optical modes are assumed to be fixed and the local GC is thought to be determined by the total intensity profile [151 – 153]. In calculations of field propagation in multicore fibre lasers, wide use is made of coupled-mode theory (CMT), in which the field of the optical mode of an entire system (supermode) is represented as a linear combination of optical modes of individual waveguides [154]. The supermode describes the propagation of a beam through a system of passive waveguides in which its shape remains unchanged and only the common phase varies, in proportion to the distance and propagation constant β.

A multicore fibre usually supports a relatively small number of modes, whose analogues in quantum mechanics are wave functions of coupled states. The supported modes are orthogonal to each other and to leaky modes. In experiments with 7 - and 19-core fibres [59, 155], different supermodes of a passive fibre were selectively excited via signal injection from single-mode fibre. Even in the limit of weak interaction between passive cores, CMT poorly describes interaction between higher order supermodes and needs to be modified [156]. The transverse gain nonuniformity, due to either the structure of the gain or its saturation, leads to interaction between supermodes. This interaction is important at field intensities typical of fibre lasers, which are far lower than those characteristic of nonlinear optics. As distinct from CMT, a method based on expansion of the field in terms of exact eigenfunctions (supermodes) allows one to rigorously derive equations for describing the effect of GC distribution nonuniformity on mode competition. Note that, even though distorting mode profiles, thermal effects in fibre have little effect on the interaction between modes and intermodal discrimination [157].

In experiments with a seven-core fibre laser [93], increasing the pump power led to a far-field intensity distribution characteristic of phased fundamental supermode lasing. In-phase mode lasing at high pump power was also observed in the case of pulse amplification in a photonic crystal fibre having seven active cores [97]. In the framework of CMT, Bochove et al. [158] proposed an explanation for spontaneous in-phase mode selection in terms of the dependence of the positive resonant nonlinear part of the RI of glass on pump and lasing intensities. Later, it was found [159] that, in the CMT approximation, phase locking of the field occurred as well in the case of a negative additional nonlinear term in the RI. The nonlinear component of the RI of the fibre core is determined by the difference in polarisability between Yb ions in their ground and excited states and is an intricate function of pump and output intensities [160].

Numerical calculations using the program described by Elkin et al. [161] showed [162] that the phase locking of light in experimental work by Huo et al. [93] was associated with gain nonuniformity due to not only gain saturation but also the structure of the active cores. In those calculations, the simplest model for local GC saturation was used: g = g₀/(1 + I/I_sat). The field phase tuning effect was found to become stronger with increasing diffractive coupling between the cores and to be essentially insensitive to index nonlinearity, with allowance for the expected value of the RI. In the case of the design considered by Huo et al. [93], the highest gain corresponded to the out-of-phase mode [163]. At the same time, the result of amplification was highly dependent on conditions at the amplifier input. In particular, if seven beams covering the active cores, with a scatter in phase under 0.3 rad, were directed to the input, the in-phase mode prevailed at the output. This result contradicts the generally accepted view that the mode having the largest small-signal GC prevails at the amplifier output.

The paradox was explained in Refs [164, 165]. In the simplest case, we can consider the competition between two supermodes identical in frequency and polarisation, but having different propagation constants ( β₁ and β₂) and transverse field distributions [ψ₁(x, y) and ψ₂(x, y)]. The total field can then be represented as E = c₁(z)ψ₁(x, y) + c₂(z)ψ₂(x, y), where c₁(z) and c₂(z) are coefficients of expansion of the field in terms of the functions ψ₁(x, y) and ψ₂(x, y), normalised by the condition ∫_S|ψ_i|²dxdy = 1 (i = 1, 2), and the integration is performed over the cross section S of the amplifier. Taking the coefficients in the form , where P_{1, 2} are the powers of the first and second modes, we can obtain the following equations for mode powers and the phase difference of mode fields, ϕ = ϕ₂ – ϕ₁:

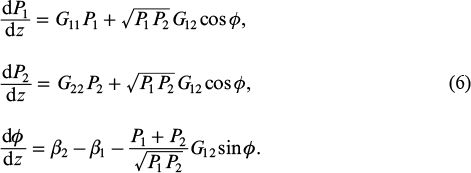
Here, the G_ij matrix elements are the overlap integrals of the mode fields and the GC distribution g(x, y, z):

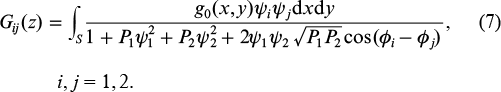
The mechanism of competition between longitudinal or transverse modes in a medium with a uniform small-signal GC has been known since studies by Kuznetsova and Rautian [166] and Anan'ev [167], respectively. In such cases, interference between counterpropagating waves leads to gain spatial hole burning and is the key cause of multimode lasing.

Spatial nonuniformity of the GC is represented by additional terms in the system of equations (6), which explicitly relate supermode fields. GC nonuniformity can result from small-signal GC nonuniformity (due to nonuniformity of pumping or doping with active additives) or saturation field nonuniformity. If a small signal coinciding with an optical mode is fed to the input of an amplifier, its propagation will be accompanied by the excitation of another mode as well. The mode cross-coupling effect occurs even in the linear amplification regime, which qualitatively distinguishes it from mode coupling in passive waveguide structures with a nonlinear field dependence of their RI [168].

If the polarisations of two modes having the same frequency are orthogonal to each other, the modes are incoherent with each other, or there is no spatial dependence of the GC, the G₁₂ terms in the system of equations (6) are zero. In all these cases, traditional views of mode competition associated with gain saturation remain unchanged. At the same time, even in the case of a standard multimode double-cladding fibre amplifier, the cross-amplification term G₁₂ is nonzero, because the small-signal GC is an explicit function of coordinates.

Analysis of the role of cross-amplification in a symmetric waveguide structure [165] shows that the terms in the first two equations in (6) are negative when averaged over z. Thus, a given negative contribution from cross-amplification will tell primarily on the lower power mode. As a result, its power may stop growing at all, whereas the higher power mode will continue to build up. Such behaviour of mode powers is illustrated by Fig. 8b, which shows the evolution of the powers of symmetric and antisymmetric modes along the length of an amplifier in a system of two parallel identical thin planar waveguides [164]. In contrast to calculations in the framework of standard transfer equations (cf. to Fig. 8a), Eqns (6) predict a higher gain for the mode whose power is higher at the amplifier input.

Zoom In Zoom Out Reset image size

In the seven-core fibre laser design described by Huo et al. [93], angular modes essentially do not eliminate the population inversion in the central core. In the case of gain saturation, this causes the in-phase mode, which has the smallest small-signal modal GC, to prevail. Calculations [163] show that, for the in-phase mode to prevail, it is sufficient that, in the field configuration formed in the early stage, the scatter in phase be less than 0.3 rad. The probability of such an event is not low. If it occurs, higher order angular modes with a lower initial power are less amplified, which leads to a better output beam quality [169]. The small-signal modal GC of the in-phase mode exceeds that of the other supermodes [163, 170] if the index step in the central core is reduced, which also can help to select the fundamental mode.

In experiments with a 2-m-long fibre amplifier having a 25-μm core diameter, Andermahr and Fallnich [171] studied the propagation of monochromatic light in the form of a coherent mixture of two spatial modes with different, but not orthogonal, polarisations. At a pump power of ∼12.3 W, the fundamental mode prevailed in one plane of polarisation at the amplifier output and the first order mode prevailed in the orthogonal plane. The ideas developed previously [164, 165] allow these results to be understood. Since there is no cross-amplification in the case of fields differing in polarisation, their evolution follows a usual path, with a proportional energy gain for each polarisation. For each polarisation, however, the contribution of the mode with the lower initial power decreases, so that the modes have orthogonal polarisations at the amplifier output [172].

Mode competition was analysed above for a monochromatic field. Four-wave mixing (FWM) can produce fields at frequencies differing from the carrier frequency of the field. FWM efficiency is limited by the necessity that two conditions be fulfilled for both the frequency difference and propagation constant (frequency and phase matching). Because of this, interaction between waves typically has the form of energy transfer between them. As predicted by Fève [173], the presence of gain in single-mode fibre causes irreversible energy transfer from the stronger wave to the weaker one, even if the phase matching condition is not fulfilled. This effect limits the power of the starting wave, which is accompanied by broadening of the output emission spectrum, as was observed in an experimental study [174]. The coupling between two distinct optical modes in a waveguide through FWM can be described in terms of spatial gain/refraction gratings [175]. Scattering by such gratings leads to power redistribution to higher order modes, degrading the output beam quality [176].

The field at the output aperture of an array in externally coupled systems can be represented as

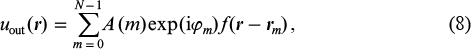
where A(m) and φ_m are the amplitude and phase of the field emitted by the mth laser and the function f (r) describes the spatial mode field distribution of a single-mode laser centred at a point with transverse coordinate r_m. In the case of a steady-state operation of an array of nonidentical lasers, these have the same emission wavelength, but the field amplitudes and phases can vary. The modes of the common cavity of the array can be determined from the condition of field reproduction after a round trip through the cavity (with allowance for amplification). The condition of the reproduction of the system of fields can be reduced to solving a system of equations characterised by a coupling matrix [9]. For a complex field envelope C(R) [i.e. C(r_m) = A(m) exp(iφ_m) at R = r_m] and a beam profile f (r – r_m), which is zero beyond the mth single-mode waveguide, the equation representing the condition of field reproduction after a round trip through the entire system has the form

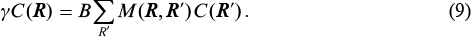
Here, the constant B takes into account the total cavity round trip phase change and the gain in the active waveguides; γ is the eigenvalue; and M(R,R') is the coupling matrix. For an infinite array of identical elements, we have |γ| = 1.

Theory of Talbot coupling between waveguide lasers in an external cavity of length L in the quasi-optical approximation was developed by Golubentsev et al. [113]. In this theory, the coupling matrix is given by

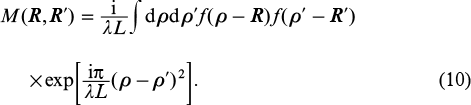
As shown in the limit of a large number of lasers [113], the diffraction loss of the self-reproducing mode in a 1D structure of N lasers with a period Λ is 1 – |γ|² ≈ π[Λ/(Na)]², where a is the radius of the emitting aperture of one laser. The loss in an array of lasers whose output end faces fill a circular aperture has the form 1 – |γ|² ≈ π^–1[μ₀Λ/(Na)]², where μ₀ ≈ 2.404 is the first zero of the zeroth-order Bessel function. The zeroth-order diffraction loss in the array is the same for all modes exactly reproducible in an infinite system (Fig. 4). Even though the in-phase mode in systems of finite size has the lowest loss [177], the difference in loss between the in-phase and other self-reproducing modes is very small, so additional measures should be taken to suppress all modes except the in-phase one.

Golubentsev et al. [113] presented explicit estimates of the loss due to a small tilt (θ) of a plane mirror, δγ ≈ (θaN²/λ)², and a shift (δL) of the mirror from the position exactly corresponding to the Talbot distance, |δγ| ≈ {(Λ/a)² [δL/(2πL_T)]}². The a/Λ ratio characterises the density of filling of a linear aperture with emitters. For a 2D laser array, this density is proportional to (a/Λ)².

In the limit of global coupling in a laser array, where each laser is coupled to the others in the same way [38], all the coupling matrix elements are identical, so that the rank of the matrix is unity. In the case of a positive real-valued coupling coefficient, the in-phase mode is selected. As shown in a review by Likhanskii and Napartovich [9], if the scatter in eigenfrequencies of individual cavities is small compared to the average mode spacing, it has a weak effect on the threshold GC of the other supermodes. One way of ensuring global coupling (see Section 2.6) is through a system of 2 × 2 couplers. In the limit of a wavelength common to the entire array, it ensures complete phase locking.

In a scheme with an external Talbot filter, the diffraction loss has a significant effect on the possibility of scaling the system. Wrage et al. [136] proposed a Talbot filter in the form of an RW for a multicore fibre laser with cores arranged along a ring. In the case of a proper adjustment of parameters, the structure of the cores, periodic in the direction of traversal of the RW, ensures zero diffraction loss, as distinct from 1D arrays, which have a finite number of cores. Global coupling between elements is assumed to be possible if the diffractive exchange radius for beam propagation is of the order of the length of the ring. For an RW of length L_T/4, this gives the inequality

In the general case, the field at the output of an N-core laser can be represented in the form (8), and the field returned to the system of cores after two passes through the RW can be represented in the form

If condition (11) is fulfilled, the following formula for the C_m coefficients can be derived [178];

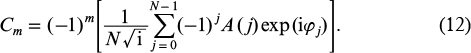
The distribution of the field returned to the multicore structure (MCS) after two passes through the RW turns out to be out of phase with the amplitudes, equal in magnitude, in all the cores. The field injected into the jth core contains a contribution from the output fields in all the cores with identical amplitudes, i.e. the coupling between the cores has a global character. If there is no gain, the eigenvalue of the out-of-phase supermode in the case of nonidentical cores is

where φ_j is the additional phase after two passes through the jth core.

Note that, in their experiments, Wrage et al. [136] observed partial broadening of the regular structure in the output beam distribution. As shown earlier [179], the 2a/Λ ratio is three times that required by condition (11), so that, if there is a large scatter in the optical length of the cores, two more modes of the MCS have losses comparable to those of the out-of-phase mode.

Another example of optical coupling approaching global coupling in properties is coupling through a cylindrical mirror located the focal length from emitting apertures (the Fourier coupling considered in Section 2.4). In experiments described by Corcoran and Rediker [63] and Corcoran and Durville [64], phase locking with the use of Fourier coupling showed high efficiency and stability to scatter in parameters of individual lasers. The principle of this method [180] is that Fourier transformation converts the field envelope profile of a periodic emitter array into the profile of the field injected into one laser and the field profile of an individual emitter into the total field envelope profile. Global coupling takes place if the quasi-optical approximation is applicable, which limits the size of laser arrays [181].

If the field emitted by a 1D array of 2N + 1 lasers is represented in the form (8), after light with a resonance wavelength λ₀ = Λ²/F travels to a mirror with a focal length F and back the distribution can be represented in the form [182]

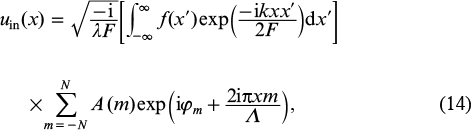
where k = 2π/λ₀ is the wavenumber.

If the field at the output of one element is thought to be a Gaussian beam with a profile f (x) = exp(–x²/a²) and the field envelope is taken in the form of a Gaussian distribution A(m) = exp( – m²Λ²/D²) of width D, then, provided the width of the envelope of the field being returned, determined by the Fourier transform of a mode of one element, is matched to the size of the frequency, Λ² = πDa, we can obtain [182] an expression for the eigenvalue of the round trip operator:

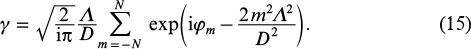
Thus, even though coupling through a Fourier filter at a large size (and small fill factor) of an array can be thought of as global, the extreme elements of the array make a small contribution to its output power and have a weak effect on phase locking efficiency. Moreover, even if all elements are identical, the diffraction loss in the Fourier filter is nonzero.

The feasibility of steady-state phase locking in a laser array depends on many parameters. The key obstacle to the phase locking of a laser array is the distinction between the eigenfrequencies of individual cavities or, in a more general case, the distinction between the optical lengths of gain elements. In the limit of global coupling between all elements, the phase locking mechanism is based on laser wavelength tuning to a value at which the difference between the gain and loss, both being strong functions of wavelength, is maximal for a considerable fraction of elements [51, 179, 182]. Figure 9 shows a typical dependence of the calculated total field power P = ∫ |u_out(x)|²dx on wavelength detuning δλ for a laser array. Note that there are peaks roughly equal in power at markedly different wavelengths.

Zoom In Zoom Out Reset image size

As mentioned in Section 5.2, in the case of a multicore fibre laser with its cores arranged along a ring, global coupling with no diffraction losses can be ensured with the use of a filter in the form of an RW. The eigenvalue for such a structure is described by (13), where the phase shifts φ_j are random quantities dependent on the length of the elements and the emission wavelength detuning δλ from a reference value. At a constant detuning δλ and parameters typical of fibre lasers, the scatter in φ_j far exceeds 2π. The main cause of the scatter in optical lengths in experiments with multicore fibre lasers [136, 137, 141] was the scatter in core radius, which can be quantified by the standard deviation Δr. At a given MCS, a supermode is generated at the wavelength corresponding to the largest difference between the gain and loss.

Averaging over random MCS's, we can obtain an asymptotic dependence for ⟨| γ|²⟩ – the maximum absolute square of the eigenvalue in the gain band (λ₀ – δλ_max, λ₀ + δλ_max):

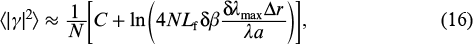
where δβ is the average modal correction to the propagation constant and C ≈ 0.577 is Euler's constant [see derivation of (16) based on extreme value statistics in Ref. [51]].

Direct numerical calculations [178, 179] confirm (Fig. 10) that ⟨| γ|²⟩ can be described by the logarithmic relation (16). In the case of identical cores, ⟨| γ|²⟩ would be independent of the number of elements. Thus, as the number of cores increases, the phase locking efficiency in a laser array with coupling through a circular Talbot filter decreases as ( lnN)/N.

Zoom In Zoom Out Reset image size

Numerical calculations [182] for a multicore fibre laser with an external Fourier cavity demonstrate that the dependence of the maximum ⟨| γ|²⟩ value in the gain band on the scatter in phase shifts in channels is in qualitative agreement with relation (16). For a seven-element array of ytterbium-doped fibre lasers with parameters corresponding to experimental data [64], numerical simulation predicts an almost perfect phase locking, whereas in the case of 15 lasers efficiency is a factor of 2 lower. Thus, even though a Fourier filter offers high selectivity (as pointed out in theoretical analysis by Apollonov et al. [183]), it ensures efficient coupling only in the case of a small laser array with a low fill factor.

6.1.1. Phase locking of a system of amplifiers in a common cavity

Fridman et al. [30] analysed 370 000 measurements of the output intensity distribution for an array of 25 (5 × 5) fibre lasers coupled through a system of mirrors in the focal plane [57]. Analysis of an array of output distributions at efficiency maxima in this system indicates that the probability that phase locking efficiency is greater than or equal to X is adequately described by the Bramwell – Holdsworth – Pinton distribution [184]:

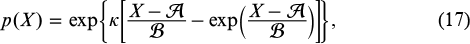
where and are the mean and width of the distribution and the parameter κ determines the degree of correlation between the measurements. The best fit was obtained at κ ≈ 1.03. Under the assumption that the distributions at neighbouring spikes are uncorrelated (κ = 1), distribution (17) reduces to a generalised Fisher – Tippett distribution, which, according to Gnedenko's theorem [185], is an asymptotic probability distribution density for a maximum in a sample of random variables. The probability density for the output power of phase-locked light is well fitted by the Vivo – Majumdar – Bohigas distribution [186] at low efficiencies and by the Majumdar – Vergassola distribution [187] at high efficiencies. These distributions correspond to the distributions of the largest and smallest eigenvalues of random positive matrices.

If a small number of longitudinal modes fall in a gain band, the probability that there is a wavelength common to the array at which a high degree of phase locking can be reached is extremely low. Fibre lasers having a dense spectrum of longitudinal modes are viable candidates for the fabrication of large arrays of phase-locked lasers. It is worth noting that there is practical interest in the ability to simultaneously phase-lock lasers in a few common longitudinal modes, as was observed in experiments [188] concerned with the phase locking of the outputs of four fibre amplifiers in a common cavity with a total round-trip path length of ∼820 m. The lasers were coupled using a system of 2 × 2 couplers. Two combinations of the differences between the amplifier lengths (measured from the length of the shortest amplifier) were considered: (1) 1.4 cm, 1 m, 5.1 m; (2) 5.1 cm, 1 m, 5.1 m. Measurements of optical and total power oscillation spectra showed that the total spectrum contained structures differing in frequency scale. The largest frequency scale was attributable to the small difference between the amplifier lengths in the two combinations: (1) 17 and (2) 4.8 GHz. In the case of combination 2, the structure was observed to have characteristic spacings between peaks, 200 and 40 MHz, corresponding to length differences of 1 and 5.1 m. Higher resolution measurements showed that each peak was split into a sequence of spikes spaced 240 kHz apart, which corresponded to longitudinal modes of the common cavity. The spikes in turn had a fine structure, which was attributed by Simpson et al. [188] to field polarisation dispersion. Since the generation of a large number of supermodes is accompanied by a considerable broadening of the emission spectrum, the threshold for SBS in the cores decreases markedly, which allows one to envisage a further rise in the power of combined lasers.

To estimate the limiting size of an array in which a high degree of phase locking is highly probable, Kouznetsov et al. [189] proposed a simplified probabilistic approach. Efficiency on the addition of a laser to an existing array was quantified by cos φ, where φ is the round-trip phase change in the added laser for a field with the supermode wavelength. In the case of an equiprobable distribution, the probability that cosφ exceeds a particular value, Y, is . For N lasers with an average length , the probability that a given wavelength lies in the gain band 2π/Δk for at least one supermode can be estimated as , which is valid if this quantity is less than unity. In such a case, the number of lasers that can be phase-locked with a given efficiency is described by the relation

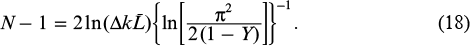
It can be obtained from (18) that, at a gain bandwidth of ∼10⁴ cm^–1, up to eight or nine 10-m-long lasers can be phase-locked with a 90 % efficiency.

6.1.2. Effect of feedback in a gain element on phase locking stability

If there is feedback in each gain element, the laser system is a coupled cavity array. We are interested primarily in stable control over laser operation by an external signal at a small-signal GC above threshold. The laser remains in an external signal-controlled operation mode at any external signal frequency detuning from the frequency of its longitudinal mode if the injection power exceeds the critical one [190]:

where G_th and G₀ are the integrated threshold GC and integrated small-signal GC, respectively, and r_m is the reflection coefficient of the output mirror. If the optical power returned to each laser is below the critical one, only some of the lasers in the system will be injection-locked, even at the maximum phase locking efficiency. Under the assumption that all the lasers in an array have identical GCs and injected powers, the injection locking condition can be represented in the form [191]

where is the integrated threshold GC for an array of identical lasers; χ is the fraction of the optical power being returned; and η_ext is the 'true' phase locking efficiency, i.e. the ratio of the output power of the laser array to the input power in the case of identical lasers.

Figure 11 (solid lines) presents numerical simulation results for a fibre laser array with an injection power P_inj half the critical one [192]. The number of injection-locked lasers at each random fibre length in the array was determined at the wavelength corresponding to the maximum in η_ext in the gain band. Next, it was averaged over 200 arrays with a given standard deviation σ(l_m). It is seen that, if there is no index nonlinearity, only a small fraction of lasers in a large array are locked by an external signal, even at a phase detuning half the critical one.

Zoom In Zoom Out Reset image size

The nature of this effect can be understood in terms of a model valid in the limit of a large array [193], in which phase changes in cavities are assumed to be uniformly distributed over the range (φ_c – δφ, φ_c + δφ). It is seen in Fig. 12 that, at a locking efficiency η ≈ 80 %, all the lasers are locked by an external signal. With decreasing phase locking efficiency, the number of states of the array with a given locking efficiency beyond the locking zone increases. This leads to a decrease in the probability that, at a given efficiency, a contribution to the total field will be made by the lasers with a phase change detuning from resonance below the critical one. In other words [194], the density of states of the system in a locked state decreases.

Zoom In Zoom Out Reset image size

A simplified model for emission phase distributions of individual elements allows one to estimate achievable efficiency for an amplifier array in a common cavity as well [191]. In particular, for the conditions used by Chang et al. [195] in an experiment with 16 fibre amplifiers in a ring configuration, we obtain η = 53 %, in agreement with the observed value.

6.1.3. Effect of nonlinearity on phase locking stability

The effect of nonlinear variations of the gain and refractive index of media with light intensity on phase locking of gain elements has been the subject of extensive studies. For a model of a laser array with coupling between nearest neighbours, Golubentsev et al. [196] showed that, for stable phase locking in the case of Kerr nonlinear with a coefficient n_K, the strength of optical coupling between the lasers, μ, should meet the conditions Re μ > 0 and n_KIm μ < 0, i.e. an imaginary term in the coupling strength is needed. Longhi and Feng [197] predicted stable in-phase mode lasing in circular arrays with coupling between nearest neighbours at Im μ = 0. To this end, the coupling coefficients for clockwise and counterclockwise light propagation in the array should differ and meet a certain relation. We have found no data on experimental implementation of such a type of coupling.

A multichannel ring cavity similar to that schematised in Fig. 2 was considered by Bochove and Shakir [198], who showed that, in this configuration, supermode selection was possible and obtained a logarithmic fit analogous to (16) for the eigenvalue of the supermode. The system was numerically simulated by Bochove et al. [199] at N = 3 with allowance for saturable gain in each fibre and the Kerr and resonant nonlinear contributions to the RI. At high pump powers (∼1 kW per channel), they found self-oscillation instability of in-phase mode lasing, which was interpreted in terms of a nonlinear contribution to the phase change in an individual cavity [199].

Between 2008 and 2018, Leger presented a series of reports concerned with a double-core fibre having a large separation between its active cores, coupled through an external interferometer. Such a configuration makes it possible to eliminate the effect of the ambient medium on phase locking accuracy. Chiang et al. [200] demonstrated that the RI of a fibre core had a contribution proportional to its GC with a Henry factor α = 7.4. This effect can compensate for the phase difference between the fields at the channel outputs, but only if the fields differ significantly in intensity [201]. It was also shown that, in an interference scheme, even slight reflection in the loss channel mitigated the requirements for phase locking accuracy on account of a reduction in intermodal discrimination value [202].

Peleš et al. [203] and Wiesenfeld et al. [204] numerically investigated in-phase mode lasing stability in a system of fibre amplifiers located in a common cavity with global coupling. Population inversion was found using rate equations for three- and four-level media [205], and the mean field in each amplifier was determined using the Rigrod formula. The coupling matrix (9) had a nondegenerate eigenvalue (M_e) and an (N – 1)-fold degenerate eigenvalue (m_e). In this model, Peleš et al. [203] derived a system of algebraic equations relating field amplitudes and GCs in fibres after a round trip through a common cavity. As a result, the in-phase supermode turned out to be stable in a few narrow regions in the (W_p τ, ζ) plane, where W_p is the pump rate; τ is the upper level lifetime; and is the coupling parameter. The addition [204] of a shift proportional to the integrated GC to the phase change over fibre improved single-mode lasing stability, but the stability and instability regions persisted.

The effect of index nonlinearity on the phase locking of a laser array locked by an external signal was analysed by Corcoran et al. [206] in the mean field approximation. Generally speaking, there are several solutions for the field in a cavity with a nonlinear medium at a given external signal intensity [207]. Corcoran et al. [206] chose the solution nearest to the eigenmode field. It was shown that the addition to the RI proportional to the gain considerably improved locking efficiency.

Napartovich et al. [192] numerically investigated a laser array with global coupling without resorting to the mean field approximation. The addition of an index component proportional to the gain was shown to slightly improve array phase locking efficiency at any nonlinearity value (Fig. 11a), with a drastic increase in the number of phase-locked lasers. It is seen in Fig. 11b that, even at a large number of lasers in an array, the number of phase-locked lasers continues to rise. As follows from Fig. 13, the likely cause of this effect is the strong dependence of the fraction of phase-locked lasers on efficiency. Figure 13 presents calculation results obtained in a simplified model with a uniform phase scatter distribution in a preset range [29].

Zoom In Zoom Out Reset image size

Modelling in a self-consistent model [191] shows that, at an optimal fraction of the optical power being returned and a nonlinear contribution to the RI, stable phase locking of 20 – 25 lasers can be expected, with phase locking efficiency η_ext of ∼70 %. In Fourier-coupled arrays where the supermode frequency is determined by several lasers located in the centre of the array, Corcoran and Durville [208] were able to achieve in-phase supermode lasing in an array of 35 semiconductor lasers, with an interference pattern contrast of 0.57.

Since the scatter in the optical length of amplifiers has a random character, the degree of phase locking should undergo large fluctuations in response to changes in parameters of the structure that determine optical lengths. Because of this, an undesirable feature of the operation of an optically coupled laser array is a tendency toward spike lasing due to fluctuation-induced random transitions to a different wavelength characterised by a similar difference between the gain and loss [75].

One possible alternative operation mode of practical interest is a transition to regular pulsations of the total output power. The development of periodic pulsations at a varied coupling strength was observed in an experiment with two coupled CO₂ lasers [39]. As the frequency of field exchange between their cavities approached the relaxation oscillation frequency, regular oscillations gave way to chaotic ones through an oscillation period doubling sequence. In the chaotic pulsation regime, the laser fields retained a high degree of coherence. In the case of two coupled fibre lasers, repetitive pulse generation was observed in a numerical experiment [209] in a wide range of laser coupling coefficients at a constant detuning of the cavity frequencies (200 kHz) and a population inversion relaxation time τ_f = 160 μs. In addition, there was a high far-field interference pattern contrast owing to the coincidence of the field phases of pulses generated at a frequency of ∼1/τ_f.

The dynamics of the operation of two coupled fibre lasers was addressed in a study reported by Zhou et al. [210], where repetitive pulse generation was due to the phase modulation of one of the lasers at a resonance frequency (23 kHz in the system in question). The resonance frequency is given by

where δ is the cavity round trip loss; τ_c is the cavity round trip time; P_p is the pump power; and is the threshold pump power. At other modulation frequencies, pulse generation was chaotic.

Dynamic operation modes in laser arrays are typically more complex (see e.g. Ref. [82]). Numerical simulation of the dynamics of the operation of 100- [211] and 1000-element [212] laser arrays with global coupling showed that an increase in the scatter in optical lengths led to spike lasing. At power maxima, the axial brightness was ∼30 % of the ideal value. This effect emerges if the finite relaxation time of laser level populations is taken into account. For phase locking, it was sufficient that the eigenfrequencies of individual lasers fall in a finite spectral range related to emission frequency uncertainty.

Simultaneous generation of a few longitudinal modes in a ring cavity with two or four fibre amplifiers coupled by 2 × 2 couplers was numerically simulated by Wu et al. [213]. The population inversion and mean field in each amplifier were described by rate equations that took into account the Kerr nonlinearity of the RI and group velocity dispersion. The output power rapidly oscillated, and the spectrum contained several narrow lines within a band ∼10 GHz in width. The simulation results agree well with experimental data [195]. Note that, for a large number of lasers (10 to 16), the obtained efficiencies exceeded those calculated in a model proposed by Kouznetsov et al. [189].

Sivaramakrishnan et al. [214] numerically investigated the stability of one supermode in a fibre amplifier array located in a common cavity. According to their results, if there is no common longitudinal mode in the gain band of a medium, the power spectrum contains several narrow lines and the order parameter oscillates at a frequency of ∼1.8 GHz. If there is only one common mode, as a result of phase perturbation in one of its channels the laser returns to single-mode operation in a few round trips, which is consistent with experimental data reported by Guillot et al. [215]. Kerr nonlinearity leads to line broadening and FWM between modes, increasing the possible number of modes being generated. On the other hand, nonlinearity causes energy leakage to higher loss modes, reducing the power of the fundamental mode.

Nair et al. [216] numerically investigated an array of semiconductor lasers with optical coupling intermediate between global and nearest neighbour coupling. Their results demonstrate that, in the case of identical lasers, taking into account the relaxation of the medium and the time delay in the coupling system leads to synchronous chaotic operation of the entire array, similar to the operation of a single laser in the Lang – Kobayashi model. If the scatter in laser parameters is taken into account [217], the laser array remains phase-locked.

Passive phase locking of pulsed lasers has been studied experimentally by many groups, but for a relatively small number of elements. In an experimental study of three fibre amplifiers in a circular configuration, with light outcoupling through a diffraction grating, Yang et al. [218] observed an interference pattern with a coherence of 0.82 at a pulse repetition rate of 2.2 MHz, peak power of 1.02 kW and pulse duration of 9.6 ns. In a study reported by Rosenstein et al. [219], two photonic crystal fibre amplifiers with a fundamental-mode diameter of 55 μm were interference-coupled with an efficiency η = 92 % in a pulse generation mode with a peak power of 0.7 MW. The 10-ns pulse duration and 1-kHz repetition rate were ensured by an acoustic Q-switch. In an experimental study of three Nd : YAG lasers coupled by nonlinear gratings in gain elements [71], one laser could operate in the Q-switching regime. This also led to an increase in interference pattern contrast.