Bifurcations, chaos and adaptive backstepping sliding mode control of a power system with excitation limitation

Chaotic oscillations in power systems may cause a lot of complex nonlinear dynamic behaviors, which may present some potential threats to the safe operation of the power grid. In 1988, Salam¹ calculated the homoclinic orbit in a two-machine system which illustrates the existence of chaotic motions in power systems. Since then, many researchers began to focus on the study of chaos in power systems. In 1993, the existence of chaos for a simple power system was first confirmed through the calculation of Lyapunov exponents and broad-band spectrum.² The nonlinear phenomena³ were observed in a single-machine-infinite-bus power system with the excitation hard-limits, and the global bifurcations including period-doubling cascades which leaded to chaotic behavior were observed. Yu et. Al.⁴ focused on three routes to chaos including the period-doubling bifurcation, torus bifurcation directly initiated by a disturbance of energy, and also revealed that chaos can lead power system to voltage collapse and angle divergence. Subramanian⁵ developed the bifurcation diagrams of steady state solutions in a power system from which the existence of various bifurcation points such as Hopf bifurcation, fold bifurcation, saddle-node bifurcation and period-doubling bifurcation were obtained, and voltage collapse and chaotic motions due to period doublings were also unearthed. Qin⁶ studied the effect of the dynamical behaviors in a simple power system with random parameter. Furthermore, with the expansion of the social power demand, the scale of power systems become gradually increasing. The important features of modern power systems are high-voltage and long-distance transmission, for which the systems often operate near their stability limits. The research on chaotic motion and stability of the power systems become extremely urgent.

According to the above researches, chaotic motions are easily observed in the power systems with the change of system parameters and random disturbances. For the general systems, the chaotic trajectory of system will have a great difference with the different initial value but their final steady state is still same. However, for the complicated power systems, the trajectories and final stable state will be influenced with the tiny changes of the initial value, which implies the power systems have the ability to exhibit a number of coexisting motions for a given system parameters. This phenomenon, called multistability, has been observed in many fields of science.^7–9 Venkatasubramanian and Ji¹⁰ reported four attractors coexisted phenomena in a power system, but no detail report on bifurcation and Lyapunov with changing parameters of system was given. Ma and Min¹¹ also investigated the coexistence of periodic orbits and chaos in a delayed power system. The existing phenomenon increases the complexity of the system and brings huge threaten to the stability of the power grid. With the break of chaotic oscillations or the coexistence of different motions, the angle divergence and voltage collapse in power system will be taken place.

Therefore, it is necessary to design controllers to prevent the instability of power system. So far a lot of control methods have been studied to suppress chaotic oscillation in power system. Wei¹² designed an adaptive controller based on the LaSalle invariance principle to suppress different undesirable bifurcations which threatened the secure and stable work of power system. Li¹³ proposed a robust adaptive fuzzy controller for a single machine bus system through static var compensator. Furtat¹⁴ investigated the robust control of multi-machine power systems with parameters uncertainties. Min¹⁵ designed a controller through the relay characteristic function to suppress chaotic motions in interconnected power system. Ni¹⁶ proposed the variable speed synergetic controller to eliminate chaotic oscillation in power system.

In this paper, the nonlinear dynamics of a single-machine-infinite bus system is studied through the bifurcation diagrams and Lyapunov exponent. The coexistence of different motions as well as the instability in power system is observed due to angle divergence. Moreover, to eliminate chaotic motions in nonlinear power system, an adaptive backstepping sliding mode controller is proposed, which can guarantee that the angle and frequency of power system keeps operating on the stable orbit. Compared to other controllers, the adaptive backstepping sliding mode controller has the advantage of adaptive backstepping control and sliding mode control which possesses more robustness to uncertainties for the tracking targets.

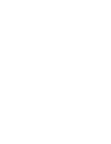
A single-machine-infinite bus system with the excitation limitation³ is presented in Fig. 1, which consists of generators, transformer, load, circuit breaker, systematic tie line and the simplified excitation model.

The single-machine-infinite bus system can be described as

where E_fdr is the input signal of wind-up limiter and the output of the wind-up limiter E_fd is shown as

and the bus voltage at the generator bus terminal is defined as

where δ is the generator angle, ω is the machine frequency, E′ is the generator voltage behind the transient reactance, H is the moment of inertia in second, D is the generator damping factor, P_m is the mechanical power, V₀ is the infinite bus voltage, x denotes the transmission line reactance, x_d denotes the synchronization reactance, $x d ′$ represents the transient reactance, $T d 0 ′$ is the open-loop time constant of the armature winding, V_ref is the reference bus voltage, T_A is the time-constant, K_A is exciter gain and E_fd0 is the reference voltage. The power system¹⁰ can exhibit periodic orbits, stable chaos and the instable divergence motions with varying the system parameters P_m, D and K_A.

In this section, through the typical bifurcation diagrams and Lyapunov exponents, the nonlinear dynamics in power system is analyzed to illustrate the effects of mechanical power P_m, generator damping factor D and exciter gain K_A. The coexistence of attractors in nonlinear systems often appear with the same parameter values with different initial conditions, which presents interesting characterics of multistable system. The route to chaos in power system in Eq. (1) is due to the period-doubling bifurcation (i.e., PDB), and the coexisting motions of different periodic-orbits are also observed. The instability of power system is caused by the angle divergence when stable chaotic oscillation is destroyed. The initial conditions, i.e, IC1 = (0.98571, -0.0004, 1.4046, 2.3282), and IC2 = (1.4378, 0.0032, 1.3389, 10.9338) in the simulations are given, respectively. The system parameters is fixed by

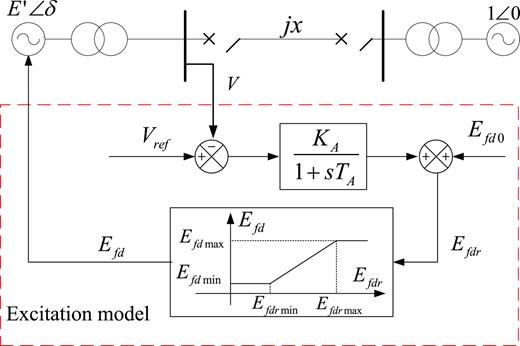
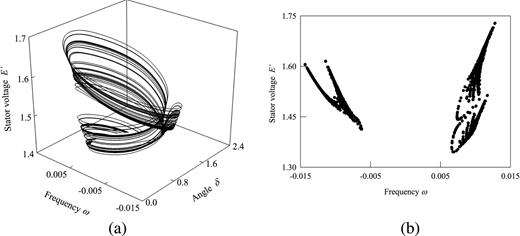
The mechanical power P_m has a great influence on stable operation in power system with excitation limitation, which determines the speed of the generator. To better understand the dynamics of power system in Eq. (1), the bifurcation diagrams and Lyapunov exponents with the parameter P_m ∈ [1.036, 1.304] are shown in Fig. 2(a) and 2(b) respectively with D = 1.4 and K_A = 150. The chaotic and periodic motions of power system can be easily observed. From Fig. 2(b), the largest exponent with increasing parameter P_m is negative for P_m ∈ [1.036, 1.2982] in which different periodic motions are presented in Fig. 2(a), while the largest exponent for P_m ∈ [1.2982, 1.301] is larger than zero, which means that chaotic motions exist. The coexisting domain of period-1 and perod-2 lies in P_m ∈ [1.0401, 1.1025] with the hatched areas for the different initial conditions, while the same motions with IC1 and IC2 are observed for the other ranges. Black dots mean the trajectories with the initial condition IC1, and red dots denote the trajectories with the initial condition IC2. The phase portraits of the coexistence at P_m = 1.05 are shown in Fig. 3(a) and 3(b). From Fig. 2(a), a switch ‘jump’ motion from period-1 to period-2 can be observed in P_m ∈ [1.1025, 1.1029] because of the non-smooth wind-up limiter. From a small periodic window in Fig. 2(a), a PDB period-doubling bifurcation is observed at P_m = 1.29403, and then periodic-4 motions appear until another PDB occurs at P_m = 1.29773. Next, the single-machine-infinite bus system begins to enter into chaotic motions at P_m = 1.2982 after a series of PDB, and four Lyapunov exponents with P_m = 1.2982 are (0.1358, 0.0, -0.1028, -1.346) in Fig, 2(b). The chaotic trajectories of power system in Eq. (1) are depicted in Fig. 4(a) with parameters P_m = 1.3, D = 1.4 and K_A = 150, and the corresponding Poincaré maps are presented in Fig. 4(b) which consist of many irregular points. Finally, with the mechanical power increasing from P_m = 1.301, the strange attractor grows larger and then disappears, which indicates the extinction of chaotic motions at a boundary crisis. In Fig. 5(a), the transient chaotic behavior for P_m = 1.305 is displayed by initially staying at t = 30.1s, and then the stable chaotic motion is broken. The machine angle δ increases monotonously along the trajectories from Fig. 5(b) so that the generator loses synchronism possibly leading to a power system break-up. The stator voltage is better behaved along the divergence while the angle quickly diverges away with any initial conditions. Thus, the collapse of power system is only caused by the machine angle instability.

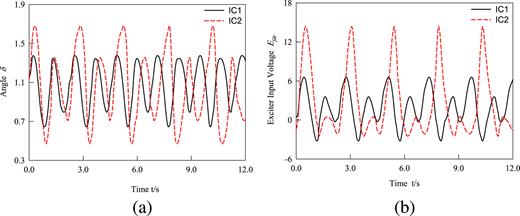
Next, it is necessary to analysis the dynamical behaviors with a damping parameter for which model the overall damping effects in the power system. The bifurcation diagrams and Lyapunov exponents are presented for D ∈ [1.36, 5.08], P = 1.3 and K_A = 150 in Fig. 6(a) and 6(b). The coexisting region in D ∈ [2.79, 3.84] is hatched with two period-2 motions for the initial conditions IC1 and IC2, while the other regions show the same behaviors. The coexistence of period-2 and period-2 with different initial conditions is plotted at D = 2.9 in Fig. 7. Time-historical machine angle δ and exciter input voltage E_fdr display two period-2 motions with varying time which agree with the bifurcation in Fig. 6(a). With the damping factor decreasing from 5.08, the different periodic motions first occur in the range D ∈ [1.433, 5.08] from Fig. 6(a), and the largest Lyapunov exponent approaches near zero or becomes negative in Fig. 6(b). Then the power system at D = 1.433 enters into the chaos through a series of PDB, and the corresponding four Lyapunov exponents with D = 1.433 are (0.1192, 0.0, -0.098, -1.334) in Fig. 3(b). Finally, the machine angle will tend to infinite with decreasing D = 1.389, which illustrates that the instability of power system with the damping factor dropping off occurs.

Furthermore, the bifurcation diagrams and Lyapunov exponents for $K A ∈ 80 , 152$ with P_m = 1.3 and D = 1.4 are represented in Fig. 8. The coexisting regions of two different period-1 are shown in K_A ∈ [84.21, 87.86], and the coexistence of period-1 and period-2 orbits is also given in K_A ∈ [87.86, 92.01] with IC1 and IC2. The same behaviors of power system with two different initial conditions occur for the remaining range of the exciter control gain K_A > 92.01. In Fig. 8, two ‘jump’ motions at K_A = 87.86 and K_A = 92.01 are observed from period-1 to period-2, which often takes place in discontinuous systems. From Fig. 7, the power system runs at stable equilibrium points for the exciter gain K_A < 84.21 and all Lyapunov exponents are less than zero. The periodic windows are observed in K_A ∈ [84.21, 141], which is in agreement with the largest Lyapunov exponent. With parameters K_A increasing from 84.21, period-2 orbits suddenly turn to period-4 orbits because PDB occurs at K_A = 123.45, and then period-8 motions appear until another PDB is found at K_A = 138.43. Next, the stable periodic behaviors disappear and chaotic motions begin to appear from K_A = 141 due to the crisis of the boundaries, and four Lyapunov exponents with K_A = 141 are (0.0134, 0.0, -0.097, -1.215) in Fig. 8(b). The gain of the excitation limitation in power system determines the stability of the generator, which often has high control values for K_A. When the gain K_A is increased from 141, the strange chaotic attractors become larger and may eventually hit the unstable limit set, resulting in the broken of chaos at K_A = 151.3. Time-plots histories of the trajectories for the power system are presented in Fig. 9 with the parameters P_m = 1.3, D = 1.4 and K_A = 170. In this case, only the machine angle monotonously increases and is quick divergent while the machine frequency ω, the generator voltage E′ and the input signal of wind-up limiter E_fdr quickly conerge to the equilibrium points which form the local stable space. Obviously, the unstable power system is caused by the divergence of machine angle without voltage collapse.

From the above discussions, the complex dynamics of the power system are investigated by changing the system parameters, and the coexisting regions, periodic motions and chaos are observed, respectively. The instability of system is caused by the divergence of machine angle because of the broken chaos. Therfore, it is necessary to design an effective controller to suppress the instability, chaos and the coexisting phenomenon in power system.

To eliminate chaotic oscillation in power system, an adaptive backstepping sliding mode controller with a simple adaptive law is proposed to keep the power system operating on a stable motion. The operational control variable in a power system can be accessible, and the control objective must be implementable easily in engineering. The machine angle δ of the generator often can be controlled at the desired value when the system is unstable, which is often the control object. The input signal of wind-up limiter E_fdr and the output of the wind-up limiter E_fd are used to change the voltage in power system, which needn’t be controlled. Thus the control objective is to propose an adaptive backstepping sliding mode control system for the output angle of power system to track the given target asymptotically. Now the designed controller u is added to the second equation of system Eq. (1), and the controlled system can be rewritten by

The adaptive backstepping sliding mode controller design procedure is shown as follows:

Step 1: Define the target as r and the output as δ, and the tracking error as

and its derivative is given by

The first Lyapunov function is described as

Let $e 2 = ω 0 ω+ c 1 e 1 − r ̇$ be the virtual control. The expression becomes $e ̇ 1 = e 2 − c 1 e 1$⁠. The time derivative of V₁ along with Eq. (7) is

The switching function of sliding mode control is defined as

and the parameters k₁, c₁ are positive. Obviously, if the switching function σ = 0, then e₁ = e₂ = 0 and $V ̇ ≤0$⁠.

Step 2: To design the controller u, the mechanical power P_m and the effect of excitation limitation in power system denote the total uncertainties. Thus the second equation of system Eq. (5) can be shown as

where F denotes the lumped uncertainty, which is assumed to be bounded, i.e., $M≥ F$⁠. The upper bound M is a positive constant which is difficult to obtain, therefore, the estimate value of lumped uncertainty is given by $F ˆ$⁠. Then the Lyapunov function is chosen

where γ is a positive constant and the error of estimation is $F ̃ = F ˆ −F$⁠.

Using equations from Eq. (7) to Eq. (12), the time derivative of V₂ is given by

According to Eq. (13), an adaptive backstepping sliding mode controller is designed as

where both h and n are positive constants. The adaptive law for $F ˆ$ is designed as

By substituting Eq. (14) and Eq. (15) into Eq. (13), then Eq. (13) becomes

where e^T = [e₁ e₂] and Q is a symmetric matrix with the form

To guarantee that Q is positive definite, the following conditions should be held by

where h, c₁, k₁ are positive constants. A sufficient condition to guarantee that Q is positive definite is as follows

According to Barbalat’s lemma, the expression $P ( t ) = e T Qe+hn σ$ will converge to zero when time t approaches to infinite. Therefore, the error e₁ and e₂ will also tend to zero as t → ∞. Finally, the stability of the adaptive backstepping sliding mode control system can be proved.

To avoid the chattering phenomena, the following relay characteristic function can be used to replace the sign function in Eq. (14) in numerical simulations

where

and r₀,s₀ are small positive constants.

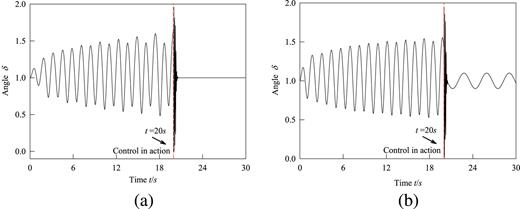
To illustrate the effects of the designed adaptive backstepping sliding controller, the following two cases are considered as the target r = 1.0 and r = 0.1sin(2t) + 1.0, respectively. In the simulation, the chaotic oscillation in power system is shown with parameters P_m = 1.3, D = 1.4 and K_A = 150. At this time, the controller u is put into effect at t =20s. Simulation results are depicted in Fig. 10, and the design parameters are given by c₁= 10, k₁ = 15 h = 25 and n = 1.5. From Fig. 10(a) and 10(b), it is observed that the chaotic motions in power system can be quickly tracked to the object for t ≥ 20s, respectively, which indicates that the proposed control method can restrain chaos and render the controlled power system asymptotically stable.

In this paper, the bifurcation diagrams and Lyapunov exponent in the power system are investigated by varying the different system parameters, in which the coexisting periodic motions and chaotic oscillation are observed. Simulation results are plotted with the phase portraits, Poincaré maps and the time-historic responses. The coexistence of period-1 with period-1 orbits, and period-2 with period-1orbits are observed with different initial conditions. The instability of power system is also observed when the machine angle becomes larger and larger for the broken of chaos. Therefore, in order to hold back the collapse of power system and guarantee the power system operates at a desire value, the adaptive backstepping slide mode controller is designed to eliminate chaotic oscillations. Finally, the effectiveness of the designed control scheme has been confirmed by the simulations.

The work is supported by the National Natural Science Foundation of China (No. 51475246) and the Natural Science Foundation of Jiangsu Province under Grant No Bk20131402.