Introduction

Graphene, two-dimensional honey-comb-like carbon lattice, is a very promising material for many optics, plasmonics and photonics applications1,2,3. In contrary to metal based plasmonics, graphene may support TE-polarized plasmon-polaritons as well, as TM-polarized ones4,5,6. TE plasmon-polaritons in suspended graphene are close to the light line and weakly localized. Such plasmon-polaritons exist when imaginary part of graphene conductivity is negative Im[σg] < 0, what corresponds to the frequency range defined by the following: 1.667 < ħω/μch < 2, where ħ is Plank constant, ω = 2πf is the angular frequency (time dependence exp-iωt]), μch is the chemical potential (or Fermi level) of graphene. Chemical potential is defined by charge-carrier concentration n: μch ≈ ħvF(πn)1/2, where vF ≈ 106 m/s is the Fermi velocity. Charge-carrier concentration may be tuned by chemical doping or electrostatic bias7,8,9. Nowadays, gate voltage allows reaching Fermi level values up to about 1 eV (or, equivalently, charge-carrier concentration ~7 · 1013 cm−2). While TM plasmons exist at ħω/μch < 1.667, which correspond to frequencies up to mid-infrared range, TE ones may be excited at higher frequencies up to visible light through telecommunication frequencies. This fact makes TE plasmons very promising for practical applications in communication technologies. Due to the small spectral range, TE-polarized plasmons have been directly observed in experiment only recently10. In bilayer graphene it is expected stronger field confinement of this mode11. In two-layer configuration at certain spacer properties both symmetric and anti-symmetric modes may exist12.

Indeed, only graphene ribbons may be used in planar geometry. Edges of the ribbons lead usually to increase of loss13. To avoid undesirable losses one may use cylindrical structures in real plasmonic devices14. TM plasmonic modes of cylindrical graphene-based waveguides were investigated in15. Graphene-based cylindrical waveguides have been analyzed in different configurations16, the single-mode realization of such waveguide was proposed17. In case of magnetically-biased graphene coating authors have paid attention to hybridization of TE and TM plasmonic modes. Nevertheless, conditions of supporting all-TE plasmonic modes by cylindrical graphene-based waveguide have never been stated yet. By the other hand, TE modes are more susceptible to radiation from the edges due to their proximity to light cone. Thus, cylindrical structures may be more suitable for practical applications of TE plasmons.

Results

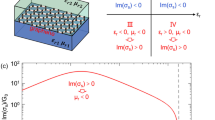
Geometry of the problem is shown in Fig. 1a. Dielectric cylinder (core of the waveguide) with dielectric permittivity (we use SI units, ε0 is electric constant) and radius R, is coated by graphene layer. Such cylinder is embedded in dielectric medium with dielectric permittivity . Both mediums are non-magnetic (μin = μout = μ0). the cylinder axis coincides with z-axis. For modeling graphene optical properties we used the standard procedure (see Methods for details). Dependencies of real and imaginary parts of graphene conductivity from its chemical potential for some frequencies are shown in Fig. 1b.

Figure 1
figure 1

Geometry of the problem (a), conductivity of graphene versus chemical potential at different frequencies (b), critical core radius versus graphene chemical potential (c) and frequency (d).

Full size image

In cylindrical geometry, only fundamental modes (i.e. ϕ-independent) may be classified into TE- and TM- polarized. Higher modes are hybrid TE-TM ones. Depending on relation between longitudinal field components Ez and Hz, one may divide modes into quasi-TE and quasi-TM polarized. Due to hybrid nature of such modes, their dispersion equations are equals.

Using appropriate boundary conditions, one may obtain dispersion equation of fundamental TE mode (see Methods for details):

In (1) In(gr) and Kn(pr) are modified Bessel functions of n-th order, , .

For further analysis let us limit ourselves by the case of real values of p and g. Both terms in right-hand side of equation (1) are positive, so, we may conclude that condition Im [σg] < 0 is necessary. But this condition is not sufficient. Let us suppose that . This condition is good satisfied near the interband transition (i.e. when 1.667 < ħω/μch < 2). Let us put iσg ≈ |Im[σg]|. Cut-off limit (i.e. p → 0) leads to critical coupling between radius of the core, frequency and dielectric permittivity:

Let us consider two limit cases. The first one, when gcrR ≪ 1, corresponds to small core radius, small difference of permittivities of the inner and the outer mediums, or low frequency. This limit leads to the following condition:

In case of small radius and low frequencies equation (3) and condition gcrR ≪ 1 can not be satisfied simultaneously. There is only one way: to reduce the difference (εout − εin). Using the limitation condition with equation (3), one may obtain the following

where we use relative permittivities and Z0 = (μ0/ε0)1/2 is the impedance of free space. Taking into account that in frequency range 100–600 THz (near infrared to visible light, wavelegth range from 500 nm to 3 μm) |Im[σg]| may reach (at ħω/μch ≈ 2) up to 10−4–10−3 S, one can estimate . So, equation (3) may be used for estimation of the minimal radius only in case of two almost identical mediums. Estimations of critical radius from equation (3) give R ∼ 1 μm. We should note that in other cases, the critical radius is greater.

In the opposite case, when gcrR ∼ 1, one may obtain:

Estimating from (5) gcrR = [(εout − εin)μ0]1/2ωR ≈ 2 · (10−2–10−1)ωR/c, one may conclude, that the case under consideration will be realized when ωR ≫ 1.5 · (109–1010) m/s. For the frequencies 100–600 THz, we will have R ≫ 1 μm. This situation is poorly suitable for practical applications and will not be considered further.

In the intermediate case, when gcrR ≈ 1, we will have . Numerical estimations shows that . We should note that such case may be realized only at fixed permittivity difference and core radius, given by . This is very difficult for practical realization.

Let us consider more detailed the case of equal core and outer mediums, which correspond to the lowest core radius. Dependencies of the critical radius, calculated from equation (3), versus the frequency of propagating waves and graphene chemical potential are shown in Fig. 1c,d.

One can see that the minimal value of critical radius corresponds to intrerband transitions of carriers in graphene ħω/μch ≈ 2. This value is comparable with the wavelength of the volume wave. Increasing of the frequency at fixed chemical potential leads to decrease of minimal value of critical radius. At fixed core radius, range of chemical potentials, when the structure supports TE plasmons, increases with increasing of frequency. Vice versa, increase of chemical potential leads to increase of the frequency range. We should to note, that at certain values of core radius the waveguide may support TE plasmons in wide frequency range. For example, at R = 1.25 μm for chemical potential 1.0 eV the frequency window is from about 425 THz to more than 600 THz, at R = 1.75 μm for chemical potential 0.8 eV–from about 330 THz, at R = 3 μm for chemical potential 0.5 eV–from about 200 THz. Thus, proposed structure may work as a high pass filter with controllable characteristics.

Main characteristics of propagating plasmon-polaritons are the effective refractive index neff = Re[h]/k0, where k0 = ω/c and propagation length LSPP = 1/(2Im[h]). Let us investigate these characteristics for guiding TE mode. For simplicity, we will put εout = εin = ε0. Core radius will be R = 1 μm. At such core radius, the structure may support TE plasmon-polaritons in frequency range from approximately 370 THz and chemical potential values from approximately 0.8 eV. Figure 2a shows dependencies of neff and LSPP from frequency and chemical potential calculated from exact dispersion equation given by (1).

Figure 2
figure 2

Characteristics of guiding TE plasmon-polaritons (a) and distance of TE plasmon mode from light line (b). Core radius R = 1 μm. Permittivities of the core and the outer mediums are equals. Filled region in (b) correspond to the values , what may be observed in some materials at near the resonance conditions or in ε-near-zero materials and metamaterials, logarithmic scale is used for both axes.

Full size image

One can see, that the maximal effective refractive index corresponds to condition ħω/μch ≈ 2. In the case under consideration localization of plasmonic mode is characterized by parameter . So, exceeding the unity by the effective refractive index describes the mode localization. TE mode of cylindrical graphene waveguide is weakly localized, similarly to the case of suspended single layer graphene4,9. The propagation length at ħω/μch ≈ 2 is close to the minimal value due to higher localization. At fixed frequency (chemical potential) propagation length increase rapidly when chemical potential (frequency) decrease (increase), while localization is almost the same. This is due to decrease of real part of graphene conductivity at ħω/μch < 2 and hence to decrease of dissipation.

Similarly to the single layer graphene and the double-layer configuration12,18, TE mode in proposed structure is very sensitive to difference between dielectric permittivities of the core and the outer medium. Calculations show that at more favorable for TE mode propagation condition of ħω/μch ≈ 2, the structure may support this mode only while for μch = 0.8 eV (f ≈ 387 THz), for μch = 0.9 eV (f ≈ 435 THz), for μch = 1.0 eV (f ≈ 484 THz) and for μch = 1.1 eV (f ≈ 532 THz). Our estimations give smaller critical values of difference between dielectric permittivities than those for double-layer configuration (for the spacer thickness 100 nm critical 12, while we have ). This is caused by the fact, that fundamental TE mode of cylindrical waveguide is better comparable with symmetric mode in planar geometry, which has not been considered in details.

The main difficulty for experimental detection and practical applications of TE plasmons in graphene is their proximity to the light line. The distance of TE modes from the light line may be described by the difference , where is the refractive index of the outer medium. As we have mentioned above, the most favorable for TE mode propagation conditions are ħω/μch = 2 and . Let us investigate how the value of permittivity will affect characteristics of TE modes. Dependence of the plasmon distance from the light line from the permittivity for different values of chemical potential and frequency, corresponding to the condition of interband transitions, is shown in Fig. 2b. Core radius is equal to 1 μm. Filled region correspond to the values . Such situation may be observed in some materials at near the resonance conditions or in ε-near-zero materials and metamaterials19,20. One can see, that at values of permittivity plasmon distance from the light line decrease almost exponentially with increasing of permittivity (logarithmic scale is used for both axes in Fig. 2b). At the difference increase slowly with decrease of permittivity. Comparing the values of for usual materials (εr > 1) with the ones for materials at near resonance conditions and ε-near-zero materials, one may conclude that in the last case the difference may be in order of magnitude greater. So, for experimental observation of TE modes may be more favorable to use ε-near-zero metamaterials.

Discussion

Let us discuss now the possible ways to reduce the critical radius. From equation (3) one can see that there is only one way–to increase the absolute value of imaginary part of the surface conductivity. This purpose may be achieved by use of few-layer graphene. Detailed investigation has shown11 that in bilayer graphene TE plasmons may departs more from light line comparing with the single graphene layer. An effective optical conductivity of randomly oriented few-layer graphene is proportional to the number of layers N21,22,23,24. Thus, the absolute value of imaginary part of conductivity will increase and critical radius value will decrease approximately N times. For example, if one will use the 5 layer graphene, all results we have obtained for the core radius of 1 μm, may be observed at core radius of about 200 nm. Experimentally, TE-plasmons have been observed at telecommunication frequencies10 (wavelength in vacuum is 1.55 μm). With taking into account the possibility of reducing the critical core radius, proposed structure may have wide perspectives in communication technologies.

High-order modes of the waveguide under investigation are described by the same dispersion equation, which was obtained by Gao et al.15 due to hybrid TE-TM fields structure. At interband transitions condition TE component will dominate in such modes. Calculations show that such modes may be supported by the structure at much larger core radius. For example, for μch = 1.0 eV (f ≈ 484 THz) and equal core and outer mediums the structure may support the mode with azimuthal distribution ~exp[iϕ] only at core radius of about some centimeters. This is not appropriate for practical applications. By the other hand, this fact shows that the proposed structure may work in single-mode regime in wide frequency range.

In conclusions, we have investigated TE plasmonic modes supported by cylindrical graphene based structure. Such modes may propagate in the structure only at core radius larger than at least 500 nm at frequencies of near-infrared-to-visible light. The most favorable condition for TE plasmons propagation is the equality of the core and the outer mediums. TE plasmons dispersion departs from the light line more significantly for low values of permittivities . Use of few-layer graphene should lead to decrease of critical radius or operating frequency. Results have a potential interest for practical design of optical devices based on TE plasmonic modes of cylindrical graphene waveguides in wide frequency range, including telecommunication frequencies.

Methods

We used cylindrical coordinates (r, ϕ, z). For obtain dispersion equation, one should to solve Maxwell’s equations inside each medium with taking into account the boundary conditions: , , and . Considering the waves propagating along cylinder axis, one may put electric and magnetic fields E, H ~ exp[−iωt + ihz].

Graphene layer was modeled as infinitesimally thin surface with the surface conductivity σg, calculated from Kubo formula25,26,27. At finite temperature it may be divided into intra- and interband contributions σg = σintra + σinter:

In (6) T is the temperature, Γ is the charge carriers scattering rate. For numerical calculations we will use T = 300 K and Γ = 0.1 meV.

For fundamental TE mode, field components may be obtained from common field distribution:

Here, I0(gr) and K0(pr) are modified Bessel functions, prime denotes the derivative with respect to the argument, , .

Using these field expressions with boundary conditions, one may obtain a system of equations with respect to constants B0 and D0:

By equating the determinant of the matrix constructed from coefficients at unknown constants, one may obtain dispersion equation (1).

Additional Information

How to cite this article: Kuzmin, D. A. et al. Transverse-electric plasmonic modes of cylindrical graphene-based waveguide at near-infrared and visible frequencies. Sci. Rep. 6, 26915; doi: 10.1038/srep26915 (2016).