Abstract
The Kibble-Zurek mechanism (KZM) predicts the density of topological defects produced in the dynamical processes of phase transitions in systems ranging from cosmology to condensed matter and quantum materials. The similarity between KZM and the Landau-Zener transition (LZT), which is a standard tool to describe the dynamics of some non-equilibrium physics in contemporary physics, is being extensively exploited. Here we demonstrate the equivalence between KZM in the Ising model and LZT in a superconducting qubit system. We develop a time-resolved approach to study quantum dynamics of LZT with nano-second resolution. By using this technique, we simulate the key features of KZM in the Ising model with LZT, e.g., the boundary between the adiabatic and impulse regions, the freeze-out phenomenon in the impulse region, especially, the scaling law of the excited state population as the square root of the quenching speed. Our results provide the experimental evidence of the close connection between KZM and LZT, two textbook paradigms to study the dynamics of the non-equilibrium phenomena.
Similar content being viewed by others
Introduction
Non-equilibrium phenomena at avoided level crossings play an essential role in many dynamical processes throughout physics and chemistry. A transition between energy levels at the avoided crossing is known as the Landau-Zener transition (LZT)1,2, which has served over decades as a textbook paradigm of quantum dynamics. LZT has recently been extensively studied3 both theoretically and experimentally in, e.g., superconducting qubits4,5,6,7, spin-transistor8 and optical lattices9,10,11,12. On the other hand, quantum phase transition may also relate to avoided level crossings and it plays an important role in nature. Recently, an elegant theoretical framework for understanding the dynamics of phase transition is provided by the Kibble-Zurek mechanism (KZM)13,14,15,16. When the parameters of a quantum system that drive the quantum phase transition are varied in time causing the system to traverse the critical point, KZM predicts that the density of the defects produced in the process follows a power law that scales with the square root of the speed at which the critical point is traversed. Due to its ubiquitous nature, this theory finds applications in a wide variety of systems ranging from cosmology to condensed matter and quantum materials17,18,19,20.
The correspondence between LZT and KZM was first pointed out by Damski21,22. It was shown that the dynamics of LZT can be intuitively described in terms of KZM of the topological defect production in nonequilibrium quantum phase transition. A widely used picture to model the dynamical process of LZT is the adiabatic-impulse approximation (AIA), which was originally developed in KZM theory. The entire dynamical process can be divided into three regions: the adiabatic, impulse and adiabatic regions, as shown in Fig. 1a. The three regions are separated by two boundaries  and
and  , where v is the quench rate and
, where v is the quench rate and  is referred to as the freeze out time. Based on AIA, the dynamics of topological defect production in non-equilibrium phase transitions can be simulated with LZT which was experimentally demonstrated using an optical interferometer23. However, some key features of the correspondence between LZT and KZM, such as the freeze out time
is referred to as the freeze out time. Based on AIA, the dynamics of topological defect production in non-equilibrium phase transitions can be simulated with LZT which was experimentally demonstrated using an optical interferometer23. However, some key features of the correspondence between LZT and KZM, such as the freeze out time  and the adiabatic-impulse-adiabatic regions, have not been investigated experimentally. Most importantly, by studying the dynamical quantum phase transition in a quantum Ising chain, it is found that the average density of defects scales as the square root of the quenching speed24,25. This universal scaling law of defect formulation as a function of quench speed, which lies at the heart of KZM, lacks adequate experimental evidence in LZT.
and the adiabatic-impulse-adiabatic regions, have not been investigated experimentally. Most importantly, by studying the dynamical quantum phase transition in a quantum Ising chain, it is found that the average density of defects scales as the square root of the quenching speed24,25. This universal scaling law of defect formulation as a function of quench speed, which lies at the heart of KZM, lacks adequate experimental evidence in LZT.
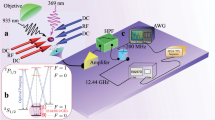
Energy level avoided crossing and experimental procedure.
(a) A typical energy structure (parameterized by time) of a two-level system. The diabatic states  ,
,  and energy eigenstates
and energy eigenstates  are denoted in the plot. (b) A schematic of time profile of the experiment consisting of three parts. During state preparation, a −π/2y (π) pulse is applied to prepare the qubit in
are denoted in the plot. (b) A schematic of time profile of the experiment consisting of three parts. During state preparation, a −π/2y (π) pulse is applied to prepare the qubit in 
 . The Landau-Zener transition is realized by chirping the microwave frequency from ωi to ωf. The final state of the qubit is obtained by state tomography.
. The Landau-Zener transition is realized by chirping the microwave frequency from ωi to ωf. The final state of the qubit is obtained by state tomography.
In this paper, we use LZT in superconducting qubits to simulate KZM of the Ising model. We develop a time-resolved method to directly investigate the quantum dynamics of LZT in the superconducting qubit. Using state tomography, we measure the time evolution of the population P+ of the instantaneous positive energy eigenstate [see Fig. 1a] for the entire LZT process. We find that P+ exhibits a rapid change near the center of the avoided crossing and varies gradually outside this region, revealing the existence of the adiabatic and impulse regions. Moreover, the freeze-out behavior predicted by KZM has also been observed and the boundary between the adiabatic and impulse region predicted by AIA is confirmed. We observe that the experimental simulated KZM of Ising model displays the theoretically predicted Kibble-Zurek scaling law. Therefore, our result demonstrate the close connection between KZM and LZT, in particular, the presence of Kibble-Zurek scaling behavior in LZT.
Results
The equivalence between KZM and LZT
The Ising model is regarded as one of the two prototypical models to understand quantum phase transitions26. After rescaling all the quantities to the dimensionless variables, we obtain the Ising model Hamiltonian

with the periodic boundary condition, where  are the Pauli-matrices operators. Here N is the total number of spins and g is a dimensionless constant driving the phase transition. The ground state of HI is a paramagnet for
are the Pauli-matrices operators. Here N is the total number of spins and g is a dimensionless constant driving the phase transition. The ground state of HI is a paramagnet for  and a ferromagnet for
and a ferromagnet for  and g = 1 corresponds to the critical point. To study the dynamics of this model, we assume that the system evolves from time ti = −∞ to tf = 0 and takes a linear quench
and g = 1 corresponds to the critical point. To study the dynamics of this model, we assume that the system evolves from time ti = −∞ to tf = 0 and takes a linear quench  , where
, where  provides a quench rate.
provides a quench rate.
By utilizing Jordan-Wigner transformation and Fourier transform, the Ising model can be simplified as a bunch of decoupled qubits with the Hamiltonian  , where the eigenenergy
, where the eigenenergy  and
and  is the pseudomomentum. Here and hereafter we set the lattice constant a = 1. The density of defects resulting from the quantum quench has the expression
is the pseudomomentum. Here and hereafter we set the lattice constant a = 1. The density of defects resulting from the quantum quench has the expression  , where pk is the excitation probability corresponding to the pseudomomentum k. We consider a special case where the system undergoes slow evolution with
, where pk is the excitation probability corresponding to the pseudomomentum k. We consider a special case where the system undergoes slow evolution with  . Under this condition, it is safe to assume that only long wavelength modes are excited, i.e.,
. Under this condition, it is safe to assume that only long wavelength modes are excited, i.e.,  and then
and then  , where {uk, vk} are Bogoliubov modes governed by the following matrix equation
, where {uk, vk} are Bogoliubov modes governed by the following matrix equation

Here  is the normalized time and
is the normalized time and  is the sweeping velocity.
is the sweeping velocity.
On the other hand, for a quantum two-level system with the diabatic basis, we consider the time-dependent Hamiltonian of a quantum two-level system in the diabatic basis  and
and 

where Δ is the tunneling amplitude and ϵ(t) is the energy difference between the two diabatic basis. We mainly consider ϵ(t) = vt with v being the speed of energy variation. The time-dependent instantaneous energy eigenstates  are
are

where cos θ = ϵ(t)/Ω(t) with  . The instantaneous energy eigenvalues of H(t) are
. The instantaneous energy eigenvalues of H(t) are  , forming an avoided level crossing at t = 0 with a gap Δ. If the system initially in the ground state traverses the avoided crossing, the Landau-Zener theory gives the probability of the qubit occupying the exciting state as PLZ ≈ exp(−πΔ2/2 ħv). LZT has received tremendous attention since quantum two-level systems, i.e., qubits, are currently considered as the best building blocks of quantum information processors.
, forming an avoided level crossing at t = 0 with a gap Δ. If the system initially in the ground state traverses the avoided crossing, the Landau-Zener theory gives the probability of the qubit occupying the exciting state as PLZ ≈ exp(−πΔ2/2 ħv). LZT has received tremendous attention since quantum two-level systems, i.e., qubits, are currently considered as the best building blocks of quantum information processors.
With the substitution v/Δ2 = χk and tΔ = τ, it is found that the dynamics of the Ising model governed by Eq. (2) is the same as LZT physics contained in Eq. (3) up to a normalized tunneling amplitude Δ25. Therefore, we can use LZT to simulate KZM of the Ising model.
A key concept of KZM is AIA. Following the arguments in refs 21,22, we consider two nontrivial schemes to relate LZT with KZM. In scheme A, the system starts far away from the avoided crossing, corresponding to ϵi → −∞ and ends also far away from the avoided crossing, corresponding to ϵf → ∞. The initial state  is the ground state of the Hamiltonian at time t = −∞. As shown in Fig. 1a, the evolution can be divided into three regions: there are two adiabatic regions
is the ground state of the Hamiltonian at time t = −∞. As shown in Fig. 1a, the evolution can be divided into three regions: there are two adiabatic regions  and
and  , where almost no transition between the instantaneous energy eigenstates
, where almost no transition between the instantaneous energy eigenstates  occurs. On the contrary, in the impulse region
occurs. On the contrary, in the impulse region  transitions between the states
transitions between the states  could occur. Quantitatively, the boundaries separating the adiabatic and impulse regions are determined by the freeze-out time
could occur. Quantitatively, the boundaries separating the adiabatic and impulse regions are determined by the freeze-out time  , where α is a dimensionless parameter, τQ = Δ/v sets the scale of the quench time and τ0 = 1/Δ, respectively. The finite density of topological defects
, where α is a dimensionless parameter, τQ = Δ/v sets the scale of the quench time and τ0 = 1/Δ, respectively. The finite density of topological defects  is caused by non-adiabatic evolution in the impulse region
is caused by non-adiabatic evolution in the impulse region  , which equals the occupation probability of
, which equals the occupation probability of  . Therefore, the density of topological defects Dn in KZM corresponds to the transition probability P+ in LZT, i.e., Dn = P+. In scheme B, the system starts from the center of the avoided crossing, i.e., ϵi = 0 and evolves to the adiabatic region till far away from the avoided crossing. Similarly, there are two regions, an impulse region
. Therefore, the density of topological defects Dn in KZM corresponds to the transition probability P+ in LZT, i.e., Dn = P+. In scheme B, the system starts from the center of the avoided crossing, i.e., ϵi = 0 and evolves to the adiabatic region till far away from the avoided crossing. Similarly, there are two regions, an impulse region  and an adiabatic
and an adiabatic  , can be defined. For both schemes, we directly measure the time-resolved P+ of LZT in our experiment and then quantitatively compare the result with the prediction of KZM.
, can be defined. For both schemes, we directly measure the time-resolved P+ of LZT in our experiment and then quantitatively compare the result with the prediction of KZM.
The time-resolved LZT
We use superconducting qubits to investigate the dynamics of the Ising model. Two samples were studied: a superconducting phase qubit (denoted as Q1 with T1 = 113 ns,  )6 and a 3D transmon (denoted as Q2 with T1 = 2.386 μs,
)6 and a 3D transmon (denoted as Q2 with T1 = 2.386 μs,  , see supplementary material). Here T1 is the energy relaxation time from state
, see supplementary material). Here T1 is the energy relaxation time from state  to state
to state  and
and  is the decoherence time including contributions from both relaxation and dephasing. Because neither the phase qubit nor the transmon qubit possess an intrinsic avoided level crossing, we use a coherent microwave field to generate an adjustable effective avoided energy level crossing27. The position and the tunneling amplitude (Δ) of the avoided crossing are determined by the frequency and amplitude of the microwave field, respectively. With this flexibility and controllability, instead of sweeping the flux bias, we chirp the microwave frequency ω while keeping the qubit frequency ω10 constant to realize LZT (see Methods). The profiles of the control and measurement pulses are illustrated in Fig. 1b.
is the decoherence time including contributions from both relaxation and dephasing. Because neither the phase qubit nor the transmon qubit possess an intrinsic avoided level crossing, we use a coherent microwave field to generate an adjustable effective avoided energy level crossing27. The position and the tunneling amplitude (Δ) of the avoided crossing are determined by the frequency and amplitude of the microwave field, respectively. With this flexibility and controllability, instead of sweeping the flux bias, we chirp the microwave frequency ω while keeping the qubit frequency ω10 constant to realize LZT (see Methods). The profiles of the control and measurement pulses are illustrated in Fig. 1b.
In our experiment, scheme A is a good approximation to LZT from −∞ to +∞ because ϵi/2π = −200 MHz and Δ/2π = 20 MHz, resulting  . The initial state is prepared in
. The initial state is prepared in  at ϵi/2π = −200 MHz. This is followed immediately by chirping ϵ to ϵf with a constant speed v = (ϵf − ϵi)/tLZ, where tLZ is the duration of the chirping operation. At the end of ϵ chirping, we perform state tomography (see supplementary material) to determine the density matrix of the qubit
at ϵi/2π = −200 MHz. This is followed immediately by chirping ϵ to ϵf with a constant speed v = (ϵf − ϵi)/tLZ, where tLZ is the duration of the chirping operation. At the end of ϵ chirping, we perform state tomography (see supplementary material) to determine the density matrix of the qubit  by measuring the expectation values
by measuring the expectation values  , where σx,y,z are the Pauli matrices. We then varied tLZ from 1 ns to 120 ns and ϵf/2π from −200 MHz to +400 MHz to obtain a complete set of experimental data. Since the avoided crossing centers at ϵ = 0, our experiments effectively cover the dynamical evolution of the system from
, where σx,y,z are the Pauli matrices. We then varied tLZ from 1 ns to 120 ns and ϵf/2π from −200 MHz to +400 MHz to obtain a complete set of experimental data. Since the avoided crossing centers at ϵ = 0, our experiments effectively cover the dynamical evolution of the system from  to
to  .
.
By converting the density matrix to the time-dependent basis  , we obtain the
, we obtain the

which shows that only  and
and  contribute to P+. The measured
contribute to P+. The measured  ,
,  and P+ for qubit Q2 are plotted in Fig. 2a–c, respectively. Shown in Fig. 2d–f are the results of numerical simulation obtained by solving the master equations (see Methods), where important system parameters, such as the relaxation and the dephasing times are determined from the pump-decay and the Ramsey fringe measurements. The good agreement between the experimental and the simulated results indicates that all essential aspects of our experiment are well controlled and understood.
and P+ for qubit Q2 are plotted in Fig. 2a–c, respectively. Shown in Fig. 2d–f are the results of numerical simulation obtained by solving the master equations (see Methods), where important system parameters, such as the relaxation and the dephasing times are determined from the pump-decay and the Ramsey fringe measurements. The good agreement between the experimental and the simulated results indicates that all essential aspects of our experiment are well controlled and understood.
The adiabatic and impulse regions
The time resolved quantum dynamics of P+(t) described above can be investigated by measuring  with nano-second time resolution. Shown in Fig. 3a are examples of P+ for qubit Q2 as a function of evolution time for various LZT duration time tLZ. In order to compare with AIA, we normalize the evolution time by the freeze-out time
with nano-second time resolution. Shown in Fig. 3a are examples of P+ for qubit Q2 as a function of evolution time for various LZT duration time tLZ. In order to compare with AIA, we normalize the evolution time by the freeze-out time  . The value of α used here is π/2, which is the same as that of AIA in this scheme21,22. In all cases P+ changes rapidly near the center of the avoided crossing and varies slowly outside the central region. This is the clear experimental evidence supporting the physical picture of AIA. Moreover, the boundaries between the adiabatic and impulse regions are demarcated by
. The value of α used here is π/2, which is the same as that of AIA in this scheme21,22. In all cases P+ changes rapidly near the center of the avoided crossing and varies slowly outside the central region. This is the clear experimental evidence supporting the physical picture of AIA. Moreover, the boundaries between the adiabatic and impulse regions are demarcated by  with no fitting parameters, confirming the validity of AIA.
with no fitting parameters, confirming the validity of AIA.
Population P+ as a function of the normalized time  and the comparison of
and the comparison of  and P+.
and P+.
(a) the evolution starting from t = −∞ with ϵi/2π = −200 MHz and ϵf/2π = 200 MHz. (b) the evolution starting from t = 0 with ϵi/2π = 0 and ϵf/2π = 400 MHz. Different LZ durations tLZ = 10 ns (red circle), 20 ns (magenta square), 40 ns (blue triangle), 80 ns (green diamond), are used to produce different LZT speed. The symbols (solid lines) are experimental (numerical) results. The red translucent (clear) regions mark the impulse (adiabatic) regions, while the boundary locates on  . The error bars are smaller than the sizes of the symbols. (c) The comparison of topological defects density
. The error bars are smaller than the sizes of the symbols. (c) The comparison of topological defects density  in KZM theory and P+ in LZT with ϵi/2π = 0. The blue symbols (green solid lines) are the experimental (numerical) results. The red dashed line shows the density
in KZM theory and P+ in LZT with ϵi/2π = 0. The blue symbols (green solid lines) are the experimental (numerical) results. The red dashed line shows the density  predicted in KZM with α = 0.784 as the best fit.
predicted in KZM with α = 0.784 as the best fit.
In scheme B, we investigate LZT by starting from the center of the avoided crossing (i.e., ϵi = 0). The system is initialized in the lower energy eigenstate at ϵi = 0 with a proper resonant π/2 pulse28,29,30. Then a time sequence similar to that in scheme A is applied. Here, ϵf/2π ranges from 0 to 400 MHz. The gap size is fixed at Δ/2π = 20 MHz, resulting a maximal ϵf/Δ = 20. Shown in Fig. 3b are examples of measured P+ as a function of the evolution time. In this case, α = π/4 according to refs 21,22. Similar adiabatic and impulse regions are observed with the boundary at  , strongly supporting AIA.
, strongly supporting AIA.
The freeze-out phenomenon
Another interesting problem is whether one can observe directly the predicted state freeze-out phenomenon in the impulse region  . According to KZM, although P± of the time-dependent basis states
. According to KZM, although P± of the time-dependent basis states  change rapidly in the impulse region, the probability amplitudes (thus
change rapidly in the impulse region, the probability amplitudes (thus  ) in the time-independent basis
) in the time-independent basis  should be frozen out. To see whether this is indeed the case, we plot the measured
should be frozen out. To see whether this is indeed the case, we plot the measured  of the qubit Q2 in Fig. 4a–c (see Methods). The line represents the freeze-out time
of the qubit Q2 in Fig. 4a–c (see Methods). The line represents the freeze-out time  is also shown in the plot. Here we use the theoretical KZM value α = π/4 because the total LZT duration is shorter than 40 ns and the effect of decoherence may not have significant effects on the result. It can be seen that
is also shown in the plot. Here we use the theoretical KZM value α = π/4 because the total LZT duration is shorter than 40 ns and the effect of decoherence may not have significant effects on the result. It can be seen that  change slowly in the impulse region, indicating that the state of the qubit is nearly frozen. In order to compare with the experimental data, we present the numerically simulated results by solving master equations without adjustable parameters for the evolution of LZT in Fig. 4d–f. The good agreement between the simulation and the experimental results supports the observation of the state freeze-out phenomenon and confirms the validity of AIA.
change slowly in the impulse region, indicating that the state of the qubit is nearly frozen. In order to compare with the experimental data, we present the numerically simulated results by solving master equations without adjustable parameters for the evolution of LZT in Fig. 4d–f. The good agreement between the simulation and the experimental results supports the observation of the state freeze-out phenomenon and confirms the validity of AIA.
One of the key features of the correspondence between KZM and LZT is  . In Fig. 3c we plot P+ as a function of tLZ for ϵf/2π = 200 MHz thus
. In Fig. 3c we plot P+ as a function of tLZ for ϵf/2π = 200 MHz thus  . In order to compare with the theory, tLZ is expressed in terms of τQ/τ0. It is found that P+ follows quite well with the behavior of the topological defects density
. In order to compare with the theory, tLZ is expressed in terms of τQ/τ0. It is found that P+ follows quite well with the behavior of the topological defects density  predicted in refs 21,22. Here, α = 0.784 is obtained from the best fit which is within 0.2% of KZM predicted value π/4. The excellent agreement between the experimental results of LZT and the theory of KZM provides strong support to the conjecture that the dynamics of the Landau-Zener model can be accurately described in terms of the Kibble-Zurek theory of the topological defect production in nonequilibrium phase transitions and vice versa.
predicted in refs 21,22. Here, α = 0.784 is obtained from the best fit which is within 0.2% of KZM predicted value π/4. The excellent agreement between the experimental results of LZT and the theory of KZM provides strong support to the conjecture that the dynamics of the Landau-Zener model can be accurately described in terms of the Kibble-Zurek theory of the topological defect production in nonequilibrium phase transitions and vice versa.
The scaling law
We now address the simulation of the scaling law predicted by KZM for the Ising model. By choosing small quenching rates  , all the relevant physics described by Eq. (2) happens in the long wavelength limit
, all the relevant physics described by Eq. (2) happens in the long wavelength limit  . In experiments, we choose a cutoff kc/π and thus vc/Δ2 = χkc to ensure that LZT probability can be neglected for
. In experiments, we choose a cutoff kc/π and thus vc/Δ2 = χkc to ensure that LZT probability can be neglected for  . For each
. For each  , we choose Nk different quasimomentum k equally distributed in
, we choose Nk different quasimomentum k equally distributed in  and measure the corresponding excitation probability
and measure the corresponding excitation probability  . Then the average density of defects can be expressed as
. Then the average density of defects can be expressed as

where the last equation is given by KZM theory. Stimulated by this prediction, we plot experimentally measured  vs.
vs.  for the qubits Q1 (red squares) and Q2 (blue squares) in Fig. 5, where Nk = 127 for each
for the qubits Q1 (red squares) and Q2 (blue squares) in Fig. 5, where Nk = 127 for each  , kc/π = 0.2 and
, kc/π = 0.2 and  . A striking feature is that
. A striking feature is that  shows a very good linear relation with
shows a very good linear relation with  . By fitting the line to a general linear function
. By fitting the line to a general linear function  , we obtain the offset N0 and slope β as summarized in Table 1. It is interesting that with the increasing of the decoherence time, the slope increases while the offset decreases. In order to confirm our observation, we did numerical simulations using T1 and
, we obtain the offset N0 and slope β as summarized in Table 1. It is interesting that with the increasing of the decoherence time, the slope increases while the offset decreases. In order to confirm our observation, we did numerical simulations using T1 and  of Q1, Q2 and infinite, shown in Fig. 5. Since there is no adjustable parameter, the agreement between the experimental data and numerical simulation results are remarkable. When the decoherence time goes to infinite, the offset tends to zero and the slope
of Q1, Q2 and infinite, shown in Fig. 5. Since there is no adjustable parameter, the agreement between the experimental data and numerical simulation results are remarkable. When the decoherence time goes to infinite, the offset tends to zero and the slope  , which is very close to the theory predicted value
, which is very close to the theory predicted value  25. Therefore, it is evident that LZT in qubit exhibits same scaling behavior of KZM of the Ising model although decoherence will quantitatively modify the value of some parameters.
25. Therefore, it is evident that LZT in qubit exhibits same scaling behavior of KZM of the Ising model although decoherence will quantitatively modify the value of some parameters.
The scaling behavior of  as a function of
as a function of  .
.
The red (blue) squares represent the experimental data measured in Q1 (Q2). The magenta, blue solid lines are the numerical simulation of the master equation with the decoherence of the phase qubit and 3D transmon, respectively. The green solid lines are the simulated results with infinite T1 and  .
.
Discussion
In our experiment, the hallmark features of the Ising model predicted by KZM, such as the existence of the adiabatic and impulse regions, the freeze-out phenomenon and scaling law, were observed. The experimental observations of the first two are in good agreement with the theoretical results because in the experiment the time of evolution is much less than T1 and  of the qubit Q2.
of the qubit Q2.
We here make several comments on our results of the scaling law. (i) In the absence of decoherence, our numerical results show that the slope  , while the theory predicts
, while the theory predicts  . The discrepancy between the numerical and the theoretical results is due to the fact that in the numerical simulation, both ϵi and ϵf are finite. the LZ transition happens in a finite range, i.e.,
. The discrepancy between the numerical and the theoretical results is due to the fact that in the numerical simulation, both ϵi and ϵf are finite. the LZ transition happens in a finite range, i.e.,  . In theory, however, β is assuming ϵf/Δ → ∞. To confirm it, we increased ϵf/Δ in numerical simulation and indeed find that β approaches
. In theory, however, β is assuming ϵf/Δ → ∞. To confirm it, we increased ϵf/Δ in numerical simulation and indeed find that β approaches  asymptotically. (ii) The offset N0 in the defect density
asymptotically. (ii) The offset N0 in the defect density  is observed for both qubits in Fig. 5. In addition, the stronger the decoherence, the larger the offset. It was found in previous studies31,32 that decoherence tends to increase the density of defects. As the decoherence rate increases, more defects are generated in the process of LZ transition. This is confirmed in our experiments, where it is found that the defect density
is observed for both qubits in Fig. 5. In addition, the stronger the decoherence, the larger the offset. It was found in previous studies31,32 that decoherence tends to increase the density of defects. As the decoherence rate increases, more defects are generated in the process of LZ transition. This is confirmed in our experiments, where it is found that the defect density  as well as the offset N0 for qubit Q1 is greater than that for qubit Q2. If the coherence time increase further, the offset will gradually approach to zero, as verified by the simulation 3 in Fig. 5. (iii) It is known that the theoretical prediction of ref. 25 is obtained in the continuum limit. So a further question is whether the finite size effect is important in our experiments. If we consider a quantum Ising spin chain with a finite length N, there will be energy splitting in the energy spectrum. In this case, if the chirping speed is too slow compared with the energy splitting caused by the finite size, then the prediction of ref. 25 would not be valid. In other words, the finite size effect sets a lower bound on the chirping speed. To be more precise, let us consider the energy splitting near zero energy where
as well as the offset N0 for qubit Q1 is greater than that for qubit Q2. If the coherence time increase further, the offset will gradually approach to zero, as verified by the simulation 3 in Fig. 5. (iii) It is known that the theoretical prediction of ref. 25 is obtained in the continuum limit. So a further question is whether the finite size effect is important in our experiments. If we consider a quantum Ising spin chain with a finite length N, there will be energy splitting in the energy spectrum. In this case, if the chirping speed is too slow compared with the energy splitting caused by the finite size, then the prediction of ref. 25 would not be valid. In other words, the finite size effect sets a lower bound on the chirping speed. To be more precise, let us consider the energy splitting near zero energy where  . Based on Eq. (2), we require χk=±π/N > 1, corresponding to
. Based on Eq. (2), we require χk=±π/N > 1, corresponding to  . In our experiments, we choose
. In our experiments, we choose  , which requires
, which requires  , a condition that is very well satisfied in our experiments. Thus the effect of finite size is negligible.
, a condition that is very well satisfied in our experiments. Thus the effect of finite size is negligible.
In conclusion, using linear chirps of microwave field and exploring the correspondence between the KZM of topological defects production and LZT, we simulated the KZM of the Ising model with a superconducting qubit system. All important predictions of KZM for the Ising model, such as the existence of adiabatic and impulse regions, the freeze-out phenomenon and especially the scaling law have been clearly demonstrated. The observed scaling behavior in the presence of decoherence sheds new light on the investigation of the effects of decoherence on KZM of non-equilibrium quantum phase transitions.
Methods
Chirp-LZT operation
In order to perform the LZT, we chirp the microwave frequency29,30 instead of sweeping the flux bias of the qubit. Concretely, with the qubit dc-biased at a fixed flux Φ, we chirp the microwave frequency from ωi to ωf, corresponding to the change of ϵ from ϵi to ϵf. Note that in our experiment, the energy difference is ϵi,f = ħ(ω01 − ωi,f), with a chirping microwave frequency  . Here we assume ħ = 1. If we set the original microwave frequency as ω01, then the chirped frequency is
. Here we assume ħ = 1. If we set the original microwave frequency as ω01, then the chirped frequency is  . Therefore, the relationship between the chirped microwave frequency
. Therefore, the relationship between the chirped microwave frequency  and the diabatic energy difference ϵi,f is given by
and the diabatic energy difference ϵi,f is given by  .
.
To chirp the microwave frequency, we apply modulation signals from a Tektronix AWG70002 to the IF (intermediate frequency) ports of a IQ mixer. Considering the original microwave waveform as Ar sin ω0t, the modulation signals applied to the I and Q ports of the IQ mixer as cos δωt and sin δωt, respectively. In this way, the modulated microwave at the output port of the mixer is 
 and the microwave frequency is chirped by tuning δω. From calibration, we find that the power of ω0 tone is at least 50 dB lower than that of ω0 + δω, indicating the negligible effect of ω0 on the qubit in the chirp operation.
and the microwave frequency is chirped by tuning δω. From calibration, we find that the power of ω0 tone is at least 50 dB lower than that of ω0 + δω, indicating the negligible effect of ω0 on the qubit in the chirp operation.
The Chirp-LZT method provides us several advantages in performing LZT. First of all, all parameters of the qubit, such as T1,  and the coupling strength between the qubit and the external driven filed, are fixed during the measurements. Second, the end points of diabatical energy sweep ϵi and ϵf would not be limited by the avoided level crossings resulting from the coupling between the qubit and microscopic two level systems (TLSs) usually presented in superconducting qubits because the microwave couples much weakly to TLSs than to the qubit. Third, it is easy to control the chirping velocity and the tunnel splitting Δ by controlling the frequency and power of the microwave. In addition, such method provides a useful tool for systems without natural avoided crossings in their energy diagram, such as transmons, to perform LZT and other similar experiments.
and the coupling strength between the qubit and the external driven filed, are fixed during the measurements. Second, the end points of diabatical energy sweep ϵi and ϵf would not be limited by the avoided level crossings resulting from the coupling between the qubit and microscopic two level systems (TLSs) usually presented in superconducting qubits because the microwave couples much weakly to TLSs than to the qubit. Third, it is easy to control the chirping velocity and the tunnel splitting Δ by controlling the frequency and power of the microwave. In addition, such method provides a useful tool for systems without natural avoided crossings in their energy diagram, such as transmons, to perform LZT and other similar experiments.
Solution of the master equation
The numerical results are obtained by solving master equations. The quantum dynamics of the superconducting qubits is described by the master equations of the time evolution of the density matrix ρ including the effects of dissipation:  , where H is the Hamiltonian of the system described by Eq. (3). The second term of this equation, Γ[ρ], describes the effects of decoherence on the evolution phenomenologically. Setting ħ = 1, the master equation can be rewritten as
, where H is the Hamiltonian of the system described by Eq. (3). The second term of this equation, Γ[ρ], describes the effects of decoherence on the evolution phenomenologically. Setting ħ = 1, the master equation can be rewritten as

Here Γ1 ≡ 1/T1 is the energy relaxation rate and  is the decoherence rate. The relationship between the density matrix and the qubit state expectation values are given by
is the decoherence rate. The relationship between the density matrix and the qubit state expectation values are given by

The numerical simulations in Figs 2, 3, 4 are straightforwardly obtained by solving Eq. (7). The simulations (solid lines) in Fig. 5 are obtained by mapping P+ as defined in Eq. (5) to the defect density  . By using v/Δ2 = χk for each chirping velocity v, we can find the corresponding momentum k with
. By using v/Δ2 = χk for each chirping velocity v, we can find the corresponding momentum k with  fixed. In this way, we obtain
fixed. In this way, we obtain  for different momentum k. Then
for different momentum k. Then  is computed from P+ using Eq. (6).
is computed from P+ using Eq. (6).
Additional Information
How to cite this article: Gong, M. et al. Simulating the Kibble-Zurek mechanism of the Ising model with a superconducting qubit system. Sci. Rep. 6, 22667; doi: 10.1038/srep22667 (2016).
References
Landau, L. D. On the theory of transfer of energy at collisions II. Physik. Z. Sowjet. 2, 46–51 (1932).
Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. London, Ser. A 137, 696–702 (1932).
Shevchenko, S. N., Ashhab, S. & Nori, F. Landau-Zener-Stückelberg interferometry. Phys. Rep. 492, 1–30 (2010).
Oliver, W. D. et al. Mach-Zehnder interferometry in a strongly driven superconducting qubit. Science 310, 1653–1657 (2005).
Sillanpää, M., Lehtinen, T., Paila, A., Makhlin, Y. & Hakonen, P. Continuous-time monitoring of Landau-Zener interference in a cooper-pair box. Phys. Rev. Lett. 96, 187002 (2006).
Tan, X. et al. Demonstration of Geometric Landau-Zener Interferometry in a Superconducting Qubit. Phys. Rev. Lett. 112, 027001 (2014).
Sun, G. et al. Tunable quantum beam splitters for coherent manipulation of a solid-state tripartite qubit system. Nat. Commun. 1, 51, Doi: 10.1038/ncomms1050 (2010).
Betthausen, C. et al. Spin-transistor action via tunable Landau-Zener transitions. Science 337, 324–327 (2012).
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012).
Salger, T., Geckeler, C., Kling, S. & Weitz, M. Atomic Landau-Zener tunneling in Fourier-synthesized optical lattices. Phys. Rev. Lett. 99, 190405 (2007).
Chen, Y.-A., Huber, S. D., Trotzky, S., Bloch, I. & Altman, E. Many-body Landau-Zener dynamics in coupled one-dimensional Bose liquids. Nat. Phys. 7, 61–67 (2011).
Zhang, D.-W., Zhu, S.-L. & Wang, Z. D. Simulating and exploring Weyl semimetal physics with cold atoms in a two-dimensional optical lattice. Phys. Rev. A 92, 013632 (2015).
Kibble, T. W. B. Topology of cosmic domains and strings. J. Phys. A: Math. Gen. 9, 1387 (1976).
Kibble, T. W. B. Some implications of a cosmological phase transition. Phys. Rep. 67, 183–199 (1980).
Zurek, W. H. Cosmological experiments in superfluid helium? Nature 317, 505–508 (1985).
Zurek, W. H. Cosmological experiments in condensed matter systems. Phys. Rep. 276, 177–221 (1996).
Chuang, I., Durrer, R., Turok, N. & Yurke, B. Cosmology in the laboratory: Defect dynamics in liquid crystals. Science 251, 1336–1342 (1991).
Ulm, S. et al. Observation of the Kibble–Zurek scaling law for defect formation in ion crystals. Nat. Commun. 4, 2290, Doi: 10.1038/ncomms3290 (2013).
Pyka, K. et al. Topological defect formation and spontaneous symmetry breaking in ion Coulomb crystals. Nat. Commun. 4, 2291, Doi: 10.1038/ncomms3291 (2013).
Navon, N., Gaunt, A. L., Smith, R. P. & Hadzibabic, Z. Critical dynamics of spontaneous symmetry breaking in a homogeneous Bose gas. Science 347, 167–170 (2015).
Damski, B. The simplest quantum model supporting the Kibble-Zurek mechanism of topological defect production: Landau-Zener transitions from a new perspective. Phys. Rev. Lett. 95, 035701 (2005).
Damski, B. & Zurek, W. H. Adiabatic-impulse approximation for avoided level crossings: From phase-transition dynamics to Landau-Zener evolutions and back again. Phys. Rev. A 73, 063405 (2006).
Xu, X.-Y. et al. Quantum simulation of Landau-Zener model dynamics supporting the Kibble-Zurek mechanism. Phys. Rev. Lett. 112, 035701 (2014).
Zurek, W. H., Dorner, U. & Zoller, P. Dynamics of a quantum phase transition. Phys. Rev. Lett. 95, 105701 (2005).
Dziarmaga, J. Dynamics of a quantum phase transition: Exact solution of the quantum Ising model. Phys. Rev. Lett. 95, 245701 (2005).
Sachdev, S. Quantum Phase Transitions (Cambridge University Press, 2001).
Sun, G. et al. Landau-Zener-Stückelberg interference of microwave-dressed states of a superconducting phase qubit. Phys. Rev. B 83, 180507 (2011).
Yan, F. et al. Rotating-frame relaxation as a noise spectrum analyser of a superconducting qubit undergoing driven evolution. Nat. Commun. 4, 2337, Doi: 10.1038/ncomms3337 (2013).
Berger, S. et al. Geometric phases in superconducting qubits beyond the two-level approximation. Phys. Rev. B 85, 220502 (2012).
Leek, P. J. et al. Observation of Berry’s phase in a solid-state qubit. Science 318, 1889–1892 (2007).
Patanè, D., Silva, A., Amico, L., Fazio, R. & Santoro, G. E. Adiabatic dynamics in open quantum critical many-body systems. Phys. Rev. Lett. 101, 175701 (2008).
Nalbach, P., Vishveshwara, S. & Clerk, A. A. Quantum Kibble-Zurek physics in the presence of spatially correlated dissipation. Phys. Rev. B 92, 014306 (2015).
Acknowledgements
This work was partly supported by the SKPBR of China (Grants No. 2011CB922104 and 2011CBA00200), NSFC (Grants No. 91321310, 11274156, 11125417, 11474153, 11474154 and 61521001), NSF of Jiangsu (Grant No. BK2012013), PAPD and the PCSIRT (Grant No. IRT1243). S. Han is supported in part by the U.S. NSF (PHY-1314861).
Author information
Authors and Affiliations
Contributions
The data were measured by M.G., G.S., Y.Z., Y.F., Y.L. and X.T. and analyzed by M.G., X.W., G.S., D.Z., Y.Y., S.Z., S.H. and P.W.; H.Y. and D.L. fabricated the sample; The theoretical framework was developed by X.W. and S.Z.; All authors contributed to the discussion of the results. Y.Y. and S.H. supervised the experiment and S.Z. supervised the theory.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Gong, M., Wen, X., Sun, G. et al. Simulating the Kibble-Zurek mechanism of the Ising model with a superconducting qubit system. Sci Rep 6, 22667 (2016). https://doi.org/10.1038/srep22667
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep22667
This article is cited by
-
Generalized Kibble-Zurek mechanism for defects formation in trapped ions
Science China Physics, Mechanics & Astronomy (2023)
-
Experimentally testing quantum critical dynamics beyond the Kibble–Zurek mechanism
Communications Physics (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

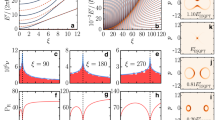


 and P+ as a function of ϵf/2π and tLZ.
and P+ as a function of ϵf/2π and tLZ.

 in LZT with ϵi/2π = 0. The white solid line marks the freeze-out time
in LZT with ϵi/2π = 0. The white solid line marks the freeze-out time  in KZM with α = π/4.
in KZM with α = π/4.