Abstract
Just as the topology of the Fermi surface defines the properties of the free electrons in metals and semiconductors, the geometry of the iso-frequency surface in the phase space of the propagating electromagnetic waves, determines the optical properties of the corresponding optical materials. Furthermore, in the direct analog to the Lifshitz transition in condensed matter physics, a change in the topology of iso-frequency surface has a dramatic effect on the emission, propagation and scattering of the electromagnetic waves. Here, we uncover a new class of such optical topological transitions in metamaterials, induced by the non-locality of the electromagnetic response inherent to these composites.
Similar content being viewed by others
Introduction
With the underlying quantum-mechanical wave nature of free electrons in solids, many optical phenomena find their close analogues in condensed matter physics - from optical solitons1 vs. charge density waves2 to Bose-Einstein Condensation3 and its optical equivalent in photorefractive crystals4. On a more basic level, both the “electronic” and “electromagnetic” material properties can be traced to the geometry of the underlying surface that constrains the phase space that is allowed to the propagating light or matter waves for a given energy. In condensed matter physics, this is the familiar Fermi surface – and change its topology from a “closed” to an “open” form in what is known as the Lifshitz transition5, leads to a profound effect on the transport properties of metals and semiconductors. First studied in metals, Lifshitz transitions have been observed in other materials such as superconductors6 and bilayer graphene7, proven to be general phenomena in condensed matters. The corresponding optical topological transitions8 (OTTs) that were recently discovered in electromagnetic metamaterials, show even more dramatic manifestations, as these optical effects are not subject to the restrictions of Fermi exclusion principle. A closed iso-frequency surface corresponds to a dielectric and reduces to a simple sphere when the material does not show any anisotropy in its electromagnetic response. An open iso-frequency surface, on the other hand, is the key property of the hyperbolic media, where the wavenumbers of the propagating waves are not limited by the frequency, essentially breaking the conventional diffraction limit and leading to a broad bandwidth singularity of the photonic density of states9 in the effective medium limit. It is this key feature of the hyperbolic metamaterials (HMMs) that lead to the recent progress in super-resolution hyperlens imaging10,11,12,13, diffraction-unlimited photolithography and sub-wavelength interference14,15. A change in the topology of the iso-frequency surface therefore has a dramatic effect on a wide range of optical phenomena.
In its simplest form a transition in the topology of the iso-frequency surface can be observed in strongly anisotropic materials at the frequency when one of the dielectric permittivity components changes sign and the iso-frequency surface transforms from a (closed) ellipsoid into an (open) hyperboloid8. Naturally, being induced by the changes of the average electromagnetic response, such a transition can be understood in the effective medium limit, which ignores the finite size of the unit cell of the material. However, as we show in the present work, the electromagnetic response of a metamaterial composite that results from a finite size of the unit cell, generally referred to as the non-locality or the spatial dispersion– can also lead to a different class of OTTs that has no counterpart in the effective medium approximation.
Aside from the direct consequences of this behavior for optical response of such media and the corresponding practical applications (in e.g. optical filters, electromagnetic modulators, etc.), this new class of OTTs introduced in the present work, has broader implications. As OTTs in electromagnetic metamaterials can be mapped onto the metric signature transitions in cosmology, the electromagnetic response of a non-local metamaterial can be connected to space-time discretization models16,17, with the metamaterial unit cell playing the role of the effective Planck length.
A hyperbolic iso-frequency surface for propagating electromagnetic waves generally implies that either one or two components of the dielectric permittivity tensor of the medium are negative. If the medium has an axis of symmetry (which is the case of most hyperbolic media studied so far18), in the effective medium limits the resulting dispersion equation for the TM-polarized waves can be expresses as,

where z is the symmetry axis of the uniaxial material, k = (kx, ky, kz) is the wavevector, ε = diag(ετ, ετ, εn) is the corresponding dielectric permittivity tensor and ω is the electromagnetic wave frequency. Note that, depending on whether only one εz = εn or two components εx = εy = ετ of the dielectric permittivity tensor are negative, the hyperbolic iso-frequency surface corresponding to the equation (1), consists respectively of two separate parts (Fig. 1a) or a single sheet (Fig. 1b).
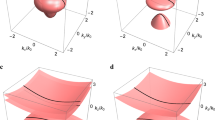
Iso-frequency surfaces of hyperbolic metamaterials and frequency-dependent anisotropic permittivity and reflectance of sapphire.
(a,b) Iso-frequency surfaces of hyperbolic metamaterials, for Re[ετ] > 0, Re[εn] < 0 (a) and Re[ετ] < 0, Re[εn] > 0 (b). Each of the two sheets forming the iso-frequency surface in panel a, is simply connected, as any closed loop it contains, can be continuously transformed into a single point. Note that this is not the case in panel (b). (c) Frequency-dependent anisotropic permittivity of sapphire, from the date of ref. 40. The solid and dashed lines show ordinarily and extraordinarily components, respectively. (d–e), Angular dependence of sapphire reflectivity of sapphire in a hyperbolic frequency bands, when iso-frequency surface is (d) and is not (e) simply-connected. The color code (green and red) in panel (c) corresponds to the colors in panels (d) and (e).
Note that these two different types of hyperbolic iso-frequency surface correspond to fundamentally different topological phases. In one case (see Fig. 1a), the iso-surface consists of two parts with each being a simply-connected topological space, while the other (Fig. 1b) is not simply-connected. The topological concept of simple connectivity (or equivalently 1-connectivity)19 describes the situation when every path between two points of a topological space can be continuously transformed, staying within the space, into any other such path while preserving the two endpoints. Alternatively, simple connectivity means that every loop on the surface can be contracted to a point. The continuous transformation of the orange loop in Fig. 1 illustrates the simple connectedness in the bottom surface in Fig. 1a and the lack of it in Fig. 1b. Note that this topological difference between the two hyperbolic iso-frequency surfaces also has profound physics implications. The lack of simple-connectedness indicates the presence of the holes in the surface - which implies the absence of the propagating waves in the corresponding range. For light incident on such material, this would imply a total (or nearly total, if the material losses are taken into account) reflection. Indeed, the reflectivity calculations of Figs. 1d,e for the two topologically different hyperbolic phases (corresponding to light incident onto sapphire, respectively in the 2nd and 3rd hyperbolic bands of sapphire - see Fig. 1c) show a qualitatively different reflectivity pattern.
In the strongly anisotropic regime the electromagnetic response of a material generally shows strong frequency variation, ε = ε(ω), leading to the hyperbolic dispersion in a limited wavelength range. This behavior is illustrated in Fig. 1c, using the example of sapphire that supports three different hyperbolic intervals (“red” and “green” regions in panel Fig. 1c). These hyperbolic bands are generally terminated at the frequencies when one of the dielectric permittivity components changes sign. As in such strongly anisotropic materials, this may not happen simultaneously with all eigenvalues of ε), a hyperbolic band is usually bounded by an “elliptical” phase (when all permittivity components are positive, “blue” regions in Fig. 1c), corresponding to a dielectric behavior, or a “metallic” one (ε < 0). Other natural hyperbolic materials (such as e.g. bismuth20, boron nitride21 and graphite22) also show a similar pattern.
Metamaterials - artificial electromagnetic composites patterned on a subwavelength scale that allow to “design” the unit cell for the desired electromagnetic response − also show the hyperbolic subbands and the corresponding topological transitions at their limits. This is illustrated in Fig. 2b–c, where we show the entire “phase diagram” for planar metamaterials. If the periodicity (h) of multilayers in Fig. 2a forming the planar metamaterial is sufficiently small compared to the free space wavenumber (k0)  , the dielectric permittivity tensor of the composite can be calculated using by the effective medium theory (EMT)23 which yields,
, the dielectric permittivity tensor of the composite can be calculated using by the effective medium theory (EMT)23 which yields,

where εM and εD are the permittivities of the metal and the dielectric, respectively, rM is the metal filling ratio and the x-y plane is parallel to the layers. For the TE-polarized waves, the corresponding effective medium dispersion is,

corresponding to either the spherical iso-frequency surface (for ετ > 0) or metallic behavior (ετ < 0) when the material does not support any TE propagating waves - see Fig. 2b. The TM-polarized modes, on the other hand, have a more complicated behavior as shown in Fig. 2c. With the dispersion defined by equation (1), the resulting phase diagram shows the metallic, the dielectric and both kinds of the hyperbolic phases, depending on the frequency (the vertical axis of Figs. 2b,c) and the unit cell composition (horizontal axis of Fig. 2b,c). Note that, similar to the case of natural hyperbolic media, for any volume fraction r ≠ 0.5, the hyperbolic range is bounded by either a “metallic” or a “dielectric” phase.
Quantitatively, OTTs, which is the optical analog of Lifshitz transition in condensed mater physics, can be characterized by the topological phase parameter p defined as,

where S is area. As can be seen from equation (4), the topological phase parameter p is essentially the scaled solid angle in the phase space that is covered by the iso-frequency surface. This topological phase parameter is equal to the unity for a closed iso-frequency surface of a dielectric, is exactly zero for a metal and lies between these two values for a hyperbolic medium. In Fig. 3, we plot the order parameter defined by equation (4) for the TM modes in planar metamaterials. Note a clearly visible difference in the values of the parameter p for the four phases (see Fig. 2c) supported by the system.
Topological phase parameter of the multilayer HMM for TM polarization.
The false-color scale representation of the topological phase parameter (p) in the multilayer hyperbolic metamaterial as a function of the metal volume fraction (horizontal axis) and the ratio of the metal and dielectric components permittivities (vertical axis), for TM-polarized propagating waves.
Using the example of a planar metamaterial (Fig. 2a) formed by the alternating layers of a dielectric with the permittivity εD = 4 and a Drude metal with the permittivity  and the plasma frequency ωp, in Fig. 4 we use the effective medium approximation (eq. (2)) to plot dispersion diagram ω(kτ, kn), where kτ and kn are the wavevector components in respectively the directions parallel and perpendicular to the layers. There, Fig. 4b corresponds to the metal volume fraction rM = 1/3 < 0.5, with a dielectric phase between two hyperbolic bands, while Fig. 4c shows the dispersion diagram for rM = 2/3 > 0.5, when a frequency bandgap (corresponding to the metallic phase) separates the topologically different hyperbolic phases. There, the geometry of the corresponding iso-frequency surface relates to the cross-section of the dispersion diagram in Fig. 4a at the given frequency ω.
and the plasma frequency ωp, in Fig. 4 we use the effective medium approximation (eq. (2)) to plot dispersion diagram ω(kτ, kn), where kτ and kn are the wavevector components in respectively the directions parallel and perpendicular to the layers. There, Fig. 4b corresponds to the metal volume fraction rM = 1/3 < 0.5, with a dielectric phase between two hyperbolic bands, while Fig. 4c shows the dispersion diagram for rM = 2/3 > 0.5, when a frequency bandgap (corresponding to the metallic phase) separates the topologically different hyperbolic phases. There, the geometry of the corresponding iso-frequency surface relates to the cross-section of the dispersion diagram in Fig. 4a at the given frequency ω.
Note that neither for rM < 0.5 nor when rM > 0.5 does the effective medium result of Fig. 4 allow for a “direct” topological transition between the hyperbolic phases of different topology. Instead, the corresponding evolution involves an intermediate phase, which can be either dielectric (rM < 0.5) or metallic (rM > 0.5).
However, the effective medium approximation (eq. (2)) used to calculate the phase space (Fig. 3) and dispersion (Fig. 4) diagrams for planar metamaterials, does not take into account the finite size of the metamaterial unit cell and the corresponding non-locality. While the resulting “spatial dispersion” effects (As the effects of the finite size of the unit cell can be incorporated into the dielectric permittivity tensor formalism via the k-dependence of ε, the corresponding mathematical description in terms of the “spatial frequency” k carries an essential similarity to that of the “temporal” frequency dispersion ε(ω). The term “spatial dispersion” originates from this mathematical connection.) are generally weak, especially for increasingly smaller size of the (subwavelength) unit cell, they may account for qualitatively new physics such as e.g. formation of additional waves23,24,25,26,27,28,29,30, double-refraction31,32 and may therefore have the potential to lead to an entire new class of OTTs, not found within the conventional effective media. In particular, we predict that essential non-locality of optical metamaterials leads to the direct transitions between two topologically different hyperbolic phases.
Indeed, the exact dispersion diagram for metal-dielectric composite of Fig. 2a does uncover the predicted topological transition. Solving for the exact propagating wave dispersion33 (see Methods) in the metal-dielectric composite having the identical material properties and geometries as before, we obtain the diagram shown in Fig. 5 at rM = 2/3. As we increase the frequency, at the critical point (ωc) the originally single-sheet connected hyperboloid (Fig. 5c) degenerates into a conical surface (Fig. 5b) which then immediately evolves into the disconnected hyperboloids of Fig. 5a. This behavior is further illustrated in the constant frequency cross-sections (see Fig. 5d–f) and the full dispersion diagram of Fig. 5g plotted in kτ-kn-ω space.
Three classes of propagating wave dispersion in multilayer HMM.
(a–f) Iso-frequency curves of the multilayer HMM in kx-ky-kz space (a–c) and in kτ-kn space (d–f) at ω/ωp = ωc/ωp+Δ (a,d), ω/ωp = ωc/ωp (b,e) and ω/ωp = ωc/ωp−Δ (c,f). Panel (g) shows the evolution of iso-frequency curve with frequency, in the range ωc/ωp − Δ ≤ ω/ωp ≤ ωc/ωp + Δ. The iso-frequency curves in panel (d–f) are superimposed in panel (g) with the same colors. In the entire plot, rM = 2/3 and Δ = 2.5 × 10−5.
Note that the conical dispersion surface at the OTT allows an arbitrarily small wavenumber including k = 0 to propagate in multilayer metamaterials. This formally allows for zero effective refractive index at the transition, thus extending the original concept of epsilon-near-zero materials34 to an entirely new class of optical modes.
Furthermore, the conical iso-frequency surface at the non-local OTT predicted in the present work, will result in the phenomenon of conical diffraction35 that manifests in the “double-refraction” of a TM-polarized beam at normal incidence upon the planar metamaterial surface. It should be straightforward to observe this effect in the standard experimental setup for optical refraction in planar metamaterials36.
In the present work, we focus on the fundamental concept and the general properties of non-local optical topological transitions. As the iso-frequency surface and its topology is a fundamental property of propagating electromagnetic waves in a medium and is directly related to the photonic density of states, such transitions will have a strong effect on a broad range of optical phenomena - from light localization and scattering to nonlinear and quantum optics. Furthermore, multilayer hyperbolic metamaterials such as the planar composite studied in the present work, facilitated by the immediate availability of the material components (e.g. transparent conducting oxides in near infrared37 and heavily-doped semiconductors mid infrared36) and well-established fabrication protocols (physical vapor deposition techniques such as molecular beam epitaxy and sputtering that enable multilayers with sub-nanometer accuracy), show immediate promise as spatial optical filters and further research is expected leading to many other applications. To further tailor the applicability of such structures, passive dielectric layers can be replaced with active dielectric layers for loss compensation38,39.
To summarize, we present that non-locality can induce a new type of OTT in electromagnetic metamaterials, with the system at the critical point corresponding to a new class of zero-index media.
Methods
Wave propagation through multilayers consisting of isotropic materials can be described by the standard transmission matrix approach33. For the case with periodic bilayers, the final dispersion equations for TE- and TM-polarized waves reduce to,

where dM (=hrM) and dD (=h(1 − rM)) are the thicknesses of the metal layer and the dielectric layer, respectively, K is the wavenumber for Bloch waves,  and
and  and kτ is the wavevector component parallel to the layers. The effective medium approximation of equation (2) is based on the second-order expansion of equation (5) in powers of kd ≪1.
and kτ is the wavevector component parallel to the layers. The effective medium approximation of equation (2) is based on the second-order expansion of equation (5) in powers of kd ≪1.
For the dispersion calculation shown in Fig. 5, loss-less Drude model was used for the metal and the permittivity of the dielectric was set to εD = 4.0 same as in Fig. 4. The plasma frequency was defined as a normalized parameter ωp = 2πc/40h (c is the speed of light) using the period (h), thus we can work in the metamaterial limit (k0h ≪ 1) at around the surface plasmon resonance frequency (ω ≈ 2πc/90h). When h ≈ 30 nm, the value of ωp (≈0.5 eV) corresponds to a typical plasma frequency of a highly-doped transparent conductive oxides which is one of the alternative plasmonic materials studied extensively in the past few years (see Ref. 37). Also note that the chosen value εD = 4.0 is consistent with the dielectric permittivities of a number of transparent oxides such as zinc oxide and titanium oxide.
Additional Information
How to cite this article: Ishii, S. and Narimanov, E. Non-local Optical Topological Transitions and Critical States in Electromagnetic Metamaterials. Sci. Rep. 5, 17824; doi: 10.1038/srep17824 (2015).
References
Eisenberg, H., Silberberg, Y., Morandotti, R., Boyd, A. & Aitchison, J. Discrete spatial optical solitons in waveguide arrays. Phys. Rev. Lett. 81, 3383–3386 (1998).
Degiorgi, L., Alavi, B., Mihály, G. & Grüner, G. Complete excitation spectrum of charge-density waves: Optical experiments on K0.3MoO3 . Phys. Rev. B 44, 7808 (1991).
Fleischer, J. W., Segev, M., Efremidis, N. K. & Christodoulides, D. N. Observation of two-dimensional discrete solitons in optically induced nonlinear photonic lattices. Nature 422, 147–150 (2003).
Sun, C. et al. Observation of the kinetic condensation of classical waves. Nat. Phys. 8, 470–474 (2012).
Lifshitz, I. M. Anomalies of electron characteristics of a metal in the high pressure region. Sov. Phys. JETP 11, 1130 (1960).
Liu, C. et al. Evidence for a Lifshitz transition in electron-doped iron arsenic superconductors at the onset of superconductivity. Nat. Phys. 6, 419–423 (2010).
Varlet, A. et al. Tunable Fermi surface topology and Lifshitz transition in bilayer graphene. Synth. Met., doi: 10.1016/j.synthmet.2015.07.006 (2015).
Krishnamoorthy, H. N. S., Jacob, Z., Narimanov, E., Kretzschmar, I. & Menon, V. M. Topological transitions in metamaterials. Science 336, 205–209 (2012).
Smolyaninov, I. I. & Narimanov, E. E. Metric signature transitions in optical metamaterials. Phys. Rev. Lett. 105, 067402 (2010).
Jacob, Z., Alekseyev, L. V. & Narimanov, E. Optical Hyperlens: Far-field imaging beyond the diffraction limit. Opt. Express 14, 8247–8256 (2006).
Salandrino, A. & Engheta, N. Far-field subdiffraction optical microscopy using metamaterial crystals: Theory and simulations. Phys. Rev. B 74, 075103 (2006).
Liu, Z., Lee, H., Xiong, Y., Sun, C. & Zhang, X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 315, 1686 (2007).
Smolyaninov, I. I., Hung, Y. J. & Davis, C. C. Magnifying superlens in the visible frequency range. Science 315, 1699 (2007).
Thongrattanasiri, S. & Podolskiy, V. A. Hypergratings: nanophotonics in planar anisotropic metamaterials. Opt. Lett. 34, 890–892 (2009).
Ishii, S., Kildishev, A. V., Narimanov, E., Shalaev, V. M. & Drachev, V. P. Sub-wavelength interference pattern from volume plasmon polaritons in a hyperbolic medium. Laser Photonics Rev. 7, 265–271 (2013).
Smolyaninov, I. I. Metamaterial’multiverse’. J. Opt. 13, 024004 (2011).
Smolyaninov, I. I. Critical opalescence in hyperbolic metamaterials. J. Opt. 13, 125101 (2011).
Poddubny, A., Iorsh, I., Belov, P. & Kivshar, Y. Hyperbolic metamaterials. Nat. Photon. 7, 948–957 (2013).
Croft, H. T., Falconer, K. J. & Guy, R. K. Unsolved problems in geometry. 149–167 (Springer-Verlag: New York,, 1991).
Alekseyev, L. V., Podolskiy, V. A. & Narimanov, E. E. Homogeneous Hyperbolic Systems for Terahertz and Far-Infrared Frequencies. Adv. Optoelectron. 2012, doi: 10.1155/2012/267564 (2012).
Caldwell, J. D. et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat. Commun. 5, 5221 (2014).
Sun, J., Zhou, J., Li, B. & Kang, F. Indefinite permittivity and negative refraction in natural material: Graphite. Appl. Phys. Lett. 98, 101901 (2011).
Rytov, S. M. Electromagnetic Propeties of a Finely Stratified Medium. Sov. Phys. JETP 2, 466–475 (1956).
Pokrovsky, A. L. & Efros, A. L. Electrodynamics of Metallic Photonic Crystals and the Problem of Left-Handed Materials. Phys. Rev. Lett. 89, 093901 (2002).
Belov, P. A. et al. Strong spatial dispersion in wire media in the very large wavelength limit. Phys. Rev. B 67, 113103 (2003).
Elser, J., Wangberg, R., Podolskiy, V. A. & Narimanov, E. E. Nanowire metamaterials with extreme optical anisotropy. Appl. Phys. Lett. 89, 261102 (2006).
Pollard, R. et al. Optical nonlocalities and additional waves in epsilon-near-zero metamaterials. Phys. Rev. Lett. 102, 127405 (2009).
Belov, P. A., Tretyakov, S. A. & Viitanen, A. J. Dispersion and Reflection Properties of Artificial Media Formed By Regular Lattices of Ideally Conducting Wires. J. Electromagnet. Wave. 16, 1153–1170 (2002).
Wells, B. M., Zayats, A. V. & Podolskiy, V. A. Nonlocal optics of plasmonic nanowire metamaterials. Phys. Rev. B 89, 035111 (2014).
Ritchie, R. H. Plasma Losses by Fast Electrons in Thin Films. Phys. Rev. 106, 874–881 (1957).
Orlov, A. A., Voroshilov, P. M., Belov, P. A. & Kivshar, Y. S. Engineered optical nonlocality in nanostructured metamaterials. Phys. Rev. B 84, 045424 (2011).
Castaldi, G., Galdi, V., Alù, A. & Engheta, N. Nonlocal transformation optics. Phys. Rev. Lett. 108, 63902 (2012).
Yeh, P. Optical waves in layered media. Vol. 95 (Wiley Online Library, 1988).
Alù, A., Silveirinha, M. G., Salandrino, A. & Engheta, N. Epsilon-near-zero metamaterials and electromagnetic sources: Tailoring the radiation phase pattern. Phys. Rev. B 75, 155410 (2007).
Peleg, O. et al. Conical diffraction and gap solitons in honeycomb photonic lattices. Phys. Rev. Lett. 98, 103901 (2007).
Hoffman, A. J. et al. Negative refraction in semiconductor metamaterials. Nat. Mater. 6, 946–950 (2007).
West, P. R. et al. Searching for better plasmonic materials. Laser Photon. Rev. 4, 795–808 (2010).
Ni, X. et al. Loss-Compensated and Active Hyperbolic Metamaterials. Opt. Express 19, 25255–25262 (2011).
Tumkur, T. et al. Control of spontaneous emission in a volume of functionalized hyperbolic metamaterial. Appl. Phys. Lett. 99, 151115 (2011).
Schubert, M., Tiwald, T. & Herzinger, C. Infrared dielectric anisotropy and phonon modes of sapphire. Phys. Rev. B 61, 8187 (2000).
Acknowledgements
This work was in part support by JSPS Postdoctoral Fellowships for Research Abroad (SI), NSF Center for Photonic and Multiscale Nanomaterials, Army Research Office MURI and Gordon and Betty Moore Foundation (EN).
Author information
Authors and Affiliations
Contributions
Both authors contributed to the calculations and the analysis of the data, discussion of the results and the preparation of the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Ishii, S., Narimanov, E. Non-local Optical Topological Transitions and Critical States in Electromagnetic Metamaterials. Sci Rep 5, 17824 (2016). https://doi.org/10.1038/srep17824
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep17824
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.