Introduction

The exponential progress of microelectronics over the last decade has been dramatically dependent on the excellent host material, silicon. The weak spin-orbit coupling and the existence of zero nuclear spin isotopes have made silicon a prime semiconductor platform for the emerging field of quantum information technology1. Shallow hydrogenic impurities (e.g., phosphorus, bismuth, and arsenic)2 offer natural Coulomb confinement to single electrons and provide access to single electron and nuclear spins for encoding quantum information3. The relatively large electronic wavefunctions of the donors allow gate control of orbital and spin properties. This has led to the demonstration of high fidelity single4 and two-qubit logic gates5,6 with exceptional spin coherence times7,8 and all-electrical spin readout and initialization9. Advanced lithographic techniques have been developed to deterministically place one to few phosphorous donors in a plane of silicon with a lattice constant precision10,11, leading to the fabrication of single-atom transistors12, few-atom thick nanowires13, and low-noise atomic spin qubits4,5.

Accurate modeling of the spin and orbital properties of shallow dopants is crucial for designing and optimizing high-performance spin qubits14. Two dominant approaches in the community are the multi-valley effective mass technique and the Slater-Koster tight-binding (TB) method, as these enable calculations at the length scale of 10–100 nm. While effective mass theory is a continuum minimal-basis approach lacking atomic resolution, Slater-Koster TB theory is an atomistic full Brillouin Zone method15. However, both these methods are semi-empirical and single-electron in nature, relying on different levels of simplifications and parameters from ab-initio methods. The ability to extend the simulations to a larger number of electrons and compute properties without fitting parameters can be achieved by ab-initio density functional theory (DFT). DFT has been extensively applied to elucidate the electronic properties of semiconductors and is currently the only approach to obtain absolute values of Fermi contact hyperfine (HF) parameters between electron and nuclear spins in multi-electron systems16. Although DFT has succeeded in providing accurate hyperfine parameters for some highly localized deep impurity systems17, it is extremely challenging to simulate relatively delocalized shallow dopant states due to the system size limitations and excessive computational burden18.

While DFT calculations on shallow dopants have improved over the years, past works were able to calculate either the hyperfine coupling or binding energy with accuracy, but not both. Swift et al.19 employed pseudopotential and extrapolation approaches with HSE and PBE functionals working in tandem, achieving outstanding accuracy in binding energy calculations of bismuth and arsenic donors in Si. However, the predefined frozen core region of Kohn–Sham orbitals results in an incomplete description of the hyperfine coupling. Smith et al.20 achieved success in the binding energy calculations directly from the wavefunctions extracted from the supercells containing 10648 atoms and the impurity potential of the phosphorus donor using an empirical model. And Gerstmann21 accurately reproduced the isotropic hyperfine and super-hyperfine parameters of shallow donors in Si using Green’s function approach. However, the empirical correction included in these methods lacks the capacity to provide an accurate evaluation of the hyperfine coupling and orbital splitting of the donor simultaneously from a single theoretical framework. In addition, electric field dependency of the hyperfine coupling, critical for quantum computing, has never been obtained from ab-initio calculations.

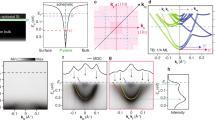
In the present work, these obstacles are overcome by using pseudopotential (PSP) and all-electron (AE) mixed Gaussian type localized basis sets combined with hybrid functional to conduct large-scale DFT calculations containing up to thousands of atoms (4096 atoms; 4 × 4 × 4 nm3). A host of important spin and orbital properties of a single phosphorus donor in silicon (Si:P), such as hyperfine coupling and its electric field dependency, super-hyperfine couplings at silicon lattice points within a few shells of the impurity, and excited orbital (valley-orbit) splitting are accurately evaluated simultaneously. To obtain consistently accurate values of all these quantities together, the wavefunction, and hence the electron density needs to be accurately described not only close to the donor nucleus but also over a large part of the silicon lattice extending over a Bohr radius of 1–2 nm. Figure 1 shows a schematic of a single P dopant as a spin qubit in a silicon host, with the corresponding charge density difference map obtained from DFT showing the electronic interactions close to the donor atom. We focus on P donors due to their technological significance in quantum computing2, but the presented methods also apply to other shallow Group V dopants in silicon. For comparison, three separate approaches are used, namely, (1) the Pseudopotential approach (PSP) in VASP22, (2) the All-Electron approach (AE) in CP2K23, and (3) the mixed Pseudopotential and All-Electron approach (PSP-AE) in CP2K. The three-pronged approaches enable us to contrast the shortcomings of each technique and help us to assess computational cost versus accuracy. We find that the use of proper basis functions, state-of-the-art functionals, and extrapolation method can yield quantitatively accurate results without significantly increasing the computational burden.

Fig. 1: Illustration of single P donor in Si host in a quantum information processor.
figure 1

A-gates above the donors control the hyperfine coupling and hence the resonance frequency of the nuclear spin qubits; J-gates between the donors control the electron-mediated coupling between adjacent nuclear spins. The black background Si region below the barrier is used to reflect a more bulk-like scenario for qubits embedded into Si at depths >10 nm. The embedded charge density difference map illustrates the electronic interaction around the donors (isosurface value of 1 × 10−3 e/Å3), where cyan area represents electron depletion and yellow area represents electron accumulation.

Full size image

Recently papers have emphazied the importance of using all-electron level basis sets in spin-Hamiltonian calculations for quantitative predictions of spin dynamics24,25. As an AE approach based on Gaussian type localized basis sets, CP2K solves the inherent problems induced by the PSP approximation such as the disregard of the core spin-polarization effect and the contribution of the exchange-correlation potential in the vicinity of the nucleus26. Hence, it provides high computational efficiency and superior accuracy for core-electron related properties such as hyperfine coupling, nuclear magnetic resonance, and g-factor27,28,29,30. Additionally, hybrid functional is employed, which can further improve the accuracy of the wavefunction amplitude and the electron localization at the donor nucleus19,31. With the combination of AE approach and hybrid functional, a value of 115.5 MHz HF constant is predicted in the present work which is in excellent agreement with the experimental value of 117 MHz32. The corresponding binding energy 1 s(A1) of the ground state and energies of excited 1 s(T2) and 1 s(E) states are found to be 46.07 meV, 37.22 meV, and 35.87 meV, respectively, in good agreement with the experimental values33,34. Furthermore, the Stark shift of the hyperfine coupling is of utmost importance for electrically tuning electron-nuclear resonance frequency of donor spin qubits and it is computed from DFT in quantitative agreement with measurements. Finally, we show that the computational burden of an AE method can be largely alleviated by using a PSP-AE mixed method which can achieve the same accuracy as the AE approach.

The method introduced in the present work, is currently, to the best of our knowledge, the only approach that can simultaneously reproduce all the important properties of shallow donors in predictive accuracy (e.g., anisotropic/isotropic hyperfine, super-hyperfine interactions, and their electric field dependency, as well as binding energy calculations). Therefore, the present work represents significant progress in ab-initio calculations of shallow spin defects and paves the way for predictive exploration of similar quantum defects in a host of emerging materials.

Results

Hyperfine coupling

The Hamiltonian describing the hyperfine interaction between an electronic spin S and a nuclear spin I is known as:

$${{{{{\rm{H}}}}}}={{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}{{{{{\rm{I}}}}}}.{{{{{\rm{S}}}}}}$$
(1)

where \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) is the isotropic or the Fermi contact hyperfine coupling at the site of the nuclear spin and is calculated by35:

$${{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}=\frac{2{\mu }_{0}}{3}{\gamma }_{e}{\gamma }_{I}\int {\delta }_{T}\left({{{{{\bf{r}}}}}}\right){\rho }_{s}\left({{{{{\bf{r}}}}}}+{{{{{{\rm{R}}}}}}}_{{{{{{\rm{I}}}}}}}\right)d{{{{{\bf{r}}}}}}$$
(2)

where \({\mu }_{0}\) is the magnetic susceptibility of free space. \({\gamma }_{e}\) and \({\gamma }_{I}\) are the electron gyromagnetic ratio and the nuclear gyromagnetic ratio of the nucleus at \({{{{{{\rm{R}}}}}}}_{{{{{{\rm{I}}}}}}}\), respectively. \({\delta }_{T}({{{{{\bf{r}}}}}})\) is a smeared out \(\delta\) function to take scalar-relativistic effects into account35 and \({\rho }_{s}\) is the spin density. For all-electron basis sets approach, the relativistic effects onto the \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) are ignored and the last term becomes \({\rho }_{s}\left({{{{{{\rm{R}}}}}}}_{{{{{{\rm{I}}}}}}}\right)\). If the nuclear spin site is the impurity site itself, we obtain the hyperfine coupling of the donor; while if the site is a silicon site in the vicinity of the donor, occupied by a 29Si isotope of 28Si, we obtain the super-hyperfine couplings.

Pseudopotential approximation approach (VASP-PSP)

In order to predict the HF constants from DFT results, a very recently proposed extrapolating method is employed in the present work with minor modification19. Briefly, since the error induced by the exponential tail of wavefunctions inversely scales with the supercell size, the calculated HF constants (\({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\)) of a variety of supercell sizes obtained from the PBE functional are plotted as a function of 1/N (Fig. 2a and Supplementary Table S1), where N represents the number of atoms in the supercell. A fitting function is then obtained based on the polynomial least-square method starting from the supercell size of n = 4 (N = 512) to n = 6 (N = 1728), which gives an expression of \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) = 7.47x2 + 72.8x + 43.6. Subsequently, an intercept value of 43.6 MHz is achieved by the extrapolation of N⟶∞ (i.e., x → 0), corresponding to the predicted HF constant.

Fig. 2: Fermi contact hyperfine parameters.
figure 2

Fitting the hyperfine constants calculated from Perdew–Burke–Ernzerhof (PBE) and Heyd, Scuseria, and Ernzerhof (HSE) functionals as a function of the supercell size (N) and extrapolating \(N\longrightarrow \infty\) to obtain the intercept value using different approaches: a Pseudopotential approximation approach (VASP-PSP), b All-electron approach (CP2K-AE), and (c) Pseudopotential approximation and all-electron mixed approach (CP2K-PSP-AE); dashed line represents the experimental value.

Full size image

In contrast to the experimental HF constant of 117 MHz32, the predicted value is significantly underestimated owing to the excess delocalization of wavefunction inherent in PBE. The use of hybrid functional can improve the description of localization. As reported, the fitting functions obtained from PBE and HSE functionals provide exactly the same slope value19. Hence the fitting function \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) from PBE is subsequently employed to fit HF results obtained from HSE at the supercell size of n = 5 (i.e., \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) = 136.9 MHz and x = 1) (Fig. 2a). This gives an intercept value of 56.7 MHz (Supplementary Table S2), showing a slight improvement over PBE. However, the HF coupling is still considerably underestimated due to the inherent problems of the PSP approximation method discussed in the introduction section.

It is worth noting that due to the excessive computational burden and lower computational efficiency of large-scale systems, a limited supercell size in the VASP-PSP and the previously reported linear-extrapolation19 approaches results in a weak convergence of the fitting function (i.e., the linear coefficient is dominant in \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\)), leading to a significant underestimation of the HF constants. This poor convergence issue and underestimation of the HF constants can be considerably eliminated by the employment of all-electron basis sets and larger supercell sizes as described in the following CP2K-AE and CP2K-PSP-AE approaches, providing a significant improvement in evaluating the core-electron dominant properties of shallow donors.

All-electron approach (CP2K-AE)

To eliminate the inherent problems induced by the PSP approach, GAPW method implemented in CP2K using an AE basis set is employed to calculate the Fermi contact HF parameter. Due to the higher computational efficiency, a larger supercell size is evaluated for the PBE approach, containing 4096 (n = 8) atoms. The calculated HF parameters for the donor are presented in Supplementary Table S1. In contrast to VASP-PSP approach, the use of AE scheme provides higher HF constants for different supercells due to the more localized nature of Gaussian type basis sets and improved description of the core spin-polarization effect. The same extrapolating method as the VASP-PSP approach is used to predict the HF constants. With the increase in supercell size, the quadratic coefficient of the polynomial fitting function becomes more dominant. The fitting function starting from the supercell size of n = 5 (N = 1000) to n = 8 (N = 4096) for PBE results gives an expression of \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) = 20.22x2 + 15.3x + 110.0 (Fig. 2b). This is subsequently employed to extrapolate HF results obtained from HSE at n = 5 (i.e., \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) = 151.0 MHz and x = 1), giving an intercept value of 115.5 MHz (Supplementary Table S2), corresponding to the final prediction of HF constant, in excellent agreement with the experimental value of 117 MHz32.

Pseudopotential approximation and all-electron mixed approach (CP2K-PSP-AE)

Although the AE approach significantly improves the inherent delocalization problem induced by the PSP method, the consideration of all electrons for each atom considerably increases the computational cost, making large-scale system calculations expensive. Therefore, a PSP and AE mixed approach is employed in the present work to efficiently and accurately evaluate the hyperfine coupling interaction for large-scale systems. To achieve consistent results in contrast to pob-DZVP AE approach, pseudopotentials from the same family (DZVP-GTH-PBE) were used. The lattice parameter, the bond length of Si–Si, and the angle of Si–Si–Si of the geometry optimized from DZVP-GTH-PBE pseudopotential using PBE are 5.479 Å, 2.373 Å, and 109.5°, consistent with the results from pob-DZVP AE approach using PBE (5.486 Å, 2.375 Å, and 109.5°, respectively).

The CP2K-PSP-AE scheme provides similar HF constants compared with CP2K-AE approach (Supplementary Table S1). The same extrapolating method starting from the supercell size of n = 5 (N = 1000) to n = 8 (N = 4096) is used, providing a fitting function of \({{{{{{\rm{A}}}}}}}_{{{{{{\rm{iso}}}}}}}^{{{{{{\rm{I}}}}}}}\) = 19.49x2 + 18.9x + 102.3 (Fig. 2c). A subsequent extrapolation on HSE results n = 5 gives an intercept value of 112.6 MHz (Supplementary Table S2), in good agreement with the experimental value and the HF constant predicted from CP2K-AE approach. Furthermore, a comparison of the computational cost of CP2K-PSP-AE mixed approach with CP2K-AE approach summarized in Supplementary Table S3 indicates a significant improvement in the computational speed (4.5–5 times faster), permitting accurate spin-density description with higher computational efficiency.

Super-hyperfine coupling

In addition to the calculation of HF parameters, super-hyperfine (SHF) interactions are evaluated. In contrast to the HF parameters which describe the wavefunction distribution on the central donor nucleus, SHF interactions depend on the wavefunction distribution in the silicon lattice sites surrounding the donor which can be occupied by the spin ½ isotope 29Si. Five shells of silicon atoms closest to the donor center are investigated, namely (1,1,1), (2,2,0), (1,1,\(\bar{3}\)), (0,0,4), and (3,3,1) in units of a0/4 with a0 being the lattice constant.

The SHF parameters are calculated in a similar way to the HF parameter through the extrapolation approach. The fitting functions are obtained starting from the supercell size of n = 4 (N = 512) to n = 6 (N = 1728) for VASP approach (Supplementary Figure S1) or n = 8 (N = 4096) for CP2K approach (Supplementary Figs. S2 and S3). These fitting functions are subsequently used to fit the SHF results obtained from HSE at the supercell size of n = 5, giving the final prediction of SHF constants. As shown in Fig. 3, the 4th-nearest-neighbor shell (0,0,4) gives the highest SHF constant owing to the Kohn–Luttinger oscillations36, consistent with the experimental results32 and data from Green’s function calculation (LMTO-GF)21. A better agreement with Green’s functional method is obtained from AE approach.

Fig. 3: Isotropic super-hyperfine parameters.
figure 3

The super-hyperfine constants for different shells calculated from different approaches as a function of distance to the donor center, including: Pseudopotential approximation approach (VASP-PSP), all-electron approach (CP2K-AE), Pseudopotential approximation and all-electron mixed approach (CP2K-PSP-AE), Green’s function approach (LMTO-GF)21, and experimental values32.

Full size image

It’s worth noting although the differences between VASP and CP2K results might be partially induced by the different optimized geometries, the consideration of the core electrons (i.e., PSP vs. AE basis sets) is the dominant factor that influences the HF and SHF calculations. These results prove that a combination of hybrid functional and AE approach can significantly improve the delocalization problem induced by PSP and PBE functional and accurately describe the spin-density of the donor state.

The anisotropic SHF constants of the five shells of silicon atoms closest to the donor center are subsequently analyzed. Since most of the anisotropic parts (kHz) are at least 3–4 orders of magnitude smaller compared with the isotropic (MHz) SHF constants, the extrapolation method is not applicable in this case due to the sensitivity and significant fluctuation of the anisotropic parts as a function of supercell size. Hence, the anisotropic constants calculated from the largest supercells (n = 6 for VASP and n = 8 for CP2K) were used as the final prediction. As shown in Supplementary Table S4, both VASP and CP2K results exhibit good agreement with the experimental value37. The only exception is the (0,0,4) results obtained from VASP which provide different values of |Bzz|(23 kHz) and |Bxy|(49 kHz) components, contradictory to the experimental measurements (41 kHz for both |Bzz| and |Bxy|). In this sense, CP2K results show better consistency with the experimental values, where an anisotropy of these values could not be resolved.

Electric-field dependent hyperfine coupling

Different from previous studies that investigate the influence of strain-induced internal field on the hyperfine coupling19,36,38, an external static electric field is employed in the present work. The presence of an external electric field (\(\vec{\varepsilon }\)) can distort the shape of the donor wavefunction and pull the wavefunction away from the donor site. This will result in a decrease in the electric field dependent hyperfine parameter A(\(\vec{\varepsilon }\)) which is proportional to \({|\Psi (\vec{\varepsilon },\vec{{R}_{I}})|}^{2}\), where \(\vec{{R}_{I}}\) represents the donor site. Experimental measurements39 have shown a quadratic dependence of the hyperfine coupling with electric field, which is parameterized as40:

$$\triangle A\left(\vec{\varepsilon }\right)={A}_{0}\left({\eta }_{2}{\varepsilon }^{2}+{\eta }_{1}\varepsilon \right)$$
(3)

where \(\triangle A\left(\vec{\varepsilon }\right)\) represents the change of hyperfine parameter in the presence of electric field \(\vec{\varepsilon }\) (i.e., \(A\left(\vec{\varepsilon }\right)-{A}_{0}\)). η2 and η1 are the coefficients of the quadratic and linear terms respectively. For bulk donors, η2 was measured to be −3.7 × 10−3 μm2/V2 for Si:Sb and η1 was found to be negligibly small. Since \(\triangle A\left(\vec{\varepsilon }\right)\) is a relative value, there is no need to employ all-electron basis sets for all atoms; hence only CP2K-PSP-AE method is used. Detailed calculation parameters are described in the Methods section.

Figure 4a shows our DFT calculations of \(\triangle A\left(\vec{\varepsilon }\right)/{A}_{0}\) as a function of the electric field magnitude for different supercell sizes. The quadratic coefficient η2 is the dominant part and decreases with the increase of supercell size, achieving a value of −2.65 × 10−3 μm2/V2 at the supercell size of n = 8 (N = 4096) (Fig. 4b and Supplementary Table S5), in good agreement with the TB results (−2.76 × 10−3 μm2/V2)40 and the experimental data for Si:Sb (−3.7 × 10−3 μm2/V2)39. Although the calculated quadratic coefficient is larger than the experimental measurement owing to the limitation of supercell size, the trend shows that it is approaching the experimental value with the increase of supercell size. In contrast, the linear coefficient η1 is relatively stable and close to zero for all supercells.

Fig. 4: Electric field dependent hyperfine coupling.
figure 4

a Electric field response of hyperfine coupling \(\triangle A/{A}_{0}\) as a function of the intensity of external electric field (\(\varepsilon\)) for various supercell sizes (n), where \(\triangle A\) represents the change of hyperfine parameter in the presence of electric field (i.e., \(A\left(\varepsilon \right)-{A}_{0}\)) and \({A}_{0}\) represents the hyperfine parameter without electric field; b quadratic (η2) and linear (η1) coefficients as a function of supercell sizes.

Full size image

The effect of electric field on the isotropic and anisotropic parts of HF and SHF interactions is further analyzed. In this part, AE basis sets were used for P donor and Si atoms located in (1,1,1) and (0,0,4) shells, while the rest Si atoms were treated with PSP in order to reduce the computational burden. (1,1,1) and (0,0,4) shells were chosen to reflect the effect of electric field on the inner and outer 29Si atoms. Compared with the isotropic parts, the value of the anisotropic parts are at least two orders of magnitudes smaller except the (1,1,1) shell (Supplementary Table S6), consistent with the experimental results37. And the change of the anisotropic parts under the effect of electric field is at least one order of magnitude smaller compared with the isotropic parts. The anisotropic parts of the HF constant of P donor are increased under electric field, due to the symmetry-breaking effect, except the |Bxy| component. In terms of the anisotropic parts of the four 29Si atoms located in inner (1,1,1) shell, only the diagonal components (i.e., |Bxx|, |Byy|, and |Bzz|) are increased under electric field, while the non-diagonal components show an opposite trend. For the anisotropic parts of the six 29Si atoms located in outer (0,0,4) shell, the effect of electric field can be summarized as two cases: (1) For Si1 and Si2 atoms which are along the electric field z-direction and located on the opposite sides of the P donor (i.e., (0,0,4) and (0,0,−4)), the diagonal components (i.e., |Bxx|, |Byy|, and |Bzz|) and one non-diagonal component (|Bxy|) are decreased under electric field, while the rest two non-diagonal components (i.e., |Bxz|, |Byz|) are increased; (2) In contrast, the anisotropic parts of the rest four Si atoms showing a different trend, with one diagonal component decreased while all the rest diagonal and non-diagonal components increased. It’s worth noting that the |Bzz| (19 kHz) and |Bxy| (27 kHz) components of (0,0,4) shell in this case are different, contradictory to the experimental measurements, showing the same issue as previously discussed in the anisotropic VASP SHF results (Supplementary Table S4). This further proves the importance of using all-electron basis sets for all atoms to correctly describe the core-electron contributions to the spin-polarization effect.

Binding energy calculation

Binding energies (E) are calculated from the Kohn–Sham eigenvalues as described in a previous work19:

$$E={\epsilon }_{{{{{{\rm{cb}}}}}}}-{\epsilon }_{{{{{{\rm{donor}}}}}}}+e\nabla V$$
(4)

where \({\epsilon }_{{{{{{\rm{cb}}}}}}}\) represents the eigenvalue of the conduction band minimum (CBM) in bulk Si and \({\epsilon }_{{{{{{\rm{donor}}}}}}}\) represents the resultant eigenvalue in P doped Si. \(\nabla V\), which is calculated by the Freysoldt method41,42, is the correction term and is used to align the Kohn–Sham levels between the bulk Si and Si:P system (Supplementary Table S7).

Pseudopotential approximation approach (VASP-PSP)

The final binding energy is predicted in a similar way to the calculation of HF constant by fitting the binding energy results from PBE as a function of the supercell size starting from n = 4 (N = 512) to n = 6 (N = 1728) using the linear least-square method. This provides a fitting function of \({E}_{{{{{{\rm{b}}}}}}}\) = 0.0312x + 0.0325 (Fig. 5a). A subsequent extrapolation to N⟶∞ (i.e., x⟶0) gives an intercept value of 32.5 meV, representing the prediction of binding energy from the PBE functional.

Fig. 5: Binding energy and exchange-splitting energy.
figure 5

The calculated binding energy and exchange-splitting energy for a single phosphorus donor in silicon as a function of supercell size: a, b Pseudopotential approximation approach using VASP (VASP-PSP); c, d Pseudopotential approximation approach using CP2K (CP2K-PSP); dashed line represents the experimental value of binding energy.

Full size image

However, the delocalization of the wavefunction and the underestimation of the exchange-splitting effect (\({\delta }^{{{{{{\rm{ex}}}}}}}\)) from PBE functional result in an underestimation of the binding energy compared with the experimental value of 45.59 meV33. Therefore, HSE functional is employed and the underestimation of \({\delta }^{{{{{{\rm{ex}}}}}}}\) in PBE is considered (Supplementary Table S7). \({\delta }^{{{{{{\rm{ex}}}}}}}\) represents the difference between the spin-up and spin-down eigenvalues of the donor state19 and it also shows a clear trend inversely scaling with the supercell size (N) (Fig. 5b), giving slope values of 0.0086 (\({s}_{{{{{{\rm{PBE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\)) and 0.0304 (\({s}_{{{{{{\rm{HSE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\)) for PBE and HSE functionals, respectively. The final HSE binding energy slope (\({s}_{{{{{{\rm{HSE}}}}}}}\)) is calculated by adding half the HSE exchange-splitting slope (\(\frac{1}{2}{s}_{{{{{{\rm{HSE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\)) on the spin-averaged PBE slope (\({s}_{{{{{{\rm{PBE}}}}}}}-\frac{1}{2}{s}_{{{{{{\rm{PBE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\))19:

$${s}_{{{{{{\rm{HSE}}}}}}}={s}_{{{{{{\rm{PBE}}}}}}}-\frac{1}{2}{s}_{{{{{{\rm{PBE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}+\frac{1}{2}{s}_{{{{{{\rm{HSE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}$$
(5)

This gives a slope value of 0.0421 (\({s}_{{{{{{\rm{HSE}}}}}}}\)), which is subsequently used to extrapolate the binding energy calculated from HSE functional at the supercell size of n = 5 to the N⟶∞ limit (i.e., \({E}_{{{{{{\rm{b}}}}}}}\) = 0.088 and \(x\) = 1) (Table 1). The resultant intercept value corresponds to the final prediction of the binding energy, with the value of 46.07 meV, in excellent agreement with the experimental value (45.59 meV).

Table 1 Calculated binding energies of ground state \({E}_{1{{{{{\rm{s}}}}}}({{{{{{\rm{A}}}}}}}_{1})}\) and energies of excited \({E}_{1{{{{{\rm{s}}}}}}({{{{{{\rm{T}}}}}}}_{2})}\) and \({E}_{1{{{{{\rm{s}}}}}}({{{{{\rm{E}}}}}})}\) states using Perdew–Burke–Ernzerhof (PBE) and Heyd, Scuseria, and Ernzerhof (HSE) functionals.
Full size table

The same method was employed to calculate the higher 1 s(T2) and 1 s(E) orbital states, giving the final prediction of 37.22 meV and 35.87 meV, respectively (Table 1 and Supplementary Figure S4), showing good agreement with the experimental value of 33.88 meV and 32.54 meV34. The splitting of these states is due to the so-called valley-orbit splitting originating from strong donor core potential. These low-manifold states in the donor spectra are responsible for several properties of donor spin qubits including the spin-lattice relaxation times43. These results indicate that HSE has the capacity of reducing the error induced by the PBE underestimation of binding energy, while the size limitation of HSE functional could be corrected by the PBE scaling, achieving significant agreement with experiments.

All-electron approach (CP2K-AE)

Unfortunately, binding energy cannot be calculated currently in this method because the output of electrostatic potential which is required for calculating the correction term (\(e\nabla V\)) is incompatible with GAPW method in CP2K.

Pseudopotential approximation approach (CP2K-PSP)

Unlike GAPW approach, electrostatic potential can be obtained with GPW method in CP2K. Therefore, the binding energy is calculated in the same method described in the VASP-PSP approach. While performing the hybrid functional calculation using the pseudopotential approximation approach in CP2K (CP2K-PSP), the auxiliary density matrix method (ADMM) was employed to reduce the computational burden and accelerate the calculation speed44. The calculated results are summarized in Table 1. The same extrapolating method is used by linearly fitting the PBE results as a function of the supercell size starting from n = 4 (N = 512) to n = 8 (N = 4096), This provides a fitting function of Eb = 0.0345x + 0.0319 (Fig. 5c). A subsequent consideration of exchange-splitting effect (\({\delta }^{{{{{{\rm{ex}}}}}}}\)) gives slope values of 0.0083 (\({s}_{{{{{{\rm{PBE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\)) and 0.0271 (\({s}_{{{{{{\rm{HSE}}}}}},{\delta }^{{{{{{\rm{ex}}}}}}}}\)) for PBE and HSE functionals, respectively (Supplementary Table S8 and Fig. 5d). The final slope of HSE binding energy (\({s}_{{{{{{\rm{HSE}}}}}}}\)) is calculated by Eq. (5) and a value of 0.0439 is achieved. A subsequent extrapolation of the binding energy from HSE functional at the supercell size of n = 5 to the N⟶∞ limit (i.e., \({E}_{{{{{{\rm{b}}}}}}}\) = 0.087 and \(x\) = 1) (Table 1) gives a final prediction of 43.03 meV. Additionally, the same method is employed to calculate the energies of excited 1 s(T2) (30.34 meV) and 1 s(E) (29.24 meV) states (Table 1 and Supplementary Figure S5), in good agreement with the experimental value and VASP-PSP results.

Conclusion

Efficient large-scale DFT calculations have been performed in the present work to evaluate the hyperfine coupling of phosphorus donors in silicon and estimate the binding energies of the donor electron’s ground and higher orbital states. Remarkable accuracy in the prediction of Fermi contact HF, its electric field dependency, and SHF has been achieved with all-electron level analysis and hybrid functional working in tandem. This highlights the importance of using all-electron level analysis to provide satisfactory elucidation of shallow donor systems. Results also reveal that a combination of pseudopotential approximation and all-electron level analysis can permit an accurate description of spin-density at the donor nucleus and generate all calculated parameters in a considerably more efficient way. Additionally, calculations of energies of the ground and excited states have exhibited outstanding agreement with the experimental value, demonstrating the predictive nature of the extrapolating approach for shallow donor systems. In the qubit architectures, the dopants are typically embedded into silicon at depths >10 nm (Fig. 1), which is larger than several Bohr radii of the dopants. Hence, the bulk-like scenario is more appropriate for these qubits. While the method introduced in the present work is focused on evaluating the properties of bulk systems, further consideration of surface effects for dopants buried a few nm below the barrier may be also achievable, owing to the superior computational efficiency of the PSP-AE mixed approach and its capacity of investigating large-scale systems containing thousands of atoms.

Methods

Pseudopotential approximation approach (VASP-PSP)

The first set of calculations were conducted with the projector augmented-wave (PAW) method implemented in the Vienna Ab-initio Simulation Package (VASP)22,45. Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional46 was employed with standard scalar-relativistic PAW pseudopotentials including four valence electrons (3s23p2) for Si and five valence electrons (3s23p3) for P. A plane-wave basis set cutoff energy of 260 eV was used. Since PBE gave a band gap value of 0.61 eV, which is significantly underestimated, the hybrid functional of Heyd, Scuseria, and Ernzerhof (HSE)47,48 with 24% of Hartree Fock mixed was employed, predicting a band gap of 1.14 eV (Supplementary Figure S6), consistent with the experimental room-temperature value of 1.13 eV49. The predicted lattice constant was 5.433 Å, consistent with the experimental value of 5.431 Å50. A variety of supercells were constructed with \(n\times n\times n\) multiples of the conventional cubic cell. The largest supercell corresponded to n = 6 containing 1728 atoms. Sampling at the Γ point can provide reliable results, hence a single k point was employed for all supercells to reduce the computational burden. For geometry optimization, the convergence criteria were set to 10−5 eV in energy and 0.01 eV/Å in force, respectively. For Si:P system, one silicon was replaced by the phosphorus dopant, and configurations of the optimized geometry in contrast to bulk silicon are summarized in Supplementary Table S9. In contrast to bulk Si, the bond lengths of Si:P system are only changed by <0.5%.

All-electron approach (CP2K-AE)

The second set of calculations was carried out with Gaussian and augmented plane-waves (GAPW) scheme in CP2K/Quickstep23,51. PBE and HSE functionals were used to describe the exchange-correlation effects46,47,48. For HSE functional, 13% of Hartree Fock mixture could most accurately reproduce the band gap (1.14 eV) and lattice constant (5.473 Å). A matrix diagonalization method was applied for wavefunction optimization. The convergence threshold on energy for self-consistent field was set to 10−5 Hartree (Ha). Double-ζ valence with polarization quality (pob-DZVP) for Si52 and 6-311G** Gaussian type basis set for P53, respectively, were used, together with a 450 Ry cutoff energy for the auxiliary plane-waves grid. The largest supercell corresponded to n = 8 containing 4096 atoms. A single k point was employed for all supercells. The geometry was optimized using Broyden-Fletcher-Goldfarb-Shanno (BFGS)54,55,56,57 and Limited-memory BFGS58 optimizers, with the convergence criteria of 3 × 10−4 Ha/Bohr and 1.5 × 10−3 Bohr for the root mean square (RMS) force and RMS atomic displacement, respectively.

Pseudopotential approximation and all-electron mixed approach (CP2K-PSP-AE)

The third set of calculations included two steps for PBE functional calculations: (1) The geometry optimization was performed with gaussian and plane-waves (GPW) scheme in CP2K/Quickstep59 in combination with Goedecker−Teter−Hutter pseudopotentials60,61 and (2) Double-ζ valence with polarization quality (pob-DZVP) for Si52 and 6-311G** Gaussian type basis set for P53, respectively, were used to perform a single-point calculation based on the optimized geometry. For hybrid functional calculations, the procedure was the same as that used in the second set of calculations (i.e., using AE scheme for both geometry optimization and single-point calculation), owing to the vastly lower computational cost of HSE in AE scheme in contrast to that in PSP approach. All the rest of the parameters and convergence criteria were the same as that used in the second set of calculations.

Electric field-dependent hyperfine parameter calculation

A static electric field was applied to evaluate its influence on hyperfine coupling. A variety of electric field values was investigated, including: 0, 2E-07, 4E-07, 6E-07, 8E-07, 10E-07, and 12E-07 (units are in a.u.). In order to consider the symmetry-breaking effect induced by the electric field, geometry relaxation of ligand atoms was performed after applying an electric field with the GAPW scheme51. Goedecker−Teter−Hutter pseudopotential for Si60,61 and modified pcH-2 Gaussian type basis set for P were used62, respectively. The rest of the parameters and convergence criteria are the same as those used in the second set of calculations.